Модуль действительного числа 10 класс мордкович: Презентация по алгебре «Модуль действительного числа. Решение уравнений с модулем» для 10 класса
Модуль действительного числа, урок по алгебре в 8 классе, презентация
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Скачать:Модуль действительного числа (PPTX)
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 8 класса
Мультимедийное учебное пособие «Алгебра за 10 минут»
Ребята, с модулем числа мы встречались и раньше. Сегодня мы обобщим все наши знания, ну и конечно узнаем что-то новое.
Определение. Модулем неотрицательного действительного числа $x$ называют само это число: $|x|=x$. Модулем отрицательного действительного числа $x$ называют противоположное число: $|x|=-x$.
Давайте запишем строгое математическое определение: $|x|=\begin {cases} x, x≥0, \\ -x, x
Например:
$|8|=8$;
$|-8|=-(-8)=8$;
2$.5. $|a|=|-a|$.
Геометрический смысл модуля действительного числа
Числовая прямая служит хорошим примером множества действительных чисел. Давайте отметим на числовой прямой две точки a и b и постараемся найти расстояние $ρ(a; b)$ между этими точками. Очевидно, что это расстояние равно $b-a$, если $b>a$.
Если $a>b$, то расстояние будет равно $a-b$.
Если $a=b$, то расстояние равно нулю, так как получается единая точка.
Все три случая мы можем описать единообразно: $ρ(a;b)=|a-b|$.
Пример.
Решите уравнение:
а) $|x-3|=6$;
б) $|x+5|=3$;
в) $|x|=2,8$;
г) $|x-\sqrt{3}|=2$.
Решение.
а) Надо найти на координатной прямой такие точки, которые удалены от точки 3 на расстояние равное 6.
$ρ(x;3)=6$.
Это точки – 9 и -3 (прибавили и отняли шестерку от тройки).
Ответ: $х=9$ и $х=-3$.
б) $|x+5|=3$, перепишем уравнение в виде $|x-(-5)|=3$.
$ρ(x;-5)=3$.
Найдем расстояние от точки -5, удаленное на 3. Такое расстояние, получается от двух точек: $х=2$ и $х=-8$.
Ответ: $х=2$ и $х=-8$.
в) $|x|=2,8$ можно представить в виде $|х-0|=2,8$ или $ρ(x;0)=2,8$.
Очевидно, что $х=-2,8$ или $х=2,8$.
Ответ: $х=-2,8$ и $х=2,8$.
г) $|x-√3|=2$ эквивалентно $ρ(x; \sqrt{3})=2$.
Очевидно, что $х=\sqrt{3}-2$ или $х=\sqrt{3}+2$.
Ответ: $x=\sqrt{3}-2$ или $x=\sqrt{3}+2$.
Пример.
Решить уравнения:
а) $|2x-8|=4$;
б) $|3-3x|=6$;
в) $|10x+5|=-2$.
Решение.
а) Преобразуем левую часть уравнения: $|2x-8|=|2(x-4)|=|2||x-4|=2|x-4|$.
Тогда уравнение можно переписать в виде: $|x-4|=2$.
Или $ρ(x;4)=2$.
Ответ: $х=6$ или $х=2$.
б) Опять же преобразуем левую часть: $|3-3x|=|-3(x-1)|=|-3||(x-1)|=3|x-1|$.
Тогда уравнение можно переписать в виде: $|x-1|=2$.
Или $ρ(x;1)=2$.
Ответ: $х=3$ или $х=-1$.
в)$|10x+5|=-2 $.
Ответ: нет корней.
График функции $y=|x|$.
Вычислить модуль мы можем из любого числа.
2}$.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Г. Мордковича (профильный уровень) 4 часа
Свойства функций
Степень с рациональным показателемАбсолютное значение — общее руководство по математическим навыкам
Что это значит?
Определения:
Абсолютное значение (или модуль) | х | действительного числа x является неотрицательным значением x независимо от его знака.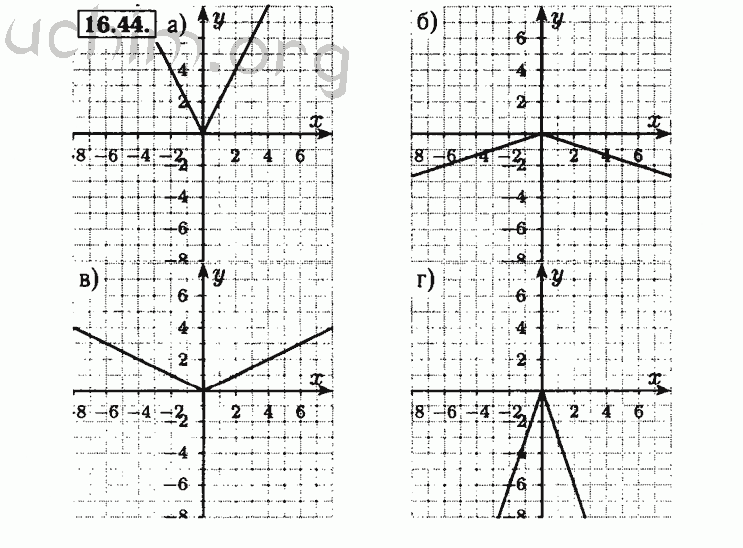
Например, абсолютное значение 5 равно 5, а абсолютное значение -5 также равно 5. Абсолютное значение числа можно рассматривать как его расстояние от нуля по линии действительных чисел. Кроме того, абсолютная величина разности двух действительных чисел есть расстояние между ними.
Абсолютное значение обладает следующими четырьмя фундаментальными свойствами:
Неотрицательность $$|a| ≥ 0$$ Положительная определенность $$|a| = 0 ⇔ a = 0$$ Мультипликативность $$|ab| = |a||b|$$ Субаддитивность $$|a + b| ≤ |а| + |b|$$
Другие важные свойства абсолютного значения включают:
Идемпотентность (абсолютное значение абсолютного значения является абсолютным значением) $$||a|| = |a|$$ Симметрия $$|-a| = |a|$$ Тождество неразличимых (эквивалентно положительной определенности) $$|a — b| = 0 ⇔ a = b$$ Неравенство треугольника (эквивалентное субаддитивности) $$|a — b| ≤ |а — с| + |c — b|$$ Сохранение деления (эквивалентно мультипликативности) $$|a / b| = |а| / |б| \space\space if \space\space b ≠ 0$$ (эквивалент субаддитивности) $$|a — b| ≥ ||а| — |b||$$
Два других полезных свойства, касающихся неравенств: $$|a| ≤ b ⇔ -b ≤ a ≤ b$$ $$|a| ≥ b ⇔ a ≤ -b \space или \space b ≤ a$$
Эти соотношения можно использовать для решения неравенств, включающих абсолютные значения.
Например: $$|x — 3| ≤ 9 ⇔ -9 < x - 3 < 9$$ $$⇔ -6 < x < 12$$
Источник:en.wikipedia.org/wiki/Absolute_value
Как это выглядит?
Абсолютное значение 5 равно 5, это расстояние от 0,5 единиц.
Абсолютное значение -5 равно 5, это расстояние от 0,5 единиц.
$$|x| = 2 $$
$$|x| > 2$$
$$Для \space |x| < 2, -2 < x < 2$$ $$For \space |x| = 4, -4 = x = 4$$
|7| = 7 означает, что абсолютное значение 7 равно 7.
|-7| = 7 означает, что абсолютное значение -7 равно 7.
|-2 — x| означает абсолютное значение -2 минус x.
-|х| означает отрицательное значение абсолютного значения x.
Тебе пригодится…
Абсолютное значение действительных чисел встречается в самых разных математических установках, например, абсолютное значение также определяется для комплексных чисел, кватернионов, упорядоченных колец, полей и векторных пространств.