Контрольная работа по алгебре 10 класс мордкович 1: Контрольные работы по алгебре 10 класс к учебнику А.Г. Мордковича
Контрольная работа № 1 | |
1 вариант 1). Для функции f (х) = х3 + 2х2 – 1. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если:
3). Построить график функции: а). у = – х + 5 б). у = х2 – 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную:
| 2 вариант 1). Для функции f (х) = 3х2 – х3 + 2. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если:
3). Построить график функции: а). у = х – 7 б). у = – х2 + 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную:
|
Контрольная работа № 2 | |
1 вариант 1). Вычислите:
2). Упростите: 3). Известно, что: Вычислить 4). Решите уравнение: 5). Докажите тождество: | 2 вариант 1). Вычислите:
2). Упростите:
3). Известно, что:
Вычислить 4). Решите уравнение:
5). Докажите тождество:
|
Контрольная работа № 3 | |
1 вариант 1). Найти наименьшее и наибольшее значения функций:
2). Упростить выражение:
3). Исследуйте функцию на четность: 4). Постройте график функции:
5). Известно, что | 2 вариант 1). Найти наименьшее и наибольшее значения функций:
2). Упростить выражение:
3). Исследуйте функцию на четность: 4). Постройте график функции:
5). Известно, что |
Контрольная работа № 4 | |
1 вариант 1). Решить уравнение:
2). Найти корни уравнения 3). Решить уравнение:
4). Найти корни уравнения 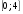 . . | 2 вариант 1). Решить уравнение:
2). Найти корни уравнения 3). Решить уравнение:
4). Найти корни уравнения |
Контрольная работа № 5 | |
1 вариант 1). Вычислить:
2). Упростить выражение:
3). Доказать тождество:
4). Решить уравнение а).
5). Зная, что | 2 вариант 1). Вычислите:
2). Упростить выражение:
3). Доказать тождество:
4). Решить уравнение а).
5). Зная, что |
Контрольная работа № 6 | |
1 вариант 1). Найдите производную функции: а). в). д). 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции 3). Прямолинейное движение точки описывается законом 4). Дана функция Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке | 2 вариант 1). Найдите производную функции: а). в). д). 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции 3). Прямолинейное движение точки описывается законом 4). Дана функция Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке |
Контрольная работа № 7 ( итоговая ) | |
1 вариант 1). Дана функция 2). Решите уравнение:
3). Упростите выражение: а). б). 4). Постройте график функции с полным исследованием функции | 2 вариант 1). Дана функция 2). Решите уравнение:
3). Упростите выражение: а). б). 4). Постройте график функции с полным исследованием функции |
Контрольная работа № 1 | |
1 вариант 1). Для функции f (х) = х3 + 2х2 – 1. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если: 3). Построить график функции: а).у = – х + 5 б).у = х2 – 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную: | 2 вариант 1). Для функции f (х) = 3х2 – х3 + 2. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если: 3). Построить график функции: а).у = х – 7 б).у = – х2 + 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную: |
Контрольная работа № 2 | |
1 вариант 1). Вычислите: 2). Упростите: 3).Известно, что: Вычислить . 4). Решите уравнение: 5). Докажите тождество: | 2 вариант 1). Вычислите: 2). Упростите: 3). Известно, что: . Вычислить . 4). Решите уравнение: . 5). Докажите тождество:
|
Контрольная работа № 3 | |
1 вариант 1). Найти наименьшее и наибольшее значения функций:
2). Упростить выражение: 3). Исследуйте функцию на четность: 4). Постройте график функции: 5). Известно, что . Докажите, что . | 2 вариант 1). Найти наименьшее и наибольшее значения функций:
2). Упростить выражение: 3). Исследуйте функцию на четность: 4). Постройте график функции: 5). Известно, что . Докажите, что . |
Контрольная работа № 4 | |
1 вариант 1). Решить уравнение: 2). Найти корни уравнения 3). Решить уравнение: 4). Найти корни уравнения | 2 вариант 1). Решить уравнение: 2). Найти корни уравнения 3). Решить уравнение: 4). Найти корни уравнения |
Контрольная работа № 5 | |
1 вариант 1). Вычислить: 2). Упростить выражение: 3). Доказать тождество: 4). Решить уравнение а). 5). Зная, что | 2 вариант 1). Вычислите: 2). Упростить выражение: 3). Доказать тождество: 4). Решить уравнение а). 5). Зная, что |
Контрольная работа № 6 | |
1 вариант 1). Найдите производную функции: а). ; б). в). д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции 3). Прямолинейное движение точки описывается законом 4). Дана функция Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке | 2 вариант 1). Найдите производную функции: а). ; б). в). д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1. 3). Прямолинейное движение точки описывается законом 4). Дана функция Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке . |
Контрольная работа № 7( итоговая ) | |
1 вариант 1). Дана функция 2). Решите уравнение: 3). Упростите выражение: а). б). 4). Постройте график функции с полным исследованием функции | 2 вариант 1). Дана функция 2). Решите уравнение: 3). Упростите выражение: а). б). . 4). Постройте график функции с полным исследованием функции . |
Экзаменационная работа за 1 полугодие. 10 класс.
Вариант 1.
Часть 1.
1.Укажите сколько натуральных чисел входят в область определения функции:
у = -2х+4 +2х+3-3 x2+10х-3.
2.Найдите по графику наименьшее значение функции: y=sin x на [π/3;7π/6]
3. Найдите значение функции: у =2 sin x + cos x, если х = — π/2.
4.В ∆АВС угол С равен 900 , ВС=21, АВ=5. Найдите sin В.
5. Решите уравнение: — cos x= 3х-1.
6.Сколько корней имеет уравнение: cos x=22 на [-π;3π].
7.Вычислите: sin (arccos x+ arccos(- x)).
8.Сколько натуральных чисел входит в область допустимых значений выражения arcsin (5-2x).
9.Вычислите: sin(-7π)+2 cos31π3 — tg7π4.
10.Найдите значение выражения: 27 sinα -15, если cos α=429 и 0
11.Найдите сумму наибольшего отрицательного и наименьшего положительного корней уравнения 4 cos2 2х =2.
12. Сколько корней имеет уравнение 3 cos х +sin х =0 на [0; π].
Часть 2.
1.Найдите значение выражения 3 tg2 х0 -1, где х0 – наименьший положительный корень уравнения 2 cos2 х + 5 sin x -4=0.
2.Точка М не лежит в плоскости параллелограмма АВСД. На отрезке АМ выбрана точка Е так, что МЕ : ЕА = 2:3.
а) постройте точку F –точку пересечения прямой МВ с плоскостью СДЕ;
б) найдите АВ, если EF=10см.
3.При каких а решения системы 3х+2у=7;х-у=а удовлетворяют неравенству х
4.Используя график функции у=f(х), где f(х) = х2 -4х+3 постройте
у=| -f ( |х| ) |.
5.Решите неравенство 6 cos 2 t + sin t > 4.
6. Решите уравнение (2 cos x -1) 4×2- 7 х+3 = 0
Экзаменационная работа за 1 полугодие. 10 класс.
Вариант 2.
Часть 1.
1.Укажите сколько натуральных чисел входят в область определения функции:
у = 2×2-5х+2 +2×2-4х10-2х.
2.Найдите по графику наибольшее значение функции: y= cos x на [π/2;4π/3]
3. Найдите значение функции: у =2 cos (x- π/2)-1, если х = — π/2.
4.В ∆АВС угол С равен 900 , АС=621, АВ=30. Найдите sin А.
5. Решите уравнение: cos x= 2х + 1.
6.Сколько корней имеет уравнение: sin x=- 22 на [-π;2π].
7.Вычислите: cos (arcsin x+ arcsin(- x)).
8.Сколько натуральных чисел входит в область допустимых значений выражения arccos (3-2x).
9.Вычислите: cos(-9π)+2 sin(-49π6) — ctg(-21π4).
10.Найдите значение выражения: 7 — 8 sinα , если cos α=-154 и 3π/2
11.Найдите сумму наибольшего отрицательного и наименьшего положительного корней уравнения 4 sin2 2х =3.
12. Сколько корней имеет уравнение cos х= sinх на [0; π].
Часть 2.
1.Найдите значение выражения 5 tg2 х0 + 2,3 , где х0 – наименьший положительный корень уравнения 6 — 6 cos х — sin2 x =0.
2.Точка М не лежит в плоскости ромба АВСД. На отрезке ВМ выбрана точка F так, что МF : FB = 1:3.
а) постройте точку K –точку пересечения прямой МC с плоскостью AFД;
б) найдите FK, если AД=16см.
3.При каких а решения системы х+ау=3;ах+4у=6 удовлетворяют неравенству х >1, у>0.
4.Используя график функции у=f(х), где f(х) = х2 +4х+3 постройте
у= — | f ( |х| ) |.
5.Решите неравенство 6 cos 2 t + sin t ≤ 4.
6. Решите уравнение (2cos 2 x — 3) 3×2- 7 х+4 = 0.

Решения контрольных работ по алгебре и началам анализа из сборника для 10 класса Глизбург В. И. (под ред. А.Г. Мордковича). Профильный уровень. Варианты 1,2,3,4. — Рукопись. — 2016.
Настоящее пособие содержит решения контрольных работ из сборника «Глизбург В. И. Алгебра и начала анализа. Контрольные работы для 10 класса общеобразовательных учреждений (профильный уровень) / В. И. Глизбург ; под ред. А. Г. Мордковича. — М. : Мнемозина, 2007. — 62 с.»
Сборник контрольных работ предназначен для тех учителей математики, которые используют в своей преподавательской деятельности УМК, созданный авторским коллективом под руководством А. Г. Мордковича для изучения в 10-м классе профильной старшей школы курса алгебры и начал анализа.
Каждый вариант контрольной работы выстроен по одной и той же схеме: задания базового (обязательного) уровня — до первой черты; задания уровня выше среднего — между первой и второй чертами; задания повышенной сложности — после второй черты. Шкала оценок за выполнение контрольной работы может выглядеть так: за успешное выполнение заданий до первой черты — оценка 3; за успешное выполнение заданий базового уровня и одного дополнительного (после первой или после второй черты) — оценка 4; за успешное выполнение заданий трех уровней — оценка 5. При этом оценку не рекомендуется снижать за одно неверное решение в первой части работы (допустимый люфт).
Страницы решебника представлены в виде слайдов. Кликните на нужный слайд, чтобы прочитать содержание страницы. Как листать слайды — читайте на странице https://gdz.math-helper.ru/kak-prosmatrivat-slaydyi/
Внимание! Рукопись не проверялась, возможны ошибки!
Содержание
Контрольная работа № 1
Контрольная работа № 2
Контрольная работа № 3
Контрольная работа № 4
Контрольная работа № 5
Контрольная работа № 6
Контрольная работа № 7
Контрольная работа № 8
Контрольная работа № 9

Курс повышения квалификации

Курс повышения квалификации

Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДБ-195686
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Контрольные работы по алгебре (10 класс)
КОНТРОЛЬНЫЕ РАБОТА
Тема: «Входная контрольная работа»
(коды КЭС: 1.3.4, 2.4.3, 2.5.1, 2.3.2, 3.1.3, 3.1.5, 3.1.4, 3.2.5, 2.3.4)
План работы:
План Входной контрольной работы по алгебре для учащихся 10 класса «А»
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
Уровень сложности(Б, П)
Примерное время выполнения, мин.
Макс. балл за задание
1
1.1
2.4
2.5
1.3.4
2.4.3
2.5.1
2.3.2
Арифметические действия с рациональными числами. Рациональные выражения и их преобразования. Свойства квадратных корней. Формулы сокращенного умножения.
РО
Б
5
1
2
3.1
3.1.3
Квадратное уравнение. Формула корней квадратного уравнения.
РО
Б
9
3
3
3.1
3.1.5
Решение уравнений высших степеней.
РО
П
8
2
4
3.2
3.1.4
Решение рациональных уравнений.
РО
Б
8
2
5
3.2
3.2.5
Квадратные неравенства.
РО
Б
7
2
6
3
2.3.4
Текстовые задачи
РО
П
8
2
Пояснение
Типы заданий:
ВО – с выбором ответа — ;
КО – с кратким ответом;
РО – с развернутым ответом
Уровень сложности:
Б – базовый;
П – повышенный
Текст контрольной работы
Вариант 1
1. Найдите значение выражения (1 балл)
—
2. Решите уравнение (1 балл за каждое уравнение)
А) 6x2-3x=0
Б) 25x2+2x-1=0
В) 25x2=1
3. Решите биквадратное уравнение (2 балла)
x4 -13x2+36=0
4. Решите неравенство (2 балла)
x2+4x+3≥0
5. (2 балла) Разность корней квадратного уравнения
x2-12x+q=0 равна 2. Найдите q.
Вариант 2
1. Найдите значение выражения (1 балл)
—
2. Решите уравнение (1 балл за каждое уравнение)
А) 5x2+20x=0
Б) x2-4x+1=0
В) 49x2=1
3. Решите биквадратное уравнение (2 балла)
x4 -29x2+100=0
4. Решите неравенство (2 балла)
x2-4x-5≥0
5. (2 балла) Разность корней квадратного уравнения
x2+x+с=0 равна 6. Найдите с.
Система оценивания
9-10 баллов (90-100%) — оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
№ 1 Тема: «« Степень с действительным показателем»
(коды КЭС: 1.1.5, 1.1.6, 1.1.7 )
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
Уровень сложности(Б, П)
Примерное время выполнения, мин.
Макс. балл за задание
1
1.3
1.1.5
1.1.6
1.1.7
РО
Б
5
2
2
1.3
1.1.5
1.1.6
1.1.7
РО
Б
5
2
3
1.3
1.1.5
1.1.6
1.1.7
РО
П
10
2
4
1.3
1.1.5
1.1.6
1.1.7
РО
П
10
2
5
1.3
1.1.5
1.1.6
1.1.7
РО
П
10
2
Пояснение
Типы заданий:
1) ВО – с выбором ответа — ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Контрольная работа №1
Тема « Степень с действительным показателем»
В – 1 В — 2
1. Вычислить:
1) 1)
2) 2)
2. Упростить выражение при
1) 1)
2) 2)
3. Сократить дробь 3. Сократить дробь
4. Сравнить числа: 4. Сравните числа
1) 1)
2) и 1. 2) и 1.
5. Найти сумму бесконечно убывающей
геометрической прогрессии,
если
Система оценивания
9-10 баллов (90-100%) — оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
5. Найти второй член бесконечно убывающей геометрической прогрессии, если сумма её членов равна , а знаменатель равен
№ 2 Тема: «« Степенная функция»
(коды КЭС: 2.1.3, 2.1.7., 3.1.4, 3.3.4 )
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
Уровень сложности(Б, П)
Примерное время выполнения, мин.
Макс. балл за задание
1
3.1
2.1.3
2.1.7.
РО
Б
5
2
2
3.1
2.1.3
2.1.7.
РО
Б
5
2
3
3.1
3.1.4
3.3.4
РО
П
10
2
4
3.1
3.1.4
3.3.4
РО
П
10
2
5
3.1
2.1.3
2.1.7.
3.1.4
3.3.4
РО
П
10
2
Пояснение
Типы заданий:
1) ВО – с выбором ответа — ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Контрольная работа №2
Тема «Степенная функция»
Вариант 1
1. Найти область определения функции .
2. Изобразить эскиз графика функции у = х7 и перечислить её основные свойства. Пользуясь свойствами этой функции:
1) сравнить с единицей (0,95)7; 2) сравнить и .
3. Решить уравнение:
1) 2) ; 3)
4. Установить, равносильны ли неравенства и <0.
5. Найти функцию, обратную к функции . Указать её область определения и множество значений. Является ли эта функция ограниченной?
Вариант 2
1. Найти область определения функции .
2. Изобразить эскиз графика функции у = х6 и перечислить её основные свойства. Пользуясь свойствами этой функции:
1) сравнить с единицей (1,001)6; 2) сравнить и .
3. Решить уравнение: 1) 2) .
3)
4. Установить, равносильны ли неравенства и .
5. Найти функцию, обратную к функции . Указать её область определения и множество значений. Является ли эта функция ограниченной?
Система оценивания
9-10 баллов (90-100%) — оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
№ 3 Тема: «« Показательная функция»
(коды КЭС: 2.1.5, 2.3.3., 3.3.6 )
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
Уровень сложности(Б, П)
Примерное время выполнения, мин.
Макс. балл за задание
1
3.1
2.1.5
2.2.3
3.3.6
РО
Б
5
1
2
3.1
2.1.5
2.2.3
3.3.6
РО
Б
5
2
3
3.1
2.1.5
2.2.3
3.3.6
РО
П
5
1
4
3.1
2.1.5
2.2.3
3.3.6
РО
П
6
2
5
3.1
2.1.5
2.2.3
3.3.6
РО
П
7
2
6
3.1
2.1.5
2.2.3
3.3.6
РО
П
7
2
Пояснение
Типы заданий:
1) ВО – с выбором ответа — ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Тема 3 «Показательная функция»
Вариант 1
1. Сравнить числа: 1) и ; 2) и .
2. Решить уравнение: 1) ; 2)
3. Решить неравенство >
4. Решить неравенство: 1) ; 2)
5. Решить систему уравнений
6. (Дополнительно) Решить уравнение
Вариант 2
1. Сравнить числа: 1) и ; 2) и .
2. Решить уравнение: 1) ; 2)
3. Решить неравенство .
4. Решить неравенство: 1) ; 2)
5. Решить систему уравнений
6. (Дополнительно) Решить уравнение
Система оценивания
9-10 баллов (90-100%) — оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
№ 4 Тема: «Логарифмическая функция»
(коды КЭС: 1.3, 1.4.5, 2.1.6, 2.2.4, 3.3.7 )
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
Уровень сложности(Б, П)
Примерное время выполнения, мин.
Макс. балл за задание
1
2.1
2.3
3.1
1.3
1.3
РО
Б
5
1
2
2.1
2.3
3.1
1.3
1.4.5
3.3.7
РО
Б
5
1
3
3.1
1.3
2.2.4
РО
Б
5
1
4
2.1
2.3
2.1.6
РО
Б
6
2
5
3.1
1.3
2.2.4
РО
П
7
2
6
2.1
2.3
2.1.6
РО
П
7
3
Пояснение
Типы заданий:
1) ВО – с выбором ответа — ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Тема 4 «Логарифмическая функция»
Вариант 1
1. Вычислите:
2. Сравните числа и
3. Решите уравнение
4. Решите неравенство
5. Решите уравнение
6. Решите неравенство:
Вариант 2
1. Вычислите:
2. Сравните числа и
3. Решите уравнение
4. Решите неравенство
5. Решите уравнение
6. Решите неравенство:
Система оценивания
9-10 баллов (90-100%) — оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
№ 5 Тема: «Тригонометрические формулы»
(коды КЭС: 1.2.3, 1.2.4, 1.2.5, 1.2.6, 1.2.7 )
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
Уровень сложности(Б, П)
Примерное время выполнения, мин.
Макс. балл за задание
1
1.3
1.2.3
1.2.4
РО
Б
6
3
2
1.3
1.2.5
1.2.6
РО
Б
4
1
3
1.3
1.2.7
РО
Б
10
2
4
1.3
1.2.5
1.2.6
РО
Б
10
2
5
1.3
1.2.5
1.2.6
РО
П
10
2
Пояснение
Типы заданий:
1) ВО – с выбором ответа — ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Тема №5 «Тригонометрические формулы»
Вариант 1
1. Найти значение выражения: 1) 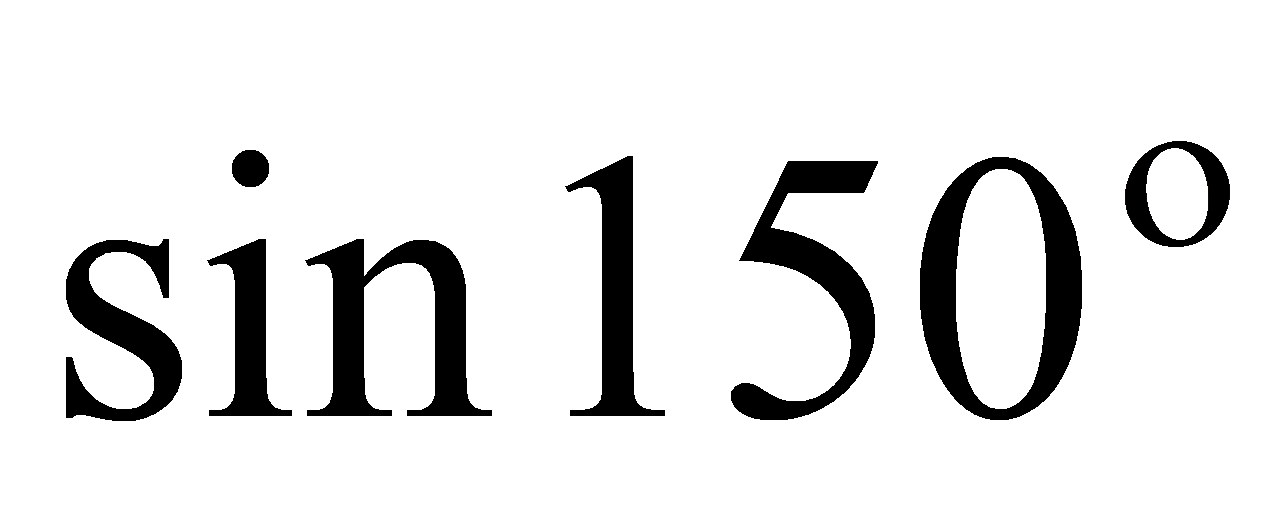 2)
2) 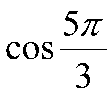 3)
3) 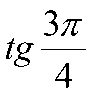
2. Вычислить: 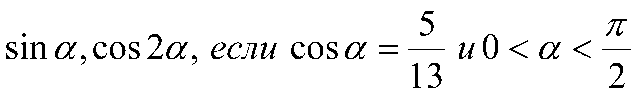
3. Упростить выражение:
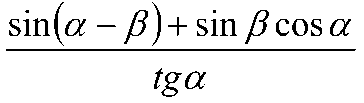
4. Доказать тождество:
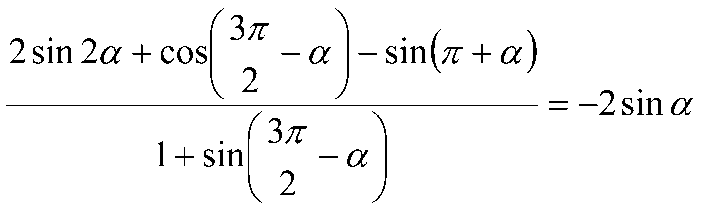
5. Решить уравнение
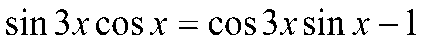
Вариант 2
1. Найти значение выражения: 1) 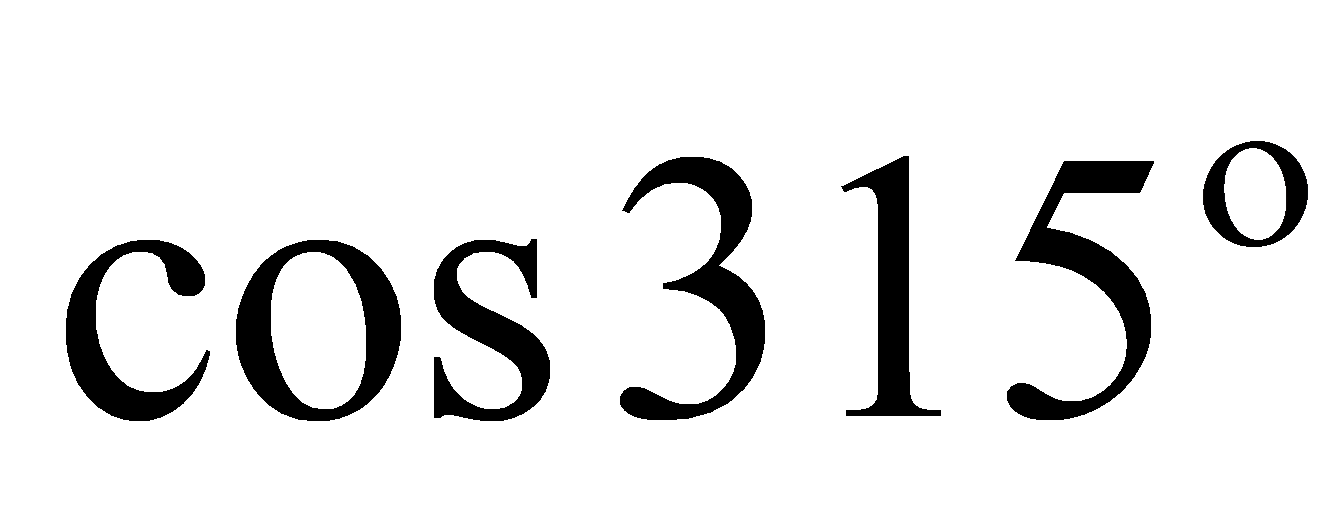 2)
2) 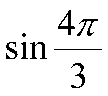 3)
3) 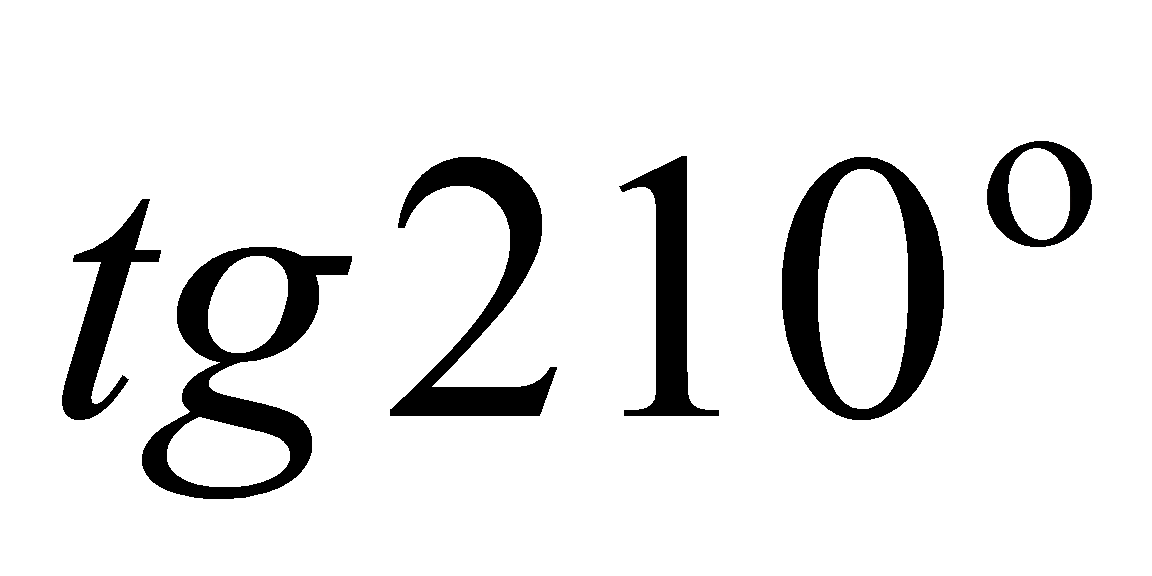
2. Вычислить: 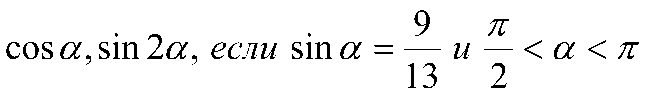
3. Упростить выражение:
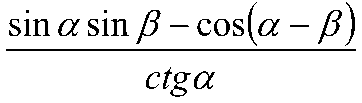
4. Доказать тождество:
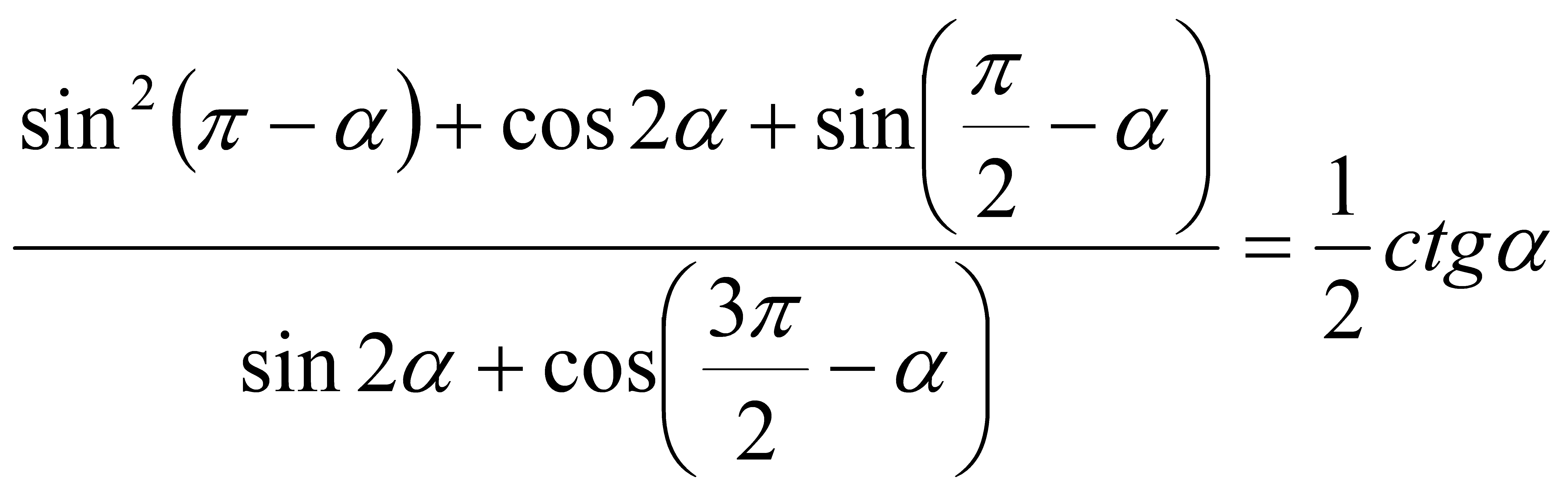
5. Решить уравнение 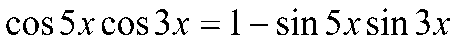
Система оценивания
9-10 баллов (90-100%) — оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
№ 6 Тема: «Тригонометрические уравнения»
(коды КЭС: 2.1.4)
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
Уровень сложности(Б, П)
Примерное время выполнения, мин.
Макс. балл за задание
1
2.1
2.1.4
РО
Б
10
2
2
2.1
2.1.4
РО
Б
10
2
3
2.1
2.1.4
РО
Б
10
3
4
2.1
2.1.4
РО
Б
10
3
Пояснение
Типы заданий:
1) ВО – с выбором ответа — ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Тема 6 «Тригонометрические уравнения»
Вариант 1
1. Решите уравнение:
2. Найдите решение уравнения на отрезке .
3. Решите уравнение:
; в)
4. Решите уравнение:
а)
Вариант 2
1. Решите уравнение:
а)
2. Найдите решение уравнения на отрезке .
3. Решите уравнение:
в)
4. Решите уравнение:
а)
Система оценивания
9-10 баллов (90-100%) — оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
Тема: «Итоговая контрольная работа»
(коды КЭС: 1.4.4.. 2.1.4, 2.2.3, 2.2.4, 3.1, 3.2, 3.3)
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
Уровень сложности(Б, П)
Примерное время выполнения, мин.
Макс. балл за задание
1
1.3
1.4.4.
2.1.4
РО
Б
5
2
2
2.1
2.2.3
РО
Б
5
2
3
2.2
2.2.4
РО
Б
10
2
4
2.3
3.1
РО
Б
10
2
5
3.1
3.2
3.3
РО
Б
10
2
Пояснение
Типы заданий:
1) ВО – с выбором ответа — ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Итоговая контрольная работа по алгебре и началам анализа.
Вариант 1
Базовый уровень
Вычислить:
а) 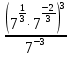 ; в)
; в) 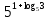 ;
;
б) 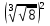 ; г)
; г) 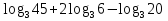 .
.
Вычислить:
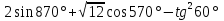 .
.
Решите уравнение:
а) 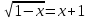 ; в)
; в) 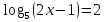 ;
;
б)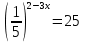 ; г)
; г) 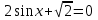 .
.
Решите неравенство:
а) 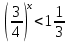 ; б)
; б)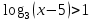 .
.
Упростите выражения:
а)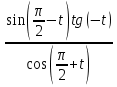 ; б)
; б)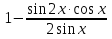 .
.
Повышенный уровень
Решите уравнение:
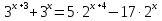 .
.
Решите уравнение:
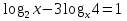 .
.
Решите уравнение:
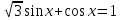 .
.
а) Решите уравнение
 .
.
б) Найдите все корни этого уравнения, принадлежащие отрезку 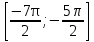 .
.
Вариант 2
Базовый уровень
Вычислить:
а) 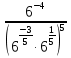 ; в)
; в) 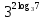 ;
;
б) 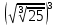 ; г)
; г) 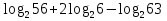 .
.
Вычислить:
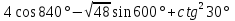 .
.
Решите уравнение:
а) 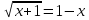 ; в)
; в) 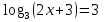 ;
;
б)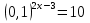 ; г)
; г) 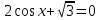 .
.
Решите неравенство:
а) 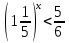 ; б)
; б)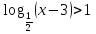 .
.
Упростите выражения:
а)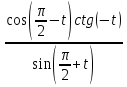 ; б)
; б)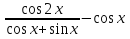 .
.
Повышенный уровень
Решите уравнение:
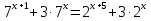 .
.
Решите уравнение:
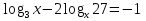 .
.
Решите уравнение:
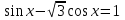 .
.
а) Решите уравнение
 .
.
б) Найдите все корни этого уравнения, принадлежащие отрезку 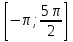 .
.
Система оценивания
9-10 баллов (90-100%) — оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»

Решения контрольных работ по алгебре и началам анализа из сборника для 10 класса Глизбург В. И. (под ред. А.Г. Мордковича). Базовый уровень. — Рукопись. — 2015.
Настоящее пособие содержит решения контрольных работ из сборника «Глизбург В. И. Алгебра и начала математического анализа. 10 класс. Контрольные работы для учащихся общеобразовательных учреждений (базовый уровень) / В. И. Глизбург ; под ред. А. Г. Мордковича. — М. : Мнемозина, 2009. — 39 с.»
Сборник контрольных работ предназначен для тех учителей математики, которые используют в своей преподавательской деятельности УМК, созданный авторским коллективом под руководством А. Г. Мордковича.
Каждый вариант контрольной работы выстроен по одной и той же схеме: задания обязательного минимума — до первой черты, задания среднего уровня — между первой и второй чертой, задания уровня выше среднего — после второй черты. Шкала оценок за выполнение контрольной работы может выглядеть так: за успешное выполнение только заданий обязательного минимума — оценка 3; за успешное выполнение заданий обязательного минимума и одного дополнительного (после первой или второй черты) — оценка 4; за успешное выполнение заданий всех трех уровней — оценка 5. При этом оценку не рекомендуется снижать за одно неверное решение в первой части работы (допустимый люфт).
Внимание! Рукопись не проверялась, возможны ошибки!
Содержание
Контрольная работа № 1
Контрольная работа № 2
Контрольная работа № 4
Контрольная работа № 5
Контрольная работа № 6
Контрольная работа № 7
Контрольная работа № 8
ВНИМАНИЕ! Все права на публикацию рукописей принадлежат сайту gdz.math-helper.ru. Копирование и распространение материалов запрещено!
Математика является предметом изучения, включающим число, формы, количество, алгебру и геометрию и их взаимосвязи. Математика является основным предметом преподавания во всех школах и колледжах.
10-й класс, SSC часть 2 Математические работы состоят из 20% объективных вопросов и вопросов с несколькими вариантами ответов. Учащиеся 10 класса могут подготовить свой предмет по математике на илмкидуня. Ilmkidunya дает уникальную возможность для ученика 10-го класса практиковать свою математику онлайн. На этой тестовой странице MCQ учащиеся 10-го класса могут оценивать себя для сдачи экзамена с отличными оценками.
Тест Мудрости по 10-й главе математики
(Урду Средний)
Практикуя свой предмет по математике онлайн, ученики -го класса найдут эту страницу очень полезной для сдачи ежегодных экзаменов.Эти онлайн-вопросы по математике имеют тысячи целей с несколькими вариантами ответов. студенты могут лучше оценить свою подготовку к математике. Эта бесплатная платформа подготовки к экзаменам по математике поможет ученикам 10-го класса с полной уверенностью сдать экзамен.
Ilmkidunya.com — первый образовательный сайт, предложивший новую аутентичную систему подготовки к онлайн-экзаменам для учащихся 10-го класса.Учащиеся 10-го класса всех учебных советов BISES могут подготовить свои экзамены в режиме онлайн через ilmkidunya. Студенты могут оценить уровень своей подготовки к ежегодным экзаменам, попробовав эти надежные и точные информативные онлайн-тесты.
Учащиеся 10-го класса могут проверять свою подготовку с помощью этой онлайн-системы тестирования столько раз, сколько захотят, пока не обнаружат, что они полностью подготовлены. Студентам 10 класса рекомендуется пройти этот онлайн-тест по предмету «Математика».Учащиеся 10-го класса всех BISES могут оценить свою подготовку к математике на ilmkiunya.
,Практический тест по промежуточной алгебре
1. Упростите выражение (4 x +2 2x ) / (2 x )
A 6
B 2 + 2 x
C 2 × 2 x
D 2 x +1
2. Упростите выражение (2x 2 -5x-12) / (2x 2 -4x-16).
A (x-6) / 2 (x-2)
B (x-6) / 2 (x + 2)
C (2x + 3) / 2 (x-2)
D (2x + 3) / 2 (x + 2)
3. Предположим, что функция f (x) является квадратичной функцией с корнями при x = 2-3i и x = 2 + 3i.Найдите f (x).
A f (x) = x 2 -4x-5
B f (x) = x 2 -4x + 13
C f (x) = x 2 -6ix-5
D f ( x) = x 2 -6ix + 13
4. Решить неравенство для x. Выбрать все, что подходит.
4x 3 + 10x 2 -24x <0
A x <-4
B -4
C 0
D x> 3/2
5. Бейсбольный мяч подбрасывается в воздух с начальной высота 6 футов. Его высота над землей (в футах) t секунд после броска определяется функцией h (t) = — 16t 2 + 46t + 6.Сколько времени (в секундах) для бейсбола, чтобы поразить землю?
A 2 секунды
B 5/2 секунды
C 3 секунды
D 4 секунды
6. Решите уравнение для x. Выбрать все, что подходит.
log 2 (8x-x 2 ) = 4
A x = -8
B x = 0
C x = 4
D x = 8
7. Рассчитать среднюю скорость изменения f между х = 1 и х = 4.
f (x) = x 3 + 3x + 1
A 6
B 20/3
C 24
D 72
8.Упростите выражение (x 3 -3x 2 + 2x-6) / (x 2 -9).
A 1
B (x-3) / (x + 3)
C (x 2 +2) / (x-3)
D (x 2 +2) / (x + 3)
9. Предположим, что угол? находится в квадранте I и потому? = 12/13. Найти загар?
Загар? = 1/13
B загар? = 13
С загар? = 5/12
D загар? = 12/5
10. Какое выражение эквивалентно 6√x + 10x?
A 2 (3x -1 + 5x)
B 2 (3x 1/2 + 5x)
C 2x (3x -1 +5)
D 2x (3x 1/2 +5 )
Ответы и пояснения
1.D
Эту проблему можно решить либо (1), отдельно упростив числитель и знаменатель, а затем упростив результат, либо (2), используя свойство распределения. Для этой проблемы мы будем использовать первый метод.
Сначала переписать 4 x как показатель степени 2, используя свойство, (b x ) y = b xy .
4 x = (2 2 ) x = 2 2x
Затем используйте это для упрощения числителя со свойством, b x x у = b х + у .
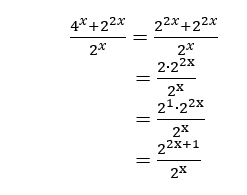
Наконец, упростите результат, используя b x / b y = b xy
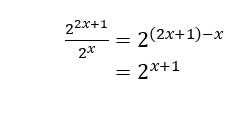
2. Упростите, упростите выражение, первый фактор числитель и знаменатель. Методом проб и ошибок числитель может быть разложен на два бинома следующим образом. 2x 2 — 5x — 12 = (2x + 3) (x -4)
Для знаменателя вычтите общий множитель, который равен 2.
2x 2 — 4x — 16
= 2 (x 2 — 2x -8)
= 2 (x-4) (x + 2)
Таким образом, факторизованная форма выражения это

Обратите внимание, что есть общий фактор (х — 4), который находится как в числителе, так и в знаменателе. Следовательно, вы можете еще больше упростить выражение, отменив его.

3. B
Корнями квадратичной функции f (x) являются значения x, для которых f (x) = 0.Квадратичная функция, записанная в виде f (x) = (x-a) (x-b), имеет корни при x = a и x = b. Поэтому, чтобы найти f (x), подставьте 2-3i и 2 + 3i для a и b в это уравнение и упростите результат. Обратите внимание, что (2-3i) (2 + 3i) = 4-9i 2 = 13.
f (x) = (xa) (xb)
= [x- (2-3i)] [x- (2 + 3i)]
= x 2 — (2-3i) x- (2+ 3i) x + (2-3i) (2 + 3i)
= x 2 -2x + 3ix-2x-3ix + 13
= x 2 -4x + 13
4. A и C
Чтобы решить, сначала фактор полином.Обратите внимание, что наибольший общий фактор (GCF) в терминах равен 2x. Вычеркните это выражение, а затем используйте метод проб и ошибок, чтобы вычислить результирующий трином.
4x 3 + 10x 2 -24x
= 2x (2x 2 + 5x-12)
= 2x (2x-3) (x + 4)
Решая для 0, мы находим, что корни многочлена: x = 0, x = 3/2 и x = -4.
Эти значения делят числовую линию на четыре интервала. Выберите номер теста из каждого интервала и определите, является ли продукт положительным или отрицательным.Для этой проблемы мы будем использовать -5, -1, 1 и 2 в качестве тестовых чисел. Подставьте эти значения в исходный полином.
x = -5:
4 (-5) 3 +10 (-5) 2 -24 (-5)
= -375 + 250 + 120
= -5
x = -1:
4 (-1) 3 +10 (-1) 2 -24 (-1)
= -4 + 10 + 24
= 30
x = 1:
4 (1) 3 + 10 (1) 2 -24 (1)
= 4 + 10-24
= -10
x = 2:
4 (2) 3 +10 (2) 2 -24 (2)
= 32 + 40-48
= 24
Таким образом, данное неравенство 4x 3 + 10x 2 -24x <0 удовлетворяется числами меньше -5 и числами от 0 до 3/2.
5. D
Бейсбол упадет на землю, когда его высота станет нулевой. В математической записи это произойдет, когда h (t) = 0. Поэтому нам нужно установить данную функцию равной нулю.
h (t) = 0
-16t 2 + 46t + 6 = 0
Теперь решите полученное уравнение. Разложите левую сторону и используйте свойство нулевого произведения, чтобы решить для t.
-2 (8t 2 -23t-3) = 0
-1 (8t + 1) (t-3) = 0
t = -1 / 8 t = 3
Ответ имеет смысл, только когда t положительный, поэтому мы можем отбросить отрицательное значение.Таким образом, калькулятор упадет на землю через 3 секунды после того, как его бросят.
6. C
nly: логарифм числа — это показатель степени, на который нужно поднять основание, чтобы получить это число. Например, поскольку 2 3 = 8, также верно, что log_2? 8 = 3. Таким образом, данное уравнение log_2? (8x-x 2 ) = 4 подразумевает, что
8x-x 2 = 2 4
Упростим это уравнение и решим для x.
8x-x 2 = 16
0 = x 2 -8x + 16
0 = (x-4) 2
x = 4
Таким образом, решение является x = 4.Проверьте это значение самостоятельно, подставив его в исходное уравнение, чтобы убедиться, что результат является верным утверждением.
7. C
Средняя скорость изменения функции f между x = a и x = b может быть рассчитана по формуле
Средняя скорость изменения = (f (b) -f (a)) / (ba)
Чтобы использовать эту формулу, сначала вычислите f (1) и f (4).
Затем используйте эти значения для расчета средней скорости изменения.
Средняя скорость изменения = (f (4) -f (1)) / (4-1)
8.D
Чтобы упростить выражение, сначала вычислите числитель и знаменатель. Числитель может быть разложен по группам следующим образом.
x 3 -3x 2 + 2x-6
= x 2 (x-3) +2 (x-3)
= (x 2 +2) (x-3)
Для знаменателя, коэффициент с использованием формулы разности квадратов, 2 -b 2 = (a + b) (ab).
x 2 -9 = (x + 3) (x-3)
Таким образом, факторизованная форма выражения составляет
(x 3 -3x 2 + 2x-6) / (x 2 -9)
= (x 2 +2) (x-3) / (x + 3) (x-3)
Обратите внимание, что существует общий фактор (x-3), который в числителе и знаменателе.Следовательно, вы можете еще больше упростить выражение, отменив его.
(x 2 +2) (x-3) / (x + 3) (x-3)
= (x 2 +2) / (x + 3)
9. C
Используйте единичный круг, чтобы смоделировать значение косинуса. В прямоугольном треугольнике функция косинуса cos? = Смежная / гипотенуза. Используя теорему Пифагора, мы находим, что длина второго отрезка равна
b = √ (c 2 -a 2 )
= √ (1 2 — (12/13) 2 )
= √ (25/169)
= 5/13
Так как функция тангенса равна tan ? = противоположно / смежно, значение загара ? — это загар ? = √ (5/13) / (12/13) = √5 / 12 В квадранте I значения косинуса и тангенса являются положительными.Поэтому загар ? = 5/12.
10. B
Все варианты включают в себя два преобразования данного выражения: выведение 2 или 2x и изменение радикала в экспоненту. Первый фактор из наибольших общих факторов (GCF) в терминах. В этом случае GCF составляет 2.
6√x + 10x
= 2 (3√x + 5x)
Кроме того, квадратный корень из x равен x, возведенному в степень 1/2.
2 (3√x + 5x)
= 2 (3x 1/2 + 5x)
.
= 2 (x 2 — 2x -8)
= 2 (x-4) (x + 2)
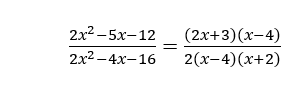
Обратите внимание, что есть общий фактор (х — 4), который находится как в числителе, так и в знаменателе. Следовательно, вы можете еще больше упростить выражение, отменив его.
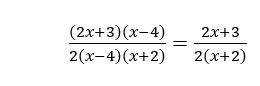
= [x- (2-3i)] [x- (2 + 3i)]
= x 2 — (2-3i) x- (2+ 3i) x + (2-3i) (2 + 3i)
= x 2 -2x + 3ix-2x-3ix + 13
= x 2 -4x + 13
= 2x (2x 2 + 5x-12)
= 2x (2x-3) (x + 4)
4 (-5) 3 +10 (-5) 2 -24 (-5)
= -375 + 250 + 120
= -5
4 (-1) 3 +10 (-1) 2 -24 (-1)
= -4 + 10 + 24
= 30
4 (1) 3 + 10 (1) 2 -24 (1)
= 4 + 10-24
= -10
4 (2) 3 +10 (2) 2 -24 (2)
= 32 + 40-48
= 24
-16t 2 + 46t + 6 = 0
-1 (8t + 1) (t-3) = 0
t = -1 / 8 t = 3
0 = x 2 -8x + 16
0 = (x-4) 2
x = 4
Чтобы использовать эту формулу, сначала вычислите f (1) и f (4).
= x 2 (x-3) +2 (x-3)
= (x 2 +2) (x-3)
= (x 2 +2) (x-3) / (x + 3) (x-3)
= (x 2 +2) / (x + 3)
= √ (1 2 — (12/13) 2 )
= √ (25/169)
= 5/13
= 2 (3√x + 5x)
= 2 (3x 1/2 + 5x)


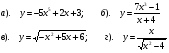
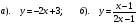
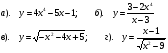
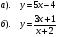
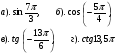
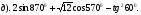
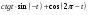
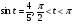 .
.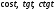 .
.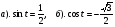
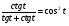 .
.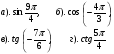
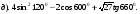
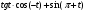
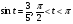 .
.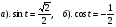 .
.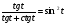 .
.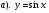 на отрезке
на отрезке 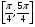
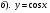 на отрезке
на отрезке 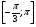 .
.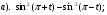
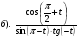
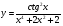
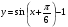
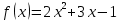 . Докажите, что
. Докажите, что 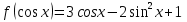 .
.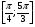 ;
;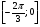
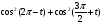
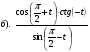
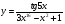
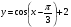
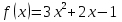 . Докажите, что
. Докажите, что 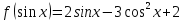
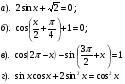
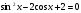 на отрезке
на отрезке 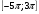 .
.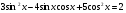
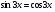
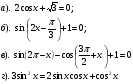
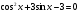 на отрезке
на отрезке 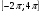 .
.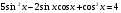
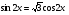 , принадлежащие отрезку
, принадлежащие отрезку 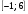 .
.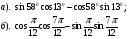
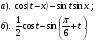
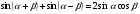
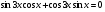
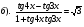
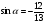 и
и 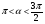 , найти
, найти 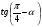 .
.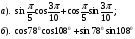
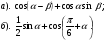
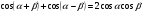
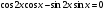
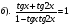
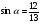 и
и 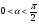 , найти
, найти 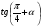 .
.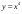 ; б).
; б). 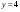 ;
; 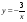 ; г).
; г). 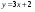 ;
; 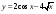 .
.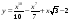 в точке х0 = 1.
в точке х0 = 1.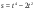 . Найдите ее скорость в момент времени
. Найдите ее скорость в момент времени 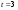 с.
с.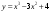 .
.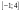 .
.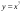 ; б).
; б). 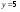 ;
;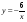 ; г).
; г). 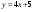 ;
;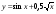 .
.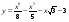 в точке х0 = 1.
в точке х0 = 1.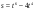 . Найдите ее скорость в момент времени t = 2с.
. Найдите ее скорость в момент времени t = 2с.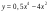 .
.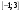 .
.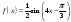 . Составить уравнение касательной к графику в точке с абсциссой
. Составить уравнение касательной к графику в точке с абсциссой 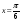 . Установить, в каких точках промежутка
. Установить, в каких точках промежутка 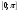 касательная к графику данной функции составляет с осью Ох угол 600.
касательная к графику данной функции составляет с осью Ох угол 600.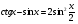
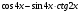 ;
;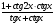 .
.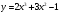 .
.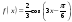 . Составить уравнение касательной к графику в точке с абсциссой
. Составить уравнение касательной к графику в точке с абсциссой 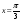 . Установить точки минимума и максимума, а также наибольшее и наименьшее значение на промежутке
. Установить точки минимума и максимума, а также наибольшее и наименьшее значение на промежутке 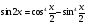
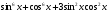 ;
;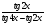 .
.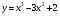 .
.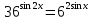 .
.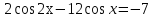 .
.