Геометрия, 10 класс: уроки, тесты, задания

Аксиомы стереометрии

1. Аксиомы стереометрии и их простейшие следствия

Параллельность прямых и плоскостей

1. Параллельность прямых, прямой и плоскости

2. Взаимное расположение прямых в пространстве. Угол между прямыми

3. Параллельность плоскостей

4. Тетраэдр и параллелепипед

Перпендикулярность прямых и плоскостей

1. Перпендикулярность прямой и плоскости

2. Перпендикуляр и наклонные. Угол между прямой и плоскостью

3. Двугранный угол. Перпендикулярность плоскостей

Многогранники

1. Понятие многогранника. Призма

2. Пирамида

3. Правильные многогранники

Векторы в пространстве

1. Понятие вектора в пространстве

2. Сложение и вычитание векторов. Умножение вектора на число

3. Компланарные векторы

www.yaklass.ru

Геометрия для 10 класса | Интернет — шпаргалка

1. Аксиомы стереометрии

1.1 Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

1.2 Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

 1.3 Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

2. Некоторые следствия из аксиом.

2.1 Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

2.2 Через две пересекающиеся прямые проходит плоскость, и притом только  одна.

3. Параллельность прямых, прямой и плоскости.

3.1 Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

3.2 Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

3.3 Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

3.4 Если две прямые параллельны третьей прямой, то они параллельны.

3.5 Прямая и плоскость называются параллельными, если они не имеют общих точек.

3.6 Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

4. Взаимное расположение прямых в пространстве. Угол между двумя прямыми.

4.1 Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости.

4.2 Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся

4.3 Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой, и притом только одна.

4.4 Если стороны двух углов соответственно сонаправлены, то такие углы равны.

5. Параллельность плоскостей.

5.1 Две плоскости называются параллельными, если они не пересекаются.

5.2 Если две пересекающиеся прямые одной        плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

6. Перпендикулярность прямой и плоскости.

6.1 Если одна из двух параллелельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.

6.2 Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

6.3 Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.

6.4 Если две прямые перпендикулярны к плоскости, то они параллельны.

6.5 Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

6.6 Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

7. Перпендикуляр и наклонные. Угол между прямой и плоскостью.

7.1 Прямая, проведённая в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной.

7.2 Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и её проекции на плоскость.

8. Двугранный угол. Перпендикулярность плоскостей.

8.1 Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости.

8.2 Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен 90⁰.

8.3 Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

8.4 Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его трёх измерений.

8.5 Сумма плоских углов многогранного угла меньше 360⁰.

9. Теорема Эйлера.

В любом выпуклом многограннике сумма числа граней и вершин больше числа рёбер на 2.

10. Призма

10.1 Площадь боковой поверхности призмы равна произведению периметра основания на высоту призмы.

11. Пространственная теорема Пифагора.

Если все плоские углы при одной из вершин тетраэдра – прямые, то квадрат площади грани, противолежащей этой вершине, равен сумме квадратов площади остальных граней.

12. Пирамида

12.1 Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

12.2 Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему.

13. Вектор

13.1 Отрезок, для которого указано, какой из его концов считается началом, а какой – концом, называется вектором.

13.2 Для любых трёх точек A, B и C имеет место равенство

13.3

13.4

13.5 Произведением ненулевого вектора на число k называется такой вектор длина которого равна причём векторы и сонаправлены при k>0 и противоположно направлены при k<0. Произведением нулевого вектора на число считается нулевой вектор.

13.6

13.7

13.8

13.9 Любой вектора можно разложить по трём данным некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.

14. Координаты точки и координаты вектора

14.1 Любой вектор можно представить в виде причём коэффициенты разложения определяются единственным образом.

14.2 Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.

14.3 Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.

14.4 Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на число.

14.5 Каждая координата середины отрезка равна полусумме соответствующих координат его концов.

14.6 Расстояние между точками вычисляется по формуле

15. Скалярное произведение векторов.

15.1 Скалярным произведением двух векторов является произведение их длин на косинус угла между ними.

15.2 Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

15.3 Скалярный квадрат вектора равен квадрату его длины.

15.4

15.5

15.6

15.7

16. Движения

16.1 Движение пространства – это отображение пространства на себя, сохраняющее расстояния между точками.

16.2 Осевой симметрией с осью a называется такое отображение пространства на себя, при котором любая точка M переходит в симметричную ей точку  относительно оси a.

16.3 Зеркальной симметрией называется такое отображение пространства на себя, при котором любая точка M переходит в симметричную ей относительно плоскости α точку M₁.

16.4 Параллельным переносом на вектор  называется отображение пространства на себя, при котором любая точка M переходит в такую точку M₁, что .

16.5 Центральным подобием с центром O и коэффициентом k ≠ 0 называется отображение пространства на себя, при котором каждая точка M переходит в точку M₁, что

17. Цилиндр и конус.

17.1 Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и L₁, называется цилиндром.

17.2 Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра.

17.3 Площадь цилиндра находится по формуле

17.4 Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом.

17.5 Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

17.6 Площадь полной поверхности конуса находится по формуле

17.7 Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую, т.е.

18. Сфера

18.1 Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.

18.2 Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

18.3 Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.

18.4 Площадь сферы вычисляется по формуле

18.5 Радиус сферы, проведённый в точку касания сферы и прямой, перпендикулярен к этой прямой

18.6 Если радиус сферы перпендикулярен к прямой, проходящей через его конец, лежащий на сфере, то эта прямая является касательной к сфере.

18.7 Отрезки касательных к сфере, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр сферы.

Понравилось это:

Нравится Загрузка…

inetshpora.wordpress.com

Угол между прямой и плоскостью. Видеоурок. Геометрия 10 Класс

На этом уроке мы введем понятие угла между прямой и плоскостью, дадим его строгое определение и решим задачи, в которых будет встречаться данный угол.

Наверняка вы слышали такое выражение: «Солнечный луч падает под углом…». (См. Рис. 1.)

Рис. 1. Падает солнечный луч

По сути, здесь идет речь об угле между прямой, частью которой является луч, и «плоскостью» земной поверхности (хотя она, конечно, не совсем плоская).

Мы привыкли, что угол бывает между двумя лучами (см. Рис. 2) или прямыми (см. Рис. 3).

Рис. 2. Угол между лучами

Рис. 3. Угол между прямыми

Как же определить угол между прямой и плоскостью?

Углом между прямой и плоскостью называют угол между прямой и ее проекцией на эту плоскость.

Чтобы построить проекцию прямой на плоскость, достаточно опустить из любых двух ее точек перпендикуляры на плоскость (спроектировать эти точки), после чего провести через них прямую – это и будет проекция (см. Рис. 4).

Рис. 4. Угол между прямой и плоскостью

Так, проекции всех точек данной прямой будут лежать на одной прямой.

---

Доказательство

Пусть  – точка пересечения прямой  и плоскости ,  и  – точки на прямой ,  и  – их проекции на плоскость . Докажем, что ,  и  лежат на одной прямой . (См. Рис. 5.)

Рис. 5. Иллюстрация к доказательству

Заметим, что , так как , . Значит если рассмотреть плоскость , то точки  и  будут принадлежать ей. Но плоскость  пересекает исходную плоскость по некоторой прямой. (См. Рис. 6.)

Рис. 6. Пересечение плоскостей

Значит раз точки ,  и  принадлежат обеим плоско

interneturok.ru

Параллельность плоскостей — урок. Геометрия, 10 класс.

Как известно из аксиом стереометрии, если плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Значит, две плоскости или пересекаются, или не пересекаются.

 

Плоскости, которые не пересекаются, называются параллельными.

Параллельные плоскости α и β обозначаются α&par;β.

Пример:

любая конструкция с полом, потолком и стенами даёт нам представление о параллельных плоскостях — пол и потолок как две параллельные плоскости, боковые стены как параллельные плоскости.

 

 

 

Признак параллельности плоскостей.

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

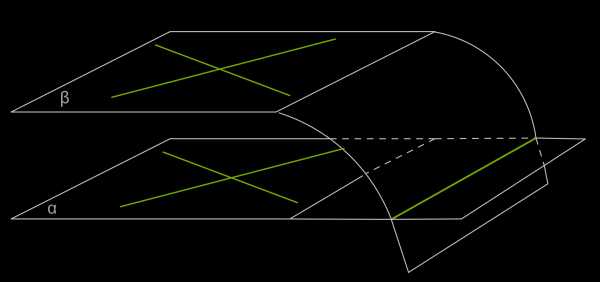
Доказательство.

Пусть α и β — данные плоскости, a1 и a2 — пересекающиеся прямые в плоскости α, а b1 и b2 — соответственно параллельные им прямые в плоскости β.

 

Допустим, что плоскости α и β не параллельны, то есть, они пересекаются по некоторой прямой \(c\).

Прямая a1 параллельна прямой b1, значит, она параллельна и самой  плоскости β.

Прямая a2 параллельна прямой b2,  значит, она параллельна и самой плоскости β (признак параллельности прямой и плоскости).

 

Прямая \(c\) принадлежит плоскости α, значит, хотя бы одна из прямых — a1 или a2 — пересекает  прямую \(c\), то есть имеет с ней общую точку. Но прямая \(c\) также принадлежит и плоскости β, значит, пересекая прямую \(c\), прямая a1 или a2 пересекает плоскость β, чего быть не может, так как прямые a1 и a2 параллельны плоскости β.

Из этого следует, что плоскости α и β не пересекаются, то есть, они параллельны.

Свойства параллельных плоскостей

Теорема 1. Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.

 

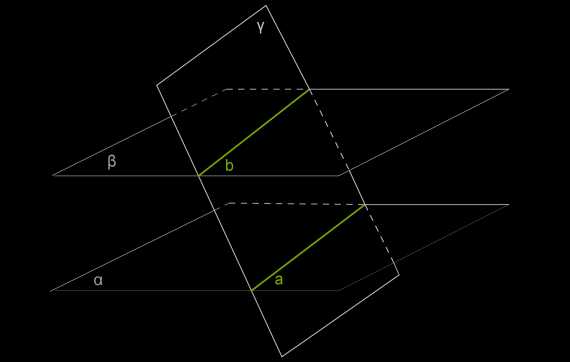
Доказательство.

Пусть α и β — параллельные плоскости, а γ — плоскость, пересекающая их.

Плоскость α пересекается с плоскостью γ по прямой \(a\).  

Плоскость β пересекается с плоскостью γ по прямой \(b\). 

 

Линии пересечения \(a\) и \(b\) лежат  в одной плоскости γ и потому могут быть либо пересекающимися, либо параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не могут иметь общих точек. Следовательно, они параллельны.

 

Теорема 2. Отрезки параллельных прямых, заключённых между двумя параллельными плоскостями, равны. 

 

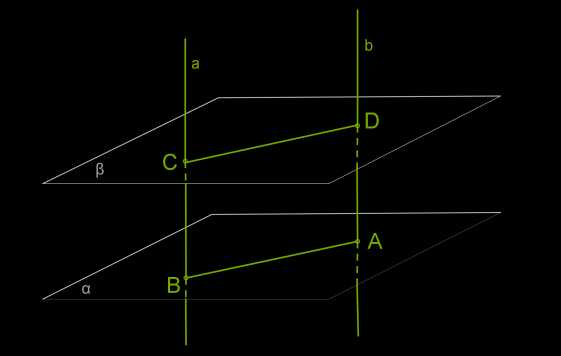
Доказательство.

Пусть α и β — параллельные плоскости, а \(a\) и \(b\) — параллельные прямые, пересекающие их.

Через прямые \(a\) и \(b\) можно провести плоскость — эти прямые параллельны, значит, определяют плоскость, причём только одну.

Проведённая плоскость пересекается с плоскостью α по прямой \(AB\), а с плоскостью β — по прямой \(CD\). 

По предыдущей  теореме прямые \(AB\) и \(CD\) параллельны. Четырёхугольник \(ABCD\) есть параллелограмм (у него противоположные стороны параллельны). А раз это параллелограмм, то противоположные стороны у него равны, то есть \(BC = AD\).

www.yaklass.ru

Введение в стереометрию — урок. Геометрия, 10 класс.

Школьный курс геометрии состоит из планиметрии и стереометрии.

 

Планиметрия изучает фигуры и их свойства на плоскости. Образно говоря, планиметрия изучает всё, что можно нарисовать или начертить на листе бумаги.

Основные объекты планиметрии — это точки, линии и замкнутые фигуры (например: квадрат, треугольник, круг, трапеция, ромб). Множество всех точек, рассматриваемых в планиметрии, образует плоскость. Множество точек в планиметрии называется фигурой. Замкнутая фигура в планиметрии — это множество точек, ограниченных линией.Стереометрия изучает фигуры и их свойства в пространстве. Образно говоря, стереометрия изучает всё, что можно склеить из бумаги, сколотить из досок, построить из кирпичей и т. п.

Основными объектами стереометрии являются точки, прямые, плоскости и замкнутые пространственные фигуры (например: куб, пирамида, параллелепипед, шар, конус). Множество всех точек, рассматриваемых в стереометрии, называется пространством. Любое множество точек называется фигурой. Замкнутая фигура в стереометрии — это множество точек, ограниченных поверхностью.

Пример:

на анимированных иллюстрациях наглядно показаны связь и различие плоских и пространственных фигур.

Ваш браузер не поддерживает HTML5 видео

Ваш браузер не поддерживает HTML5 видео

Так как каждая прямая и каждая плоскость содержат какие-либо точки, то прямая и плоскость тоже являются фигурами стереометрии.
Плоскость бесконечна и делит пространство на две части.

Точки обозначаются прописными латинскими буквами: \(A, B, C, D, E, F…\)
Прямые обозначаются строчными латинскими буквами: \(a, b, c, d, e, f…\)
Плоскости обозначаются греческими буквами: α,β,γ и т. д.

www.yaklass.ru

ПОУРОЧНЫЕ РАЗРАБОТКИ ПО ГЕОМЕТРИИ 10 класс — разработки уроков — авторские уроки — план-конспект урока

ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА

Введение. АКСИОМЫ СТЕРЕОМЕТРИИ И ИХ СЛЕДСТВИЯ

Урок 1. Предмет стереометрии. Аксиомы стереометрии

Урок 2. Некоторые следствия из аксиом

Урок 3. Решение задач на применение аксиом стереометрии и их следствий

Урок 4. Решение задач на применение аксиом стереометрии и их следствий

Урок 5. Решение задач на применение аксиом стереометрии и их следствий. Самостоятельная работа

Глава I. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

§ 1. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ, ПРЯМОЙ И ПЛОСКОСТИ

Урок 6. Параллельные прямые в пространстве

Урок 7. Параллельность прямой и плоскости

Урок 8. Решение задач по теме «Параллельность прямой и плоскости»

Урок 9. Решение задач по теме «Параллельность прямой и плоскости»

Урок 10. Решение задач по теме «Параллельность прямой и плоскости»

§ 2. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ В ПРОСТРАНСТВЕ

Урок 11. Скрещивающиеся прямые

Урок 12. Углы с сонаправленными сторонами. Угол между прямыми

Урок 13. Решение задач по теме «Взаимное расположение прямых в пространстве. Угол между двумя прямыми»

Урок 14. Решение задач по теме «Параллельность прямых и плоскостей»

Урок 15. Контрольная работа по теме «Аксиомы стереометрии. Взаимное расположение прямых, прямой и плоскости»

§ 3. ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ

Урок 16. Параллельные плоскости

Урок 17. Свойства параллельных плоскостей

§ 4. ТЕТРАЭДР. ПАРАЛЛЕЛЕПИПЕД

Урок 18. Тетраэдр

Урок 19. Параллелепипед

Урок 20. Задачи на построение сечений

Урок 21. Задачи на построение сечений

Урок 22. Закрепление свойств параллелепипеда

Урок 23. Контрольная работа № 1

Урок 24. Зачет № 1

Глава II. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

§ 1. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ

Урок 25. Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости

Урок 26. Признак перпендикулярности прямой и плоскости

Урок 27. Теорема о прямой, перпендикулярной к плоскости

Урок 28. Решение задач на перпендикулярность прямой и плоскости

Урок 29. Решение задач на перпендикулярность прямой и плоскости

Урок 30. Решение задач на перпендикулярность прямой и плоскости

§ 2. ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ. УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ

Урок 31. Расстояние от точки до плоскости. Теорема о трех перпендикулярах

Урок 32. Угол между прямой и плоскостью

Урок 33. Повторение теории. Решение задач на применение теоремы о трех перпендикулярах (ТПП), на угол между прямой и плоскостью

Урок 34. Решение задач на применение ТТП, на угол между прямой и плоскостью

Урок 35. Повторение (решение задач на теорему о 3-х перпендикулярах)

Урок 36. Угол между прямой и плоскостью (повторение)

§ 3. ДВУГРАННЫЙ УГОЛ. ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ

Урок 37. Двугранный угол

Урок 38. Признак перпендикулярности двух плоскостей

Урок 39. Прямоугольный параллелепипед

Урок 40. Решение задач на свойства прямоугольного параллелепипеда

Урок 41. Перпендикулярность прямых и плоскостей (повторение)

Урок 42. Решение задач

Урок 43. Контрольная работа по теме «Перпендикулярность прямых и плоскости»

Урок 44. Зачет № 2

Глава III. МНОГОГРАННИКИ

§ 1. ПОНЯТИЕ МНОГОГРАННИКА. ПРИЗМА

Урок 45. Понятие многогранника

Урок 46. Призма. Площадь поверхности призмы

Урок 47. Повторение теории, решение задач на вычисление площади поверхности призмы

Урок 48. Решение задач на вычисление площади поверхности призмы

§ 2. ПИРАМИДА

Урок 49. Пирамида

Урок 50. Правильная пирамида

Урок 51. Решение задач по теме «Пирамида»

Урок 52. Решение задач по теме «Пирамида». Самостоятельная работа

Урок 53. Усеченная пирамида. Площади поверхности усеченной пирамиды

§ 3. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ

Урок 54. Симметрия в пространстве. Понятие правильного многогранника. Элементы симметрии правильных многогранников

Урок 55. Контрольная работе № 3.1 по теме «Многогранники»

Урок 56. Зачет № 3 по теме «Многогранники. Площадь поверхности призмы, пирамиды»

Глава IV. ВЕКТОРЫ В ПРОСТРАНСТВЕ

§ 1. ПОНЯТИЕ ВЕКТОРА В ПРОСТРАНСТВЕ

Урок 57. Понятие векторов. Равенство векторов

§ 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО

Урок 58. Сложение и вычитание векторов. Сумма нескольких векторов

Урок 59. Умножение вектора на число

§ 3. КОМПЛАНАРНЫЕ ВЕКТОРЫ

Урок 60. Компланарные векторы. Правило параллелепипеда

Урок 61. Разложение вектора по трем некомпланарным векторам

Урок 62. Зачет по теме «Векторы в пространстве»

ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ

Урок 63. Итоговое повторение. Аксиомы стереометрии и их следствия

Урок 64. Параллельность прямых и плоскостей

Урок 65. Повторение (теорема о трех перпендикулярах, угол между прямой и плоскостью)

Урок 66. Контрольная работа № 5

Урок 67. Повторение. Векторы в пространстве, их применение к решению задач

Урок 68. Заключительный урок-беседа по курсу геометрии

ПРИЛОЖЕНИЯ

Приложение 1. Контрольные и самостоятельные работы

Урок 5. Самостоятельная работа

Урок 9. Самостоятельная работа обучающего характера

Урок 10. Проверочная самостоятельная работа

Урок 14. Работа по карточкам

Урок 15. Контрольная работа по теме «Аксиомы стереометрии. Взаимное расположение прямых, прямой и плоскости»

Урок 17. Самостоятельная работа

Урок 23. Контрольная работа № 1

Урок 30. Самостоятельная работа

Урок 53. Тест

Урок 55. Контрольная работа № 3.1 по теме «Многогранники»

Урок 63. Теоретический тест с последующей самопроверкой

Урок 66. Контрольная работа № 5

Урок 67. Мини-тест по теории

Приложение 2. Плакаты № 1, 2, 3, 4, рекомендуемые к урокам № 51, 52, 53

compendium.su

Геометрия (10 класс) — Викиверситет

Геометрия. Учебник для 10-11 классов общеобразовательных учреждений. Автор: Погорелов А. В.

Темы[править]

§1 Аксиомы стереометрии и их простейшие следствия
1. Аксиомы стереометрии.
Стереометрия — это раздел геометрии, в котором изучаются фигуры в пространстве. Основными фигурами являются точка, прямая и плоскость.

Аксиома
Через 3 точки, не лежащие на одной прямой, проходит плоскость и притом только одна.

Аксиома
Если 2 плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Аксиома
Если 2 точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

2. Существование плоскости, проходящей через данную прямую и данную точку.

Теорема
Через прямую и не лежащую на ней точку можно провести плоскость, и при том только одну.

3. Пересечение прямой с плоскостью.

Теорема
Через 2 пересекающиеся прямые можно провести плоскость и притом только одну.

Следствие теоремы
плоскость и не лежащая на ней прямая либо не пересекаются, либо пересекаются в одной точке.

4. Замечание к аксиоме I
Аксиома I стереометрии носит другой смысл чем подобная аксиома планиметрии. Теперь она утверждает вообще существование точек, не лежащих на данной прямой. Из этого не следует существование точек вне прямой на плоскости, это требует доказательства. 5. Развиение пространства на две полупространства.

Теорема
Плоскость разбивает пространство на два полупространства. Если точки Х и Y принадлежат одному полупространству, то отрезок ХY не пересекает плоскость. Если же точки Х и Y принадлежат разным полупространствам, то отрезок ХY пересекает плоскость.

• Контрольные вопросы и задачи(стр. 10-11)

§2 Параллельность прямых и плоскостей
7. Параллельные прямые в пространстве.
8. Признак параллельности прямых.
9. Признак параллельности прямой и плоскости.
10. Признак параллельности плоскостей.
11. Существование плоскости параллельной данной плоскости.
12. Свойства параллельных плоскостей.
13. Изображение пространственных фигур на плоскости.

• Контрольные вопросы и задачи(стр. 20-24)

§3 Перпендикулярность прямых и плоскостей
14. Перпендикулярность прямых в пространстве.
15. Признак перпендикулярности прямой и плоскости.
16. Построение перпендикулярных прямой и плоскости.
17. Свойства перпендикулярных прямой и плоскости.
18. Перпендикуляр и наклонная.
19. Теорема о трех перпендикулярах.
20. Признак перпендикулярности плоскостей.
21. Расстояние между скрещивающимися прямыми.
22. Применение ортогонального проектирования в техническом черчении.

• Контрольные вопросы и задачи(стр. 35-41)

Внимание! Требуется преподаватель для создания учебной программы. Вы можете помочь проекту, написав её.

ru.wikiversity.org