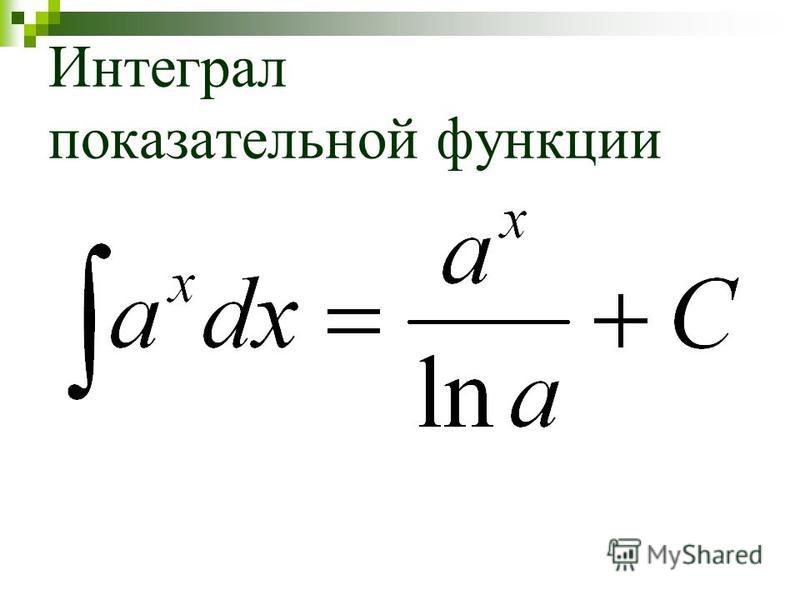Производная степенной функции урок 11 класс: Производная степенной функции

Содержание

Разработка урока по теме «Производная степенной функции. Применение производной в решении задач физики» 11 класс

Главная / Старшие классы / Алгебра

Скачать

260 КБ, 859163.doc Автор: Короткова Татьяна Александровна, 1 Апр 2015

Урок соответствует технологии модульного обучения.

Автор: Короткова Татьяна Александровна

Тип	Название материала	Автор	Опубликован
документ	Разработка урока по теме «Производная степенной функции. Применение производной в решении задач физики» 11 класс	Короткова Татьяна Александровна	1 Апр 2015
презентация, документ	Применение производной к исследованию функции в решении задач при подготовке к ЕГЭ. 11 класс.	Манькова Ирина Геннадьевна	31 Мар 2015
документ	Интегрированный урок (физика и математика) в 11 классе по теме: «Применение производной при решении физических зхадач» 16.04.2014г Интегрированный урок «Применение производной при решении физических задач» (11-й класс)	Сарангова Жанна Валерьевна	21 Мар 2015
документ	Проверочная работа по теме «Производная степенной функции» и «Правила дифференцирования» составлена к учебнику «Алгебра и начало математического анализа 10-11 класс» (авторы: Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева и д	Акинина Татьяна Николаевна	16 Янв 2016
документ	Повторительно-обобщающий урок в 11 классе по теме: «Применение производной к исследованию функции»	Шаршина Юлия Юрьевна	16 Мая 2015
презентация, документ	Интегрированный урок алгебры и физики «Применение производной при решении физических задач» (11-й класс) Интегрированный урок «Применение производной при решении физических задач» (11-й класс) Интегрированный урок «При	Манджиева Лидия Батма-Халгаевна	11 Апр 2016
документ	Разработка урока по теме «Применение производной к исследованию функции» 10 класс	Зайцева Галина Геннадиевна	4 Апр 2015
презентация, документ	Разработка урока по теме: «Производная функции»	Груздева Светлана Ивановна	1 Апр 2015
документ	Интегрированный урок по теме «Применение производной в решении физических задач»	Бельцов Александр Владимирович	21 Мар 2015
разное	Методическая разработка по теме: «Применение векторно-координатного метода в решении стереометрических задач»	Симакова Наталья Борисовна	21 Мар 2015
документ	Конспект урока по теме «Возрастание и убывание функций» (11 класс, учебник Ш. А Алимова и др.) Конспект урока по математике в 11-м классе Тема раздела: «Применение производной к исследованию функций» Тема: «Возрастание и убывани	Макевит Ирина Владимировна	12 Мая 2015
документ	Разработка метапредметного урока по математике и физике по теме «Производная в математике и физике» в 11 классе Разработка метапредметного урока по математике и физике по теме «Производная в математике и физике» в 11 классе ( с исп	Моргунова Татьяна Юрьевна	20 Мар 2015
презентация	урок по теме » Применение производной к исследованию функции»-11 класс-презентация	Коровашкова Алла Дмитриевна	21 Мар 2015
документ	урок по теме » Применение производной к исследованию функции»-11 класс	Коровашкова Алла Дмитриевна	21 Мар 2015
документ	Урок по теме «Применение производной к исследованию функций на примере отыскания оптимальных решений экстремальных задач» (деловая игра), 10 класс	Заббарова Фирая Масгудовна	16 Янв 2016
документ	Конспект урока по алгебре в 11 классе Применение графика производной к исследованию свойств функции	Лиц Людмила Юрьевна	15 Окт 2015
презентация, документ	Урок алгебры в 11 классе «Применение производной при решении задач ЕГЭ».	Данилова Оксана Михайловна	17 Окт 2015
документ	«Применение производной в решении практических задач на наибольшее и наименьшее значение» 10 класс	Седлина Лариса Михайловна	15 Окт 2015
презентация, документ	Методическая разработка обобщающего урока 11 класс по теме «Область определения функции» Диск	Васильева Жанна Витальевна	4 Апр 2015
документ	Методическая разработка по теме: «Применение векторно-координатного метода в решении стереометрических задач»	Симакова Наталья Борисовна	21 Мар 2015
разное	Методическая разработка по теме: «Из опыта работы подготовки школьников к олимпиадам по математике». Принцип Дирихле и его применение при решении задач Инварианты и их применение при решении задач Полуинварианты. Метод крайнего. Литература.	Неверовская Светлана Владимировна	1 Апр 2015
документ	Разработка урока по алгебре для 11 класса. Тема: «Применение производной в различных областях науки»	Савченко Татьяна Александровна	31 Мар 2015
документ	Урок математики в 3 классе по теме «Упражнение в решении арифметических задач»	Пенькова Елена Владимировна	11 Мая 2015
разное	Методическая разработка урока по теме «Применение производной»	Кончанин Светлана Равильевна	4 Апр 2015
документ	Урок по алгебре и началам анализа с применение ОЭР в 11 классе по теме: Число е. Производная показательной функции.	Маханова Самига Галимжановна	26 Окт 2015
документ	Применение производной к исследованию функции. Повторение. 11 класс.	Архипова Ирина Викторовна	4 Ноя 2015
документ	Применение производной при исследовании функции — 11 класс	Маргарита Геннадьевна Березина	16 Окт 2015
разное	Разработка урока по геометрии в 11 классе «Метод координат при решении стереометрических задач»	Уртюкова Мая Андреевна	23 Сен 2015
презентация, документ	Разработка учебного занятия по теме» Применение производной к исследованию функций и построеннию графиков. Схема исследования функции»	Воронкова Ольга Николаевна	1 Апр 2015
документ	Мастер-класс по теме: «Методы активизации родителей в решении воспитательно — образовательных задач ДОУ»	Еняшина Елена Александровна	3 Авг 2015
документ	Урок в 11 классе «Применение графика производной к исследованию свойств функции»	Лиц Людмила Юрьевна	6 Дек 2015
документ	Сценарий урока 10 класса по теме «Исследование функции с помощью производной.» Решение задач	Карабовская Ирина Борисовна	10 Июл 2015
документ	Разноуровневая контрольная работа по теме: » Применение непрерывности и производной.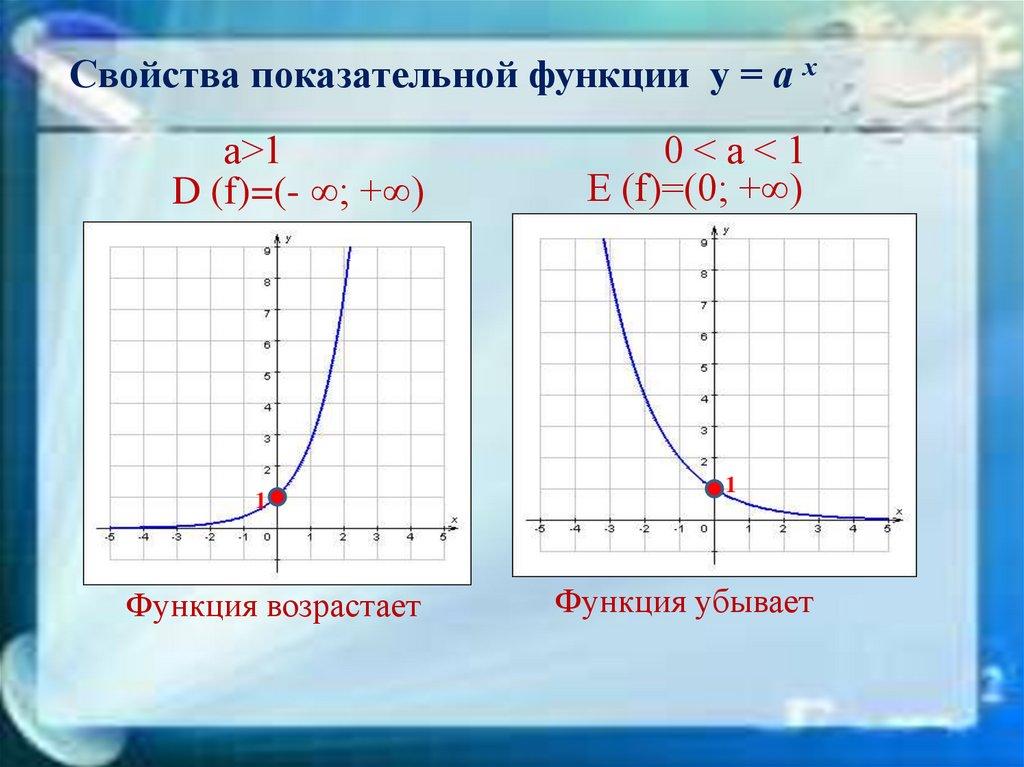 Касательная к графику функции «. 10 класс	Куликова Елена Георгиевна	7 Мая 2015
документ	Индивидуальный лист достижения обучающегося по теме : «Применение непрерывности и производной функции» 10 класс	Куликова Елена Георгиевна	27 Мая 2015
документ	План открытого урока 11 кл.- Применение комбинаторики при решении задач по теории вероятностей	Маргарита Геннадьевна Березина	16 Окт 2015
разное	Открытый урок по теме «Применение производной к исследованию функции»	Крапивина Светлана Владимировна	1 Апр 2015
разное	урок-КВН в 10 классе по теме»Применение непрерывности и производной к исследованию функции».	Лидия Павловна Рязанова	31 Мар 2015
документ	Применение тригонометрических подстановок при решении алгебраических задач 11 класс	Шишкина Елена Павловна	20 Фев 2016
презентация, документ	Урок- консультация в 11 классе «Применение координатно-векторного метода при решении задач С2″	Закирова Ильсеяр Салихзяновна	21 Мар 2015
документ	методическая разработка урока «Производная и её применение» Учитель математики Г.Е. Манасян Тема: «Производная и ее применение»	Манасян Григорий Ервандович	6 Дек 2015

Степенная функция и ее производная.

11-й класс

Ткач Наталья Васильевна, учитель математики

Разделы: Математика, Конкурс «Презентация к уроку»

Класс: 11

Презентация к уроку

Загрузить презентацию (1 МБ)

(Учебник под редакцией А.Н. Колмогорова, базовый уровень)

Цели: ввести понятие степенной функции, рассмотреть ее свойства, формулу производной степенной функции.

Вывод формулы производной степенной функции
Закрепить навыки распознавания функций по заданному графику;
Закрепить навыки построения графиков
Развивать зрительную память, внимание, умение анализировать, сравнивать, обобщать

Оборудование:

Проектор. На уроке используется презентация «Степенная функция и ее производная»:
- при повторении теоретического материала на экране высвечиваются повторяемые формулы, примеры, иллюстрирующие основные определения.
- при самопроверке самостоятельной работы на экране появляются эталонные ответы на соответствующие задания.
На столах лежат конверты с карточками для исследовательской работы, для организации самостоятельной работы, которые учащиеся используют на различных этапах урока.

Комбинированный урок

ознакомление с темой урока, постановка его целей и задач;
проверка домашнего задания;
проверка знаний и умений учащихся по пройденному материалу;
изложение нового материала;
первичное закрепление изученного;
подведение итогов урока и постановка домашнего задания

I. Мотивационная беседа

Как выдумаете, зачем надо изучать математику? Ответ на этот вопрос вы найдете, если вспомните, что означает в переводе с греческого слово «математика». «Математика» — знание, наука. Именно поэтому, если человек был сведущ в математике, то это всегда означало высшую степень учености. А умение правильно видеть и слышать – первый шаг к мудрости. Хочется, чтобы сегодня все ученики вашего класса показали, насколько они мудры и насколько сведущие люди в математике 11 класса. Итак, тема «Степенная функция и ее производная».

II.

Проверка домашнего задания

(Взаимопроверка по составленным учениками карточек по проверке производной показательной и логарифмической функции.) Учитель подводит итоги проверки домашней работы. Может контролировать ответы учащихся, корректирует и дополняет записи в тетрадях.

Учитель подводит итоги выполнения классом домашнего задания.

Прежде чем перейдем к изучению новой темы, необходимо вспомнить теоретический материал.

Систематизация знаний и умений по пройденному материалу

Для подготовки учащихся к усвоению нового материала повторяются и систематизируются их знания и умения в процессе устного решения упражнений на готовых чертежах.

Слайд. Установите вид зависимости. Запишите формулу.

Слайд. Какие из формул обозначают показательную, логарифмическую и степенную функции?

Слайд. Определить график, какой функции изображен?

Слайд с теоретическими вопросами. Для повторения основных формул используется презентация. На экране последовательно появляются левые части формул, и после ответа учащихся к ним присоединяется правая часть. Если учащиеся не называют какое-либо формулу, то его напоминает учитель. При завершении опроса все формулы высвечиваются на экране.

III. Исследовательская работа

Учитель: А сейчас проведем исследовательскую работу.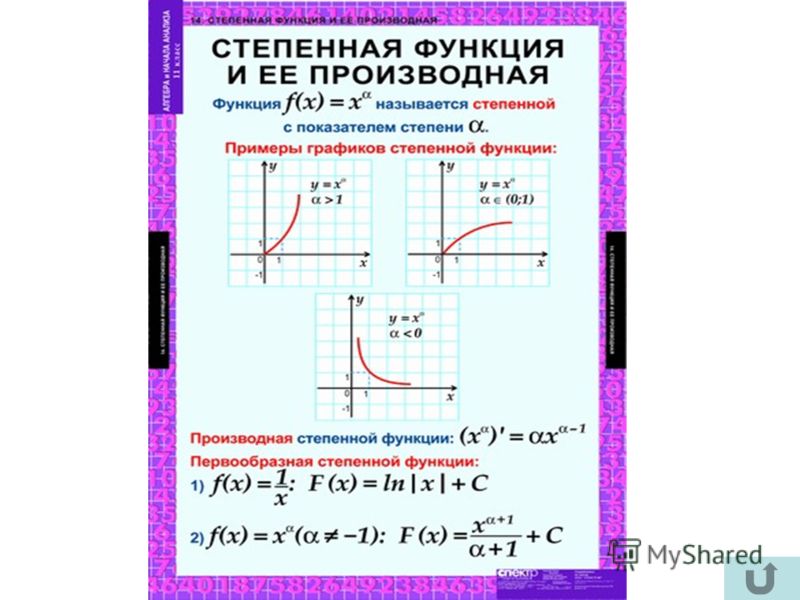 Получите задания.

Чему равна производная у = , где n натуральное число?
Запишите, чему равна производная у = х – n?
Сделайте вывод, для любого справедлива формула …, где m любое целое число.
Вспомните, чему равна производная ?
Чему равна производная ?
Сделайте вывод, …, где — любое рациональное число.
Найдите доказательство этой формулы в учебнике на стр.260 3-й абзац сверху.

Слайд. Формула производной степенной функции. (Вывод с доказательством записывается в тетради).

IV. Первичное закрепление изученного

Для закрепления изученного учащимся предлагается сначала прочитать содержание п.43 учебника. Затем учитель отвечает на возникшие у ребят вопросы.

Работа в группах. Каждой группе раздаются листы с заданиями.

Слайд. Тест на соответствие (после выполнения, физминутка)

Слайд. Графический диктант.

Разноуровневая самостоятельная работа.

V. Постановка домашнего задания

На дом задается содержание п.41-43 и решить задачи №559(б,в), 562(в,г), 563(б,г), 564(а,в). Обратите внимание на то, что необходимо знать формулы производной не только степенной функции, но и всех ранее изученных. Уметь доказывать вывод формулы производной степенной функции. Самостоятельно познакомиться с первообразной степенной функции.

VI. Подведение итогов

Вы замечательно поработали. Посчитайте свои баллы, я поставлю вам оценки.

Еще раз проверить формулы производных и графики.

VII. Резервные задания

12.01.2014

Исчисление I — Производные

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т. е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

В этой главе мы начнем рассмотрение следующей важной темы в классе исчисления — производных. Эта глава посвящена почти исключительно поиску производных. В этой главе мы рассмотрим одно из них. Мы оставим большинство приложений производных до следующей главы.

Вот список тем, затронутых в этой главе.

Определение производной. В этом разделе мы определяем производную, даем различные обозначения для производной и работаем над несколькими задачами, иллюстрирующими, как использовать определение производной для фактического вычисления производной функции.

Интерпретация производной – В этом разделе мы даем несколько наиболее важных интерпретаций производной. Мы обсуждаем скорость изменения функции, скорость движущегося объекта и наклон касательной к графику функции.

Формулы дифференцирования. В этом разделе мы даем большинство общих формул производных и свойств, используемых при нахождении производной функции. Примеры в этом разделе в основном сосредоточены на многочленах, корнях и, в более общем плане, переменных, возведенных в степень.

Правило произведения и частного. В этом разделе мы приведем две наиболее важные формулы для дифференцирования функций. Мы обсудим Правило произведения и Правило частного, позволяющие нам дифференцировать функции, которые до этого момента мы не могли дифференцировать.

Производные триггерных функций. В этом разделе мы обсудим дифференцирование триггерных функций. Даны производные всех шести тригонометрических функций, и мы показываем вывод производных от \(\sin(x)\) и \(\tan(x)\).

Производные экспоненциальной и логарифмической функций. В этом разделе мы выводим формулы для производных экспоненциальной и логарифмической функций.

Производные обратных триггерных функций. В этом разделе мы приводим производные всех шести обратных триггерных функций. Покажем вывод формул арксинуса, арккосинуса и арктангенса.

Производные гиперболических функций. В этом разделе мы определяем гиперболические функции, даем соотношения между ними и некоторые основные сведения о гиперболических функциях. Мы также приводим производные каждой из шести гиперболических функций и показываем вывод формулы для гиперболического синуса.

Цепное правило. В этом разделе мы обсудим одну из наиболее полезных и важных формул дифференцирования — Цепное правило. Имея в руках цепное правило, мы сможем различать гораздо более широкий спектр функций. Как вы увидите на протяжении остальных курсов по математическому анализу, многие производные, которые вы будете использовать, будут включать цепное правило!

Неявное дифференцирование. В этом разделе мы обсудим неявное дифференцирование. Не каждую функцию можно явно записать в терминах независимой переменной, например. y = f(x), но нам все равно нужно знать, что такое f'(x). Неявное дифференцирование позволит найти производную в этих случаях. Знание неявной дифференциации позволит нам сделать одно из наиболее важных применений деривативов — относительные ставки (следующий раздел).

Связанные ставки – В этом разделе мы обсудим единственное применение деривативов в этом разделе, Связанные ставки. В задачах о связанных скоростях нам задают скорость изменения одной величины в задаче и просят определить скорость одной (или нескольких) величин в задаче. Часто это один из самых сложных разделов для студентов. В этом разделе мы работаем с несколькими задачами, поэтому, надеюсь, к концу этого раздела вы получите достаточное представление о том, как работают эти задачи.

Производные высшего порядка. В этом разделе мы определяем понятие производных высшего порядка, даем краткое описание производной второго порядка и показываем, как работает неявное дифференцирование для производных высшего порядка.

Логарифмическое дифференцирование. В этом разделе мы обсудим логарифмическое дифференцирование. Логарифмическое дифференцирование дает альтернативный метод дифференцирования произведений и частных (иногда более простой, чем использование правила произведения и частного). Однако более важным является тот факт, что логарифмическое дифференцирование позволяет нам дифференцировать функции, имеющие вид одной функции, возведенной в другую функцию, т.е. есть переменные как в основании, так и в показателе степени функции.

Математические онлайн-заметки Pauls

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Добро пожаловать в мои онлайн-уроки и заметки по математике. Целью этого сайта является предоставление полного набора бесплатных онлайновых (и загружаемых) заметок и/или учебных пособий для занятий, которые я преподаю в Университете Ламара. Я пытался написать заметки/учебники таким образом, чтобы они были доступны для всех, кто хочет изучить предмет, независимо от того, посещаете ли вы мои занятия или нет. Другими словами, они не предполагают, что у вас есть какие-либо предварительные знания, кроме стандартного набора предварительных материалов, необходимых для этого класса. Другими словами, предполагается, что вы знаете алгебру и тригонометрию до прочтения примечаний к Исчислению I, знаете исчисление I до прочтения примечаний к Исчислению II, и т. д. . Предположения о вашем прошлом, которые я сделал, даны с каждым описанием ниже.

Я хотел бы поблагодарить Шейна Ф., Фреда Дж., Майка К. и Дэвида А. за все опечатки, которые они нашли и прислали мне! Я пытался проверить эти страницы и найти как можно больше опечаток, однако просто невозможно обнаружить их все, когда вы также являетесь человеком, написавшим материал. Фред, Майк и Дэвид обнаружили довольно много опечаток, которые я пропустил, и были достаточно любезны, чтобы отправить их мне. Еще раз спасибо, Фред, Майк и Дэвид!

Если вы являетесь одним из моих нынешних студентов и ищете домашние задания, у меня есть набор ссылок, которые приведут вас на нужные страницы, перечисленные здесь.

В настоящее время я получил заметки/учебники для своего класса алгебры (математика 1314), исчисления I (математика 2413), исчисления II (математика 2414), исчисления III (математика 3435) и дифференциальных уравнений (математика 3301) онлайн. У меня также есть пара обзоров/дополнений. Среди обзоров/дополнений, которые у меня есть, есть обзор алгебры/триггеров для моих студентов, изучающих математику, учебник для начинающих по комплексным числам, набор распространенных математических ошибок и несколько советов о том, как изучать математику.

Я также сделал большинство страниц этого сайта доступными для скачивания. Эти загружаемые версии представлены в формате pdf. Каждая тема на этом сайте доступна для полной загрузки, а в случае очень больших документов я также разделил их на более мелкие части, которые в основном соответствуют каждой из отдельных тем. Чтобы получить загружаемую версию любой темы, перейдите к этой теме, а затем в меню «Загрузить » вам будет предложена возможность загрузить тему.

Вот полный список всех тем, которые в настоящее время доступны на этом сайте, а также краткое описание каждой из них.

Шпаргалки и таблицы

Шпаргалки по алгебре — это столько общих фактов, свойств, формул и функций по алгебре, сколько я только мог придумать. Также включена страница с распространенными ошибками по алгебре. Доступны две версии шпаргалки. Один полноразмерный и в настоящее время состоит из четырех страниц. Другая версия представляет собой сокращенную версию, которая содержит точно такую же информацию, как и полная версия, за исключением того, что она только что была уменьшена, поэтому две страницы печатаются на лицевой стороне, а две страницы — на обратной стороне одного листа бумаги.

Шпаргалки по триггерам. Вот набор общих фактов, свойств и формул триггеров. Единичный круг (полностью заполненный) также включен. Доступны две версии шпаргалки. Один полноразмерный и в настоящее время состоит из четырех страниц. Другая версия представляет собой сокращенную версию, которая содержит точно такую же информацию, как и полная версия, за исключением того, что она только что была уменьшена, поэтому две страницы печатаются на лицевой стороне, а две страницы — на обратной стороне одного листа бумаги.

Шпаргалки по математическому анализу. Это серия памятных листов по математическому анализу, которые охватывают большую часть стандартного курса по математическому анализу I и несколько тем из курса по математическому анализу II. Здесь есть четыре разных шпаргалки. В одном содержится вся информация, в другом — только информация о лимитах, в третьем — только информация о производных, а в последнем — только информация об интегралах. Каждая шпаргалка поставляется в двух версиях. Один полноразмерный, а другой уменьшенный, с точно такой же информацией, что и полноразмерная версия, которая печатает две страницы на передней и / или обратной стороне каждой страницы бумаги.

Общие производные и интегралы. Здесь представлен набор общих производных и интегралов, которые регулярно используются в исчислении I или исчислении II класса. Также включены напоминаний о нескольких методах интеграции. здесь доступны две версии шпаргалки. Один полноразмерный и в настоящее время состоит из четырех страниц. Другая версия представляет собой сокращенную версию, которая содержит точно такую же информацию, как и полная версия, за исключением того, что она только что была уменьшена, поэтому две страницы печатаются на лицевой стороне, а две страницы — на обратной стороне одного листа бумаги.

Таблица преобразований Лапласа. Вот список преобразований Лапласа для класса дифференциальных уравнений. В этой таблице приведены многие из часто используемых преобразований и формул Лапласа. В настоящее время он состоит из двух страниц, причем первая страница представляет собой преобразования Лапласа, а вторая — некоторую информацию/факты о некоторых записях.

Заметки для занятий

Во всех классах, за исключением дифференциальных уравнений, есть практические задачи (с решениями), которые вы можете использовать на практике, а также набор задач с заданиями (без решений/ответов), которые могут использовать преподаватели, если они желание.

Алгебра (математика 1314) [Примечания] [Практические задачи] [Задачи с заданиями] — Темы, включенные в этот набор заметок/учебника:

Предварительные занятия — свойства экспонент, рациональные экспоненты, отрицательные экспоненты, радикалы, многочлены, факторинг, рациональные выражения, комплексные числа
Решение уравнений и неравенств — Линейные уравнения, Квадратные уравнения, Заполнение квадрата, Квадратная формула, Применение линейных и квадратных уравнений, Приведение к квадратной форме, Уравнения с радикалами, Линейные неравенства, Полиномиальные и рациональные неравенства, Абсолютные уравнения и неравенства.
Графики и функции — графические линии, окружности и кусочные функции, определение функции, обозначение функции, композиция функций, обратные функции.
Общие графики — параболы, эллипсы, гиперболы, абсолютное значение, квадратный корень, постоянная функция, рациональные функции, сдвиги, отражения, симметрия.
Полиномиальные функции — деление многочленов, нули/корни многочленов, нахождение нулей многочленов, построение графиков многочленов, дроби.
Экспоненциальные и логарифмические функции — экспоненциальные функции, логарифмические функции, решение экспоненциальных функций, решение логарифмических функций, приложения.
Системы уравнений — метод подстановки, метод исключения, расширенная матрица, нелинейные системы.

Заметки/учебник по алгебре предполагают, что вы уже знакомы с основами алгебры. В частности, предполагается, что разделы показателей и факторинга будут для вас скорее обзором. Кроме того, предполагается, что вы знакомы с основами графических уравнений. Графики конкретных типов уравнений подробно описаны в примечаниях, однако предполагается, что вы понимаете базовую систему координат и то, как наносить точки на график.

Исчисление I (Математика 2413) [Примечания] [Практические задачи] [Задачи с заданиями] — Темы, включенные в этот набор заметок/учебника:

Обзор алгебры и триггеров — триггерные функции и уравнения, экспоненциальные функции и уравнения, логарифмические функции и уравнения.
Пределы — концепции, определение, вычисления, односторонние пределы, непрерывность, пределы, включающие бесконечность, правило L’Hospitals
Производные — определение, интерпретации, производные формулы, степенное правило, правило произведения, частное правило, цепное правило, производные высшего порядка, неявное дифференцирование, логарифмическое дифференцирование, производные триггерных функций, экспоненциальные функции, логарифмические функции, обратные триггерные функции и гиперболический триггер Функции.
Применение производных — связанные скорости, критические точки, минимальные и максимальные значения, возрастающие/убывающие функции, точки перегиба, вогнутость, оптимизация
Интегрирование — Определение, Неопределенные интегралы, Определенные интегралы, Правило подстановки, Вычисление определенных интегралов, Основная теорема исчисления
Применение интегралов — среднее значение функции, площадь между кривыми, тела вращения, работа.

Заметки/руководство по Исчислению I предполагают, что у вас есть практические знания по Алгебре и Тригонометрии. Есть некоторый обзор нескольких тем по алгебре и триггерам, но по большей части предполагается, что у вас есть приличный опыт в алгебре и триггерах. Эти примечания предполагают отсутствие предварительных знаний исчисления.

Исчисление II (Math 2414) [Примечания] [Практические задачи] [Задачи с заданиями] — Темы, включенные в этот набор заметок/учебника:

Методы интегрирования — интегрирование по частям, интегралы с триггером Функции, Подстановки триггеров, Интегрирование с использованием дробей, Интегралы С участием корней, Интегралов с участием квадратов, Стратегия интегрирования, Неправильный Интегралы, сравнительный тест для несобственных интегралов и аппроксимация определенного Интегралы.
Применение интегралов — длина дуги, площадь поверхности, центр масс/центроид, гидростатическое давление и сила, вероятность.
Параметрические уравнения и полярные координаты — параметрические уравнения и кривые, расчет с помощью параметрических уравнений (касательные, площади, длина дуги и площадь поверхности), полярные координаты, расчет с полярными координатами (касательные, площади, длина дуги и площадь поверхности).
Последовательности и ряды — Последовательности, ряды, сходимость/расхождение рядов, абсолютные ряды, интегральный тест, сравнительный тест, предельный сравнительный тест, тест чередующихся рядов, тест отношений, тест корня, оценка значения ряда, степенной ряд, ряд Тейлора , Биномиальная серия
Векторы — Основы, Величина, Единичный вектор, Арифметика, Скалярный продукт, Крест Продукт, Проекция
Трехмерная система координат — уравнения прямых, уравнения плоскостей, квадратичные поверхности, функции многих переменных, векторные функции, пределы, производные и интегралы векторных функций, касательные векторы, нормальные векторы, бинормальные векторы, кривизна, цилиндрические координаты, сферические Координаты

Примечания/руководство по исчислению II предполагают, что у вас есть практические знания исчисления I, включая пределы, производные и интегрирование (вплоть до базовой замены). Также предполагается, что вы достаточно хорошо знаете Trig. Некоторые темы в значительной степени зависят от триггера и знания триггерных функций.

Исчисление III (Math 3435) [Примечания] [Практические задачи] [Задачи с заданиями] — Темы, включенные в этот набор заметок/учебника:

Трехмерная система координат — уравнения прямых, уравнения плоскостей, квадратичные поверхности, функции многих переменных, векторные функции, пределы, производные и интегралы векторных функций, касательные векторы, векторы нормалей, бинормальные векторы, кривизна, цилиндрические координаты , Сферические координаты
Частные производные — пределы, частные производные, частные производные высшего порядка Производные, дифференциалы, цепное правило, производные по направлению, градиент.
Применение частных производных — касательная плоскость, нормальная линия, относительный экстремум, абсолютный экстремум, оптимизация, множители Лагранжа.
Множественные интегралы — повторные интегралы, двойные интегралы, двойные интегралы в полярных координатах, тройные интегралы, тройные интегралы в цилиндрических координатах, тройные интегралы в сферических координатах, замена переменных, площадь поверхности.
Линейные интегралы — векторные поля, линейные интегралы по длине дуги, линейные интегралы по отношению к x и y , линейные интегралы векторных полей, основная теорема линейных интегралов, консервативные векторные поля, потенциальные функции, теорема Грина, Завиток, Дивергенция.
Поверхностные интегралы — параметрические поверхности, поверхностные интегралы, поверхностные интегралы векторных полей, теорема Стокса, теорема о дивергенции.

Заметки/руководство по исчислению III предполагают, что у вас есть практические знания исчисления I, включая пределы, производные и интегрирование. Также предполагается, что читатель хорошо знаком с несколькими темами Calculus II, включая некоторые методы интегрирования, параметрические уравнения, векторы и знание трехмерного пространства.

Дифференциальные уравнения (Math 3301) [Заметки]

— Темы, включенные в этот набор заметок/учебника:

Дифференциальные уравнения первого порядка — линейные уравнения, уравнения с разделителями, точные уравнения, равновесные решения, задачи моделирования.
Дифференциальные уравнения второго порядка. Однородные и неоднородные дифференциальные уравнения второго порядка, фундаментальный набор решений, неопределенные коэффициенты, вариации параметров, механические колебания
Преобразования Лапласа — Определение, Обратные преобразования, Ступенчатые функции, Функции Хевисайда, Дельта-функция Дирака, Решение IVP, Неоднородная IVP, Непостоянный коэффициент IVP, Интеграл свертки.
Системы дифференциальных уравнений — матричная форма, собственные значения/собственные векторы, фазовая плоскость, неоднородные системы, преобразования Лапласа.
Решения серии — Решения серии, Дифференциальные уравнения Эйлера.
Дифференциальные уравнения высшего порядка — n ^-й-й порядок дифференциальных уравнений, неопределенные коэффициенты, вариация параметров, 3 x 3 системы дифференциальных уравнений.
Краевые задачи и ряды Фурье — Краевые задачи, собственные значения и собственные функции, ортогональные функции, синусоидальные ряды Фурье, косинусные ряды Фурье, ряды Фурье.
Дифференциальные уравнения в частных производных — уравнение теплопроводности, волновое уравнение, уравнение Лапласа, разделение переменных.

Эти примечания предполагают отсутствие предварительных знаний дифференциальных уравнений. Однако требуется хорошее понимание исчисления. Это включает в себя практические знания дифференциации и интеграции.

Обзоры и дополнения

Обзор алгебры/триггеров — это обзор алгебры и триггеров это было первоначально написано для моих студентов исчисления I. Это все еще ориентировано в основном по отношению к студентам, изучающим исчисление, со случайными комментариями о том, как тема будет использоваться в классе исчисления. Тем не менее, кому нужен обзор некоторых базовой алгебры, тригонометрических, экспоненциальных функций и логарифмов следует найти информация об использовании.

Не все темы, изучаемые на занятиях по алгебре или триггерам, рассматриваются в этом обзор. В основном я освещал темы, которые имеют особое значение для студентов. на уроке исчисления. Я включил пару тем, которые не так важны на занятиях по математическому анализу, но иногда у студентов возникают проблемы с этим. По мере того, как будет время, я буду добавлять и другие разделы.

Обзор представляет собой набор задач с первым решением, содержащим подробную информацию о том, как работать с этим типом задач. Более поздние решения обычно не такие подробные, но могут содержать дополнительную/новую информацию по мере необходимости.

Учебник по комплексным числам. Это краткое введение в некоторые основные идеи, связанные с комплексными числами. Рассматриваемые темы представляют собой краткий обзор арифметики с комплексными числами, комплексного сопряжения, модуля, полярной и экспоненциальной формы, а также вычислительных мощностей и корней комплексных чисел.

Обратите внимание, что в этом учебнике предполагается, что вы, по крайней мере, видели некоторые комплексные числа до чтения. Цель этого документа — немного выйти за рамки того, что видит большинство людей, впервые знакомящихся с комплексными числами, скажем, на уроках алгебры в колледже. Кроме того, этот документ никоим образом не претендует на то, чтобы дать полное представление о комплексных числах, и я не охватываю все используемые концепции (это сам по себе целый класс).

Распространенные математические ошибки. Как и в случае с алгеброй/триггером, просмотрите это изначально был написан для моего класса исчисления I. Однако только один из пяти разделы, которые я дал здесь, непосредственно касаются темы исчисления. другие четыре раздела представляют собой более общие ошибки или охватывают ошибки алгебры и триггеров. В первых четырех разделах есть пара примеров исчисления, но в во всех этих случаях я также пытался привести примеры, не связанные с исчислением.