Презентация преобразование выражений содержащих радикалы 11 класс мордкович – Презентация к уроку по алгебре (11 класс) на тему: Презентации 11 класс
Презентация к уроку по алгебре (11 класс) на тему: Презентации 11 класс
Слайд 1
Статистическая обработка данныхСлайд 2
Статистика (лат . « status ») состояние дел это отрасль знаний, в которой излагаются общие вопросы сбора, измерения и анализа массовых статистических (количественных или качественных) данных; изучение количественной стороны массовых общественных явлений в числовой форме.
Слайд 3
результат количество результатов результат количество результатов результат кол ─ во результатов Многоугольник распределений Гистограмма распределений
Слайд 4
результат количество результатов результат количество результатов « »: « »: « »: « »: Круговая диаграмма
Слайд 5
Этапы статистической обработки данных 3. Построить графики распределения данных 4. Получить паспорт данных измерения объём , размах , мода измерения, среднее (или среднее арифметическое ) 1. Упорядочить и сгруппировать данные измерения 2. Составить таблицу распределения данных
Слайд 6
результат количество результатов результат количество результатов ‒ объём измерения ‒ размах измерения ‒ мода измерения ‒ среднее
Слайд 7
результат количество результатов результат количество результатов варианта кратность ряд данных сгруппированный ряд данных Средняя варианта — медиана измерения.
Слайд 8
объём : размах : медиана : среднее : Пример: На уроке физкультуры 14 школьников прыгали в высоту, а учитель записывал их результаты: . Получить сгруппированный ряд данных и таблицу распределения. Найти объём, размах, моду, среднее и медиану измерени я . Решение: варианта кратность варианта кратность мода :
Слайд 9
варианта кратность варианта кратность варианта кратность
Слайд 10
варианта сумма кратность частота варианта сумма кратность частота
Слайд 11
варианта сумма кратность частота частота, варианта сумма кратность частота
Слайд 12
Пример: Составить таблицу распределения данных и таблицу распределения частот. Решение: варианта сумма кратность частота частота, варианта сумма кратность частота варианта кратность
Слайд 13
На испытательном стенде оружейного завода пристреливают готовые ружья, т.е . уточняют и корректируют их прицел. Выстрелы Ружьё А Ружьё Б Выстрелы Ружьё А Ружьё Б Среднее для ружья А : Среднее для ружья Б :
Слайд 14
Числовую характеристику данных измерения, отвечающую за разброс данных вокруг среднего значения, называют дисперсией . — средним квадратическим отклонением . Алгоритм вычисления дисперсии : среднее значение ; о тклонение данных от : ; квадраты отклонений: ;
Слайд 15
Выстрелы из ружья А (среднее: ) результат отклонение квадрат отклонения результат отклонение квадрат отклонения
Слайд 16
Выстрелы из ружья Б (среднее: ) результат отклонение квадрат отклонения результат отклонение квадрат отклонения
Слайд 17
Выстрелы из ружья А (среднее: ) результат отклонение квадрат отклонения результат отклонение квадрат отклонения Выстрелы из ружья Б (среднее: ) результат отклонение квадрат отклонения результат отклонение квадрат отклонения
Слайд 18
Этапы статистической обработки данных 3. Построить графики распределения данных 4. Получить паспорт данных измерения объём , размах , мода измерения, среднее (или среднее арифметическое ) 1. Упорядочить и сгруппировать данные измерения 2. Составить таблицу распределения данных
Слайд 19
Каждое значение, полученное в ходе измерений, называют вариантой . Число повторений данной варианты, называют её кратностью .
Слайд 20
Числовую характеристику данных измерения, отвечающую за разброс данных вокруг среднего значения, называют дисперсией . — средним квадратическим отклонением . Алгоритм вычисления дисперсии : среднее значение ; о тклонение данных от : ; квадраты отклонений: ;
nsportal.ru
«Свойства корня n-ой степени. Преобразование выражений, содержащих радикалы».
Открытый урок в 11 классе по теме:
«Свойства корня n-ой степени. Преобразование выражений, содержащих радикалы».

Учитель ГБОУ ЦО № 1602
г. Москвы
Гайваль О. Н.
Урок в 11 классе по теме: «Свойства корня n-ой степени. Преобразование выражений, содержащих радикалы».
Тип урока: урок обобщающего повторения.
Цели:
Обобщение знаний и умений по данной теме; подготовка к контрольной работе.
Развитие логического мышления, интуиции, умения устанавливать причинно-следственные связи, математической речи.
Воспитание умения проводить оценку и самооценку знаний и умений, высокой работоспособности и организованности, аккуратности ведения записей в тетради и на доске.
Ход урока.
Устный счёт.
Фронтальная работа с классом. Задания через проектор показаны на экране.
34, 43, 24, 53, 25, 33,
(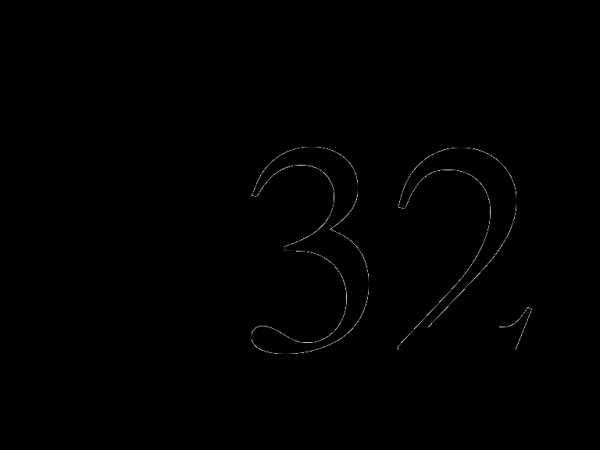 )2, (
)2, (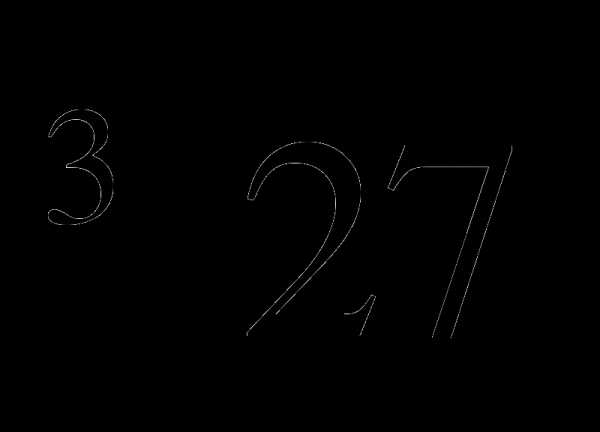 )3, (
)3, (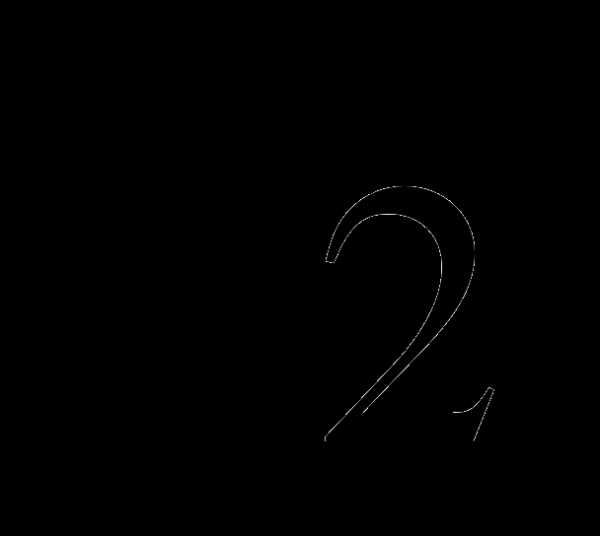 )8, (
)8, (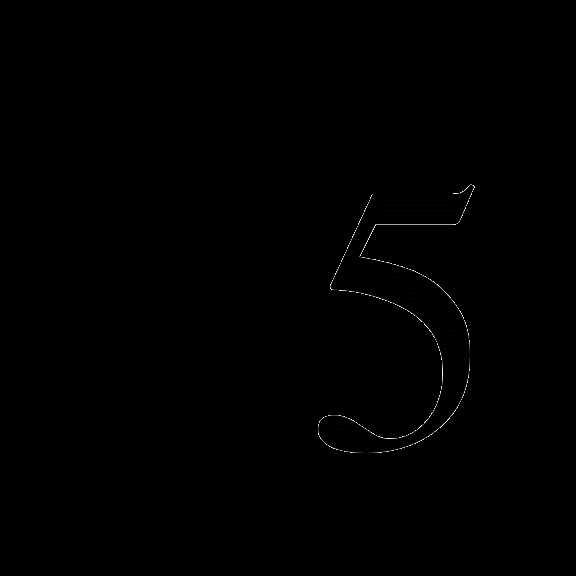 )4, (
)4, (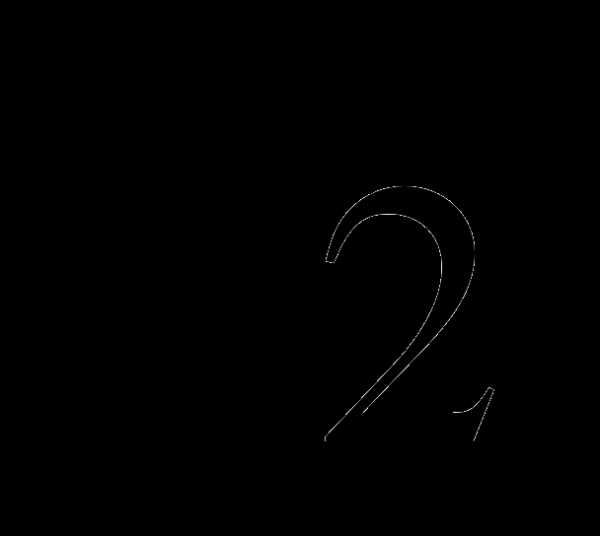 ) 10, (
) 10, ( )4, (
)4, (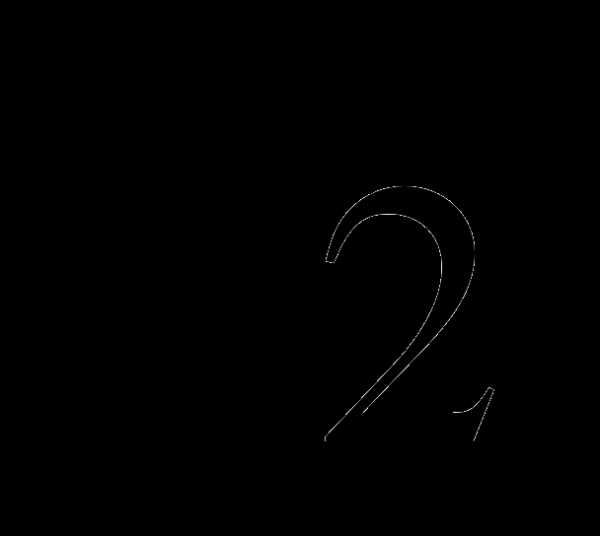 )6,
)6,
 ,
, 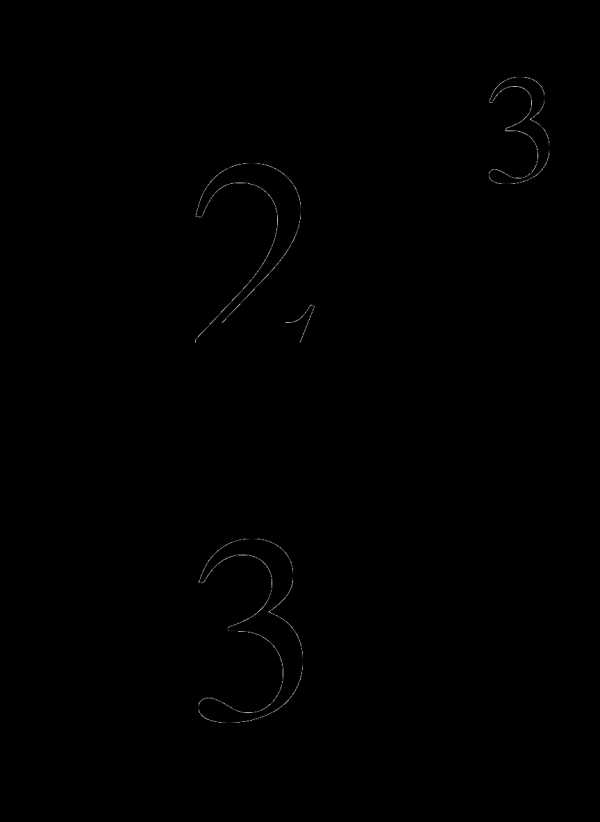 ,
,  ,
,  ,
, 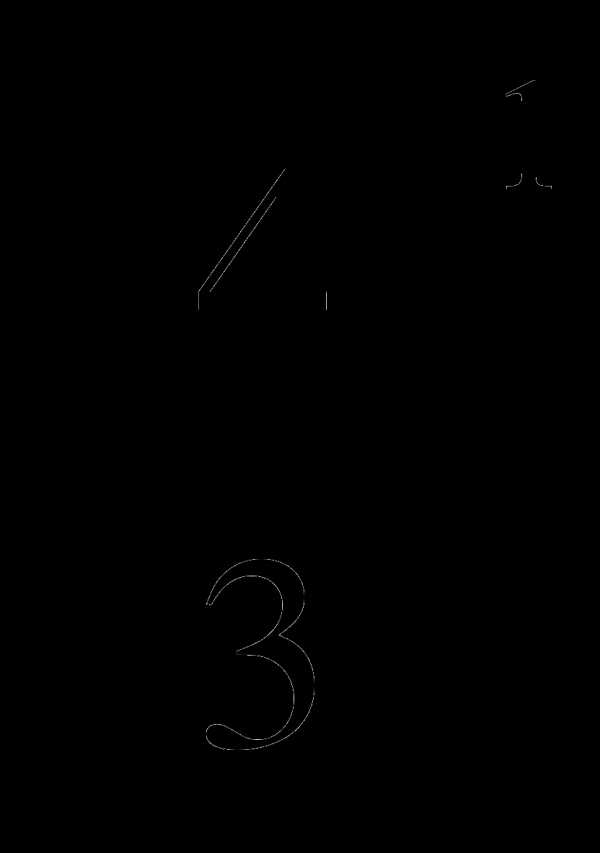 ,
, 
Работа в группах.
Опрос теории по свойствам корня n-ой степени. Опрос ведут консультанты с выставлением оценок.
Работа у доски.
№ 1105 (б, г), 1188 (а, б).
Упростить выражение: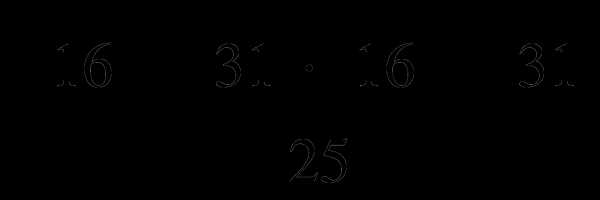
Тест. Проверка применять свойства на практике. После окончания работы проводится взаимопроверка в парах.
1. Упростите:  .
.
а) а; б) 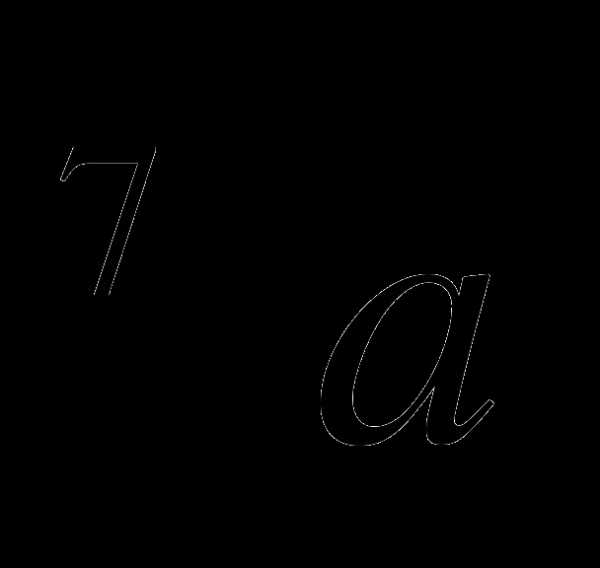 ; в) 1; г)
; в) 1; г) 
2. Вычислите: 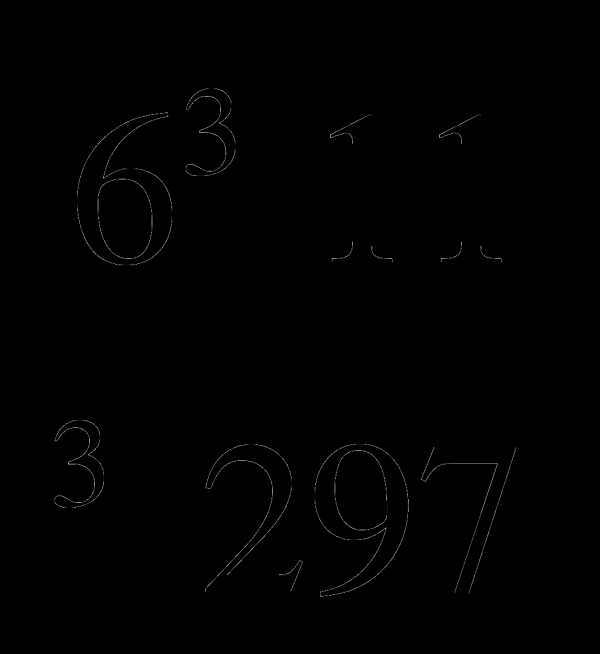 .
.
а)  , б) 2, в)
, б) 2, в) 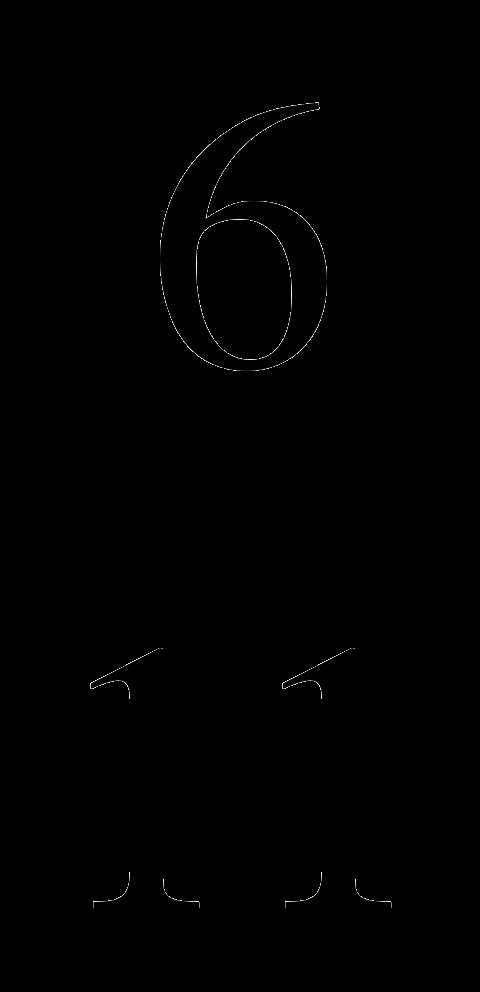 , г) 3.
, г) 3.
3. Вычислите: 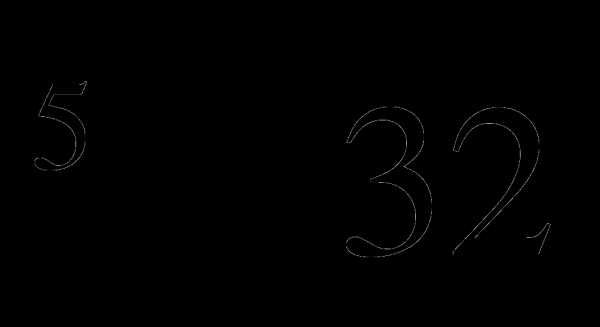 —
— 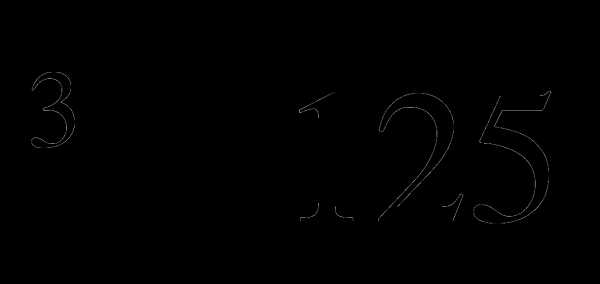 .
.
а) -7, б) -3, в) 3, г) 7.
4. Найдите значение выражения: .
а) 12, б) 6, в) 3, г) 9.
5. Задайте формулой функцию, график которой изображён на рисунке:
а) у = 
 ,
,в) у = 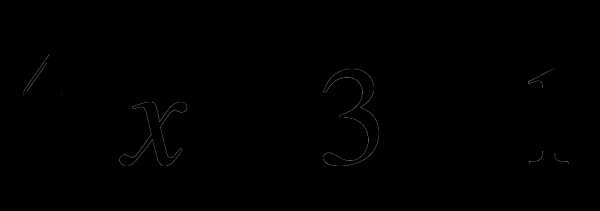 , г) у =
, г) у = 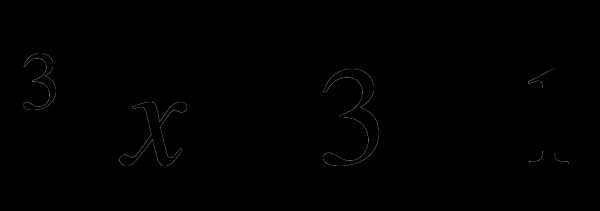 .
.
6. Укажите область значений функции у =  .
.
а) (-∞; +∞), б) [0; +∞),
в) множество положительных чисел, г) [ — 3; +∞).
7. Вычислите: 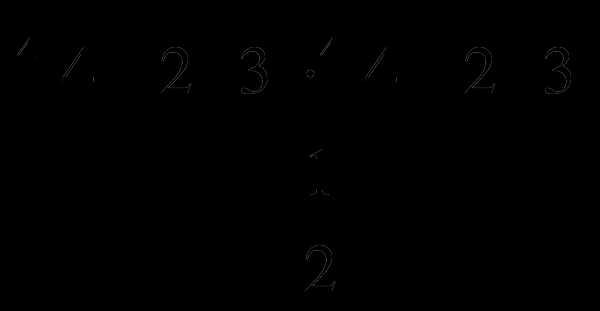 .
.
а) 8, б) 4, в) 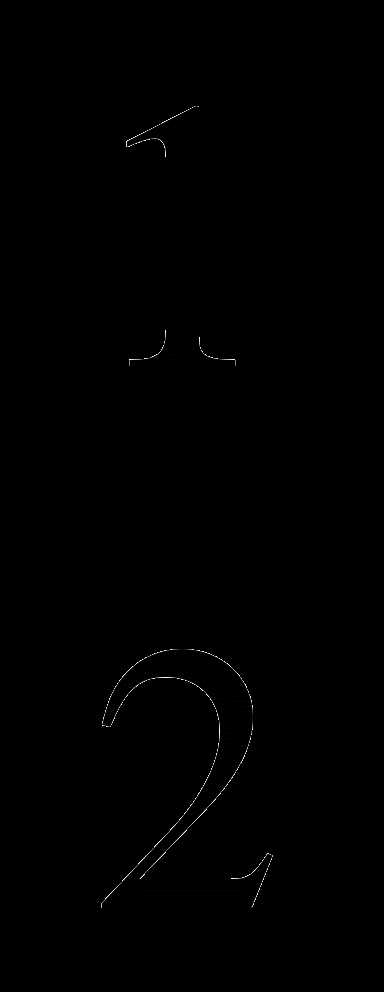 , г) 2.
, г) 2.

Вариант 2.
1. Упростите: 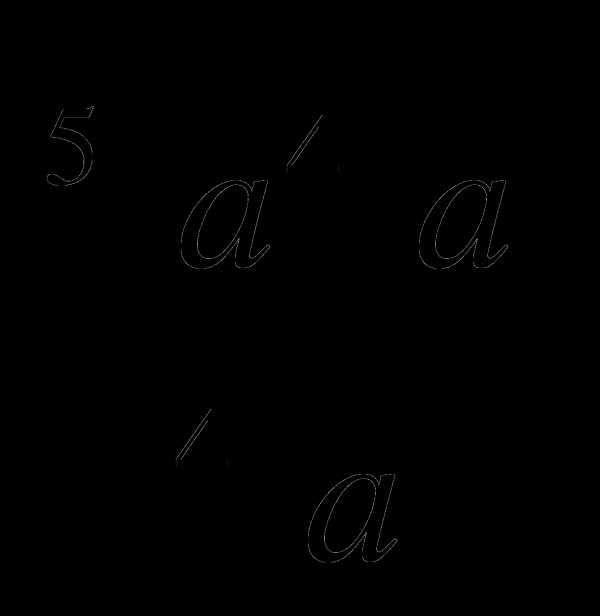 .
.
а)  ; б)
; б) 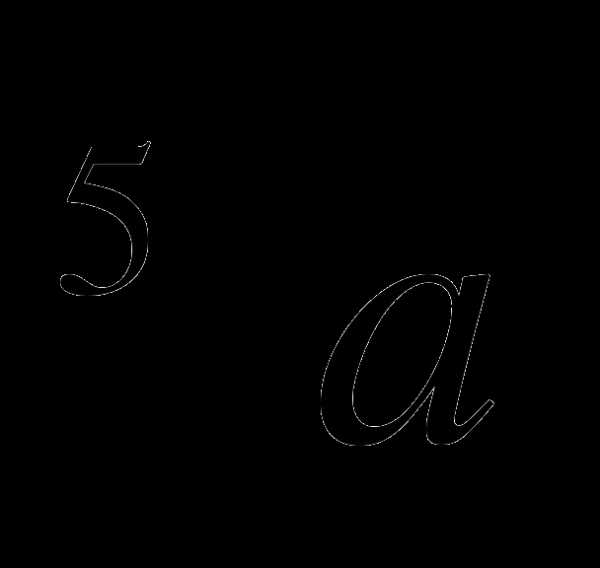 ; в) а; г). 1
; в) а; г). 1
2. Вычислите:  .
.
а) 1, б) 3, в) 0,3 , г) 1,5.
, г) 1,5.
3. Вычислите: 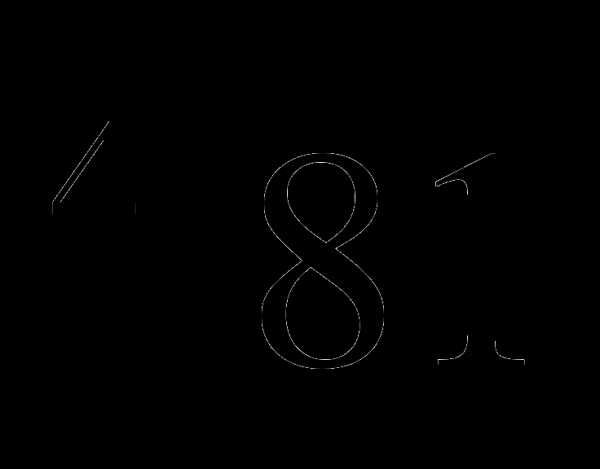
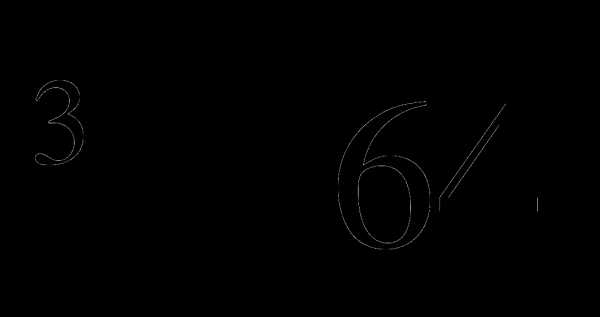 .
.а) -1, б) 7, в) -7, г) 1.
4. Найдите значение выражения: .
а) 15, б) 10, в) 30, г) 6.
5. Задайте формулой функцию, график которой изображён на рисунке:
а) у =  , б) у =
, б) у =  ,
,
в) у =  , г) у =
, г) у =  .
.
6. Укажите область значений функции у = 
а) (-∞; +∞), б) [1; +∞),
в) множество положительных чисел, г) [ 0; +∞).
7. Вычислите: 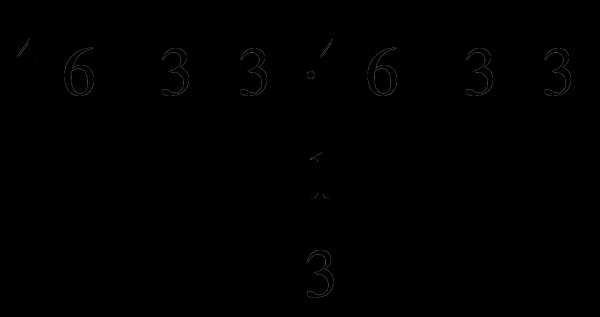 .
.
а) 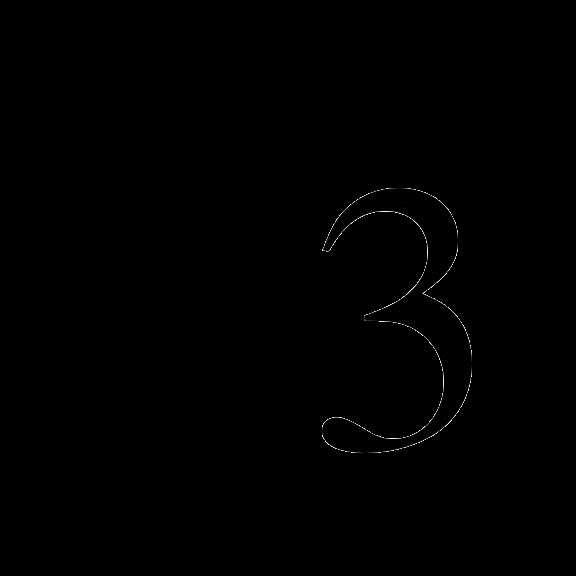 , б) 1, в) 3, г)
, б) 1, в) 3, г) .
.

5. Домашнее задание. № 1189, № 1195 (а, б), 1102 (а, б).
Ответы и решения
1. . Ответ: в).
2. 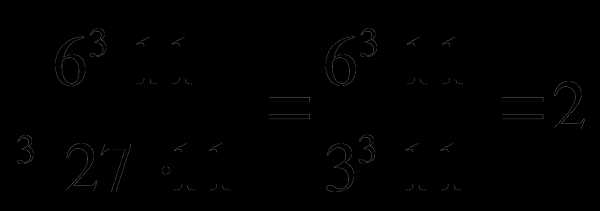 . Ответ: б).
. Ответ: б).
3. -2 –(-5) = -2 + 5 = 3. Ответ: в).
4. . Ответ: б).
5. Ответ: г).
6. Ответ: б).
7. .
Ответ: г).
Вариант 2.
1. . Ответ: г).
2. . Ответ: в).
3. 3 – (-4) = 3 + 4 = 7. Ответ: б).
4. . Ответ: в).
5. Ответ: а).
6. Ответ: г).
7. .
Ответ: в).
infourok.ru
Преобразование выражений, содержащих радикалы
Вопросы занятия:
· ввести понятие «радикал»;
· рассмотреть примеры, в которых выполняются преобразования выражений с радикалами.
Материал урока
На прошлых уроках мы с вами познакомились с корнем n—ой степени из а, рассмотрели основные свойства корня. На сегодняшнем уроке мы будем решать задачи на преобразование выражений с радикалами, используя все, что мы изучали на предыдущих уроках.
Повторим основные понятия.
Корнем n-ой степени из неотрицательного числа a называют такое неотрицательное число, при возведении которого в степень n получается число а.
Корнем нечётной степени n-ой из отрицательного числа а называют такое отрицательное число, при возведении которого в степень n получается а.
Обозначают:
Число а – это подкоренное число, число n – показатель корня.
Перечислим основные свойства
Прежде чем приступить к решению упражнений, давайте отметим некоторые важные моменты.
Верно ли что:
Нет, так как, например:
Верно ли что:
Нет, так как, например:
В данном случае справедлива формула:
Эта же формула справедлива для любого чётного показателя степени.
Для нечётного показателя степени имеем другую формулу.
Рассмотрим несколько примеров.
Пример.
Пример.
Пример.
Пример.
Пример.
Пример.
Пример.
Пример.
Пример.
Пример.
Ещё раз хотелось бы обратить ваше внимание, что решая задачи с радикалами, в первую очередь мы должны обратить внимание на то, какой знак может иметь подкоренное выражение. И только после этого приступать к преобразованию выражений.
videouroki.net
Методическая разработка по алгебре (11 класс) на тему: Конспект урока по алгебре и началам анализа в 11 классе «Степень с рациональным показателем», с презентацией.
Конспект
урока по алгебре и началам анализа в 11 классе
по теме: «Степень с рациональным показателем»
Тип урока: урок рефлексии (повторительно-обобщающий урок)
Вид урока: Урок — практикум, с применением ИКТ.
Оборудование урока, средства обучения: компьютер, интерактивная доска, оценочные листы, карточки с заданиями, дешифраторами, опорные сигнальные схемы, презентация.
Цели урока (слайд 2):
Обучающие:
- Повторить и обобщить знания учащихся по теме “Степень с рациональным показателем”.
- Актуализировать опорные знания учащихся.
- Проконтролировать уровень усвоения материала.
- Ликвидировать пробелы в знаниях и умениях учащихся.
- Формировать навыки самоконтроля учащихся.
Развивающие:
- Развивать познавательную активность учащихся.
- Развивать умение применять знания на практике.
Воспитывающие:
- Воспитывать заинтересованность каждого ученика в работе, сознательный интерес к предмету, к истории математики.
План урока.
- Сообщение темы и цели урока (2 мин.).
- Актуализация знаний с опорой на сигнальную схему (5 мин.).
- Устная работа «Математическая разминка» (6 мин.).
- Исторический момент. Решение уравнений с использованием свойств степени (8 мин.).
- Преобразование выражений, содержащих радикалы и степени с дробным показателем.
(15 мин).
- Самостоятельная работа на основе заданий из ЕГЭ (5 мин).
- Задание на дом, комментирование (2 мин.).
- Подведение итогов урока. (2 мин.).
ХОД УРОКА
I. Организационный момент. Сообщение целей урока.
Учитель:
Мы закончили изучение темы “Степень с рациональным показателем и её свойства” и сегодня повторим и систематизируем те знания, которые были приобретены вами в результате изучения темы. Ваша задача — показать, как вы усвоили изученный материал, и как вы умеете применять полученные знания при решении конкретных задач.
На столе у каждого из вас есть оценочный лист. В него вы будете вносить свою оценку за каждый этап урока. В конце урока вы выставите средний балл за урок.
Оценочный лист
Ф/И/ учащегося__________________________________________
Задание | Актуализация знаний (повторение теории) | Математическая разминка. (устная работа) | Исторический момент (решение уравнений с использованием свойств степени) | Преобразование выражений, содержащих радикалы и степени | Проверь себя (с\р) | Итого |
Оценка | — | — |
II. Актуализация знаний.
Проверка знания учащимися основных понятий и правил, умений объяснять их сущность, аргументировать свои суждения.
Ученикам предлагается на индивидуальных листах заполнить таблицу.
Потом учащиеся выставляют себе отметки в оценочном листе, сравнив ответы с опорной сигнальной схемой.
Критерий оценивания: 2 верных ответа – 1 балл.
Предлагается заполнить таблицу индивидуально (слайд 3):
№ п/п | Вопрос | Ответ | Ограничения для: |
1 | Закончи определение: степенью числа а с рациональным показателем r =m/n называется ……. | Число √ a | m- целое, а>0, n- натуральное, n>1 |
2 | Каким может быть число а в степени r | больше 0 | а>0, r- рациональное |
3 | Чему равно: 0 в степени r? | 0 | r>0 |
4 | Чему равно: 0 в степени r, где r | не имеет смысла | |
5 | Чему равно а в степени 0? | 1 | а>0 |
6 | Запишите свойства степени с рациональным показателем. | a ∙ a = a | а>0; b>0; n,s — рациональные |
a : a = a | |||
( a ) = a | |||
(ab) = a b | |||
(a/b) = a /b | |||
a n>0; a > b при n | если 0 n — рациональное | ||
а > а , при а>1; а 0 | n– рациональное, n > s |
III. Устная работа «Математическая разминка»
Учитель: Применим знание определения и свойств степени с рациональным показателем, выполнив следующие задания устно.
1. Представить выражение х22 в виде произведения двух степеней с основанием х, если один из множителей равен:
(слайд 4)
х2, х5,5, х1/4, х1,2, х0
2. Упростить:
(слайд 5)
а) х 1/2∙ √х;
б) у 5/8∙ у 1/4 : у 1/8 ;
в) с 1,4 с -0,3 с 2,9.
3. Вычислите:
(слайд 6)
а) 4-2 :; б) 9-4 : 3-6 ; в) .
4. Имеет ли смысл выражение:
(слайд 7)
2; (-5); (-0,2); 0; 0 -10.
5. Сравните:
(слайд 8)
и .
Учитель:
А сейчас самостоятельно вычислите устно и составьте слово, используя дешифратор. (слайд 9)
Выполнив это задание, вы, ребята, узнаете фамилию немецкого математика, который ввел термин — “показатель степени”.
1) (-8)1/3; 2) 811/2; 3) (3/5)-1; 4) (5/7)0 .
5) 27-1/3; 6) (2/3)-2; 7) 161/2 ∙ 1251/3 .
Слово: 1234567 (Штифель)
Л | Т | Н | Р | Ш | О | Ь | И | Е | Ф | К | А | Д | Ю |
9/4 | 9 | 5 | 11 | -2 | 4/9 | 20 | 5/3 | 1/3 | 1 | 3 | 8 | 64 | 2 |
(слайд 10)
IV. Исторический момент. (слайд 11)
Задание. Решить уравнения и составить слово, используя дешифратор. Каждый учащийся получает индивидуальное задание.
Карточка № 1
1) х1/3=4; 2) у-1=3/5; 3) а1/2= 2/3; 4) х-0,5 х1,5 = 1; 5) у1/3 =2
6) а2/7а12/7 = 25; 7) а1/2 : а = 1/3.
Слово: 1234567 (Диофант)
Карточка № 2
1) х1/3=4; 2) у-1= 3; 3) ( х+6)1/2 = 3; 4) у1/3 =2; 5) (у-3)1/3=2;
6) а1/2 : а = 1/3
Cлово: 123456 (Декарт)
Карточка № 3
1) а2/7а12/7 = 25; 2) (х-12)1/3 =2; 3) х-0,7 х3,7 = 8;
4) а1/2 : а = 1/3; 5) а1/2= 2/3.
Cлово: 123451 (Ньютон)
(слайд 12)
Дешифратор
Л | Т | Н | Р | Ш | О | Ь | И | Е | Ф | К | А | Д | Ю |
9\4 | 9 | 5 | 11 | -2 | 4\9 | 20 | 5\3 | 1\3 | 1 | 3 | 8 | 64 | 2 |
Учащиеся выставляют себе отметки в оценочном листе, используя критерий оценивания «один неправильный ответ – минус один балл».
Историческая справка: (учитель)
(слайд 13)
Диофант — греческий учёный, живший в III веке, в своей книге «Арифметика» ввёл символы для первых шести степеней неизвестного и обратных им величин.
Рене Декарт – жил во Франции, в XVII в, ввёл современные обозначения степени (типа а4, а5 ).
Исаак Ньютон – английский математик (1643–1727), ввёл современные определения и обозначения степени с нулевым, отрицательным и дробным показателем.
V. Преобразование выражений, содержащих радикалы и степени с дробным показателем. (15 мин.)
Задание №51 а), № 49 г),№ 47 г), стр.282 — 283, учебник для 10-11 класса под ред. А.Н.Колмогорова. Решение заданий у доски с объяснением, «сильными» учениками.
(слайд 14)
VI. Самостоятельная работа на основе заданий из ЕГЭ. (10 мин.)
(слайд 15)
Вариант 1
1. Вычислить: по1 баллу
а) 272/3; б) 160,75 + 4 ∙ ( 1/25)1\2
2. Упростить выражение: по 2 балла
а) х1/2 ∙ х 3/4 ; б)( х-5/6 )-2/3;
в) х-1/3 : х3/4; г) (0,04х7/8)-1/2
3. Решить уравнение: по 3 балла
а) х1/3 = 4; б) 2х1/6 — 11/3 =0
4. Упростить выражение: 4 балла
(а + 3а1/2): (а1/2+3)
5. Найти значение выражения: 5 баллов
(у1/2 -2)-1 — (У1/2 +2)-1 , при у=18
Проверка (слайд 16)
Учащиеся выставляют себе отметки в оценочном листе, используя критерий оценивания:
(слайд 17)
“5” – 24–25баллов;
“4”– 20–23баллов;
“3” – 13–19баллов;
“2” – менее 13 баллов.
VII. Задание на дом.
(слайд 18)
Тематический тест из материалов ЕГЭ, 1 вариант.
- Подведение итогов урока.
(слайд 19)
Выставление среднего балла за урок.
Учитель.
(слайд 20)
Ребята, на доске вы видите высказывания английского математика Джеймса Джозефа Сильвестра о математике
“Математика – это музыка разума,
Музыка – это математика чувств”.
Не правда ли, романтично?
К чувствам мы можем отнести различного рода переживания. В этом году одной из причин ваших и моих переживаний является успешная сдача ЕГЭ и, как следствие, поступление в ВУЗ. Очень хочется, чтобы преобладали положительные эмоции. Должна быть уверенность, а это наши знания и навыки. Сегодня на уроке мы внесли очередной вклад в вашу подготовку к ЕГЭ, повторяя понятие степени с рациональным показателем.
nsportal.ru
Урок по алгебре на тему «Преобразование выражений, содержащих радикалы»(10класс)
Тема урока: Преобразование выражений, содержащих радикалы
Цель занятия: Обеспечить овладение всеми обучающимися алгоритмическими приемами преобразований выражений, содержащих радикалы
Задачи:
Обучающая: систематизировать знания свойств корня п-ой степени; отработать практические умения решения заданий ЕГЭ по математике.
Развивающая: развивать логическое мышление учащихся, вырабатывать умение сравнивать, делать выводы, делать самопроверку, развивать интерес к изучению математики; Воспитательная: воспитывать навыки самостоятельной работы при выборе способа решения задач, воспитание настойчивости и целеустремленности, воспитание математическо грамотности
Тип урока: комбинированный
Оборудование: Компьютер, тетради обучающихся, раздаточный материал
Структура урока:
1) Организационный момент, вступительная беседа учителя-
2) Актуализация опорных знаний
3) Постановка цели и задач учебного занятия.
4) Первичное усвоение новых знаний
5)Закрепление изученного материала
6)Обобщение и систематизация знаний
7)Подведение итогов работы. Рефлексия
8) Домашнее задание
Ход урока.
11.Организационный этап
Здравствуйте, садитесь.
Командир группы, доложите явку учащихся
2. Актуализация знаний.
Ребята, на прошлом уроке мы изучили свойства корня n-ой степени. Сегодня мы посмотрим, как их применять при решении различных задач которые могут встретиться на практике.
2.1 Устные упражнения
2.2 Математический диктант
3.Постановка цели и задач учебного занятия.
Мотивация учебной деятельности обучающихся через обозначение проблемы:
3.1.Выражения, содержащие операцию извлечения корня, называют иррациональными выражениями.
3.2
Что нужно сделать? составить алгоритм преобразования выражений, содержащих радикалы.
Правильно, вы сформулировали цель занятия: составить алгоритм преобразования выражений, содержащих радикалы



Я хочу обратить внимание на то ,что полученные знания и навыки вы в дальнейшем будете применять в профессиональной деятельности: например для написания программы на языке программирования нужно уметь произвести математические алгоритмы действий и только потом приступать к программированию.
4.Первичное усвоение новых знаний
4.1Повторим Алгоритм преобразований выражений, содержащих радикалы:
1.Чтобы внести множитель под знак радикала, нужно его возвести в соответствующую степень;
2Чтобы вынести множитель из под знака радикала, нужно его разложить на множители.
5. Закрепление изученного материала
5.1Решение упражнений
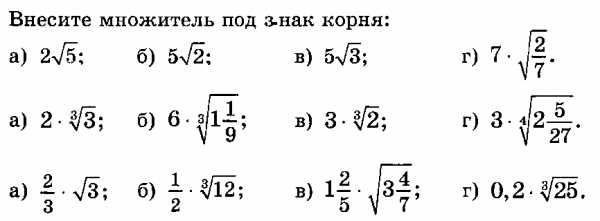
5.2Я хочу обратить внимание еще раз на то, что данная тема очень важная, так как из года в год на Е Г Э всегда присутствуют задания с радикалами. Поэтому сегодня хочется показать все многообразие заданий по этой теме,
задания ЕГЭ по математике.
6. Обобщение и систематизация знаний- с/р и критерии
7. Подведение итогов работы.7.1 Вывод по занятию.
Как вы считаете, цель занятия: составить алгоритм преобразования выражений, содержащих радикалы, достигнута? Повторим его.
7.2 Рефлексия. Закончите предложение:
• Сегодня на уроке мне понравилось…….
• Сегодня на уроке я узнал………
• Сегодня на уроке я научился……..
8. Постановка домашнего задания
Домашнее задание:


infourok.ru
Презентация к уроку по алгебре (8 класс) на тему: Преобразование выражений содержащих квадратные корни.
Урок алгебры в 8 классе
Тема «Преобразование выражений содержащих квадратные корни»
Цели урока:
- Формирование у учащихся знаний о разложении выражений, содержащих квадратные корни на множители с использованием формул сокращенного умножения.
- Развитие умений использовать ранее полученных знаний при разложении на множители выражений содержащих корни.
- Воспитывать собранность, умение самостоятельно действовать, интерес к предмету.
Цель ученика: Приобрести навык преобразования выражений с квадратными корнями.
Тип урока: Урок изучения новых знаний и способов действий.
Методы урока: объяснительно-иллюстративный.
Оборудование урока: доска, проектор с экраном, карточки
План урока.
- Организационный момент.
Сообщение темы урока . (слайды 1-2)
Ребята каждый из вас сегодня получил «фигуренка» в течение урока на каждом этапе вы будете закрашивать какую – то его часть цветами светофора : зеленый- все понятно, желтый – есть вопросы, красный – сложно, нужно разобрать еще раз .
- Актуализация знаний.
— устный счет (презентация)(слайды 3-5)
— повторить формулы сокращенного умножения.(слайд 6)
III. Работа по теме урока.
Мы с вами изучили свойства квадратных корней и выполняли преобразования выражений содержащих квадратные корни. Сегодня рассмотрим еще некоторые. Давайте рассмотрим пример №1 ( слайд 7). Какую формулу нужно применить?…
Решим №423 (а, в).
Рассмотрим пример №2 (слайд 8).
Решим №423 (е, ж)
Рассмотрим пример №3 (слайд9 )
Решим №428 (а, б, в), №429(а, б)
В нашем учебнике есть рублика : «Для тех кто хочет знать больше…». Небольшое выступление ученика. Всегда хочется узнать кто придумал обозначения или ввел какие-то символы. Так вот…
Средневековые математики обозначали квадратный корень символом Rx. Современное обозначение впервые употребил немецкий математик Кристоф Рудольф {Ch. Rudolff), из школы коссистов, в 1525 году. Происходит этот символ от стилизованной первой буквы того же слова radix. Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт для иной цели, и эта черта вскоре слилась со знаком корня.
Сейчас мы с вами рассмотрим преобразование двойных радикалов.(слайд 10 )
А теперь разберем задание №425 (а). Учитель дает возможность проявить себя сильным ученикам, но если они затрудняются, то помогает.
- Обучающая самостоятельная работа
Вариант 1 | Вариант 2 |
а) (а + ; б 2. Сократите дробь
| 1. Выполните действия а) (; б) 2. Сократите дробь
|
Ребята выполняют задания самостоятельно, если нужно консультируются у учителя. После окончания работы ответы выводятся на экран.
- Итог урока. Рефлексия. Домашнее задание.
Сегодня мы рассмотрели некоторые способы преобразования выражений содержащих квадратные корни. Какие Далее учитель делает заключение о тех заданиях к которым нужно вернуться ориентируясь на «фигуренков» .
Фигуренок
nsportal.ru
Методическая разработка по алгебре (11 класс) на тему: Методическая разработка урока в 11 классе для подготовки к ЕГЭ на тему: «Преобразование иррациональных выражений».
Методическая разработка урока в 11 классе для подготовки к ЕГЭ на тему:
«Преобразование иррациональных выражений».
Обобщающее повторение.
Цели:
-обобщить и систематизировать знания по теме «Преобразование иррациональных выражений»
-учиться применять полученные знания в задачах ЕГЭ части В и как элемент задачи части С.
Оборудование: раздаточные материалы, настенные таблицы.
Ход урока.
- Организационный момент.
- Проверка домашнего задания.
- Проговаривание в парах свойств степени с действительным показателем и свойств корня n-ой степени, а так же формул сокращённого умножения. Оценивание друг друга и сравнение с шаблоном, представленным в таблице.
- Выполнение заданий по планшетам для устного счета по одному заданию в произвольном порядке преимущественно те задания, которые вызвали затруднения при выполнении домашней работы. (Приложение №1)
- Работа в малых группах (по 4 человека) над карточками-ошибками, на которых представлены математические софизмы, суть которых и требуется пояснить. (Приложение №2).
- Решение упражнений.
- Упростите выражение
При a>
- Найдите целое число, равное разности
При условии, что a>242
- Найти наименьшее значение функции
f(x)=
при решении этого упражнения находим область определения функции и упрощаем выражение, задающее функцию, остальное доделываем дома
- Рефлексия. Решение теста. (Приложение №3)
- Итог урока.
Приложение №1
1 столбец. Представить в виде степени.
2 столбец. Представить в виде корня n-степени.
3 столбец. Разложить на множители.
4 столбец. Представить в виде степени.
| |||
| |||
ПРИЛОЖЕНИЕ №2.
КАРТОЧКИ – ОШИБКИ.
№1
Все числа равны между собой.
Возьмём два произвольных не равных между собой числа a и b
.
Слева и справа стоят полные квадраты, т.е. можем записать
Извлекая из обеих частей равенства квадратный корень, получим
a-b=b-a
или 2a=2b, или окончательно a=b.
№2
Половина любого числа равна половине ему противоположного.
Возьмём произвольное число a и положим
x=-
Тогда 2x+a=0 или после умножения на a получим 2ax + =0.
Прибавляя к обеим частям этого равенства , имеем
Так как ,то предыдущее равенство можно записать в виде
,
а после извлечения квадратного корня из обеих частей последнего равенства получаем
.
Поскольку по условию x=-, то из равенства имеем, и поэтому получаем окончательно .
№3
Квадратный корень из отрицательного числа существует.
Пусть a – произвольное положительное число, и положим x=-a. Тогда , а т.к. , то
.
Извлекая из обеих частей равенства корень четвертой степени, получаем
.
Но корень из произведения двух множителей равен произведению корней из этих множителей, т.е. ,
что, в свою очередь, может быть представлено в виде
x=.
Последнее равенство можно записать так:
x=.
Возвращаясь к исходному случаю x=-a, получаем, что , а разделив обе части равенства на , получим , т.е. квадратный корень из отрицательного числа (-a) и равен минус квадратному корню из числа a.
№4
Сумма любых двух одинаковых чисел равна нулю.
Возьмем произвольное неравное нулю число a и напишем уравнение x=a. Умножая обе его части на (-4а), получим -4ах=-4. Прибавляя к обеим частям этого равенства и перенеся член влево с противоположным знаком, получим
,
откуда, замечая, что слева стоит полный квадрат, имеем
,
или x-2a=x.
Заменяя в последнем равенстве х на равное ему число а, получим а-2а=а, или –а=а, откуда 0=а+а, т.е. сумма двух произвольных одинаковых чисел а равна нулю.
Приложение 3
Вариант 1
А1. Выполните действия:
.
А2. Найдите значение выражения
при k=5.
В1. Найдите значение выражения
, если
Вариант 2
А1. Упростите выражение:
А2. Найдите значение выражения
при а=2
В1. Найдите значение выражения
, если
nsportal.ru

