Презентация осевая и центральная симметрия 11 класс: Презентация по теме: «Центральная симметрия» (11 класс)
«Центральная и осевая симметрии» | Презентация к уроку по геометрии (8 класс) по теме:
Слайд 1
Центральная и осевая симметрии
Слайд 2
План урока Теоретическая самостоятельная работа с самопроверкой. Изучение нового материала с использованием презентации. Закрепление нового материала с использованием презентации.
Слайд 3
Ответы к тесту Вариант №1. Ч В заданиях вставьте пропущенные слова в определениях и теоремах. 1. *** называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. а) прямоугольник б) трапеция в) ромб г) четырехугольник 2.Прямоугольник – это ***, у которого все углы прямые. а) трапеция б) четырехугольник в) ромб г) параллелограмм 3. Диагонали ромба являются *** его углов. а) медианами б) высотами в) средними линиями г ) биссектрисами 4. *** называется четырехугольник, у которого только две противолежащие стороны параллельны. а) прямоугольник б) параллелограмм в) трапеция г) ромб 5. У параллелограмма противолежащие стороны равны, противолежащие *** равны. а) вершины б) углы в) прямые г) отрезки 6. Ромб – это ***, у которого все стороны равны. а) четырехугольник б) прямоугольник в) квадрат г) параллелограмм 7. *** параллелограмма пересекаются и точкой пересечения делятся пополам. а) вершины б) стороны в) углы г) диагонали 8. Диагонали *** равны. а) четырехугольника б) ромба в) прямоугольника г) трапеции Вариант №2. В заданиях вставьте пропущенные слова в определениях и теоремах. 1. *** называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. а) четырехугольник б) трапеция в) ромб г) прямоугольник 2.Прямоугольник – это ***, у которого все углы прямые. а) трапеция б) параллелограмм в) ромб г) четырехугольник 3. Диагонали ромба являются *** его углов. а) медианами б) высотами в) биссектрисами г) средними линиями 4. *** называется четырехугольник, у которого только две противолежащие стороны параллельны. а) прямоугольник б ) трапеция в) параллелограмм г) ромб 5.
У параллелограмма противолежащие стороны равны, противолежащие *** равны. а) вершины б) углы в) прямые г) отрезки 6. Ромб – это ***, у которого все стороны равны. а) четырехугольник б) прямоугольник в) квадрат г) параллелограмм 7. *** параллелограмма пересекаются и точкой пересечения делятся пополам. а) вершины б) стороны в) углы г) диагонали 8. Диагонали *** равны. а) четырехугольника б) ромба в) прямоугольника г) трапеции Вариант №2. В заданиях вставьте пропущенные слова в определениях и теоремах. 1. *** называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. а) четырехугольник б) трапеция в) ромб г) прямоугольник 2.Прямоугольник – это ***, у которого все углы прямые. а) трапеция б) параллелограмм в) ромб г) четырехугольник 3. Диагонали ромба являются *** его углов. а) медианами б) высотами в) биссектрисами г) средними линиями 4. *** называется четырехугольник, у которого только две противолежащие стороны параллельны. а) прямоугольник б ) трапеция в) параллелограмм г) ромб 5. У параллелограмма противолежащие стороны равны, противолежащие *** равны. а) вершины б) отрезки в) прямые г) углы 6. Ромб – это ***, у которого все стороны равны. а) параллелограмм б) прямоугольник в) квадрат г) четырехугольник 7. *** параллелограмма пересекаются и точкой пересечения делятся пополам. а) вершины б) диагонали в) углы г) стороны 8. Диагонали *** равны. а) четырехугольника б ) прямоугольника в) ромба г) трапеции
У параллелограмма противолежащие стороны равны, противолежащие *** равны. а) вершины б) отрезки в) прямые г) углы 6. Ромб – это ***, у которого все стороны равны. а) параллелограмм б) прямоугольник в) квадрат г) четырехугольник 7. *** параллелограмма пересекаются и точкой пересечения делятся пополам. а) вершины б) диагонали в) углы г) стороны 8. Диагонали *** равны. а) четырехугольника б ) прямоугольника в) ромба г) трапеции
Слайд 4
Ответы к тесту Вариант №1. 1 г 2 г 3 г 4 в 5 б 6 г 7 г 8 в Вариант №2. 1 а 2 б 3 в 4 б 5 г 6 а 7 б 8 б
Слайд 5
Центральная и осевая симметрии
Слайд 7
Точки А и А 1 называются симметричными относительно точки О , если О — середина отрезка АА 1 . О — центр симметрии А А 1 О Точка О считается симметричной самой себе. Центральная симметрия
Слайд 8
Какие из точек симметричны относительно точки О ? N N 1 О M M 1 Q P
Слайд 9
Задание1 Построить треугольник, симметричный АВС относительно точки О . О В А С А 1 С 1 В 1 Построение.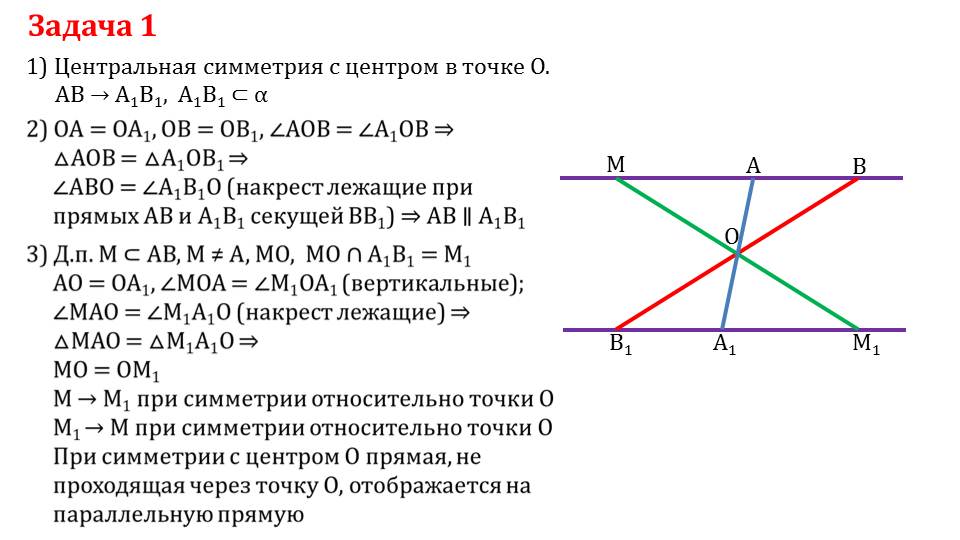
Слайд 10
Фигура называется симметричной относительно точки О , если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. О О Примеры фигур, имеющих центр симметрии. О О
Слайд 11
Осевая симметрия Две точки А и А 1 называются симметричными относительно прямой n , если эта прямая проходит через середину отрезка АА 1 и перпендикулярна к нему. n А А 1 n – ось симметрии О
Слайд 12
Какие из точек симметричны относительно прямой b ? b N N 1 M M 1 A A P
Слайд 13
b С В А А 1 В 1 С 1 Задание 2 Построить треугольник, симметричный АВС относительно прямой b Построение.
Слайд 14
Фигура называется симметричной относительно прямой n , если для каждой точки фигуры симметричная ей точка относительно прямой n также принадлежит этой фигуре. Примеры фигур, имеющих ось симметрии.
Слайд 15
Примеры фигур, обладающих центральной и осевой симметрией.
Симметрия и осевая симметрия — презентация по геометрии 11 класс
Слайды и текст этой презентации
| Слайд №1 | |
Симметрия. Осевая симметрия. Осевая симметрия. Подготовила : Ученица 11 «А» класса Пустовалова Василиса. | |
| Слайд №2 | |
| Содержание: Определение симметрии, виды симметрии. Осевая симметрия. Теорема. | |
| Слайд №3 | |
| Симметрия – (от греч.) соразмерность, пропорциональность, одинаковость в расположении частей. Виды симметрии: 1. осевая симметрия 2. центральная 3. зеркальная 4. параллельный перенос. | |
| Слайд №4 | |
| Осевой симметрией с осью a называется такое отображение пространства на себя, при котором любая точка M переходит в симметричную ей точку M1 относительно оси a. Симметрия простейших фигур | |
| Слайд №5 | |
| Докажем , что осевая симметрия есть движение. | |
| Слайд №6 | |
| Z Y X O O M M1 1) Обозначим точку О – центр симметрии и введем прямоугольную систему координат Оxyz с началом в точке О.  | |
| Слайд №7 | |
| Z Y X O O M M1 2) Установим связь между координатами двух точек: M(x; y; z) и M1(x1; y1; z1). Z0 (M) = M1. | |
| Слайд №8 | |
| Z Y X O O M M1 3)Если М Оz , то Оz ММ1 и проходит через середину. 4) Т. к. Оz М1, то z = z1. | |
| Слайд №9 | |
| Z Y X O O A B A1 B1 5) Рассмотрим А(x1; y1; z1), В(x2; y2; z2) 6) А—> А1, В—> В1, тогда А1(-x1; -y1; z1), В1(-x2; -y2; z2) | |
| Слайд №10 | |
| Z Y X O O A B A1 B1 тогда АВ=А1В1, т.е. Sоz — движение. 7) Докажем, что расстояние между симметричными точками А1 и В1 равно АВ | |
| Слайд №11 | |
| По формуле расстояния между двумя точками находим : тогда АВ=А1В1, т. тогда АВ=А1В1, т.е. Sоz — движение, что и требовалось доказать. | |
- Автор: Виктория
- Распечатать
Оцените статью:
(2 голоса, среднее: 4.5 из 5)
Поделитесь с друзьями!
Большой сборник презентаций в помощь школьнику.
закрыть
Скопируйте этот код и вставьте его на своем сайте:
<div><strong><a href=»https://volna.org/geometrija/simmietriia_i_osievaia_simmietriia.html»
title=»Симметрия и осевая симметрия — презентация по геометрии 11 класс» target=»_blank»
>Симметрия и осевая симметрия — презентация по геометрии 11 класс</a></strong><iframe
src=»https://volna. org/iframe/302/» frameborder=»0″ marginwidth=»0″ marginheight=»0″
scrolling=»no»
allowfullscreen></iframe></div>
org/iframe/302/» frameborder=»0″ marginwidth=»0″ marginheight=»0″
scrolling=»no»
allowfullscreen></iframe></div>
Осевая и центральная симметрия
Осевая симметрия является преобразованием, поэтому каждая точка $$P$$ на плоскости отображает другую точку $$P’$$ также на плоскости, так что ось $$e$$ будет серединным перпендикуляром к отрезку $$PP’$$. Осевые симметрии являются обратными изометриями, потому что они сохраняют расстояния между его точками и его гомологичными точками, но его ориентация обратна. Осевая симметрия возникает не только между предметом и его отражением, поскольку многие фигуры, которые могут разбиваться на две части посредством линии, симметричны относительно линии. Эти объекты имеют одну (или несколько) осей симметрии.
Осевая симметрия возникает, когда точки одной фигуры совпадают с точками другой фигуры, принимая за отсчет линию, известную под названием оси симметрии. В осевой симметрии мы находим то же явление, что и в изображении, отраженном в зеркале.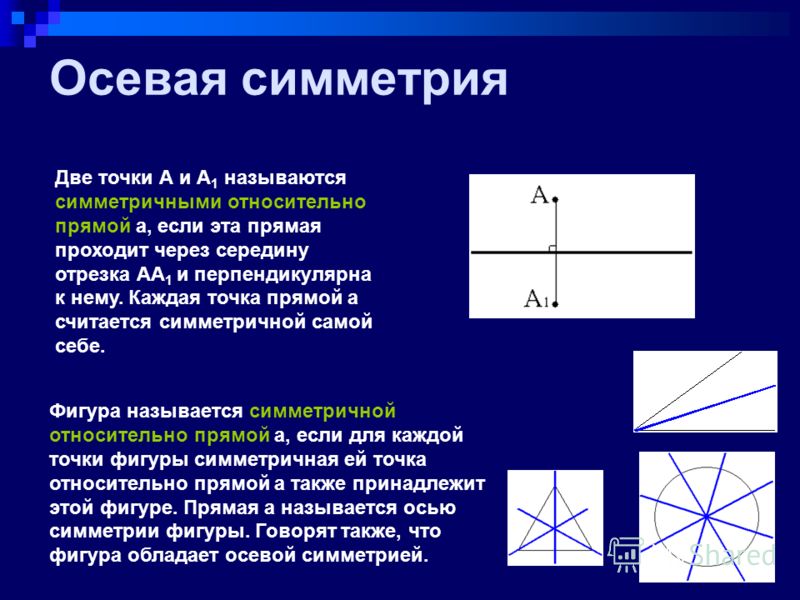
Мы называем точки, принадлежащие симметричной фигуре, гомологичными точками, то есть $$A’$$ гомологична $$A$$, $$B’$$ гомологична $$B$$, и $$C’$$ гомологичен $$C$$. Кроме того, существующие расстояния между точками исходной фигуры равны расстояниям между точками симметричной фигуры. В этом случае: Осевая симметрия также может иметь место в объекте относительно одной или нескольких осей симметрии.
Если мы изогнем фигуру по прочерченной оси симметрии, мы можем ясно заметить, что точки противоположных частей совпадают, то есть обе части соответствуют.
Далее мы изучим выражение осевых симметрий в координатах.
Пусть $$P ‘= (x, y)$$ и $$P ‘= (x’, y ‘)$$ — две точки плоскости, выразим ее в координатах в соответствии с положением ее оси:
Ось симметрии является осью координат Y:
В этом случае алгебраическое представление преобразования можно выполнить с помощью следующей системы:
$$$ \begin{pmatrix} x’ \\ y’ \end{pmatrix} = \begin{pmatrix} -1 и 0 \\ 0 и 1 \end{pmatrix} \cdot \begin{pmatrix} х \\ у \end{pmatrix} $$$
Далее мы собираемся вычислить симметрию точки $$P$$ с помощью симметрии, осью которой является их координатная ось.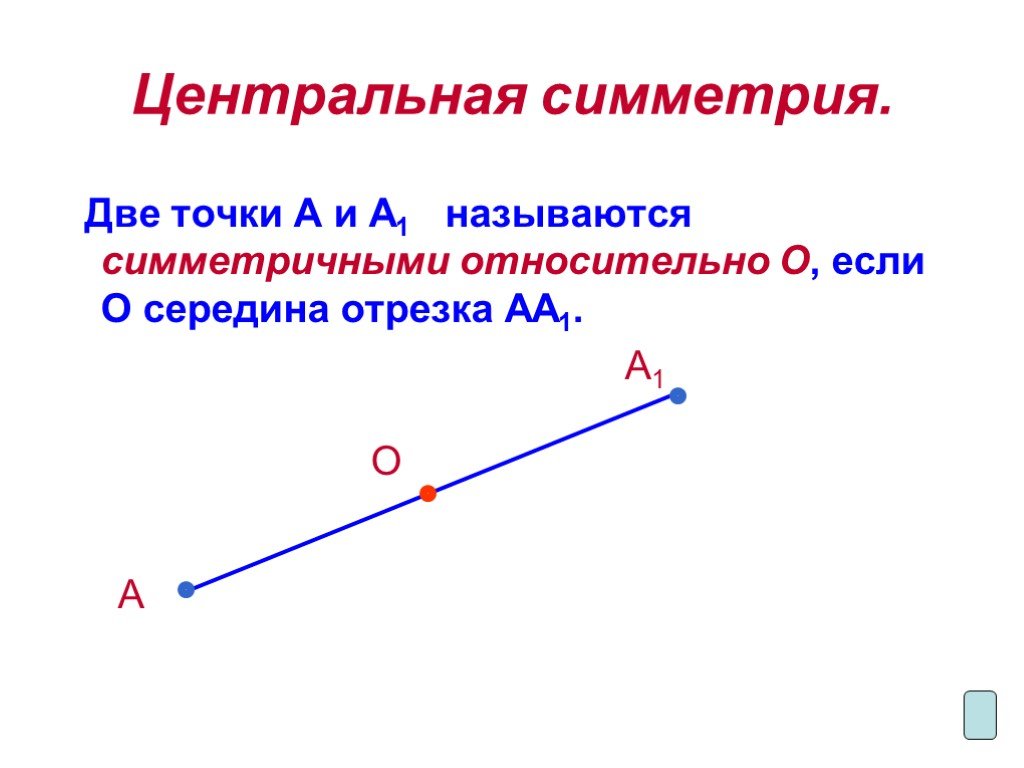 Пусть $$P = (2,2)$$ — точка плоскости, тогда ее симметрия вычисляется с помощью следующей системы уравнений:
Пусть $$P = (2,2)$$ — точка плоскости, тогда ее симметрия вычисляется с помощью следующей системы уравнений:
$$$ \begin{pmatrix} x’ \\ y’ \end{pmatrix} = \begin{pmatrix} -1 и 0 \\ 0 и 1 \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 2 \end{pmatrix} \Стрелка вправо \влево\{ \begin{array}{l} x’=-2 \\ y’=2 \end{массив} \Правильно. $$$
Следовательно, симметричной точкой относительно оси координат y является точка $$P’=(-2,2)$$.
Ось симметрии является осью координат x:
В этом случае алгебраическое представление преобразования можно выполнить с помощью следующей системы: $$$ \begin{pmatrix} x’ \\ y’ \end{pmatrix} = \begin{pmatrix} 1 и 0 \\ 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} х \\ у \end{pmatrix} $$$
Продолжаем предыдущий пример, вспомним, что у нас была точка P с координатами $$(2,2)$$ и в предыдущем примере мы вычислили ее симметричную относительно оси координат $$y$$. Теперь мы вычислим ее симметричную относительно оси координат $$x$$ и назовем эту новую точку $$P»$$. Вычислим ее координаты с помощью следующей системы уравнений:
Вычислим ее координаты с помощью следующей системы уравнений:
$ $$ \begin{pmatrix} x’ \\ y’ \end{pmatrix} = \begin{pmatrix} 1 и 0 \\ 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 2 \end{pmatrix} \Rightarrow \left\{ \begin{array}{l} x’=2 \\ y’=-2 \end{array} \Правильно. $$$
Таким образом, симметричной точкой относительно оси координат x является точка $$P»=(2,-2)$$.
Чтобы закончить осевые симметрии, мы собираемся изучить, что происходит с композицией осевых симметрий:
Композицией двух симметрий с параллельными осями $$e$$ и $$e’$$ является трансляция, вектор которой имеет длину, удвоенную расстояние между осями, направление перпендикулярно осям и его смысл тот это идет от $$e$$ до $$e’$$.
- Композиция двух симметрий с перпендикулярными осями $$e$$ и $$e’$$ является центральной симметрией относительно точки пересечения двух осей симметрии.
Возьмем снова точку $$P = (2,2)$$ и применим к ней симметрию относительно оси координат y, а затем симметрию относительно оси координат $$x$$. \circ$$.
\circ$$.
Точка является центром симметрии фигуры, если она определяет центральную симметрию.
Далее мы увидим выражение в координатах центральной симметрии, изменяющей центр симметрии.
Координаты с помощью центральной симметрии $$O=(0,0)$$:
На следующем изображении мы видим, как ведет себя центральная симметрия, являющаяся центром начала координат точки:
Далее треугольник и его гомолог видны с помощью симметрии:
В обоих случаях преобразование связано со следующей системой: $$$ \begin{pmatrix} x’ \\ y’ \end{pmatrix} = \begin{pmatrix} -1 и 0 \\ 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} х \\ у \end{pmatrix} $$$
Зная отрезок $$AB$$, образованный точками $$A = (1,0)$$ и $$B = (2,3)$$, вычислим его симметрию относительно центра координат . Для этого вычислим симметрию точек $$A$$ и $$B$$. Точно, симметрия $$A$$ равна $$A’$$:
$$$ \begin{pmatrix} x’ \\ y’ \end{pmatrix} =
\begin{pmatrix} -1 и 0 \\ 0 & -1 \end{pmatrix} \cdot
\begin{pmatrix} 1 \\ 0 \end{pmatrix}
\стрелка вправо \влево\{ \begin{array}{l} x’=-1 \\ y’=0 \end{массив}
\Правильно.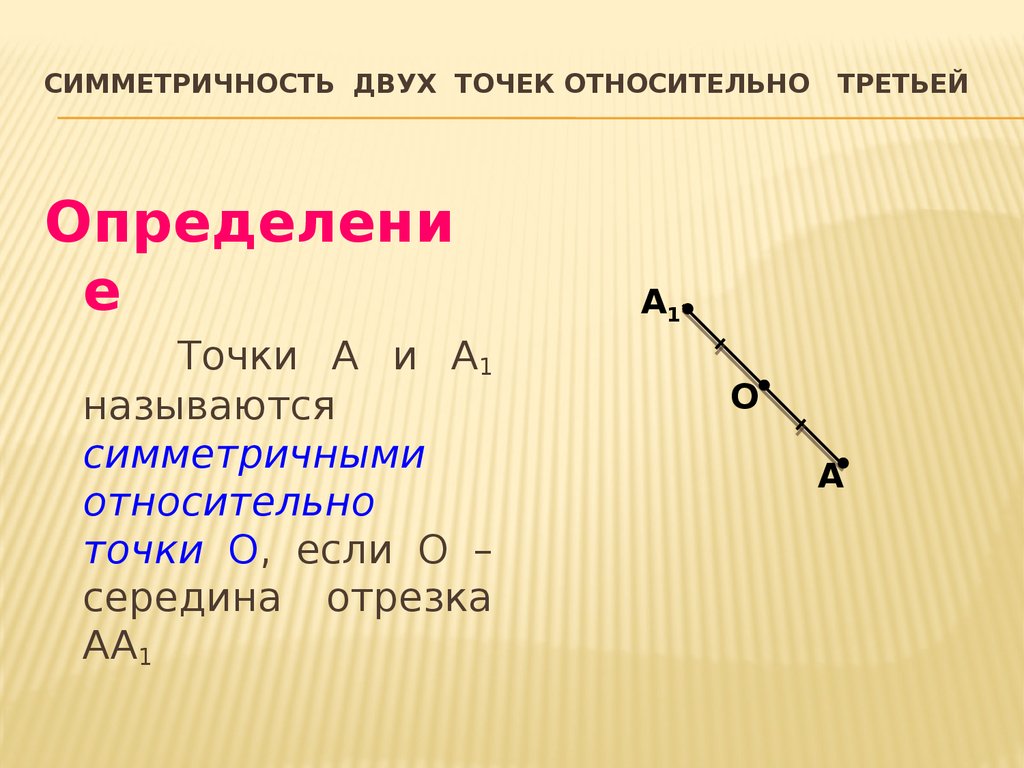 $$$
$$$
Следовательно, $$A ‘= (-1,0)$$ . Симметрия точки $$B$$ равна $$B’$$:
$$$ \begin{pmatrix} x’ \\ y’ \end{pmatrix} = \begin{pmatrix} -1 и 0 \\ 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 3 \end{pmatrix} \стрелка вправо \влево\{ \begin{array}{l} x’=-2 \\ y’=-3 \end{массив} \Правильно. $$$
Следовательно, симметрией отрезка $$AB$$ является отрезок $$A’B’$$, проходящий через точки $$A’ = (-1,0)$$ и $$B ‘= ( -2, -3)$$.
Координаты с помощью центральной симметрии $$O=(a, b)$$:
Точка $$P’$$, гомологичная точке $$P=(x, y)$$ посредством центральной симметрии центра $$O=(a, b)$$:
А фигура, гомологичная треугольнику, имеет такой вид:
Следовательно, связанная с ним система: $$$ \begin{pmatrix} x’ \\ y’ \end{pmatrix} = \begin{pmatrix} -1 и 0 \\ 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} х \\ у \end{pmatrix} + \begin{pmatrix} 2a \\ 2b \end{pmatrix} $$$
, где мы помним, что значения $$(a, b)$$ являются координатами центра симметрии.

Мы собираемся рассмотреть центр центральной симметрии $$O = (1,2)$$ и хотим вычислить симметрию относительно $$O$$ точки $$A = (3,7)$ $. Тогда для системы уравнений, связанной с центральной симметрией с началом $$O=(a, b)$$, координаты симметричной точки равны:
$$$ \begin{pmatrix} x’ \\ y’ \end{pматрица} = \begin{pmatrix} -1 и 0 \\ 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} 3 \\ 7 \end{pmatrix} + \begin{pmatrix} 2\cdot 1 \\ 2\cdot 2 \end{pmatrix} \Rightarrow \left\{ \begin{array}{l} x’=-3+2=-1 \\ y’=-7+4=-3 \end{array} \Правильно. $$$ 9\circ$$, поэтому получается та же цифра, что называется регрессией. Это инволютивное преобразование.
Симметрия | Биология, типы, примеры и факты
биологическая симметрия
Все медиа
- Связанные темы:
- бирадиальная симметрия радиальная симметрия мезаксоническое состояние двусторонняя симметрия сферическая симметрия
Просмотреть весь связанный контент →
симметрия , в биологии упорядоченное повторение частей животного или растения.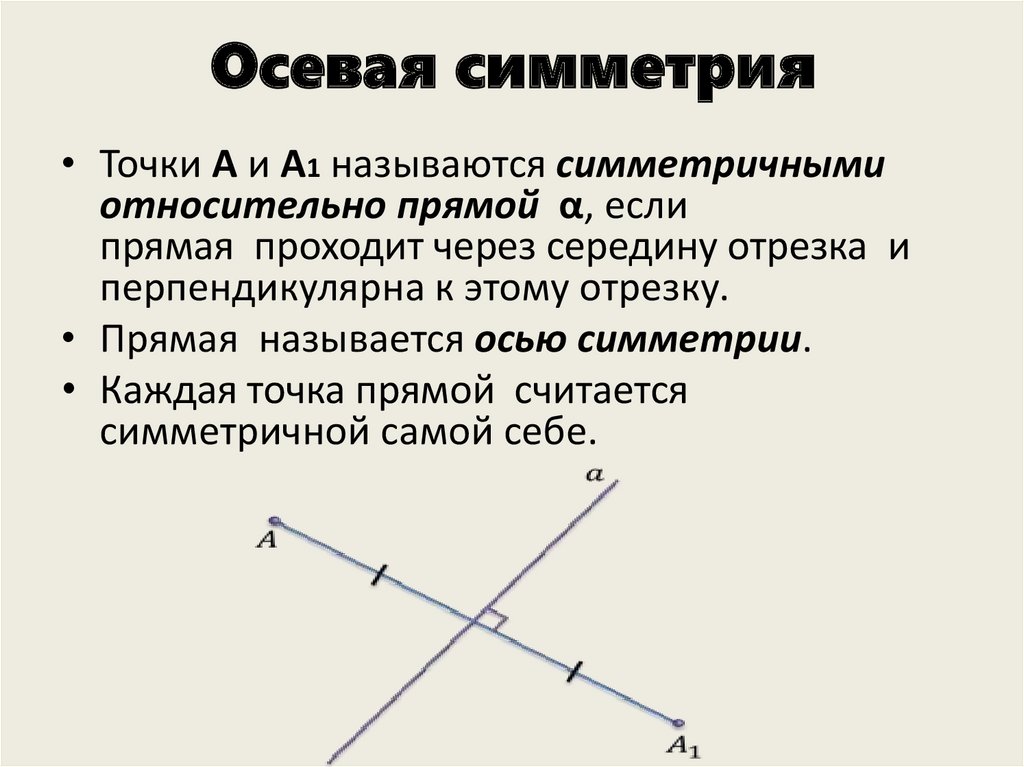 В частности, симметрия относится к соответствию частей тела по размеру, форме и относительному положению на противоположных сторонах разделительной линии или распределенных вокруг центральной точки или оси. За исключением радиальной симметрии, внешняя форма мало связана с внутренней анатомией, так как животные самого разного анатомического строения могут иметь один и тот же тип симметрии.
В частности, симметрия относится к соответствию частей тела по размеру, форме и относительному положению на противоположных сторонах разделительной линии или распределенных вокруг центральной точки или оси. За исключением радиальной симметрии, внешняя форма мало связана с внутренней анатомией, так как животные самого разного анатомического строения могут иметь один и тот же тип симметрии.
Симметрия у животных
Некоторые животные, особенно большинство губок и амебоидных простейших, лишены симметрии, имея либо неправильную форму, различную для каждой особи, либо форму, подвергающуюся постоянным изменениям. Однако подавляющее большинство животных имеет определенную симметричную форму. Среди животных встречаются четыре таких типа симметрии: сферическая, радиальная, бирадиальная и двусторонняя.
Britannica Quiz
Biology Bonanza
Что означает слово «миграция»? Сколько пар ног у креветки? От ядовитых рыб до биоразнообразия — узнайте больше об изучении живых существ в этой викторине.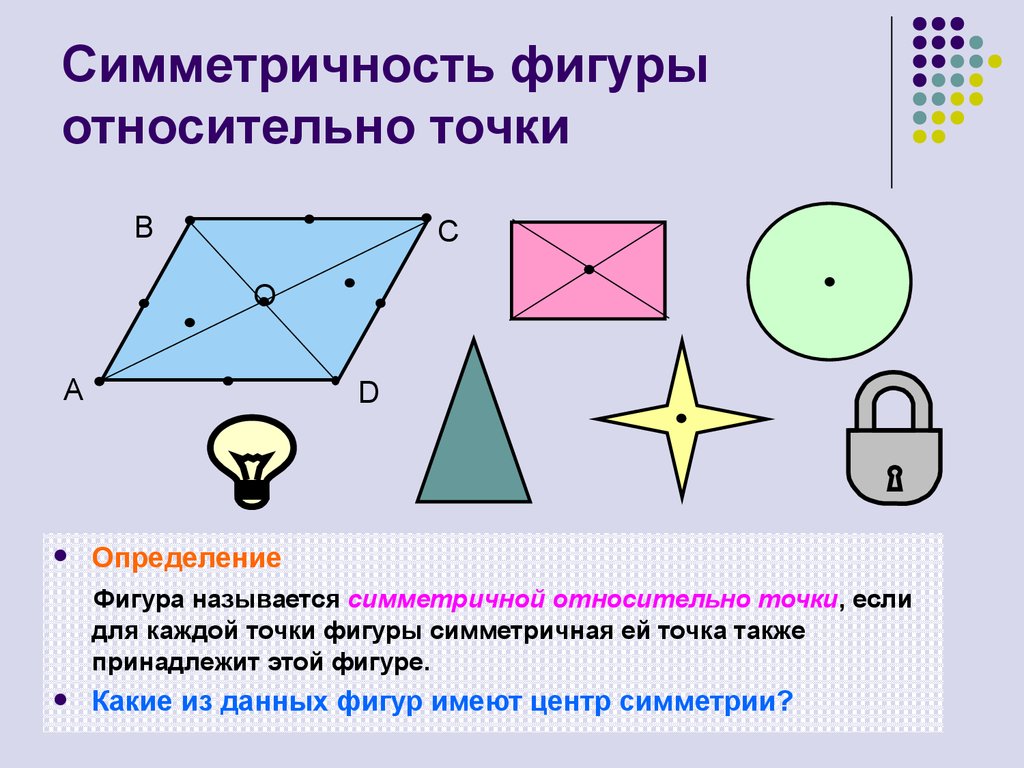
При сферической симметрии, представленной только группами простейших Radiolaria и Heliozoia, тело имеет форму сферы, а части расположены концентрически вокруг центра сферы или расходятся от него. У такого животного нет ни концов, ни сторон, и любая плоскость, проходящая через центр, разделит животное на равнозначные половины. Сферический тип симметрии возможен только у мельчайших животных с простым внутренним строением, так как у сфер внутренняя масса велика по отношению к площади поверхности и становится слишком большой для эффективного функционирования с увеличением размера и сложности.
При радиальной симметрии тело имеет общую форму короткого или длинного цилиндра или чаши с центральной осью, от которой расходятся части тела или вдоль которой они расположены правильным образом. Главная ось гетерополярна, т. е. с непохожими концами, один из которых несет рот и называется оральным, или передним, концом, а другой, называемый аборальным, или задним, концом, образует задний конец животное и может нести анус. Следовательно, главная ось называется орально-аборальной или переднезадней осью. За исключением животных, имеющих нечетное число частей, расположенных по кругу (как у пятилучевых морских звезд), любая плоскость, проходящая через эту ось, разделит животное на симметричные половины. Животные, имеющие три, пять, семь и т. д. частей в круге, обладают симметрией, которую можно назвать соответственно трехлучевой, пятилучевой, семилучевой и т. д.; только определенные плоскости, проходящие через ось, будут делить таких животных на симметричные половины. Радиальная симметрия встречается у книдарий (включая медуз, актиний и кораллов) и иглокожих (таких как морские ежи, офиуры и морские звезды).
Следовательно, главная ось называется орально-аборальной или переднезадней осью. За исключением животных, имеющих нечетное число частей, расположенных по кругу (как у пятилучевых морских звезд), любая плоскость, проходящая через эту ось, разделит животное на симметричные половины. Животные, имеющие три, пять, семь и т. д. частей в круге, обладают симметрией, которую можно назвать соответственно трехлучевой, пятилучевой, семилучевой и т. д.; только определенные плоскости, проходящие через ось, будут делить таких животных на симметричные половины. Радиальная симметрия встречается у книдарий (включая медуз, актиний и кораллов) и иглокожих (таких как морские ежи, офиуры и морские звезды).
В бирадиальной симметрии кроме переднезадней оси имеются еще две другие оси или плоскости симметрии, расположенные под прямым углом к ней и друг к другу: сагиттальная, или срединная вертикально-продольная, и поперечная, или поперечная, оси. Таким образом, такое животное имеет не только два конца, но и две пары симметричных сторон.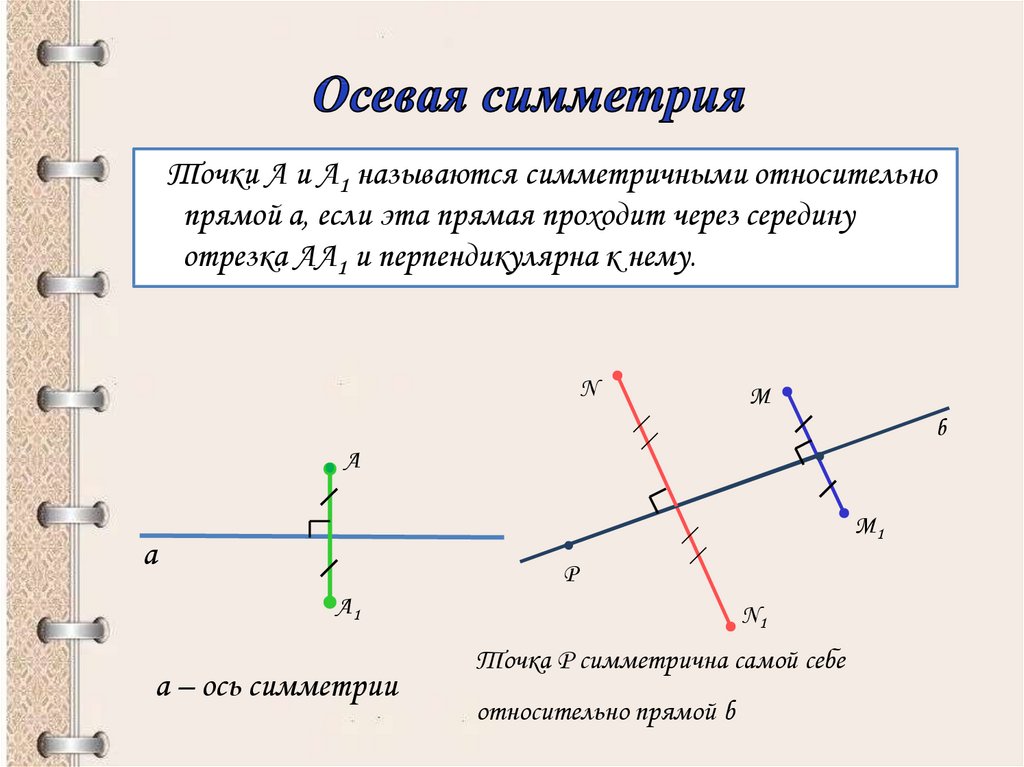 У бирадиального животного есть только две плоскости симметрии: одна проходит через переднезаднюю и сагиттальную оси, а другая — через переднезаднюю и поперечную оси. Бирадиальная симметрия имеет место в гребенчатых желе.
У бирадиального животного есть только две плоскости симметрии: одна проходит через переднезаднюю и сагиттальную оси, а другая — через переднезаднюю и поперечную оси. Бирадиальная симметрия имеет место в гребенчатых желе.
При билатеральной симметрии имеются те же три оси, что и при бирадиальной симметрии, но только одна пара симметричных сторон, латеральные стороны, поскольку две другие стороны, называемые дорсальной (задней) и вентральной (брюшной) поверхностями, неодинаковы. Таким образом, только одна плоскость симметрии разделит билатеральное животное на симметричные половины, срединная продольная или сагиттальная плоскость. Двусторонняя симметрия характерна для подавляющего большинства животных, в том числе для насекомых, рыб, амфибий, рептилий, птиц, млекопитающих и большинства ракообразных.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подписаться сейчас
Симметрия в цветах
Понятие симметрии также применяется в ботанике. Цветок считается симметричным, если каждая мутовка состоит из равного числа частей или когда части любой одной мутовки кратны частям предыдущей. Так, симметричный цветок может иметь пять чашелистиков, пять лепестков, пять тычинок и пять плодолистиков, или число любых из этих частей может быть кратно пяти.
Цветок считается симметричным, если каждая мутовка состоит из равного числа частей или когда части любой одной мутовки кратны частям предыдущей. Так, симметричный цветок может иметь пять чашелистиков, пять лепестков, пять тычинок и пять плодолистиков, или число любых из этих частей может быть кратно пяти.
Число частей в пестичной (женской) мутовке часто не соответствует количеству частей в других мутовках, но в таких случаях цветок все же называется симметричным, если остальные мутовки нормальные. Цветок, в котором части расположены попарно, двумерный; в тройках, четверках или пятерках, трехчленных, четырехчленных или пятичленных соответственно. Трехмерная симметрия является правилом для однодольных растений, пятичленная наиболее распространена среди двудольных, хотя двудольные и четырехчленные цветки также встречаются в последней группе.
Когда разные члены каждой мутовки одинаковы, цветок правильный и называется актиноморфным или радиально-симметричным, как у петунии, лютика и шиповника.


 е. Sоz — движение.
е. Sоz — движение.