Преобразование иррациональных выражений 11 класс презентация – Презентация к уроку по алгебре (11 класс) на тему: Презентации 11 класс | скачать бесплатно
Презентация «Иррациональные уравнения» для 11 класса
Просмотр содержимого документа
«Презентация «Иррациональные уравнения» для 11 класса»

- Вот другой взгляд- высокий: учитесь , читайте , размышляйте и извлекайте из всего самое полезное . Когда ум просветлеет , вы узнаете, кто вы и что вы.
Н.И.Пирогов

Иррациональные уравнения


Цели урока
- Обобщить и систематизировать знания и умения при решении иррациональных уравнений, рассмотреть способы решения типовых уравнений
- Развивать умение выделять главное, существенное в изучаемом материале, обобщать факты и понятия, развивать самостоятельность, мышление, познавательный интерес.
- Содействовать формированию мировоззренческих понятий.

Устная работа

Определение
- Иррациональными называются уравнения, в которых переменная содержится под знаком корня или под знаком операции возведения в дробную степень.

Посторонние корни
- Основными причинами появления посторонних корней является возведение обеих частей уравнения в одну и ту же чётную степень, расширение области определения и др.
- По этим причинам необходимой частью решения иррационального уравнения является проверка , либо использование области определения заданного уравнения.

- В некоторых случаях можно сделать вывод о решении иррационального уравнения, не прибегая к преобразованиям.
- Например, уравнения
не имеют решения.

Устно:
Какие из следующих уравнений являются иррациональными?
а) х + √ х = 2 б) х + √ х = 0
в) х √7 = 11+х
д) у + √ у ² +9 = 2 е ) √ х – 1 = 3
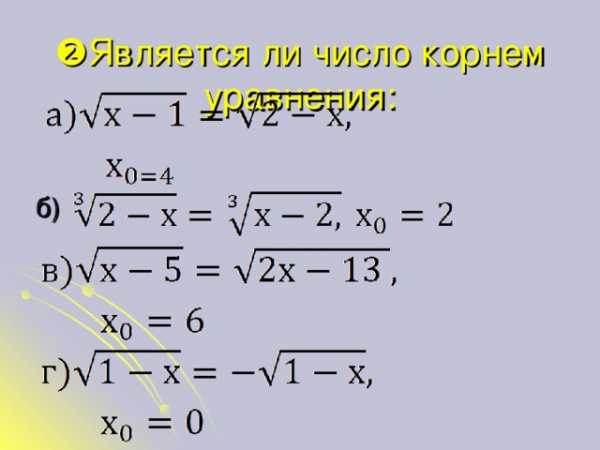
❷ Является ли число корнем уравнения:
б)

Метод возведения обеих частей уравнения в одну и ту же степень
- Преобразовать обе части уравнения к виду
2 . Возвести обе части в n -ую степень
3. Учитывая, что получаем:
4. Решить полученное уравнение и выполнить проверку (или ОДЗ)

Пример
Воспользуемся формулой куба разности двух чисел
(a -b
=
Ответ: -109; 80.

Если квадратных корней в иррациональном уравнении много, то приходится возводить в квадрат несколько раз:

Решение:
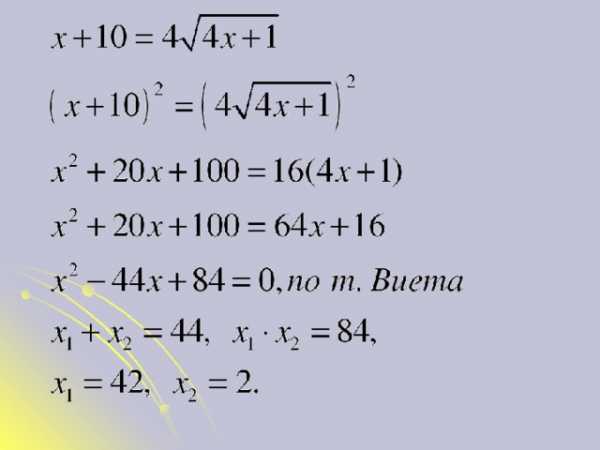

Проверка

Равносильные переходы

Примеры:
Ответ:5
Ответ:11

Уравнения, в которых одно или несколько подкоренных выражений точные квадраты. Пример

Метод замены переменной
- Ввести новую переменную
- Решить уравнение, отбросить посторонние корни
- Вернуться к первоначальному неизвестному

- Введение вспомогательной переменной в ряде случаев приводит к упрощению уравнения.
- Чаще всего в качестве новой переменной используют входящий в уравнение радикал.
- При этом уравнение становится рациональным относительно новой переменной.

Пример 1
Решение
ОДЗ: x≠1,x≠0.
Обозначим+
=
=t
, где t≠ 0 .
Ответ: -1/511; 2

Пример 2
Пусть
тогда исходное уравнение примет вид:
у 1 = -7, у 2 = 6

Решая уравнение
получим:
х = 3,
х = — 4,5
Ответ: -4,5;3.

Самостоятельная работа

Решите уравнение
Вариант 1
Вариант 2
а)
а)
б)
б)
в)
в)
г)
г)
Ответы:
а) 2; 9 . б)17 в)2;3 г)0
а)0 ; 5 б)10 в)-5;-2 г) -2; 2.
Вариант 1:
Вариант 2:

ДОМАШНЕЕ ЗАДАНИЕ
п. 33
№ 423(б)
№ 424(б, в)
425 (в, г)

Итоги урока
—
—

Рефлексия
- Ваше настроение

Спасибо за урок!
multiurok.ru
Урок+ презентация по алгебре на тему»Решение иррациональных уравнений» 11 класс
Урок по алгебре для11 класса.Тема: Решение Иррациональных уравнений
Якуценя Елена Петровна
Цели урока:
Обобщение и систематизация способов решения иррациональных уравнений.
Решение более сложных типов иррациональных уравнений .
Развивать память, внимание, логическое мышление, математическую речь.
Уметь адекватно анализировать свою работу.
Верить в свои силы.
Учиться работать продуктивно и с интересом .
Ход урока
1. Организационный момент.
1 слайд.
Иррациональные уравнения.
“Мне приходится делить время между политикой и уравнениями,
однако, уравнения, по-моему, гораздо важнее.
Эйнштейн
Здравствуйте, ребята. Добрый день, уважаемые учителя, приглашаю Вас на урок алгебры в 11 классе “Иррациональные уравнения”.
Эйнштейн говорил так: “Мне приходится делить время между политикой и уравнениями. Однако, уравнения, по-моему, гораздо важнее. Политика существует для данного момента, а уравнения будут существовать вечно”.
Как Вы знаете, прославился он именно уравнением, названным “уравнение Эйнштейна”. Вот и мы займемся уравнениями.
Сообщение целей урока слайд 2
Мы постараемся достичь всех целей урока, а для того чтобы вы смогли проанализировать свою работу я раздам вам рабочую карту, в которой вы будете отмечать успешность выполнения заданий символами:
Рабочая карта ученика 11 класса __________________________________
Теория
кроссворд
Тест
2. Метод
возведения в степень, равную показателю корня
Метод составления смешанной системы
3. Метод введения новой переменной
Метод умножения на сопряженное выражение
Самостоятельная
работа
Начало урока
Итог урока
Оценка
“!” – владею свободно
“+” — могу решать, иногда ошибаюсь
“-” — надо еще поработать
Перед тем как перейти к следующему этапу нашего урока проверим выполнение домашнего задания. Тетради с решенными уравнениями вы мне сдадите, а теорию мы повторим устно в виде кроссвордов.
История развития теории иррациональности знает много ученых – исследователей. Назовем некоторых из них, отвечая на вопросы теории, которая является фундаментом для решения иррациональных уравнений.
4 слайд: На экране появляются вопросы с 1 по 6 –ой и первый кроссворд.
Что требуется для полученных значений переменной при решении иррациональных уравнений? (проверка)
Способ, которым проводится проверка решений иррациональных уравнений. (подстановка)
Как называется знак корня?( радикал)
Сколько решений имеет уравнение х2 = а, если а < 0? (ноль)
Как называются уравнения, в которых под знаком корня содержится переменная? (иррациональное)
Как называется корень второй степени? (квадратный)
Получилось имя Евклид. Евклид – это великий ученый, он жил в 3 веке до нашей эры в Древней Греции. Известно, что он был приглашен в Александрию царем Птолемеем I Сотером для организации математической школы. Он был человеком мягкого характера, очень скромного, но независимого. Он сказал, что познание мира ведет к совершенствованию души. Предлагаю эти слова взять эпиграфом нашего урока.
Понятие иррациональности ассоциируется с изображением корня. Греческие математики вместо слов “извлечь корень” говорили “найти сторону квадрата по его заданной величине (площади)”. Знак корня впервые появился в 1525 году. За это время его изображение менялось. Кто ввел это изображение?
Об этом мы узнаем, ответив на следующие вопросы:
3 слайд: На экране вопросы и следующий кроссворд.
Сколько решений имеет уравнение х2=0. (одно)
Корень какой степени существует из любого числа? (нечетной )
Как называется корень третей степени? (кубический)
Сколько решений имеет уравнение х2=а, если а >0 ? (два)
Как называется корень уравнения, который получается в результате неравносильных преобразований? (постороннний)
Корень какой степени существует только из неотрицательного числа? (четной)
И так впервые изображение корня ввёл Декарт, французский ученый. Им положено начало исследования важных свойств алгебраических уравнений.
4 слайд: На экране вопросы и следующий кроссворд.
Кто же ввел современное изображение корня? Ответим на вопросы .
Как называется равенство двух алгебраических выражений? (уравнение)
Как называют значение переменной, при котором уравнение обращается в верное числовое равенство (корень)
Какая черта личности поможет при решении иррациональных уравнений? (трудолюбие)
Какой должен быть взгляд на уравнения, что бы не вычисляя сказать ответ? (пристальный)
Как называют уравнения, если они имеют одни и те же корни или не имеют корней вообще? (равносильные)
Как называется иррациональное выражение, содержащее противоположное арифметическое действие? (сопряженное)
Это Ньютон – английский физик, открывший основные законы природы, законы Ньютона. Он ввёл современное изображение корня.
Итак, мы повторили теорию решения иррациональных уравнений, которая является фундаментом для познания мира.
Отметьте в своих рабочих карточках как вы справились с заданием.
Об истории возникновения понятия иррациональных чисел подготовила небольшое сообщение Солтыбай Ботагоз.
История иррациональных чисел восходит к удивительному открытию Пифагорийцев ещё в VI веке до н.э. А началось все с простого, казалось бы вопроса – каким числом выражается длина диагонали квадрата со стороной 1?
Пифагорийцы доказали, что √2 – нельзя выразить отношением некоторых целых чисел m и n. √2 – по их мнению вообще не было числом. Открыв новый математический объект они пришли в полное замешательство. В основе всеобщей гармонии мира, считали они, должны лежать целые числа и их отношения. Никаких других чисел они не знали. И вдруг эта гармония рушится – существуют величины, которые отношением целых чисел, в принципе – не являются.
В переводе с латыни “irrationalis” – “неразумный”. Любопытно, что в средневековой Европе наряду с “irrationalis” в ходу был еще и другой термин “surdus” – “глухой” или “немой”. Судя по такому названию, математикам средневековья иррациональные числа представлялись чем-то настолько “неразумным”, что “ни высказать, ни выслушать”. Удивление и досада, с которыми древние математики в начале восприняли иррациональные числа, впоследствии, сменились интересом и пристальным вниманием к новым математическим объектам.
Спасибо Ботагоз, за интересное сообщение. А сейчас откройте рабочие тетради, запишите число и тему урока. Сейчас мы решим небольшой тест, составленный из иррациональных уравнений. С помощью этого теста мы узнаем, в какой работе Евклида была описана необходимость введения иррациональных чисел, по которой потом занимались все творцы современной математики: Декарт и Ферма, Ньютон и Лейбниц, Колмогоров и Понтрягин. Решите уравнения у доски, и запишите буквы, под которыми находятся интервалы, содержащие корни уравнений
Эта древняя книга называлась «НАЧАЛА «она оказала наибольшее влияние на развитие европейской цивилизации.
2.2.Работаем устно.
Основные методы решения иррациональных уравнений.
Иррациональные уравнения можно решать различными методами мы с вами закрепим 4 их них:
Решение уравнений каждого метода у доски. Проверяем по слайдам. Одновременно с этим по одному человеку у доски будут решать иррациональны уравнения по карточкам.
4. Завершим наш урок самостоятельной работой.
Проверка по готовым слайдам.
5. Итоги урока. Сделайте выводы с помощью рабочей картыЮкак вы можете оценить свои знания, полученные на сегодняшнем уроке.
6. Задание на дом. № 126, № 127
Спасибо за урок. До свидания.
infourok.ru
Презентация и конспект по алгебре на тему «ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ЛОГАРИФМИЧЕСКИХ ВЫРАЖЕНИЙ» (11 класс)
Дата: 22.12.2016
Класс:11Б
ТЕМА: «ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ
ЛОГАРИФМИЧЕСКИХ ВЫРАЖЕНИЙ»
Знания и навыки, которыми должны овладеть учащиеся после изучения данного урока:
знать определение логарифма числа, основное логарифмическое тождество, свойства логарифмов;
уметь выполнять преобразования выражений, содержащих логарифмы, вычислять логарифмы.
Ход урока:
1) Логарифм – это греческое слово, которое состоит из 2-х слов: “логос”- отношение, “аритмос”- число. Значит, логарифм есть число, измеряющее отношение. В публикации тысяча шестьсот четырнадцатого года сообщалось, что Непер изобрёл логарифмы. Позже им были составлены логарифмические таблицы, которые теперь известны нам как таблицы Брадиса. Менее чем за одно столетие таблицы распространились по всему миру и сделались незаменимым вычислительным средством. В дальнейшем они были, как бы встроены в удобное устройство, чрезвычайно ускоряющее процесс вычисления – логарифмическую линейку, которой пользовались до семидесятых годов двадцатого века.
Приложение 1.
2) Логарифмом положительного числа b по основанию a, причём а больше нуля и не равно единицы, называется показатель степени, в которую нужно возвести число a, чтобы получить число b.
Это равенство, выражающее определение логарифма, называется основным логарифмическим тождеством.
ЦОР 1
Поработаем устно:
ЩЕЛЧОК
Приложение 2.
Равенство означает, что
Из определения логарифма получаются следующие важные равенства:
Например:
Приложение 3.
Перейдем к заданиям ЕНТ:
Приложение 4.
3) Для логарифма по основанию десять существует специальное обозначение и название десятичный логарифм.
Логарифм по основанию е называется натуральным логарифмом.
Например,
4) Из определения логарифма вытекают следующие его свойства. Все свойства формулируются и доказываются только для положительных значений переменных, содержащихся под знаками логарифмов.
Логарифм произведения двух положительных чисел по основанию а равен сумме логарифмов этих чисел с тем же основанием.
ЦОР 2
Например,
Задание 1.
Задание 2. Упростите выражение
Воспользуемся решением предыдущего примера. Заменим
Обратите внимание на то, что логарифм в квадрате, поэтому и сумму необходимо возвести в квадрат. Применяя формулу квадрата суммы, раскроем скобки. Приведём подобные слагаемые.
5) Логарифм частного равен разности логарифмов делимого и делителя.
ЦОР 3
Рассмотрим применение этой формулы на примере:
Задание 1. Найдите значение выражения , если
Задание 2. Найдите значение b по его логарифму
6) Логарифм степени по основанию а, равен произведению показателя степени на логарифм по тому же основанию.
ЦОР 4
Например,
Задание 1. Вычислите , если
Упростим выражение
Формула
называется формулой перехода к новому основанию.
Задание 1. Выразить через логарифм с основанием 2.
Задание 2. Вычислите
ЦОР 5
8)
ЦОР 6
Например,
Задание 1. Вычислите
Задание 2. Вычислите
9) К логарифмическим преобразованиям можно приступать, только в том случаи, если вы запомнили все свойства логарифмов. Повторив их, рассмотрим задания на преобразования логарифмических выражений с другой стороны.
Для преобразования суммы или разности логарифмических выражений иногда достаточно использовать определение логарифма, а чаще всего свойства логарифма произведения или частного.
Задание 1. Вычислите
Решим двумя способами.
1 способ, используя определение логарифма:
2 способ, опираясь на свойство логарифма частного:
Задание 2. Найдите значение выражения
Применим сначала формулу логарифма произведения, затем определение логарифма.
Основное логарифмическое тождество используется при преобразовании выражений, содержащих логарифм в показателе степени. Идея таких операций заключается в получении равных основания степени и основания логарифма.
Иногда необходимо преобразовывать выражение по свойствам логарифма и по свойствам степени, так же можно легко перейти от одного основания к другому, используя формулу перехода. В других случаях следует применять несколько свойств.
Задание 3. Вычислите
Задание 4. Найдите значение выражения
Задание 5. Найдите значение выражения
Задание 6. Представьте в виде разности логарифмов
Наибольшую трудность представляют преобразования логарифмических выражений, находящихся под радикалом. В процессе преобразований приходится рассматривать модули логарифмических выражений, для раскрытия которых требуется сравнить иррациональные числа или рациональное и иррациональное число. Будем действовать последовательно. Рассмотрим выражение, стоящее под внутренним радикалом.Подставим в исходное выражение.
Раскроем модуль, учитывая, что знаменатель положителен, а числитель отрицателен.
Меняем знаки в числителе и упрощаем.
Получим исходное выражение, равное разности логарифмов.
Такие и подобные примеры вам могут встретиться при решении заданий Единого Государственного экзамена.. Следует отметить, что с преобразованием логарифмических выражений можно встретиться и при решении уравнений и неравенств или исследовании функций, поэтому в неявном виде они могут присутствовать и в заданиях групп В и С.
10) Подведение итогов. Вопросы:
Логарифм по основанию 10 называется
- основным логарифмом
2) Какие значения может принимать x в выражении
Строго положительные3) Чему равен
a4) Чему равен
a5) Укажите соотношение, которое верно для всех x ≠ 0.
6) Укажите верное соотношение для формулы перехода к новому основанию.
7) Укажите верное равенство при
11) Контрольное тестирование.
infourok.ru
Конспект урока «Преобразование иррациональных выражений»
Домашняя работа
«Преобразование выражений, содержащих радикалы»
В – I
Вынесите множитель из-под знака корня:
а) б)
Упростите выражение:
а) б) .
Освободитесь от иррациональности в знаменателе дроби .
Расположите числа в порядке возрастания.
…………………………………………………………………
Домашняя работа
«Преобразование выражений, содержащих радикалы»
В – II
Вынесите множитель из-под знака корня:
а) б)
Упростите выражение:
а) б) .
Освободитесь от иррациональности в знаменателе дроби .
Расположите числа в порядке возрастания.
…………………………………………………………………
Домашняя работа
«Преобразование выражений, содержащих радикалы»
В – I
Вынесите множитель из-под знака корня:
а) б)
Упростите выражение:
а) б) .
Освободитесь от иррациональности в знаменателе дроби .
Расположите числа в порядке возрастания.
…………………………………………………………………
Домашняя работа
«Преобразование выражений, содержащих радикалы»
В – II
Вынесите множитель из-под знака корня:
а) б)
Упростите выражение:
а) б) .
Освободитесь от иррациональности в знаменателе дроби .
Расположите числа в порядке возрастания.
…………………………………………………………………
infourok.ru
Конспект обзорного урока «Преобразование рациональных и иррациональных выражений» (11 класс)
Обзорный урок на тему
«Преобразование рациональных и иррациональных выражений»
Цели: 1) актуализировать знания и умения по преобразованию выражений (свойства степени, корня, логарифма, тригонометрических функций)
2) решать типовые задачи из сборника заданий итоговой аттестации выпускников.
Ход урока
1. Организационный момент.
Класс делится по группам в соответствии с разделами:
1) Свойства степени с рациональным показателем;
2) Свойства корня, решение сложного радикала;
3) Свойства логарифма;
4) Свойства тригонометрических функций.
2. Актуализация знаний.
Каждая группа на бумажном планшете выписывает основные свойства тех функций, которые были распределены, таблички крепятся к доске, происходит обсуждение и запись основных свойств.
Далее среди групп раздаются карточки с заданиями обязательного компонента подготовки.
Группа «Степень с рациональным показателем»Упростите
1)
2)
Группа «Свойства корня»
Упростите
1)
2)
Группа «Логарифм»
Упростите
1) . Найдите
2) . Найдите
Группа «Свойства тригонометрических функций»
Упростите
1)
2)
Учащиеся решают задания в течение 10 минут. При этом у них есть возможность решить задания других групп. После этого учащиеся из каждой группы выходят к доске и показывают решение, обязательно указывая свойства, которые они использовали на планшетах, прикрепленных к доске.
Если задание не решено ни одной группой, задание решаем всем классом.
3. Формирование умений и навыков
В следующей части урока учащиеся решают пробные задания итоговой аттестации (Задания итоговой аттестации среди выпускников средней школы. Алматы: НЦТ, 2017). Та группа, которая решает задание быстрее всех получает балл и показывает решение у доски.
1. (В19.2) Упростите выражение
Решение:
Ответ:
2. (В23. 01) Вычислите
Решение:
Ответ: 2
3. (В17. 02) Выразите через a и b, если и
Решение:
Ответ:
3. Рефлексия
Один участник из каждой группы называет самые используемые свойства из своей группы. После чего происходит обмен вопросами между группами. Группа, ответившая на большее количество вопросов получает балл. Подводятся итоги урока, выставляются оценки по группам.
4. Домашнее задание.
infourok.ru
Урок по алгебре в 11-м классе по теме: «Иррациональные уравнения»
Разделы: Математика
Цель: Расширение и углубление представления о методах решения иррациональных уравнений.
I. Вступление:
Определение иррационального уравнения
Методы решения иррациональных уравнений (возведение обеих частей в одну и ту же степень, введение новых переменных).
II. Рассмотрение новых методов решения иррациональных уравнений.
1. Метод возведения обеих частей в одну и ту же степень
№1. .
Если в уравнении несколько радикалов, то уравнение приходится возводить в степень неоднократно. В этом случае обычно один из радикалов уединяют, т. е. располагают в одной из частей уравнения, а всё остальное переносят в другую частью.
, (посторонний корень)
Ответ: 2.
Мы выполнили проверку, т. к. возведение обеих частей уравнения в одну и ту же степень может привести к появлению посторонних корней, потому, например, что неверное равенство при возведении в квадрат может дать верное неравенство (н.), но при возведении в квадрат получим (в.)
№2. .
Возведём обе части уравнения в куб.
или .
Подстановкой найденных значений х в данное уравнение убеждаемся, что его корнем является только х = -0,5.
Ответ: -0,5.
Замечание! При возведении в куб в первый раз мы получаем равносильное уравнение. Однако дальнейшая замена выражения на выражение могла привести к появлению постороннего корня, что показала проверка.
2. Метод введения новых переменных
Ещё один из способов избавиться от радикалов – ввести новую переменную.
№3. .
Уединим корень в правую часть.
, сравнив выражения в левой части и под знаком радикала, заметим
, пусть, , тогда , имеем . Проверим их
Ответ:
Умение удачно ввести новую переменную приходит не сразу. Удачный выбор новой переменной делают уравнение более прозрачным. Поэтому нет смысла торопиться начинать преобразовывать, сначала лучше убедиться в том, нельзя ли уравнение записать проще, введя новую переменную.
№4. .
Пусть , .
, возведём обе части в квадрат.
,
,
,
. Проверка показывает, что – посторонний корень. Получим: .
Ответ: .
3. Метод оценки или использования области значений функции
№5. .
то следовательно, т.е. данное уравнение не имеет смысла.
Ответ:
№6. .
Перепишем его так: . следовательно, получим
Ответ:
№7. .
Избавимся от иррациональности в знаменателях дробей левой части уравнения, получим
.
После возведения в квадрат обеих частей получим
Левая часть в своей области определения >0, следовательно , корней нет.
Ответ:
4. Функционально-графический метод
№8. .
1) Рассмотрим функцию Найдём Знаки видны на рисунке 1.
Получим, что х = 0, х = 3 – точка минимума, х = 1 – точка максимума.
График функции изобразим схематично (рисунок 2).
Заметим, что .
2) Рассмотрим функцию .
Преобразуем её:
.
Заметим, что .
3) Так как , то заданное уравнение сводится к системе уравнений:
Оба этих уравнения, как мы уже отметили, обращаются в верное равенство при . Это единственный корень уравнения.
Ответ: 3.
5. Векторный метод
№9.
Найдём ОДЗ: .
Пусть , то , 2, т. е. . Так как , где – угол между векторами u и v, то , следовательно, и – коллинеарны, поэтому соответствующие координаты пропорциональны:
х = 1,44,
Ответ: 1,44.
6. Прямое использование ОДЗ
№10. .
Нахождение ОДЗ в этом уравнении представляет собой достаточно трудоёмкую работу (попробуйте!) и совершенно ненужную задачу. Возведём обе части в квадрат:
,
,
, (посторонний корень).
Ответ: 1.
№11.
В этом уравнении нахождение ОДЗ приносит несомненную пользу.
Графически переменные можно видеть на рисунке 3.
Используя числовую прямую, выясним, что ОДЗ состоит из х = 0 и х = 1. Проверка показывает, что х = 0 – посторонний корень.
Ответ: 1.
Итак, лучше искать ОДЗ или делать проверку? Истина, как всегда, посередине.
7. Метод мажорант
№12. .
Преобразуем подкоренные выражения, выделив полный квадрат, тогда
Значение левой части , значение правой части . Равенство при условии, что обе части равны 5 при одном и том же значении х.
х = -1. Проверим и убедимся в том, что х = -1 – корень уравнения.
Ответ: -1.
8. Преобразование выражения
№13. ОДЗ .
или .
Решение стандартно.
Ответ: -1; 0; 3.
9. Использование монотонности функции
№14. .
ОДЗ , .
Левая часть уравнения – сумма убывающих функций, а правая – возрастающая функция, следовательно, уравнение имеет единственный корень. Так как , то . Подберём х, он равен 7.
Ответ: 7.
Обзор “новинок”
№ 15. ОДЗ
x+3=0 или x+3=3x-9
x=3 (не удовлетворяет) x=6
Если , то
Ответ: -6; 6
№ 16.
5 — 2cos2x > 0, 2 — cos2,5x > 0, при всех X R
7 – 3cos2,5x = 4;
cos2,5x = 1, x = 4/5 n, n Z
Ответ: 4/5 n Z
№ 17.
,
Ответ: -1.
№ 18.
ОДЗ
Ответ: -П; П
III. Выводы
IV. Домашнее задание. Разобрать решения этих уравнений, решить их самостоятельно и свериться.
12.01.2007
xn--i1abbnckbmcl9fb.xn--p1ai
Разработка зачетной работы по алгебре по теме «Тождественные преобразования иррациональных алгебраических выражений» (11 класс)
Зачётная работа по теме: « Тождественные преобразования иррациональных алгебраических выражений» (№1)
I .Выполните преобразования выражений, содержащих степени с рациональными показателями:
1.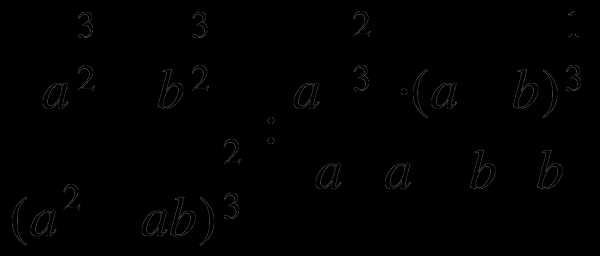 ,вычислите, если a=1,2 ; b=0,6.
,вычислите, если a=1,2 ; b=0,6.
2. 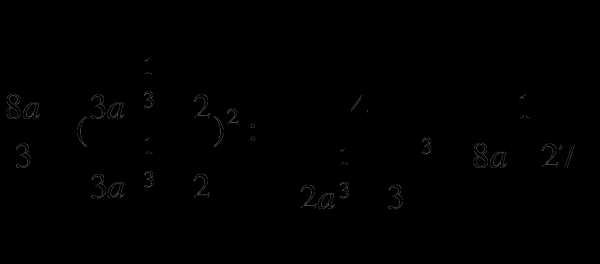 3.
3.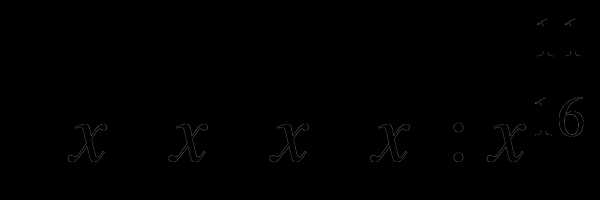
4. , вычислите, если a=72,25 ; b=12,25 5.
6. 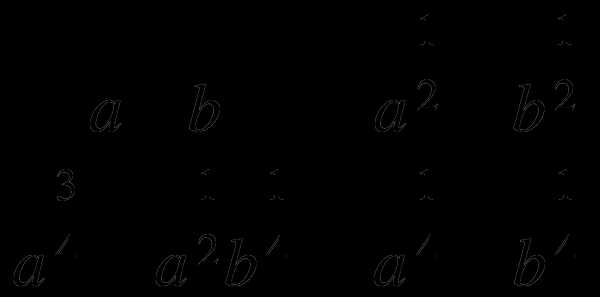 , вычислите, если a=
, вычислите, если a=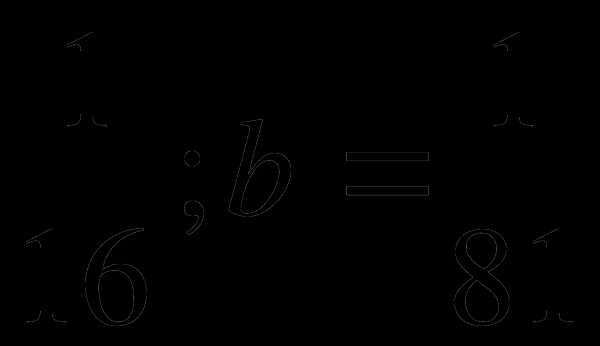
7.
8.  9.
9.
II.Выполните преобразование иррациональных выражений:
1.
2.
3.
4.
5. 6., если
7.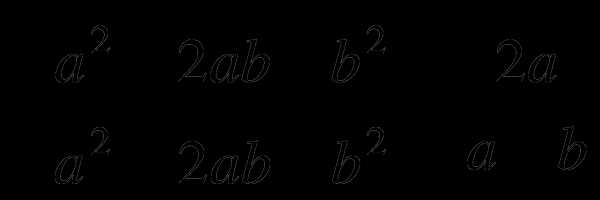 , если 8.
, если 8.
9.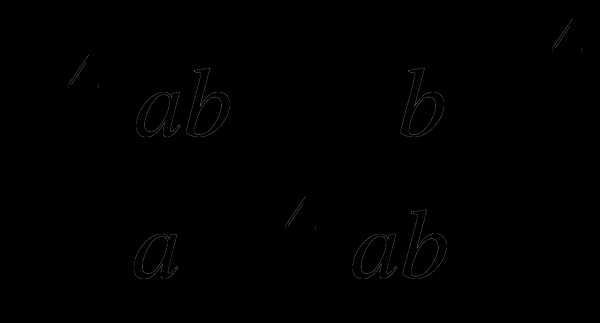 10.
10.
11., если 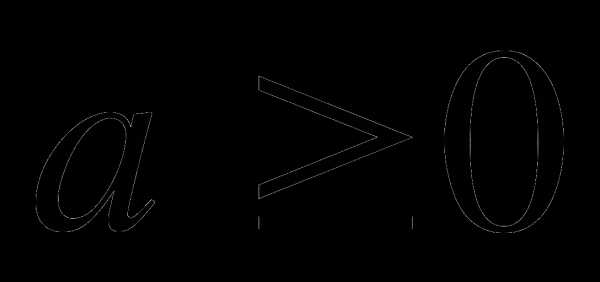
12.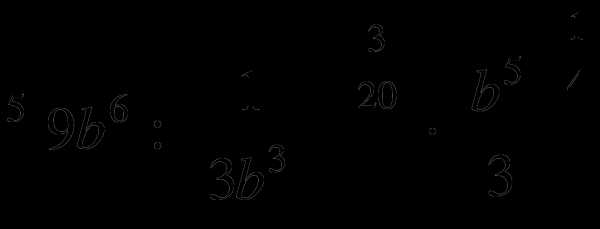 13.
13. 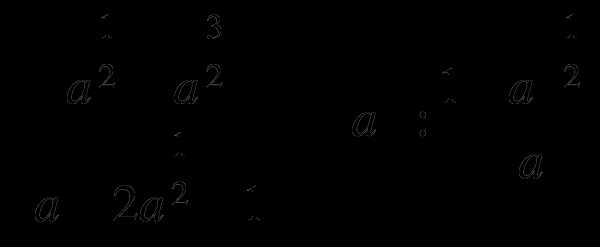
14.
15.
16.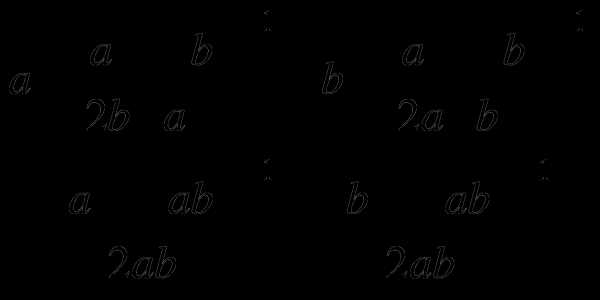
17.
18.
19.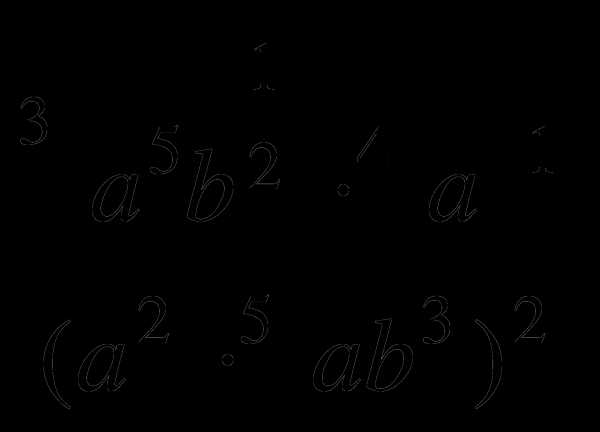 20.
20.
infourok.ru

