Повторение 11 класс тригонометрия: Решение тригонометрических уравнений. Алгебра 11 класс. Вводное повторение – Урок-повторение по теме «Тригонометрические уравнения и неравенства» (11-й класс)
Цель:
- Повторить и систематизировать раннее изученный материал по решению простейших тригонометрических уравнений.
- Повторить методы решения уравнений.
- Решить сложные уравнения, встречающиеся на ЕГЭ.
- Проверить усвоение материала.
1 урок: «Повторение теоретического материала и решение простейших уравнений» (используя компьютерную презентацию).
2-3 уроки: «Семинар по решению одного уравнения несколькими способами».
4-5 уроки: Решение более сложных уравнений, предложенными способами.
6 урок: Контрольное тестирование по теме, с использованием компьютерной программы.
Урок №1: «Повторение теоретического материала и решение простейших уравнений»
Цель (слайд 2)
- Повторить и систематизировать раннее изученный материал по решению простейших тригонометрических уравнений.
- Решение уравнений, с выбором ответов.
- Воспитывать умение применять полученные знания.
Ход урока:
- Решение уравнений вида .
- Решение уравнений вида
- Решение уравнений вида и
- Итог урока.
Решение сложных уравнений сводится к решению простейших уравнений:
и
Вспомним, как они решаются. (Используется презентация, «по щелчку мышки»)
1. Решение простейших тригонометрических уравнений вида: (слайд 3)
.
где
Частные случаи (слайд 4)
Решить уравнения:
Ответ: .
Ответ: .
Ответ: .
Решите самостоятельно и найдите правильный ответ (найти соответствие):
№ уравнения | Уравнение | № ответа | Ответ |
1 | a | ||
2 | b | ||
3 | c | ||
4 | d | ||
5 | e |
2. Решение простейших тригонометрических уравнений вида: (слайд 5)
, где
Частные случаи: (слайд 6)
Решить уравнения:
Ответ: .
Ответ: .
Ответ: .
Решите самостоятельно и найдите правильный ответ (найти соответствие):
№ уравнения | Уравнение | № ответа | Ответ |
1. | a | ||
2. | b | корней нет | |
3. | c | ||
4. | d | ||
5. | e |
3. Решение простейших тригонометрических уравнений вида: (слайд 7)
Решить уравнения:
1.
Ответ: .
2.
Ответ: .
3.
Ответ: .
Решите самостоятельно и найдите правильный ответ (найти соответствие)
№ уравнения | Уравнение | № ответа | Ответ |
1. | a | ||
2. | b | ||
3. | c | ||
4. | d |
Решение простейшего тригонометрического уравнения вида:
решение аналогичное предыдущему случаю.
4. Итог урока:
Сегодня на уроке мы повторили решение простейших тригонометрических уравнений. На следующем уроке будем повторять методы решения тригонометрических уравнений, для этого класс разбивается на 7 небольших групп, каждая из которых покажет выбранный метод решения уравнения:
.
Приложение
Можно обращаться за консультацией.
Дома повторить пункты № 9,11, учебник под редакцией А.Н.Колмогорова, стр. 93-106, учебник под редакцией А.Г.Мордковича.
 Описание слайда: 2 слайд
Описание слайда: 2 слайд  Описание слайда:
Описание слайда:Тригонометрия-это часть геометрии, где с помощью тригонометрических функций связываются элементы треугольника. Тригонометрия-это объект математического анализа, где тригонометрические уравнения изучаются методами алгебры.
3 слайд Описание слайда:
Описание слайда:Тригонометрия в древности являлась вспомогательным разделом астрономии. Древнегреческие ученые разработали «тригонометрию хорд». Древнеиндийские ученые заменили хорды синусами. В VIII веке математики Востока превратили тригонометрию в самостоятельную математическую дисциплину. Ими были введены другие тригонометрические функции и составлены таблицы. Окончательный вид тригонометрия приобрела в XVIII веке в трудах Л.Эйлера.
4 слайд
Синусом угла α называется отношение ординаты точки В к R. Косинусом угла α называется отношение абсциссы точки В к R. Тангенсом угла α называется отношение ординаты точки В к ее абсциссе. Котангенсом угла α называется отношение абсциссы точки В к ее ординате. R α R B (x;y) y x
5 слайд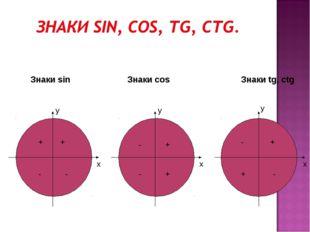 Описание слайда:
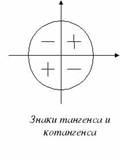
Описание слайда:x x x y y y Знаки sin Знаки cos Знаки tg, ctg + + — — — — + + — + + —
6 слайд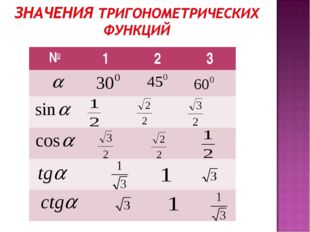 Описание слайда:
Описание слайда:№ 1 2 3
7 слайд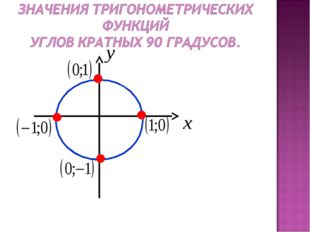 Описание слайда:
Описание слайда:  Описание слайда:
Описание слайда:sin² α + cos² α = 1 tg α · ctg α = 1 tg α = sin α ÷ cos α ctg α = cos α ÷ sin α 1 + tg² α = 1 ÷ cos² α 1 + ctg² α = 1 ÷ sin² α
9 слайд Описание слайда: 10 слайд
Описание слайда: 10 слайд  Описание слайда:
Описание слайда:sin (α + β) = sin α · cos β + sin β · cos α sin (α — β) = sin α · cos β — sin β · cos α cos (α + β) = cos α · cos β — sin α · sin β cos (α — β) = cos α · cos β + sin α · sin β tg (α + β) = (tg α + tg β) ÷ (1 — tg α · tg β) tg (α — β) = (tg α — tg β) ÷ (1 + tg α · tg β) ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β — ctg α) ctg (α — β) = (ctg α · ctg β — 1) ÷ (ctg β + ctg α)
11 слайд
cos 2α = cos² α — sin² α cos 2α = 2cos² α — 1 cos 2α = 1 — 2sin² α sin 2α = 2sin α · cos α tg 2α = (2tg α) ÷ (1 — tg² α) ctg 2α = (ctg² α — 1) ÷ (2ctg α)
12 слайд Описание слайда: 13 слайд
Описание слайда: 13 слайд  Описание слайда:
Описание слайда:cost = a sint = a
14 слайд Описание слайда: 15 слайд
Описание слайда: 15 слайд 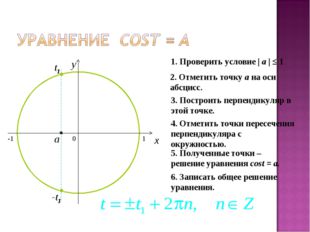 Описание слайда:
Описание слайда:0 x y 2. Отметить точку а на оси абсцисс. 3. Построить перпендикуляр в этой точке. 4. Отметить точки пересечения перпендикуляра с окружностью. 5. Полученные точки – решение уравнения cost = a. 6. Записать общее решение уравнения. 1. Проверить условие | a | ≤ 1 a t1 -t1 -1 1
16 слайд Описание слайда:
Описание слайда:0 x y 2. Отметить точку а на оси ординат. 3. Построить перпендикуляр в этой точке. 4. Отметить точки пересечения перпендикуляра с окружностью. 5. Полученные точки – решение уравнения sint = a. 6. Записать общее решение уравнения. 1. Проверить условие | a | ≤ 1 a t1 π-t1 -1 1
17 слайд Описание слайда:
Описание слайда:1 1 х у 0
18 слайд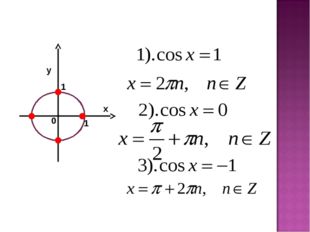 Описание слайда:
Описание слайда:1 1 х у 0
19 слайд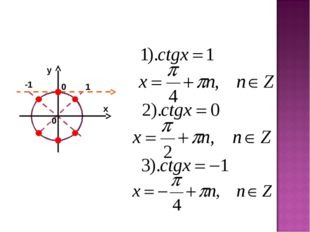 Описание слайда:
Описание слайда:0 х у 0 1 -1
20 слайд Описание слайда:
Описание слайда:0 x y -1 1
21 слайд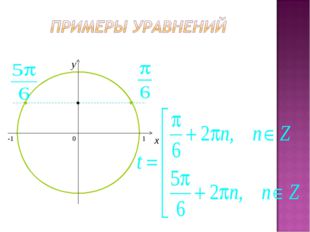 Описание слайда:
Описание слайда:0 x y -1 1
22 слайд Описание слайда:
Описание слайда:cost >a, cost ≤ a sint >a, sint ≤ a
23 слайд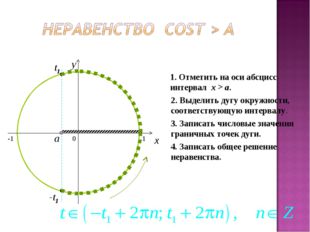 Описание слайда:
Описание слайда:0 x y 1. Отметить на оси абсцисс интервал x > a. 2. Выделить дугу окружности, соответствующую интервалу. 3. Записать числовые значения граничных точек дуги. 4. Записать общее решение неравенства. a t1 -t1 -1 1
24 слайд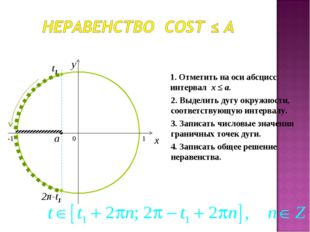 Описание слайда:
Описание слайда:0 x y 1. Отметить на оси абсцисс интервал x ≤ a. 2. Выделить дугу окружности, соответствующую интервалу. 3. Записать числовые значения граничных точек дуги. 4. Записать общее решение неравенства. a t1 2π-t1 -1 1
25 слайд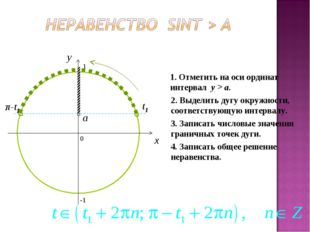 Описание слайда:
Описание слайда:0 x y 1. Отметить на оси ординат интервал y > a. 2. Выделить дугу окружности, соответствующую интервалу. 3. Записать числовые значения граничных точек дуги. 4. Записать общее решение неравенства. a t1 π-t1 -1 1
26 слайд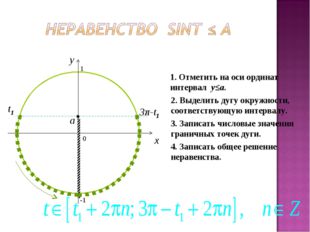 Описание слайда:
Описание слайда:0 x y 1. Отметить на оси ординат интервал y≤a. 2. Выделить дугу окружности, соответствующую интервалу. 3. Записать числовые значения граничных точек дуги. 4. Записать общее решение неравенства. a 3π-t1 t1 -1 1
27 слайд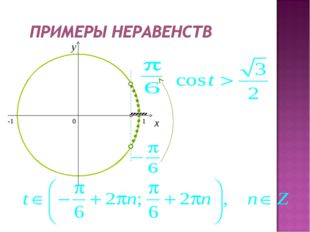 Описание слайда:
Описание слайда:0 x y -1 1
28 слайд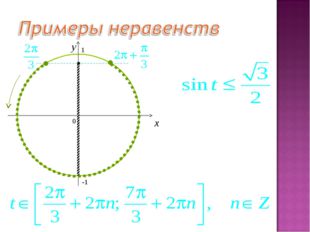 Описание слайда:
Описание слайда:0 x y -1 1

Курс повышения квалификации
Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДВ-117009
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Выберите документ из архива для просмотра:
Выбранный для просмотра документ Тренажер 1 Вычисления и преобразования со степенями и корнями.doc
Выбранный для просмотра документ Тренажер 10 Значения тригонометрических функций.doc
Выбранный для просмотра документ Тренажер 11 Формулы приведения.doc
Выбранный для просмотра документ Тренажер 12 Основные формулы тригонометрии.doc
Выбранный для просмотра документ Тренажер 13 Основные формулы тригонометрии.doc
Выбранный для просмотра документ Тренажер 14 Простейшие тригонометрические уравнения.doc
Выбранный для просмотра документ Тренажер 15 Простейшие тригонометрические неравенства.doc
Выбранный для просмотра документ Тренажер 16 Область определения тригонометрических функций.doc
Выбранный для просмотра документ Тренажер 17 Периодичность тригонометрических функций.doc
Выбранный для просмотра документ Тренажер 18 Четность тригонометрических функций.doc
Выбранный для просмотра документ Тренажер 19 Монотонность тригонометрических функций.doc
Выбранный для просмотра документ Тренажер 2 Преобразование уравнений.doc
Выбранный для просмотра документ Тренажер 3 Показательные уравнения.doc
Выбранный для просмотра документ Тренажер 4 Показательные неравенства.doc
Выбранный для просмотра документ Тренажер 5 Вычисление логарифмов.doc
Выбранный для просмотра документ Тренажер 6 Логарифмические уравнения.doc
Выбранный для просмотра документ Тренажер 7 Логарифмические неравенства.doc
План — конспект урока по алгебре в 11 классе Тема урока: «Повторение. Преобразование тригонометрических выражений»
Учитель математики — Григоренко С. В.
Пояснительная записка
Вашему вниманию представлен урок алгебры в 11 классе по теме «Повторение. Преобразование тригонометрических выражений». Данный урок является уроком повторения, применения знаний и умений по материалу, пройденному в 10 классе, проводится в форме турнира и относится к нетрадиционным видам уроков.
Основная цель по содержанию – повторение основных формул тригонометрии в преобразовании тригонометрических выражений.
Урок опирается на знания, полученные учащимися при изучении тем раздела: «Тригонометрические формулы», пройденного в курсе алгебры 10 класса. Материал, рассмотренный на данном уроке, является очень важным в курсе, так как является основой при преобразовании тригонометрических выражений и при решении тригонометрических уравнений.
Материалы урока могут быть использованы учителями, преподающими математику на базовом уровне. Учебник для общеобразовательных учреждений «Алгебра 10-11» Ш. А. Алимов и др.
Цель Повторение основных формул тригонометрии и их применение в преобразовании тригонометрических выражений. Помочь учащимся осознать практическую значимость учебного материала.
Задачи
Образовательные: воспроизведение и коррекция опорных знаний по теме; совершенствование навыков применения основных тригонометрических формул и формул приведения; формирование навыков решения экзаменационных задач.
Развивающие: развивать вычислительные навыки, логическое мышление учащихся, умение обобщать, систематизировать на основе сравнения, делать выводы; развивать память, речь.
Воспитательные: воспитывать чувство взаимопомощи, сотрудничества, серьезное отношение к своим учебным обязанностям.
Тип урока: обобщающее повторение.
Форма урока: Практикум с элементами исследования
Оборудование: дидактические карточки с заданиями, таблицы с формулами, компьютер, мультимедийный проектор.
Основные этапы урока:
Организационный момент
Мотивация
Турнир
Подведение итогов урока
Ход урока
Учащиеся рассажены за 3 стола (по 2 парты) группами по 6 человек в группе
1.Организационный момент: Приветствие учащихся, сообщение темы урока, цели (повторить тригонометрические формулы и их использование при преобразовании тригонометрических выражений), создание благоприятной, дружеской атмосферы. (слайд 1) — 2 минуты
2.Мотивация
Для успешного решения задач по тригонометрии необходимо уверенное владение многочисленными формулами. Тригонометрические формулы надо помнить. Разучивание тригонометрических формул в школе не для того чтобы вы всю оставшуюся жизнь вычисляли синусы и косинусы, а для того чтобы ваш мозг приобрел способность работать. Правильно выбранная формула часто позволяет существенно упростить решение, поэтому весь изученный материал данной темы стоит держать в зоне своего внимания. Знания, умения, навыки полученные в процессе работы гарантируют успешное выполнение соответствующих заданий ЕГЭ.
Девиз урока: «Не бойтесь формул! Учитесь владеть этим инструментом Человеческого гения! В формулах заключено величие и могущество разума…» (Марков А.А.) (слайд 2)
Сегодня наш урок будет проходить в форме математического турнира между тремя командами. Победит та команда, которая наберет большее количество очков. Желаю всем командам удачи!
Команды сообщают о готовности к соревнованию. – 3 минуты
3. Турнир
Тур 1. Викторина
Правила конкурса. Командам предлагается ответить на вопросы. Право ответа предоставляется той команде, которая первой поднимет руку. В случае неправильного ответа, на вопрос может ответить другая команда. За каждый правильный ответ команда получает 1 балл. (слайды 2 – 15) — 10 минут
Тур 2. Теоретический «Кто больше знает формул тригонометрии?».
Команды в течение 5 минут записывают на листках известные тригонометрические формулы. За каждую правильно записанную формулу команде присуждается 1 балл.
(слайд 16)
Тур 3. Вычислите
Каждой команде предлагается карточка, в которой содержатся задания на вычисление тригонометрических выражений. Команды коллективно выполняют задания в течение 10 минут. По истечении времени, команды сдают свои решения. Каждый верный ответ оценивается в 1 балл. (слайд 17) + приложение 1
Тур 4. Упрощение выражений
Командам предлагается выполнить задания на упрощение тригонометрических выражений (всего 7 заданий). На решение каждого задания командам предоставляется до 2 минут. Но это время может быть сокращено. Право первоочередного ответа предоставляется команде, поднявшей руку первой. Участник команды выходит к доске и показывает решение. Если решение неверно, то на вопрос может ответить другая команда. За каждое верное решение команде присуждается 1 балл.
(слайды 18-25) – 20 минут
4.Подведение итогов турнира.
Объявление количества баллов, которые набрала каждая из команд
4.Подведение итогов урока.
Выставление оценок. (Капитаны оценивают участников своей команды, команда оценивает капитана)
Благодарю вас за труд, старание и надеюсь, что урок был для вас, ребята, интересным соревнованием математических знаний и умений. Не забывайте закреплять полученные знания и умения.
Один из известных венгерских математиков Дьордь Пойа сказал такие слова «Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их!»
5.Постановка домашнего задания
Тренажер «Преобразование тригонометрических выражений». (Приложение 2)
Приложение 2
Тренажер «Преобразование тригонометрических выражений»
1.Упростить выражения:
а) 1 – cos2 б) sin2 — 1
в) cos2 + ( 1 – sin2) г) sin2 + 2 cos2 — 1
д) ( 1 — sin)(1 + sin) е) (cos- 1)( cos+1)
ё) 1 — sin2 — cos2 ж) cos2 — (1 — 2 sin2 )
з) sincostq и) sincosctq — 1
к) sin2 + cos2 +tq2 л) tqctq+ ctq2
м) н)
2.Докажите, что при всех допустимых значениях значение выражения не зависит от :
а) б)
в) г)
д) (sin+cos)2 – 2sincos е) sin4+ cos4+2sin2cos2
ё) ж)
3. Докажите тождество:
а) (sin+sin)(sin- sin) – (cos+cos)( cos- cos) = 0
б) ctq2 — cos2 = ctq2 cos2
в) = sin2cos2 г) +2sincos= 1
д) = cos- sin е) (1+tq)2 + (1 — tq)2 =
ё) = 2tq ж) = tqtq
Приложение 1
ВЫЧИСЛИТЕ
1.Найдите значение выражения:
2 sin- 2 cos+ 3 tq — ctq
2.Известно, что .
Найдите: sin , если cos = — 0,6.
3.Найдите значения тригонометрических функций угла , если известно, что:
сtq = — 2,5 и — угол IV четверти.
4.Вычислите
а) ;
б) .
В)
Г)
Д)
Приложение 3
Турнир «Преобразование тригонометрических выражений»
2
3
Приложение 4
Презентация



























На этом уроке мы повторим тригонометрические уравнения и вычисления.
В начале урока мы вспомним определения прямой и обратной задачи для некоторой функции и повторим определения основных тригонометрических функций. Решим несколько простейших тригонометрических уравнений и более сложное уравнение с использованием замены переменной.
В конце урока мы вспомним формулы двойного и половинного аргумента, а также формулу универсальной тригонометрической подстановки и решим обобщенную задачу на эту тему.
Тема: Повторение курса алгебры 10 класса
Урок: Тригонометрические уравнения, вычисления
С любой конкретной функцией связаны две задачи: прямая и обратная.
Пусть 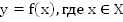 .
.
Прямая задача:
Дано: задано значение аргумента 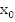 .
.
Найти: соответствующее значение функции 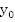 .
.
Обратная задача:
Дано: задано значение функции 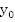 .
.
Найти: множество всех значений аргумента 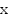 , при которых
, при которых 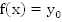 (найти все значения
(найти все значения 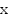 , удовлетворяющие данному соотношению).
, удовлетворяющие данному соотношению).
Решение прямой и обратной задачи зависит от закона, по которому каждому значению аргумента ставится в соответствие единственное значение функции.
Напомним каждый из этих законов для тригонометрических функций.
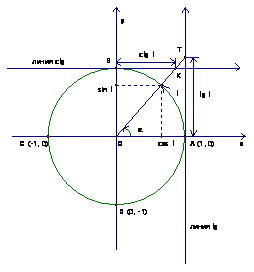
Рис. 1.
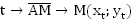
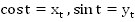
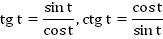
Таким образом, заданы функции 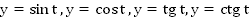 .
.
Заметим, что 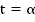 , если
, если 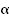 вычислять в радианах.
вычислять в радианах.
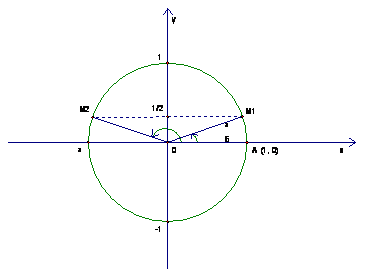
После сделанных напоминаний рассмотрим подробно следующее уравнение:
Дано: 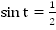 .
.
Найти: все значения аргумента 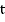 , синус которых равен
, синус которых равен  .
.
Начнем с повторения основных типов заданий, которые мы рассмотрели в теме «Тригонометрия» и решим несколько нестандартных задач.
Задача №1. Выполнить перевод углов в радианы и градусы: а) 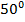 ; б)
; б) 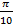 .
.
а) Воспользуемся формулой перевода градусов в радианы
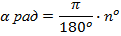
Подставим в нее указанное значение 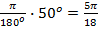 .
.
б) Применим формулу перевода радиан в градусы
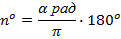
Выполним подстановку 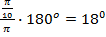 .
.
Ответ. а) 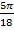 ; б)
; б) 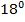 .
.
Задача №2. Вычислить: а) 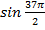 ; б)
; б) 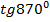 .
.
а) Поскольку угол далеко выходит за рамки табличного, уменьшим его с помощью вычитания периода синуса. Т.к. угол указан в радианах, то и период будем рассматривать как 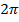 .
.
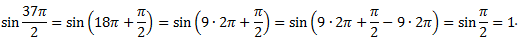
б) В данном случае ситуация аналогичная. Поскольку угол указан в градусах, то и период тангенса будем рассматривать как 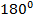 .
.
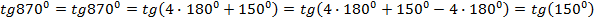
Полученный угол хоть и меньше периода, но больше 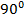 , а это значит, что он относится уже не к основной, а к расширенной части таблицы. Чтобы не тренировать лишний раз свою память запоминанием расширенной таблицы значений тригофункций, вычтем период тангенса еще раз:
, а это значит, что он относится уже не к основной, а к расширенной части таблицы. Чтобы не тренировать лишний раз свою память запоминанием расширенной таблицы значений тригофункций, вычтем период тангенса еще раз:
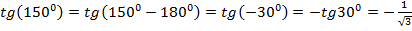 .
.
Воспользовались нечетностью функции тангенс.
Ответ. а) 1; б) 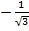 .
.
Задача №3. Вычислить 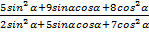 , если
, если 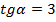 .
.
Приведем все выражение к тангенсам, разделив числитель и знаменатель дроби на 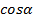 . При этом, можем не бояться, что
. При этом, можем не бояться, что 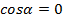 , т.к. в таком случае значения тангенса не существовало бы.
, т.к. в таком случае значения тангенса не существовало бы.
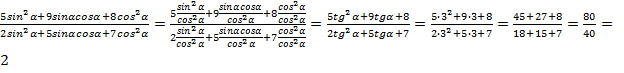
Ответ. 2.
Задача №4. Упростить выражение 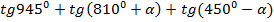 .
.
Указанные выражения преобразовываются с помощью формул приведения. Просто они непривычно записаны с использованием градусов. Первое выражение вообще представляет собой число. Упростим все тригофункции по очереди:
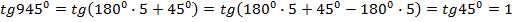
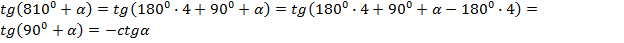
Т.к. 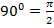 , то функция меняется на кофункцию, т.е. на котангенс, и угол
, то функция меняется на кофункцию, т.е. на котангенс, и угол 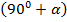 попадает во вторую четверть, в которой у исходного тангенса знак отрицательный.
попадает во вторую четверть, в которой у исходного тангенса знак отрицательный.
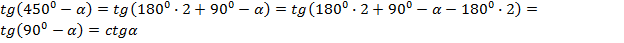
По тем же причинам, что и предыдущем выражении, функция меняется на кофункцию, т.е. на котангенс, а угол 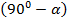 попадает в первую четверть, в которой у исходного тангенса знак положительный.
попадает в первую четверть, в которой у исходного тангенса знак положительный.
Подставим все в упрощаемое выражение:
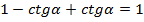 .
.
Ответ. 1.
Задача №5. Упростить выражение 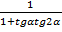 .
.
Распишем тангенс двойного угла по соответствующей формуле и упростим выражение:
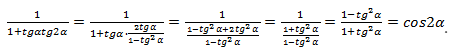
Последнее тождество является одной из формул универсальной замены для косинуса.
Ответ.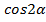 .
.
Задача №6. Вычислить 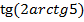 .
.
Главное, это не сделать стандартной ошибки и не дать ответ, что выражение равно 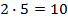 . Воспользоваться основным свойством арктангенса нельзя пока возле него присутствует множитель в виде двойки. Чтобы от него избавиться распишем выражение по формуле тангенса двойного угла
. Воспользоваться основным свойством арктангенса нельзя пока возле него присутствует множитель в виде двойки. Чтобы от него избавиться распишем выражение по формуле тангенса двойного угла 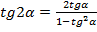 , при этом относимся к
, при этом относимся к 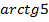 , как к обыкновенному аргументу.
, как к обыкновенному аргументу.
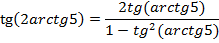
Теперь уже можно применять основное свойство арктангенса, вспомним, что на его численный результат ограничений нет.
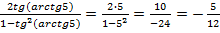 .
.
Ответ.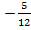 .
.
Задача №7. Решить уравнение 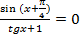 .
.
При решении дробного уравнения, которое приравнивается к нулю, всегда указывается, что числитель равен нулю, а знаменатель нет, т.к. на ноль делить нельзя.
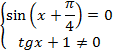
Первое уравнение представляет собой частный случай простейшего уравнения, которое решается с помощью тригонометрической окружности. Вспомните самостоятельно этот способ решения. Второе неравенство решается как простейшее уравнение по общей формуле корней тангенса, но только с записью знака неравно.
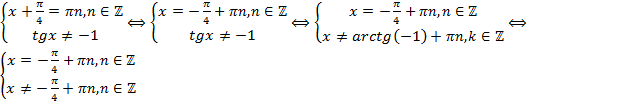
Как видим, одно семейство корней исключает другое точно такое же по виду семейство не удовлетворяющих уравнению корней. Т.е. корней нет.
Ответ. Корней нет.
Задача №8. Решить уравнение 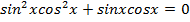 .
.
Сразу заметим, что можно вынести общий множитель и проделаем это:
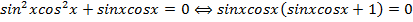
Уравнение свелось к одной из стандартных форм, когда произведение нескольких множителей равно нулю. Мы уже знаем, что в таком случае или один из них равен нулю или другой, или третий. Запишем это в виде совокупности уравнений:
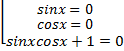
Первые два уравнения являются частными случаями простейших, с подобными уравнениями мы уже многократно встречались, поэтому сразу укажем их решения. Третье уравнение приведем к одной функции с помощью формулы синуса двойного угла.
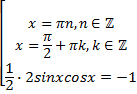
Решим отдельно последнее уравнение:
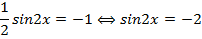
Данное уравнение не имеет корней, т.к. значение синуса не могут выходить за пределы 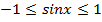 .
.
Таким образом, решением является только два первых семейства корней, их можно объединить в одно, что легко показать на тригонометрической окружности:
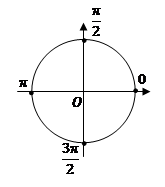 |
Это семейство всех половин 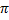 , т.е.
, т.е. 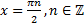
Ответ.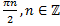 .
.
Перейдем к решению тригонометрических неравенств. Сначала разберем подход к решению примера без использования формул общих решений, а с помощью тригонометрической окружности.
Задача №9. Решить неравенство 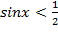 .
.
Изобразим на тригонометрической окружности вспомогательную линию, соответствующую значению синуса равному  , и покажем промежуток углов, удовлетворяющих неравенству.
, и покажем промежуток углов, удовлетворяющих неравенству.
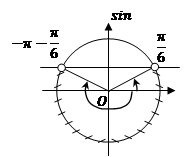 |
Очень важно понять, как именно указывать полученный промежуток
Материалы к зачету по теме «Тригонометрические уравнения и неравенства»
ПРОСТЕЙШИЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
1. Уравнение sin x = a имеет решение, если −1 ≤ a ≤ 1.
x1 = α1; x2 = α2. Учитывая периодичность функции синус, получиммножества корней уравнения sin x = a:
|
2. Уравнение cos x = a имеет решение, если −1 ≤ a ≤ 1.
Учитывая периодичность функции косинус, получиммножества корней уравнения cos x = a:
|
3. Уравнение tg x = a имеет решение при любом а, так как область значений тангенса — вся числовая ось.
Значит уравнение tg x = a на этом интервале имеет единственный корень. Учитывая, что тангенспериодическая функция, то множества решений уравнения записывают так: tg x — это ордината точки Т, пересечения прямой ОР1с линией тангенсов Р0Т. |
4. Уравнение сtg x = a имеет решение при любом а, так как область значений котангенса — вся числовая ось.
Уравнение сtg x = a имеет единственный корень. Учитывая, что котангенс периодическая функция, то множества решений уравнения записывают так:
Исключением из приведенных выше рассуждений является то, что линия котангенсов параллельна оси абсцисс.
ЧАСТНЫЕ СЛУЧАИ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
sin x = a и cos x = a.
Уравнение | Решение |
Тригонометрический лист для класса 11
(1) Укажите квадрант, в котором лежит угол каждой данной меры:
(i) 25◦ (ii) 825◦ (iii) −55◦ (iv) 328◦ (v) -230◦
Solution
9 ) Для каждого заданного угла найдите общий угол с мерой θ, такой что 0◦ ≤ θ <360◦(i) 395◦ (ii) 525◦ (iii) 1150◦ (iv) −270◦ (v) −450◦
Solution
(3) Если cosθ — b sinθ = c, показать, что sinθ + b cosθ = ± √a2 + b2 — c2.Solution
(4) Если sinθ + cosθ = m, показать, что cos6θ + sin6θ = 4–3 (m2–1) 2/4, где m2 ≤ 2. Solution
(5) If (cos4 α / cos700064 α / cos700064 α / + (sin4 α / sin2 β) = 1, докажите, что
(i) sin4 α + sin4 β = 2sin2 α sin2 β
(ii) (cos4 β / cos2 (7) Solution (8) Если tan2 θ = 1 — k2, показать, что sec θ + tan3 θ cosec θ = (2-k2) 3/2. Также найдите значения k, для которых этот результат выполняется. Solution (9) Если sec θ + tanθ = p, получить значения sec θ, tan θ и sin θ в терминах p Solution (10) Если cot θ (1 + sinθ) = 4m и cot θ (1 — sin θ) = 4n, то докажите, что (m2 — n2) 2 = mn Solution (11) Если cosec θ — sinθ = a3 и sec θ — cos θ = b3, то докажите, что a2b2 Вопрос 1: Если кроватка θ (1 + sin θ) = 4м и кроватка θ (1 — sin θ) = 4n, то докажите, что (m2 — n2) 2 = mn Ответ: 9000ot000θ θ2 (1 000 и 000) θ 2 (1 000 и 000) θ 2 (1 000 и 000) θ 2 (1 000 и 000) θ 2 (1 000 и 000) θ 2 (1 000 и 000) θ 2 (1 000 и 000) θ 2 (1 000 и 000) θ 2 (1 000 и 000) θ 2 (1 000 и 000) θ 1 (2 000 000 000) θ 1 (2 000 000 000) 0 000 (2 000) = 2 000 1 cot θ (1 — sin θ) = 4n m = [cot θ (1 + sin θ)] / 4 n = [cot θ (1 — sin θ)] / 4 m2 = [cot θ (1 + sin θ) / 4] 2 = [Cot2 θ (1 + sin θ) 2/16] — (1) n2 = [cot θ (1-sin θ) / 4] 2 = [cot2 θ (1-sinθ) 2/16] — — (2) (1) — (2) L.H.S m2 — n2 = [cot2 θ (1 + грех θ) 2 — cot2 θ (1 + грех θ) 2] / 16 = [cot2 θ (1 + sin2θ + 2sinθ) — cot2 θ (1 + sin2θ -2sinθ)] / 16 = (4 cot2 θ sinθ / 16) = (θ cot2 грех θ / 4) (m2 — n2) 2 = (θ cot4 sin2 θ) / 16 = [(cos4 θ / sin4 θ) ⋅ sin2 θ] / 16 = (1/16) (cos4 θ / sin2 θ) — (1) л.H.S m = [cot θ (1 + sin θ)] / 4 n = [cot θ (1 — sin θ)] / 4 mn = [cot θ (1 + sin θ) / 4] [cot θ (1 — sin θ) ) / 4] = cot2 θ (1 — sin2 θ) / 16 = cot2 θ (cos2 θ) / 16 = (cos2 θ / sin2 θ) ⋅ (cos2 000) 000) (cos4 θ / sin2 θ) — (2) RHS Вопрос 2: Если cosec θ — sinθ = a3 и sec θ — cosθ = b3, то докажите, что a20009000 Answer: Given, что: cosec θ — θ = грех a3 (1 / θ грех) — грех θ = a3 (1 — sin2θ) / грех θ = a3 cos2θ / грех θ = a3 —— (1) sec θ — соз = (sin2θ / COS θ) / (cos2θ / грех θ) = (sin2θ / COS θ) ⋅ (син θ / cos2θ) = (sin3θ / cos3θ) b3 / a3 = tan3θ tanθ = б / a sin θ = Ь / √ (b2 + a2) cos θ = a / √ (b2 + a2) При применении значений sin θ и cos θ в (1) cos2θ / sin θ = a39 (39) √ (b2 + A90 0082)] 2 / [б / √ (b2 + a2)] = a3 ab√ (b2 + a2) = 1 Taking квадраты с обеих сторон, мы get a2b2 (b2 + a2) = 1 Hence доказана. Вы также можете посетить следующие веб-страницы по различным предметам в математике. WORD PROBLEMS HCF и LCM слово problems Word проблемы на простых уравнений Word задач на линейных уравнений Word задач на квадратичных задачах equations Algebra слово problems Word на trains Area и слова problems Word задач по прямой вариации и обратных вариационных задач Word на единичных проблем price Word на скорости блок проблем Word по сравнению rates Converting периметра словесные задачи с обычными единицами преобразование словосочетаний с метрическими единицами Сложные задачи по простым интересам Сложные задачи по сложным процентам 3Словые задачи по типам углов Дополнительные и дополнительные угловые задачи по словам0000000002929 6 Trigonometry слово problems Percentage проблема слова Profit и потеря слова проблема Markup и уценка проблема слова проблема Decimal слово problems Word по проблемам fractions Word на смешанном fractrions One шага уравнения в словах problems Linear неравенств слова problems Ratio и пропорции слове problems Time и работа слово проблема problems Word на множества и Венна проблемой diagrams Word на ages Pythagorean теореме словесные задачи Процент числа проблемных слов Сложные задачи на постоянной скорости Средние задачи на средней скорости Словые задачи на сумму углов треугольника 180 градусов ТРУДНЫЕ ТЕМЫ 0004 Percentage shortcuts Times таблица shortcuts Time, скорость и расстояние shortcuts Ratio и пропорция shortcuts Domain и диапазон рационального functions Domain и диапазона рациональных функций с рациональным holes Graphing functions Graphing рациональных функций с holes Converting дробей, чтобы fractions Decimal представление рационального numbers Finding квадратного корня, используя длинный division L. Для полного решения должны быть получены «все возможные значения», удовлетворяющие уравнению. Когда мы пытаемся решить тригонометрическое уравнение, мы пытаемся найти все наборы значений θ, которые удовлетворяют данному уравнению. Иногда в простых уравнениях и когда легко нарисовать график уравнения, можно найти решение, просто просмотрев график. A функция f (x) называется периодической, если существует T> 0 такое, что f (x + T) = f (x) для всех x в области определения функции f (x). Иллюстрация: Общее решение cos θ = 0 cos θ = 0 ⇒ x = π / 2. Это возможно, только если OP совпадает с OY или OY’ , когда OP совпадает с OY, θ = π / 2, 5π / 2, 9π / 2 или, -3π / 2, -7π / 2 .. ……… (1) , когда OP совпадает с OY’ θ = -3π / 2, -7π / 2 или, -π / 2, -5π / 2 ………… (2) Таким образом, из (1) и (2) следует, что общее решение cos θ = 0 есть θ (2n + 1) π / 2, где n = 0, ± 1, ± 2 ……… Для получения дополнительной информации о тригонометрических уравнениях см. Приведенное ниже видео: Мы знаем, что когда sin θ = k, k должно быть таким, чтобы –1 ≤ k ≤ 1 Мы всегда можем найти некоторые α ∈ [–π / 2, π / 2] Поскольку sin (-π) / 2 = -1 и sin π / 2 = 1, так что sinθ = k, то есть α = sin-1k i.e. sinθ = sinα, α ∈ [–π / 2, π / 2] ⇒ sin θ — sin α = 0 ⇒ 2 sin {(θ — α) / 2} cos {θ + α) / 2} = 0 из вышеприведенного уравнения, которое должно быть удовлетворено, либо sin {(θ — α) / 2) = 0 и, следовательно, ((θ — α) / 2) = целое кратное π ∴ θ — α = 2nπ i. Иллюстрация: Найти общее решение уравнения sin θ = 1/2 Решение: Мы знаем, что sin θ = 1/2 = sin π / 6. Иллюстрация: Решите уравнение sin 6x + sin 4x = 0. Решение: Применение формул для суммы синусов, т. Е. sin A + sin B = sin (A + B) / 2. cos (A-B) / 2, у нас есть sin 5x cos x = 0 ……… (1) Если ‘x’ является решением уравнения, то верно хотя бы одно из следующих уравнений: sin 5x = 0 или cos x = 0 ……… (2) И наоборот, если x является решением одного из уравнений (2), то это также решение уравнения (1).Таким образом, уравнение (1) эквивалентно уравнению (2). Решения уравнения (2) имеют вид x = nπ / 5, x = (2n + 1) π / 2, где n = 0, ± 1, ± 2 …… Все эти значения x и только эти значения являются решениями исходного уравнения. Решение: Знаки приобретают большое значение в случае тригонометрических функций. Студенты обычно склонны упоминать общие решения sin и tan θ, что неправильно, поскольку это не даст нам полного решения. sin θ отрицательно в 3-м и 4-м квадранте, а tan θ положительно в 1-м и 3-м квадранте. Так как правило, 3-й квадрант и при θ = 4π / 3 оба удовлетворены. ∴ Общее решение 2nπ + 4π / 3. Это потому, что в интервале [0, 2π] оно выполняется только при 4π / 3. Снова в [2π, 4π] оно выполняется при 2π + 4π / 3 и так далее. Иллюстрация: Найти общее решение cos 3θ = sin 2θ. Решение: Это можно решить двумя разными способами. Method 1: Мы можем записать данное уравнение как cos 3θ = cos (π / 2 — 2θ) ⇒ 3θ = 2nπ + (π / 2 — 2θ), где n = 0, ± 1, ± 2 …… или 5θ = 2nπ + π / 2, а также θ = 2nπ — π / 2 или θ = (4n + 1) π / 10 и θ = (4n – 1) π / 2, где n ∈ I …… (A) Метод 2: sin 2θ = sin (π / 2 — 3θ) 2θ = nπ + (–1) n (π / 2 — 3θ). Случай I: Когда n четное, n = 2 м, где m = 0, ± 1, ± 2 …… 2θ = 2mπ + π / 2 — 3θ θ = (4m + 1) π / 10, где m ∈ I …….(В) Case II: Когда n нечетно, n = (2m + 1) 2θ = (2m + 1) π — (π / 2 — 3θ) θ = — (4m + 1) π / 2, где m = 0, ± 1, ± 2 …… (B) Примечание: Без сомнения, решения, полученные обоими методами для нечетных значений n, различны, но, как показано на приведенной ниже диаграмме, вы можете видеть, что все возможные значения θ могут быть получены обоими данными решениями: от B от A для m = 0, θ = — π / 2, для n = 0, θ = — π / 2 для m = 1, θ = — 5π / 2, для n = 1, θ = + 3π / 2 для m = 2, θ = — 9π / 2, для n = 2, θ = + 7π / 2 для m = –1, θ = — 3π / 2, для m = –1, θ = — 5π / 2 для m = –2, θ = 7π / 2 для m = –2, θ = — 9π / 2 Приятно, что sin2 θ = k, k ∈ [0, 1] Мы можем найти такое α, что ⇒ sin2 θ = sin2α, где α = sin-1 √k i.е. (sinθ — sinα) (sinθ + sinα) = 0 любой грех θ — грех α = 0 θ = nπ + (–1) nα, где n = 0, ± 1, ± 2 ……… (1) или sin θ + sin α = 0 sin θ = — sin α θ = nπ — (–1) nα, где n = 0, ± 1, ± 2 …… .. (2) Из (1) и (2) получаем общее решение уравнения с заданным θ = nπ ± α, где n = 0, ± 1, ± 2 …… и α = sin-1 √k Иллюстрация: Решить уравнение 7tan2 θ — 9 = 3 с2θ Решение: Дано, 7tan2θ — 9 = 3 с2θ или 7tan2θ — 9 = 3 (1 + tan2θ) Примечание: Мы не можем определить уникальный метод решения тригонометрических уравнений.В каждом случае успех в решении тригонометрического уравнения зависит, в частности, от знания и умения применять тригонометрическую формулу и практики решения задач. Многие тригонометрические формулы являются истинными равенствами для всех значений переменной, встречающейся в них. Иллюстрация: Решите уравнение: cos θ = 0 cos θ = cos π / 2 ⇒ θ = 2nπ + π / 2 Важно: Следующие советы и шаги помогут вам систематически решать тригонометрические уравнения. 1. Попробуйте уменьшить уравнение с точки зрения одного тригонометрического отношения предпочтительно sin θ или cos θ. e.g. sin θ — k1 = 0 ⇒ θ = nπ + (–1) n sin-1 k1 cos θ — k2 = 0 ⇒ θ = 2nπ + cos–1 k2. Внимание: Необходимо проверить, что k1, k2 ∈ [–1, 1].Не пишите вслепую так, как есть, поскольку это будет абсурдно, если они не принадлежат [–1, 1] . Иллюстрация: Решите уравнение 5sin θ — 2 cos2θ — 1 = 0 Решение: Дано, 5 sin θ — 2 cos2θ — 1 = 0 или 5 sin θ — 2 (1 — sin2θ) — 1 = 0 Сначала рассмотрим случай, когда sin θ = -3, Но этот случай невозможен, так как диапазон синуса равен [-1, 1]. Уравнение не определено для нечетного кратного π / 2. 1. Если в уравнении участвует tan θ или sec θ, θ ≠ нечетное кратное π / 2. 2. Если в уравнении участвует cot θ или cosec θ, θ ≠ кратна π или 0. Тригонометрия полна формул, и студентам рекомендуется изучить все тригонометрические формулы, включая основы тригонометрии, чтобы оставаться конкурентоспособными на экзаменах JEE и других инженерных экзаменах.Студенты должны практиковать различные задачи тригонометрии, основанные на тригонометрических соотношениях и основах тригонометрии, чтобы познакомиться с этой темой. Вы можете сослаться на некоторые из перечисленных ниже ресурсов: Читать подробнее, купить учебные материалы Trigonometry составить учебные записки, заметки о пересмотре, видео-лекции, вопросы за прошлый год и др. Также посмотрите другие учебные материалы по математике здесь.00000000000000


Период функции:

Общее решение уравнения sin θ = k.
Общее решение sin2 θ = k, где k ∈ [0, 1]
или 4tan2θ = 12
или tan2θ = 3
или tan2θ = (tan π / 3) 2
⇒ θ = nπ + π / 3, где n = 0, ± 1, ± 2 …………
Решение: Мы можем решить это, чтобы получить две формы
cos θ = 0 ⇒ θ = (2n + 1) π / 2
или θ = (4n + 1) π / 2.
Если у нас есть выбор для преобразования проблемы в синус или косинус, то форма косинуса удобнее по сравнению с формой синуса. Это связано с тем, что в общем решении синуса нам придется иметь дело с (–1) n, что неудобно по сравнению с обработкой +, полученной в форме косинуса.
2. Факторизовать многочлен с точки зрения этих отношений.
3. Для LHS, чтобы быть нулем, решите для каждого фактора. И запишите общее решение для каждого фактора на основе стандартных результатов, полученных ранее в этом разделе.
или 2 sin2 θ + 5 sin θ — 3 = 0
или (sinθ + 3) (2 sinθ — 1) = 0
∴ грех θ = -3 или грех θ = ½Некоторые ключевые моменты, которые следует отметить:

