Осевая симметрия

Сегодня на уроке мы вспомним такое понятие как осевая симметрия на плоскости, введём понятие осевой симметрии в пространстве, проверим, будет ли осевая симметрия движением пространства.

Давайте вспомним, что фигура называется симметричной относительно прямой , если для каждой точки фигуры симметричная ей точка относительно прямой  также принадлежит этой фигуре. Прямая  называется осью симметрии фигуры. Про такую фигуру говорят, что она обладает осевой симметрией.

Давайте приведём примеры таких фигур из жизни и геометрии.

Ещё мы давали такое определение:

Точки  и  называются симметричными относительно прямой , если прямая  проходит через середину отрезка  и перпендикулярна к этому отрезку.

Прямая  называется осью симметрии.

Каждая точка прямой  считается симметричной самой себе.

В курсе планиметрии мы доказывали, что осевая симметрия является движением.

Напомним это доказательство.

Пусть точки М и N – какие-нибудь точки плоскости, а точки М₁, и N₁ – симметричные им точки относительно прямой А. Здесь может быть несколько вариантов расположения точек на плоскости.

Рассмотрим один из таких вариантов.

По построению симметричных точек относительно прямой А, прямая А перпендикулярна прямым ММ₁ и NN₁ и делит эти отрезки пополам, значит, в треугольниках МОМ₁ и NОN₁ отрезки ОК и ОЕ будут являться медианами и высотами, проведёнными к основанию, то есть это равнобедренные треугольники.

.

.

Заменив отрезок  равным ему отрезком , а отрезок  – равным ему отрезком , получим, что .

Вывод: таким образом, мы доказали, что расстояние между точками М и N равно расстоянию между симметричными им точками М один и N₁.

Получаем, что осевая симметрия – пример движения плоскости.

В пространстве осевой симметрией с осью  мы назовем такое отображение пространства на себя, при котором любая точка  переходит в симметричную ей точку  относительно оси .

Теперь давайте проверим, будет ли осевая симметрия в пространстве движением пространства.

Для этого введём прямоугольную систему координат Оxyz так, чтобы ось Оz совпала с осью симметрии. Теперь давайте попробуем найти связь между координатами точки М с координатами x, y, z и точки М₁ с координатами x₁, y₁,z₁, симметричных относительно оси Оz.

Если точка М не лежит на оси Оz, то по определению оси симметрии, ось Оz проходит через середину отрезка ММ

1 и перпендикулярна к этому отрезку. Поскольку Оz – середина отрезка ММ₁, и абсциссы и ординаты точек оси Оz равны нулю, то можно записать, что  и .

То есть , .

Условие того, что ось Оz перпендикулярно прямой ММ₁ даёт нам, то что аппликаты точек М и М₁ равны .

Если же точка М лежит на оси Оz, то она отображается сама на себя, по определению оси симметрии, значит, и в этом случае будут выполнятся полученные равенства.

Вывод: для симметричный точек относительно оси Оz абсциссы и ординаты противоположны, а аппликаты равны.

Возникает вопрос, а если ось симметрии совпадает не с осью Оz, а, например, Оx или Оy. Тогда связь между координатами симметричных точек М и М₁ будет такая: если ось симметрии проходит через ось Оx, то точки М и М₁ имеют такие координаты , .

Если осью симметрии будет ось Оy, то точки М и М

1 имеют такие координаты , .

Теперь давайте рассмотрим любые две точки  и . По только что доказанным формулам для координат симметричных точек получим, что точка . Точка .

Теперь давайте найдём расстояние .

Получим, что .

Теперь давайте найдём расстояние между точками  и .

Очевидно, что оба эти выражения равны, то есть получим, что . То есть расстояние между точками при осевой симметрии в пространстве сохраняется, значит, осевая симметрия в пространстве также является движением, но уже не плоскости, а пространства.

Задача: найти координаты точек, в которые переходят точки , ,  при осевой симметрии относительно координатных осей.

Решение: сначала найдём координаты точек в которые переходит точки , ,  при осевой симметрии относительно оси Ох.

Если точка  симметрична точке  относительно оси  то справедливы формулы: .

Точка  отобразится в точку .

Точка  отобразится в точку .

Точка  отобразится в точку .

Если точка  симметрична точке  относительно оси  то справедливы формулы: .

Точка  отобразится в точку .

Точка  отобразится в точку .

Точка  отобразится в точку .

Если точка  симметрична точке  относительно оси  то справедливы формулы: .

Точка  отобразится в точку .

Точка  отобразится в точку .

Точка  отобразится в точку .

Итоги:

Сегодня на уроке мы ввели понятия осевой симметрии в пространстве. Показали, что и в пространстве осевая симметрия будет примером движения. Решили несколько задач.

videouroki.net

Презентация по геометрии (11 класс) на тему «Центральная и осевая симметрии»

Центральная и осевая симметрии.

Пусть каждой точке М пространства соответствует некоторая точка М₁.

М₁

М

В таком случае говорят, что задано отображение пространства на себя. Можно сказать, что при данном отображении точка М переходит (отображается) в точку М₁.

Под движением пространства понимают отображение пространства на себя, при котором любые две точки А и В

переходят (отображаются) в какие-то точки А₁ и В₁ так, что А₁В₁ = АВ.

А₁

В₁

А

В

(Как и для плоскости)

Движение пространства – это отображение пространства на себя, сохраняющее расстояния между точками.

Центральная симметрия является движением.

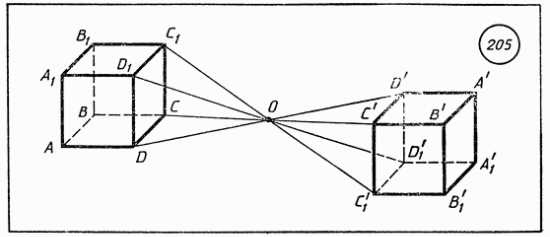
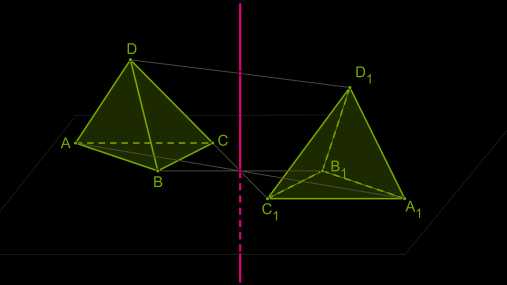
Осевая симметрия является движением.

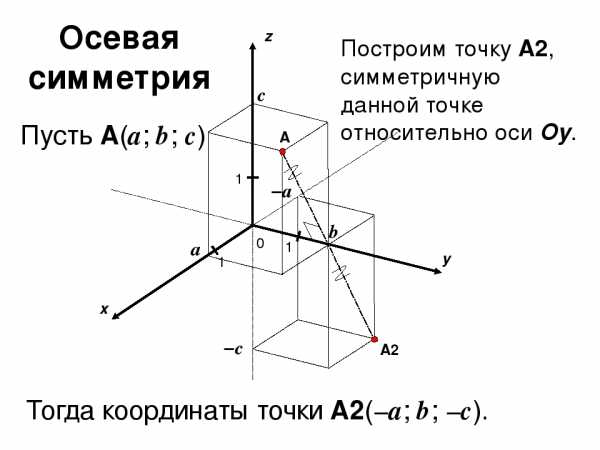
Вопросы и задания.

1. Дана точка М (1; 1; 1). Какие координаты имеет симметричная ей точка относительно точки О (0; 0; 0)?

2. Дана точка М (– 5; – 5; – 5). Какие координаты имеет симметричная ей точка относительно точки О (0; 0; 0)?

3. Дана точка М (– 5; 1; – 5). Какие координаты имеет симметричная ей точка относительно точки О (0; 0; 0)?

4. Дана точка М (– 5; у; – 5). Какие координаты имеет симметричная ей точка относительно оси Оу?

5. Дана точка М (х; – 5; – 5). Какие координаты имеет симметричная ей точка относительно оси Ох?

Домашнее задание: п. 54, 55, № 478 (а,б), 479.

infourok.ru

Осевая и центральная симметрия — сообщение доклад (6, 8 класс) (описание для детей)

Симметрия является неотъемлемой частью мира, в котором мы живем. Мы восхищаемся красотой природы, архитектурными сооружениями, механическими приборами и шедеврами искусства, не задумываясь над тем, что в основе их создания лежит симметрия.

«Симметрия» с греческого языка переводится как гармония, соразмерность, красота. Впервые термин стал широко употреблять Пифагор в до н.э. Им он обозначил трехмерное изображение геометрических фигур и их частей в пространстве. Также ученый определил отклонение от симметрии как асимметрию.

Существует два основных виды симметрии: осевая и центральная.

Осевая симметрия или зеркальная – это симметрия относительно оси. То есть одна половинка фигуры полностью соразмерна с другой относительно прямой. Так если согнуть листок пополам, то каждая точка одной половины листа будет иметь своего двойника на другой половине, а сам сгиб станет осью симметрии.

Зеркальную симметрию можно наблюдать в природе: листья растений симметричны относительно среднего стебля, крылья бабочки являются зеркальным отображением друг друга, человек и животные обладают симметрией в расположении частей тела. Архитектурные сооружения также являются ярким примером осевой симметрии. Фасады зданий, особенно античных, вызывают чувства строгости и восхищения красотой именно благодаря симметрии их частей. Симметрия в архитектуре служит не только для эстетического удовольствия наблюдателей, но и гарантирует зданиям и сооружениям прочность и надежность конструкции.

Центральная симметрия – это симметрия относительно точки. У такой симметрии обязательно есть неподвижный центр, при вращательных действиях на 180° относительно него фигура переходит сама в себя. Благодаря этому свойству центральная симметрия получила второе название – поворотная. С древнейших времен ее эталоном считается круг, и действительно, как бы мы не поворачивали его вокруг центра, каждая точка окружности переходит в соответствующую ей. В природе ярким примером центральной симметрии являются снежинки; цветы таких растений, как одуванчик, мать-и-мачеха, а также ромашки, если количество ее лепестков четное; шестеренки механизмов.

Вариант 2

Наверное, каждый слышал такие понятия, как «симметрия», «симметрично» и тому подобное. Но есть такие люди, которые не понимают значение данных синонимов. Так что же такое симметрия? Где ее применяют? И какие разновидности существуют?

Краткий экскурс о симметрии в общих чертах.

Постараюсь объяснить понятие симметрии на некотором примере. Представьте обыкновенную бабочку. Так, а теперь надо провести через нее линию. Когда линия окончательно проведена, необходимо посмотреть на правую и левую части рисунка. Если эти 2 части рисунка одинаковы по размерам и пропорциям, то это можно называть симметричной моделью. Короче говоря, симметрия – это полная соразмерность частей тела по отношению к линии. Где же применяется симметрия? Ну, симметрия встречается везде, где только можно. Геометрия, физика, биология, химия, культура – все это содержит симметрию, причем каждая отличается друг от друга. Еще существует понятие асимметрии. То есть, отсутствие правильной соразмерности. Еще стоит отметить, что симметрия не всегда бывает точной.

Некоторые виды симметрии, их характеристика и применение.

Всего наберется с десяток разных видов симметрий. Но рассмотреть необходимо только те, которые часто встречаются. Сразу стоит сказать, что обе из них находят применение в решении задач по геометрии. Итак, вот 2 главных вида симметрии:

Осевая симметрия.

Этот вид симметрии делится на 4 группы, отличающиеся друг от друга.

1) Отражательная симметрия – это зеркальное движение, в котором точки, не перемещающиеся никуда, соединены в одну линию – ось симметрии. Прямоугольник и параллелограмм – отличные примеры.

2) Вращательная симметрия – это осевая симметрия, которая относительна поворотам вокруг оси.

3) Осевая симметрия n – го порядка – это симметрия относительно поворотов на 360 градусов вокруг оси.

4) Зеркально поворотная осевая симметрия n – го порядка – то же самое, только перпендикулярно оси.

Центральная симметрия.

Это преобразование, при котором каждая точка А переходит в точку А1, при этом она симметрична предыдущей относительно оси О. Данная симметрия – это, по сути, тот же поворот на 180 градусов в планиметрии. Центральную симметрию от осевой отличает то, что в первом случае присутствует движение.

Картинка к сообщению Осевая и центральная симметрия

Популярные сегодня сообщения и доклады

• Доклад Растения пустыни 4 класс окружающий мир сообщение

  Пустыня считается местом, где кроме песков не может быть жизни, но это ошибочное мнение. В пустыне можно встретить разных животных, насекомых, ящериц, а это значит, что в пустыне могут прорас

• Доклад Иоганн Себастьян Бах (сообщение)

  Иоганн Себастьян Бах (1685-1750 гг.) относится к величайшим представителям всемирной классической музыки. Бах является уроженцем небольшого немецкого провинциального городка Эйзенах и появляе

• Доклад на тему Животные и насекомые лугов сообщение

  Мир животных необычайно разнообразен. Они густо заселяют наш Земной шар. Где только не встретишь животных: в горах или же на лугах, в сухой пустыне и, напротив, в глубоком водоёме.

• Доклад на тему Прыжки сообщение

  Современный спорт сейчас очень тяжело представить без такого вида упражнений, как прыжки. Они являются одной из главных частей всех олимпиад.

• Доклад на тему Правильное питание 2, 3, 4, 7 класс сообщение

  Правильное питание является одной из основ здоровья. Если мы посмотрим древние медицинские трактаты, то там пища практически всегда воспринимается как лекарство. Древние люди, когда глубоко р

• Доклад Большой Кремлевский дворец сообщение

  Большой кремлевский дворец является одним из построек в составе Московского Кремля, одним из его дворцов. Период его постройки – а это примерно 1838-1840 года, приходится на период правления

doklad-i-referat.ru

Осевая и центральная симметрия — урок. Математика, 6 класс.

Симметрия — слово греческого происхождения, как и многие другие слова, которые связаны с математикой. Оно означает соразмерность, наличие определённого порядка, закономерности в расположении частей. Смотря на объекты вокруг, мы не раз восклицаем: «Какая симметрия!»

 

Люди с давних времён использовали симметрию в рисунках, орнаментах, предметах быта, в архитектуре, художестве, строительстве.

Но симметрия широко распространена и в природе, где не было вмешательства человеческой руки. Её можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел, в порхающей бабочке, загадочной снежинке, морской звезде.

 

 

Пока рассмотрим две симметрии на плоскости: относительно точки и прямой.

Центральная  симметрия

Симметрию относительно точки называют центральной симметрией.

Точки M и M1 симметричны относительно некоторой точки  \(O\), если точка \(O\) является серединой отрезка MM1.

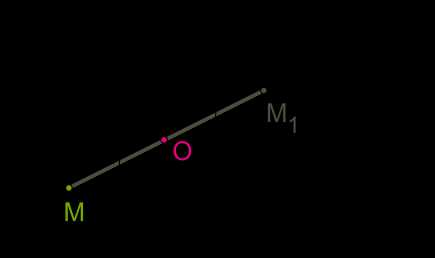
Точка \(O\) называется центром симметрии.

 

Алгоритм построения центрально-симметричных фигур.

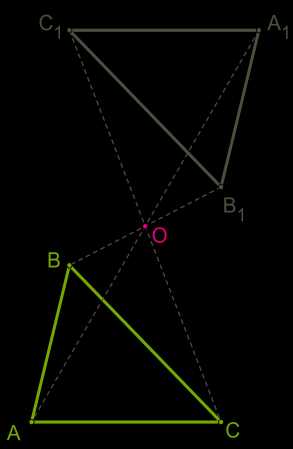
Построим треугольник A1B1C1, симметричный треугольнику \(ABC\) относительно центра (точки) \(O\):

 

1. для этого соединим точки \(A\), \(B\), \(C\) с центром \(O\) и продолжим эти отрезки;
2. измерим отрезки \(AO\), \(BO\), \(CO\) и отложим с другой стороны от точки \(O\) равные им отрезки AO=OA1;BO=OB1;CO=OC1;
3. соединим получившиеся точки отрезками и получим треугольник A1B1C1, симметричный данному треугольнику \(ABC\).

Фигуры, симметричные относительно некоторой точки, равны.

Фигура симметрична относительно центра симметрии, если для каждой этой точки фигуры симметричная ей точка также лежит на этой фигуре. Такая фигура имеет центр симметрии (фигура с центральной симметрией).

Есть фигуры с центральной симметрией, это, например, окружность и параллелограмм. У окружности центр симметрии — это её центр, у параллелограмма центр симметрии — это точка, в которой пересекаются его диагонали. Есть очень много фигур, у которых нет центра симметрии.

Осевая симметрия

Осевая симметрия — это симметрия относительно проведённой прямой (оси).

Точки M и M1 симметричны относительно некоторой прямой (оси симметрии), если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии от оси симметрии.

 

Алгоритм построения фигуры, симметричной относительно некоторой прямой.

 

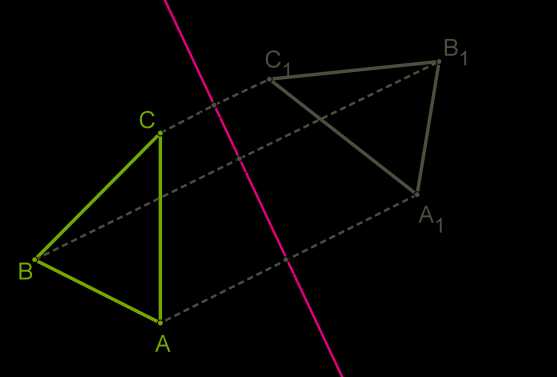
Построим треугольник A1B1C1, симметричный треугольнику \(ABC\) относительно красной прямой:

 

1. для этого проведём из вершин треугольника \(ABC\) прямые, перпендикулярные оси симметрии, и продолжим их дальше на другой стороне оси.
2. Измерим расстояния от вершин треугольника до получившихся точек на прямой и отложим с другой стороны прямой такие же расстояния.
3. Соединим получившиеся точки отрезками и получим треугольник A1B1C1, симметричный данному треугольнику \(ABC\).

Фигуры, симметричные относительно прямой, равны.

Фигура считается симметричной относительно прямой, если для каждой точки рассматриваемой фигуры симметричная для неё точка относительно данной прямой также находится на этой фигуре. Прямая является в этом случае осью симметрии фигуры.

Иногда у фигур несколько осей симметрии:

• для неразвёрнутого угла существует единственная ось симметрии — это биссектриса данного угла.
• Для равнобедренного треугольника есть единственная ось симметрии.
• Для равностороннего треугольника — три оси.
• Для прямоугольника и ромба существуют две оси симметрии.
• Для квадрата — целых четыре.
• Для окружности осей симметрии бесчисленное множество — это каждая прямая, которая проходит через центр этой фигуры.
• Есть фигуры без осей симметрии — это параллелограмм и треугольник, все стороны которого различны.

www.yaklass.ru

Движения в пространстве — урок. Геометрия, 11 класс.

 

Движение в пространстве определяется так же, как и на плоскости.

Движением называется преобразование, при котором сохраняются расстояния между точками.

Под движением пространства понимается отображение пространства на себя, при котором любые две точки A и B переходят (отображаются) в некие точки A1 и B1 так, что AB=A1B1.

 

Иными словами, движение пространства — это отображение пространства на себя, сохраняющее расстояния между точками. Так же, как и для движения на плоскости, доказывается, что:

при движении в пространстве

 

— прямые переходят в прямые,

— полупрямые — в полупрямые,

— отрезки — в отрезки,

— сохраняются углы между прямыми.

Обрати внимание!

Новым свойством движения в пространстве является то, что движение переводит плоскости в плоскости.

В пространстве, так же как и на плоскости, две фигуры называются равными, если они совмещаются движением.

Виды движения в пространстве

1. Центральная симметрия (симметрия относительно точки).

 

2. Осевая симметрия (симметрия относительно прямой).

 

3. Зеркальная симметрия (симметрия относительно плоскости).

 

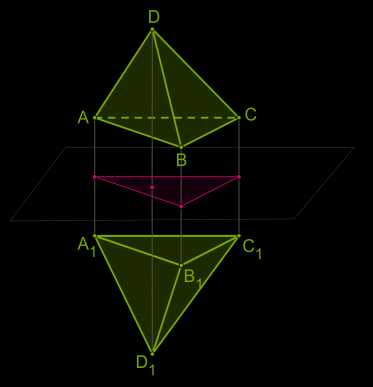
4. Параллельный перенос (точки переносятся на данный вектор).

 

5. Поворот на данный угол вокруг данной точки.

www.yaklass.ru

Реферат — Осевая симметрия — n1.doc

Реферат — Осевая симметрия
скачать (227.5 kb.)

Доступные файлы (1):

---

n1.doc

Реклама MarketGid:

Физико-Математический факультет

Кафедра алгебры, геометрии,

Теории и методики обучения математики

Осевая симметрия
Выполнил:

СОДЕРЖАНИЕ

ОПРЕДЕЛЕНИЕ И СВОЙСТВА 3

ОСЕВОЙ СИММЕТРИИ ПЛОСКОСТИ 3

РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ ОСЕВОЙ СИММЕТРИИ 6

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ 10

ОПРЕДЕЛЕНИЕ И СВОЙСТВА

ОСЕВОЙ СИММЕТРИИ ПЛОСКОСТИ

Точки М и М₁ называются симметричными относительно заданной прямой L, если эта прямая является серединным перпендикуляром к отрезку МM₁ (рис 1). Каждая точка прямой L симметрична сама себе. Преобразование плоскости, при котором каждая точка отображается на симметричную ей точку относительно данной прямой L, называется осевой симметрией с осью L и обозначается S_L: S_L (M) = M₁.

Точки М и М₁ взаимно симметричны относительно L, поэтому S_L(M₁)=M. Следовательно, преобразование, обратное осевой симметрии, есть та же осевая симметрия: S_L^-1 = S_L, S_{L °} S_L = E. Иначе говоря, осевая симметрия плоскости является инволютивным преобразованием.

Образ данной точки при осевой симметрии можно просто построить, пользуясь только одним циркулем. Пусть L – ось симметрии, A и B – произвольные точки этой оси (рис 2). Если и S_L(M) = M₁, то по свойству точек серединного перпендикуляра к отрезку имеем: AM = AM₁ и BM = BM₁. Значит, точка M₁ принадлежит двум окружностям: окружности с центром A радиуса AM и окружности с центром B радиуса BM (M – данная точка).

Фигура F и её образ F₁ при осевой симметрии называются симметричными фигурами относительно прямой L (рис 3).

Теорема. Осевая симметрия плоскости есть движение.

Если А и В – любые точки плоскости и S_L(A) = A₁, S_L(B) = B₁, то надо доказать, что A₁B₁ = AB. Для этого введем прямоугольную систему координат OXY так, чтобы ось OX совпала с осью симметрии. Точки А и В имеют координаты А(x₁,-y₁) и B(x₁,-y₂).Точки А₁ и В₁ имеют координаты A₁(x₁,y₁) и B₁(x₁,y₂) (рис 4 – 8). По формуле расстояния между двумя точками находим:

, .

Из этих соотношений ясно, что АВ=А₁В₁, что и требовалось доказать.

Из сравнения ориентаций треугольника и его образа получаем, что осевая симметрия плоскости есть движение второго рода.

Осевая симметрия отображает каждую прямую на прямую. В частности, каждая из прямых, перпендикулярных оси симметрии, отображается этой симметрией на себя.

Теорема. Прямая, отличная от перпендикуляра к оси симметрии, и её образ при этой симметрии пересекаются на оси симметрии или ей параллельны.

Доказательство. Пусть дана прямая, не перпендикулярная оси L симметрии. Если m ? L= P и S_L(m)=m₁, то m₁?m и S_L(P)=P, поэтому Pm₁ (рис 9). Если же m || L , то m₁ || L , так как в противном случае прямые m и m₁ пересекались бы в точке прямой L, что противоречит условию m ||L (рис 10).

В силу определения равных фигур, прямые, симметричные относительно прямой L, образуют с прямой L равные углы (рис 9).

Прямая L называется осью симметрии фигуры F, если при симметрии с осью L фигура F отображается на себя: S_L (F) =F. Говорят, что фигура F симметрична относительно прямой L.

Например, всякая прямая, содержащая центр окружности, является осью симметрии этой окружности. Действительно, пусть М – произвольная точка окружности ? с центром О, ОL, S_L(M)= M₁. Тогда S_L(O) = O и OM₁=OM, т. е. M₁ є ?. Итак, образ любой точки окружности принадлежит этой окружности. Следовательно, S_L(?)=?.

Осями симметрии пары непараллельных прямых служат две перпендикулярные прямые, содержащие биссектрисы углов между данными прямыми. Осью симметрии отрезка является содержащая его прямая, а также серединный перпендикуляр к этому отрезку.

Рассмотрим наиболее типичные ситуации применения осевой симметрии в задачах.

ЗАДАЧА 1

Точки M и N симметричны вершине C треугольника ABC относительно прямых, содержащих биссектрисы его углов A и B. Доказать, что точка P касания стороны AB с вписанной в треугольник окружностью является серединой отрезка MN.

РЕШЕНИЕ. Пусть Q и T – точки касания вписанной окружности соответственно со сторонами BC и CA(рис 11).

Так как биссектриса угла принадлежит его оси симметрии и AT = AP,

BQ = BP, то точка P служит образом точек Q и T при указанных осевых симметриях. Поскольку, CQ = CT, то и MP = NP.
ЗАДАЧА 2

Продолжения боковых сторон AD и BC равнобочной трапеции ABCD пересекаются в точке S. Доказать, что окружности, описанные около треугольников ACS и BDS, пересекаются в центре окружности, описанной около данной трапеции.

РЕШЕНИЕ. Пусть M – вторая точка пересечения окружностей ACS и BDS(рис 12).

Прямая SM является осью симметрии этих окружностей и трапеции, поэтому она содержит центр окружности, описанной около трапеции. Далее, ASM = BSM => AM = MC =>AM = MC. Так как, кроме того, AM = MB и DM = MC, то точка М равноудалена от всех вершин трапеции.
ЗАДАЧА 3

Внутри острого угла дана точка А. Построить треугольник ABC наименьшего периметра, вершины B и C, которого принадлежат сторонам угла.

РЕШЕНИЕ. Построим точки M и N, симметричные точке А относительно сторон данного угла. Прямая MN пересекает стороны угла в искомых точках B и C (рис 13).

Действительно, если B₁ и C₁ – какие-либо другие точки на сторонах угла, то

A₁B₁ + B₁C₁ +C₁A₁ = MB₁ + B₁C₁ + C₁N > MN = MB + BC + CN = AB +BC +CA

Следовательно, треугольник ABC имеет наименьший периметр. Вместе с этим доказано, что он единственный.
ЗАДАЧА 4

Дана прямая m и две окружности ? и Я в полуплоскости с границей m. Найти на прямой m точку, касательные из которой к данным окружностям образуют с прямой m равные углы.

РЕШЕНИЕ. Пусть М – искомая точка прямой m, а t и p – касательные к ? и Я, проходящие через М и образующие с прямой M равные углы (рис 14).

Прямая m – ось симметрии прямых p и t. Поэтому если окружность Я₁ симметрична Я относительно m, то прямая t касается Я_1. Таким образом, для нахождения искомой точки M достаточно построить общую касательную к окружностям ? и Я₁. При заданном расположении окружностей ? и Я окружности ? и Я₁ имеют четыре общих касательных. Следовательно, задача имеет четыре решения. На рисунке показано только одно из них.

ЗАДАЧА 5

Три данные прямые a, b и c проходят через центр окружности ?. Построить треугольник, описанный около ?, вершины которого лежат на данных прямых.

РЕШЕНИЕ. Пусть треугольник ABC искомый и Aa, Вb, Cc (рис 15).

Пусть m = S_a(c) и n = S_b(c), то точка P касания стороны AB с окружностью ? принадлежит оси симметрии прямых m и n (задача 1). Построив точку P, строим прямую AB. Касательная к окружности ? в точке P, пересекаясь с прямыми a и b, даёт точки A и B. Касательная в одной из этих точек пересекает прямую с в третьей искомой точке C.

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1. 
   Яглом И.М.– геометрические преобразования;
   
2. 
   Понарин Я.П.– Элементарная геометрия, том 1;
   
3. 
   Дорофеев С.Н.– Геометрические преобразования в примерах и задачах.
   

---

Скачать файл (227.5 kb.)

---

gendocs.ru

Симметрия, осевая симметрия — презентация, доклад, проект

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать её на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: [email protected]

Мы в социальных сетях

Социальные сети давно стали неотъемлемой частью нашей жизни. Мы узнаем из них новости, общаемся с друзьями, участвуем в интерактивных клубах по интересам

ВКонтакте >

Что такое Myslide.ru?

Myslide.ru — это сайт презентаций, докладов, проектов в формате PowerPoint. Мы помогаем учителям, школьникам, студентам, преподавателям хранить и обмениваться своими учебными материалами с другими пользователями.

---

Для правообладателей >

myslide.ru