Олимпиадные задания по физике 11 класс с решениями – 11
Олимпиада по физике 11 класс школьный тур
Школьный тур олимпиады
Физика
11 класс
Стеклянный шарик падает в воду с ускорением 5,8м/с2. Найти плотность стекла, если плотность воды равна 1000кг/м3 (15 баллов)
2. Шарик массой , заряд которого , подвешен на нити длиной . Над точкой подвеса на расстоянии от нее помещен заряд . Шарик отклоняют от положения равновесия на угол и отпускают. Найти скорость шарика и силу натяжения нити при прохождении шариком положения равновесия. Значение электрической постоянной ε0 = 8,85·10–12 Ф/м.
(35баллов)
3. По двум параллельным проводникам, находящимся друг от друга на расстоянии , перемещают перемычку с постоянной скоростью . Между проводниками включены последовательно два конденсатора, причем отношение их емкостей . Вся система находится в постоянном магнитном поле, вектор индукции которого ортогонален плоскости, в которой лежат проводники. Какова индукция магнитного поля, если на конденсаторе напряжение .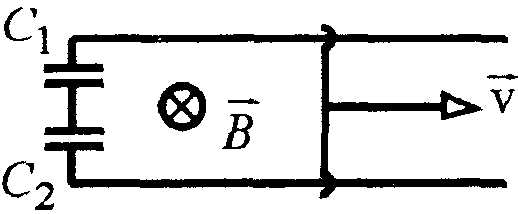
(30 баллов)
4. Экспериментатор набрал на улице мокрого снега, имеющего температуру 0°С, поместил его в морозильную камеру и начал через равные промежутки времени измерять его температуру, занося данные в журнал (первая запись была сделана сразу после начала эксперимента). Однако впоследствии журнал был испорчен, так что удалось прочитать только значения температуры, соответствующие десятой и одиннадцатой записям: –0,5 °С и –4 °С соответственно. Определите по этим данным массовую долю воды в мокром снеге. Удельная теплоемкость льда 2,1·103Дж/(кг·°С), удельная теплота плавления льда 3,35·105 Дж/кг.
(20 баллов)
Решения заданий школьной олимпиады
школьников по физике
11 класс
1. Стеклянный шарик падает в воду с ускорением 5,8 м/с2. Найти плотность стекла, если плотность воды равна 1000 кг/м3 (15 баллов)
Решение

2. Шарик массой , заряд которого , подвешен на нити длиной . Над точкой подвеса на расстоянии от нее помещен заряд . Шарик отклоняют от положения равновесия на угол и отпускают. Найти скорость шарика и силу натяжения нити при прохождении шариком положения равновесия. Значение электрической постоянной ε0 = 8,85·10–12 Ф/м. (35баллов)
Решение
Будем отсчитывать потенциальную энергию от положения равновесия. С учетом потенциальной энергии электростатического взаимодействия, из закона сохранения энергии имеем
(1)
Здесь и расстояния между зарядами в момент, когда шарик отклонен от положения равновесия и в положении равновесия соответственно.
Очевидно .
По теореме косинусов находим
Из (1) получаем
.
Подставляя сюда выражения для и окончательно находим
.
Вычисляя по полученной формуле, находим .
Найдем силу натяжения нити в положении равновесия шарика. Под действием сил натяжения нити , тяжести и кулона шарик движется по дуге окружности, т.е. ускорено :
.
Выбирая ось направленную вертикально вверх, для проекция сил на эту ось находим:
,
.
Ответ: , .
3. По двум параллельным проводникам, находящимся друг от друга на расстоянии , перемещают перемычку с постоянной скоростью . Между проводниками включены последовательно два конденсатора, причем отношение их емкостей . Вся система находится в постоянном магнитном поле, вектор индукции которого ортогонален плоскости, в которой лежат проводники. Какова индукция магнитного поля, если на конденсаторе напряжение .
(30 баллов)
Решение
Модуль ЭДС индукции, возникающей при перемещении перемычки в магнитном поле с индукцией , равен
.
Общая емкость последовательно соединенных конденсаторов и равна
.
Таким образом, заряд накопленный конденсаторами равен
.
Следовательно
.
Но при последовательном соединении , где заряд на емкости .
Отсюда
.
Ответ:
4. Экспериментатор набрал на улице мокрого снега, имеющего температуру 0°С, поместил его в морозильную камеру и начал через равные промежутки времени измерять его температуру, занося данные в журнал (первая запись была сделана сразу после начала эксперимента). Однако впоследствии журнал был испорчен, так что удалось прочитать только значения температуры, соответствующие десятой и одиннадцатой записям: –0,5 °С и –4 °С соответственно. Определите по этим данным массовую долю воды в мокром снеге. Удельная теплоемкость льда 2,1·10
(20 баллов)
Решение
Пусть интервал времени, через который производится измерение температуры, равен T, тогда, в соответствии с записями в журнале, температура стала равной t1=–0,5°С через 9T, а t2=–4°С – через 10T. В течение первого интервала времени вся имевшаяся в мокром снеге вода замерзла. Тогда, считая мощность отъема тепла в морозильной камере постоянной, запишем уравнения теплового баланса:
От начала эксперимента до 10-го измерения:
9TP=φmλ+cm|t1|;
от 10-го до 11-го измерения:
TP=cm (|t2|–|t1|), где P – мощность отъема тепла, m – масса снега, φ – массовая доля воды в мокром снеге. Из полученных уравнений несложно найти
φ=c(9|t2|–10|t1|)/λ
Подставляя численные значения, получаем φ ≈0,19. Ответ: 19%.
infourok.ru
Физика 11 класс, муниципальный (второй) этап, г. Москва, 2016 год
Задача 1
Стоя на движущемся вниз эскалаторе, мальчик подбросил монетку, как ему показалось, вертикально вверх, и через τ = 1 с поймал её. Скорость эскалатора V = 1 м/с, а угол его наклона к горизонту α = 30⁰. На какое максимальное расстояние от точки бросания удалялась монетка? В течение какого времени монетка поднималась вверх в системе отсчёта, связанной со стенами шахты эскалатора? Ускорение свободного падения можно считать равным 10 м/с
Возможное решение
Максимальное расстояние, на которое монетка удалялась от точки её бросания, проще всего искать в системе отсчёта, связанной с эскалатором. В этой системе отсчёта начальная скорость монетки направлена вертикально, следовательно,
Возможны также решения, в которых ищется максимальное расстояние от монетки до точки бросания (точка пространства) в системе отсчёта, связанной со стенами шахты эскалатора. ТАКОЕ РЕШЕНИЕ ТОЖЕ СЛЕДУЕТ СЧИТАТЬ ПРАВИЛЬНЫМ. В этой системе отсчёта вертикальная составляющая начальной скорости монетки равна
(за положительное выбрано направление вверх), а горизонтальная составляющая начальной скорости монетки равна
ν2 =V∙cosα.
В момент максимального удаления монетки от точки броска, вектор смещения r должен быть перпендикулярен вектору скорости монетки ν (это равносильно тому, что в данный момент расстояние между монеткой и точкой броска не уменьшается и не увеличивается). Пусть ν0 — начальная скорость монетки, тогда
Момент времени, когда векторы r и ν перпендикулярны, найдём из условия равенства нулю их скалярного произведения:
Проекция вектора ν0 на ось, направленную вертикально вверх, равна ν1, поэтому
По теореме Пифагора
Получаем уравнение на t
Аналогичное уравнение можно получить аналитически. Расстояние между монеткой и точкой броска будет меняться со временем по закону
Расстояние r будет максимально тогда, когда максимален квадрат расстояния r2. Продифференцировав выражение для r
решение t = 0 соответствует минимуму функции r2(t). Поскольку мы ищем максимум, то уравнение можно сократить на t. Получим квадратное уравнение
решив которое, найдём что расстояние максимально в момент времени
Второй корень квадратного уравнения рассматривать не нужно, поскольку он больше 1 с (то есть соответствует моменту времени после того, как мальчик поймал монетку). Максимальное расстояние между монеткой и точкой броска
r(tm) ≈ 1,09 м.
Из закона сложения скоростей получаем, что в системе отсчёта, связанной со стенами шахты эскалатора, вертикальная составляющая начальной скорости монетки равна: g(τ/2) – V∙sinα. Тогда
Ответ: t = 0,45 с
Критерии оценивания
| Найдено максимальное расстояние от монетки до точки её бросания (либо в системе отсчёта мальчика, либо в системе отсчёта стен шахты) | 4 балла |
| Применён закон сложения скоростей | 2 балла |
| Найдено время t | 4 балла |
Задача 2
Рисунок 2.1
Льдинка с вмороженным в неё металлическим слитком подвешена на лёгкой нити и частично погружена в цилиндрический стакан с водой так, что лёд не касается стенок стакана. Площадь дна стакана S = 100 см2 . Для того, чтобы удержать льдинку в таком положении, нить перекидывают через идеальный блок, к оси которого прикладывают вертикально направленную силу F = 10 Н. На другой конец нити вешают подходящий противовес. На сколько изменится уровень воды в стакане после того, как льдинка растает? Повысится он или понизится? Масса слитка m = 100 г, плотность металла ρ = 10 000 кг/м
Возможное решение
Рисунок 2.2
Рассмотрим внешние силы, действующие на содержимое стакана, в которое включим воду, льдинку и слиток. Сила тяжести компенсируется двумя направленными вверх внешними силами – силой натяжения нити F/2 и силой реакции дна стакана. Последняя, в свою очередь, равна по модулю силе давления на дно со стороны жидкости. Из условия равновесия содержимого стакана в исходном состоянии следует:
где h1 – высота уровня воды в исходном состоянии.
После таяния льдинки масса содержимого сохраняется, но изменяется уровень воды в стакане и, следовательно, давление воды около дна. Кроме этого, на содержимое перестаёт действовать сила F/2, но на дно с силой
начинает действовать слиток. Новое условие равновесия содержимого имеет вид:
S∙ρ0∙g∙h2 + N = mсодерж∙g
где h1 – высота уровня воды в исходном состоянии.
Вычитая из первого уравнения второе, получим выражение для изменения уровня воды в стакане:
Так как эта величина положительная, то уровень воды в стакане повысится.
Критерии оценивания
| Записано условие равновесия содержимого в исходном состоянии | 2 балла |
| Записано условие равновесия содержимого в конечной ситуации | 2 балла |
| Получено выражение для изменения уровня жидкости | 2 балла |
| Получено численное значение для изменения уровня жидкости | 2 балла |
| Явно указано, что уровень повысится | 2 балла |
| (Если задача решалась через объём погружённой льдинки и изменение объёмов при таянии, то за верное выражение для изменения уровня – 6 баллов.) |
Задача 3
Один моль аргона участвует в процессе, в ходе которого теплоёмкость остаётся постоянной и равной C =10 Дж/К. При этом аргон увеличил свой объём, совершив работу A = 40 Дж. Найдите изменение температуры аргона и подведённое к нему количество теплоты.
Возможное решение
Запишем для данного процесса первое начало термодинамики:
т. е. газ охлаждался. Подведённое к газу количество теплоты равно:
Q = C∙∆T = – 162 Дж,
т. е. газ в данном процессе отдавал теплоту.
Критерии оценивания
| Записано первое начало термодинамики | 4 балла |
| Найдено изменение температуры газа | 2 балла |
| Найдено количество теплоты | 2 балла |
| Указано, что газ тепло отдавал (получен ответ со знаком минус) | 2 балла |
Задача 4
Электрическая цепь представляет собой проволочную сетку, состоящую из звеньев, имеющих одинаковые сопротивления R.
Одно звено заменено на вольтметр, сопротивление которого тоже равно R. К сетке подключён источник напряжения U0 = 14 В так, как показано на рисунке. Найдите показание вольтметра.
Рисунок 4.1
Возможное решение
Изобразим схематически токи, текущие в звеньях сетки, учитывая её симметрию и закон Ома для участка цепи. Согласно этому закону, силы тока в параллельных звеньях, находящихся под одинаковым напряжением, обратно пропорциональны сопротивлениям этих звеньев. При изображении токов также нужно учитывать закон сохранения электрического заряда для узлов сетки – сумма токов, втекающих в узел, должна быть равна сумме токов, вытекающих из узла.
Рисунок 4.2
Точки подключения источника напряжения расположены на вертикальной оси симметрии сетки. Поэтому токи, текущие налево и направо от оси симметрии сетки, вытекающие из данного узла или втекающие в данный узел, должны быть одинаковыми. Обозначим токи, текущие налево и направо от верхнего среднего узла сетки, через I. Тогда ток, втекающий в верхний средний узел, равен 2I. При обходе левой (и правой) верхней четверти сетки суммарное падение напряжения должно быть равно нулю. Следовательно, токи, текущие налево и направо от центрального узла сетки, одинаковы и равны 4I. Значит, токи, текущие вниз от левого среднего и от правого среднего узла сетки, равны 5I.
Выразим напряжение источника U0 через ток I. Для того чтобы сделать это, мысленно сложим схему пополам вдоль вертикальной оси симметрии. Тогда сопротивления всех звеньев, не лежащих на оси симметрии, уменьшатся в 2 раза, а текущие по ним токи увеличатся в 2 раза. Суммарное сопротивление всех звеньев, подключённых к источнику (за исключением звена, находящегося непосредственно между клеммами источника), равно 7R/5. Текущий через эти звенья ток равен 10I. Поэтому падение напряжения во внешней цепи между клеммами источника равно U0 = 14IR. Отметим, что это заодно позволяет найти ток, текущий через звено между точками подключения источника напряжения.
Он равен 14 I и течёт от центрального узла сетки к нижнему среднему узлу.
Для вольтметра можно записать: Uv = 4∙IR.
Отсюда Uv = 4∙U0 / 14 = 2∙U0 / 7 = 4В.
Ответ: Uv = 4В
Критерии оценивания
| Установлено распределение токов в звеньях сетки | 3 балла |
| Найдена связь между током, текущим через вольтметр, и токами в других частях цепи | 1 балл |
| Установлена связь между напряжением источника и током, текущим в какой-либо части цепи | 2 балла |
| Установлена связь между показанием вольтметра и током, текущим через него | 1 балл |
| Получено выражение для связи напряжения источника и показания вольтметра | 2 балла |
| Получен численный ответ для показания вольтметра | 1 балл |
Задача 5
Электрическая цепь состоит из соединённых последовательно идеального источника напряжения с ЭДС E = 12 В, резистора, разомкнутого ключа и заряженного до напряжения 2∙E конденсатора (полярность указана на схеме). Ключ замыкают.
Определите напряжение U на конденсаторе в тот момент, когда количество теплоты, выделившееся в резисторе, окажется в 3 раза меньше энергии, оставшейся в конденсаторе.
Возможное решение
Полярность зарядки конденсатора всегда останется такой же, какой она была вначале. Поскольку исходное напряжение на конденсаторе превышает ЭДС источника, то после замыкания ключа ток в цепи потечёт против часовой стрелки. К интересующему нас моменту времени заряд, протекший через источник (и подзарядивший его), равен q = C∙(2E – U) . Запишем закон сохранения энергии с учётом выделившегося количества теплоты и работы, совершённой источником:
Отсюда, с учётом того, что
получим:
Ответ: U = 18 В
Критерии оценивания
| Определена начальная энергия конденсатора | 1 балл |
| Найден протёкший через источник заряд | 1 балл |
| Найдена работа, совершённая источником | 1 балл |
| Записан закон сохранения энергии | 4 балла |
| Получено выражение для напряжения на конденсаторе | 2 балла |
| Получено численное значение напряжения на конденсаторе | 1 балл |
Общие рекомендации по оцениванию работы
- За каждое верно выполненное действие баллы складываются.
- При арифметической ошибке (в том числе ошибке при переводе единиц измерения) оценка снижается на 1 балл.
- Максимум за 1 задание – 10 баллов.
- Всего за работу – 50 баллов.
olimpiadnye-zadanija.ru
Задачи олимпиадные, задачи Капицы по физике, сборник задач
Эта брошюра — последняя в серии — необычна. Весь год наши читатели получали информацию о новых проблемах физики, астрономии, математики, о последних достижениях и открытиях. А теперь мы даем им возможность узнать о самих себе.
«Знаете ли вы физику? » — так можно было бы озаглавить брошюру академика П. Л. Капицы. Но это название, вероятно, оказалось бы слишком упрощенным.
Задачи Капицы иногда очень трудны, и не решить их не значит не знать физику. Но они и не таковы, чтобы их невозможно было решить новичку. Некоторые из них даже довольно просты. Но ни одна не поддастся вам, если вы не умеете вникать в сущность физического процесса. Многие задачи настолько содержательны, что подробное их решение с анализом превращается в небольшое научное исследование.
Как видите, полная пестрота. Но попробуйте в ней разобраться. И если это вам удастся, вы сможете заявить: Я понимаю физику.
Напечатанные в этом сборнике задачи были составлены мной для студентов Московского физико-технического института, когда в 1947— 1949 гг. я там читал курс общей физики. В этот сборник вошли также задачи, которые давались на экзаменах при поступлении в аспирантуру Института физических проблем Академии наук СССР. Эти задачи собрали вместе и подготовили к печати студенты физтеха, недавно окончившие институт И. Ш. Слободецкий и Л. Г. Асламазов.
При составлении этих задач я преследовал определенную цель, поэтому они были составлены не обычным образом. Чтобы их решение для читателя представляло интерес, следует сделать некоторые разъяснения.
Хорошо известно, какое большое значение имеет решение задач при изучении точных наук, таких, как математика, механика, физика и др. Решение задач дает возможность самому студенту не только проверить свои знания, но и, главное, тренирует его в умении прикладывать теоретические знания к решению практических проблем. Для преподавателя задачи являются одним из наиболее эффективных способов — проверять, насколько глубоко понимает студент предмет, не являются ли его знания только накоплением заученного наизусть. Кроме того, при обучении молодежи решением задач — можно еще воспитывать и выявлять творческое научное мышление. Хорошо известно, что для плодотворной научной работы требуются не только знания и понимание, но, главное, еще самостоятельное аналитическое и творческое мышление. Как одно из эффективных средств воспитания, выявления и оценки этих качеств при обучении молодежи и были составлены эти задачи.
Я стремился осуществить эту цель, составляя большинство задач таким образом, что они являются постановкой небольших проблем, и студент должен на основании известных физических законов проанализировать и количественно описать заданное явление природы. Эти явления природы выбраны так, чтобы они имели либо научный, либо практический интерес, и при этом нами учитывалось, что уровень знаний студентов должен быть достаточным, чтобы выполнить задание.
Обычно задачи ставятся так, чтобы подходов к их решению было несколько, с тем чтобы и в выборе решения могла проявиться индивидуальность студента. Например, 4-ю задачу о траектории полета самолета, при которой в кабине была бы невесомость, можно решить стандартным способом, написав уравнение движения самолета в поле тяжести Земли и приравнять нулю равнодействующую сил, действующих на точку, находящуюся в самолете. Другой способ решения более прост: принять, что если самолет следует траектории свободно летящего тела, которая в земном поле близка к параболе, тогда тело, находящееся в самолете, может быть в состоянии невесомости. Более любознательный студент может углубить вопрос и выяснить, что требуется при полете самолета для того, чтобы во всех точках кабины самолета было одновременно состояние невесомости. Далее можно разобрать вопрос, какие навигационные приборы нужны, чтобы пилот мог вести самолет по нужной для осуществления невесомости траектории и т.п. Характерной чертой наших задач является то, что они не имеют определенного законченного ответа, поскольку студент может по мере своих склонностей и способностей неограниченно углу биться в изучение поставленного вопроса. Ответы студента дают возможность оценить склонность и характер его научного мышления, что особенно важно при отборе в аспирантуру. Самостоятельное решение такого рода задач дает студенту тренировку в научном мышлении и вырабатывает в нем любовь к научным проблемам. Кроме проблемного характера этих задач, в большинстве из них есть еще одна особенность: в них не заданы численные величины физических констант и параметров и их представляется выбрать самим решающим. Так, например, в той же 4-й задаче о невесомости в самолете требуется определить время, в продолжение которого она может осуществляться, и при этом говорится, что выбирается современный самолет. Потолок полета этого самолета и его предельную скорость представляется выбрать самому студенту. Это мы делаем потому, что практика преподавания показывает, что обычно у нас мало заботятся о том, чтобы ученый и инженер в процессе своего учения научились конкретно представлять себе масштабы тех физических величин, с которыми им приходится оперировать: ток, скорость, напряжение, прочность, температуру и пр.
При решении научных проблем ученому всегда приходится в своем воображении ясно представлять величину и относительную значимость тех физических величин, которые служат для описания изучаемого явления. Это необходимо, чтобы уметь выбирать те из них, которые являются решающими при опытном изучении данного явления природы. Поэтому надо приучать смолоду ученых, чтобы символы в формулах, определяющие физические величины, всегда представляли для них конкретные количественные значения. Для физика, в отличие от математика, как параметры, так и переменные величины в математическом уравнении должны являться конкретными количествами. В моих задачах я к этому приучаю студентов тем, что они сами должны в литературе отыскивать нужные для решения величины. Студенты физтеха с интересом относятся к этим задачам и часто подвергали их совместному обсуждению. Когда эти задачи давались нами на экзаменах, то необходимое условие при решении — полная свобода в пользовании литературой. Обычно на экзаменах давалось несколько задач (до 5), так чтобы предоставить экзаменующемуся по своему вкусу выбрать 2-3 из них. По выбору задач тоже можно было судить о склонностях студента. Для аспирантских экзаменов составлялись новые и более сложные задачи, но здесь разрешалось экзаменующемуся не только пользоваться литературой, но и консультацией.
На решение каждой из задач я обычно давал около часа. Задачи должны были быть решены в письменном виде, но способности и характер студента в основном выявляются при устном обсуждении написанного текста. Чем ярче способности молодого ученого, тем скорее можно их выявить. Обычно обсуждение всех этих задач не брало у нас больше часа.
Воспитание и обучение молодых ученых теперь являются большой и самостоятельной государственной задачей. У нас в стране, кроме физико-технического института, имеется еще несколько высших учебных заведений, которые ставят перед собой задачу воспитания научных кадров. Несомненно, преподавание в таких вузах имеет свою специфику, и оно отличается от преподавания в вузах, которые готовят кадры для нашей промышленности и народного хозяйства. Мне думается, что при выработке методов преподавания решение задач-проблем, подобных собранным в этой книге, может быть широко использовано не только при преподавании физики, но и других областей точных наук: математики, механики, химии и др. Перед тем как решить крупную научную проблему, ученым надо уметь ее решать в малых формах. Поэтому решение задач, аналогичных приведенным в этом сборнике, является хорошей подготовкой для будущих научных работников.
Академик П.Л.Капица
Знаменитые задачи Капицы воскрешают в памяти студенческие годы и тот энтузиазм, с которым мы, молодежь, учились у Петра Леонидовича постигать физику. Самое главное то, что эти задачи доставляют самое настоящее эстетическое наслаждение. Хотя различными издательствами выпущено много отличных задачников по физике, но до сих пор не существует столь блестящей подборки, какую дал Капица. Эти задачи-огромный мир физики, науки, вызывающей сильную жажду мыслить и побеждать.
В последовательности задач нет видимой системы, каждая следующая возникает как бы сама собой и независимо от предыдущей. В то же время в подборке ничего нельзя убавить или изменить- в ней все стоит на своем месте, как стоят на месте руны Калевалы, имеющие самостоятельное значение и слабо связанные между собой сюжетной линией.
Вероятно, будет полезно сказать несколько слов о том методе, которого придерживается Капица в обучении физике и который привел его к созданию специального цикла задач и вопросов.
Петр Леонидович читал у нас на физико-техническом факультете МГУ (ныне МФТИ) курс общей физики с экспериментальным уклоном. Параллельный курс с теоретическим уклоном читал академик Ландау.
Разумеется, лекции Капицы были событием, и на них являлись не только все студенты, хотя посещение занятий было у нас не обязательным, но и масса посторонних людей. Знаменитый ученый тщательно готовился к каждой встрече со студентами- это было ясно по той четкости, с которой производились на глазах у пораженной аудитории оригинальные и сложные опыты. Никто из нас не забудет, как ассистент стрелял из лука, демонстрируя технику изготовления кварцевых нитей, как заряжали добровольцев электричеством, как двигались на длинном столе шары, делая для нас наглядными строгие законы механики. Но теперь, через 17 лет, когда вспоминаешь о лекциях Капицы, то прежде всего возникает в памяти даже не феерия блестящих экспериментов, а небольшие «лирические отступления» лектора от основной темы- короткие рассказы Капицы о физиках и физике. В этих, как бы возникающих по случайной ассоциации, вставках было основное: суть той школы, которую стремился сформировать Петр Леонидович.
Всякий выдающийся ученый создает школу, и в этом, вероятно, его главная заслуга. Школу не заменят никакие учебники. Ученый передает своим последователям не только знания, но и нечто гораздо более ценное: метод мышления, отношение к работе и к самому себе, свое индивидуальное представление о цели науки. Самое усиленное штудирование книг и статей не может оставить в душе того следа, который оставляет живое слово учителя, окруженного в глазах молодежи ореолом мудрости и авторитета.
Капица прививал нам бескорыстную любовь к физике и бескомпромиссную научную честность. Он рассказывал про удивительного человека по имени Кавендиш, который сделал замечательные открытия и не опубликовал их, ибо не стремился к славе, а работал из чистой любознательности. Он внес для нас полную четкость в запутанный тогда вопрос о приоритете в открытии, объяснив, что приоритет принадлежит не тому, кто первый упомянул о чем-то, а тому, кто первый оценил важность этого и поставил восклицательный знак. Он добавлял все новые штрихи к портрету великого Резерфорда- своего учителя. Слушая Капицу, мы начинали понимать, что физика не промежуточное звено между математикой и техникой, не синтез философии и опытных знаний, а ни на что не похожая, совершенно особая и прекрасная наука. И из студентов мы незаметно для самих себя становились физиками.
Секрет воздействия Капицы состоит в том, что он учит углубленному проникновению в механизм процесса и открывает тем самым для ученика новый мир. Он призывает не к формальному знанию, а к пониманию явления, заставляет ученика стать не свидетелем, а как бы участником физического явления. Именно для этого Капица широко использует свое любимое средство- задачи.
Я хорошо помню свой первый в жизни университетский экзамен по физике. Первый курс, зимняя сессия. Экзаменатор- заведующий кафедрой академик Капица.
Получив билет с вопросами, я начал сосредоточенно готовиться и исписал несколько листов бумаги. С бьющимся сердцем сел за стол перед Петром Леонидовичем. Каково же было мое удивление, когда он сразу отодвинул в сторону все мои труды, положил передо мной чистый лист бумаги и спросил:
—При ударе биллиардного шара в борт угол падения равен углу отражения или нет?
Так начался самый интересный в моей жизни экзамен. Необычные задачи сыпались на меня одна за другой и каждая требовала догадки и творческого напряжения. Это был не опрос, выяснявший, какой оценки заслужила моя работа в течение семестра, это был урок, давший мне больше пользы, чем любая лекция.
Когда я вышел с экзамена, ребята интересовались: трудные задачи дает Капица? Я не смог ответить на этот вопрос. Задачи были разные: одни я не мог решить, другие мог, но все они одинаково нравились мне и никакая из них не вызывала трепета, который возникает у студента перед каверзными вопросами экзаменатора
Петр Леонидович рассказывал на лекции, что один известный английский профессор давал своим ученикам такие задачи, которые сам не мог решить. «Если не решат-не надо,а решат- науке польза будет»,-говорил великий физик. Один раз дал- никто не решил, другой раз дал- снова никто не решил, а третий раз дал- один из студентов решил. Этот студент был Максвелл. «Нам тоже нужны Максвеллы»,- добавлял Петр Леонидович
—Ну и как же с Максвеллами?-может спросить читатель.- Есть они среди тех, кто почти двадцать лет тому назад прослушал свою первую университетскую лекцию? Сбылись надежды их воспитателя- академика Капицы?
На этот вопрос можно ответить так: подождем еще немного. Чем больше проходит времени, тем бесспорнее все становится на свои места. Но ясно одно: задачи Петра Леонидовича, составленные, чтобы заинтересовать молодежь физикой, «сработали». Они продолжают работать и сейчас. Доказательство тому- то чувство любопытства и заинтересованности, с которым вы держите в руках эту книжку.
В.Тростников
© Дизайн и верстка сайта: Журавлева С.В., Журавлев А.А.
physics-is-cool.ucoz.net
Олимпиада по физике школьный тур 11 класс 2015-2016 уч г с решениями
Решение школьного этапа всероссийской олимпиады
школьников по физике в 2015 — 2016 учебном году
класс.
1.Рыбка в опасности. Проплывая со скоростью V мимо большого коралла, маленькая рыбка почувствовала опасность и начала движение с постоянным (по модулю и направлению) ускорением a = 2 м/с2 . Через время t = 5 с после начала ускоренного движения её скорость оказалась направленной под углом 90 к начальному направлению движения и была в два раза больше начальной. Определите модуль начальной скорости V, с которой рыбка плыла мимо коралла.
Решение 1: Воспользуемся векторным уравнением
V кон = V + a*t . Учитывая, что Vкон = 2V и что
V кон V, его можно изобразить в виде векторного треугольника скоростей. Используя теорему Пифагора, находим ответ: V = at = 4,5 м/с.
√5
Правильность (ошибочность) решения
Баллы
Полное верное решение
10
Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.
8
Построен треугольник скоростей
5
При помощи теоремы Пифагора найден ответ
5
Если задача решалась аналитически, первые 5 баллов даются за записанную систему уравнений (зависимости проекций скорости от времени)
5
Получен верный ответ
5
Есть отдельные уравнения, относящиеся к сути задачи при отсутствии решения (или при ошибочном решении).
0-1
Решение неверное, или отсутствует.
0
2. Два одинаковых шарика, массой каждый, заряжены одинаковыми знаками, соединены нитью и подвешены к потолку (рис.). Какой заряд должен иметь каждый шарик, чтобы натяжение нитей было одинаковым? Расстояние между центрами шариков  . Чему равно натяжение каждой нити?
. Чему равно натяжение каждой нити?
Коэффициент пропорциональности в законе Кулона k = 9·109 Нм2/Кл2.
Решение 2:
На рисунке представлены силы действующие на оба тела. Из него видно, что
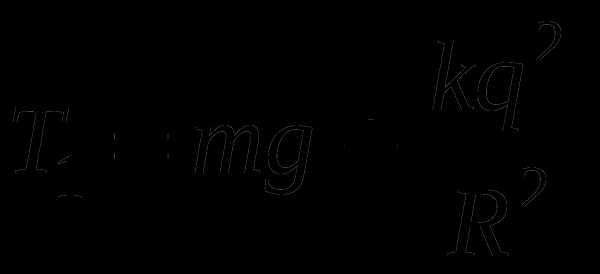
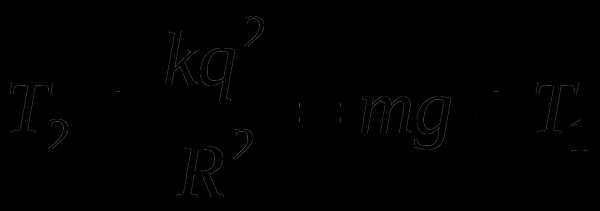
Учитывая, что находим
Кл.
Правильность (ошибочность) решения
Баллы
Полное верное решение
10
Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.
8
Решение в целом верное, однако, содержит существенные ошибки (не физические, а математические).
5-6
Сделан рисунок с действующими силами, записан 2 закон Ньютона для 1 и 2 тела.
5
Получен верный ответ
5
Есть понимание физики явления, но не найдено одно из необходимых для решения уравнений, в результате полученная система уравнений не полна и невозможно найти решение.
2-3
Есть отдельные уравнения, относящиеся к сути задачи при отсутствии решения (или при ошибочном решении).
0-1
Решение неверное, или отсутствует.
0
Задача 3.
В калориметре находится вода массой mв = 0,16 кг и температурой tв = 30 оC. Для того,
чтобы охладить воду, из холодильника в стакан переложили лед массой mл = 80 г. В
холодильнике поддерживается температура tл = –12 оC. Определите конечную температуру в
калориметре. Удельная теплоёмкость воды Cв = 4200 Дж/(кг* оC), удельная теплоёмкость льда
Cл = 2100 Дж/(кг* оC), удельная теплота плавления льда λ = 334 кДж/кг.
Решение 3:
Так как неясно, каким будет конечное содержимое калориметра (растает ли весь лёд?)
будем решать задачу «в числах».
Количество теплоты, выделяемое при охлаждении воды: Q1 = 4200*0,16*30 Дж = 20160
Дж.
Количество теплоты, поглощаемое при нагревании льда: Q2 = 2100*0,08*12 Дж = 2016
Дж.
Количество теплоты, поглощаемое при таянии льда: Q3 = 334000*0,08 Дж = 26720 Дж.
Видно, что количества теплоты Q1 недостаточно для того, чтобы расплавить весь лёд
(Q1 < Q2 + Q3). Это означает, что в конце процесса в сосуде будут находится и лёд, и вода, а
температура смеси будет равна t = 0 оC.
Правильность (ошибочность) решения
Баллы
Полное верное решение
10
Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.
8
Решение в целом верное, однако, содержит существенные ошибки (не физические, а математические).
5-6
Записана формула для расчета количества теплоты для 1, 2 и 3 процесса(по 2 балла за каждую формулу)
Получен верный ответ
5
Есть понимание физики явления, но не найдено одно из необходимых для решения уравнений, в результате полученная система уравнений не полна и невозможно найти решение.
2-3
Есть отдельные уравнения, относящиеся к сути задачи при отсутствии решения (или при ошибочном решении).
0-1
Решение неверное, или отсутствует.
0
Задача 4
Экспериментатор собрал электрическую цепь, состоящую из разных батареек с
пренебрежимо малыми внутренними сопротивлениями и одинаковых плавких
предохранителей, и нарисовал ее схему (предохранители на схеме обозначены черными
прямоугольниками). При этом он забыл указать на рисунке часть ЭДС батареек. Однако
э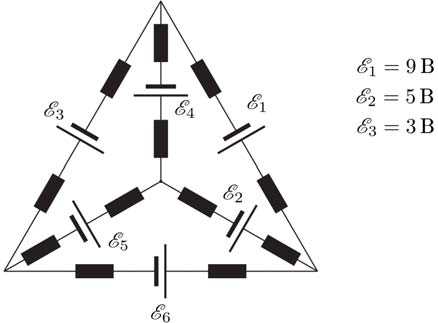 кспериментатор помнит, что в тот день при проведении опыта все предохранители остались
кспериментатор помнит, что в тот день при проведении опыта все предохранители остались
целыми. Восстановите неизвестные значения ЭДС.
Решение 4:
Если бы при обходе какого-либо замкнутого контура алгебраическая сумма ЭДС была
бы не равной нулю, то в этом контуре возник бы очень большой ток (из-за малости
внутренних сопротивлений батареек), и предохранители перегорели бы. Поскольку такого не
произошло, можно записать следующие равенства:
E1− E2 − E4 = 0, откуда E4 = 4 В,
E3 +E5 − E4 = 0, откуда E5 = 1 В,
E5 +E2 − E6 = 0, откуда E6 = 6 В.
Правильность (ошибочность) решения
Баллы
Полное верное решение
10
Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.
8
Сформулирована идея о равенстве нулю суммы ЭДС при обходе любого контура
4
Правильно найденные значения трех неизвестных ЭДС – по 2 балла за каждую
6
Есть понимание физики явления, но не найдено одно из необходимых для решения уравнений, в результате полученная система уравнений не полна и невозможно найти решение.
2-3
Есть отдельные уравнения, относящиеся к сути задачи при отсутствии решения (или при ошибочном решении).
0-1
Решение неверное, или отсутствует.
0
infourok.ru
Олимпиада по физике 7-11 классов с решениями
XLVI Всероссийская олимпиада школьников по физике. Ленинградская область. Муниципальный этап
7 класс
На графике показана зависимость пути, пройденного телом от времени. Какой из графиков соответствует зависимости скорости этого тела от времени?

2. Из пункта A в пункт B выехал автомобиль «Волга» со скоростью 90 км/ч. В то же время навстречу ему из пункта B выехал автомобиль «Жигули». В 12 часов дня машины проехали мимо друг друга. В 12:49 «Волга» прибыла в пункт B, а ещё через 51 минуту «Жигули» прибыли в A. Вычислите скорость «Жигулей».
3. Материальная точка движется по окружности радиусом R=2 м с постоянной по модулю скоростью, совершая полный оборот за 4 с. Определите среднюю скорость по перемещению за первые 3 с движения
4. Тело движется так, что скорости его в течение каждого из n равных промежутков времени равны соответственно V1 ,V2, V3, …..Vn. Какова средняя скорость тела?
XLVI Всероссийская олимпиада школьников по физике. Ленинградская область. Муниципальный этап
8 класс
К
 убик 3 плавает в жидкостях 1 и 2 как показано на рисунке. В жидкости 1 находится 2/3 объема кубика. Плотности жидкостей 1 и 2. Найти плотность материала кубика 3.
убик 3 плавает в жидкостях 1 и 2 как показано на рисунке. В жидкости 1 находится 2/3 объема кубика. Плотности жидкостей 1 и 2. Найти плотность материала кубика 3.
2. Междугородный автобус прошел 80 км за 1 час. Двигатель развивал мощность 70 кВт при КПД 25%. Сколько дизельного топлива (плотность 800 кг/м3, удельная теплота сгорания 42 106 Дж/кг) сэкономил водитель, если норма расхода горючего 40 л на 100 км пути?
3. Человек переправляется на лодке из пункта А в пункт В, находящийся на кратчайшем расстоянии от А на другом берегу. Скорость лодки относительно воды 2,5 м/c, скорость течения реки 1,5 м/c. Какое минимальное время потребуется ему для переправы, если ширина реки равна 800 м?
4. Тело проходит одинаковые участки пути с постоянными в пределах участка скоростями V1 , V2 , V3, ….. Vn .Определите среднюю скорость на всем пути.
XLVI Всероссийская олимпиада школьников по физике. Ленинградская область. Муниципальный этап
9 класс
Полый шарик из алюминия находясь в воде, растягивает пружину динамометра с силой 0.24 Н, а в бензине с силой 0,33 Н. Найти объем полости. Плотности алюминия, воды и бензина соответственно =2,7 103 кг/м3, в = 103 кг/м3 и Б =0,7 103 кг/м3. Выталкивающей силой воздуха пренебречь. Ускорение свободного падения g = 10 м/c2.
На наклонном дне сосуда, наполненного водой, покоится на маленьких подставках алюминиевый кубик с ребром a = 10 см. Определите суммарную силу трения между кубиком и подставками. Угол наклона дна сосуда к горизонту = 30°, плотности алюминия и воды соответственно a = 2,7 • 103 кг/м3, в = 103 кг/м3. Ускорение свободного падения g = 10 м/c2.
Камень, брошенный под углом 300 к горизонту, дважды был на одной высоте h; спустя время t1 = 3 c и время t2 = 5 c после начала движения. Найти начальную скорость тела. Ускорение свободного падения Земли равно 9,81 м/c2.
Ускорение свободного падения на поверхности Солнца 264,6 м/c2, а радиус Солнца в 108 раз больше радиуса Земли. Определите отношение плотностей Земли и Солнца. Ускорение свободного падения Земли равно 9,81 м/c2.
Для измерения температуры 66 г воды в нее погрузили термометр, имеющий теплоемкость СТ= 1,9 Дж/К, который показывал температуру в помещении t2=17,80С. Какова действительная температура воды, если термометр показывает 32,4 0С. Теплоемкость воды с=4,2 кДж/K?
XLVI Всероссийская олимпиада школьников по физике. Ленинградская область. Муниципальный этап
10 класс
1. Пузырек воздуха поднимается со дна водоема, имеющего глубину H . Найти зависимость радиуса пузырька воздуха от глубины его положения в текущий момент времени, если его объем на глубине H равен V.
2. За время t1 = 40 c в цепи состоящей из трех одинаковых проводников соединенных параллельно и включенных в сеть, выделилось некоторое количество теплоты Q. За какое время выделится такое же количество теплоты, если проводники соединить последовательно?
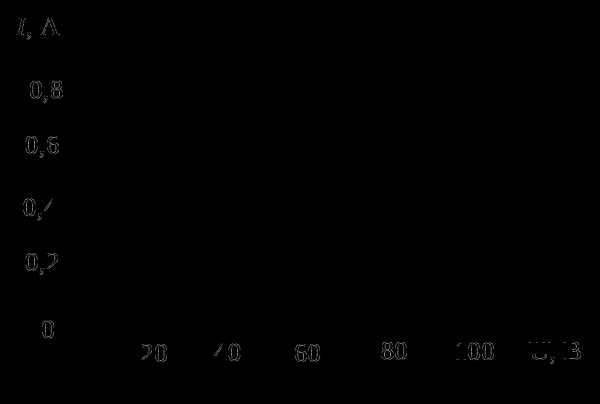
3. Можно ли две лампы накаливания мощностью 60 Вт и 100 Вт, рассчитанные на напряжение 110 В, включить последовательно в сеть напряжением 220 В, если допустимо превышение напряжения на каждой лампе не более 10% от номинального? Вольтамперная характеристика (зависимость силы тока в лампе от приложенного напряжения) показана на рисунке.
4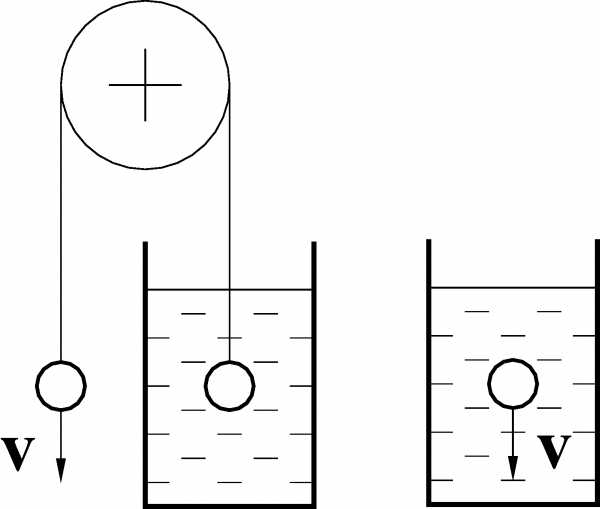 . Два одинаковых шара плотности ρ соединены невесомой нитью, переброшенной через блок. Правый шар, погруженный в вязкую жидкость плотности ρ0, поднимается с установившейся скоростью v. Определить отношение ρ/ρ0, если установившаяся скорость свободно падающего в жидкости шара также равна v. Ускорение свободного падения g.
. Два одинаковых шара плотности ρ соединены невесомой нитью, переброшенной через блок. Правый шар, погруженный в вязкую жидкость плотности ρ0, поднимается с установившейся скоростью v. Определить отношение ρ/ρ0, если установившаяся скорость свободно падающего в жидкости шара также равна v. Ускорение свободного падения g.
5. Спортсмены бегут с одинаковыми скоростями v колонной длины l0 . Навстречу бежит тренер со скоростью u (u
XLVI Всероссийская олимпиада школьников по физике. Ленинградская область. Муниципальный этап
11 класс
1. Колесо радиуса R катится без проскальзывания с постоянной скоростью центра колеса v. С верхней точки обода колеса срывается камешек. Через какое время колесо наедет на этот камешек? Радиус колеса R, ускорение свободного падения g.
2. Муравей бежит от муравейника по прямой так, что скорость его обратно пропорциональна расстоянию до центра муравейника. В тот момент, когда муравей находится в точке А на расстоянии l1 = 1 м от центра муравейника его скорость v1= 2 см/с. За какое время муравей добежит от точки А до точки В, которая находится на расстоянии l2 = 2 м от центра муравейника?
3. Какой максимальный объём воды плотностью ρ1 = 1,0 г/см3 можно налить в H-образную несимметричную трубку с открытыми верхними концами, частично заполненную маслом плотностью ρ2 = 0,75 г/см3? Площадь горизонтального сечения вертикальных частей трубки равна S. Объёмом горизонтальной части трубки можно пренебречь. Вертикальные размеры трубки и высота столба масла приведены на рисунке (высоту h считать заданной).
Примечание. Затыкать открытые концы трубки, наклонять её или выливать из неё масло запрещено.
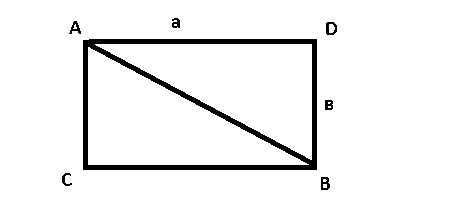
4. Чему равно сопротивление проволочного каркаса в виде прямоугольника со сторонами а и в и диагональю, если ток течет от точки А к точке В? Сопротивление единицы длины провода .
Движение материальной точки описывается уравнением х(t)=0,2 sin(3,14t), где х выражается в метрах, t – в секундах. Определите путь, пройденный точкой за 10 с движения.
Возможные решения
7 класс
На графике показана зависимость пути, пройденного телом от времени. Какой из графиков соответствует зависимости скорости этого тела от времени?

Решение: Правильный ответ Г.
2. Из пункта A в пункт B выехал автомобиль «Волга» со скоростью 90 км/ч. В то же время навстречу ему из пункта B выехал автомобиль «Жигули». В 12 часов дня машины проехали мимо друг друга. В 12:49 «Волга» прибыла в пункт B, а ещё через 51 минуту «Жигули» прибыли в A. Вычислите скорость «Жигулей».
Решение: Волга» проехала путь от пункта A до места встречи с «Жигулями» за время tx, а «Жигули» этот же участок проехали за t1 = 100 минут. В свою очередь, «Жигули» проехали путь от пункта B до места встречи с «Волгой» за время tx, а «Волга» этот же участок проехала за t2 = 49 минут. Запишем эти факты в виде уравнений:
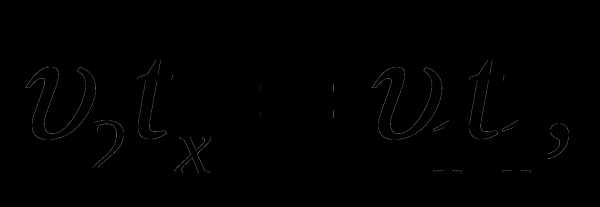
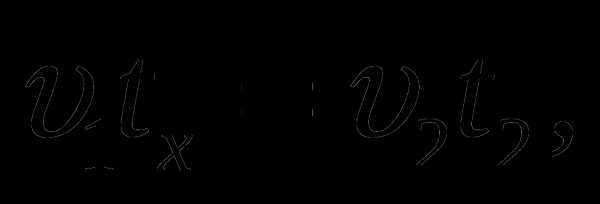
где υ1 – скорость «Жигулей», а υ2 – скорость «Волги». Поделив почленно одно уравнение на другое, получим:
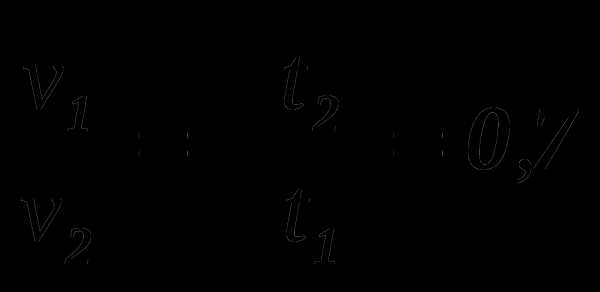 .
.
Отсюда υ1 = 0,7υ2 = 63 км/ч.
3. Материальная точка движется по окружности радиусом R=2 м с постоянной по модулю скоростью, совершая полный оборот за 4 с. Определите среднюю скорость по перемещению за первые 3 с движения
Решение: Перемещение материальной точки за 3 с составляет 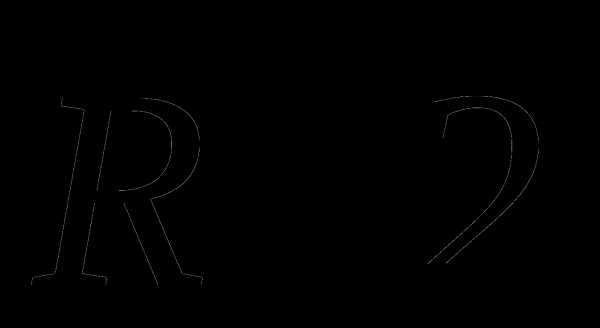
Средняя скорость по перемещению равна 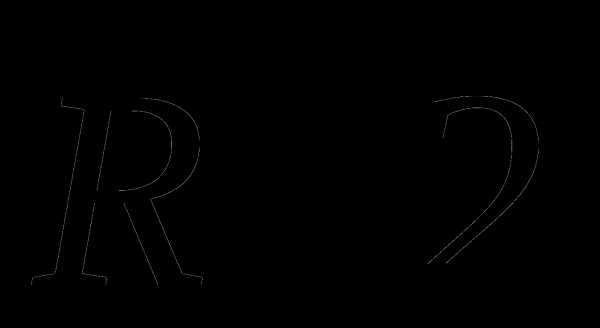 /3
/3
4. Тело движется так, что скорости его в течение каждого из n равных промежутков времени равны соответственно V1 ,V2, V3, …..Vn. Какова средняя скорость тела?
Решение: 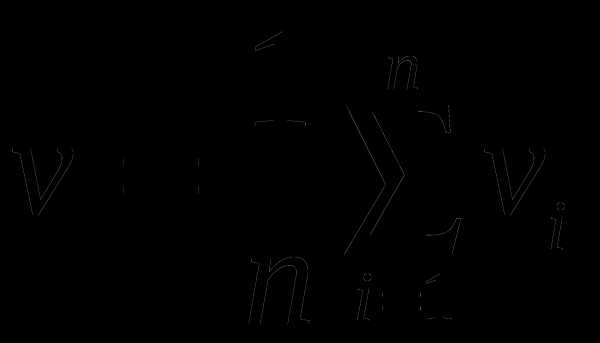
XLVI Всероссийская олимпиада школьников по физике. Ленинградская область. Муниципальный этап
Возможные решения
8 класс
К
 убик 3 плавает в жидкостях 1 и 2 как показано на рисунке. В жидкости 1 находится 2/3 объема кубика. Плотности жидкостей 1 и 2. Найти плотность материала кубика 3.
убик 3 плавает в жидкостях 1 и 2 как показано на рисунке. В жидкости 1 находится 2/3 объема кубика. Плотности жидкостей 1 и 2. Найти плотность материала кубика 3.
Решение: F1 mg =F1+F2 F2
3 gV = 1 gV 2/3 +2 gV 1/3
mg 3 = 12/3 +21/3
3 = (21 + 2)/3
2. Междугородный автобус прошел 80 км за 1 час. Двигатель развивал мощность 70 кВт при КПД 25%. Сколько дизельного топлива (плотность 800 кг/м3, удельная теплота сгорания 42 106 Дж/кг) сэкономил водитель, если норма расхода горючего 40 л на 100 км пути?
Решение: КПД = A/Q =Nt/rm = Nt/rV
V= Nt/rКПД
Вычисления: V= 0,03 м3; из пропорции 80/100 = x/40 определяем норму расхода горючего на 80 км х = 32 (литра)
V=32-30=2 (литра)
3. Человек переправляется на лодке из пункта А в пункт В, находящийся на кратчайшем расстоянии от А на другом берегу. Скорость лодки относительно воды 2,5 м/c, скорость течения реки 1,5 м/c. Какое минимальное время потребуется ему для переправы, если ширина реки равна 800 м?
Решение: Для переправы за минимальное время необходимо, чтобы вектор результирующей скорости v был направлен перпендикулярно берегу
4. Тело проходит одинаковые участки пути с постоянными в пределах участка скоростями V1 , V2 , V3, ….. Vn .Определите среднюю скорость на всем пути.
Решение: 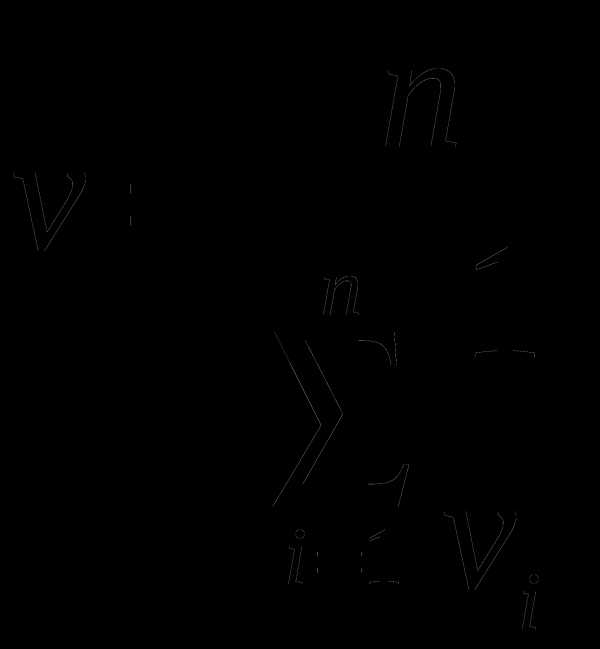

XLVI Всероссийская олимпиада школьников по физике. Ленинградская область. Муниципальный этап
Возможные решения
9 класс
Полый шарик из алюминия находясь в воде, растягивает пружину динамометра с силой 0.24 Н, а в бензине с силой 0,33 Н. Найти объем полости. Плотности алюминия, воды и бензина соответственно =2,7 103 кг/м3, в = 103 кг/м3 и Б =0,7 103 кг/м3. Выталкивающей силой воздуха пренебречь. Ускорение свободного падения g = 10 м/c2.
Решение:
На наклонном дне сосуда, наполненного водой, покоится на маленьких подставках алюминиевый кубик с ребром a = 10 см. Определите суммарную силу трения между кубиком и подставками. Угол наклона дна сосуда к горизонту = 30°, плотности алюминия и воды соответственно a = 2,7 • 103 кг/м3, в = 103 кг/м3. Ускорение свободного падения g = 10 м/c2.
Решение: Кубик находится в равновесии под действием трех сил: силы тяжести mg, архимедовой силы FA и силы реакции со стороны подставок, которую, в свою очередь, удобно разложить на две составляющие: нормальную к наклонному дну составляющую силы реакции N и силу трения о подставки Fтр.
Отметим, что наличие подставок, на которых покоится кубик, играет в задаче важную роль, т.к. именно благодаря им вода окружает кубик со всех сторон, и для определения силы, с которой вода действует на него, можно воспользоваться законом Архимеда. Если бы кубик лежал непосредственно на дне сосуда и вода под него не подтекала, то результирующая поверхностных сил давления воды на кубик не выталкивала бы его наверх, а наоборот, еще сильнее прижимала бы ко дну. В нашем случае на кубик действует выталкивающая сила FA = a3g, направленная вверх.
Проектируя все силы на координатную ось, параллельную дну сосуда, запишем условие равновесия кубика в виде: Fтр = (mg – FA) sin.
Учитывая, что масса кубика m = aa3, получаем ответ: Fтр =(a – в)a3g sin = 8,5 (Н).
Камень, брошенный под углом 300 к горизонту, дважды был на одной высоте h; спустя время t1 = 3 c и время t2 = 5 c после начала движения. Найти начальную скорость тела. Ускорение свободного падения Земли равно 9,81 м/c2.
Решение: Движение тела в вертикальном направлении описывается уравнением:
Отсюда при y = h получим;
Используя свойства корней квадратного уравнения, согласно которым
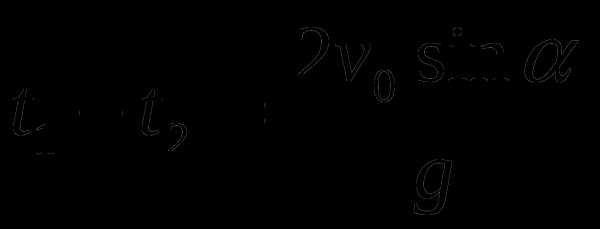 получим
получим
Ускорение свободного падения на поверхности Солнца 264,6 м/c2, а радиус Солнца в 108 раз больше радиуса Земли. Определите отношение плотностей Земли и Солнца. Ускорение свободного падения Земли равно 9,81 м/c2.
Решение: Применим закон всемирного тяготения для определения g
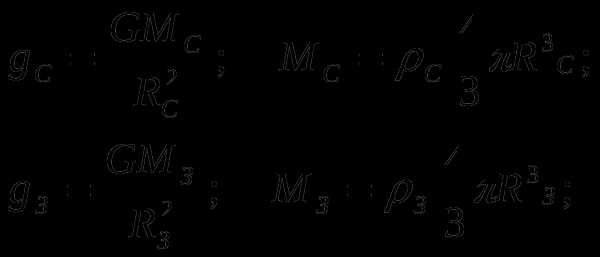
Для измерения температуры 66 г воды в нее погрузили термометр, имеющий теплоемкость СТ= 1,9 Дж/К, который показывал температуру в помещении t2=17,80С. Какова действительная температура воды, если термометр показывает 32,4 0С. Теплоемкость воды с=4,2 кДж/K?
Решение: Термометр при погружении его в воду получил количество теплоты .
Это количество теплоты отдано ему водой; следовательно .
Отсюда
XLVI Всероссийская олимпиада школьников по физике. Ленинградская область. Муниципальный этап
Возможные решения
10 класс
1. Пузырек воздуха поднимается со дна водоема, имеющего глубину H . Найти зависимость радиуса пузырька воздуха от глубины его положения в текущий момент времени, если его объем на глубине H равен V.
Решение: Давление на дне водоема: на глубине h:
Объем пузырька на глубине h: 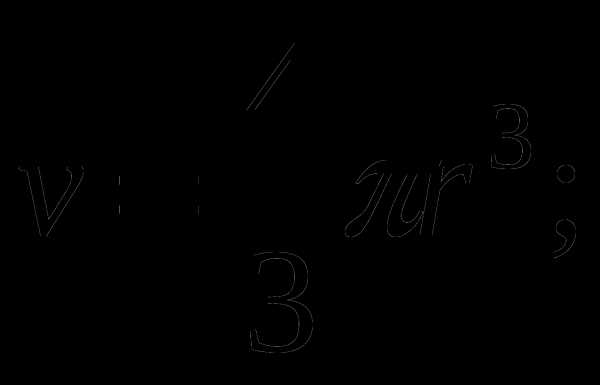

Отсюда 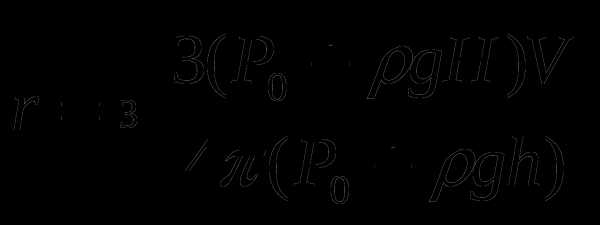
2. За время t1 = 40 c в цепи состоящей из трех одинаковых проводников соединенных параллельно и включенных в сеть, выделилось некоторое количество теплоты Q. За какое время выделится такое же количество теплоты, если проводники соединить последовательно?
Решение:
3. Можно ли две лампы накаливания мощностью 60 Вт и 100 Вт, рассчитанные на напряжение 110 В, включить последовательно в сеть напряжением 220 В, если допустимо превышение напряжения на каждой лампе не более 10% от номинального? Вольтамперная характеристика (зависимость силы тока в лампе от приложенного напряжения) показана на рисунке.

Решение: При номинальном напряжении Uн=110 В ток, текущий через лампу мощностью Р1= 60 Вт равен А. При последовательном соединении ламп такой же ток пойдет через лампу мощностью Р2= 100 Вт. Согласно вольтамперной характеристике этой лампы, при токе 0,5 А напряжение на этой лампе должно быть
А. При последовательном соединении ламп такой же ток пойдет через лампу мощностью Р2= 100 Вт. Согласно вольтамперной характеристике этой лампы, при токе 0,5 А напряжение на этой лампе должно быть  В. Следовательно, при последовательном соединении двух ламп напряжение на лампе мощностью 60 Вт достигает номинального уже при напряжении в сети
В. Следовательно, при последовательном соединении двух ламп напряжение на лампе мощностью 60 Вт достигает номинального уже при напряжении в сети 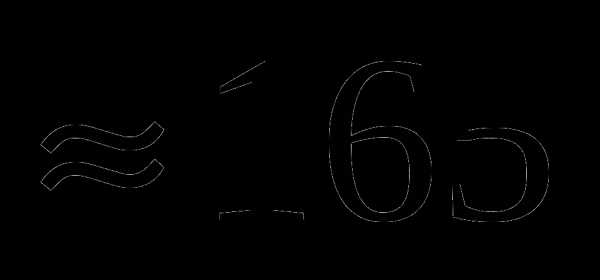 В. Поэтому при напряжении в сети 220 В напряжение на этой лампе будет превышать номинальное больше, чем на 10%, и лампа перегорит.
В. Поэтому при напряжении в сети 220 В напряжение на этой лампе будет превышать номинальное больше, чем на 10%, и лампа перегорит.
4 . Два одинаковых шара плотности ρ соединены невесомой нитью, переброшенной через блок. Правый шар, погруженный в вязкую жидкость плотности ρ0, поднимается с установившейся скоростью v. Определить отношение ρ/ρ0, если установившаяся скорость свободно падающего в жидкости шара также равна v. Ускорение свободного падения g.
. Два одинаковых шара плотности ρ соединены невесомой нитью, переброшенной через блок. Правый шар, погруженный в вязкую жидкость плотности ρ0, поднимается с установившейся скоростью v. Определить отношение ρ/ρ0, если установившаяся скорость свободно падающего в жидкости шара также равна v. Ускорение свободного падения g.
Решение: Силы сопротивления движению шаров из-за равенства их установившихся скоростей одинаковы в обоих случаях, хотя и направлены в противоположные стороны.
Запишем динамическое уравнение движения в проекциях на ось оу, направленную вертикально вверх, для первого и второго случаев (движения системы тел и падения одного шарика в жидкости, соответственно):
T – mg = 0
T + FA – mg – Fc = 0
FA – mg + Fc = 0 ,
где mg –модуль силы тяжести, Т – модуль силы натяжения нити, FA – модуль выталкивающей силы, Fc — модуль силы сопротивления.
Решая систему уравнений, получим, 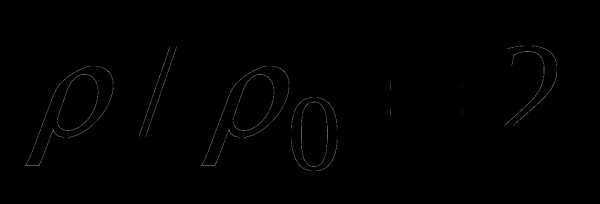 .
.
5. Спортсмены бегут с одинаковыми скоростями v колонной длины l0 . Навстречу бежит тренер со скоростью u (u
Решение: Время, в течение которого все спортсмены, начиная с первого и кончая последним в колонне, повстречаются с тренером, равно
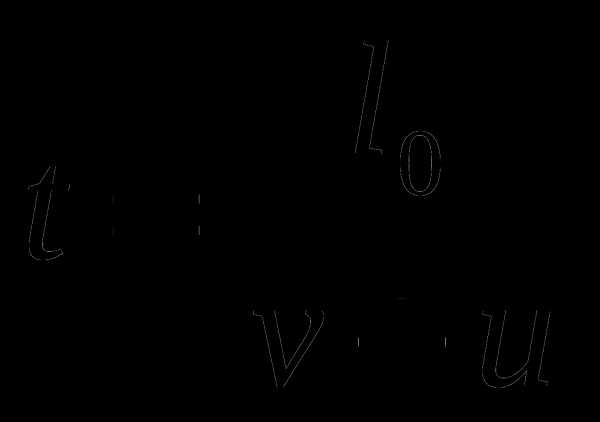 .
.
В тот момент, когда последний спортсмен поравняется с тренером, первый будет находиться от него на расстоянии
.
Такова и будет длина колонны, когда все спортсмены развернутся.
XLVI Всероссийская олимпиада школьников по физике. Ленинградская область.
Муниципальный этап
Возможные решения
11 класс
1. Колесо радиуса R катится без проскальзывания с постоянной скоростью центра колеса v. С верхней точки обода колеса срывается камешек. Через какое время колесо наедет на этот камешек? Радиус колеса R, ускорение свободного падения g.
Решение: Если ось колеса движется со скоростью v, без проскальзывания, то скорость нижней точки равна 0, а верхней, как и горизонтальная скорость камушка, равна 2v.
Время падения камушка
Время движения оси по горизонтали в два раза больше.
Значит, наезд произойдет через 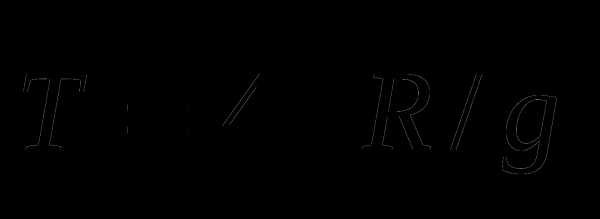 .
.
2. Муравей бежит от муравейника по прямой так, что скорость его обратно пропорциональна расстоянию до центра муравейника. В тот момент, когда муравей находится в точке А на расстоянии l1 = 1 м от центра муравейника его скорость v1= 2 см/с. За какое время муравей добежит от точки А до точки В, которая находится на расстоянии l2 = 2 м от центра муравейника?
Решение: Скорость муравья меняется со временем не по линейному закону. Поэтому средняя скорость на разных участках пути различна, и пользоваться для решения известными формулами для средней скорости мы не можем. Разобьем путь муравья от точки А до точки В на малые участки, проходимые за одинаковые промежутки времени  . Тогда
. Тогда
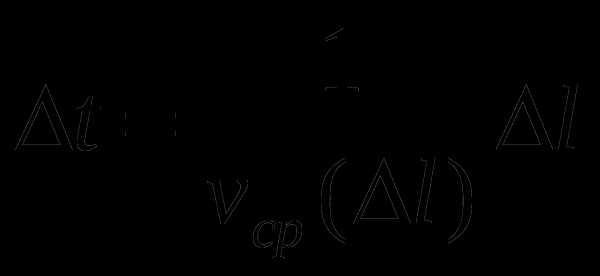 , где
, где 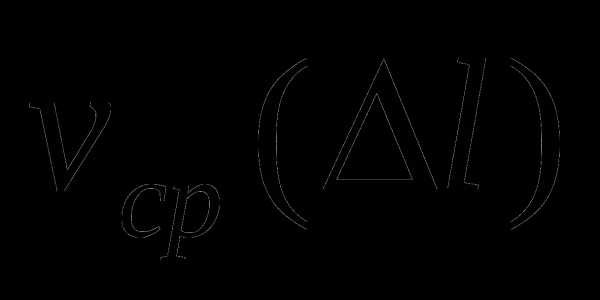 — средняя скорость на данном отрезке
— средняя скорость на данном отрезке  .
.
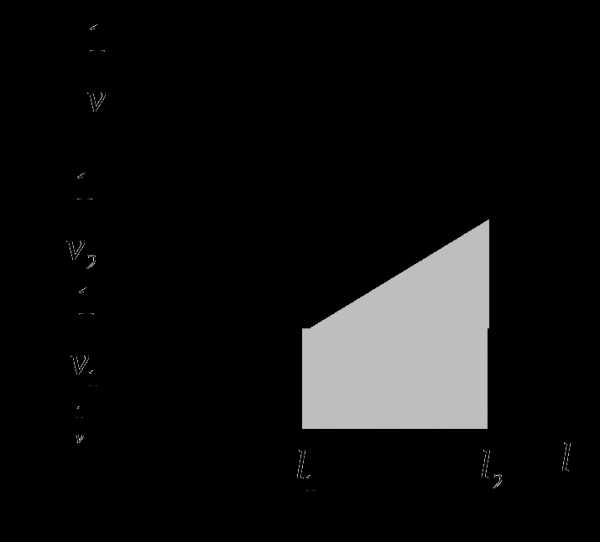 Построим график зависимости величины
Построим график зависимости величины 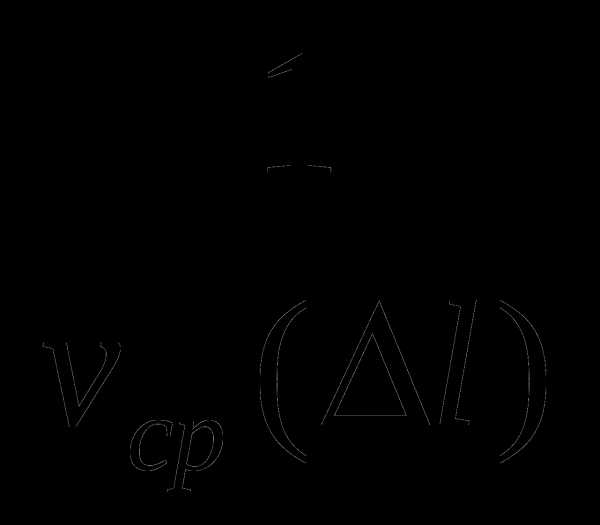 от
от 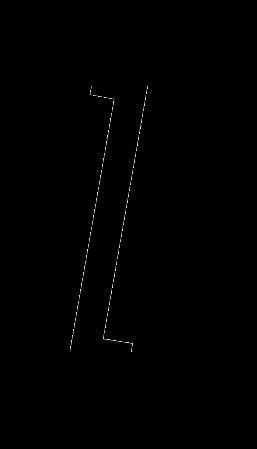 (см. рисунок). Искомое время
(см. рисунок). Искомое время  численно равно заштрихованной на рисунке площади:
численно равно заштрихованной на рисунке площади:
.
Учитывая, что 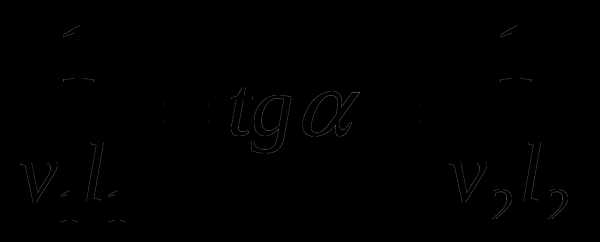 , найдем соотношение между обратными величинами скоростей:
, найдем соотношение между обратными величинами скоростей: 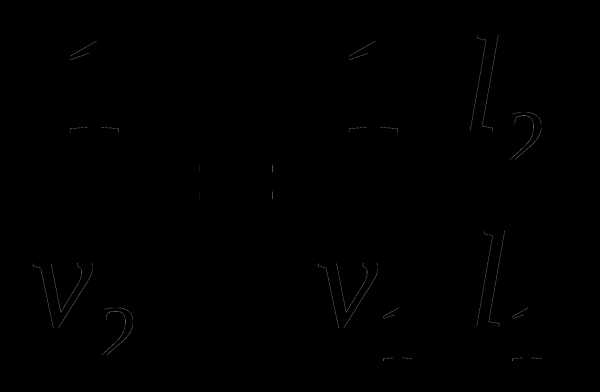 . Подставляя полученное равенство в последнее выражение для
. Подставляя полученное равенство в последнее выражение для  , получим: .
, получим: .
После подстановки, найдем значение с.
3. Какой максимальный объём воды плотностью ρ1 = 1,0 г/см3 можно налить в H-образную несимметричную трубку с открытыми верхними концами, частично заполненную маслом плотностью ρ2 = 0,75 г/см3? Площадь горизонтального сечения вертикальных частей трубки равна S. Объёмом горизонтальной части трубки можно пренебречь. Вертикальные размеры трубки и высота столба масла приведены на рисунке (высоту h считать заданной).
Примечание. Затыкать открытые концы трубки, наклонять её или выливать из неё масло запрещено.
Решение: Важно, чтобы в коротком колене осталось как можно меньше масла. Тогда в высокой трубке можно будет создать столб максимальной высоты, превышающей 4h на х. Для этого начнём наливать воду в правое колено. Так будет продолжаться до тех пор, пока уровень воды не достигнет 2h в правом колене, а уровень масла, соответственно, – 3h в левом. Дальнейшее вытеснение масла невозможно, так как граница раздела масло-вода в правом колене станет выше соединительной трубки, и в левое колено начнёт поступать вода. Процесс добавления воды придётся прекратить, когда верхняя граница масла в правом колене достигнет верха колена. Условие равенства давлений на уровне соединительной трубки даёт:
откуда x = (ρ1 — ρ2)h/ρ2. Окончательно, высота столба воды, который удалось налить (4h + х), а, следовательно, максимальный объем воды будет 4,33hS.
4. Чему равно сопротивление проволочного каркаса в виде прямоугольника со сторонами а и в и диагональю, если ток течет от точки А к точке В? Сопротивление единицы длины провода .

Решение:
R
5. Движение материальной точки описывается уравнением х(t)=0,2 sin(3,14t), где х выражается в метрах, t – в секундах. Определите путь, пройденный точкой за 10 с движения.
Решение: Движение описывается уравнением:
;
отсюда Т=1 с За время 10 с точка совершит 10 полных колебаний. За время одного полного колебания точка проходит путь равный 4 амплитудам.
Полный путь равен 10x 4x 0,2 = 8 м
infourok.ru
Физика | Олимпиадные задания
Содержание Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 1 Содержание ↑ Систему грузов, имеющих массы m и 3m, тянут с помощью подвижного блока по гладкой горизонтальной поверхности. При каких значениях силы F грузы не будут проскальзывать друг по другу, если коэффициент трения между ними μ? Массами блоков и нити можно пренебречь. Нить […]
Содержание Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 1 Содержание ↑ Два шарика брошены одновременно навстречу друг другу с одинаковыми начальными скоростями: один с поверхности земли вертикально вверх, другой с высоты Н вертикально вниз. Найдите эти скорости, если известно, что шарики встретились на высоте H/4. Возможное решение Направим ось x вверх и […]
Содержание Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 1 Содержание ↑ Электричка без начальной скорости с постоянным ускорением начинает заезжать в тоннель, имеющий длину L. Машинист в головном вагоне заметил, что он проехал тоннель за время t = 38 с. Сколько времени находился в тоннеле кондуктор, сидящий в конце последнего вагона, если […]
Содержание Задание 1 Задание 2 Задание 3 Задание 4 Задание 1 Содержание ↑ Мотоциклист выехал из города со скоростью v = 60 км/ч, одновременно ему навстречу из деревни выехал велосипедист со скоростью u. Через время t = 30 мин они встретились. Затем мотоциклист доехал до деревни, и сразу же с удвоенной скоростью поехал назад, и успел в город одновременно […]
Содержание Задание 1 Задание 2 Задание 3 Задание 4 Задание 1 Содержание ↑ В ящик с жесткими стенками, имеющий форму куба объемом 1 м3 и массой 300 кг, насыпали стальные шары диаметром 20 мм плотностью 7800 кг/м3. Затем ящик потрясли и добавили в него столько шаров, что больше уже не получается засунуть ни одного шара (то […]
Содержание Задача 1 Возможное решение Критерии оценивания Задача 2 Возможное решение Критерии оценивания Задача 3 Возможное решение Критерии оценивания Задача 4 Возможное решение Критерии оценивания Задача 5 Возможное решение Критерии оценивания Задача 1 Содержание ↑ Колесо обозрения радиусом R = 60 м вращается с постоянной угловой скоростью в вертикальной плоскости, совершая полный оборот за время T […]
Содержание Задача 1 Возможное решение Критерии оценивания Задача 2 Возможное решение Критерии оценивания Задача 3 Возможное решение 1 Возможное решение 2 Критерии оценивания Задача 4 Возможное решение Критерии оценивания Задача 5 Возможное решение Критерии оценивания Задача 1 Содержание ↑ Три небольших одинаковых шарика закреплены на прямой лёгкой спице, один из концов которой шарнирно прикреплён к потолку. […]
Содержание Задача 1 Возможное решение Критерии оценивания Задача 2 Возможное решение Критерии оценивания Задача 3 Возможное решение Критерии оценивания Задача 4 Возможное решение Критерии оценивания Задача 5 Возможное решение Критерии оценивания Задача 1 Содержание ↑ Саша, Коля и Дима приняли участие в соревнованиях по бегу на дистанцию L = 200 м. На старте друзья располагались на […]
Содержание Задача 1 Возможное решение Критерии оценивания Задача 2 Возможное решение Критерии оценивания Задача 3 Возможное решение 1 Критерии оценивания Возможное решение 2 Критерии оценивания Задача 4 Возможное решение Критерии оценивания Задача 1 Содержание ↑ Турист проехал на велосипеде за один день 40 км. При этом с 9.00 до 11.20 он ехал со скоростью, которая равномерно […]
Содержание Задача 1 Возможное решение Критерии оценивания Задача 2 Возможное решение Критерии оценивания Задача 3 Возможное решение Критерии оценивания Задача 1 Содержание ↑ Почтальон Печкин, двигаясь на велосипеде с постоянной скоростью, объехал одну за другой улицы деревни, доставляя корреспонденцию. Линия, вдоль которой двигался почтальон, показана на рисунке. Во сколько раз быстрее проехал бы Печкин расстояние от […]
Задача 1 Стоя на движущемся вниз эскалаторе, мальчик подбросил монетку, как ему показалось, вертикально вверх, и через τ = 1 с поймал её. Скорость эскалатора V = 1 м/с, а угол его наклона к горизонту α = 30⁰. На какое максимальное расстояние от точки бросания удалялась монетка? В течение какого времени монетка поднималась вверх в […]
Задача 1 Небольшой брусок через систему блоков связан нерастяжимой нитью с длинной тележкой, которая может катиться по горизонтальной поверхности. Брусок кладут на тележку и приводят в движение с постоянной скоростью ν = 2 м/с, направленной горизонтально вдоль тележки (см. рис. 1.1). Какую скорость относительно бруска будет иметь тележка в тот момент, когда угол между наклонной […]
Задача 1 Массивная горизонтальная плита движется вниз с постоянной скоростью V = 4 м/с. Над плитой на нити неподвижно относительно земли висит мячик. В тот момент, когда расстояние между плитой и мячиком было равно h = 1 м, нить оборвалась. Через какое время после обрыва нити мячик догонит плиту? На какое максимальное расстояние от плиты […]
Задача 1 Машина проехала расстояние L = 160 км от города до деревни за время T = 2 часа. Её скорость на первом, хорошем, участке пути была на ∆V = 10 км/час больше средней скорости на всём пути, а на втором, плохом, участке – на ∆V = 10 км/час меньше средней скорости на всём пути. […]
Задача 1 На полный обгон теплоходом каравана барж потребовалось t1 = 2 минуты, а катер обгонял теплоход t2 = 1 мин. Какое время t3 потребуется катеру на обгон каравана барж? Известно, что катер совсем маленький, а длина каравана в три раза больше длины тНа полный обгон теплоходом каравана барж потребовалось t1 = 2 минуты, а […]
olimpiadnye-zadanija.ru
Олимпиада по физике 7-11 класс
Школьный этап олимпиады по физике.
9 класс
1. Движения поездов.
Экспериментатор Глюк наблюдал за встречным движением скорого поезда и электрички. Оказалось, что каждый из поездов прошел мимо Глюка за одно и тоже время t1 = 23c. А в это время друг Глюка, теоретик Баг, ехал в электричке и определил, что скорый поезд прошел мимо него за t2 = 13c. Во сколько раз отличаются длины поезда и электрички?
2. Расчет электрических цепей.
Каково сопротивление цепи при разомкнутом и замкнутом ключе? R1 = R4 = 600 Ом, R2 = R3 = 1,8 кОм.
3. Калориметр.
В калориметр с водой, температура которой t0, бросили кусочек льда, имевшего температуру 0 оС. После установления теплового равновесия оказалось, что четверть льда не растаяло. Считая известными массу воды М, ее удельную теплоемкость с, удельную теплоту плавления льда λ, найдите начальную массу кусочка льда m.
4. Цветные стекла.
На тетради написано красным карандашом «отлично» и «зеленым» — «хорошо». Имеются два стекла – зеленое и красное. Через какое стекло нужно смотреть, чтобы увидеть слово «отлично»? Свой ответ поясните.
5. Колба в воде.
Колба из стекла плотностью 2,5 г/см3 вместимостью 1,5 л имеет массу 250 г. Груз, какой массы надо поместить в колбу, чтобы она утонула в воде? Плотность воды 1 г/см3.
Ответы, указания, решения к олимпиадным задачам
1. Экспериментатор Глюк наблюдал за встречным движением скорого поезда и электрички. Оказалось, что каждый из поездов прошел мимо Глюка за одно и тоже время t1 = 23c. А в это время друг Глюка, теоретик Баг, ехал в электричке и определил, что скорый поезд прошел мимо него за t2 = 13c. Во сколько раз отличаются длины поезда и электрички?
Решение.
Пусть скорость скорого поезда:его длина —
Для электрички соответственно:ее длина —
Следовательно:
Скорость сближения поезда и электрички равна сумме их скоростей. Поэтому:
Выразим из (1) уравнения скорость поезда, из (2) – скорость электрички, подставим в (3).
Решая полученное уравнение, найдем отношение длин поезда и электрички:
Критерии оценивания:
Запись уравнения движения скорого поезда – 1 балл
Запись уравнения движения электрички – 1 балл
Запись уравнения движения при сближении скорого поезда и электрички – 2 балла
Решение уравнения движения, запись формулы в общем виде – 5 баллов
Математические расчеты –1 балл
2. Каково сопротивление цепи при разомкнутом и замкнутом ключе? R1 = R4 = 600 Ом, R2 = R3 = 1,8 кОм.
Решение.
При разомкнутом ключе: Ro = 1,2 кОм.
При замкнутом ключе: Ro = 0,9 кОм
Эквивалентная схема при замкнутом ключе:
Критерии оценивания:
Нахождение общего сопротивления цепи при разомкнутом ключе – 3 балла
Эквивалентная схема при замкнутом ключе – 2 балла
Нахождение общего сопротивления цепи при замкнутом ключе – 3 балла
Математические вычисления, перевод единиц измерения – 2 балла
3. В калориметр с водой, температура которой t0, бросили кусочек льда, имевшего температуру 0 оС. После установления теплового равновесия оказалось, что четверть льда не растаяло. Считая известными массу воды М, ее удельную теплоемкость с, удельную теплоту плавления льда λ, найдите начальную массу кусочка льда m.
Решение.
Поскольку не весь лед растаял, то после установления теплового равновесия в калориметре находится и вода, и лед.
Это возможно только при температуре плавления льда, значит конечная температура системы равна 0 оС.
Четверть льда не растаяло, значит, растаяло (расплавилось) три четверти льда.
Вода, охладившись до нуля градусов Цельсия, отдает количество теплоты:
Теплоту, необходимую для плавления, лед получил от воды:
Согласно уравнению теплового баланса:
Следовательно,
Критерии оценивания:
Составление уравнения количества теплоты, отданного холодной водой – 2 балла
Составление уравнения количества теплоты, необходимого для плавления льда – 3 балла
Запись уравнения теплового баланса – 1 балл
Решение уравнения теплового баланса (запись формулы в общем виде, без промежуточных вычислений) – 3 балла
Вывод единиц измерения для проверки расчетной формулы – 1 балл
4. На тетради написано красным карандашом «отлично» и «зеленым» — «хорошо». Имеются два стекла – зеленое и красное. Через какое стекло нужно смотреть, чтобы увидеть слово «отлично»? Свой ответ поясните.
Решение.
Если красное стекло поднести к записи красным карандашом, то она не будет видна, т.к. красное стекло пропускает только красные лучи и весь фон будет красным.
Если же рассматривать запись красным карандашом через зеленое стекло, то на зеленом фоне мы увидим слово «отлично», написанное черными буквами, т.к. зеленое стекло не пропускает красные лучи света.
Чтобы увидеть слово «отлично» в тетради, нужно смотреть через зеленое стекло.
Критерии оценивания:
5. Колба из стекла плотностью 2,5 г/см3 вместимостью 1,5 л имеет массу 250 г. Груз какой массы надо поместить в колбу, чтобы она утонула в воде? Плотность воды 1 г/см3.
Решение.
Чтобы колба утонула в воде, необходимо, чтобы она полностью погрузилась в воду. Условия плавания колбы:
Объем колбы больше ее вместимости на объем стекла, из которого она изготовлена:
Сила тяжести, действующая на колбу с грузом:
Сила Архимеда, действующая на колбу при полном погружении:
Решаем систему двух уравнений: =
Критерии оценивания:
Запись условия плавания тел – 1 балл
Запись формулы нахождения силы тяжести, действующей на колбу с грузом – 2 балла
Запись формулы нахождения силы Архимеда, действующей на колбу, погруженную в воду – 3 балла
Решение системы двух уравнений – 3балла
Математические вычисления – 1 балл
infourok.ru


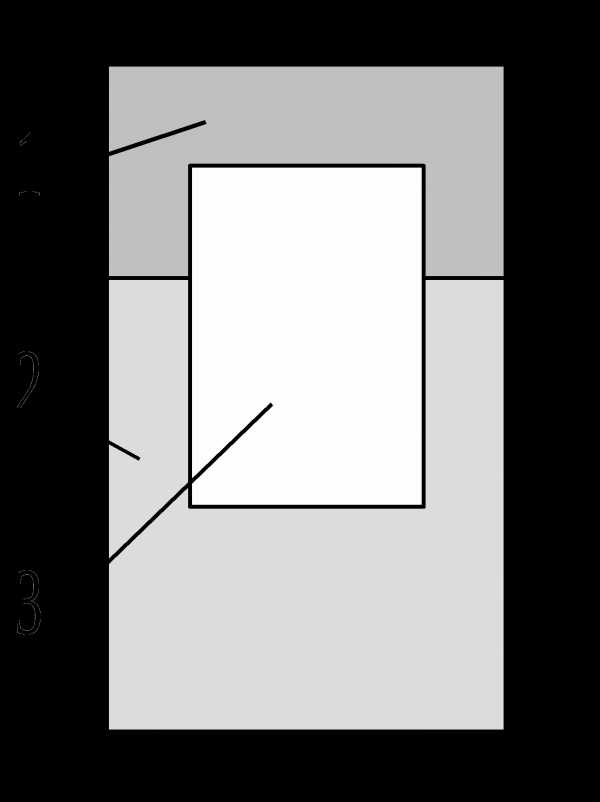 убик 3 плавает в жидкостях 1 и 2 как показано на рисунке. В жидкости 1 находится 2/3 объема кубика. Плотности жидкостей 1 и 2. Найти плотность материала кубика 3.
убик 3 плавает в жидкостях 1 и 2 как показано на рисунке. В жидкости 1 находится 2/3 объема кубика. Плотности жидкостей 1 и 2. Найти плотность материала кубика 3.