Презентация по теме «Изменчивость» 11 класс | Презентация к уроку по биологии (11 класс) на тему:

Слайд 1

Изменчивость

Слайд 2

Наследственность – способность живых организмов передавать свои признаки по наследству Изменчивость – способность живых организмов приобретать новые признаки

Слайд 3

Изменчивость модификационная наследственная

Слайд 4

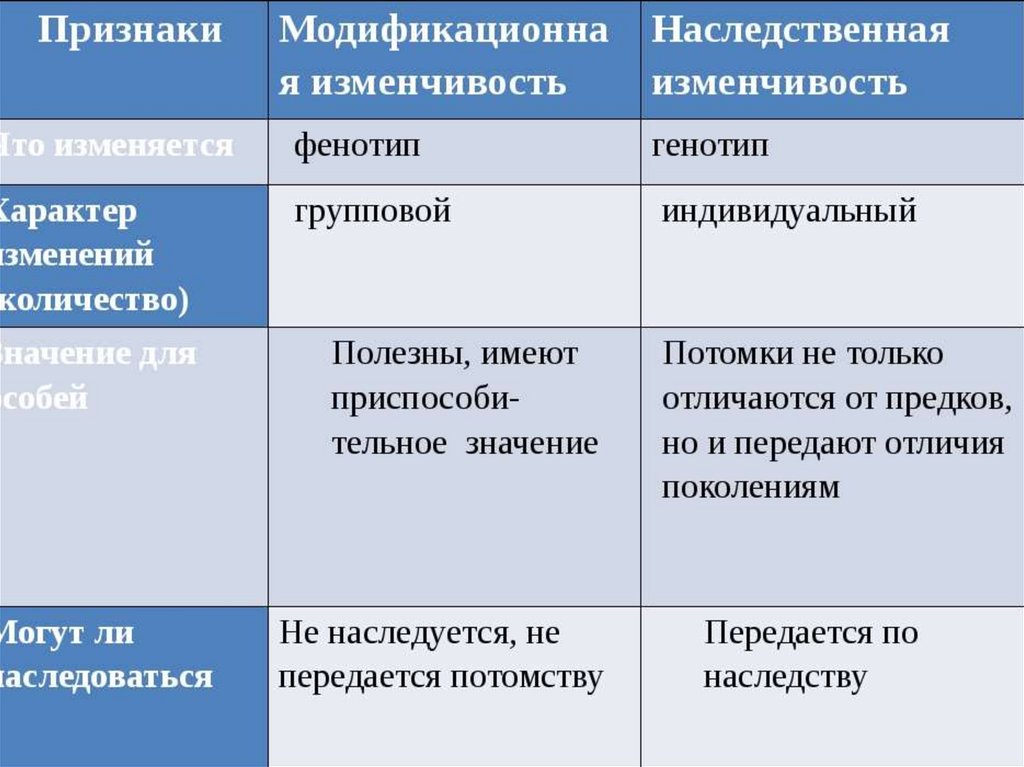
Модификационная изменчивость – зависит от условий жизни и условий окружающей среды

Слайд 5

Разная форма листьев у стрелолиста

Слайд 6

Разный размер у коров

Слайд 7

Есть признаки, которые она затрагивает (рост, вес, размер, форма, плодовитость) Есть признаки, которые она не затрагивает (цвет волос/глаз, особенности внутр.органов ) Модификационная изменчивость

Слайд 8

Все признаки проявляются в пределах «нормы реакции» Норма реакции – способность проявления признака

Слайд 9

Модификационная изменчивость не передается по наследству зависит от условий возможна в пределах нормы реакции

Слайд 10

Наследственная изменчивость – зависит от изменений в генах Бывает 2 типов:

Слайд 11

Комбинативная изменчивость (разная комбинация попавших генов) половина от папы кроссинговер случайность половина от мамы оплодотворения гамет Перекрещивание участков хромосом

Слайд 12

Мутационная изменчивость – нарушение структуры генов

Слайд 13

Мутационная изменчивость Генная (внутри одного гена) А-Т-Т-А- Г -Ц-А-А-Ц-Ц-Г-А-А-Т Т-А-А-Т- Т -Г-Т-Т-Г-Г-Ц-Т-Т-А НЕПРАВИЛЬНЫЙ ГЕН НЕПРАВИЛЬНЫЙ БЕЛОК Нарушение обмена веществ ( например, фенилкетонурия )

Слайд 14

Мутационная изменчивость 2. Хромосомная (внутри хромосомы) часть хромосомы пропадает ( делеция ) часть хромосомы дублируется( дупликация ) часть хромосомы переворачивается ( инверсия ) часть хромосомы перескакивает на другую хромосому ( транслокация )

Слайд 15

Делеция Дупликация Инверсия Транслокация

Слайд 16

Мутационная изменчивость 3. Геномная (в количестве хромосом) недостающая хромосома лишняя хромосома (синдром Дауна полиплоидия у растений +)

Слайд 17

Мутационная изменчивость 4. Соматическая (в неполовых клетках уже после оплодотворения) не передается по наследству

Слайд 18

Мутационная изменчивость 5. Цитоплазматическая (в ДНК митохондрий или рибосом) Передается только по материнской линии

Слайд 19

Наследственная изменчивость передается по наследству зависит от генов возможны любые проявления

Слайд 20

Мутационные факторы : причины , увеличивающие частоту мутаций радиация химия вирусы

Слайд 21

Репарация – способность клетки к устранению повреждений и восстановлению молекулы ДНК.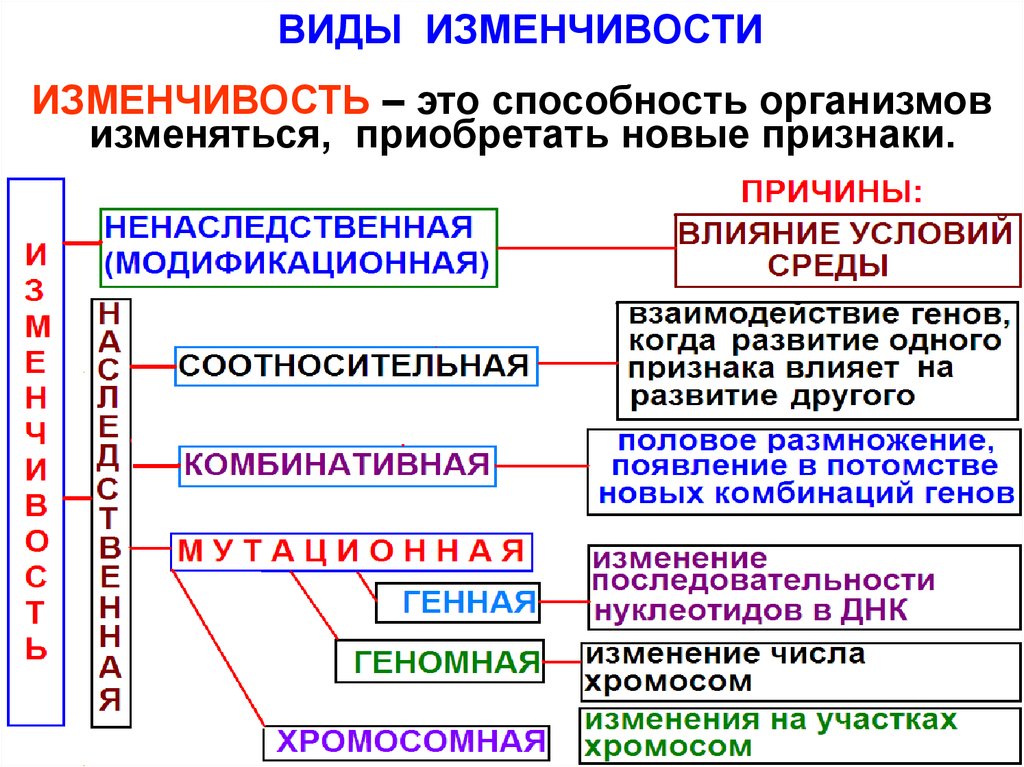 С помощью ферментов распознаются поврежденные участки, отделяются , по 2 цепочке строится нужный участок, встраивается в молекулу.

Слайд 23

Мутации : вредные нейтральные (если участок ДНК не отвечал за образование белка) полезные*

Наследственная изменчивость. Типы мутаций. (11 класс)

Похожие презентации:

Эндокринная система

Анатомо — физиологические особенности сердечно — сосудистой системы детей

Хронический панкреатит

Топографическая анатомия верхних конечностей

Анатомия и физиология сердца

Мышцы головы и шеи

Эхинококкоз человека

Черепно-мозговые нервы

Анатомия и физиология печени

Топографическая анатомия и оперативная хирургия таза и промежности

Тетрадь
для работ по биологии
ученика (цы) 11 класса
МБОУ «Средняя общеобразовательная
школа №22»
Ф.И. (в родительном падеже)

2. 06 сентября Тема: Наследственная изменчивость. Типы мутаций

Цели урока — изучить:
-виды наследственной изменчивости;
-типы мутаций, их причины;
— продолжить формирование учебнопознавательной, коммуникативной и
информационной компетенций.

3. 1.Наследственная изменчивость

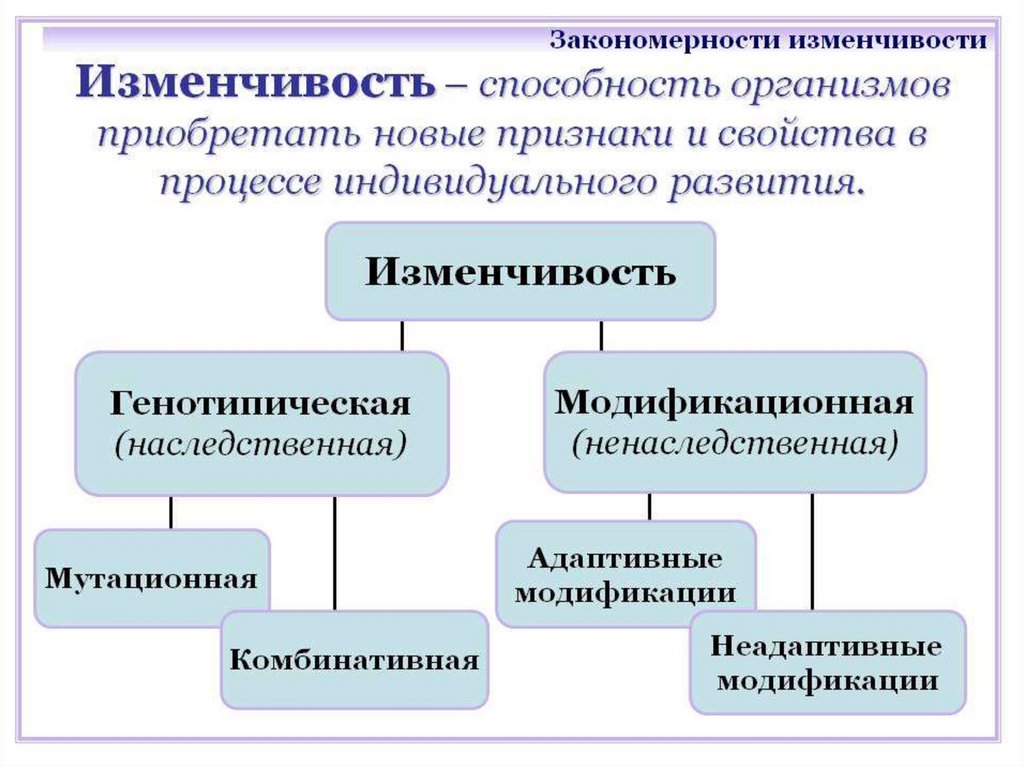
Изменчивость – всеобщее свойство всех
организмов изменяться в ходе онтогенеза.
Различают 2 вида изменчивости:
наследственную и ненаследственную.
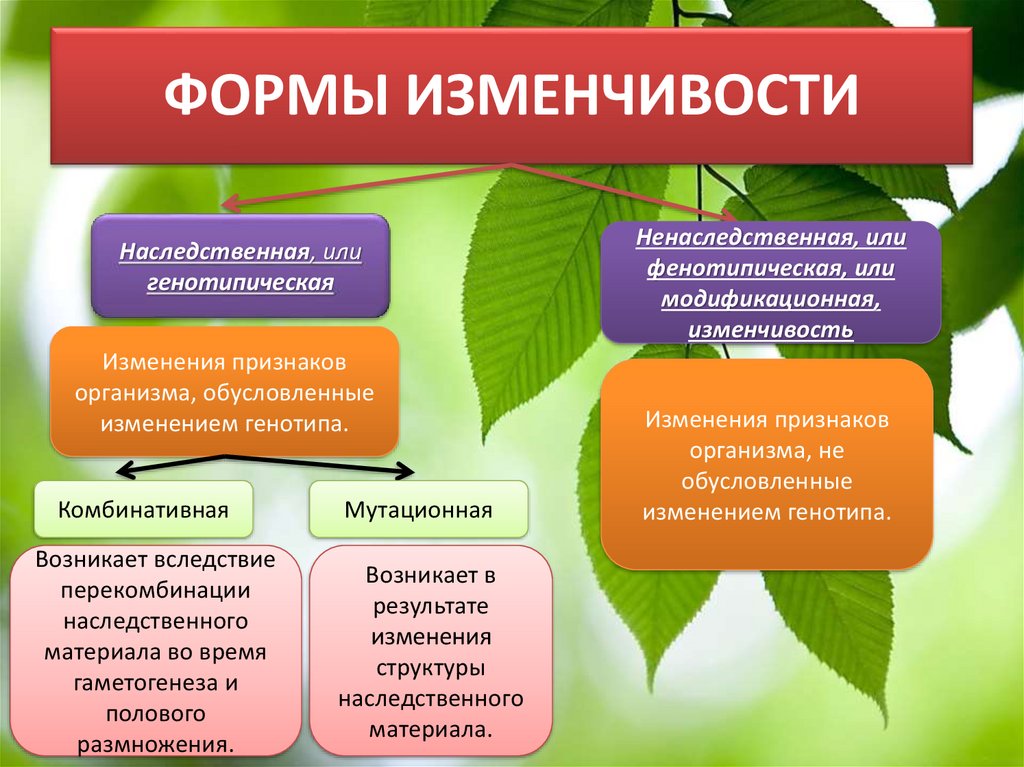
Наследственная изменчивость – основа
биоразнообразия и эволюции видов.
Различают 2 вида наследственной
изменчивости: комбинативная и мутационная.

4. 1.Комбинативная изменчивость

случайная комбинация генов в генотипе

6. 2. Мутационная изменчивость (мутации) – внезапно возникающие стойкие изменения генов и хромосом, передающиеся по наследству

7. 3. Классификация мутаций

основана на характере изменения
структуры отдельных генов, хромосом и
генома в целом.
В рамках этой классификации
различают следующие типы мутаций:
геномные;
хромосомные;
генные.
Типы мутаций
Геномные
приводят к изменению
общего числа хромосом
Хромосомные
связаны с изменением
структуры хромосом
Генные
связаны с изменением
последовательности
нуклеотидов в молекуле
ДНК
Цитоплазматическая
результат изменения
ДНК клеточных
органоидов –
пластид, митохондрий

9.

4.Геномные мутации (изменение общего числа хромосом)1) Полиплоидия — образование организмов
геном которых представлен более чем двумя (3n,
4n, 6n и т. д.) наборами хромосом (46 – 92)
В зависимости от происхождения среди
полиплоидов различают:
аллополиплоидию, у организмов имеются наборы
хромосом, полученные при гибридизации от
разных видов,
аутополиплоидию, у организмов происходит
увеличение числа наборов хромосом собственного
генома, кратное n.
Примеры геномных мутаций
различают 2 вида:
Полиплоидия — кратное
увеличение числа хромосом
У карпа (2п=10хр – 20хр.)
Анеуплоидия – уменьшение
или увеличение общего
числа хромосом (2п)

11.  3.1. Анеуплоидия – изменение числа хромосом, не кратное гаплоидному набору. Причина — не расхождение хромосом во время мейоза пример: полид

3.1. Анеуплоидия
– изменение числа хромосом,
не кратное гаплоидному набору. Причина — не
расхождение хромосом во время мейоза
пример: полидактилия (многопалость)
2 n +1 (46+1)
трисомия
2 n – 1 (46-1)
моносомия
2 n + 2 (45+2)
тетросомия
2 n — 2 (46-2)
нулесомия

12.

Причина анеуплоидии-не расхождение хромосом во время мейоза — возраст матери более 35 летСиндром Дауна – трисомия по 21 паре хромосомнаследственное заболевание возникает из-за
того, что в 21 хромосомной паре не две
гомологичные хромосомы, а три (46+1).

13. Болезнь Дауна –трисомия 21 пары хр.

Волчья пасть (расщелина неба) наследственное заболевание возникает из-за
того, что в 15 хромосомной паре не 2
гомологичные хромосомы, а 3 (2п+1-трисомия).
Расщелина зашивается в 2-х дневном возрасте
до операции
после операции

15. 5. Хромосомные мутации

При хромосомных мутациях происходят крупные
перестройки структуры отдельных хромосом
наблюдаются: потеря (делеция) или удвоение
(дубликация) части генетического материала
одной или нескольких хромосом;
изменение ориентации
(инверсия) сегмента
хромосом;
перенос части
генетического материала с
одной хромосомы на
другую (транслокация)
Хромосомные мутации

17.

6. Генные мутацииНа генном уровне изменения первичной
структуры ДНК генов под действием мутаций
менее значительны, чем при хромосомных
мутациях, однако генные мутации
встречаются более часто. В результате
генных мутаций происходят:
-замена, делеция и вставка одного или
нескольких нуклеотидов;
-транслокация, дубликация и инверсия
различных частей гена.
В том случае, когда под действием
мутации изменяется лишь один нуклеотид,
говорят о точечных мутациях.

18. Генные (точечные) серповидно-клеточная анемия

Последствия точковых
мутаций
1) сохранение смысла кодона из-за
вырожденности генетического кода;
2) изменение смысла кодона, приводящее
к замене аминокислоты в
соответствующем месте полипептидной
цепи;
3) образование бессмысленного кодона с
преждевременной терминацией;
4) обратная замена.
В генетическом коде имеются три
бессмысленных кодона: амбер —
УАГ, охр — УАА и опал — УГА
7. Медико-генетическое консультирование
позволяет определить во время планирования
беременности риск наследственных заболеваний,
среди которых:
-фенилкетонурия;
-гемофилия А;
-болезнь Дауна
Мутагены — вещества,
вызывающие изменения ДНК, генов
МУТАГЕНЫ
НЕКОТОРЫЕ
ЛЕКАРСТВЕННЫЕ
ПРЕПАРАТЫ
РЕНТГЕНОВСКИЕ
ЛУЧИ
ЯДОВИТЫЕ
ВЕЩЕСТВА
(КОЛХИЦИН)
КАНЦЕРОГЕННЫЕ
ВЕЩЕСТВА
РАДИОАКТИВНЫЕ
ВЕЩЕСТВА
(1867-1939)
Ботаник-микробиолог,
библиотекарь
Императорского
ботанического сада и
профессор Петроградского
женского медицинского
института.
Индуцированные мутации,
вызванные облучением (радиацией),
впервые были обнаружены
советским ученым Г.А. Надсоном
Наиболее известные работы связаны с
развитием радиационной биологии.
Доказал на низших грибах возможность
искусственного получения мутаций под
действием ионизирующей радиации
(совместно с Г.С.Филипповым).
Химический
мутагенез был
впервые изучен
В. В.Сахаровым и
М.Е. Лобашовым
Некоторые вещества: аммиак, азотистая
кислота, антибиотики усиливают
мутагенный эффект во много раз по
сравнению со спонтанными. Они получили
название супермутагенов.
СПОНТАННЫЙ (САМОПРОИЗВОЛЬНЫЙ)
МУТАГЕНЕЗ
Факторы
Внешние
(экзогенные)
Внутренние
(эндогенные)
•Естественный
радиационный фон
•Высокие и низкие
температуры
Химические
соединения, спонтанно
возникающие
в процессе обмена
веществ
ПОЛИПЛОИДНЫЕ
ФОРМЫ
•ОШИБКИ ПРОЦЕССОВ
РЕПЛИКАЦИИ
•РЕКОМБИНАЦИИ ДНК
8.Цитоплазматическая изменчивость
-внеядерная, обусловлена генами ДНК-пластид
Пример — пестролистность фиалки, дифенбахии.

27. Закрепление

1. Найдите соответствие :
тетросомия
2n – 2
нулесомия
2n + 2
трисомия
2n-1
моносомия
6n
полиплоидия
2n+1
анеуплоидия
4n
2. Решите задачу
Определите тип мутации. Лабораторную
крысу (после воздействия радиацией)
скрестили с нормальным самцом.
Потомства нет, почему?

28. Домашнее задание

Читать § 28, отвечать на вопросы 1-6 устно,
решить задачу №3 на стр. 65.
Творческое задание
Подготовить презентацию «Растения –
полиплоиды»

29. Спасибо за работу на уроке

Будьте здоровы!

30. Генные

На генном уровне изменения первичной структуры ДНК генов
под действием мутаций менее значительны, чем при
хромосомных мутациях, однако генные мутации встречаются
более часто. В результате генных мутаций происходят замены,
делеции и вставки одного или нескольких нуклеотидов,
транслокации, дупликации и инверсии различных частей гена. В
том случае, когда под действием мутации изменяется лишь один
нуклеотид, говорят о точечных мутациях. Поскольку в состав ДНК
входят азотистые основания только двух типов — пурины и
пиримидины, все точковые мутации с заменой оснований
разделяют на два класса: транзиции и трансверсии. Возможны
четыре генетических последствия точковых мутаций: 1)
сохранение смысла кодона из-за вырожденности генетического
кода , 2) изменение смысла кодона, приводящее к замене
аминокислоты в соответствующем месте полипептидной цепи , 3)
образование бессмысленного кодона с преждевременной
терминацией. В генетическом коде имеются три бессмысленных
кодона: амбер — UAG, охр — UAA и опал — UGA, 4) обратная
замена.

English     Русский Правила

Меры изменчивости

Меры изменчивости

Автор(ы)

Дэвид М. Лейн

Предпосылки

процентили, Распределения, Меры центральной тенденции

Цели обучения

1. Определить относительную изменчивость двух распределений
2. Вычислить диапазон
3. Вычислить межквартильный диапазон
4. Вычислить дисперсию населения
5. Оценить дисперсию по выборке
6. Вычислить стандартное отклонение от дисперсии

Что такое изменчивость?

Изменчивость относится к тому, насколько «распространен» группа баллов есть. Чтобы понять, что мы подразумеваем под разбросом, рассмотрим графики на рис. 1. Эти графики представляют результаты двух тестов. Средний балл за каждый тест составляет 7,0. Несмотря на равенство средств, вы можете видеть, что дистрибутивы совершенно разные. Конкретно, баллы по викторине 1 более плотно упакованы, а баллы по викторине 2 более разбросаны. Различия между учащимися были значительными. больше в викторине 2, чем в викторине 1.

Викторина 1

Тест 2

Рисунок 1. Гистограммы двух тестов.

Термины изменчивость, разброс и дисперсия синонимы и указывают на то, насколько распространено распределение. Только как в разделе о центральной тенденции, где мы обсуждали меры центра распределения баллов, в этой главе мы обсудим меры изменчивости распределения.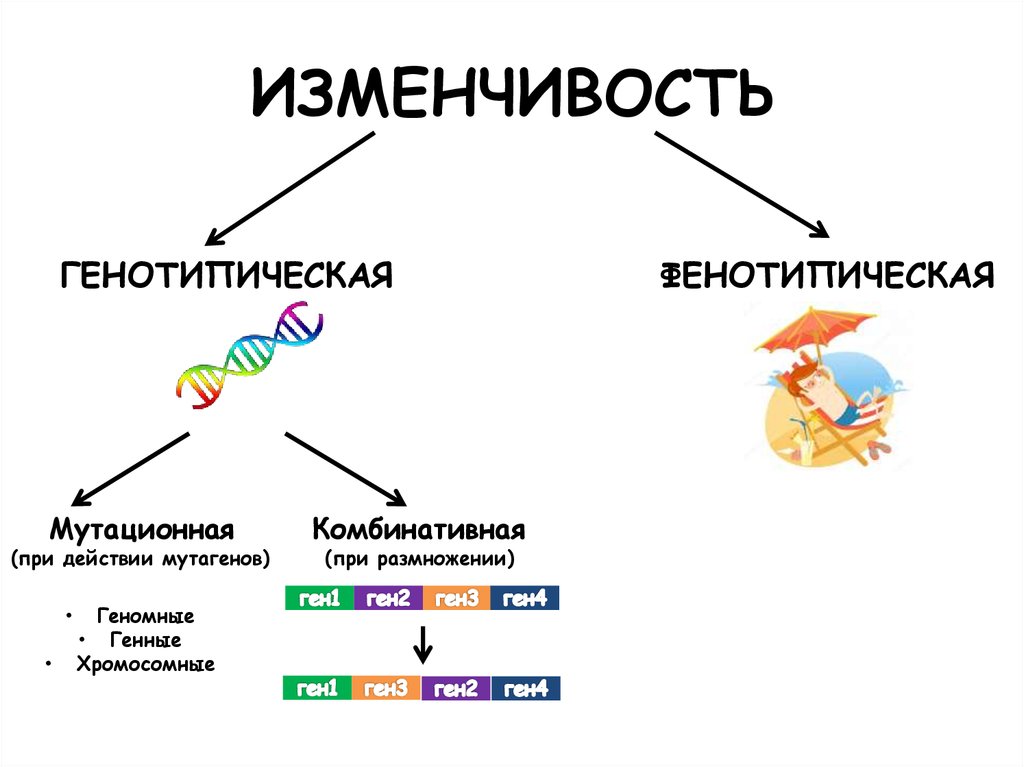

Существует четыре часто используемых меры изменчивости: размах, межквартильный размах, дисперсия и стандартное отклонение. В следующих нескольких абзацах мы рассмотрим каждый из этих четырех меры изменчивости более подробно.

Диапазон
Диапазон является простейшей мерой изменчивости вычислить, и тот, который вы, вероятно, сталкивались много раз в твоей жизни. Диапазон — это просто наивысший балл минус самый низкий балл. Возьмем несколько примеров. Каков диапазон из следующей группы чисел: 10, 2, 5, 6, 7, 3, 4? Хорошо, наибольшее число 10, а наименьшее число 2, поэтому 10 — 2 = 8. Диапазон равен 8. Возьмем другой пример. Здесьs набор данных с 10 числами: 99, 45, 23, 67, 45, 91, 82, 78, 62, 51. Какой диапазон? Наибольшее число — 99, а наименьшее число 23, поэтому 99 — 23 равно 76; диапазон 76.

Теперь рассмотрим две викторины, показанные на рис. 1. В викторине 1 самый низкий балл равен 5, а самый высокий балл равен 9. Следовательно, диапазон равен 4. Диапазон на викторине 2 был больше: самый низкий оценка была 4, а самая высокая оценка была 10. Таким образом, диапазон 6.

Межквартильный диапазон

Межквартильный диапазон (IQR) – это диапазон средних 50% баллов в дистрибутив. Он рассчитывается следующим образом:

IQR = 75-й процентиль — 25-й процентиль

Для теста 1 75-й процентиль равен 8, а 25-й процентиль равен 6. Таким образом, межквартильный размах равен 2. Для викторины 2, которая имеет большее распространение, 75-й процентиль равен 9, 25-й процентиль равен 5, а межквартильный диапазон равен 4. Напомним, что при обсуждении бокса участки, 75-й процентиль назвали верхним шарниром, а 25-й процентиль нижняя петля.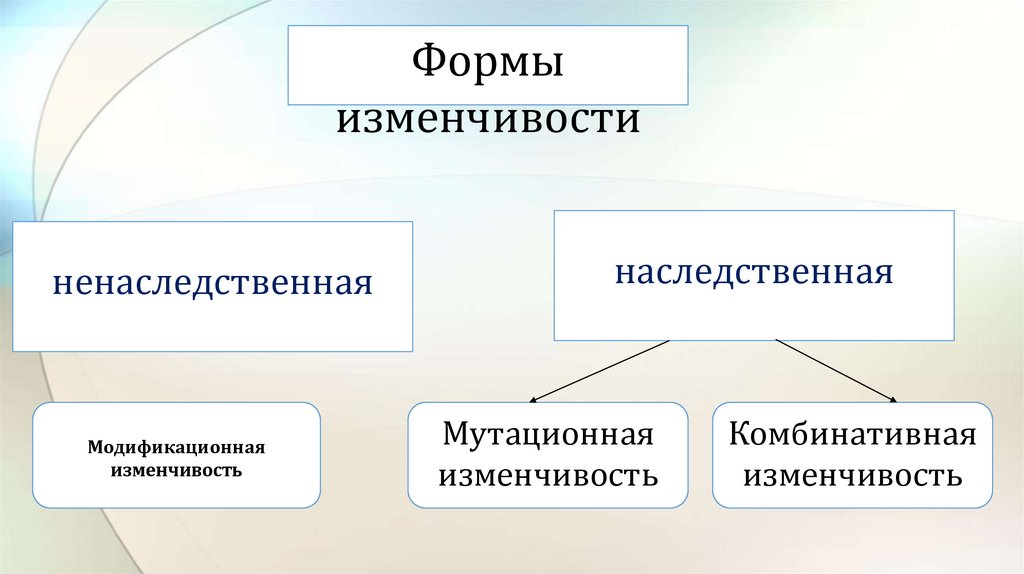

Используя эту терминологию, межквартильный размах называется H-спредом.

Родственная мера изменчивости называется полуинтерквартильным спектр. Полуинтерквартильный диапазон определяется просто как межквартильный размах, разделенный на 2. Если распределение симметрично, медиана плюс или минус полумежквартильный диапазон содержит половина баллов в раздаче.

Дисперсия

Изменчивость также можно определить с точки зрения того, как близкие баллы в распределении находятся к середине распределение. Используя среднее значение как меру середины распределения, дисперсия определяется как среднеквадратическая разница баллов от среднего. Данные теста 1 показаны на Таблица 1. Средний балл 7,0. Поэтому графа «Отклонение от среднего» содержит оценку минус 7. Столбец «Квадрат Отклонение» — это просто возведение предыдущего столбца в квадрат.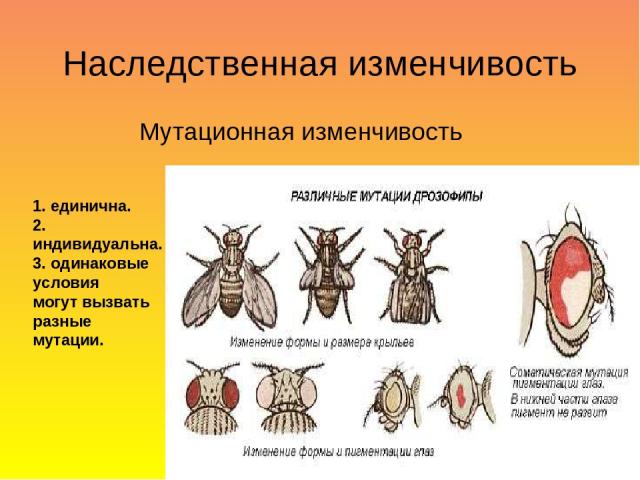

Таблица 1. Расчет дисперсии баллов за тест 1.

Баллы	Отклонение от среднего	Квадрат отклонения
9	2	4
9	2	4
9	2	4
8	1	1
8	1	1
8	1	1
8	1	1
7	0	0
7	0	0
7	0	0
7	0	0
7	0	0
6	-1	1
6	-1	1
6	-1	1
6	-1	1
6	-1	1
6	-1	1
5	-2	4
5	-2	4
Средства
7	0	1,5

Одна вещь, которая важна заметить, что среднее отклонение от среднего равно 0. Так будет всегда. Среднее квадратов отклонений составляет 1,5. Таким образом, дисперсия составляет 1,5. Аналогичные расчеты с викториной 2 показывают, что его дисперсия составляет 6,7. Формула для дисперсия:

где σ ² — дисперсия, μ — среднее значение, а N — количество чисел. Для викторины 1, мк = 7 и N = 20,

Если дисперсия в выборке используется для оценки дисперсии населения, то предыдущая формула занижает следует использовать дисперсию и следующую формулу:

, где s ² — оценка дисперсии, а M — выборочное среднее. Обратите внимание, что М является средним выборки, взятой из населения со средним значением μ. Поскольку на практике дисперсия обычно вычисляется в выборке, эта формула используется чаще всего. Моделирование «оценка дисперсия» иллюстрирует смещение в формуле с N в знаменателе.

Возьмем конкретный пример. Предположим, что баллы 1, 2, 4 и 5 были отобраны из большей популяции. Оценить дисперсия населения, которую вы бы вычислили s ² следующим образом:

 М = (1 + 2 + 4 + 5)/4 = 12/4 = 3.

с ² = [(1-3) ² + (2-3) ² + (4-3) ² + (5-3) ² ]/(4-1)

   = (4 + 1 + 1 + 4)/3 = 10/3 = 3,333

Есть альтернативные формулы, которые могут быть проще использовать, если вы делаете расчеты с помощью ручного калькулятора. Обратите внимание, что эти формулы подвержены ошибке округления, если ваши значения очень велики и/или у вас очень большое количество наблюдений.

и

Для этого примера

Стандартное отклонение

Стандарт отклонение — это просто квадратный корень из дисперсии.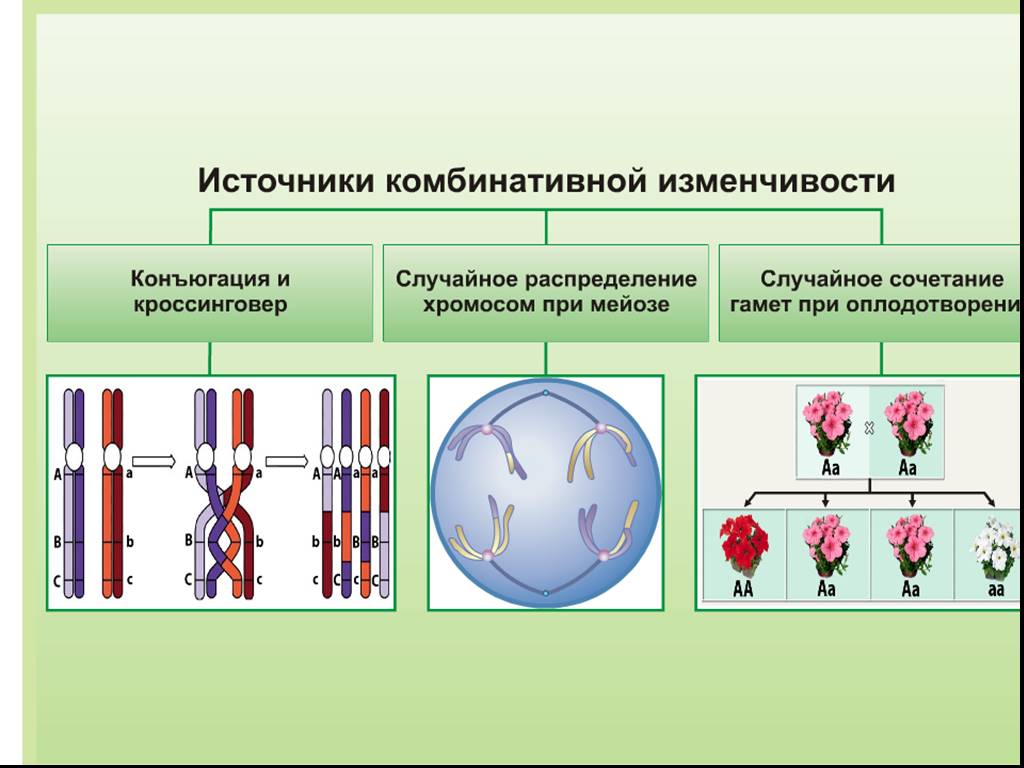 Этот делает стандартные отклонения двух распределений викторины 1.257 и 2.203. Стандартное отклонение является особенно полезная мера изменчивости при нормальном распределении или приблизительно нормальное (см. главу о нормальном распределении), потому что доля распределения в пределах заданного числа стандартных отклонений от среднего можно вычислить. Например, 68% дистрибутива в пределах одного стандартного отклонения от среднего и приблизительно 95% распределения находится в пределах двух стандартных отклонений среднего. Следовательно, если бы у вас было нормальное распределение со средним значением 50 и стандартным отклонением 10, то 68% распределения будет между 50 — 10 = 40 и 50 +10 =60. Точно так же около 95% распределения будет между 50 — 2 x 10 = 30 и 50 + 2 x 10 = 70. Символ для генеральной совокупности стандартное отклонение σ; символ для оценки, вычисленной в выборке, — s. Фигура 2 показаны два нормальных распределения. Красное распределение имеет среднее значение 40 и стандартное отклонение. из 5; синее распределение имеет среднее значение 60 и стандартное отклонение 10. Для красного распределения 68% распределения находится между 35 и 45; для синего распределения 68% находятся между 50 и 70.

Рисунок 2. Нормальные распределения со стандартным отклонения 5 и 10.

q1=c(9,9,9,8,8,8,8,7,7,7,7,7,6,6,6,6,6,6,5,5)
IQR(q1, тип = 6)
[1] 2
x=c(1,2,4,5)
var(x)
[1] 3,333333
sd(q1)
[1] 1,256562
q2=c(10,10 ,9,9,9,8,8,8,7,7,7,6,6,6,5,5,4,4,3,3)
sd(q2)
[1] 2,202869

Пожалуйста, ответьте на вопросы:

обратная связь

Меры изменчивости: размах, межквартильный размах, дисперсия и стандартное отклонение

Мера изменчивости представляет собой сводную статистику, представляющую величину дисперсии в наборе данных. Насколько распространены ценности? В то время как мера центральной тенденции описывает типичное значение, меры изменчивости определяют, насколько далеко точки данных имеют тенденцию отходить от центра. Мы говорим об изменчивости в контексте распределения значений. Низкая дисперсия указывает на то, что точки данных, как правило, плотно сгруппированы вокруг центра. Высокая дисперсия означает, что они имеют тенденцию падать дальше.

В статистике изменчивость, дисперсия и разброс являются синонимами, обозначающими ширину распределения. Точно так же, как существует несколько мер центральной тенденции, существует несколько мер изменчивости. В этом сообщении блога вы узнаете, почему понимание изменчивости ваших данных имеет решающее значение. Затем я исследую наиболее распространенные меры изменчивости — размах, межквартильный размах, дисперсию и стандартное отклонение. Я помогу вам определить, какой из них лучше всего подходит для ваших данных.

На двух приведенных ниже графиках графически показаны различия для распределений с одинаковым средним значением, но большей и меньшей дисперсией. На панели слева показано распределение, плотно сгруппированное вокруг среднего значения, в то время как распределение на правой панели более разбросано.

Связанный пост : Показатели центральной тенденции: среднее, медиана и мода

Почему важно понимать изменчивость

Давайте сделаем шаг назад и сначала разберемся, почему понимание изменчивости так важно. Аналитики часто используют среднее значение для обобщения центра совокупности или процесса. Хотя среднее значение имеет значение, люди часто еще больше реагируют на изменчивость. Когда распределение имеет более низкую изменчивость, значения в наборе данных являются более согласованными. Однако, когда изменчивость выше, точки данных более непохожи, и экстремальные значения становятся более вероятными. Следовательно, понимание изменчивости помогает понять вероятность необычных событий.

В некоторых ситуациях экстремальные значения могут вызвать проблемы! Вы когда-нибудь видели отчет о погоде, где метеоролог показывает сильную жару и засуху в одном районе и наводнение в другом? Было бы неплохо усреднить их вместе! Часто мы чувствуем дискомфорт в крайностях больше, чем в среднем.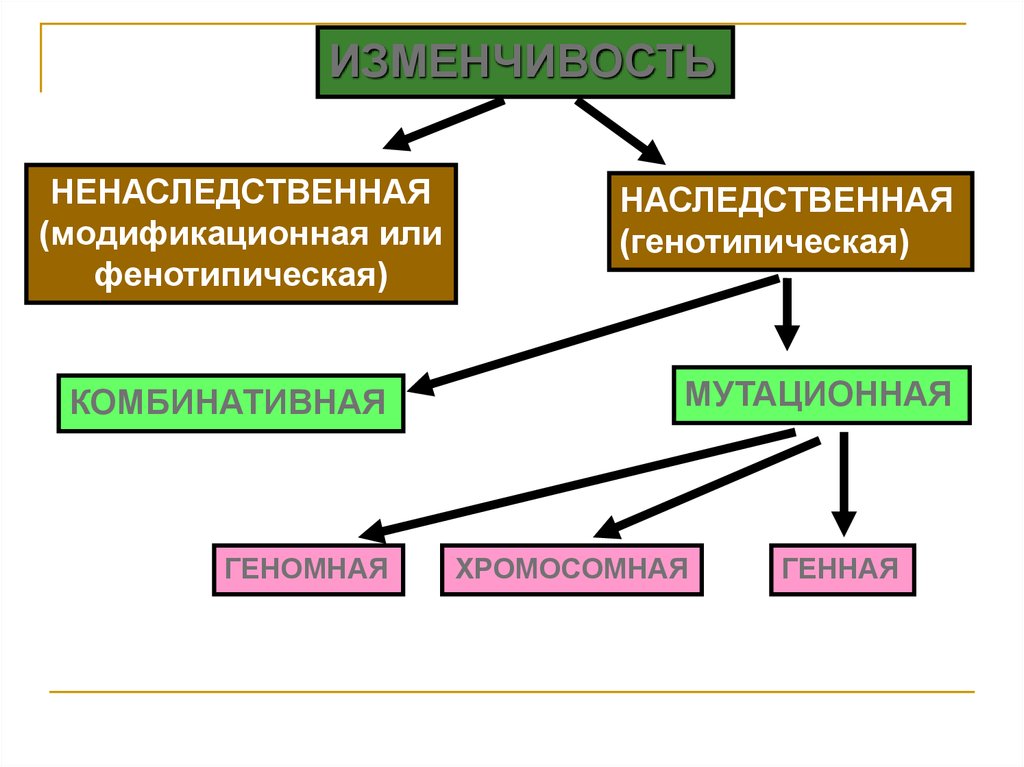 Понимание того, что изменчивость вокруг среднего дает важную информацию.

Изменчивость повсюду. Время, которое вы тратите на дорогу до работы, немного меняется каждый день. Когда вы неоднократно заказываете любимое блюдо в ресторане, оно каждый раз не одно и то же. Детали, сходящие с конвейера, могут казаться идентичными, но они имеют несколько разные длину и ширину.

Все это примеры реальной изменчивости. Некоторая степень изменчивости неизбежна. Однако слишком большое несоответствие может вызвать проблемы. Если ваша утренняя поездка на работу занимает намного больше времени, чем среднее время в пути, вы опоздаете на работу. Если ресторанное блюдо сильно отличается от обычного, оно может вам совсем не понравиться. И, если изготовленная деталь слишком сильно отличается от спецификации, она не будет работать должным образом.

Некоторые отклонения неизбежны, но проблемы возникают в крайних случаях. Распределения с большей изменчивостью дают наблюдения с необычно большими и малыми значениями чаще, чем распределения с меньшей изменчивостью.

Изменчивость также может помочь вам оценить неоднородность образца.

Пример различных величин изменчивости

Давайте рассмотрим два гипотетических ресторана-пиццерии. Они оба рекламируют среднее время доставки 20 минут. Когда мы голодны, они оба звучат одинаково хорошо! Однако эта эквивалентность может быть обманчива! Чтобы определить ресторан, в котором вы должны заказать, когда вы голодны, нам нужно проанализировать их изменчивость.

Предположим, мы изучаем их время доставки, вычисляем изменчивость для каждого места и определяем, что их изменчивость различна. Мы рассчитали стандартные отклонения для обоих ресторанов — это показатель, к которому мы вернемся позже в этом посте. Насколько существенна эта разница в быстрой доставке пиццы своим клиентам?

Графики ниже показывают распределение времени доставки и дают ответ. Ресторан с более изменчивым временем доставки имеет более широкую кривую распределения. Я использовал одинаковые шкалы на обоих графиках, чтобы вы могли визуально сравнить два распределения.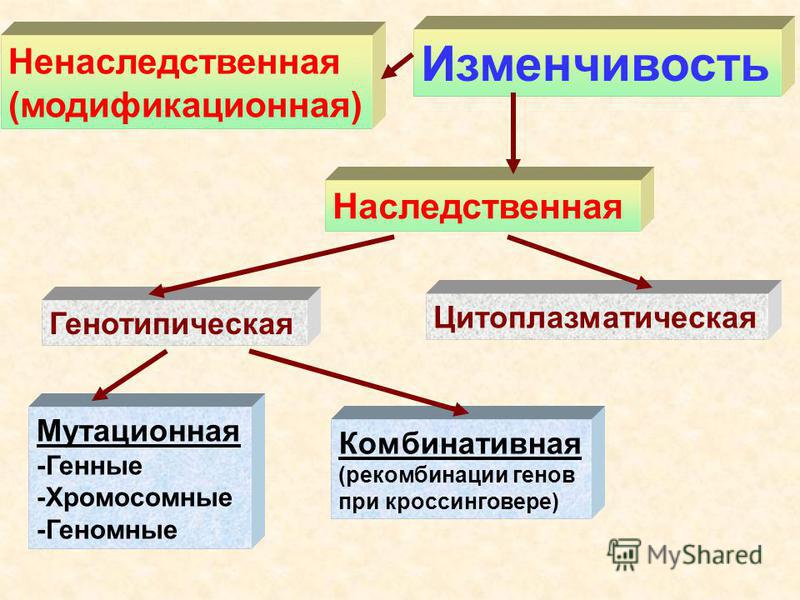

На этих графиках мы считаем неприемлемым 30-минутное ожидание или дольше. Ведь мы голодны! Заштрихованная область на каждой диаграмме представляет долю времени доставки, которое превышает 30 минут. Почти 16% доставок для ресторана с высокой вариативностью превышают 30 минут. С другой стороны, только 2% доставок занимают слишком много времени в ресторане с низкой изменчивостью. У них обоих среднее время доставки составляет 20 минут, но я знаю, где бы я разместил свой заказ, когда проголодался!

Как показывает этот пример, центральная тенденция не предоставляет полной информации. Нам также необходимо понять изменчивость в середине распределения, чтобы получить полную картину. Теперь давайте перейдем к различным способам измерения изменчивости!

Диапазон

Начнем с диапазона, потому что это наиболее простая для расчета и понимания мера изменчивости. Диапазон набора данных — это разница между наибольшим и наименьшим значениями в этом наборе данных.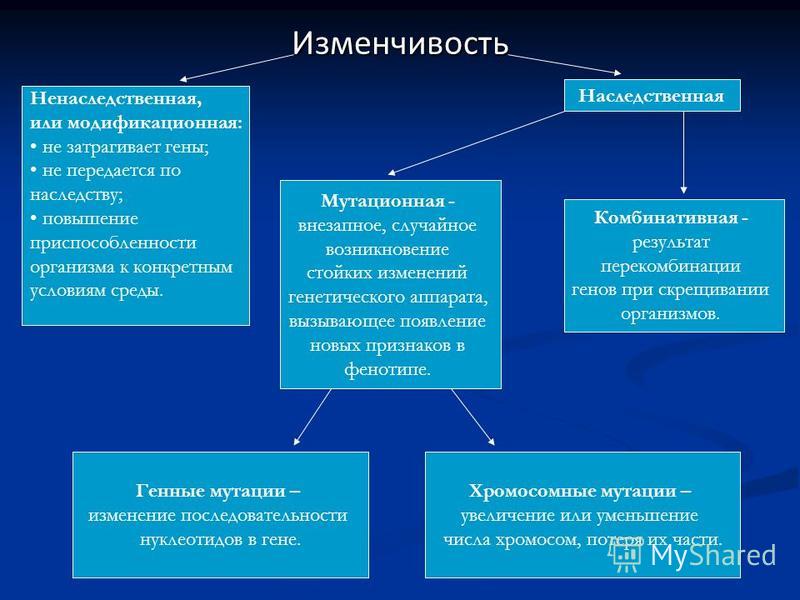 Например, в двух приведенных ниже наборах данных набор данных 1 имеет диапазон 20–38 = 18, а набор данных 2 имеет диапазон 11–52 = 41. Набор данных 2 имеет более широкий диапазон и, следовательно, большую изменчивость, чем набор данных 19.0003

Хотя диапазон легко понять, он основан только на двух самых крайних значениях в наборе данных, что делает его очень восприимчивым к выбросам. Если одно из этих чисел необычно высокое или низкое, оно влияет на весь диапазон, даже если оно нетипично.

Кроме того, на диапазон влияет размер набора данных. В целом, вы с меньшей вероятностью будете наблюдать экстремальные значения. Однако по мере увеличения размера выборки у вас появляется больше возможностей для получения этих экстремальных значений. Следовательно, когда вы берете случайные выборки из одной и той же совокупности, диапазон имеет тенденцию увеличиваться по мере увеличения размера выборки. Следовательно, используйте диапазон для сравнения изменчивости только в том случае, если размеры выборки схожи.

Подробнее читайте в моем посте Диапазон в статистике.

Межквартильный диапазон (IQR) . . . и другие Процентили

Межквартильный диапазон представляет собой среднюю половину данных. Чтобы визуализировать это, подумайте о среднем значении, которое делит набор данных пополам. Точно так же вы можете разделить данные на кварталы. Статистики называют эти кварталы квартилями и обозначают их от низкого к высокому как Q1, Q2 и Q3. Нижний квартиль (Q1) содержит четверть набора данных с наименьшими значениями. Верхний квартиль (Q4) содержит четверть набора данных с самыми высокими значениями. Межквартильный диапазон — это средняя половина данных, которая находится между верхним и нижним квартилями. Другими словами, межквартильный диапазон включает 50% точек данных, которые попадают между Q1 и Q3. IQR — красная область на графике ниже.

Межквартильный размах является надежной мерой изменчивости, аналогично тому, как медиана является надежной мерой центральной тенденции. Ни на один из показателей резко не влияют выбросы, потому что они не зависят от каждого значения. Кроме того, межквартильный диапазон отлично подходит для асимметричных распределений, как и медиана. Как вы узнаете, когда у вас есть нормальное распределение, стандартное отклонение говорит вам о проценте наблюдений, которые отклоняются от среднего на определенное расстояние. Однако это не работает для асимметричных распределений, и IQR — отличная альтернатива.

Я разделил приведенный ниже набор данных на квартили. Межквартильный диапазон (IQR) простирается от нижней границы Q2 до верхней границы Q3. Для этого набора данных диапазон составляет 39 – 20 = 19.

 

Связанные сообщения : Квартиль: определение, поиск и использование, межквартильный диапазон: определение и использование, и что такое робастная статистика?

Использование других процентилей

Когда у вас асимметричное распределение, я считаю, что представление медианы с межквартильным диапазоном является особенно хорошей комбинацией. Межквартильный диапазон эквивалентен области между 75-м и 25-м процентилем (75 – 25 = 50% данных). Вы также можете использовать другие процентили для определения разброса различных пропорций. Например, диапазон между 97,5-й процентиль и 2,5-й процентиль покрывают 95% данных. Чем шире эти диапазоны, тем выше изменчивость в вашем наборе данных.

Связанный пост : Процентили: Интерпретация и расчеты

Дисперсия

Дисперсия — это среднеквадратичное отличие значений от среднего. В отличие от предыдущих мер изменчивости, дисперсия включает в расчет все значения путем сравнения каждого значения со средним значением. Чтобы вычислить эту статистику, вы вычисляете набор квадратов разностей между точками данных и средним значением, суммируете их, а затем делите на количество наблюдений. Следовательно, это среднеквадратическая разница.

Существуют две формулы для дисперсии в зависимости от того, рассчитываете ли вы дисперсию для всей совокупности или используете выборку для оценки дисперсии совокупности.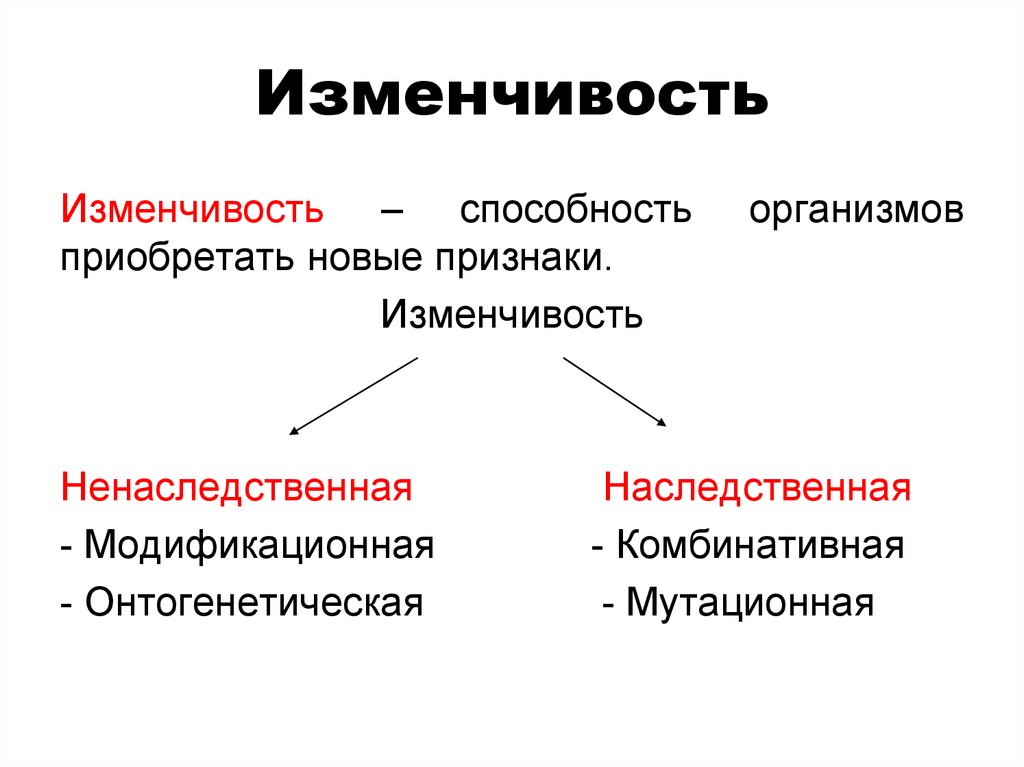 Уравнения приведены ниже, а затем я работаю с примером в таблице, чтобы воплотить его в жизнь.

Дисперсия совокупности

Формула дисперсии всей совокупности следующая:

— количество точек данных, которое должно включать все население.

Выборочная дисперсия

Чтобы использовать выборку для оценки дисперсии совокупности, используйте следующую формулу. Использование предыдущего уравнения с выборочными данными приводит к недооценке изменчивости. Поскольку обычно невозможно измерить всю совокупность, статистики гораздо чаще используют уравнение выборочной дисперсии.

В уравнении s ² — выборочная дисперсия, а M — выборочное среднее. N-1 в знаменателе корректирует тенденцию выборки к недооценке дисперсии генеральной совокупности.

Пример расчета выборочной дисперсии

Я рассмотрю пример, используя формулу для выборки на наборе данных с 17 наблюдениями в таблице ниже. Цифры в скобках представляют собой соответствующий номер столбца таблицы.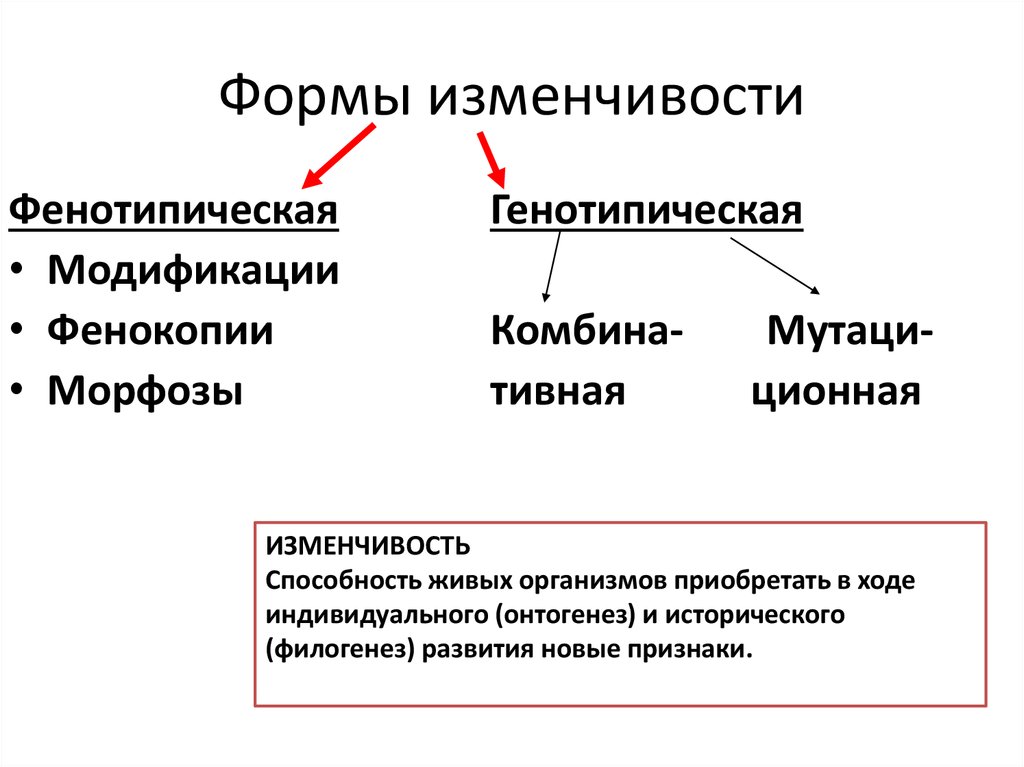 Процедура включает в себя каждое наблюдение (1), вычитание среднего значения выборки (2) для вычисления разницы (3) и возведение этой разницы в квадрат (4). Затем я суммирую квадраты разностей в нижней части таблицы. Наконец, я беру сумму и делю на 16, потому что использую уравнение выборочной дисперсии с 17 наблюдениями (17 — 1 = 16). Дисперсия для этого набора данных составляет 201.

Поскольку в расчетах используются квадраты разностей, дисперсия выражается в квадратах, а не в исходных единицах данных. Хотя более высокие значения дисперсии указывают на большую изменчивость, нет интуитивной интерпретации конкретных значений. Несмотря на это ограничение, различные статистические тесты используют дисперсию в своих расчетах. Например, прочитайте мой пост о F-тесте и ANOVA.

Хотя трудно интерпретировать саму дисперсию, стандартное отклонение решает эту проблему!

Подробности читайте в моем посте про дисперсию.

Стандартное отклонение

Стандартное отклонение — это стандартная или типичная разница между каждой точкой данных и средним значением. Когда значения в наборе данных сгруппированы ближе друг к другу, у вас меньше стандартное отклонение. С другой стороны, когда значения разбросаны больше, стандартное отклонение больше, потому что стандартное расстояние больше.

Для удобства стандартное отклонение использует исходные единицы данных, что облегчает интерпретацию. Следовательно, стандартное отклонение является наиболее широко используемой мерой изменчивости. Например, в примере с доставкой пиццы стандартное отклонение 5 указывает на то, что типичное время доставки составляет плюс-минус 5 минут от среднего значения. Его часто указывают вместе со средним значением: 20 минут (стандартное отклонение 5).

Стандартное отклонение равно квадратному корню из дисперсии. Напомним, что дисперсия измеряется в квадратах. Следовательно, квадратный корень возвращает значение в натуральных единицах. Символом стандартного отклонения как параметра генеральной совокупности является σ, а s представляет его как выборочную оценку. Чтобы вычислить стандартное отклонение, рассчитайте дисперсию, как показано выше, а затем извлеките из нее квадратный корень. Вуаля! У вас стандартное отклонение!

В разделе дисперсии мы рассчитали дисперсию 201 в таблице.

Следовательно, стандартное отклонение для этого набора данных равно 14,177.

Стандартное отклонение аналогично среднему абсолютному отклонению. Оба используют исходные единицы данных и сравнивают значения данных со средними для оценки изменчивости. Однако есть различия. Чтобы узнать больше, прочитайте мой пост о среднем абсолютном отклонении (MAD).

Люди часто путают стандартное отклонение со стандартной ошибкой среднего. Обе меры оценивают изменчивость, но они имеют совершенно разные цели. Чтобы узнать больше, прочитайте мой пост «Стандартная ошибка среднего».

Связанный пост : Использование стандартного отклонения

Эмпирическое правило для стандартного отклонения нормального распределения

Когда у вас есть нормально распределенные данные или примерно так, стандартное отклонение становится особенно ценным. Его можно использовать для определения доли значений, попадающих в заданное число стандартных отклонений от среднего значения. Например, при нормальном распределении 68% значений будут находиться в пределах +/- 1 стандартного отклонения от среднего. Это свойство является частью эмпирического правила. Это правило описывает процент данных, которые попадают в определенные числа стандартных отклонений от среднего значения для колоколообразных кривых.

Среднее +/- стандартное отклонение	Процент содержащихся данных
1	68%
2	95%
3	99,7%

Давайте еще раз взглянем на пример доставки пиццы, где у нас есть среднее время доставки 20 минут и стандартное отклонение 5 минут. Используя эмпирическое правило, мы можем использовать среднее значение и стандартное отклонение, чтобы определить, что 68% времени доставки приходится на период от 15-25 минут (20 +/- 5) до 9 минут. 5% попадут между 10-30 минутами (20 +/- 2*5).

Похожие сообщения : Нормальное распределение и эмпирическое правило

Что лучше — диапазон, межквартильный диапазон или стандартное отклонение?

Во-первых, вы, вероятно, заметили, что я не включил дисперсию в качестве одного из параметров в заголовке выше. Это связано с тем, что дисперсия выражена в квадратах и ​​не дает интуитивной интерпретации. Итак, я вычеркнул это из списка. Давайте рассмотрим остальные три меры изменчивости.

При сравнении выборок одинакового размера рассмотрите возможность использования диапазона в качестве меры изменчивости. Это достаточно интуитивная статистика. Просто имейте в виду, что один выброс может сбить диапазон. Диапазон особенно подходит для небольших выборок, когда у вас недостаточно данных для надежного расчета других показателей, а вероятность получения выброса также ниже.

При асимметричном распределении медиана является лучшим показателем центральной тенденции, и имеет смысл сочетать ее либо с межквартильным диапазоном, либо с другими диапазонами на основе процентилей, поскольку все эти статистические данные делят набор данных на группы с определенными пропорциями.