Алгебра 11 класс контрольная работа тригонометрические функции – Картотека по алгебре (11 класс) по теме: Контрольные работы по алгебре и началам анализа в 11 классе
Урок алгебры 11 класс , контрольная работа по теме»Тригонометрические функции»
Контрольная работа № 1
Тригонометрические функции
Вариант 1
А1. Найдите область определения функции  .
.
А2. Найдите множество значений функции .
А3. Выяснить, является ли данная функция четной или нечетной:
А4. Докажите, что функция является периодической с периодом Т = p.
А5. Сравните числа:  .
.
A6. Найдите значение функции .
В1. Сравните числа: 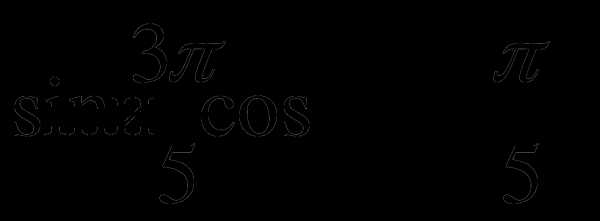 .
.
В2. Найдите все корни уравнения , принадлежащие промежутку [0;2p].
С1. Найдите наибольшее и наименьшее значение функции на отрезке 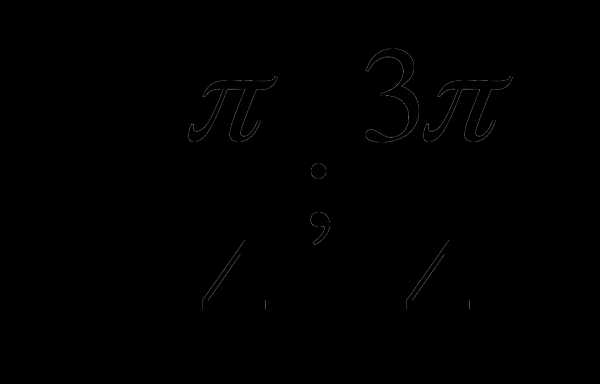
С2. Постройте график функции .
Нормы оценок: «3» — 5А, «4» — 4А + 1В, «5» — 3А + 1В +1С или 2А + 2В + 1С.
_________________________________________________________________
Контрольная работа № 1.
Тригонометрические функции
Вариант 2
А1. Найдите область определения функции .
А2. Найдите множество значений функции .
А3. Выясните, является ли данная функция четной или нечетной: .
А4. Докажите, что функция у = tg 3x является периодической с периодом Т =  .
.
А5. Сравните числа: sin  и sin
и sin  .
.
A6. Найдите значение функции .
В1. Сравните числа: 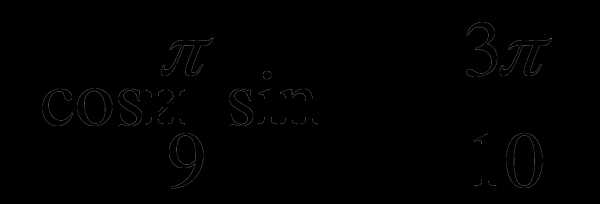 .
.
В2.Найти все корни уравнения , принадлежащие промежутку [-p;p].
С1. Найдите наибольшее и наименьшее значение функции на отрезке 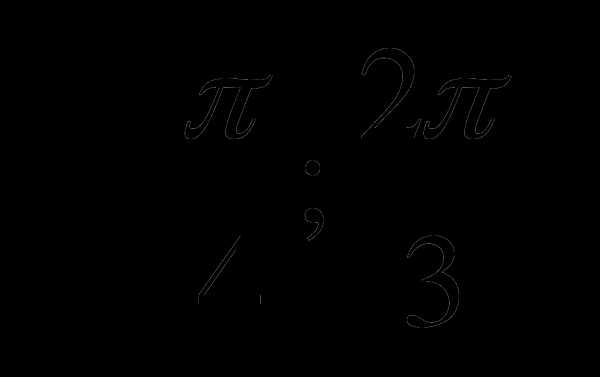 .
.
С2. Построить график функции 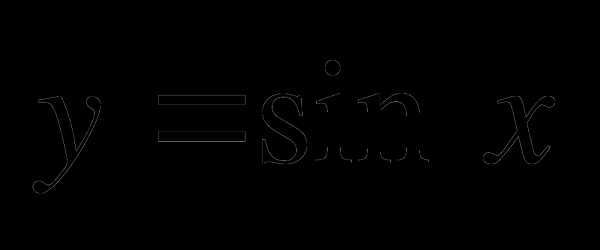 .
.
Нормы оценок: «3» — 5А, «4» — 4А + 1В, «5» — 3А + 1В +1С или 2А + 2В + 1С.
Контрольная работа № 1
Тригонометрические функции
Вариант 3
А1. Найдите область определения функции у = sin  .
.
А2. Найдите множество значений функции у = 1 –2sin x.
А3. Выяснить, является ли данная функция четной или нечетной: у = 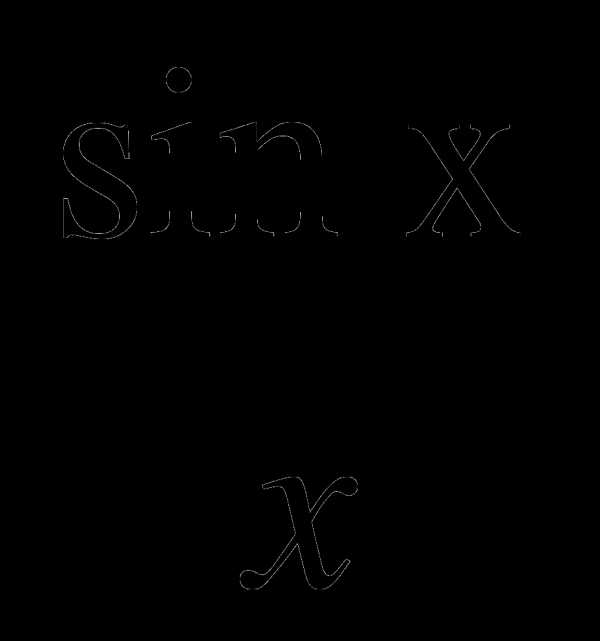 .
.
А4. Докажите, что функция у = cos  является периодической с периодом Т=3p.
является периодической с периодом Т=3p.
А5. Сравните числа: tg  и tg
и tg  .
.
A6. Найдите значение функции у=3cos при х =
при х =  .
.
В1. Сравните числа: sin  и cos
и cos  .
.
В2. Найдите все корни уравнения 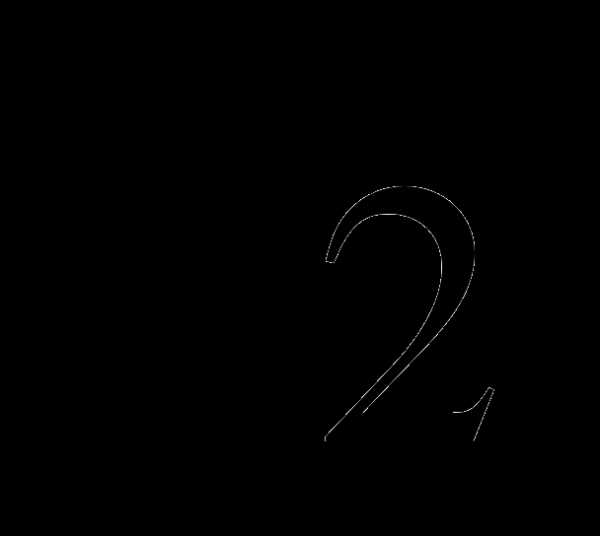 sin x = 1, принадлежащие промежутку [-p;p].
sin x = 1, принадлежащие промежутку [-p;p].
С1. Найдите наибольшее и наименьшее значение функции у=4tgx на отрезке 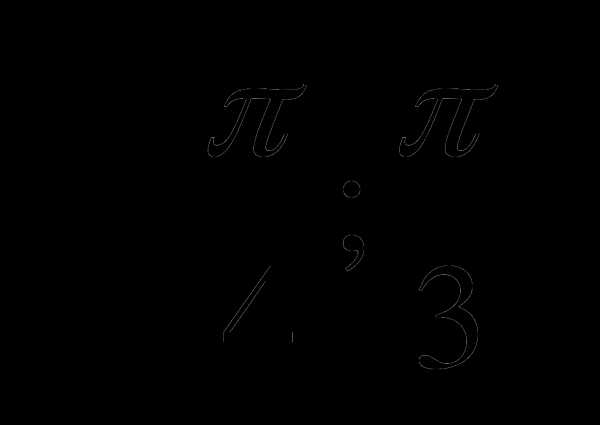
С2. Построить график функции 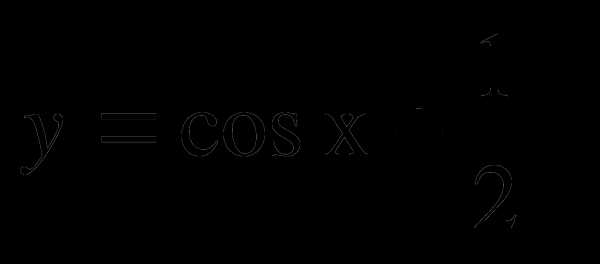 .
.
Нормы оценок: «3» — 5А, «4» — 4А + 1В, «5» — 3А + 1В +1С или 2А + 2В + 1С.
Контрольная работа № 1
Тригонометрические функции
Вариант 4
А1. Найти область определения функции у = cos  .
.
А2. Найти множество значений функции у = 3sin x.
А3. Выяснить, является ли данная функция четной или нечетной: у = tg x – x3.
А4. Доказать, что функция у = cos  является периодической с периодом Т=3p.
является периодической с периодом Т=3p.
А5. Возрастает или убывает функция у = sin x на отрезке 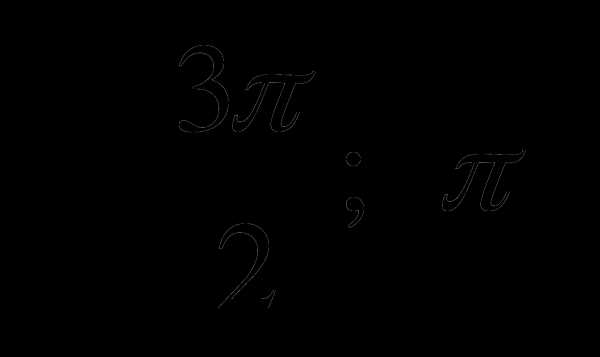 ?
?
A6. Найдите значение функции у=4sin при х =
при х =  .
.
В1. Сравните числа: cos  и sin
и sin  .
.
В2. Найдите все корни уравнения 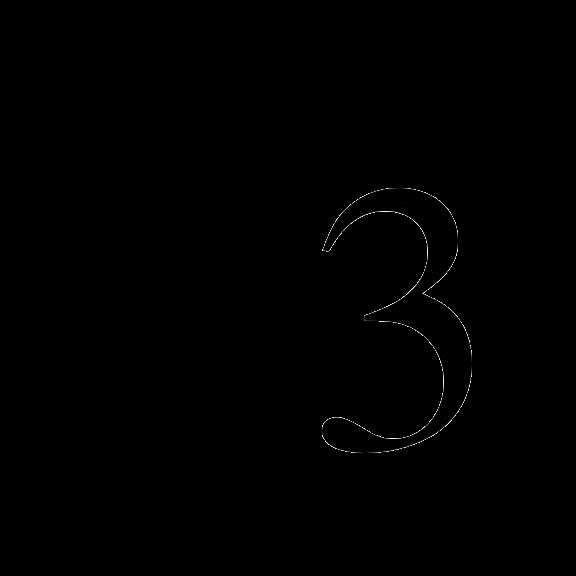 + 2cos x = 0, принадлежащие промежутку
+ 2cos x = 0, принадлежащие промежутку
[0; 2p].
С1. Найдите наибольшее и наименьшее значение функции у=4cosx на отрезке 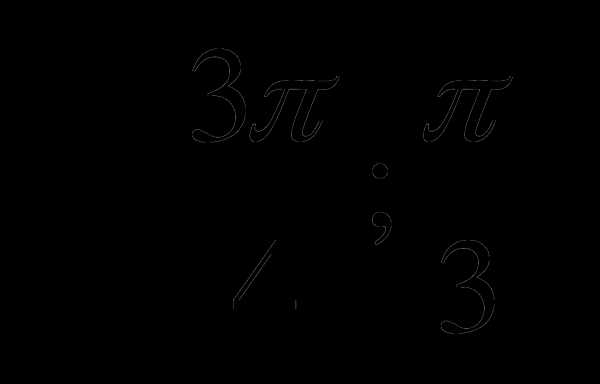 .
.
С2. Построить график функции у = |sin x| +1
Нормы оценок: «3» — 5А, «4» — 4А + 1В, «5» — 3А + 1В +1С или 2А + 2В + 1С.
infourok.ru
Подготовка к контрольной работе «Тригонометрические функции» конспект урока с презентацией и карточками для проведения контрольной работы в 11 классе по алгебре и началам анализа – УчМет
Автор Турукина Е.В.
Муниципальное бюджетное общеобразовательное учреждение
МБОУ Еткульская СОШ с.Еткуль Еткульского района Челябинской области
Класс 11
Тема Подготовка к контрольной работе по теме «Тригонометрические функции»
Цели:
1.Повторить определение четной (нечетной) функции, свойства и построение графиков тригонометрических функций
2.Воспитание мотивов учения
3.Развитие умения применять теорию на практике
План урока
Устная работа (слайд 3)
Функция у=f(x), для которой область определения симметрична относительно начала координат и выполняется равенство f(-x)=f(x)
Функция у= f(x), для которой область определения симметрична относительно относительно начала координат и выполняется равенство f(-x)=-f(x)
2.Проверить функцию на четность (слайд 4)
а) у= Sin x+ Cos x (ни четная ни нечетная)
б) у= х2 + Сos x (четная)
в) y= Sin x +2tg x (нечетная)
г) y = Cos2x –Sin2x (четная)
3.Найти область определения и область значений функции (слайд 5)
а) у= Сos 2x
б) y=2sin 0,5 x
в) y= -0,5 Cos2x
г) y=0,4Sinx +2
д) y= -0,07Cos x
е) y=5tg x +1
Ответы: а) Д(у)=R, Е(у)=[-1;1]
б) Д(у)=R, Е(у)=[-2;2]
в) Д(у)=R, Е(у)=[-0,5;0,5]
г) Д(у)=R, Е(у)=[1,6;2,4]
д) Д(у)=R,Е(у)=[-0,07;0,07]
е) Е(у)=R Д(у) : все х≠π/2 +πn, где n€Z
4.Найти наибольшее и наименьшее значение функции (слайд 6)
Ответ : у наибольшее =5, у наименьшее=1
Ответ : у наибольшее =9, у наименьшее=1
5.Повторим построение графиков тригонометрических функций(слайд 8-11)
6.Запишем домашнее задание: готовиться к контрольной работе, выполнить №717(а), 767,(766, 719)
7. При наличии времени можно предложить учащимся построить графики функций
1. у= 2Sin x -1
2. y= -0,5Cos x+2
3. y=2Sin0,5x
4. y= Cos2x+3
5. y= 3Sin2x-0,5
6. y= Cos(x — π/3 )7. y= Sin (x+ π/4 )
Следующий урок контрольная работа
Используемая литература
1. Учебник Алгебра и начала анализа для 10-11 класса
Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров, Н.Е.Федорова, М.И. Шабунин
Москва, Просвещение , 2010 год
2. Готовимся к Единому Государственному Экзамену Математика
Л.О. Денищева, Е.М.Бойченко, Ю.А.Глазков и др.
Москва, Дрофа, 2009
3. Учебно-тренировочные материалы для подготовки учащихся
ЕГЭ Математика 2009 ,Интеллект –центр
4. Дидактические материалы по алгебре и началам анализа 11 класс
М.И. Шабунин, М.В.Ткачева, Н.Е.Федорова, Р.Г. Газарян
Москва, Просвещение, 2008 год
5. А.П.Ершова, В.В.Голобородько Алгебра и начала анализа 10-11 классы. Математика. Самостоятельные и контрольные работы. Разноуровневые дидактические материалы. Москва, «Илекса» 2008
www.uchmet.ru
1 вариант № 1 Найти область определения и множество значений функции У= У=2 №2 Исследовать функцию на четность или нечетность У= У= №3 Доказать, что функция у= периодическая и найти ее наименьший положительный период. №4 Найти все принадлежащие отрезку корни уравнения №5 Найти все принадлежащие отрезку⦋-π;2π⦌ решения неравенства соs≥ | 2 вариант № 1 Найти область определения и множество значений функции У= У=3 №2 Исследовать функцию на четность или нечетность У= У= №3 Доказать, что функция у= периодическая и найти ее наименьший положительный период. №4 Найти все принадлежащие отрезку корни уравнения №5 Найти все принадлежащие отрезку⦋-3π;0⦌ решения неравенства соs≤ | 3 вариант № 1 Найти область определения и множество значений функции У= У=2 №2 Исследовать функцию на четность или нечетность У= У= №3 Доказать, что функция у= периодическая и найти ее наименьший положительный период. №4 Найти все принадлежащие отрезку корни уравнения №5 Найти все принадлежащие отрезку⦋-2π;π⦌ решения неравенства соs≥ | 4 вариант №1 Найти область определения и множество значений функции У= У= №2 Исследовать функцию на четность или нечетность У= У= №3 Доказать, что функция у= периодическая и найти ее наименьший положительный период. №4 Найти все принадлежащие отрезку корни уравнения №5 Найти все принадлежащие отрезку⦋-0.5π;2.5π⦌ решения неравенства sin≤ | 5 вариант №1 Найти область определения и множество значений функции У= У=2 №2 Исследовать функцию на четность или нечетность У= У= №3 Доказать, что функция у= периодическая и найти ее наименьший положительный период. №4 Найти все принадлежащие отрезку корни уравнения №5 Найти все принадлежащие отрезку⦋-π;2π⦌ решения неравенства соs≥ | 6 вариант №1 Найти область определения и множество значений функции У= У=2 №2 Исследовать функцию на четность или нечетность У= У= №3 Доказать, что функция у= периодическая и найти ее наименьший положительный период. №4 Найти все принадлежащие отрезку корни уравнения №5 Найти все принадлежащие отрезку⦋-2π;π⦌ решения неравенства tg≥1 | 7 вариант №1 Найти область определения и множество значений функции У= У= №2 Исследовать функцию на четность или нечетность У= У= №3 Доказать, что функция у= периодическая и найти ее наименьший положительный период. №4 Найти все принадлежащие отрезку корни уравнения №5 Найти все принадлежащие отрезку⦋-π;2π⦌ решения неравенства | 8 вариант №1 Найти область определения и множество значений функции У= У=2 №2 Исследовать функцию на четность или нечетность У= У= №3 Доказать, что функция у= периодическая и найти ее наименьший положительный период. №4 Найти все принадлежащие отрезку корни уравнения №5 Найти все принадлежащие отрезку⦋-2π;π⦌ решения неравенства соs≤ |
nsportal.ru
Тест по алгебре (11 класс) по теме: Бланки двух вариантов контрольной работы по алгебре и началам анализа в 11 классе по теме «Тригонометрические функции» (базовый уровень)
По теме: методические разработки, презентации и конспекты
контрольные работы по алгебре и началам анализа 10-11 классКонтрольные работы проводятся по прохождении тем для классов с базовым уровнем обучения и углубленным. Самостоятельные(проверочные) или зачетные работы провожу на уроках систематизации и обобщения зна…
Полугодовая контрольная работа по алгебре и началам анализа в 10 классеИтоговая контрольная работы за 1 полугодие по алгебре и началам анализа (УМК Ю.М.Колягина и др.) на 4 варианта….
Контрольные работы по алгебре и началам анализа в 11 классеКонтрольные работы…
Контрольная работа по алгебре и началам анализа для 11 класса по теме «Первообразная и интеграл»Контрольная работа по алгебре и началам анализа для 11 класса по теме «Первообразная и интеграл» в 2-х вариантах…
Контрольная работа по алгебре и началам анализа для 11 класса по теме «Обобщение понятия степени»Контрольная работа по алгебре и началам анализа для 11 класса по теме «Обобщение понятия степени» в 2-х вариантах…
Контрольная работа по алгебре и началам анализа для 11 класса по теме » Комбинаторика»Контрольная работа по алгебре и началам анализа для 11 класса по теме » Комбинаторика»…
Стартовая диагностическая работа ( 4 варианта с ответами) по алгебре и началам анализа в 11 классе в формате ЕГЭ (профиль)1.Работа состоит из 10 заданий: 1 часть 1-9 (кроме геометрии), 2 часть (10)2. Время написания работы: 60 минут.3. Максимальный бал за всю работу: 11 баллов…
nsportal.ru
Контрольная работа по алгебре 11 кл «Тригонометрические функции» 8 вариантов
Контрольная работа № 1 ВАРИАНТ 1 А 11
Найти область определения и множество значений функции y = sin x + 2.
Выяснить, является ли функция
y = x2 + cos x чётной или нечётной.
Доказать, что наименьший положительный период функции y = cos 2 x равен π.
Найти принадлежащие отрезку [- π; π] корни уравнения
 с помощью графика функции.
с помощью графика функции.Построить график функции y = cos x — 1 и найти значение аргумента, при которых функция возрастает, принимает наибольшее значение.
_________________________________________
Контрольная работа № 1 ВАРИАНТ 2 А 11
Найти область определения и множество значений функции y = 3 cos x.
Выяснить, является ли функция y = x3 sin x чётной или нечётной.
Доказать, что наименьший положительный период функции
 равен 4π.
равен 4π.Найти принадлежащие отрезку [0; 2,5π] корни уравнения
 с помощью графика функции.
с помощью графика функции.Построить график функции
 и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.
и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.
_________________________________________
Контрольная работа № 1 ВАРИАНТ 3 А 11
Найти область определения и множество значений функции y = — sin x +3.
Выяснить, является ли функция
y = x — cos x чётной или нечётной.
Доказать, что наименьший положительный период функции y = sin 2x равен π.
Найти принадлежащие отрезку [- π/2; π] корни уравнения
 с помощью графика функции.
с помощью графика функции.Построить график функции y = cos x +2 и найти значение аргумента, при которых функция возрастает, принимает наибольшее значение.
_________________________________________
Контрольная работа № 1 ВАРИАНТ 4 А 11
Найти область определения и множество значений функции y = -5 cos x.
Выяснить, является ли функция y = —x2 + sin x чётной или нечётной.
Доказать, что наименьший положительный период функции
 равен 6π.
равен 6π.Найти принадлежащие отрезку [- π/2; 2,5π] корни уравнения
 с помощью графика функции.
с помощью графика функции.Построить график функции
 и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.
и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.
_________________________________________
Контрольная работа № 1 ВАРИАНТ 5 А 11
Найти область определения и множество значений функции y = cos x -1.
Выяснить, является ли функция
y = sin x –x2 чётной или нечётной.
Доказать, что наименьший положительный период функции
 равен 10π.
равен 10π.Найти принадлежащие отрезку [0; 2π] корни уравнения
 с помощью графика функции.
с помощью графика функции.Построить график функции y = cos x +3 и найти значение аргумента, при которых функция возрастает, принимает наибольшее значение.
_________________________________________
Контрольная работа № 1 ВАРИАНТ 6 А 11
Найти область определения и множество значений функции y = -2 sin x.
Выяснить, является ли функция y = —x4 cos x чётной или нечётной.
Доказать, что наименьший положительный период функции
 равен 4π.
равен 4π.Найти принадлежащие отрезку [- π/2; π] корни уравнения
 с помощью графика функции.
с помощью графика функции.Построить график функции
 и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.
и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.
_________________________________________
Контрольная работа № 1 ВАРИАНТ 7 А 11
Найти область определения и множество значений функции y = — cos x -2.
Выяснить, является ли функция
y = x3 + cos x чётной или нечётной.
Доказать, что наименьший положительный период функции y = sin 4 x равен π.
Найти принадлежащие отрезку [- π; π/2] корни уравнения
 с помощью графика функции.
с помощью графика функции.Построить график функции y = sin x +2 и найти значение аргумента, при которых функция возрастает, принимает наибольшее значение.
_________________________________________
Контрольная работа № 1 ВАРИАНТ 8 А 11
Найти область определения и множество значений функции y = -5 sin x.
Выяснить, является ли функция y = x2 +sin x чётной или нечётной.
Доказать, что наименьший положительный период функции
 равен 6π.
равен 6π.Найти принадлежащие отрезку [- π/2; 2,5π] корни уравнения
 с помощью графика функции.
с помощью графика функции.Построить график функции
 и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.
и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.
_________________________________________
infourok.ru
Контрольная работа по алгебре 11 класс
КОНТРОЛЬНАЯ РАБОТА № 1 (ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ) – 11кл.
Вариант № 1 Вариант № 2
Найти область определения функции
а) а)
б) б)
в) в)
г) г)
Выяснить, является функция четной или нечетной
Найти множество значений функции
Изобразить схематически график функции
;
на
и опишите её свойства.
Решите с помощью графика уравнения
а) а)
на
б) б)
на
Решите неравенство
а) а)
на
б) б)
на
7*) Найти наибольшее и наименьшее значения функции:
8*) Построить график функции . При каких значениях х функция возрастает [убывает]?
multiurok.ru
Вариант1 1.Найти область определения и множество значений функции у=5 cos х . 2. Выяснить является функция у=2sin x – tg x четной или нечетной? 3.Изобразить график функции у= sin x на интервале ( — 2п; 2п) и решить уравнение sin x = 0,5. 4.Найти наибольшее и наименьшее значения функции у= 6sin x cos х + 3 5. Построить график функции у= cos х + 2. При каких значениях функция убывает; возрастает? | Вариант2 1.Найти область определения и множество значений функции у=0,5 sin х . 2. Выяснить является функция у=2cos x – x четной или нечетной? 3.Изобразить график функции у= cos x на интервале ( — 2п; 2п) и решить уравнение cos x = -0,5. 4.Найти наибольшее и наименьшее значения функции у= 6cos 5. Построить график функции у= sin х + 2. При каких значениях функция убывает; возрастает? | Вариант3 1.Найти область определения и множество значений функции у= cos х + 4 2. Выяснить является функция у = 3sin x + tg x четной или нечетной? 3.Изобразить график функции у= sin x на интервале ( — 2п; 2п) и решить уравнение sin x = -1. 4.Найти наибольшее и наименьшее значения функции у= 8sin x cos х — 2 5. Построить график функции у= cos х — 1. При каких значениях функция убывает; возрастает? | Вариант6 1.Найти область определения и множество значений функции у=sin х — 3 2. Выяснить является функция у = cos x +3 x четной или нечетной? 3.Изобразить график функции у= cos x на интервале ( — 2п; 2п) и решить уравнение cos x = -1. 4.Найти наибольшее и наименьшее значения функции у= 5cos 5. Построить график функции у= sin х — 1. При каких значениях функция убывает; возрастает? | Вариант5 1.Найти область определения и множество значений функции у= 5cos х . 2. Выяснить является функция у=sin x –5 tg x четной или нечетной? 3.Изобразить график функции у= sin x на интервале ( — 2п; 2п) и решить уравнение sin x = 1. 4.Найти наибольшее и наименьшее значения функции у= 10sin x cos х + 2 . 5. Построить график функции у= cos х + 1. При каких значениях функция убывает; возрастает? | Вариант6 1.Найти область определения и множество значений функции у=sin х + 2 2. Выяснить является функция у=2cos x – x четной или нечетной? 3.Изобразить график функции у= cos x на интервале ( — 2п; 2п) и решить уравнение cos x = 1. 4.Найти наибольшее и наименьшее значения функции у= 8cos 5. Построить график функции у= sin х + 1. При каких значениях функция убывает; возрастает? | Вариант7 1.Найти область определения и множество значений функции у=cos х + 11 2. Выяснить является функция у=sin x –2tg x четной или нечетной? 3.Изобразить график функции у= sin x на интервале ( — 2п; 2п) и решить уравнение sin x = 1. 4.Найти наибольшее и наименьшее значения функции у= 6sin x cos х + 3 5. Построить график функции у= cos х + 3. При каких значениях функция убывает; возрастает? | Вариант8 1.Найти область определения и множество значений функции у=0,5 sin х . 2. Выяснить является функция у=2cos x – x четной или нечетной? 3.Изобразить график функции у= cos x на интервале ( — 2п; 2п) и решить уравнение cos x = -1. 4.Найти наибольшее и наименьшее значения функции у= 6cos 5. Построить график функции у= sin х +3. При каких значениях функция убывает; возрастает? |
kopilkaurokov.ru


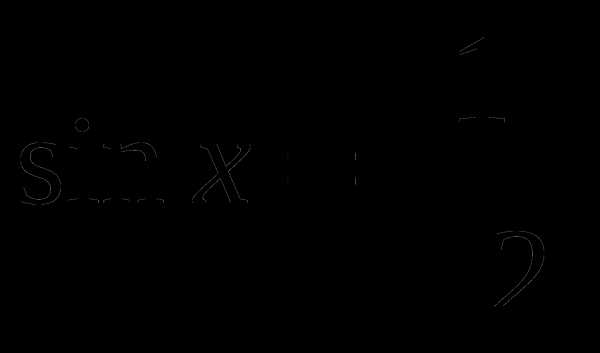 с помощью графика функции.
с помощью графика функции.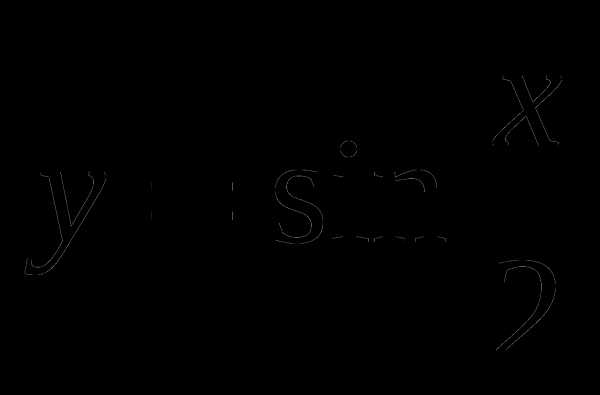 равен 4π.
равен 4π.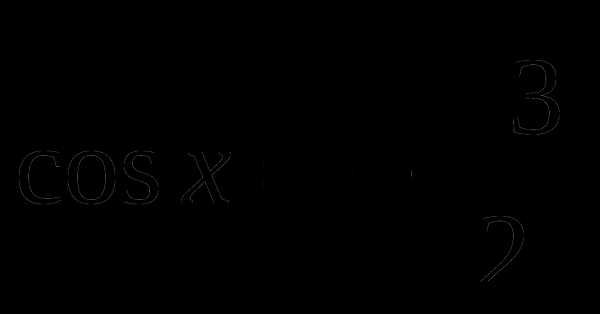 с помощью графика функции.
с помощью графика функции.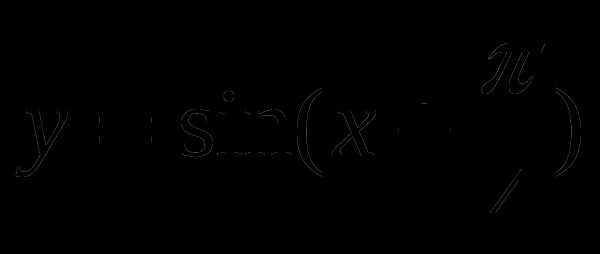 и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.
и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.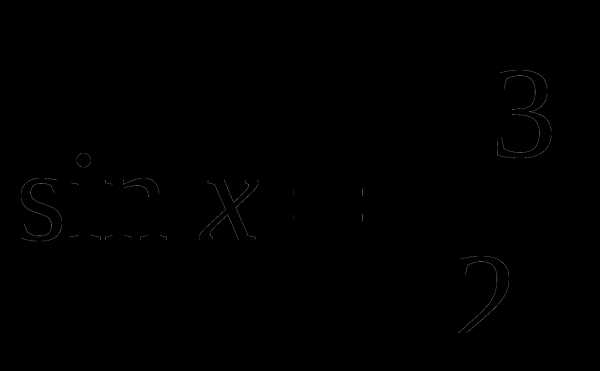 с помощью графика функции.
с помощью графика функции.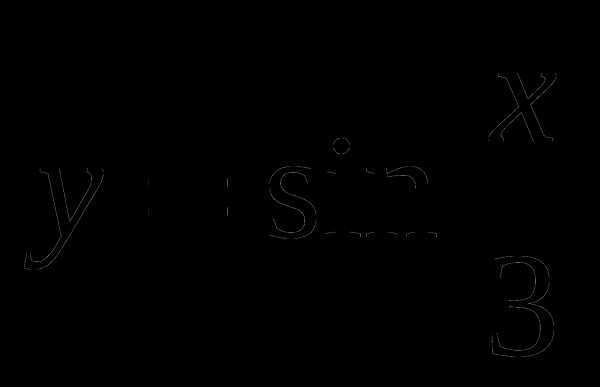 равен 6π.
равен 6π.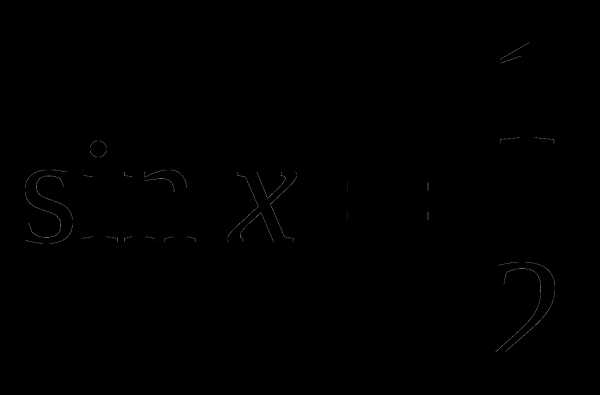 с помощью графика функции.
с помощью графика функции.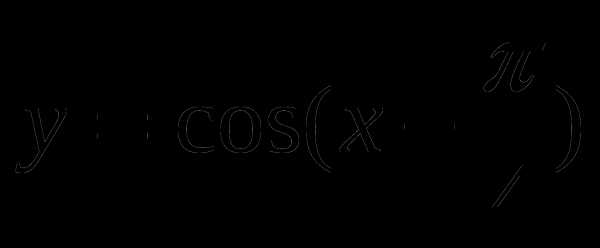 и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.
и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.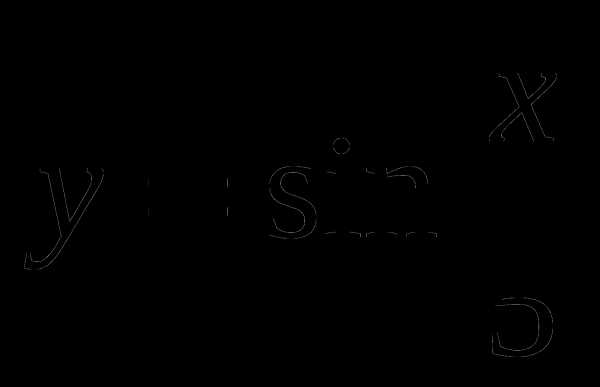 равен 10π.
равен 10π. с помощью графика функции.
с помощью графика функции. равен 4π.
равен 4π.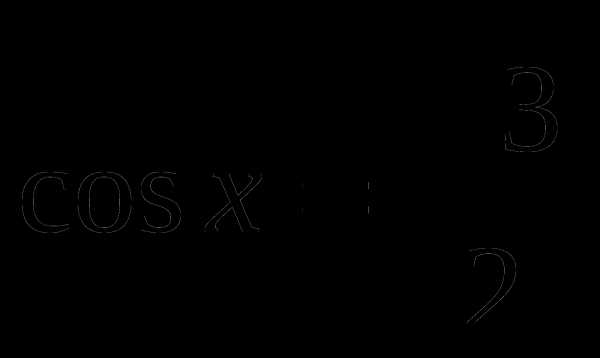 с помощью графика функции.
с помощью графика функции.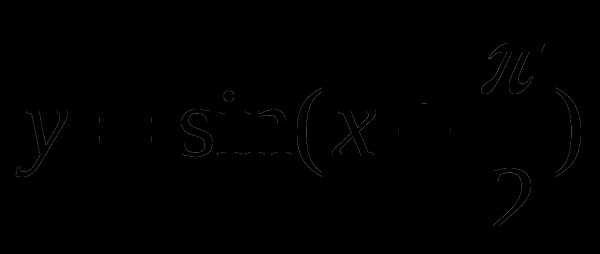 и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.
и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.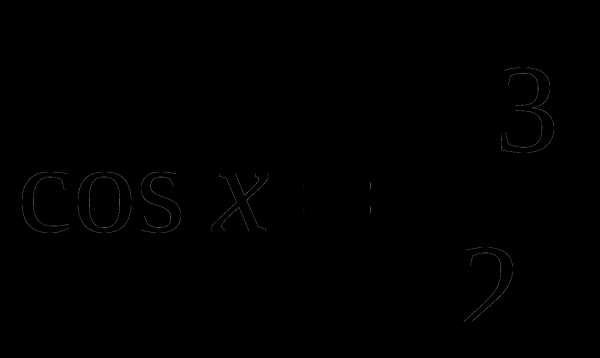 с помощью графика функции.
с помощью графика функции. равен 6π.
равен 6π.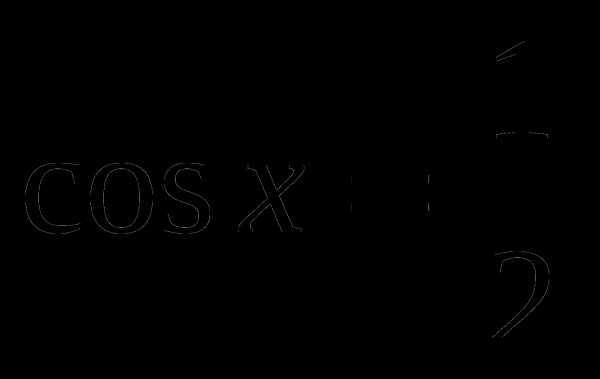 с помощью графика функции.
с помощью графика функции.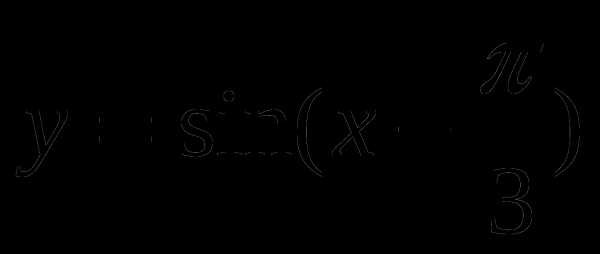 и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.
и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.