Симметрия в природе доклад – Реферат «Симметрия в природе» | Социальная сеть работников образования
Реферат «Симметрия в природе» | Социальная сеть работников образования
Муниципальное бюджетное общеобразовательное учреждение
Средняя общеобразовательная школа №3
Реферат по математике на тему:
«Симметрия в природе»
Подготовила: ученик 6 класса «В» Звягинцев Денис
Учитель: Курбатова И.Г.
с. Безопасное, 2012г.
Содержание
Введение…………………………………………………………………………3
Раздел I. Симметрия в математике………………………………………………5
Глава 1. Центральная симметрия………………………………………………..5
Глава 2. Осевая симметрия……………………………………………………….6
Глава 4. Зеркальная симметрия…………………………………………………7
Раздел II. Симметрия в живой природе………………………………………….8
Глава 1. Симметрия в живой природе. Асимметрия и симметрия…………8
Глава 2. Симметрия растений…………………………………………………10
Глава 3. Симметрия животных………………………………………………….12
Глава 4. Человек – существо симметричное…………………………………14
Заключение……………………………………………………………………….16
- Введение
Тема реферата была выбрана после изучения раздела «Осевая и центральная симметрия». Остановился именно на этой теме не случайно, хотелось узнать принципы симметрии, её виды, разнообразие её в живой и неживой природе.
Под симметрией (от греч. symmetria — соразмерность) в широком смысле понимают правильность в строении тела и фигуры. Учение о симметрии представляет собой большую и важную ветвь тесно связанную с науками разных отраслей. С симметрией мы часто встречаемся в искусстве, архитектуре, технике, быту. Так, фасады многих зданий обладают осевой симметрией. В большинстве случаев симметричны относительно оси или центра узоры на коврах, тканях, комнатных обоях. Симметричны многие детали механизмов, например, зубчатые колеса.
Было интересно, потому что данная тема затрагивает не только математику, хотя она и лежит в её основе, но и другие области науки, техники, природы. Симметрия, как мне кажется, является фундаментом природы, представление о котором слагалось в течение десятков, сотен, тысяч поколений людей.
Я обратил внимание на то, что во многих вещах, в основе красоты многих форм, созданных природой, составляет симметрия, точнее, все её виды — от простейших до самых сложных. Можно говорить о симметрии, как о гармонии пропорций, как о «соразмерности», регулярности и упорядоченности.
Нам это важно, потому что для многих людей математика – скучная и сложная наука, но математика – не только цифры, уравнения и решения, но и красота в строении геометрических тел, живых организмов и даже является фундаментом для многих наук от простых до самых сложных.
Цели реферата были следующими:
- раскрыть особенности видов симметрии;
- показать всю привлекательность математики как науки и её взаимосвязь с природой в целом.
Задачи:
- сбор материала по теме реферата и его обработка;
- обобщение обработанного материала;
- выводы о проделанной работе;
- оформление обобщенного материала.
Раздел I. Симметрия в математике
Глава 1. Центральная симметрия
Понятие центральной симметрии следующее: «Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры». Поэтому говорят, что фигура обладает центральной симметрией.
Понятия центра симметрии в «Началах» Евклида нет, однако в 38-ом предложении XI книги содержится понятие пространственной оси симметрии. Впервые понятие центра симметрии встречается в XVI в. В одной из теорем Клавиуса, гласящей: «если параллелепипед рассекается плоскостью, проходящей через центр, то он разбивается пополам и, наоборот, если параллелепипед рассекается пополам, то плоскость проходит через центр». Лежандр, который впервые ввёл в элементарную геометрию элементы учения о симметрии, показывает, что у прямого параллелепипеда имеются 3 плоскости симметрии, перпендикулярные к ребрам, а у куба 9 плоскостей симметрии, из которых 3 перпендикулярны к рёбрам, а другие 6 проходят через диагонали граней.
Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм. Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма – точка пересечения его диагоналей. Любая прямая также обладает центральной симметрией. Однако, в отличие от окружности и параллелограмма, которые имеют только один центр симметрии, у прямой их бесконечно много – любая точка прямой является её центром симметрии. Примером фигуры, не имеющей центра симметрии, является произвольный треугольник.
В алгебре при изучении чётных и нечётных функций рассматриваются их графики. График чётной функции при построении симметричен относительно оси ординат, а график нечётной функции – относительно начала координат, т.е. точки О. Значит, нечётная функция обладает центральной симметрией, а чётная функция – осевой.
Таким образом, две центрально симметричные плоские фигуры всегда можно наложить друг на друга, не выводя их из общей плоскости. Для этого достаточно одну из них повернуть на угол 180° около центра симметрии.
Как в случае зеркальной, так и в случае центральной симметрии плоская фигура непременно имеет ось симметрии второго порядка, но в первом случае эта ось лежит в плоскости фигуры, а во втором – перпендикулярна к этой плоскости.
Глава 2. Осевая симметрия
Понятие осевой симметрии представлено следующим образом: «Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая a называется осью симметрии фигуры». Тогда говорят, что фигура обладает осевой симметрией.
В более узком смысле осью симметрии называют ось симметрии второго порядка и говорят об «осевой симметрии», которую можно определить так: фигура (или тело) обладает осевой симметрией относительно некоторой оси, если каждой её точке Е соответствует такая принадлежащая этой же фигуре точка F, что отрезок EF перпендикулярен к оси, пересекает её и в точке пересечения делится пополам. Рассмотренная выше (гл. 1) пара треугольников обладает (кроме центральной) еще осевой симметрией. Её ось симметрии проходит через точку С перпендикулярно к плоскости чертежа.
Приведём примеры фигур, обладающих осевой симметрией. У неразвернутого угла одна ось симметрии — прямая, на которой расположена биссектриса угла. Равнобедренный (но не равносторонний) треугольник имеет также одну ось симметрии, а равносторонний треугольник— три оси симметрии. Прямоугольник и ромб, не являющиеся квадратами, имеют по две оси симметрии, а квадрат— четыре оси симметрии. У окружности их бесконечно много — любая прямая, проходящая через её центр, является осью симметрии.
Имеются фигуры, у которых нет ни одной оси симметрии. К таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник.
Глава 3. Зеркальная симметрия
Зеркальная симметрия хорошо знакома каждому человеку из повседневного наблюдения. Как показывает само название, зеркальная симметрия связывает любой предмет и его отражение в плоском зеркале. Говорят, что одна фигура (или тело) зеркально симметрично другой, если вместе они образуют зеркально симметричную фигуру (или тело).
Игрокам в бильярд издавна знакомо действие отражения. Их «зеркала» — это борта игрового поля, а роль луча света исполняют траектории шаров. Ударившись о борт возле угла, шар катится к стороне, расположенной под прямым углом, и, отразившись от неё, движется обратно параллельно направлению первого удара.
Важно отметить, что два симметричных друг другу тела не могут быть вложены или наложены друг на друга. Так перчатку правой руки нельзя надеть на левую руку. Симметрично зеркальные фигуры при всём своём сходстве существенно отличаются друг от друга. Чтобы убедиться в этом, достаточно поднести лист бумаги к зеркалу и попытаться прочесть несколько слов, напечатанных на ней, буквы и слова просто-напросто будут перевёрнуты справа налево. По этой причине симметричные предметы нельзя называть равными, поэтому их называют зеркально равными.
Рассмотрим пример. Если плоская фигура ABCDE симметрична относительно плоскости Р (что возможно лишь в случае взаимной перпендикулярности плоскостей ABCDE и Р), то прямая KL, по которой пересекаются упомянутые плоскости, служит осью симметрии (второго порядка) фигуры ABCDE. Обратно, если плоская фигура ABCDE имеет ось симметрии KL, лежащую в её плоскости, то эта фигура симметрична относительно плоскости Р, проведённой через KL перпендикулярно к плоскости фигуры. Поэтому ось КЕ можно назвать также зеркальной L прямой плоской фигуры ABCDE.
Две зеркально симметричные плоские фигуры всегда можно наложить
друг на друга. Однако для этого необходимо вывести одну из них (или обе) из их общей плоскости.
Вообще зеркально равными телами (или фигурами) называются тела (или фигуры) в том случае, если при надлежащем их смещении они могут образовать две половины зеркально симметричного тела (или фигуры).
Раздел II. Симметрия в живой природе
Глава 1. Симметрия в живой природе. Асимметрия и симметрия
Симметрией обладают объекты и явления живой природы. Она не только радует глаз и вдохновляет поэтов всех времен и народов, а позволяет живым организмам лучше приспособиться к среде обитания и просто выжить.
В живой природе огромное большинство живых организмов обнаруживает различные виды симметрии (формы, подобия, относительного расположения). Причем организмы разного анатомического строения могут иметь один и тот же тип внешней симметрии.
Внешняя симметрия может выступить в качестве основания классификации организмов (сферическая, радиальная, осевая и т.д.) Микроорганизмы, живущие в условиях слабого воздействия гравитации, имеют ярко выраженную симметрию формы.
Асимметрия присутствует уже на уровне элементарных частиц и проявляется в абсолютном преобладании в нашей Вселенной частиц над античастицами. Известный физик Ф. Дайсон писал: «Открытия последних десятилетий в области физики элементарных частиц заставляют нас обратить особое внимание на концепцию нарушения симметрии. Развитие Вселенной с момента ее зарождения выглядит как непрерывная последовательность нарушений симметрии. В момент своего возникновения при грандиозном взрыве Вселенная была симметрична и однородна. По мере остывания в ней нарушается одна симметрия за другой, что создает возможности для существования все большего и большего разнообразия структур. Феномен жизни естественно вписывается в эту картину. Жизнь — это тоже нарушение симметрии»
Молекулярная асимметрия открыта Л. Пастером, который первым выделил «правые» и «левые» молекулы винной кислоты: правые молекулы похожи на правый винт, а левые — на левый. Такие молекулы химики называют стереоизомерами.
Молекулы стереоизомеры имеют одинаковый атомный состав, одинаковые размеры, одинаковую структуру — в то же время они различимы, поскольку являются зеркально асимметричными, т.е. объект оказывается нетождественным со своим зеркальным двойником. Поэтому здесь понятия «правый-левый» — условны.
В настоящее время хорошо известно, что молекулы органических веществ, составляющие основу живой материи, имеют асимметричный характер, т.е. в состав живого вещества они входят только либо как правые, либо как левые молекулы. Таким образом, каждое вещество может входить в состав живой материи только в том случае, если оно обладает вполне определенным типом симметрии. Например, молекулы всех аминокислот в любом .живом организме могут быть только левыми, сахара ~ только правыми. Это свойство живого вещества и его продуктов жизнедеятельности называют дисимметрией. Оно имеет совершенно фундаментальный характер. Хотя правые и левые молекулы неразличимы по химическим свойствам, живая материя их не только различает, но и делает выбор. Она отбраковывает и не использует молекулы, не обладающие нужной ей структурой. Как это происходит, пока не ясно. Молекулы противоположной симметрии для нее яд.
Если бы живое существо оказалось в условиях, когда вся пища была бы составлена из молекул противоположной симметрии, не отвечающей дисимметрии этого организма, то оно погибло бы от голода. В неживом веществе правых и левых молекул поровну. Дисимметрия — единственное свойство, благодаря которому мы можем отличить вещество биогенного происхождения от неживого вещества. Мы не можем ответить на вопрос, что такое жизнь, но имеем способ отличить живое от неживого. Таким образом, асимметрию можно рассматривать как разграничительную линию между живой и неживой природой. Для неживой материи характерно преобладание симметрии, при переходе от неживой к живой материи уже на микроуровне преобладает асимметрия. В живой природе асимметрию можно увидеть всюду. Очень удачно это подметил в романе «Жизнь и судьба» В. Гроссман: «В большом миллионе русских деревенских изб нет и не может быть двух неразличимо схожих. Все .живое неповторимо.
Симметрия лежит в основе вещей и явлений, выражая нечто общее, свойственное разным объектам, тогда как асимметрия связана с индивидуальным воплощением этого общего в конкретном объекте. На принципе симметрии основан метод аналогий, предполагающий отыскание общих свойств в различных объектах. На основе аналогий создаются физические модели различных объектов и явлений. Аналогии между процессами позволяют описывать их общими уравнениями.
Глава 2. Симметрия растений
Изображения на плоскости многих предметов окружающего нас мира имеют ось симметрии или центр симметрии. Многие листья деревьев и лепестки цветов симметричны относительно среднего стебля.
Среди цветов наблюдаются поворотные симметрии разных порядков. Многие цветы обладают характерным свойством: цветок можно повернуть так, что каждый лепесток займёт положение соседнего, цветок же совместится с самим собой. Такой цветок обладает осью симметрии. Минимальный угол, на который нужно повернуть цветок вокруг оси симметрии, чтобы он совместился с самим собой, называется элементарным углом поворота оси. Этот угол для различных цветов не одинаков. Для ириса он равен 120є, для колокольчика – 72є, для нарцисса – 60є . Поворотную ось можно характеризовать и с помощью другой величины, называемой порядком оси и показывающей, сколько раз произойдет совмещение при повороте на 360є. Те же цветы ириса, колокольчика и нарцисса обладают осями третьего, пятого и шестого порядков соответственно. Особенно часто среди цветов встречается симметрия пятого порядка. Это такие полевые цветы как колокольчик, незабудка, зверобой, лапчатка гусиная и др.; цветы плодовых деревьев – вишня, яблоня, груша, мандарин и др., цветы плодово-ягодных растений – земляника, ежевика, малина, шиповник; садовые цветы – настурция, флокс и др.
В пространстве существуют тела, обладающие винтовой симметрией, т. е. совмещающиеся со своим первоначальным положением после поворота на угол вокруг оси, дополненного сдвигом вдоль той же оси.
Винтовая симметрия наблюдается в расположении листьев на стеблях большинства растений. Располагаясь винтом по стеблю, листья как бы раскидываются во все стороны и не заслоняют друг друга от света, крайне необходимого для жизни растений. Это интересное ботаническое явление носит название филлотаксиса, что буквально означает строение листа. Другим проявлением филлотаксиса оказывается устройство соцветия подсолнечника или чешуи еловой шишки, в которой чешуйки располагаются в виде спиралей и винтовых линий. Такое расположение особенно четко видно у ананаса, имеющего более или менее шестиугольные ячейки, которые образуют ряды, идущие в различных направлениях.
Глава 3. Симметрия животных
Внимательное наблюдение обнаруживает, что основу красоты многих форм, созданных природой, составляет симметрия, точнее, все её виды – от простейших до самых сложных. Симметрия в строение животных – почти общее явление, хотя почти всегда встречаются исключения из общего правила.
Под симметрией у животных понимают соответствие в размерах, форме и очертаниях, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии. Строение тела многих многоклеточных организмов отражает определённые формы симметрии, такие как радиальную (лучевая) или билатеральную (двусторонняя), которые являются основными типами симметрии. Кстати, склонность к регенерации (восстановление) зависит от типа симметрии животного.
В биологии о радиальной симметрии идёт речь, когда через трёхмерное существо проходят две или более плоскости симметрии. Эти плоскости пересекаются в прямой. Если животное будет вращаться вокруг этой оси на определённый градус, то оно будет отображаться само на себе. В двухмерной проекции радиальная симметрия может сохраняться, если ось симметрии направлена перпендикулярно к проекционной плоскости. Иными словами, сохранение радиальной симметрии зависит от угла наблюдения.
При радиальной или лучистой симметрии тело имеет форму короткого или длинного цилиндра либо сосуда с центральной осью, от которого отходят в радиальном порядке части тела. Среди них встречается так называемая пентасимметрия, базирующаяся на пяти плоскостях симметрии.
Радиальная симметрия характерна для многих стрекающих, а также для большинства иглокожих, кишечнополостных. Взрослые формы иглокожих приближаются к радиальной симметрии, в то время как их личинки билатерально симметричны.
Лучевую симметрию мы также видим у медуз, кораллов, актиний, морских звёзд. Если вращать их вокруг собственной оси, они несколько раз «совместятся сами с собой». Если отрезать у морской звезды любое из пяти щупалец, оно сумеет восстановить всю звезду. От радиальной симметрии различаются двулучевая радиальная симметрия (две плоскости симметрии, к примеру, гребневики), а также билатеральная симметрия (одна плоскость симметрии, к примеру, двусторонне-симметричные).
При билатеральной симметрии осей симметрии три, но симметричных сторон только одна пара. Потому что две другие стороны – брюшная и спинная – друг на друга не похожи. Этот вид симметрии характерен для большинства животных, в том числе насекомых, рыб, земноводных, рептилий, птиц, млекопитающих. Например, черви, членистоногие, позвоночные. У большинства многоклеточных (у человека в том числе) другой тип симметрии – двусторонняя. Левая половина их тела — это как бы «отражённая в зеркале правая». Этот принцип, однако, не относится к отдельным внутренним органам, что демонстрирует, например, расположение печени или сердца у человека. Плоский червь планария имеет двустороннюю симметрию. Если разрезать его вдоль оси тела или поперёк, из обеих половинок вырастут новые черви. Если же измельчить планарию как-нибудь иначе — скорее всего ничего не выйдет.
Можно сказать также, что каждое животное (будь то насекомое, рыба или птица) состоит из двух энантиоморфов – правой и левой половин. Энантиоморфы – пара зеркально асимметричных объектов (фигур), являющихся зеркальным изображением один другого (например, пара перчаток). Иными словами – это объект и его зазеркальный двойник при условии, что сам объект зеркально асимметричен.
Сферическая симметрия имеет место у радиолярий и солнечников, тело которых сферической формы, а его части распределены вокруг центра сферы и отходят от неё. У таких организмов нет ни передней, ни задней, ни боковых частей тела, любая плоскость, проведённая через центр, делит животное на одинаковые половинки.
Губки и пластинчатые не проявляют симметрию.
Глава 4. Человек — существо симметричное
Не станем пока разбираться, существует ли на самом деле абсолютно симметричный человек. У каждого, разумеется, обнаружится родинка, прядь волос или какая-нибудь другая деталь, нарушающая внешнюю симметрию. Левый глаз никогда не бывает в точности таким, как правый, да и уголки рта находятся на разной высоте, во всяком случае, у большинства людей. И всё же это лишь мелкие несоответствия. Никто не усомнится, что внешне человек построен симметрично: левой руке всегда соответствует правая и обе руки совершенно одинаковы! НО! Здесь стоит остановиться. Если бы наши руки и в самом деле были совершенно одинаковы, мы могли бы в любой момент поменять их. Было бы возможно, скажем, путем трансплантации пересадить левую ладонь на правую руку, или, проще, левая перчатка подходила бы тогда к правой руке, но на самом деле это не так. Каждому известно, что сходство между нашими руками, ушами, глазами и другими частями тела такое же, как между предметом и его отражением в зеркале. Многие художники обращали пристальное внимание на симметрию и пропорции человеческого тела, во всяком случае, до тех пор, пока ими руководило желание в своих произведениях как можно точнее следовать природе.
Известны каноны пропорций, составленные Альбрехтом Дюрером и Леонардо да Винчи. Согласно этим канонам, человеческое тело не только симметрично, но и пропорционально. Леонардо открыл, что тело вписывается в круг и в квадрат. Дюрер занимался поисками единой меры, которая находилась бы в определенном соотношении с длиной туловища или ноги (такой мерой он считал длину руки до локтя). В современных школах живописи в качестве единой меры чаще всего принимается размер головы по вертикали. С известным допущением можно считать, что длина туловища превосходит размер головы в восемь раз. На первый взгляд это кажется странным. Но нельзя забывать, что большинство высоких людей отличаются удлинённым черепом и, наоборот, редко можно встретить низкорослого толстяка с головой удлинённой формы. Размеру головы пропорциональна не только длина туловища, но и размеры других частей тела. По этому принципу построены все люди, оттого-то мы, в общем, похожи друг на друга. Однако наши пропорции согласуются лишь приблизительно, а потому люди лишь похожи, но не одинаковы. Во всяком случае, все мы симметричны! К тому же некоторые художники в своих произведениях особенно подчёркивают эту симметрию. И в одежде человек тоже, как правило, старается поддерживать впечатление симметричности: правый рукав соответствует левому, правая штанина — левой. Пуговицы на куртке и на рубашке сидят ровно посередине, а если и отступают от нее, то на симметричные расстояния. Но на фоне этой общей симметрии в мелких деталях мы умышленно допускаем асимметрию, например, расчесывая волосы на косой пробор — слева или справа или делая асимметричную стрижку. Или, скажем, помещая на костюме асимметричный кармашек на груди. Или, надев кольцо на безымянный палец только одной руки. Лишь на одной стороне груди носятся ордена и значки (чаще на левой). Полная безукоризненная симметрия выглядела бы нестерпимо скучно. Именно небольшие отклонения от неё и придают характерные, индивидуальные черты.И вместе с тем порой человек старается подчеркнуть, усилить различие между левым и правым. В средние века мужчины одно время щеголяли в панталонах со штанинами разных цветов (например, одной красной, а другой черной или белой). В не столь отдалённые дни были популярны джинсы с яркими заплатами или цветными разводами. Но подобная мода всегда недолговечна. Лишь тактичные, скромные отклонения от симметрии остаются на долгие времена.
Заключение
С симметрией мы встречаемся везде ~ в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Принципы симметрии играют важную роль в физике и математике,химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии. Существует множество видов симметрии как в растительном, так и в животном мире, но при всем многообразии живых организмов, принцип симметрии действует всегда, и этот факт еще раз подчеркивает гармоничность нашего мира.
Еще одним интересным проявлением симметрии жизненных npoifeccoe являются биологические ритмы (биоритмы), циклические колебания биологических процессов и их характеристик (сокращения сердца, дыхание, колебания интенсивности деления клеток, обмена веществ, двигательной активности, численности растений и животных), зачастую связанные с приспособлением организмов к геофизическим циклам. Исследованием биоритмов занимается особая наука — хронобиология. Помимо симметрии существует также понятие ассиметрии; Симметрия лежит в основе вещей и явлений, выражая нечто общее, свойственное разным объектам, тогда как асимметрия связана с индивидуальным воплощением этого общего в конкретном объекте.
nsportal.ru
Доклад на тему Симметрия в природе 5 класс сообщение
Симметрию, по праву, можно назвать воплощением красоты и гармонии. Что же это такое? Симметрией называют закономерное расположение одинаковых частей, относительно оси или центра. С детства мы привыкаем к ней, потому что, очень многие предметы, которые нас окружают, являются ее воплощением.
Если внимательно посмотреть на природу, то можно заметить, что симметрия проявляет себя даже в мелких деталях. Она, несомненно, радует человеческий глаз, является вдохновением для многих писателей и художников. Помимо этого, она является отличным помощником для живых организмов и помогает им приспособиться к среде обитания.
Для растений характерной является симметрия конуса. Ярким примером послужит дерево. Среди цветов можно заметить радиальную симметрию. Зеркальная симметрия присуща листьям деревьев и некоторым цветочным растениям. Рассмотрим лист с дерева. У него строгая, закономерная форма. Две половинки зеркально расположены и являются симметричными. Зеркальную симметрию так же можно встретить среди цветов и плодов. Симметрия у животных понимается как соответствие размеров и форм. Зеркальная симметрия является самой характерной для животного мира. Ярким представителем данного вида является бабочка. Посмотрите на ее крылья:они расположены строго симметрично и поражают своей красотой.
Красивые примеры симметрии в природе.
Пчелы, однозначно, знают толк в точных науках. Во все времена люди удивлялись, насколько, совершенны формы в медовых сотах. Они создают настоящее произведение искусства. Подсолнухи, так же могут похвастаться уникальной симметрией, с которой мы знакомы как последовательностью Фибоначи. Брокколи романеско считается уникальным примером фрактальной симметрии, который имеет форму спирали. Даже снежинки образуются по законам порядка. Все они имеют разные узоры, но каждая из них обладает строгой симметрией. Паутина имеет радиальную симметрию. Ее нити расположены на одинаковом расстоянии друг от друга и образуют неповторимую форму. А, теперь, взгляните на себя: две руки и две ноги, располагаются симметрично туловища. Человек является ярким примером воплощением гармонии.
У каждого из нас есть врожденное стремление к красоте. Природа, всегда, будет удивлять нас необыкновенными явлениями, такими как радуга, снег, капли дождя, цветы, растения, животные. Все это является предметом симметрии и гармонии. Если задуматься, то к симметрии можно отнести регулярность смены дня и ночи, времени года. Взгляните на мир и он поразит вас своей уникальностью и красотой.
Симметрия в природе.
Симметрию, по праву, можно назвать воплощением красоты и гармонии. Что же это такое? Симметрией называют закономерное расположение одинаковых частей, относительно оси или центра. С детства мы привыкаем к ней, потому что, очень многие предметы, которые нас окружают, являются ее воплощением.
Если внимательно посмотреть на природу, то можно заметить, что симметрия проявляет себя даже в мелких деталях. Она, несомненно, радует человеческий глаз, является вдохновением для многих писателей и художников. Помимо этого, она является отличным помощником для живых организмов и помогает им приспособиться к среде обитания.
Для растений характерной является симметрия конуса. Ярким примером послужит дерево. Среди цветов можно заметить радиальную симметрию. Зеркальная симметрия присуща листьям деревьев и некоторым цветочным растениям. Рассмотрим лист с дерева. У него строгая, закономерная форма. Две половинки зеркально расположены и являются симметричными. Зеркальную симметрию так же можно встретить среди цветов и плодов. Симметрия у животных понимается как соответствие размеров и форм. Зеркальная симметрия является самой характерной для животного мира. Ярким представителем данного вида является бабочка. Посмотрите на ее крылья:они расположены строго симметрично и поражают своей красотой.
Красивые примеры симметрии в природе.
Пчелы, однозначно, знают толк в точных науках. Во все времена люди удивлялись, насколько, совершенны формы в медовых сотах. Они создают настоящее произведение искусства. Подсолнухи, так же могут похвастаться уникальной симметрией, с которой мы знакомы как последовательностью Фибоначи. Брокколи романеско считается уникальным примером фрактальной симметрии, который имеет форму спирали. Даже снежинки образуются по законам порядка. Все они имеют разные узоры, но каждая из них обладает строгой симметрией. Паутина имеет радиальную симметрию. Ее нити расположены на одинаковом расстоянии друг от друга и образуют неповторимую форму. А, теперь, взгляните на себя: две руки и две ноги, располагаются симметрично туловища. Человек является ярким примером воплощением гармонии.
У каждого из нас есть врожденное стремление к красоте. Природа, всегда, будет удивлять нас необыкновенными явлениями, такими как радуга, снег, капли дождя, цветы, растения, животные. Все это является предметом симметрии и гармонии. Если задуматься, то к симметрии можно отнести регулярность смены дня и ночи, времени года. Взгляните на мир и он поразит вас своей уникальностью и красотой.
5 класс
Симметрия в природе

Популярные доклады
- Доклад-сообщение Планета Сатурн 2, 4, 5 класс кратко
Шестой планетой Солнечной системы принято считать Сатурн. Сияние этого небесного объекта смогли заметить древние жители, жившие на территории теперешнего Ирака. Немного позже ее разглядели и греки, давшие этой планете название Кронос,
- Доклад на тему Библия 4, 5, 8 класс сообщение
В мире множество различных религий. Самые распространенные из них: христианство, мусульманство, буддизм, конфуцианство. Библия – главная книга всех христиан. Она удивительна и невероятна по определению.
- Доклад-сообщение Пирамиды Древнего Египта 5 класс
Не найдется тех, кто ничего не слышал о пирамидах Древнего Египта. Это величественные, монументальные сооружения, созданные несколько тысячелетий назад. За столько лет не утихают споры об этих сооружениях, появляются новые мифы и теории относительно
more-dokladov.ru
Симметрия в природе
Симметрия в природе
Радионов М.А. 11МБОУ СОШ № 30
Хосонова Ф.Ю. 11МБОУ СОШ № 30
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Гуляя осенью в роще, я собрал красивые опавшие листья и принес их домой. Мой папа (Радионов А. А., научный сотрудник Южного математического института ВНЦ РАН), глядя на них, проронил фразу: вот ещё один пример симметрии в природе. Я заинтересовался и первым делом посмотрел в словаре С.И.Ожегова, что означает слово «симметрия», а потом стал приставать к отцу с расспросами: как он определил, что перед нами «симметрия» и каких видов бывает симметрия? Это и послужило поводом изучить этот вопрос.
Цель работы: показать, какие виды симметрии наблюдаются в природе, и как они описываются при помощи математики.
Моей задачей было:
— дать описание различных видов симметрии;
— попытаться самостоятельно найти математические соотношения в строении листьев деревьев.
Объект исследования: кленовые и виноградные листья.
Предмет исследования: симметрия в природных объектах.
Методы, используемые в работе: анализ литературы по теме, научный эксперимент.
Данная работа относится к реферативно-экспериментальной.
Значимость полученных результатов заключается в том, что листья растений могут быть изучены математически, измерены инструментально и симметричность этих природных объектов может быть проверена.
Симметрия в окружающей нас природе
Симметрия (древнегреческое – «соразмерность») – закономерное расположение подобных (одинаковых) частей тела или форм живого организма относительно центра или оси симметрии. При этом подразумевается, что соразмерность – часть гармонии, правильного сочетания частей целого [7].
Гармония – греческое слово, обозначающее «согласованность, соразмерность, единство частей и целого». Внешне гармония может проявляться в симметрии и пропорциональности.
Симметрия очень распространенное явление, ее всеобщность служит эффективным методом познания природы. В живой природе симметрия не абсолютна и всегда содержит некоторую степень асимметрии. Асимметрия – (греческое «без» и «симметрии») – отсутствие симметрии.
Внимательно рассматривая природные явления, можно увидеть общее даже в самых незначительных вещах и деталях, найти проявления симметрии. Форма листа дерева не является случайной: она строго закономерна. Листок как бы склеен из двух более или менее одинаковых половинок, одна из которых расположена зеркально относительно другой. Симметрия листка повторяется для всех листиков данного дерева. Это пример зеркальной симметрии – когда объект можно разделить на правую и левую или верхнюю и нижнюю половины воображаемой осью, называемой осью зеркальной симметрии. Находящиеся по разные стороны оси половинки почти идентичны друг другу. Зеркало в точности воспроизводит то, что оно «видит», но рассмотренный порядок является обращенным: правая рука у двойника в зеркале оказывается левой. Зеркальную симметрию можно обнаружить повсюду: в листьях и цветах растений. Более того, зеркальная симметрия присуща телам почти всех живых существ (Приложение №1, рис. а).
Многие цветы обладают радиальной симметрией: внешний вид узора не изменится, если его повернуть на некоторый угол вокруг его центра. Такая симметрия называется поворотной симметрией или осевой симметрией. При этой симметрии лист или цветок, поворачиваясь вокруг оси симметрии, переходит сам в себя. Если разрезать стебель растения или ствол дерева, то на срезе зачастую отчетливо видна радиальная симметрия в виде полосок (Приложение №1, рис. б).
Поворот на определенное число градусов, сопровождаемый увеличением размера вдоль оси поворота (или уменьшением размера или же без изменения размера), порождает винтовую симметрию – симметрию винтовой лестницы (Приложение №1, рис. в).
Симметрия подобия. Еще один вид симметрии – симметрия подобия, связанная с одновременным увеличением или уменьшением подобных частей фигуры и расстояний между ними. Такую симметрию демонстрируют все растущие организмы: маленький росток любого растения содержит все особенности зрелого растения. Симметрия подобия повсеместно проявляется в природе на всем, что растет: в растущих предметах растений, животных и кристаллов (Приложение №1, рис. г).
В математике самоподобные геометрические объекты называются фракталами [1,4-6]. Для фракталов характерно, что малая часть геометрической кривой подобна всей кривой. На рисунке представлен процесс построения самоподобных кривой Коха и снежинки Коха (первые 4 шага). (приложение №2)
Любой отрезок построенной таким образом кривой имеет бесконечную длину. Фракталы характеризуются фрактальной размерностью. Термин фрактал и фрактальная размерность были введены математиком Бенуа Мандельбротом в 1975 г [6]. Фрактальная размерность была введена как коэффициент, описывающий геометрически сложные формы, для которых детали являются более важными, чем полный рисунок.
Размерность 2 означает, что любую кривую мы можем однозначно определить двумя числами. Поверхность сферы двумерна (ее можно определить с помощью двух углов широты и долготы). Размерность определяется следующим образом: для одномерных объектов – увеличение в два раза их линейного размера приводит к увеличению размеров тоже в два раза. Для двумерных объектов увеличение в два раза линейных размеров приводит к увеличению размера (площадь прямоугольника) в четыре раза. Для 3-х мерных объектов увеличение линейных размеров в два раза приводит к увеличению объема в восемь раз.
Размерность D может быть определена математически с помощью правила:
где N –N число деталей, – коэффициент масштаба, D – размерность.
Отсюда для размерности получим формулу:
Возьмем отрезок, поделим его на три равные части (N = 3), каждая полученная часть будет длиной в 3 раза меньше (), чем длина начального отрезка:
следовательно для отрезка размерность равняется одному.
Аналогично для площади: если измерить площадь квадрата, а затем измерить площадь квадрата со стороной длинною от длины стороны начального квадрата, то она окажется в 9 раз меньше (N = 9) площади начального квадрата:
для плоской фигуры размерность равняется двум. Для пространственной фигуры, такой как куб, вычисленная размерность равняется трем.
Аналогичные вычисления для кривой Коха дают результат:
следовательно фракталам соответствует не целая, а дробная размерность.
Проведение научного эксперимента
Обоснование выбора:
В качестве экспериментального материала выбраны опавшие листья деревьев: клена и винограда на внешний вид симметричные (осевая, зеркальная симметрия).
Последовательность эксперимента:
— Измерение площади левой и правой частей листа;
— Измерение углов между прожилками на листе;
— Измерение длин прожилок, имеющихся на листе;
— Запись полученных результатов;
— Поиск математических закономерностей;
— Выводы по полученным результатам.
Список того, что надо изучить на листе дерева:
Симметрия;
Углы;
Фракталы;
Геометрическая прогрессия;
Логарифмы.
Рассмотрение опавших листьев показало, что листья симметричны относительно своей оси. Более подробное рассмотрение показывает, что симметрия незначительно нарушается на краях листа, а в некоторых случаях и внутри поверхности листа.
Чтобы убедиться, насколько левая и правая части листа одинаковы, были проведены следующие измерения:
1) измерение площади левой и правой частей листа;
2) измерение углов, под которым пересекаются прожилки в левой и правой частях листа;
3) измерение длины основных прожилок в левой и правой частях листа;
4) измерение длины вторичных прожилок в левой и правой частях листа;
5) измерение длины самых мелких прожилок листа.
Для удобства проведения измерений все листы были сначала отсканированы, а затем распечатаны на бумаге на черно-белом принтере с точным сохранением размеров и деталей изображения. На бумажном изображении листа и проводились измерения. Для измерения площади левой и правой частей листа на изображение дополнительно накладывалась сетка с шагом 5 мм. Площади левой или правой частей листа подсчитывались по количеству заполняемых листом маленьких квадратиков площадью 5×5 мм2. Некоторые квадратики оказывались частично заполненными: заполненные более половины учитывались при подсчете, а заполненные менее чем на половину не учитывались в подсчетах.
На фотографиях показан процесс проведения измерений (Приложение № 3).
Кленовый лист
1) измерение площади левой части показало 317 квадратиков по 25 мм2 или 79,25 квадратных сантиметров. Измерение правой части показало 312 квадратиков по 25 мм2 или 78 квадратных сантиметров. С учетом погрешности в точности измерений полученный результат говорит о том, что приблизительно площади левой и правой частей листа одинаковы (Приложение №4, рис. 1).
2) Определение углов, под которыми расходятся прожилки листа от его основания показывает, что эти углы приблизительно одинаковы и составляют около 25 градусов. В правой части листа при движении по часовой стрелки от середины листа, первая прожилка отстоит на 26 градусов, вторая — на 52 градуса, третья — на 74 градуса. А в левой части листа при движении против часовой стрелки от оси листа, первая прожилка отклоняется на 24 градуса, вторая — на 63 градуса, третья — на 80 градусов. На рисунке 2 Приложения №4 представлены эти измерения: видно, что при всей симметричности листа, наблюдаются некоторые незначительные нарушения симметрии.
3) Измерения длин прожилок. На рисунке вместе с углами отмечены измеренные длины основных прожилок. В тех случаях, когда прожилка листа оказывалась сильно искривленной, её длина измерялась по длине ломанной кривой: изогнутая прожилка делилась на три приблизительно одинаковые части и каждая часть измерялась как прямая — линейкой. Длина основных прожилок в правой части листа составила 30,2 см. В левой части листа — 30,6 см. Общая длина вместе с центральной прожилкой — 75 см.
Дополнительно, были измерены длины всех вторичных, малых прожилок листа, которые выходят не из основания листа. В левой части листа их суммарная длина равняется 52,6 см, а в правой части листа — 51.1 см. Общая длина составляет 103,7 см (Приложение №4, рис. 3).
Удивительно, но суммарная длина малых прожилок листа больше, чем длина главных прожилок листа. В левой части отношение этих длин равняется 1,72. В правой части — 1,69. Полученные отношения близки друг другу, но не равны в точности.
Виноградный лист
1) Измерение углов, под которыми расходятся прожилки листа винограда от его основания показывает, что эти углы приблизительно одинаковы и составляют около 40 градусов. В правой части листа таких прожилок две и при движении по часовой стрелки от середины листа, первая прожилка отстоит на 41 градус, вторая — на 86 градусов. В левой части листа при движении против часовой стрелки от оси листа, первая прожилка отклоняется на 41 градус, вторая — на 80 градусов. На рисунке 1 Приложения №5 представлены эти измерения. Здесь же отмечены длины основных прожилок листа.
Не менее интересно измерение углов, под которыми пересекаются вторичные прожилки (которые отходят не от центра основания листа). Эти измерения представлены на рисунке 2 Приложения №5: для вторичных прожилок листа наблюдается больший разброс значений углов, под которыми они пересекаются с другими прожилками, но в среднем этот угол составляет приблизительно 60 градусов. Этот средний угол одинаков как в левой части листа, так и в правой его части. Здесь же отмечены длины этих вторичных прожилок.
2) Измерение длин прожилок. Длина основных (исходящих из основания листа) в левой части листа равна 16 см. В правой части листа — 16,4 см. Длина с центральной прожилкой — 44,4 см.
Длина вторичных прожилок в левой части листа составляет 41,2 см, а правой части — 43 см. В сумме общая длина вторичных прожилок составляет 84,2 см. Для виноградного листа длина вторичных прожилок приблизительно в два раза больше, чем длина основных прожилок листа.
Для виноградного листа удается измерить и длину сетки самых мелких прожилок. Они отчетливо видны на задней поверхности листа. Измерения длин самых маленьких прожилок проводились при помощи подсчета их количества на половине расстояния между двумя вторичными прожилками, после чего найденное количество умножалось на их длину одной из них (приблизительно половина расстояния между двумя основными прожилками). При этом из подсчета могли выпадать мелкие прожилки, которые не соединяются с основными прожилками и находятся между более крупных прожилок.
Измеренная таким образом длина самых мелких прожилок в левой части листа составила 110,7 см, а в правой части листа — 133,9 см. Общая длина самых мелких прожилок — 244,6 см (Рис. 3, Приложение №5).
Удивительный вывод состоит в том, что чем меньше прожилки, тем больше их общая длина. В левой части листа отношение измеренных длин:
самые мелкие прожилки / вторичные прожилки = 110,7 / 41,2 = 2,69;
вторичные прожилки / основные прожилки = 41,2 / 16,0 = 2,57.
В правой части аналогичные отношения есть
133,9 / 43,0 = 3,11,
43,0 / 16,4 = 2,62.
Полученные отношения длин точнее для отношения вторичных к основным прожилкам, поскольку эти длины измеряются более точно. Для левой части отношение длины самых мелких прожилок к длине вторичных прожилок также дает приблизительно такое же значение около 2,7. Только в правой части листа это отношение заметно больше и равно 3,11.
Из измерения длин и углов пересечения прожилок можно сделать следующие выводы.
В левой и правой частях листа наблюдаются приблизительно одинаковые углы между основными и вторичными прожилками.
Также в левой и правой частях приблизительно одинаковы и длины основных и вторичных прожилок.
Отношение длин вторичных прожилок к длине основных прожилок приблизительно равно 2,6. Это означает, что при переходе от основных прожилок к вторичным — их длина увеличивается в 2,6 раза. Отношение длин самых мелких прожилок к длине вторичных прожилок равном 2,7 для левой части листа и 3,1 для правой части листа. Это означает, что при переходе от вторичных прожилок к самым мелким — их длина увеличивается в 2,7 раза (3,1 для правой части листа).
Найденная закономерность может объясняться фрактальной структурой листа: при переходе от крупного масштаба к более мелкому масштабу наблюдается приблизительно один коэффициент увеличения длины соответствующих прожилок.
Для углов пересечения прожилок разного масштаба говорить о фрактальной структуре нельзя. Основные прожилки пересекаются по углом в 40 градусов, вторичные — под углом в 60 градусов, а самые мелкие — приблизительно под углом 90 градусов.
Применим формулу фрактальной размерности для листа винограда.
для левой части листа:
количество основных: 2;
длина основных: 16,0 см;
количество вторичных: 12;
длина вторичных 41,2 см;
количество самых мелких прожилок: 407;
длина самых мелких прожилок 110,7 см;
1)
2)
3)
Вычисления фрактальной размерности для геометрического фрактала на этапах 2) и 3) должны дать близкие значения. Полученные цифры различаются более чем в два раза. Это говорит о том, что прожилки виноградного листа не образуют геометрического фрактала. Аналогичный вывод следует из сравнения углов, под которыми пересекаются прожилки разных уровней (40, 60, 90 градусов).
Заключение
В своей работе я на конкретном примере показал, что природные симметричные листья деревьев подчиняются математическим законам. Однако, даже с учетом погрешности измерений, исследованные мною листья не являются совершенно симметричными — в левой и правой частях листа найдены отличия, то есть в живой природе симметрия не абсолютна и всегда содержит некоторую степень асимметрии. Например, длина основных прожилок листа клена в левой части составляет 30,6 см, а в правой — 30,2 см. В процентном выражении это отличие составляет 1,3 %. Для виноградного листа такое же отличие составляет 2,5 %.
При переходе от большего масштаба прожилок листа к меньшему масштабу этих прожилок наблюдается приблизительно одинаковый коэффициент увеличения длин соответствующих прожилок. Этот коэффициент равняется 2,6 (для листа винограда) и сохраняется при переходе от самых крупных прожилок к более мелким, а от них — при переходе к самым мелким прожилкам.
Такое поведение прожилок не является фрактальной структурой виноградного листа: измерение фрактальной размерности дает различные значения для прожилок разного уровня. Наблюдающаяся сложная структура прожилок листьев образуется для снабжения водой и питательными веществами всей площади листа растения. По всей видимости, фрактальная структура прожилок листьев не всегда является наилучшей (оптимальной) формой для выполнения этой задачи растением.
Список использованной литературы:
Ссылки на монографии и учебные пособия
1.Пайтген Х.О., Рихтер П.Х., Красота фракталов. Образы комплексных динамических систем//Мир.- М., 1993 г., 206 с. ISBN 5-03-001296-6
2. Тарасов Л.В. Этот удивительно симметричный мир//Просвещение.-М.,1982-с.176
2. Ссылки на статьи из энциклопедий и словарей
3. Ожегов С.И. Словарь русского языка // Русский язык.-20-е изд. М.,1988-с.585
3. Ссылки на материалы интернет-ресурсов
4.Википедия, Фрактальная размерность. https://ru.wikipedia.org/wiki/Фрактальная_размерность
5. Фракталы вокруг нас. http://sakva.net/fractals_rus/
6. Ивановский А. Фрактальная геометрия мира. http://w-o-s.ru/article/4003
7. Симметрия в природе. http://wonwilworl.blogspot.ru/2014/01/blog-post.html
Приложение №1
Рис. а
Рис. б
Рис. в
Рис. г
Приложение № 2
Кривая Коха
Снежинки Коха
Приложение №3
Приложение №4
Рис. 1
Рис. 2
Рис. 3
Приложение №5
Рис. 1
Рис. 2
Рис. 3
Просмотров работы: 1292
school-science.ru
Wonder Wild World : Симметрия в природе
Симметрия (др.-греч. — «соразмерность») — закономерное расположение подобных (одинаковых) частей тела или форм живого организма, совокупности живых организмов относительно центра или оси симметрии. При этом подразумевается, что соразмерность – часть гармонии, правильного сочетания частей целого.
Совершенство — высшая степень, предел какого-либо положительного качества, способности, или мастерства.
Симметрия – основополагающий принцип устройства мира.
Симметрия – распространенное явление, ее всеобщность служит эффективным методом познания природы. Симметрия в природе нужна, чтобы сохранять устойчивость. Внутри внешней симметрии лежит внутренняя симметрия построения, гарантирующая равновесие.
Симметрия – проявление стремления материи к надежности и прочности.
Симметричные формы обеспечивают повторяемость удачных форм, поэтому более устойчивы к различным воздействиям. Симметрия многообразна.
В природе и, в частности, в живой природе симметрия не абсолютна и всегда содержит некоторую степень асимметрии. Асимметрия — (греч. α- — «без» и «симметрия») — отсутствие симметрии.
Симметрия, как и пропорция, почиталась необходимым условием гармонии и красоты.
Существует очень сложная многоуровневая классификация типов симметрий. Здесь мы не будем рассматривать эти сложности классификации, отметим лишь принципиальные положения и вспомним простейшие примеры.
На самом верхнем уровне различают три типа симметрии: структурную, динамическую и геометрическую. Каждый из этих типов симметрии на следующем уровне делится на классическую и неклассическую.
Ниже располагаются следующие иерархические уровни. Графическое изображение всех уровней подчинения даёт разветвлённую дендрограмму.
В быту мы чаще всего сталкиваемся с так называемой зеркальной симметрией. Это такое строение объектов, когда их можно разделить на правую и левую или верхнюю и нижнюю половины воображаемой осью, называемой осью зеркальной симметрии. При этом половины, находящиеся по разные стороны оси – идентичны друг другу.Отражение в плоскости симметрии. Отражение – это наиболее известная и чаще других встречающаяся в природе разновидность симметрии. Зеркало в точности воспроизводит то, что оно «видит», но рассмотренный порядок является обращенным: правая рука у вашего двойника в действительности окажется левой, так как пальцы расположены на ней в обратном порядке. Зеркальную симметрию можно обнаружить повсюду: в листьях и цветах растений. Более того, зеркальная симметрия присуща телам почти всех живых существ, и такое совпадение отнюдь не случайно. Зеркальной симметрией обладает все, допускающее разбиение на две зеркально равные половинки. Каждая из половинок служит зеркальным отражением другой, а разделяющая их плоскость называется плоскостью зеркального отражения, или просто зеркальной плоскостью.
Поворотная симметрия. Внешний вид узора не изменится, если его повернуть на некоторый угол вокруг оси. Симметрия, возникающая при этом, называется поворотной симметрией. Листья и цветы многих растений обнаруживают радиальную симметрию. Это такая симметрия, при которой лист или цветок, поворачиваясь вокруг оси симметрии, переходит в себя. На поперечных сечениях тканей, образующих корень или стебель растения, отчетливо бывает видна радиальная симметрия. Соцветия многих цветков также обладают радиальной симметрией.
Радиально-лучевой симметрией обладают цветы, грибы, деревья. Здесь можно отметить, что на не сорванных цветах и грибах, растущих деревьях плоскости симметрии ориентированы всегда вертикально. Определяя пространственную организацию живых организмов, прямой угол организует жизнь силами гравитации. Биосфера (пласт бытия живых существ) ортогональна вертикальной линии земного тяготения. Вертикальные стебли растений, стволы деревьев, горизонтальные поверхности водных пространств и в целом земная кора составляют прямой угол. Прямой угол, лежащий в основе треугольника, правит пространством симметрии подобий, а подобие, как уже говорилось, – есть цель жизни. И сама природа, и первородная часть человека находятся во власти геометрии, подчинены симметрии и как сущности, и как символы. Как бы ни были выстроены объекты природы, каждый имеет свой основной признак, который отображен формой, будь то яблоко, зерно ржи или человек.
Примеры радиальной симметрии.

Простейший вид симметрии зеркальная (осевая), возникающая при вращении фигуры вокруг оси симметрии.
В природе зеркальная симметрия характерна для растений и животных, которые произрастают или двигаются параллельно поверхности Земли. Например, крылья и туловище бабочки можно назвать эталоном зеркальной симметрии.




Осевая симметрия это результат поворота абсолютно одинаковых элементов вокруг общего центра. При этом они могут располагаться под любым углом и с различной частотой. Главное, чтобы элементы вращались вокруг единого центра. В природе, примеры осевой симметрии чаще всего можно найти среди растений и животных, которые растут или перемещаются перпендикулярно к поверхности Земли.
 |
| Симметрия, возникающая при вращении фигуры вокруг центра вращения, называется центральной. |

Также существует винтовая симметрия. Трансляцию можно комбинировать с отражением или поворотом, при этом возникают новые операции симметрии.
Поворот на определенное число градусов, сопровождаемый трансляцией на расстояние вдоль оси поворота, порождает винтовую симметрию — симметрию винтовой лестницы.
Пример винтовой симметрии – расположение листьев на стебле многих растений.
Если рассматривать расположение листьев на ветке дерева мы заметим, что лист отстоит от другого, но и повернут вокруг оси ствола.
Листья располагаются на стволе по винтовой линии, чтобы не заслонять друг от друга солнечный свет. Головка подсолнечника имеет отростки, расположенные по геометрическим спиралям, раскручивающимся от центра наружу. Самые молодые члены спирали находятся в центре. В таких системах можно заметить два семейства спиралей, раскручивающихся в противоположные стороны и пересекающихся под углами, близкими к прямым.Но какими бы интересными и привлекательными ни были проявления симметрии в мире растений, там еще много тайн, управляющих процессами развития. Вслед за Гете, который говорил о стремлении природы к спирали, можно предположить, что движение это осуществляется по логарифмической спирали, начиная всякий раз с центральной, неподвижной точки и сочетая поступательное движение (растяжение) с поворотом вращения.

На основании этого можно сформулировать в несколько упрощенном и схематизированном виде (из двух пунктов) общий закон симметрии, ярко и повсеместно проявляющийся в природе:
1. Все, что растет или движется по вертикали, т.е. вверх или вниз относительно земной поверхности, подчиняется радиально-лучевой симметрии в виде веера пересекающихся плоскостей симметрии. Листья и цветы многих растений обнаруживают радиальную симметрию. Это такая симметрия, при которой лист или цветок, поворачиваясь вокруг оси симметрии, переходит в себя. На поперечных сечениях тканей, образующих корень или стебель растения, отчетливо бывает видна радиальная симметрия. Соцветия многих цветков также обладают радиальной симметрией.
2. Все то, что растет и движется горизонтально или наклонно по отношению к земной поверхности, подчиняется билатеральной симметрии, симметрии листка.
Этому всеобщему закону из двух постулатов подчиняются не только цветы, животные, легкоподвижные жидкости и газы, но и твердые, неподатливые камни. Этот закон влияет на изменчивые формы облаков. В безветренный день они имеют куполовидную форму с более или менее ясно выраженной радиально-лучевой симметрией. Влияние универсального закона симметрии является по сути дела чисто внешним, грубым, налагающим свою печать только на наружную форму природных тел. Внутреннее их строение и детали ускользают из-под его власти. Симметрия основана на подобии. Она означает такое соотношение между элементами, фигурами, когда они повторяют и уравновешивают друг друга.Симметрия подобия. Еще один тип симметрии — симметрия подобия, связанная с одновременным увеличением или уменьшением подобных частей фигуры и расстояний между ними. Примером такого рода симметрии служит матрешка. Очень широко распространена такая симметрия в живой природе. Ее демонстрируют все растущие организмы.
Основой эволюции живой материи является симметрия подобия. Рассмотрим цветок розы или кочан капусты. Важную роль в геометрии всех этих природных тел играет подобие их сходных частей. Такие части, конечно, связаны между собой каким-то общим, еще не известным нам геометрическим законом, позволяющим выводить их друг из друга. Симметрия подобия, осуществляющаяся в пространстве и во времени, повсеместно проявляется в природе на всем, что растет. А ведь именно к растущим формам относятся бесчисленные фигуры растений, животных и кристаллов. Форма древесного ствола – коническая, сильно вытянутая. Ветви обычно располагаются вокруг ствола по винтовой линии. Это не простая винтовая линия: она постепенно сужается к вершине. Да и сами ветви уменьшаются по мере приближения к вершине дерева. Следовательно, здесь мы имеем дело с винтовой осью симметрии подобия.
Живая природа в любых ее проявлениях обнаруживает одну и ту же цель, один и тот же смысл жизни: всякий живой предмет повторяет себя в себе подобном. Главной задачей жизни является жизнь, а доступная форма бытия заключается в существовании отдельных целостных организмов. И не только примитивные организации, но и сложные космические системы, такие как человек, демонстрируют поразительную способность буквально повторять из поколения в поколение одни и те же формы, одни и те же скульптуры, черты характера, те же жесты, манеры.
Природа обнаруживает подобие как свою глобальную генетическую программу. Ключ в изменении тоже заключается в подобии. Подобие правит живой природой в целом. Геометрическое подобие – общий принцип пространственной организации живых структур. Лист клена подобен листу клена, березы – листу березы. Геометрическое подобие пронизывает все ветви древа жизни. Какие бы метаморфозы ни претерпевала в процессе роста в дальнейшем живая клетка, принадлежащая целостному организму и выполняющая функцию его воспроизведения в новый, особенный, единичный объект бытия, она является точкой «начала», которая в итоге деления окажется преобразована в объект, подобный первоначальному. Этим объединяются все виды живых структур, по этой причине и существуют стереотипы жизни: человек, кошка, стрекоза, дождевой червь. Они бесконечно интерпретируются и варьируются механизмами деления, но остаются теми же стереотипами организации, формы и поведения.

Для живых организмов симметричное расположение частей органов тела помогает сохранять им равновесие при передвижении и функционировании, обеспечивает их жизнестойкость и лучшее приспособление к окружающему миру, что справедливо и в растительном мире. Например, ствол ели или сосны чаще всего прямой и ветви равномерно расположены относительно ствола. Дерево, развиваясь в условиях действия силы тяжести, достигает устойчивого положения. К вершине дерева ветви его становятся меньше в размерах – оно приобретает форму конуса, поскольку на нижние ветви, как и на верхние, должен падать свет. Кроме того, центр тяжести должен быть как можно ниже, от этого зависит устойчивость дерева. Законы естественного отбора и всемирного тяготения способствовали тому, что дерево не только эстетически красиво, но устроено целесообразно.
Получается, что симметрия живых организмов связана с симметрией законов природы. На житейском уровне, когда мы видим проявление симметрии в живой и неживой природе, то невольно испытываем чувство удовлетворения тем всеобщим, как нам кажется, порядком, который царит в природе.
По мере упорядочения живых организмов, их усложнения в ходе развития жизни асимметрия все больше и больше превалирует над симметрией, вытесняя ее из биохимических и физиологических процессов. Однако и здесь имеет место динамический процесс: симметрия и асимметрия в функционировании живых организмов тесно связаны. Внешне человек и животные симметричны, однако их внутреннее строение существенно асимметрично. Если у низших биологических объектов, например низших растений, размножение идет симметрично, то у высших имеет место явная асимметрия, например разделение полов, где каждый пол вносит в процесс самовоспроизведения свойственную только ему генетическую информацию. Так, устойчивое сохранение наследственности есть проявление в известном смысле симметрии, а в изменчивости проявляется асимметрия. В целом же глубокая внутренняя связь симметрии и асимметрии в живой природе обусловливает ее возникновение, существование и развитие.
Вселенная есть асимметричное целое, и жизнь в таком виде, в каком она представляется, должна быть функцией асимметрии Вселенной и вытекающих отсюда следствий. В отличие от молекул неживой природы молекулы органических веществ имеют ярко выраженный асимметричный характер (хиральность). Придавая большое значение асимметрии живого вещества, Пастер считал ее именно той единственной, четко разграничивающей линией, которую в настоящее время можно провести между живой и неживой природой, т.е. тем, что отличает живое вещество от неживого. Современная наука доказала, что в живых организмах, как и в кристаллах, изменениям в строении отвечают изменения свойств.
В общем смысле мы можем считать, что возникновение жизни в целом связано со спонтанным нарушением имевшейся до того в природе зеркальной симметрии.
Предполагают, что возникшая асимметрия произошла скачком в результате Большого Биологического Взрыва (по аналогии с Большим Взрывом, в результате которого образовалась Вселенная) под действием радиации, температуры, электромагнитных полей и т.д. и нашла свое отражение в генах живых организмов. Этот процесс, по существу, также является процессом самоорганизации. Источникwonwilworl.blogspot.com
Научно-исследовательская работа по теме «Симметрия в природе»
Муниципальное казенное общеобразовательное учреждение
Большевистская средняя общеобразовательная школа
НАУЧНО — ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
по теме:
«Симметрия в природе»
Выполнила: Берсенева Виктория Владимировна — ученица 9 класса Большевистской СОШ
Руководитель: Фаляхова Людмила Леонидовна – учитель математики
с. Сарапулка, 2015
Содержание
Введение…………………………………………………………………………..3
Раздел I. Симметрия в математике………………………………………………4
Глава 1. Центральная симметрия………………………………………………..5
Глава 2. Осевая симметрия………………………………………………………7
Глава 4. Зеркальная симметрия…………………………………………………8
Раздел II. Симметрия в живой природе……………………………………… 11
Глава 1. Симметрия в живой природе. Асимметрия и симметрия……… 11
Глава 2. Симметрия растений…………………………………………………14
Глава 3. Симметрия животных………………………………………………….16
Глава 4. Человек – существо симметричное……………………………………18
Заключение……………………………………………………………………….21
Литература……………………………………………………………………….22
2
«Природа формулирует свои законы
языком математики…»
Галилео Галилей
Введение
Я люблю свое село Сарапулку, протекающую реку Иня. С удовольствием фотографирую растения , животных, всю природу в окрестностях села. После изучения темы в геометрии «Осевая и центральная симметрия» я обратила внимание, что на фотографиях цветы растения животные симметричны и решила исследовать и узнать принципы симметрии, её виды, разнообразие её в живой и неживой природе.
Под симметрией (от греч. symmetria — соразмерность) в широком смысле понимают правильность в строении тела и фигуры. Учение о симметрии представляет собой большую и важную ветвь тесно связанную с науками разных отраслей. С симметрией мы часто встречаемся в искусстве, архитектуре, технике, быту. Так, фасады многих зданий обладают осевой симметрией. В большинстве случаев симметричны относительно оси или центра узоры на коврах, тканях, комнатных обоях. Симметричны многие детали механизмов, например, зубчатые колеса.
Было интересно, потому что данная тема затрагивает не только математику, хотя она и лежит в её основе, но и другие области науки, техники, природы. Симметрия, как мне кажется, является фундаментом природы, представление о котором слагалось в течение десятков, сотен, тысяч поколений людей. Я обратила внимание на то, что во многих вещах, в основе красоты многих форм, созданных природой, составляет симметрия, точнее, все её виды — от простейших, до самых сложных. Можно говорить о симметрии, как о гармонии пропорций, как о «соразмерности», регулярности и упорядоченности.
3
Нам это важно, потому что для многих людей математика – скучная и сложная наука, но для меня математика – не только цифры, уравнения и решения, но и красота в строении геометрических тел, живых организмов и даже является фундаментом для многих наук.
Цели исследовательской работы:
раскрыть особенности видов симметрии в природе;
показать всю привлекательность математики, как науки и её взаимосвязь с природой в целом.
Задачи:
подбор материала по симметрии, исследование и его обработка данных;
Систематизация и обобщение собранного материала;
выводы о проделанной работе;
оформление обобщенного материала.
4.
Раздел I. Симметрия в математике
Глава 1. Центральная симметрия
Понятие центральной симметрии следующее: «Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О, называется центром симметрии фигуры». Поэтому говорят, что фигура обладает центральной симметрией.
Понятия центра симметрии в «Началах» Евклида нет, однако в 38-ом предложении XI книги содержится понятие пространственной оси симметрии. Впервые понятие центра симметрии встречается в XVI в. В одной из теорем Клавиуса, гласящей: «если параллелепипед рассекается плоскостью, проходящей через центр, то он разбивается пополам и, наоборот, если параллелепипед рассекается пополам, то плоскость проходит через центр». Лежандр, который впервые ввёл в элементарную геометрию элементы учения о симметрии, показывает, что у прямого параллелепипеда имеются 3 плоскости симметрии, перпендикулярные к ребрам, а у куба 9 плоскостей симметрии, из которых 3 перпендикулярны к рёбрам, а другие 6 проходят через диагонали граней.

Евклид Симметрия в архитектуре Лежандр
5
Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм. Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма – точка пересечения его диагоналей. Любая прямая также обладает центральной симметрией. Однако, в отличие от окружности и параллелограмма, которые имеют только один центр симметрии, у прямой их бесконечно много – любая точка прямой является её центром симметрии. Примером фигуры, не имеющей центра симметрии, является произвольный треугольник.
В алгебре при изучении чётных и нечётных функций рассматриваются их графики. График чётной функции при построении симметричен относительно оси ординат, а график нечётной функции – относительно начала координат, т.е. точки О. Значит, нечётная функция обладает центральной симметрией, а чётная функция – осевой.
Таким образом, две центрально симметричные плоские фигуры всегда можно наложить друг на друга, не выводя их из общей плоскости. Для этого достаточно одну из них повернуть на угол 180° около центра симметрии. Как в случае зеркальной, так и в случае центральной симметрии плоская фигура непременно имеет ось симметрии второго порядка, но в первом случае эта ось лежит в плоскости фигуры, а во втором – перпендикулярна к этой плоскости. 6.
Глава 2. Осевая симметрия
Понятие осевой симметрии представлено следующим образом: «Фигура называется симметричной относительно прямой m, если для каждой точки фигуры симметричная ей точка относительно прямой, m также принадлежит этой фигуре. Прямая m, называется осью симметрии фигуры». Тогда говорят, что фигура обладает осевой симметрией
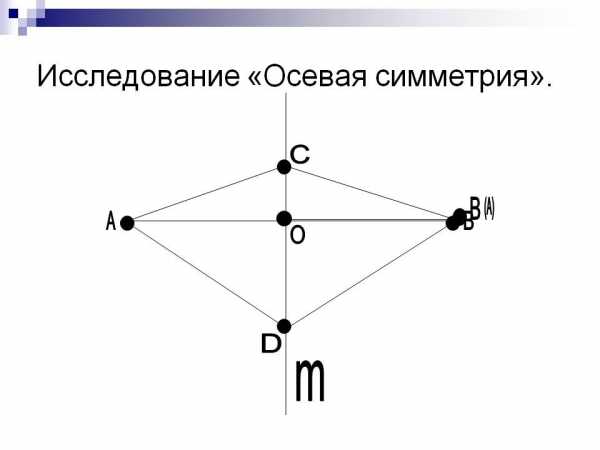
В более узком смысле осью симметрии называют ось симметрии второго порядка и говорят об «осевой симметрии», которую можно определить так: фигура (или тело) обладает осевой симметрией относительно некоторой оси, если каждой её точке С, соответствует такая принадлежащая этой же фигуре точка Д, что отрезок АВ перпендикулярен к оси, пересекает её и в точке пересечения делится пополам. Рассмотренная выше пара треугольников обладает (кроме центральной) еще осевой симметрией. Её ось симметрии проходит через точку О перпендикулярно к плоскости чертежа.
Приведём примеры фигур, обладающих осевой симметрией. У неразвернутого угла одна ось симметрии — прямая, на которой расположена биссектриса угла.
7.
Равнобедренный (но не равносторонний) треугольник имеет также одну ось симметрии, а равносторонний треугольник— три оси симметрии. Прямоугольник и ромб, не являющиеся квадратами, имеют по
две оси симметрии, а квадрат— четыре оси симметрии. У окружности их бесконечно много — любая прямая, проходящая через её центр, является осью симметрии.
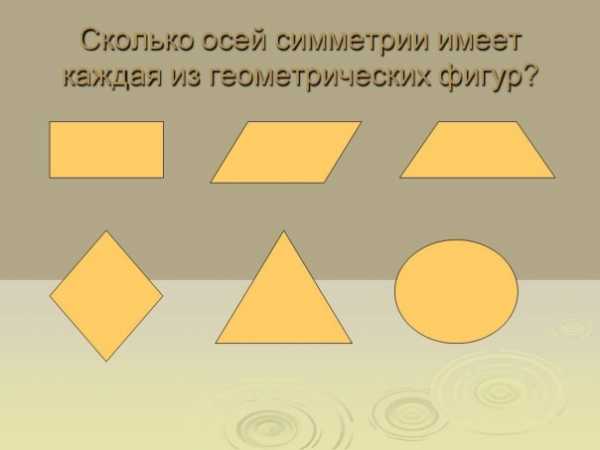
Имеются фигуры, у которых нет ни одной оси симметрии. К таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник.
Глава 3. Зеркальная симметрия
Зеркальная симметрия хорошо знакома каждому человеку из повседневного наблюдения. Как показывает само название, зеркальная симметрия связывает любой предмет и его отражение в плоском зеркале. Говорят, что одна фигура (или тело) зеркально симметрично другой, если вместе они образуют зеркально симметричную фигуру (или тело).
Я очень люблю фотографировать природу. Наше село расположено вдоль реки Иня. И когда весной разливается река, то на дальних лугах можно увидеть красивую картину, когда в воде отражаются: облака, лес, трава.
8

О нашей природе пишут стихи, рассказы. Одним из воспевателей был Анатолий Перович Бондарев. Он родился в Сарапулке, жил, рос. Много стихов написал, некоторые впоследствии стали песнями.


Дальние луга залитые водой Отражение заката в пруду


Река Иня Сельский пруд вблизи с. Сарапулка
Песня о родном селе
Сарапулка моя- Солнце пламенем жжет
Дорогое село, А река холодит,
Радость, горе, нужда- И пчела на цветок
Все быльем поросло. За пыльцою летит.
Я пою о селе, Окунусь с головой
Где родился и рос, В рябь лазури –реки,
Где мужал и взрослел, Полетят над волною
Где ходил на покос. Брызги , как мотельки
Запах свежей травы И на дальних лугах
На покосе полей, Как в перине посплю,
Звонкий смех детворы И в лесных родниках
У седых тополей Жажду я утолю.
Игрокам в бильярд издавна знакомо действие отражения. Их «зеркала» — это борта игрового поля, а роль луча света исполняют траектории шаров. Ударившись о борт возле угла, шар катится к стороне, расположенной под прямым углом, и, отразившись от неё, движется обратно параллельно направлению первого удара.
Важно отметить, что два симметричных друг другу тела не могут быть вложены или наложены друг на друга. Так перчатку правой руки нельзя надеть на левую руку. Симметрично зеркальные фигуры при всём своём сходстве существенно отличаются друг от друга. Чтобы убедиться в этом, достаточно поднести лист бумаги к зеркалу и попытаться прочесть несколько слов, напечатанных на ней, буквы и слова просто-напросто будут перевёрнуты справа налево. По этой причине симметричные предметы нельзя называть равными, поэтому их называют зеркально равными.
Две зеркально симметричные плоские фигуры всегда можно наложить
друг на друга. Однако для этого необходимо вывести одну из них (или обе) из их общей плоскости. Вообще зеркально равными телами (или фигурами) называются тела (или фигуры) в том случае, если при надлежащем их смещении они могут образовать две половины зеркально симметричного тела (или фигуры).
Раздел II. Симметрия в живой природе
Глава 1. Симметрия в живой природе. Асимметрия и симметрия
Симметрией обладают объекты и явления живой природы. Она не только радует глаз и вдохновляет поэтов всех времен и народов, а позволяет живым организмам лучше приспособиться к среде обитания и просто выжить.
В живой природе огромное большинство живых организмов обнаруживает различные виды симметрии (формы, подобия, относительного расположения). Причем организмы разного анатомического строения могут иметь один и тот же тип внешней симметрии.
Внешняя симметрия может выступить в качестве основания классификации организмов (сферическая, радиальная, осевая и т.д.) Микроорганизмы, живущие в условиях слабого воздействия гравитации, имеют ярко выраженную симметрию формы.
Асимметрия присутствует уже на уровне элементарных частиц и проявляется в абсолютном преобладании в нашей Вселенной частиц над античастицами. Известный физик Ф. Дайсон писал: «Открытия последних десятилетий в области физики элементарных частиц заставляют нас обратить особое внимание на концепцию нарушения симметрии. Развитие Вселенной с момента ее зарождения выглядит как непрерывная последовательность нарушений симметрии. В момент своего возникновения при грандиозном взрыве Вселенная была симметрична и однородна. По мере остывания в ней нарушается одна симметрия за другой, что создает возможности для существования все большего и большего разнообразия структур. Феномен жизни естественно вписывается в эту картину. Жизнь — это тоже нарушение симметрии»
Молекулярная асимметрия открыта Л. Пастером, который первым выделил «правые» и «левые» молекулы винной кислоты: правые молекулы похожи на правый винт, а левые — на левый. Такие молекулы химики называют стереоизомерами.
Молекулы стереоизомеры имеют одинаковый атомный состав, одинаковые размеры, одинаковую структуру — в то же время они различимы, поскольку являются зеркально асимметричными, т.е. объект оказывается нетождественным со своим зеркальным двойником. Поэтому здесь понятия «правый-левый» — условны.
В настоящее время хорошо известно, что молекулы органических веществ, составляющие основу живой материи, имеют асимметричный характер, т.е. в состав живого вещества они входят только либо как правые, либо как левые молекулы. Таким образом, каждое вещество может входить в состав живой материи только в том случае, если оно обладает вполне определенным типом симметрии. Например, молекулы всех аминокислот в любом .живом организме могут быть только левыми, сахара ~ только правыми. Это свойство живого вещества и его продуктов жизнедеятельности называют дисимметрией. Оно имеет совершенно фундаментальный характер. Хотя правые и левые молекулы неразличимы по химическим свойствам, живая материя их не только различает, но и делает выбор. Она отбраковывает и не использует молекулы, не обладающие нужной ей структурой. Как это происходит, пока не ясно. Молекулы противоположной симметрии для нее яд.
Если бы живое существо оказалось в условиях, когда вся пища была бы составлена из молекул противоположной симметрии, не отвечающей дисимметрии этого организма, то оно погибло бы от голода. В неживом веществе правых и левых молекул поровну. Дисимметрия — единственное свойство, благодаря которому мы можем отличить вещество биогенного происхождения от неживого вещества. Мы не можем ответить на вопрос, что такое жизнь, но имеем способ отличить живое от неживого. Таким образом, асимметрию можно рассматривать как разграничительную линию между живой и неживой природой. Для неживой материи характерно преобладание симметрии, при переходе от неживой к живой материи уже на микроуровне преобладает асимметрия. В живой природе асимметрию можно увидеть всюду. Очень удачно это подметил в романе «Жизнь и судьба» В. Гроссман: «В большом миллионе русских деревенских изб, нет и не может быть двух неразличимо схожих. Все живое — неповторимо.
Симметрия лежит в основе вещей и явлений, выражая нечто общее, свойственное разным объектам, тогда как асимметрия связана с индивидуальным воплощением этого общего в конкретном объекте. На принципе симметрии основан метод аналогий, предполагающий отыскание общих свойств в различных объектах. На основе аналогий создаются физические модели различных объектов и явлений. Аналогии между процессами позволяют описывать их общими уравнениями.
Глава 2. Симметрия растений
Изображения на плоскости многих предметов окружающего нас мира имеют ось симметрии или центр симметрии. Многие листья деревьев и лепестки цветов симметричны относительно среднего стебля.


Среди цветов наблюдаются поворотные симметрии разных порядков. Многие цветы обладают характерным свойством: цветок можно повернуть так, что каждый лепесток займёт положение соседнего, цветок же совместится с самим собой. Такой цветок обладает осью симметрии. Минимальный угол, на который нужно повернуть цветок вокруг оси симметрии, чтобы он совместился с самим собой, называется элементарным углом поворота оси. Этот угол для различных цветов не одинаков. Для ириса он равен 120є, для колокольчика – 72є, для нарцисса – 60є . Поворотную ось можно характеризовать и с помощью другой величины, называемой порядком оси и показывающей, сколько раз произойдет совмещение при 

повороте на 360є. Те же цветы ириса, колокольчика и нарцисса обладают осями третьего, пятого и шестого порядков соответственно.
Особенно часто среди цветов встречается симметрия пятого порядка. Это такие полевые цветы как колокольчик, незабудка, зверобой, лапчатка гусиная и др.; цветы плодовых деревьев – вишня, яблоня, груша, мандарин и др., цветы плодово-ягодных растений – земляника, ежевика, малина, шиповник; садовые цветы – настурция, флокс и др.


В пространстве существуют тела, обладающие винтовой симметрией, т. е. совмещающиеся со своим первоначальным положением после поворота на угол вокруг оси, дополненного сдвигом вдоль той же оси.
Винтовая симметрия наблюдается в расположении листьев на стеблях большинства растений. Располагаясь винтом по стеблю, листья как бы раскидываются во все стороны и не заслоняют друг друга от света, крайне необходимого для жизни растений. Это интересное ботаническое явление носит название филлотаксиса, что буквально означает строение листа. Другим проявлением филлотаксиса оказывается устройство соцветия подсолнечника или чешуи еловой шишки, в которой чешуйки располагаются в виде спиралей и винтовых линий. Такое расположение особенно четко видно у ананаса, имеющего более или менее шестиугольные ячейки, которые образуют ряды, идущие в различных направлениях.


Глава 3. Симметрия животных
Внимательное наблюдение обнаруживает, что основу красоты многих форм, созданных природой, составляет симметрия, точнее, все её виды – от простейших до самых сложных. Симметрия в строение животных – почти общее явление, хотя почти всегда встречаются исключения из общего правила.
Под симметрией у животных понимают соответствие в размерах, форме и очертаниях, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии. Строение тела многих многоклеточных организмов отражает определённые формы симметрии, такие как радиальную (лучевая) или билатеральную (двусторонняя), которые являются основными типами симметрии. Кстати, склонность к регенерации (восстановление) зависит от типа симметрии животного.


В биологии о радиальной симметрии идёт речь, когда через трёхмерное существо проходят две или более плоскости симметрии. Эти плоскости пересекаются в прямой. Если животное будет вращаться вокруг этой оси на определённый градус, то оно будет отображаться само на себе. В двухмерной проекции радиальная симметрия может сохраняться, если ось симметрии направлена перпендикулярно к проекционной плоскости. Иными словами, сохранение радиальной симметрии зависит от угла наблюдения.
При радиальной или лучистой симметрии тело имеет форму короткого или длинного цилиндра либо сосуда с центральной осью, от которого отходят в радиальном порядке части тела. Среди них встречается так называемая пентасимметрия, базирующаяся на пяти плоскостях симметрии.
Радиальная симметрия характерна для многих стрекающих, а также для большинства иглокожих, кишечнополостных. Взрослые формы иглокожих приближаются к радиальной симметрии, в то время как их личинки билатерально симметричны.
Лучевую симметрию мы также видим у медуз, кораллов, актиний, морских звёзд. Если вращать их вокруг собственной оси, они несколько раз «совместятся сами с собой». Если отрезать у морской звезды любое из пяти щупалец, оно сумеет восстановить всю звезду. От радиальной симметрии различаются двулучевая радиальная симметрия (две плоскости симметрии, к примеру, гребневики), а также билатеральная симметрия (одна плоскость симметрии, к примеру, двусторонне-симметричные).
При билатеральной симметрии осей симметрии три, но симметричных сторон только одна пара. Потому что две другие стороны – брюшная и спинная – друг на друга не похожи. Этот вид симметрии характерен для большинства животных, в том числе насекомых, рыб, земноводных, рептилий, птиц, млекопитающих. Например, черви, членистоногие, позвоночные. У большинства многоклеточных (у человека в том числе) другой тип симметрии – двусторонняя. Левая половина их тела — это как бы «отражённая в зеркале правая». Этот принцип, однако, не относится к отдельным внутренним органам, что демонстрирует, например, расположение печени или сердца у человека. Плоский червь планария имеет двустороннюю симметрию. Если разрезать его вдоль оси тела или поперёк, из обеих половинок вырастут новые черви. Если же измельчить планарию как-нибудь иначе — скорее всего ничего не выйдет.
Можно сказать также, что каждое животное (будь то насекомое, рыба или птица) состоит из двух энантиоморфов – правой и левой половин. Энантиоморфы – пара зеркально асимметричных объектов (фигур), являющихся зеркальным изображением один другого (например, пара перчаток). Иными словами – это объект и его зазеркальный двойник при условии, что сам объект зеркально асимметричен.
Сферическая симметрия имеет место у радиолярий и солнечников, тело которых сферической формы, а его части распределены вокруг центра сферы и отходят от неё. У таких организмов нет ни передней, ни задней, ни боковых частей тела, любая плоскость, проведённая через центр, делит животное на одинаковые половинки.
Губки и пластинчатые не проявляют симметрию.
Глава 4. Человек — существо симметричное
Не станем пока разбираться, существует ли на самом деле абсолютно симметричный человек. У каждого, разумеется, обнаружится родинка, прядь волос или какая-нибудь другая деталь, нарушающая внешнюю симметрию. Левый глаз никогда не бывает в точности таким, как правый, да и уголки рта находятся на разной высоте, во всяком случае, у большинства людей. И всё же это лишь мелкие несоответствия. Никто не усомнится, что внешне человек построен симметрично: левой руке всегда соответствует правая и обе руки совершенно одинаковы! НО! Здесь стоит остановиться. Если бы наши руки и в самом деле были совершенно одинаковы, мы могли бы в любой момент поменять их. Было бы возможно, скажем, путем трансплантации пересадить левую ладонь на правую руку, или, проще, левая перчатка подходила бы тогда к правой руке, но на самом деле это не так. Каждому известно, что сходство между нашими руками, ушами, глазами и другими частями тела такое же, как между предметом и его отражением в зеркале. Многие художники обращали пристальное внимание на симметрию и пропорции человеческого тела, во всяком случае, до тех пор, пока ими руководило желание в своих произведениях как можно точнее следовать природе.
Известны каноны пропорций, составленные Альбрехтом Дюрером и Леонардо да Винчи. Согласно этим канонам, человеческое тело не только симметрично, но и пропорционально. Леонардо открыл, что тело вписывается в круг и в квадрат. Дюрер занимался поисками единой меры, которая находилась бы в определенном соотношении с длиной туловища или ноги (такой мерой он считал длину руки до локтя). В современных школах живописи в качестве единой меры чаще всего принимается размер головы по вертикали. С известным допущением можно считать, что длина туловища превосходит размер головы в восемь раз. На первый взгляд это кажется странным. Но нельзя забывать, что большинство высоких людей отличаются удлинённым черепом и, наоборот, редко можно встретить низкорослого толстяка с головой удлинённой формы. Размеру головы пропорциональна не только длина туловища, но и размеры других частей тела. По этому принципу построены все люди, оттого-то мы, в общем, похожи друг на друга. Однако наши пропорции согласуются лишь приблизительно, а потому люди лишь похожи, но не одинаковы. Во всяком случае, все мы симметричны! К тому же некоторые художники в своих произведениях особенно подчёркивают эту симметрию. И в одежде человек тоже, как правило, старается поддерживать впечатление симметричности: правый рукав соответствует левому, правая штанина — левой. Пуговицы на куртке и на рубашке сидят ровно посередине, а если и отступают от нее, то на симметричные расстояния. Но на фоне этой общей симметрии в мелких деталях мы умышленно допускаем асимметрию, например, расчесывая волосы на косой пробор — слева или справа или делая асимметричную стрижку. Или, скажем, помещая на костюме асимметричный кармашек на груди. Или, надев кольцо на безымянный палец только одной руки. Лишь на одной стороне груди носятся ордена и значки (чаще на левой). Полная безукоризненная симметрия выглядела бы нестерпимо скучно. Именно небольшие отклонения от неё и придают характерные, индивидуальные черты.И вместе с тем порой человек старается подчеркнуть, усилить различие между левым и правым. В средние века мужчины одно время щеголяли в панталонах со штанинами разных цветов (например, одной красной, а другой черной или белой). В не столь отдалённые дни были популярны джинсы с яркими заплатами или цветными разводами. Но подобная мода всегда недолговечна. Лишь тактичные, скромные отклонения от симметрии остаются на долгие времена.
Заключение
С симметрией мы встречаемся везде ~ в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии. Существует множество видов симметрии как в растительном, так и в животном мире, но при всем многообразии живых организмов, принцип симметрии действует всегда, и этот факт еще раз подчеркивает гармоничность нашего мира.
Еще одним интересным проявлением симметрии являются биологические ритмы (биоритмы), циклические колебания биологических процессов и их характеристик (сокращения сердца, дыхание, колебания интенсивности деления клеток, обмена веществ, двигательной активности, численности растений и животных), зачастую связанные с приспособлением организмов к геофизическим циклам. Исследованием биоритмов занимается особая наука — хронобиология. Помимо симметрии, существует также понятие ассиметрии. Симметрия лежит в основе вещей и явлений, выражая нечто общее, свойственное разным объектам, тогда как асимметрия связана с индивидуальным воплощением этого общего в конкретном объекте.
Литература
1.Урманцев Ю. А. “Симметрия природы и природа симметрии”.
Москва, Мысль, 1974г..
2. А.П. Бондырев « Под небом Сарапулки»
2. http://www.worldnatures.ru
3. http://otherreferats
4. http://ru.wikipedia.org
infourok.ru
Симметрия в природе
Симметрия в природе является объективным свойством, одним из основных в современном естествознании. Это универсальная и общая характеристика нашего материального мира.
Симметрия в природе – это понятие, которое отражает существующий в мире порядок, соразмерность и пропорциональность между элементами различных систем или объектов природы, равновесие системы, упорядоченность, устойчивость, то есть определенный элемент гармонии.
Симметрия и асимметрия – понятия противоположные. Последнее отражает разупорядочение системы, отсутствие равновесия.
Формы симметрий
Современное естествознание определяет ряд симметрий, отражающих свойства иерархии отдельных уровней организации материального мира. Известны различные виды или формы симметрий:
- пространственно-временные;
- калибровочные;
- изотопические;
- зеркальные;
- перестановочные.
Все перечисленные виды симметрий можно подразделить на внешние и внутренние.
Внешняя симметрия в природе (пространственная или геометрическая) представлена огромным многообразием. Это относится к кристаллам, живым организмам, молекулам.
Внутренняя симметрия скрыта от наших глаз. Она проявляется в законах и математических уравнениях. Например, уравнение Максвелла, определяющее взаимосвязь магнитных и электрических явлений, или свойство гравитации Эйнштейна, связывающее пространство, время и тяготение.
Для чего нужна симметрия в жизни?
Симметрия в живых организмах была сформирована в процессе эволюции. Самые первые организмы, зародившиеся в океане, имели идеальную сферическую форму. Для того чтобы внедриться в иную среду, им приходилось адаптироваться к новым условиям.
Одним из способов подобной адаптации является симметрия в природе на уровне физических форм. Симметричным расположением частей тела обеспечивается равновесие при движении, жизнестойкость и адаптация. Внешние формы человека и крупных животных имеют довольно симметричный вид. В растительном мире тоже присутствует симметрия. Например, конусообразная форма кроны ели имеет симметричную ось. Это вертикальный ствол, для устойчивости утолщенный книзу. Также симметрично по отношению к нему расположены отдельные ветви, а форма конуса позволяет рационально использовать кроной световой поток солнечной энергии. Внешняя симметрия животных помогает им сохранять равновесие при движении, обогащаться энергией из окружающей среды, используя ее рационально.
В химических и физических системах симметрия присутствует тоже. Так, наиболее устойчивыми являются молекулы, которые обладают высокой симметрией. Кристаллы – это высокосимметричные тела, в их структуре периодически повторяются три измерения элементарного атома.
Асимметрия
Иногда внутреннее расположение органов в живом организме бывает асимметричным. Например, сердце располагается у человека слева, печень – справа.
Растения в процессе жизнедеятельности из почвы поглощают химические минеральные соединения из молекул симметричной формы и в своем организме преобразуют их в асимметричные вещества: белки, крахмал, глюкозу.
Асимметрия и симметрия в природе – это две противоположные характеристики. Это категории, которые всегда находятся в борьбе и единстве. Разные уровни развития материи могут носить свойства то симметрии, то асимметрии.
Если предположить, что равновесие является состоянием покоя и симметрии, а движение и неравновесное вызвано асимметрией, то можно сказать, что понятие равновесия в биологии не менее важно, чем в физике. Биологическая форма движения материи характеризуется принципом устойчивости термодинамического равновесия биологических систем. Именно асимметрию, которая является устойчивым динамическим равновесием, можно считать ключевым принципом при решении проблемы зарождения жизни.
fb.ru
Симметрия в природе
ВВЕДЕНИЕ : Проблеме симметрии посвящена поистине необозримая литература. Отучебников и научных монографий до произведений, апеллирующих не столько к чертежу и формуле, сколько к художественному образу, и сочетающих в себе научную достоверность с литературной отточенностью. В «Кратком Оксфордском словаре» симметрия определяется как «красота,обусловленная пропорциональностью частей тела или любого целого,равновесием, подобием, гармонией, согласованностью» (сам термин «симметрия» по-гречески означает «соразмерность», которую древние философы понимали как частный случай гармонии — согласования частей в рамках целого) . Симметрия является одной из наиболее фундаментальных и одной из наиболее общих закономерностей мироздания: неживой, живой природы и общества. С симметрией мы встречаемся всюду. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков человеческого знания; его широко используют все без исключения направления современной науки. Что же такое симметрия? Почему симметрия буквально пронизывает весь окружающий нас мир? Существуют, в принципе, две группы симметрий. К первой группе относится симметрия положений, форм, структур. Это та симметрия, которую можно непосредственно видеть. Она может быть названа геометрической симметрией. Вторая группа характеризует симметрию физических явлений и законов природы. Эта симметрия лежит в самой основе естественнонаучной картины мира: ее можно назвать физической симметрией. На протяжении тысячелетий в ходе общественной практики и познания законов объективной действительности человечество накопило многочисленные данные, свидетельствующие о наличии в окружающем мире двух тенденций: с одной стороны, к строгой упорядоченности, гармонии, а с другой — к их нарушению. Люди давно обратили внимание на правильность формы кристаллов, цветов, пчелиных сот и других естественных объектов и воспроизводили эту пропорциональность в произведениях искусства, в создаваемых ими предметах, через понятие симметрии. «Симметрия, — пишет известный ученый Дж. Ньюмен, — устанавливает забавное и удивительное родство между предметами, явлениями и теориями, внешне, казалось бы, ничем не связанными: земным магнетизмом, женской вуалью, поляризованным светом, естественным отбором, теорией групп, инвариантами и преобразованиями, рабочими привычками пчел в улье, строением пространства, рисунками ваз, квантовой физикой, лепестками цветов, интерференционной картиной рентгеновских лучей, делением клеток морских ежей, равновесными конфигурациями кристаллов, романскими соборами, снежинками, музыкой, теорией относительности…». Слово «симметрия» имеет двойственное толкование. В одном смысле симметричное означает нечто весьма пропорциональное, сбалансированное; симметрия показывает тот способ согласования многих частей, с помощью которого они объединяются в целое. Второй смысл этого слова — равновесие. Еще Аристотель говорил о симметрии как о таком состоянии, которое характеризуется соотношением крайностей. Из этого высказывания следует, что Аристотель, пожалуй, был ближе всех к открытию одной из самых фундаментальных закономерностей Природы — закономерности о ее двойственности. Характерно, что к наиболее интересным результатам наука приходила именно тогда, когда устанавливались факты нарушения симметрии. Следствия, вытекающие из принципа симметрии, интенсивно разрабатывались физиками в прошлом веке и привели к ряду важных результатов. Такими следствиями законов симметрии являются, прежде всего, законы сохранения классической физики. В настоящее время в естествознании преобладают определения категорий симметрии и асимметрии на основании перечисления определенных признаков. Например, симметрия определяется как совокупность свойств: порядка, однородности, соразмерности, гармоничности. Все признаки симметрии во многих ее определениях рассматриваются равноправными, одинаково существенными, и в отдельных конкретных случаях, при установлении симметрии какого-то явления, можно пользоваться любым из них. Так, в одних случаях симметрия — это однородность, в других — соразмерность и т. д. То же самое можно сказать и о существующих в частных науках определениях асимметрии. ЗНАЧЕНИЕ СИММЕТРИИ В ПОЗНАНИИ ПРИРОДЫ Идея симметрии часто являлась отправным пунктом в гипотезах и теориях ученых прошлого. Вносимая симметрией упорядоченность проявляется, прежде всего, в ограничении многообразия возможных структур, в сокращении числа возможных вариантов. В качестве важного физического примера можно привести факт существования определяемых симметрией ограничений разнообразия структур молекул и кристаллов. Поясним эту мысль на следующем примере. Допустим, что в некоторой отдаленной галактике обитают высокоразвитые существа, увлекающиеся среди прочих занятий также играми. Мы можем ничего не знать о вкусах этих существ, о строении их тела и особенностях психики. Однако достоверно, что их игральные кости имеют одну из пяти форм — тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. Всякая иная форма игральной кости в принципе исключена, поскольку требование равновероятности выпадения при игре любой грани предопределяет использование формы правильного многогранника, а таких форм только пять. Идея симметрии часто служила ученым путеводной нитью при рассмотрении проблем мироздания. Наблюдая хаотическую россыпь звезд на ночном небе, мы понимаем, что за внешним хаосом скрываются вполне симметричные спиральные структуры галактик, а в них — симметричные структуры планетных систем. Симметрия внешней формы кристалла является следствием ее внутренней симметрии — упорядоченного взаимного расположения в пространстве атомов (молекул). Иначе говоря, симметрия кристалла связана с существованием пространственной решетки из атомов, так называемой кристаллической решетки. Согласно современной точке зрения, наиболее фундаментальные законы природы носят характер запретов. Они определяют, что может, а что не может происходить в природе. Так, законы сохранения в физике элементарных частиц являются законами запрета. Они запрещают любое явление, при котором изменялась бы «сохраняющаяся величина», являющаяся собственной «абсолютной» константой (собственным значением) соответствующего объекта и характеризующая его «вес» в системе других объектов. И эти значения являются абсолютными до тех пор, пока такой объект существует. В современной науке все законы сохранения рассматриваются именно как законы запрета. Так, в мире элементарных частиц многие законы сохранения получены как правила, запрещающие те явления, которые никогда не наблюдаются в экспериментах. Видный советский ученый академик В. И. Вернадский писал в 1927 году: «Новым в науке явилось не выявление принципа симметрии, а выявление его всеобщности». Действительно, всеобщность симметрии поразительна. Симметрия устанавливает внутренние связи между объектами и явлениями, которые внешне никак не связаны. Всеобщность симметрии не только в том, что она обнаруживается в разнообразных объектах и явлениях. Всеобщим является сам принцип симметрии, без которого по сути дела нельзя рассмотреть ни одной фундаментальной проблемы, будь то проблема жизни или проблема контактов с внеземными цивилизациями. Принципы симметрии лежат в основе теории относительности, квантовой механики, физики твердого тела, атомной и ядерной физики, физики элементарных частиц. Эти принципы наиболее ярко выражаются в свойствах инвариантности законов природы. Речь при этом идет не только о физических законах, но и других, например, биологических. Примером биологического закона сохранения может служить закон наследования. В основе его лежат инвариантность биологических свойств по отношению к переходу от одного поколения к другому. Вполне очевидно, что без законов сохранения (физических, биологических и прочих) наш мир попросту не смог бы существовать.
Следует выделить аспекты, без которых симметрия невозможна:
1) объект — носитель симметрии; в роли симметричных объектов могут выступать вещи, процессы, геометрические фигуры, математические выражения, живые организмы и т.д.
2) некоторые признаки — величины, свойства, отношения, процессы, явления — объекта, которые при преобразованиях симметрии остаются неизменными; их называют инвариантными или инвариантами.
3 )изменения (объекта), которые оставляют объект тождественным самому себе по инвариантным признакам; такие изменения называются преобразованиями симметрии;
4) свойство объекта превращаться по выделенным признакам в самого себя после соответствующих его изменений.
Важно подчеркнуть, что инвариант вторичен по отношению к изменению; покой относителен, движение абсолютно.
Таким образом, симметрия выражает сохранение чего-то при каких-то изменениях или сохранение чего-то несмотря на изменение. Симметрия предполагает неизменность не только самого объекта, но и каких-либо его свойств по отношению к преобразованиям, выполненным над объектом. Неизменность тех или иных объектов может наблюдаться по отношению к разнообразным операциям — к поворотам, переносам, взаимной замене частей, отражениям и т.д. В связи с этим выделяют разные типы симметрии.
ПОВОРОТНАЯ СИММЕТРИЯ. Говорят, что объект обладает поворотной симметрией, если он совмещается сам с собой при повороте на угол 2?/n, где n может равняться 2, 3, 4 и т.д. до бесконечности. Ось симметрии называется ось осью n-го порядка.
ПЕРЕНОСНАЯ (ТРАНСЛЯЦИОННАЯ) СИММЕТРИЯ . О такой симметрии говорят тогда, когда при переносе фигуры вдоль прямой на какое-то расстояние а либо расстояние, кратное этой величине, она совмещается сама с собой.
Прямая, вдоль которой производится перенос, называется осью переноса, а расстояние а — элементарным переносом или периодом. С данным типом симметрии связано понятие периодических структур или решеток, которые могут быть и плоскими, и пространственными.
mirznanii.com

