На площадь задача – Задачи на нахождение площади. Математика 4 класс.

Содержание

Задачи на нахождение площади. Математика 4 класс.

Задача 1

Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь?

Решение:
1) 8 ∙ 7 = 56
Ответ: Площадь прямоугольника 56 м².

Задача 2

Площадь витрины квадратной формы 64м². Узнай ее периметр.

Решение:
1) 1) 64 : 8 = 8 (сторна витрины)
2) 2) 8 ∙ 4 = 32 (периметр витрины)
Ответ: 32 м.

Задача 3

Длина прямоугольника 9 дм, ширина 7 см. Найдите его площадь.

Решение:
1) 1) 90 ∙ 7 = 630
Ответ: 630 см².

Задача 4

Два прямоугольных участка имеют одинаковую площадь. Длина первого — 48 м, а ширина 30 м. Чему равна длина второго участка, если его ширина на 6 м больше ширины первого участка?

Решение:
1) 48 ∙ 30 = 1440 (площадь первого участка)

2) 30 + 6 = 36 (ширина второго участка)
3) 1440 : 36 = 40
Ответ: длина второго участка 40 м.

Задача 5

Один прямоугольный участок имеет длину 36 м, а ширину 20 м. Найдите ширину другого участка с такой же площадью, если его длина на 6 м меньше длины первого участка.

Решение:
1) 36 ∙ 20 = 720 (площадь первого участка)
2) 36 – 6 = 30 (длина другого участка)
3) 720 : 30 = 24
Ответ: ширина другого участка 24 м.

Задача 6

У какой фигуры площадь больше и на сколько: у квадрата со стороной 4 см или у прямоугольника со сторонами 2 см и 6 см?

Решение:
1) 4 ∙ 4 = 16 (площадь квадрата)
2) 2 ∙ 6 = 12 (площадь прямоугольника)
3) 16 — 12 = 4
Ответ: площадь квадратата больше на 4 см.

Задача 7

Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.

Решение:
1) 6 ∙ 6 = 36
2) 6 ∙ 4 = 24
Ответ: площадь квадрата 36 см², периметр квадрата 24 см.

Задача 8

У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.

Решение:
1) 7 ∙ 5 = 35
2) 7 ∙ 2 = 14
3) 5 ∙ 2 = 10
4) 10 + 14 = 24
Ответ: площадь прямоугольника 35 м², периметр прямоугольника 24 см.

Задача 9

Сторона клумбы квадратной формы 8 м. 7/16 всей площади клумбы засажено ромашками, а остальная площадь – незабудками. На какой площади клумбы посажены незабудки?

Решение:
1) 8 ∙ 8 = 64 (площадь клумбы)
2) 64 : 16 = 4(1/16 клумбы)

3) 4 ∙ 7 = 28 (плошадь клумбы засаженая ромашками)
4) 64 – 28 = 36
Ответ: незабудками засажено 36 м².

Задача 10

Длина прямоугольника 6 см. Чему равна его площадь, если периметр составляет 18 см?

Решение:
1) 6 ∙ 2 = 12
2) 18 – 12 = 6
3) 6 : 2 = 3 (ширина прямоугольника)
4) 3 ∙ 6 = 18
Ответ: площадь прямоугольника 18 м².

Задача 11

Площадь прямоугольного стола 4800 кв см. Его ширина 60 см. Чему равен его периметр?

Решение:
1) 4800 : 60 = 80 (длина стола)
2) 60 ∙ 2 = 120 см
3) 80 ∙ 2 = 160 см
4) 120 + 160 = 280 см
Ответ: периметр стола 280 см.

Задача 12

Периметр прямоугольника 40 см. Одна сторона 5 см. Чему равна его площадь?

Решение:
1) 5 ∙ 2 = 10
2) 40 – 10 = 30
3) 30 : 2 = 15 (другая сторона прямоугольника)
4) 5 ∙ 15 = 75
Ответ: площадь прямоугольника 75 см².

Задача 13

Площадь квадрата 49 кВ дм. Узнайте его периметр.

Решение:
1) 49 : 7 = 7 (сторона квадрата)
2) 7 ∙ 4 = 28 (периметр квадрата)
Ответ: периметр квадрата равен 28 дм.

Задача 14

Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.

Решение:
1) 4 ∙ 2 = 8 (длина окна)
2) 4 ∙ 8 = 32
Ответ: площадь окна равна 32 м².

Задача 15

Длина участка земли 54 м. ширина — 48 м. 5/9 площади засажено картофелем. Остальная часть участка – капустой. Какая площадь засажена капустой?

Решение:
1) 54 ∙ 48 = 2592 (площадь участка земли)
2) 2592 : 9 = 288 (1/9 площади)
3) 288 ∙ 5 = 1440 (5/9 площади)
4) 2592 – 1440 = 1152
Ответ: капустой засадили 1152 м².

mat-zadachi.ru

Площади фигур — задачи.

Кто подзабыл формулы – тому сюда. Еще очень удобно открыть статью с формулами в соседнем окне, чтобы они были перед глазами.

1. Найдите площадь параллелограмма, если две его стороны равны 14 и 12, а угол между ними равен 30°.

По формуле площади параллелограмма через длины его сторон и синус угла между ними:

2. Периметр равностороннего треугольника равен 30. Найдите его площадь, делённую на .

Для того, чтобы найти площадь, необходимо знать сторону. Нам дан периметр, и, поскольку все стороны равны, найдем длину стороны: . Теперь воспользуемся формулой площади равностороннего треугольника: . Разделим на и запишем ответ: 25.

Однако, формулу площади равностороннего треугольника не все помнят. Как же решить эту задачу без формулы? Проведем высоту треугольника из вершины к основанию. Так как треугольник равносторонний, то высота его будет и медианой, и разделит основание пополам:

Имеем прямоугольный треугольник с гипотенузой 10 и катетом 5. По теореме Пифагора находим высоту:

Теперь по общеизвестной формуле площади треугольника находим: . В ответ записываем результат, разделенный на .

Ответ: 25.

3. В равнобедренном треугольнике боковая сторона равна 10, а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, делённую на .

Можем найти высоту треугольника и основание, воспользовавшись определением косинуса и синуса, и затем площадь. Также нам известны две боковые стороны и угол между ними, поэтому можем воспользоваться формулой . Решим задачу обоими способами: ,

, здесь b – половина основания.

Находим площадь: .

Теперь вторым способом:

Ответ:

4. В треугольнике одна из сторон равна 10, другая равна , а угол между ними равен 60°. Найдите площадь треугольника.

Второй способ из предыдущей задачи – единственный для этой задачи:

Ответ: 75.

5. В прямоугольнике одна сторона равна 6, а диагональ равна 10. Найдите площадь прямоугольника.

Для того, чтобы найти площадь, нужна вторая сторона. Ее можно найти по теореме Пифагора:

Найдем площадь:

Ответ: 48.

6. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.

Как известно, диагонали ромба перпендикулярны друг другу и точкой пересечения делятся пополам. Поэтому треугольник АВС прямоугольный, его гипотенуза 5, один из катетов 3. Второй катет можем найти по теореме Пифагора: . Значит, диагонали ромба – 6 и 8, а зная их, найдем площадь:

Ответ: 24.

7. Периметр ромба равен 24, а косинус одного из углов равен . Найдите площадь ромба.

Здесь воспользуемся формулой для отыскания площади параллелограмма по двум сторонам и синусу угла между ними: . Но у нас имеется косинус, а не синус. Найдем синус из основного тригонометрического тождества:

Все стороны ромба равны, найдем их, зная периметр:

Площадь ромба:

Ответ: 12.

8. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 45°. Найдите площадь треугольника, деленную на

В этой задаче нас хотят запутать, задав в условии основание треугольника. На самом деле совершенно неважно, каково его основание, так как треугольник равнобедренный, и нам известны боковые стороны и угол между ними, значит, можем воспользоваться формулой площади по двум сторонам и углу между ними:

Делим результат на и записываем ответ:

Ответ: 25

9. В прямоугольнике диагональ равна 10, угол между ней и одной из сторон равен 30°, длина этой стороны . Найдите площадь прямоугольника, деленную на .

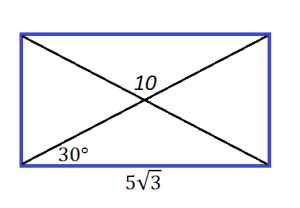Найдем вторую сторону четырехугольника, чтобы потом определить площадь. Воспользуемся определением синуса, так как ищем мы противолежащий катет:

Площадь равна:

Есть другой путь решения этой задачи, если сообразить, что угол между диагоналями равен . Тогда площадь можем отыскать так:

Делим нашу найденную площадь на , и записываем ответ: 25.

10. Радиус круга равен 3, а длина ограничивающей его окружности равна .Найдите площадь круга. В ответ запишите площадь, деленную на .

Если дан радиус круга, то мы без проблем определим его площадь и без знания длины окружности, верно?

Делим результат на , получаем 9 и записываем это число в ответ.

11. Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен . Найдите площадь трапеции, если её основания равны 6 и 9.

Найдем высоту трапеции. Катет, лежащий против угла в , вдвое меньше гипотенузы, поэтому высота равна 2,5.

Определяем площадь:

Ответ: 18,75

12. Найдите площадь прямоугольника, если его периметр равен 92, а отношение соседних сторон равно 3:20.

Полупериметр прямоугольника равен 46. Полупериметр – это сумма длинной и короткой сторон. Их отношение равно 3:20, то есть три части и двадцать частей. Тогда одна часть: . Тогда длинная сторона – 40 (), а короткая – 6. Площадь прямоугольника

Ответ: 240.

13. Периметр равнобедренного треугольника равен 392, а основание – 192. Найдите площадь треугольника.

Тут годится единственная формула – это формула Герона: . Раз треугольник равнобедренный, значит, можно их найти: . p – половина периметра: .

Считаем площадь: .

Ответ: 2688.

easy-physic.ru

Задачи по геометрии на тему «Площадь»

ПЛОЩАДЬ

№1. Периметр квадрата равен 20см. Прямоугольник имеет такую же площадь, что и квадрат, а одна из его сторон равна 10см. Найдите периметр прямоугольника.

I уровень

1) по определению стороны квадрата равны, значит 20:4=5(см) – сторона квадрата.

2) по теореме площадь квадрата равна квадрату его стороны, т.е. S=5²=25(см²), значит и площадь прямоугольника равна 25 см²

3)25:10=2,5(см) – вторая сторона прямоугольника

4)Р=10·2+2,5·2=25 см

Формулы нахождения периметра и площади квадрата и прямоугольника.

выполнить чертеж с помощью линейки и угольника

применять указанные формулы

решение требует знаний полученных еще в пропедевтическом курсе геометрии

для решения необходимы знания и умения I уровня

№2. Дано: рисунок 1.

Найти: S_АВС

I уровень

1) по свойству катет прямоугольного треугольника, лежащий против угла в 30^о, равен половине гипотенузы, т.е. ВН=1/2ВС=·8=4(см)

2) по теореме площадь треугольника равна половине произведения его основания на высоту, S_АВВС= ВН·АС= 18 см²

Свойство прямоугольного треугольника

Теорему о нахождении площади треугольника

выделять на чертеже прямоугольный треугольник, его катет и гипотенузу

анализировать чертеж

задача по готовому чертежу

задача для актуализации знаний учащихся на следующем уроке после введения теоремы о площади треугольника

для решения необходимы знания и умения I уровня

№3 Дано: АО=4; ВО=9; СО=5;DО=8;

S_АОС=15.

Найти: S_BOD

I уровень

АОС=DОВ — вертикальные углы
S_DOB : S_AOC= S_DOB= S_AOC = ·15 = 54

Понятие вертикальных углов

Теорема об отношении площадей треугольников с равным углом

выделять на чертеже вертикальные углы

применять указанную теорему

задача по готовому чертежу

после изучения площади треугольника, для ее решения необходимы знания и умения I уровня

№4.Сторона параллелограмма равна 21 см, а высота проведенная к ней 15 см. Найдите площадь параллелограмма.

№5. Сторона треугольника равна 5см, а высота, проведенная к ней, в 2 раза больше стороны. Найдите площадь треугольника.

№6. В трапеции основания равны 6 и 10 см, а высота равна полусумме длин оснований. Найдите площадь трапеции.

№7. Стороны параллелограмма равны 6 и 8 см, а угол между ними равен 30^о. Найдите площадь параллелограмма.

№8 Диагонали ромба относятся как 2:3, а их сумма равна 25 см. Найдите площадь ромба.

№9 Сторона параллелограмма равна 17 см, а его площадь 187 см². Найдите площадь ромба.

№10 Сторона треугольника равна 18 см, а высота, проведенная к ней, в 3 раза меньше стороны. Найдите площадь треугольника.

II УРОВЕНЬ

№1. В треугольнике АВС А=, ВС = 10 см, а высота BD делит сторону АС на отрезки AD = 6см, DC = 8 см. Найдите площадь треугольника и высоту, проведенную к стороне ВС.

II уровень

Рассмотрим ΔАBD: А=45^о, D=90^о, т.к. сумма острых углов прямоугольного треугольника равна 90^о, то ABD=45^о;
ВАD=ABD, значит ΔABD — равнобедренный AD=BD=6см;
S_ABC=1⁄2АС·BD=1⁄2·(6+8)·6=42см²
S_ABC=1⁄2АН·BС

42=1/2АН10

42=5АН

АН=8,4см

Свойства прямоугольного треугольника

Понятие равнобедренного треугольника и его свойство

Теорема о нахождении площади треугольника по стороне и опущенной к ней высоте

выполнить чертеж с помощью линейки и угольника

анализировать чертеж

выделять на чертеже прямоугольный треугольник

применять указанную теорему

в задаче применяется материал из разных глав учебника, свойства прямоугольного треугольника изучаются в 7 классе, равнобедренный треугольник еще раньше,

учащимся необходимо анализировать и применять более одного факта, для ее решения необходимы знания и умения II уровня

№2. В параллелограмме ABCD высоты равны 10 и 5 см, площадь параллелограмма равна 60 см². Найдите стороны параллелограмма.

II уровень

1) S_ABCD=ВН·AD=5AD=60

AD=ВС=12см

2)S_ABCD=DК·AВ=10AВ=60

AB=CD=6см

Определение параллелограмма

Понятие периметра

Теорема о нахождении площади параллелограмма

выполнить чертеж с помощью линейки и угольника

анализировать чертеж

вводить неизвестное

находить стороны параллелограмма по периметру и стороне

применять указанную теорему

необходимо построить высоту к боковой стороне, выразить из уравнения (теоремы) неизвестное;

учащимся необходимо применять более одного факта, для решения задачи необходимы знания и умения II уровня

№3. В равнобедренном треугольнике АВС высота АН в 4 раза меньше основания ВС, равного 16 см. Найдите площадь ΔАВС.

II уровень

1) АН = 1/4ВС = 1/4·16 = 4 см;

2) S_ABC= 1/2ВС·АН = 1/2·16·4 = 32 см²

Теорема о нахождении площади треугольника по стороне и опущенной к ней высоте

выполнить чертеж с помощью линейки и угольника

применять указанную теорему

В задаче содержится избыточные данные

№4 В равнобедренном треугольнике АВС высота ВН равна 12 см, а основание АС в 3 раза больше высоты ВН. Найдите площадь ΔАВС.

№5 В параллелограмме АВСD стороны равны 14 и 8 см, высота, проведенная к большей стороне, равна 4 см. Найдите площадь параллелограмма и вторую высоту.

№6 Площадь трапеции равна 320 см², а высота трапеции равна 8 см. Найдите основания трапеции, если длина одного из оснований составляет 60% длины другого.

№7 В треугольнике АВС стороны АВ и ВС равны соответственно 14 и 18 см. Сторона АВ продолжена за точку А на отрезок АМ, равный АВ. Сторона ВС продолжена за точку С на отрезок КС, равный половине ВС. Найдите площадь ΔМВК, если площадь ΔАВС равна 126 см².

№8. В ромбе АВСК из вершины В и С опущены высоты ВМ и СН на прямую АК. Найдите площадь четырехугольника МВСН, если площадь ромба равна 67 см².

№9 В ромбе АВСD на стороне ВС отмечена точка К такая, что КС:ВК=3:1. Найдите площадь ΔАВК, если площадь ромба равна 48 см².

№10 В равнобедренной трапеции АВСМ большее основание АМ равно 20 см, высота ВН отсекает от точки АМ отрезок АН, равный 6 см. Угол ВАМ равен 45^о. Найдите площадь трапеции.

III УРОВЕНЬ

№1. Площадь параллелограмма равна 48 см², а его периметр 40 см. Найдите стороны параллелограмма, если высота, проведенная к одной из них, в три раза меньше стороны.

III уровень

1) Пусть высота ВН=х, тогда AD=3х;

2) S_ABCD=ВН·AD=х·3х=48

3х²=48; х²=16; х=4

АD=3х=12см

3)AD=ВС=4см;

Р_ABCD=2(AB+BC)=40

2(АВ+12)=40

АВ+12=20

АВ=8

Определение параллелограмма

Понятие периметра

Теорема о нахождении площади параллелограмма

выполнить чертеж с помощью линейки и угольника

анализировать чертеж

вводить неизвестное

находить стороны параллелограмма по периметру и стороне

применять указанную теорему

Ход решения задачи не очевиден, необходимо проанализировать данные, узнать что объединяет площадь и периметр, ввести неизвестное;

учащимся необходимо применять более одного факта, для решения задачи необходимы знания и умения III уровня

№2. В равнобедренной трапеции высота, проведенная из вершины тупого угла, делит большее основание на два отрезка, больший из которых равен 20 см. Найдите площадь трапеции, если ее высота равна 12 см.

III уровень

1)Проведем дополнительное построение: продолжим сторону ВС, а из вершины D проведем перпендикуляр к стороне ВС, точка пересечения –Р;

2)ΔАВН=ΔCDР, т.к.

ВН=РD (по теореме Фалеса)

АВ=СД (т.к. трапеция равнобедренная), значит S_ABH=S_CPD

3)S_ABCD=S_ABH+S_BCDN= S_CPD+S_BCDN₌S_BPDH

4) PBDH- прямоугольник, значит S_BPDH=ВН·HD= 12·20=240 см²

Определение параллелограмма

Определение прямоугольника

Теорема Фалеса

Признак равенства прямоугольных треугольников

Свойство площади фигур

Теорема о нахождении площади параллелограмма.

Теорема о нахождении площади прямоугольника

выполнить чертеж с помощью линейки и угольника

анализировать чертеж

производить дополнительное построение

применять указанные теоремы

Ход решения задачи не очевиден, необходимо проанализировать данные, необходимо произвести дополнительное построение;

применяется материал изученный начиная с 7 класса;

учащимся необходимо применять более одного факта, для решения задачи необходимы знания и умения III уровня

№3. В трапеции АВСD ВС и AD – основания, ВС:AD=3:4. Площадь трапеции равна 70 см². Найдите площадь ΔАВС.

III уровень

1) Т.к. РА=СН (теорема Фалеса), то S_ABC:S_ACD=ВС:AD=3:4

2) S_ABCD=S_ABC+S_ACD=70 см²,

3+4=7

70:7=10

3·10=30, т.е. S_ABC =30 см²

Теорема Фалеса

Теорема о нахождении площади трапеции

Следствие из теоремы о площади треугольника: отношение площадей с равными высотами

выполнить чертеж с помощью линейки и угольника

анализировать чертеж

производить дополнительное построение

применять указанные теоремы

учащимся необходимо применять более одного факта, для решения задачи необходимы знания и умения III уровня

№4 В трапеции АВСD ВС и AD – основания, ВС:AD=4:5. Площадь треугольника АСD равна 35 см². Найдите площадь трапеции.

№5 В треугольнике АВС АВ=х, АС=у, А=15^о, а в треугольнике МРК КР=х, МК=у, К=165^о. Сравните площади этих треугольников.

№6 В равнобедренной трапеции угол между диагоналями равен 90^о, высота трапеции равна 8 см. Найдите площадь трапеции.

№7 В прямоугольном ΔАВС точка О – середина медианы СН, проведенной к гипотенузе АВ, АС=6 см, ВС=8 см. Найдите площадь треугольника ОВС.

№8 Площадь параллелограмма равна 50 см², а его периметр 34 см. Найдите стороны параллелограмма, если одна из них в 2 раза больше проведенной к ней высоты.

№9 В ромбе АВCD диагонали равны 5 см и 12 см. На диагонали АС взята точка М так, что АМ:МС=4:1. Найдите площадь треугольника АМD/

№10 В треугольнике АВС В=130^о, АВ=а, ВС=b, а в параллелограмме МРКН МР=а, МН=b, М=50^о. Найдите отношение площади треугольника у площади параллелограмма.

infourok.ru

Задачи на нахождение периметра и площади

Площадь одной клетки равна 1см.
Найдите площадь фигуры, изображённой на рисунке A.
Найдите площадь фигуры, изображённой на рисунке B.
Найдите площадь фигуры, изображённой на рисунке C.
Найдите площадь фигуры, изображённой на рисунке D.
Найдите площадь фигуры, изображённой на рисунке E.

Определение:
Неправильный четырехугольник – фигура, у которой стороны не равны и не параллельны.
Решение:
разобьём неправильные четырехугольники A, B, D на два прямоугольных треугольника и прямоугольник, а неправильные четырехугольники C, E на два прямоугольных треугольника и квадрат.
Применив формулы площади треугольника, квадрата и прямоугольника легко решим поставленную задачу
Фигура A
S = a · b — формула площади прямоугольника, тогда
3 · 4 = 12 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ ·1 · 5 = 2,5 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника
½ ·2 · 4 = 4 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры A
12 + 2,5 + 4 = 18,5 см²
Ответ: площадь фигуры A 18,5 см²
Фигура B
S = a · b — формула площади прямоугольника, тогда
5 · 1 = 5 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ ·6 · 5 = 15 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ ·1 · 1 = 0,5 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры B
5 + 15 + 0,5 = 18,5 см²
Ответ: площадь фигуры B 20,5 см²
Фигура C
S = a · a; S = a² — формула площади квадрата, тогда
5 · 5 = 25 см² — площадь квадрата a
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 6 = 3 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 5 = 2,5 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры C
25 + 3 + 2,5 = 30,5 см²
Ответ: площадь фигуры C 30,5 см²
Фигура D
S = a · b — формула площади прямоугольника, тогда
3 · 4 = 12 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ ·1 · 5 = 2,5 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ ·2 · 4 = 4 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры A
12 + 2,5 + 4 = 18,5 см²
Ответ: площадь фигуры A 18,5 см²
Фигура E
S = a · a; S = a² — формула площади квадрата, тогда
2 · 2 = 4 см² — площадь квадрата a
S = ½ · a · h — формула площади треугольника, тогда
½ · 3 · 4 = 6 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 2 · 2 = 2 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры E
4 + 6 + 2 = 12 см²
Ответ: площадь фигуры E 12 см²

xn--80abl6aqcjc8ic.xn--p1ai

Дидактический материал «Задачи на нахождение площади».

Просмотр содержимого документа
«Дидактический материал «Задачи на нахождение площади».»

Задачи на нахождение площади

1.Найти площадь и периметр прямоугольника со сторонами 7 см и 5 см.

2.Длина прямоугольника 8 дм, ширина 7 дм. Найдите его площадь и периметр.

3. Площадь витрины квадратной формы 64 кв.м. Узнайте ее периметр.

4. Длина прямоугольника 9 дм, ширина 7 см.Найдите его площадь и периметр.

5. Длина прямоугольника 9 м, ширина 8 дм. Найдите его площадь и периметр.

6. Ширина прямоугольника 2 дм, а его длина 42 см. Найти площадь и периметр.

7.Длина стола 3 м, а его ширина 12 дм. Найти площадь и периметр стола.

8. Длина доски 3 м 2 дм, а ее ширина 4 дм. Найти площадь и периметр доски.

9. Высота окна 160 см, ширина -15 дм. Найти площадь и периметр окна.

10. Периметр участка прямоугольной формы 300 м. Его ширина 52 м. Чему равна его площадь.

11.Длина участка прямоугольной формы 82 м. Ширина в 2 раза меньше. Найти площадь и периметр участка.

12. Два участка обнесены оградой одинаковой длины. Первый участок имеет длину 60 м, а ширину 40 м. Второй участок квадратный. Найти периметр и площадь обоих участков.

13. Периметр квадрата 48 см. Чему равна его площадь?

14. Ширина комнаты 3 м, а длина 500 см. Найти площадь и периметр комнаты.

15.Высота двери 190 см. Ширина 90 см. Найти площадь и периметр.

16. Длина прямоугольника равна стороне квадрата с периметром 64 см, а ширина его в два раза меньше. Найти площади прямоугольника и квадрата.

17. Найти площади всех возможных прямоугольников с периметром 12 см, если длина их сторон выражена целым числом см. У какого прямоугольника площадь наибольшая?

18. Участок длиной 18 м и шириной 10 м увеличили в длину на 2 м и уменьшили в ширину на 3 м. Как изменилась площадь участка?

19. Сколько краски пойдет на окраску стены длиной 6 м и высотой 4 м, если на окраску 1 кв.м. требуется 200 г краски?

20.В коридоре длиной 12 м и шириной 5 м нужно покрыть пол квадратными плитками. Сколько потребуется плиток, если площадь каждой плитки 1 кв.дм.?

21.У какой фигуры площадь больше и на сколько: у квадрата со стороной 4 см или у прямоугольника со сторонами 2 см и 6 см.

22. Периметр прямоугольника 30 см, а ширина 3 см.Найти периметр квадрата такой же площади.

23.Периметр прямоугольника 40 см. Одна сторона 5 см.Чему равна его площадь?

24. Длина прямоугольника 6 см. Чему равна его площадь, если периметр составляет 18 см?

25.Окно имеет форму прямоугольника. Высота окна 2 м, ширина 1 м 2 дм. Чему равна площадь окна?

multiurok.ru

Решаем задачи на нахождение площади и периметра

Прежде, чем решать задачи на нахождение периметра и площади геометрических фигур, напомню, что….

I уровень

1.Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь.

2.Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.

3.У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.

4.Найдите периметр и площадь прямоугольника со сторонами 6 см и 8 см.

5.Длина прямоугольника 8 дм, ширина 5 дм. Найди его площадь.

6.Вычисли площадь прямоугольника, длины сторон которого равны 6 мм и 8 мм.

7.Ширина прямоугольника 7 дм, а длина 12 дм. Вычисли площадь.

8.Длина прямоугольника 9 дм, ширина 7 см. Найди его площадь.

9.Длина стороны квадрата 6 см. Узнай площадь.

10.Вычисли периметр квадрата со стороной 4 см.

11.Ширина прямоугольника равна 9 дм, а длина на 6 дм больше. Найдите его площадь.

12.Длина прямоугольника равна 5 дм, ширина — на 4 см меньше. Найдите Р и S этого прямоугольника.

13.Начерти прямоугольник, длина одной стороны которого 2 см, а длина другой в 3 раза больше. Найди его периметр и площадь.

14.Начерти прямоугольник, длина одной стороны которого 6 см, а длина другой в 2 раза больше. Найди его периметр и площадь.

15.Начерти прямоугольник, ширина которого равна 2 см, а длина на 3 см больше. Вычисли его периметр.

16.Сторона квадрата равна 3 см. Чему равен периметр?

17.Лист бумаги имеет квадратную форму. Его сторона равна 10 см. Чему равен периметр?

18.Начерти квадрат со стороной 6 см. Найдите его периметр. Периметр квадрата равен 28 см. Чему равна его сторона?

19.Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычисли площадь окна.

20.Ширина прямоугольника 4 дм, а длина в 5 раз больше ширины. Найди площадь прямоугольника.

21.Площадь прямоугольника 36 см², его длина 9 см. Чему равна ширина прямоугольника?

II уровень

1.Начерти прямоугольник, длина одной стороны которого 2 см, а длина другой в 4 раза больше. Найди его периметр и площадь.

2.Длина прямоугольника равна 5 дм, ширина — на 4 см меньше. Найдите Р и S этого прямоугольника.

3.Дано: прямоугольник, а = 8 дм, в — на 2 см меньше. Найди Р и S.

4.Длина прямоугольника 12 см, а его ширина на 2 см меньше. Найдите площадь и периметр прямоугольника.

5.Сумма двух сторон квадрата 12 дм. Найдите периметр и площадь квадрата.

6.Найдите длину прямоугольника по его ширине – 8 дм и периметру–30 дм.

7.Периметр квадрата равен 32 см. Чему равна его сторона?

8.Периметр треугольника 21 см. Надите длину третьей стороны этого треугольника, если длины двух сторон 7 см и 8 см.

9.Периметр прямоугольника 20 см. Длина его стороны 6 см. Узнайте ширину прямоугольника и начертите его.

10.Площадь прямоугольника равна 270 кв.см, его длина 9 дм. Найдите периметр этого прямоугольника.

11.Периметр прямоугольника равен 54 м. Найдите площадь этого прямоугольника, если одна его сторона равна 18 м.

12.Найдите площадь квадрата, периметр которого равен 360 мм.

13. Периметр прямоугольника 40 см. Одна сторона 5 см.Чему равна его площадь?

14. Начерти квадрат, периметр которого равен периметру прямоугольника со сторонами 2 см и 6 см.

15. Дачный участок прямоугольной формы имеет длину 20 м и ширину 12 м. Какой длины забор надо поставить вокруг участка?

16. Периметр квадрата равен периметру треугольника со сторонами 6 см, 3 см и 7 см. Чему равна длина стороны квадрата?

17. У какой фигуры площадь больше и на сколько: у квадрата со стороной 4см или у прямоугольника со сторонами 2 см и 6 см?

18. Периметр прямоугольника равен 54 м. Найди площадь этого прямоугольника, если одна его сторона равна 18 м.

19. Периметр квадратной песочницы 12 м. Найдите площадь этой песочницы.

20. Напишите все возможные варианты длины и ширины прямоугольника, если его периметр 24 см.

Составила Кислова Людмила Борисовна

www.klass39.ru

ВЕСЬ СПИСОК ЗАДАЧ с решениями на тему: «Площадь круга»

Радиус окружности 2 см

Найти площадь круга.

Диаметр окружности 2 см

Найти площадь круга.

Длина окружности 5 м

Найти площадь круга

Две окружности,

имеющие общий центр, образуют кольцо. Радиус внешней окружности равен 10 см, а внутренней 8 см. Найти площадь этого кольца.

В окружность вписан квадрат.

Найти площадь закрашенной области, если радиус окружности равен 3 м.

Окружность вписана в квадрат.

Найти площадь закрашенной области, если сторона квадрата равна 2 м.

Равносторонний треугольник

со стороной 1 м вписан в окружность. Найти площадь круга, ограниченного этой окружностью.

Равносторонний треугольник

с высотой 3 м вписан в окружность. Найти площадь круга, ограниченного этой окружностью.

Равносторонний треугольник

вписан в окружность. Найти площадь круга, ограниченного этой окружностью, если известно, что длина отрезка ОК равна 2 м.

Прямоугольный треугольник

вписан в окружность Найти площадь круга, ограниченного этой окружностью, если известны катеты треугольника, a=4см и b=7см.

Прямоугольный треугольник

вписан в окружность Найти площадь круга, ограниченного этой окружностью, если катет треугольника равен 2м, а противоположный этому катету угол, составляет 30°.

Прямоугольный треугольник АВС

вписан в окружность Найти площадь круга, ограниченного этой окружностью, если размер клеток составляет 1см на 1см.

www-formula.ru