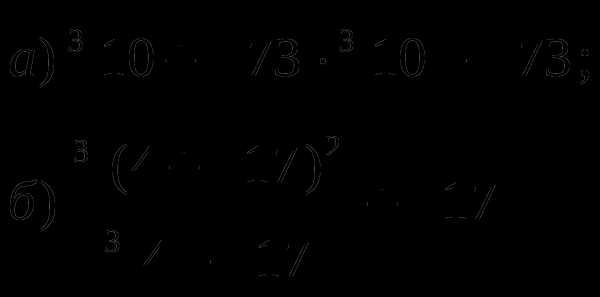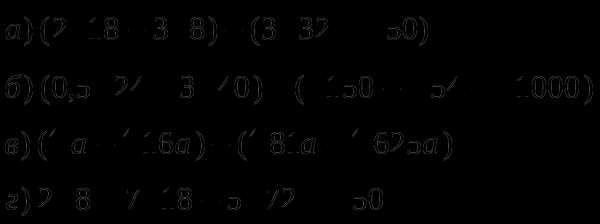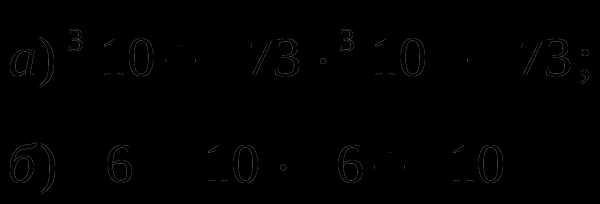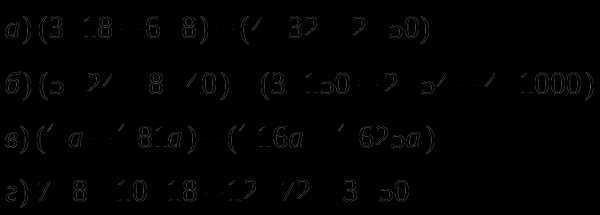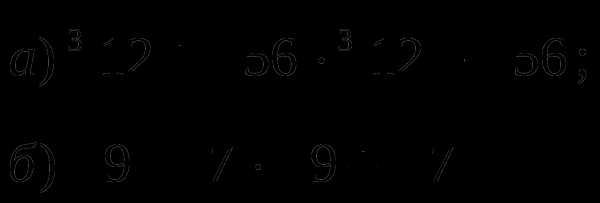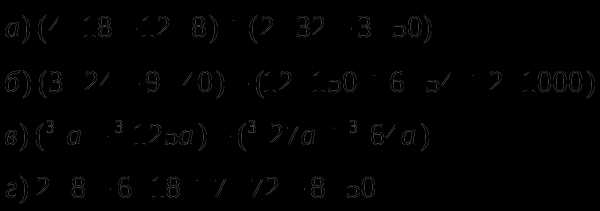Математика в техникуме 1 курс – Методическое пособие для студентов 1 курса при изучении дисциплины «Математика»

Содержание

Математика 1 курс техникума

ГАПОУ СО «Верхнесалдинский авиаметаллургический техникум»

к календарно-тематическому плану работы преподавателя

по предмету математика на 1 семестр 2017/18 учебный год

п/п

ВИД ЗАНЯТИЯ

Г р у п п а ТМ -120

№ группы

по плану

по факту

по плану

по факту

по плану

по факту

Роль математики в современном обществе. Действительные числа. Комплексные числа.

Действия над комплексными числами. Способы решения линейных уравнений.

Действия над комплексными числами. Способы решения неравенств. Иррациональные уравнения.

Иррациональные уравнения.

Иррациональные уравнения. Погрешности и вычисления с помощью микрокалькулятора

Практическая работа №1. Комплексные числа. Действия над комп. числами.

Практическая работа №2. Способы решения линейных уравнений и неравенств.

Погрешности и вычисления с помощью микрокалькулятора. Функции. Область определения и множество значений; график функции; способы задания.

Функции. Область определения и множество значений; график функции; способы задания.

Свойства функции: монотонность, четность, нечётность, ограниченность, периодичность. Обратные функции. График обратной функции. Арифм. Операции над функциями. Сложная функция (композиция).

График обратной функции. Арифм. Операции над функциями. Сложная функция (композиция).

Геометрические преобразования графиков функций.

Практическая работа №3. Область определения и множество значений функции. Построение графиков функций, заданных различными способами.

Степень с действительным показателем. Действия над степенями.

Свойства степеней с рациональным показателем.

Степенная функция, её свойства и графики.

Показательная функция, её свойства и графики. Показательные уравнения.

Показательные уравнения.

Показательные неравенства.

Логарифмы, свойства логарифмов.

Логарифмирование, потенцирование.

Логарифмическая функция, её свойства и графики.

Десятичные, натуральные логарифмы. Связь между ними .

Формулы перехода от одного логарифма к другому. Логарифмические уравнения.

Логарифмические неравенства. Углы и их измерения.

Практическая работа №4. Степень с действительным показателем. Действия над степенями.

Практическая работа №5. Свойства степеней с рациональным показателем.

Практическая работа №6. Степенная функция, её свойства и графики.

Практическая работа №7. Показательная функция, её свойства и графики. Показательные уравнения.

Углы и их измерения.

Тригонометрические функции числового аргумента и их свойства.

Тригонометрические функции числового аргумента и их свойства.Основные формулы тригонометрии.

Основные формулы тригонометрии.График, свойства тригонометрической функции синус.

График, свойства тригонометрической функции синус.График, свойства тригонометрической функции косинус.

График, свойства тригонометрической функции косинус. График, свойства тригонометрической функции тангенс.

График, свойства тригонометрической функции тангенс. График, свойства тригонометрической функции котангенс.

График, свойства тригонометрической функции котангенс Обратные тригонометрические функции.

Решение простейших тригонометрических уравнений (частные случаи).

Формулы приведения.

Формулы двойного и половинного аргумента.

Формулы сложения.

Формулы суммы и разности двух тригонометрических функций.

Преобразование произведения тригонометрических выражений.

Преобразование в сумму или разность тригонометрических выражений.

Практическая работа №8. Тригонометрические функции числового аргумента и их свойства.

Практическая работа №9. График, свойства тригонометрической функции синус.

Практическая работа №10. График, свойства тригонометрической функции косинус, тангенс.

Практическая работа №11. График, свойства тригонометрической функции котангенс. Обратные тригонометрические функции.

Контрольная работа.

Прямоугольная (декартова) система координат в пространстве. Формула расстояния между двумя точками.

Уравнение сферы.

43,

Векторы. Модуль вектора. Равенство векторов. Сложение векторов. Умножение вектора на число. Разложение вектора по единичным векторам.

45,

Угол между векторами. Проекция вектора на ось.

Координаты вектора. Скалярное произв. векторов.

Использование координат и векторов при решении мат и прикл. Задач.

П.р 12. « Прямоугольная (декартова) система координат в пространстве. Формула расстояния между двумя точками. Уравнение сферы.»

П. р 13. «Векторы. Модуль вектора. Равенство векторов. Сложение векторов. Умножение вектора на число. Разложение вектора по единичным векторам.»

П. р 14. «Угол между векторами. Проекция вектора на ось.»

П. р 15. «Координаты вектора. Скалярное произв. векторов.»

П. р 16. «Использование координат и векторов при решении мат и прикл. Задач.»

Аксиомы стереометрии и следствия из них.

Взаимное расп. прямых в пространстве.

Перпендикуляр и наклонные.

Параллельное проектирование. Свойства.

Теорема о трех перпендикулярах.

59,

Взаимное расположение двух плоскостей в пространстве.

Связь между параллельностью и перпендикулярностью.

П. р 17. «Аксиомы стереометрии и следствия из них. Параллел. прямой и плоскости»

П. р 18. «Перпендикуляр и наклонные. Сечение многогранников плоскостью.»

Числовые последовательности. Предел числ. Послед.

Преподаватель Крюкова.Е.И.

infourok.ru

Экзаменационные работы по математике для 1 курса СПО

Программа итогового экзамена по математике

Для успешной подготовки к итоговому экзамену по математике студентам следует обратить особое внимание на повторение тем, согласно стандарта.

Тригонометрия:

Основные формулы тригонометрии. Функции и их графики. Решение тригонометрических уравнений и неравенств.

Производная:

Правила вычисления производных. Производная сложной функции. Производная показательной функции. Метод интервалов. Применение производной к исследованию функции.

Первообразная:

Основное свойство первообразной. Правила нахождения первообразных.

Понятие степени:

Корень n-ой степени и его свойства. Степень с рациональным показателем. Решение иррациональных уравнений.

5. Показательная и логарифмическая функции:

Показательная функция. Решение показательных уравнений и неравенств. Логарифмы и их свойства. Логарифмическая функция. Решение логарифмических уравнений и неравенств. Свойства функций.

6. Стереометрия:

Многогранники. Тела вращения.

Критерии оценивания экзаменационной работы

1 задание: Степень с рациональным показателем – 1 балл

2 задание: Степень с рациональным показателем – 1 балл

3 задание: Свойства логарифмической функции – 1 балл

4 задание: Основные тригонометрические формулы –

2 балла

5 задание: Основные тригонометрические формулы–2 балла

6 задание: Решение тригонометрических уравнений– 1 балл

7 задание: Решение иррациональных уравнений – 2 балла

8 задание: Решение показательных уравнений – 2 балла

9 задание: Метод интервалов — Решение иррациональных уравнений – 1 балл

10 задание: Свойства тригонометрических функций – 1 балл

11 задание: Вычисление производных — 1 балл

12 задание: Нахождение первообразной функции – 1 балл

13 задание: Решение логарифмических уравнений – 1 балл

14 задание: Нахождение максимального и минимального значений функции – 2 балла

15 задание: Свойства тел в стереометрии – 1 балл

16 задание: Площадь криволинейной трапеции – 3 балла

17 задание: Построение графика логарифмической функции – 3 балла

18 задание: Решение показательных неравенств — 3 балла

19 задание: Многогранники — 3 балла

20 задание: Тела вращения — 3 балла

Каждый вариант состоит из 20 заданий. Максимальный балл за тест – 35.

0 – 14 баллов — «2» («неудовлетворительно»)

15 – 19 баллов — «3» («удовлетворительно»)

20 – 29 баллов — «4» («хорошо»)

30 – 35 баллов — «5» («отлично» )

Вариант 1

Вычислите 29 – 15. (1 балл)

Упростите выражение . (1 балл)

3) Упростите выражение – 2. (1 балл)

4) Найдите значение , если = -0,8 и . (2 балла)

5) Упростите выражение 7cos²α – 5 + 7sin²α. (2 балла)

6) Решите уравнение = 1. (1 балл)

7) Найти корень уравнения = -х. (2 балла)

8) Найти корень уравнения = 8. (2 балла)

9) Решите неравенство ≤0. (1 балл)

10) Найдите множество значений функции у =– 2. (1 балл)

11) Найдите производную функции f(x) = . (1 балл)

12) Укажите первообразную функции f(x) = 2х + 4х³ – 1. (1 балл)

13) Решите равнение + = . (1 балл)

14) Найдите точки максимума функции у = х³ – 3х² . (2 балла)

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 2; 1. (1 балл)

16) Вычислите площадь фигуры (S), ограниченной линиями у = 4 – х², у = 0, х = 0, х = 2. (3балла)

17) Укажите область определения функции у =. (3балла)

18) Найдите наибольшее целое решение неравенства – 1 0. (3балла)

19) Площади двух граней прямоугольного параллелепипеда равны 56дм² и 192дм², а длина их общего ребра 8дм. Найдите объем параллелепипеда. (3балла)

20) Образующая конуса равна 12см и составляет с плоскостью основания угол 30⁰. Найдите объем конуса, считая = 3. (3балла)

Вариант 2

Вычислите 7 — 3∙. (1 балл)

Упростите выражение . (1 балл)

3) Упростите выражение + — . (1 балл)

4) Найдите значение, если = и 0. (2 балла)

5) Упростите выражение -3sin²α — 6 – 3cos²α. (2 балла)

6) Найти корень уравнения = -х. (1 балл)

7) Решите уравнение = 1. (2 балла)

8) Найти корень уравнения = 125. (2 балла)

9) Решите неравенство ≤ 0. (1 балл)

10) Найдите множество значений функции у = + 4. (1 балл)

11) Найдите производную функции f(x) = . (1 балл)

12) Укажите первообразную функции f(x) = 3х²+ 2х -4. (1 балл)

13) Решите равнение + = (1 балл)

14) Найдите точку минимума функции у = х² — 1. (2 балла)

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 3; 6. (1 балл)

16) Вычислите площадь фигуры (S), ограниченной линиями у = х³+ 1, у = 0, х = 0, х = 2. (3балла)

17) Укажите область определения функции у =. (3балла)

18) Найдите наименьшее целое решение неравенства – 1 0. (3балла)

19) Площади двух граней прямоугольного параллелепипеда равны 35см² и 42см², а длина их общего ребра 7см. Найдите объем параллелепипеда. (3балла)

20) Образующая конуса равна 24см и составляет с плоскостью основания угол 30⁰. Найдите объем конуса, считая = 3. (3балла)

Вариант 3

1) Вычислите 2∙ – 0,9 (1 балл)

2) Упростите выражение (1 балл)

3) Упростите выражение — + (1 балл)

4) Найдите значение , если = — и (2 балла)

5) Упростите выражение -4sin²α +5 – 4cos²α (2 балла)

6) Найти корень уравнения = -х (1 балл)

7) Решите уравнение = -1 (2 балла)

8) Найти корень уравнения = 16 (2 балла)

9) Решите неравенство ≥0 (1 балл)

10) Найдите множество значений функции у = – 1 (1 балл)

11) Найдите производную функции f(x) = (1 балл)

12) Укажите первообразную функции f(x) = 5х⁴ – 2х + 1 (1 балл)

13) Решите равнение + = (1 балл)

14) Найдите точку максимума функции у = 4х – х⁴ (2 балла)

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 6; 6; 7 (1 балл)

16) Вычислите площадь фигуры (S), ограниченной линиями у = 1 – х³, у = 0, х = 0, х = 1. (3балла)

17) Укажите область определения функции у =. (3балла)

18) Найдите наибольшее целое решение неравенства – 1 0. (3балла)

19) Площади двух граней прямоугольного параллелепипеда равны 20см² и 45см², а длина их общего ребра 5см. Найдите объем параллелепипеда. (3балла)

20) Образующая конуса равна 18дм и составляет с плоскостью основания угол 30⁰. Найдите объем конуса, считая = 3. (3балла)

Вариант 4

1)Вычислите 27 – 14. (1 балл)

2)Упростите выражение . (1 балл)

3) Упростите выражение – 2. (1 балл)

4) Найдите значение , если = 0,6 и . (2 балла)

5) Упростите выражение 4cos²α – 5 + 4sin²α. (2 балла)

6) Решите уравнение = -1. (1 балл)

7) Найти корень уравнения = -х. (2 балла)

8) Найти корень уравнения = 25. (2 балла)

9) Решите неравенство ≤0. (1 балл)

10) Найдите множество значений функции у =– 3. (1 балл)

11) Найдите производную функции f(x) = . (1 балл)

12) Укажите первообразную функции f(x) = 2х³+ 4х⁵ – 2. (1 балл)

13) Решите равнение + = . (1 балл)

14) Найдите точки максимума функции у = х⁴ – 8х² (2 балла)

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 6; 3; 1. (1 балл)

16) Вычислите площадь фигуры (S), ограниченной линиями у = -4х – х², у = 0, х = -3, х = -1. (3балла)

17) Укажите область определения функции у =. (3балла)

18) Найдите наибольшее целое решение неравенства 0. (3балла)

19) Площади двух граней прямоугольного параллелепипеда равны 42дм² и 182дм², а длина их общего ребра 7дм. Найдите объем параллелепипеда. (3балла)

Вариант 5

Вычислите 24 — 3∙. (1 балл)

Упростите выражение . (1 балл)

3) Упростите выражение + — . (1 балл)

4) Найдите значение, если = и 0. (2 балла)

5) Упростите выражение -8sin²α — 7 – 8cos²α. (2 балла)

6) Найти корень уравнения = -х. (1 балл)

7) Решите уравнение = -1. (2 балла)

8) Найти корень уравнения = 64. (2 балла)

9) Решите неравенство ≤ 0. (1 балл)

10) Найдите множество значений функции у = + 1. (1 балл)

11) Найдите производную функции f(x) = . (1 балл)

12) Укажите первообразную функции f(x) = 6х⁵+ 2х³-1. (1 балл)

13) Решите равнение + = (1 балл)

14) Найдите точку минимума функции у = 3х⁵ – 5х^3. (2 балла)

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 3; 1. (1 балл)

16) Вычислите площадь фигуры (S), ограниченной линиями у = 2-х³, у = 1, х = -1, х = 1. (3балла)

17) Укажите область определения функции у =. (3балла)

18) Найдите наименьшее целое решение неравенства – 1 ≥ 0. (3балла)

19) Площади двух граней прямоугольного параллелепипеда равны 54 см² и 66 см², а длина их общего ребра 6 см. Найдите объем параллелепипеда. (3балла)

20) Образующая конуса равна 30см и составляет с плоскостью основания угол 30⁰. Найдите объем конуса, считая = 3. (3балла)

Вариант 6

1) Вычислите 7∙ – 11 (1 балл)

2) Упростите выражение (1 балл)

3) Упростите выражение — + (1 балл)

4) Найдите значение , если = — и (2 балла)

5) Упростите выражение 5sin²α +5 +5cos²α (2 балла)

6) Найти корень уравнения = -х (1 балл)

7) Решите уравнение = 0 (2 балла)

8) Найти корень уравнения = 27 (2 балла)

9) Решите неравенство ≥0 (1 балл)

10) Найдите множество значений функции у = – 2 (1 балл)

11) Найдите производную функции f(x) = (1 балл)

12) Укажите первообразную функции f(x) = 7х⁶ – 4х³ + 5 (1 балл)

13) Решите равнение + = (1 балл)

14) Найдите точку максимума функции у = х⁴ – 2х²+4 (2 балла)

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 5; 4; 6 (1 балл)

16) Вычислите площадь фигуры (S), ограниченной линиями у = х² – 4х+5, у = 0, х = 0, х = 4. (3балла)

17) Укажите область определения функции у =. (3балла)

18) Найдите наименьшее целое решение неравенства – 1 ≥0. (3балла)

19) Площади двух граней прямоугольного параллелепипеда равны 32см² и 96см², а длина их общего ребра 4см. Найдите объем параллелепипеда. (3балла)

20) Образующая конуса равна 30дм и составляет с плоскостью основания угол 30⁰. Найдите объем конуса, считая = 3. (3балла)

Вариант 7

1.Вычислите 29 – 15. (1 балл)

2.Упростите выражение . (1 балл)

3) Упростите выражение – 2. (1 балл)

4) Найдите значение , если = -0,8 и . (2 балла)

5) Упростите выражение 7cos²α – 5 + 7sin²α. (2 балла)

6) Решите уравнение = 1. (1 балл)

7) Найти корень уравнения = -х. (2 балла)

8) Найти корень уравнения = 8. (2 балла)

9) Решите неравенство ≤0. (1 балл)

10) Найдите множество значений функции у =– 2. (1 балл)

11) Найдите производную функции f(x) = . (1 балл)

12) Укажите первообразную функции f(x) = 2х + 4х³ – 1. (1 балл)

13) Решите равнение + = . (1 балл)

14) Найдите точки максимума функции у = х³ – 3х² . (2 балла)

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 2; 1. (1 балл)

16) Вычислите площадь фигуры (S), ограниченной линиями у = 4 – х², у = 0, х = 0, х = 2. (3балла)

17) Укажите область определения функции у =. (3балла)

18) Найдите наибольшее целое решение неравенства – 1 0. (3балла)

Вариант 8

1.Вычислите 7 — 3∙. (1 балл)

2.Упростите выражение . (1 балл)

3) Упростите выражение + — . (1 балл)

4) Найдите значение, если = и 0. (2 балла)

5) Упростите выражение -3sin²α — 6 – 3cos²α. (2 балла)

6) Найти корень уравнения = -х. (1 балл)

7) Решите уравнение = 1. (2 балла)

8) Найти корень уравнения = 125. (2 балла)

9) Решите неравенство ≤ 0. (1 балл)

10) Найдите множество значений функции у = + 4. (1 балл)

11) Найдите производную функции f(x) = . (1 балл)

12) Укажите первообразную функции f(x) = 3х²+ 2х -4. (1 балл)

13) Решите равнение + = (1 балл)

14) Найдите точку минимума функции у = х² — 1. (2 балла)

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 3; 6. (1 балл)

16) Вычислите площадь фигуры (S), ограниченной линиями у = х³+ 1, у = 0, х = 0, х = 2. (3балла)

17) Укажите область определения функции у =. (3балла)

18) Найдите наименьшее целое решение неравенства – 1 0. (3балла)

Вариант 9

1) Вычислите 2∙ – 0,9 (1 балл)

2) Упростите выражение (1 балл)

3) Упростите выражение — + (1 балл)

4) Найдите значение , если = — и (2 балла)

5) Упростите выражение -4sin²α +5 – 4cos²α (2 балла)

6) Найти корень уравнения = -х (1 балл)

7) Решите уравнение = -1 (2 балла)

8) Найти корень уравнения = 16 (2 балла)

9) Решите неравенство ≥0 (1 балл)

10) Найдите множество значений функции у = – 1 (1 балл)

11) Найдите производную функции f(x) = (1 балл)

12) Укажите первообразную функции f(x) = 5х⁴ – 2х + 1 (1 балл)

13) Решите равнение + = (1 балл)

14) Найдите точку максимума функции у = 4х – х⁴ (2 балла)

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 6; 6; 7 (1 балл)

16) Вычислите площадь фигуры (S), ограниченной линиями у = 1 – х³, у = 0, х = 0, х = 1. (3балла)

17) Укажите область определения функции у =. (3балла)

18) Найдите наибольшее целое решение неравенства – 1 0. (3балла)

Вариант 10

1)Вычислите 27 – 14. (1 балл)

2)Упростите выражение . (1 балл)

3) Упростите выражение – 2. (1 балл)

4) Найдите значение , если = 0,6 и . (2 балла)

5) Упростите выражение 4cos²α – 5 + 4sin²α. (2 балла)

6) Решите уравнение = -1. (1 балл)

7) Найти корень уравнения = -х. (2 балла)

8) Найти корень уравнения = 25. (2 балла)

9) Решите неравенство ≤0. (1 балл)

10) Найдите множество значений функции у =– 3. (1 балл)

11) Найдите производную функции f(x) = . (1 балл)

12) Укажите первообразную функции f(x) = 2х³+ 4х⁵ – 2. (1 балл)

13) Решите равнение + = . (1 балл)

14) Найдите точки максимума функции у = х⁴ – 8х² (2 балла)

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 6; 3; 1. (1 балл)

16) Вычислите площадь фигуры (S), ограниченной линиями у = -4х – х², у = 0, х = -3, х = -1. (3балла)

17) Укажите область определения функции у =. (3балла)

18) Найдите наибольшее целое решение неравенства 0. (3балла)

Вариант 11

Вычислите 24 — 3∙. (1 балл)

Упростите выражение . (1 балл)

3) Упростите выражение + — . (1 балл)

4) Найдите значение, если = и 0. (2 балла)

5) Упростите выражение -8sin²α — 7 – 8cos²α. (2 балла)

6) Найти корень уравнения = -х. (1 балл)

7) Решите уравнение = -1. (2 балла)

8) Найти корень уравнения = 64. (2 балла)

9) Решите неравенство ≤ 0. (1 балл)

10) Найдите множество значений функции у = + 1. (1 балл)

11) Найдите производную функции f(x) = . (1 балл)

12) Укажите первообразную функции f(x) = 6х⁵+ 2х³-1. (1 балл)

13) Решите равнение + = (1 балл)

14) Найдите точку минимума функции у = 3х⁵ – 5х^3. (2 балла)

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 3; 1. (1 балл)

16) Вычислите площадь фигуры (S), ограниченной линиями у = 2-х³, у = 1, х = -1, х = 1. (3балла)

17) Укажите область определения функции у =. (3балла)

18) Найдите наименьшее целое решение неравенства – 1 ≥ 0. (3балла)

Вариант 12

1) Вычислите 7∙ – 11 (1 балл)

2) Упростите выражение (1 балл)

3) Упростите выражение — + (1 балл)

4) Найдите значение , если = — и (2 балла)

5) Упростите выражение 5sin²α +5 +5cos²α (2 балла)

6) Найти корень уравнения = -х (1 балл)

7) Решите уравнение = 0 (2 балла)

8) Найти корень уравнения = 27 (2 балла)

9) Решите неравенство ≥0 (1 балл)

10) Найдите множество значений функции у = – 2 (1 балл)

11) Найдите производную функции f(x) = (1 балл)

12) Укажите первообразную функции f(x) = 7х⁶ – 4х³ + 5 (1 балл)

13) Решите равнение + = (1 балл)

14) Найдите точку максимума функции у = х⁴ – 2х²+4 (2 балла)

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 5; 4; 6 (1 балл)

16) Вычислите площадь фигуры (S), ограниченной линиями у = х² – 4х+5, у = 0, х = 0, х = 4. (3балла)

17) Укажите область определения функции у =. (3балла)

18) Найдите наименьшее целое решение неравенства – 1 ≥0. (3балла)

Вариант 13

1)Вычислите 29 – 15. (1 балл)

2)Упростите выражение . (1 балл)

3) Упростите выражение – 2. (1 балл)

4) Найдите значение , если = -0,8 и . (2 балла)

5) Упростите выражение 7cos²α – 5 + 7sin²α. (2 балла)

6) Решите уравнение = 1. (1 балл)

7) Найти корень уравнения = -х. (2 балла)

8) Найти корень уравнения = 8. (2 балла)

9) Решите неравенство ≤0. (1 балл)

10) Найдите множество значений функции у =– 2. (1 балл)

11) Найдите производную функции f(x) = . (1 балл)

12) Укажите первообразную функции f(x) = 2х + 4х³ – 1. (1 балл)

13) Решите равнение + = . (1 балл)

14) Найдите точки максимума функции у = х³ – 3х² . (2 балла)

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 2; 1. (1 балл)

16) Вычислите площадь фигуры (S), ограниченной линиями у = 4 – х², у = 0, х = 0, х = 2. (3балла)

17) Укажите область определения функции у =. (3балла)

18) Найдите наибольшее целое решение неравенства – 1 0. (3балла)

Вариант 14

1)Вычислите 7 — 3∙. (1 балл)

2)Упростите выражение . (1 балл)

3) Упростите выражение + — . (1 балл)

4) Найдите значение, если = и 0. (2 балла)

5) Упростите выражение -3sin²α — 6 – 3cos²α. (2 балла)

6) Найти корень уравнения = -х. (1 балл)

7) Решите уравнение = 1. (2 балла)

8) Найти корень уравнения = 125. (2 балла)

9) Решите неравенство ≤ 0. (1 балл)

10) Найдите множество значений функции у = + 4. (1 балл)

11) Найдите производную функции f(x) = . (1 балл)

12) Укажите первообразную функции f(x) = 3х²+ 2х -4. (1 балл)

13) Решите равнение + = (1 балл)

14) Найдите точку минимума функции у = х² — 1. (2 балла)

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 3; 6. (1 балл)

16) Вычислите площадь фигуры (S), ограниченной линиями у = х³+ 1, у = 0, х = 0, х = 2. (3балла)

17) Укажите область определения функции у =. (3балла)

18) Найдите наименьшее целое решение неравенства – 1 0. (3балла)

Вариант 15

1) Вычислите 2∙ – 0,9 (1 балл)

2) Упростите выражение (1 балл)

3) Упростите выражение — + (1 балл)

4) Найдите значение , если = — и (2 балла)

5) Упростите выражение -4sin²α +5 – 4cos²α (2 балла)

6) Найти корень уравнения = -х (1 балл)

7) Решите уравнение = -1 (2 балла)

8) Найти корень уравнения = 16 (2 балла)

9) Решите неравенство ≥0 (1 балл)

10) Найдите множество значений функции у = – 1 (1 балл)

11) Найдите производную функции f(x) = (1 балл)

12) Укажите первообразную функции f(x) = 5х⁴ – 2х + 1 (1 балл)

13) Решите равнение + = (1 балл)

14) Найдите точку максимума функции у = 4х – х⁴ (2 балла)

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 6; 6; 7 (1 балл)

16) Вычислите площадь фигуры (S), ограниченной линиями у = 1 – х³, у = 0, х = 0, х = 1. (3балла)

17) Укажите область определения функции у =. (3балла)

18) Найдите наибольшее целое решение неравенства – 1 0. (3балла)

Вариант 16

1)Вычислите 27 – 14. (1 балл)

2)Упростите выражение . (1 балл)

3) Упростите выражение – 2. (1 балл)

4) Найдите значение , если = 0,6 и . (2 балла)

5) Упростите выражение 4cos²α – 5 + 4sin²α. (2 балла)

6) Решите уравнение = -1. (1 балл)

7) Найти корень уравнения = -х. (2 балла)

8) Найти корень уравнения = 25. (2 балла)

9) Решите неравенство ≤0. (1 балл)

10) Найдите множество значений функции у =– 3. (1 балл)

11) Найдите производную функции f(x) = . (1 балл)

12) Укажите первообразную функции f(x) = 2х³+ 4х⁵ – 2. (1 балл)

13) Решите равнение + = . (1 балл)

14) Найдите точки максимума функции у = х⁴ – 8х² (2 балла)

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 6; 3; 1. (1 балл)

16) Вычислите площадь фигуры (S), ограниченной линиями у = -4х – х², у = 0, х = -3, х = -1. (3балла)

17) Укажите область определения функции у =. (3балла)

18) Найдите наибольшее целое решение неравенства 0. (3балла)

Вариант 17

1)Вычислите 24 — 3∙. (1 балл)

2)Упростите выражение . (1 балл)

3) Упростите выражение + — . (1 балл)

4) Найдите значение, если = и 0. (2 балла)

5) Упростите выражение -8sin²α — 7 – 8cos²α. (2 балла)

6) Найти корень уравнения = -х. (1 балл)

7) Решите уравнение = -1. (2 балла)

8) Найти корень уравнения = 64. (2 балла)

9) Решите неравенство ≤ 0. (1 балл)

10) Найдите множество значений функции у = + 1. (1 балл)

11) Найдите производную функции f(x) = . (1 балл)

12) Укажите первообразную функции f(x) = 6х⁵+ 2х³-1. (1 балл)

13) Решите равнение + = (1 балл)

14) Найдите точку минимума функции у = 3х⁵ – 5х^3. (2 балла)

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 3; 1. (1 балл)

16) Вычислите площадь фигуры (S), ограниченной линиями у = 2-х³, у = 1, х = -1, х = 1. (3балла)

17) Укажите область определения функции у =. (3балла)

18) Найдите наименьшее целое решение неравенства – 1 ≥ 0. (3балла)

Вариант 18

1) Вычислите 7∙ – 11 (1 балл)

2) Упростите выражение (1 балл)

3) Упростите выражение — + (1 балл)

4) Найдите значение , если = — и (2 балла)

5) Упростите выражение 5sin²α +5 +5cos²α (2 балла)

6) Найти корень уравнения = -х (1 балл)

7) Решите уравнение = 0 (2 балла)

8) Найти корень уравнения = 27 (2 балла)

9) Решите неравенство ≥0 (1 балл)

10) Найдите множество значений функции у = – 2 (1 балл)

11) Найдите производную функции f(x) = (1 балл)

12) Укажите первообразную функции f(x) = 7х⁶ – 4х³ + 5 (1 балл)

13) Решите равнение + = (1 балл)

14) Найдите точку максимума функции у = х⁴ – 2х²+4 (2 балла)

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 5; 4; 6 (1 балл)

16) Вычислите площадь фигуры (S), ограниченной линиями у = х² – 4х+5, у = 0, х = 0, х = 4. (3балла)

17) Укажите область определения функции у =. (3балла)

18) Найдите наименьшее целое решение неравенства – 1 ≥0. (3балла)

Вариант 19

1)Вычислите 29 – 15. (1 балл)

2)Упростите выражение . (1 балл)

3) Упростите выражение – 2. (1 балл)

4) Найдите значение , если = -0,8 и . (2 балла)

5) Упростите выражение 7cos²α – 5 + 7sin²α. (2 балла)

6) Решите уравнение = 1. (1 балл)

7) Найти корень уравнения = -х. (2 балла)

8) Найти корень уравнения = 8. (2 балла)

9) Решите неравенство ≤0. (1 балл)

10) Найдите множество значений функции у =– 2. (1 балл)

11) Найдите производную функции f(x) = . (1 балл)

12) Укажите первообразную функции f(x) = 2х + 4х³ – 1. (1 балл)

13) Решите равнение + = . (1 балл)

14) Найдите точки максимума функции у = х³ – 3х² . (2 балла)

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 2; 1. (1 балл)

16) Вычислите площадь фигуры (S), ограниченной линиями у = 4 – х², у = 0, х = 0, х = 2. (3балла)

17) Укажите область определения функции у =. (3балла)

18) Найдите наибольшее целое решение неравенства – 1 0. (3балла)

Вариант 20

1)Вычислите 7 — 3∙. (1 балл)

2)Упростите выражение . (1 балл)

3) Упростите выражение + — . (1 балл)

4) Найд

infourok.ru

Пакет заданий по математике для студентов 1 курса Башкирского строительно-архитектурного колледжа

Содержание

Пояснительная записка -2-

2. Проверочные задания по темам:

2.1 Вычисление пределов. Раскрытие неопределенностей. -3-

2.2 Линейные уравнения и неравенства -7-

2.3 Преобразование выражений, содержащих радикалы и степени с дробными показателями. -11-

2.4 Иррациональные уравнения -12-

2.5 Корень п-ой степени и его свойства -13-

2.6 Определение и свойства логарифма -17-

2.7 Логарифмические уравнения -18-

2.8 Практикум решения показательных уравнений -23-

2.9 Показательные уравнения -26

2.10 Правильная пирамида -30-

2.11. Индивидуальная контролирующая проверочная работа по теме: «Пирамида» -31-

2.12 Цилиндр. Конус. Шар. -35-

Пояснительная записка.

Курс математики – один из базовых курсов, на которые опираются общепрофессиональные и специальные дисциплины, дисциплины специализации.

Для закрепления теоретических знаний и приобретения необходимых практических умений программной дисциплины по математике предусматриваются практические занятия, которые рекомендуются проводить после изучения соответствующей темы.

Данная методическая разработка составлена для преподавателей математики для оказания методической помощи для выдачи заданий студентам 1 курса колледжей и техникумов. В данной методической разработке предложены такие темы, как вычисление пределов, раскрытие неопределенностей, линейные уравнения и неравенства, преобразование выражений, содержащих радикалы и степени с дробными показателями, иррациональные уравнения, корень п-ой степени и его свойства, определение и свойства логарифма, логарифмические и показательные уравнения, пирамида, цилиндр, конус, шар.

В результате решения практических заданий студент должен иметь представление:

о роли и месте математики в современном мире, общности ее понятий и представлений;

о методах решения некоторых практических задач с использованием элементов математического анализа.

Знать:

базовые понятия дифференциального исчисления;

способы решения простейших видов показательных и логарифмических уравнений;

способы решения простейших и иррациональных уравнений;

способы раскрытия неопределенностей при вычислении пределов;

2. Проверочные задания по темам:

2.1 Вычисление пределов. Раскрытие неопределенностей

Н
айти пределы функций

вариант 1.

2.1 Вычисление пределов. Раскрытие неопределенностей

Найти пределы функций

вариант 2.

2.1 Вычисление пределов. Раскрытие неопределенностей.

Н
айти пределы функций

вариант 3.

2.1 Вычисление пределов. Раскрытие неопределенностей.

Н
айти пределы функций

вариант 4.

2. 2 Линейные уравнения и неравенства

Р
ешить неравенства:

Решить уравнения:

2.2 Линейные уравнения и неравенства

Р
ешить неравенства:

Р
ешить уравнения:

2.2 Линейные уравнения и неравенства

Р
ешить уравнения:

Решите неравенства:

2.2 Линейные уравнения и неравенства

Р
ешить уравнения:

Решить неравенства:

2.3 Преобразование выражений, содержащих радикалы

и степени с дробными показателями.

У
простите выражения:

2.4 Иррациональные уравнения

Р

ешить уравнения:

2.5 Корень п-ой степени и его свойства

1 вариант.

В
ычислить:
Н
айдите значение числового выражения:

П
редставьте выражение в виде дроби, знаменатель которой не содержит знака корня:

Н
айдите значение выражения:

В
ыполнить действия:
Р
ешить уравнения:

2.5 Корень п-ой степени и его свойства

2 вариант.

В
ычислить:
Н
айдите значение числового выражения:

П
редставьте выражение в виде дроби, знаменатель которой не содержит знака корня:

Н
айдите значение выражения:

В
ыполнить действия:
Р
ешить уравнения:

2.5 Корень п-ой степени и его свойства

3 вариант.

В
ычислить:
Н
айдите значение числового выражения:

П
редставьте выражение в виде дроби, знаменатель которой не содержит знака корня:

Н
айдите значение выражения:

В
ыполнить действия:
Решить уравнения:

2.5 Корень п-ой степени и его свойства

4 вариант.

В
ычислить:
Н
айдите значение числового выражения:

П
редставьте выражение в виде дроби, знаменатель которой не содержит знака корня:

Н
айдите значение выражения:

В
ыполнить действия:
Решить уравнения:

2.6 Определение и свойства логарифма

В
ычислить логарифмы:

Вычислите:

Найдите А по его логарифму:

2.7 Логарифмические уравнения

Решите уравнения:

2.7. Логарифмические уравнения

В
ариант 1

Решить уравнение:

Д
ополнительные задания:

2.7. Логарифмические уравнения

Вариант 2

Р
ешить уравнение:

Дополнительные задания:

2.7. Логарифмические уравнения

Вариант 3

Решить уравнение:

Дополнительные задания:

2.7. Логарифмические уравнения

Вариант 4

Решить уравнение:

Дополнительные задания:

2. 8. Практикум по решению показательных уравнений

Вариант №1

Решите уравнения

2^х=4
3^х=81
4^х=2

5^х= ;
=4;
7^х=1

=25;
7^–х= –;

=1
2^6–х=2^3х–2
2^х– 2^х–2 =3

3^х+3– 2•3^х–1–4•3^х–2 =17

Решите уравнение вынесением за скобки

2^х+2^х–1 +2^х–2 56

10^х+10^х–1=1100

3^х+3^3–х=12

Решите уравнение графически

2^х=х–1

2.8. Практикум по решению показательных уравнений

Вариант №2

9^х=27
3^х=9
4^х=64

6^х= ;
=27;
8^х=1

=36;
8^–х= –;

=1
3^5–х=3^2х–1
5^х+1– 5 =500

2•3^х+1 +2•3^2–х =56

Решите уравнение вынесением за скобки

2•3^3х–1+27^х–2/3=^{9^х–1+2•3^2х–1}

6^х+6^х+2=222

Решите уравнение графически

0,5^х =2х

2.8. Практикум по решению показательных уравнений

Вариант №3

5^х=25
6^х=216
100^х=10000

8^х= ;
=125;
5^х=1

=16;
5^–х= –;

=1
4^9–х=4^2х–7
3^х–2– 3^х–3 =36

2^х+ 2^х–1 +2^х–2 =3^х–3^х–1+3^х–2

Решите уравнение вынесением за скобки

3^х+1–4:3^х–1=45

2^х+2^х+2=40

2^2х+6+2^х+7=17

Решите уравнение графически

х =3^х–2

2.9. Показательные уравнения

вариант 1

Р
ешить показательные уравнения:

2.9. Показательные уравнения

вариант 2

Р

ешить показательные уравнения:

2.9. Показательные уравнения

вариант 3

Р
ешить показательные уравнения:

2.9. Показательные уравнения

вариант 4

Решить показательные уравнения:

2.10. Правильная пирамида

Задача № 1

Боковое ребро правильной треугольной пирамиды равно 5 см., а высота – 3 см. Найдите площадь полной поверхности.

Задача № 2

Апофема правильной шестиугольной пирамиды равна 5 см, а высота – 4 см. Найдите площадь боковой поверхности.

Задача № 3.

В правильной треугольной пирамиде боковые грани наклонены к основанию под углом 60⁰. Расстояние от вершины основания до боковой грани равно 3. Найдите площадь боковой поверхности пирамиды.

Задачи № 4

В правильной четырехугольной пирамиде боковые грани наклонены к основанию под углом 60⁰, а расстояние от середины стороны основания до противоположной боковой грани равно 4. Найдите площадь боковой поверхности.

2.11. Индивидуальная контролирующая проверочная работа.

Вариант 1

Найдите высоту правильной шестиугольной пирамиды, если сторона ее основания равна а, апофема h

Сторона основания правильной четырехугольной пирамиды равна а, а высота h. Определить полную поверхность пирамиды.

Найдите высоту правильной треугольной пирамиды, у которой боковая поверхность равна
60 см², а полная поверхность 108 см².

2.11. Индивидуальная контролирующая проверочная работа по теме: «Пирамида»

Вариант 2

Найдите высоту правильной треугольной пирамиды, если сторона ее основания равна а, а апофема h.

Боковое ребро правильной четырехугольной пирамиды, равное 12 см, образует с плоскостью основания угол в 60⁰. Найдите боковую поверхность^{пирамиды.}

Найдите высоту правильной треугольной пирамиды, у которой площадь основания равна
27см², а полная поверхность 72см^2.

2.11. Индивидуальная контролирующая проверочная работа по теме: «Пирамида»

Вариант 3

Сторона основания правильной четырехугольной пирамиды равна а. Двугранные углы при основании равны . Определите полную поверхность.

Найдите величину двугранного угла при основании правильной четырехугольной пирамиды, если ее боковые ребра наклонены к плоскости основания под углом 30⁰.

Найдите высоту правильной треугольной пирамиды, у которой площадь основания равна
27см², а полная поверхность 72см².

2.11. Индивидуальная контролирующая

проверочная работа по теме: «Пирамида»

Вариант 4

Найдите величину двугранного угла при основании правильной четырехугольной пирамиды, если ее боковые ребра наклонены к плоскости основания под углом 60⁰.

Высота боковой грани правильной четырехугольной пирамиды равна 10 см. Определите полную поверхность пирамиды, если боковая грань наклонна к плоскости основания под углом 60^0.

Найдите высоту правильной треугольной пирамиды, у которой боковая поверхность равна
60см², а полная поверхность 108см².

2.12. Задания по теме: «Цилиндр. Конус. Шар».

Вариант 1

1. Длина окружности основания цилиндра равна 12, высота 10 см. Найти объем цилиндра.

2. Осевым сечением конуса является правильный треугольник. Образующая конуса равна 6v3. Вычислить высоту конуса.

3. Через середину радиуса шара проведено сечение, найти площадь, если радиус шара равен 6 см.

2.12. Задания по теме: «Цилиндр. Конус. Шар».

Вариант 2

1. Осевым сечением цилиндра является квадрат, площадь которого 8 см². Вычислите боковую поверхность цилиндра.

2. Осевым сечением конуса является правильный треугольник, площадь которого 64 см² . Найти объем цилиндра.

3. Осевым сечением цилиндра является квадрат, площадь которого 64 см² . Найти объем цилиндра.

2.12. Задания по теме: «Цилиндр. Конус. Шар».

Вариант 3

1. Длина окружности основания цилиндра равна 12, высота 10 см. Найти объем цилиндра.

3. Через середину радиуса шара проведено сечение, найти площадь, если радиус шара равен 6 см.

2.12. Задания по теме: «Цилиндр. Конус. Шар».

Вариант 4

1. Осевым сечением цилиндра является квадрат, площадь которого 8 см². Вычислите боковую поверхность цилиндра.

2. Осевым сечением конуса является правильный треугольник, площадь которого 64 см² . Найти объем цилиндра.

Осевым сечением цилиндра является квадрат, площадь которого 64 см² . Найти объем цилиндра.

Список литературы:

1. Лисичкин В.Т., Соловейчик И.Л.

Математика: Учеб. Пособие для техникумов.- М.:

Высшая школа, 2005

2. Алгебра и начала анализа. Учебник для 10-11 кл. средней школы./ А.М. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и др.: Под ред. А.Н. Колмогоров.- 2-е изд.- М.: Просвещение, 2008.

3. Апанасов П.Т., Орлов М.И.

Сборник задач по математике: Учебное пособие для техникумов.- М.: Высшая школа, 1987.

4. М.И.Башмаков.

Математика.- 2-е издание- М.: «Высшая школа». Учебное пособие для профессионально- технических училищ, 2001

5. Геометрия: Учебник для 10-11 кл. средней школы/ Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев и др.- М.: Просвещение, 2008

www.metod-kopilka.ru

Конспекты лекций СПО по математике 1 курс

Государственное бюджетное образовательное учреждение

среднего профессионального образования

«Губернский колледж г.Сызрани»

Технический профиль

КОНСПЕКТ ЛЕКЦИЙ
(тезисы лекций/СПО/ 1 курс)
Преподаватель Барабанова Л.Н.
РАССМОТРЕНО ОДОБРЕНО
на заседании ПЦК Методическим советом
естественнонаучного цикла технического профиля
Протокол № _ ГБОУ СПО «ГК г. Сызрани»
от «_» _ 2014 г. протокол № от «» 2014 г.
Председатель ___
Барабанова Л.Н. Методист _
Барабанова Л.Н.
Преподаватель _ Барабанова Л.Н.
Методические рекомендации для студентов СПО 1 курса разработаны преподавателем для использования их при самостоятельном изучении
материала по математике.
УТВЕРЖДАЮ
Заместитель директора
Руководитель технического профиля
_______ В.В. Колосов
ТЕМА: «ТРИГОНОМЕТРИЧЕСКИЕ ВЫРАЖЕНИЯ»
План лекции.
Определения синуса, косинуса, тангенса, котангенса. Свойства синуса, косинуса, тангенса, котангенса.
Радианная мера угла. Соотношения между тригонометрическими функциями одного и того же угла.
Применение основных тригонометрических формул к преобразованию выражений.
Формулы приведения.
Формулы сложения.
Формулы двойного угла.
Формулы половинного угла. Формулы суммы и разности тригонометрических функций.
Контрольные вопросы для самоподготовки.
Учебник: Алгебра и начала анализа 10 – 11. Колмогоров А.Н. М. Просвещение, 2005г. Вопросы № 1 – 10, страница 88 – 91.
Литературные источники.
Учебник: Алгебра и начала анализа 10 – 11. Колмогоров А.Н. М. Просвещение, 2005г. § 1, пункт 1.
ТЕМА : « ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ».
План лекции.
Тригонометрические функции и их графики.
Функции и их графики.
Четные и нечетные функции. Периодичность тригонометрических функций.
Возрастание и убывание функций. Экстремумы.
Исследование функций.
Контрольные вопросы для самоподготовки.
Учебник: Алгебра и начала анализа 10 – 11. Колмогоров А.Н. М. Просвещение, 2005г. Вопросы № 10 – 15, страница 91 – 92.
Литературные источники.
Учебник: Алгебра и начала анализа 10 – 11. Колмогоров А.Н. М. Просвещение, 2005г. § 1, пункт 2. § 2, пункт 3, 4, 5, 6.
ТЕМА: «ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ».
План лекции.
Арксинус, арккосинус, арктангенс, арккотангенс.
Решение простейших тригонометрических уравнений.
Решение тригонометрических уравнений.
Решение тригонометрических уравнений и систем уравнений.
Контрольные вопросы для самоподготовки.
Учебник: Алгебра и начала анализа 10 – 11. Колмогоров А.Н. М. Просвещение, 2005г. Вопросы № 22, 23, 24, страница 93 – 94.
Литературные источники.
Учебник: Алгебра и начала анализа 10 – 11. Колмогоров А.Н. М. Просвещение, 2005г. § 3, пункт 8, 9, 11.
ТЕМА: «ПРОИЗВОДНАЯ».
План лекции.
Приращение функции
Понятие о производной.
Правила вычисления производных.
Производная сложной функции.
Производные тригонометрических функций.
Примеры вычисления производных.
Контрольные вопросы для самоподготовки.
Учебник: Алгебра и начала анализа 10 – 11. Колмогоров А.Н. М. Просвещение, 2005г. Вопросы № 1 – 3, страница 166.
Литературные источники.
Учебник: Алгебра и начала анализа 10 – 11. Колмогоров А.Н. М. Просвещение, 2005г. § 4, пункт 12, 13, 15,16, 17.
ТЕМА: «ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ».
План лекции.
Метод интервалов.
Касательная к графику функции.
Производная в физике и технике.
Признак возрастания (убывания) функции.
Критические точки функции, максимумы и минимумы.
Применение производной к исследованию функции.
Наибольшее и наименьшее значение функции.
Контрольные вопросы для самоподготовки.
Учебник: Алгебра и начала анализа 10 – 11. Колмогоров А.Н. М. Просвещение, 2005г. Вопросы № 4, 5, 9, 10, 11, страница 167 – 168.
Литературные источники.
Учебник: Алгебра и начала анализа 10 – 11. Колмогоров А.Н. М. Просвещение, 2005г. § 5, пункт 18, 19, 21, § 6, пункт 22, 23, 24, 25.
ТЕМА: «ПЕРВООБРАЗНАЯ»
План лекции.
Определение первообразной.
Основное свойство первообразной
Правила нахождения первообразных.
Площадь криволинейной трапеции.
Контрольные вопросы для самоподготовки.
Учебник: Алгебра и начала анализа 10 – 11. Колмогоров А.Н. М. Просвещение, 2005г. Вопросы № 1 – 4, страница 199 – 200.
Литературные источники.
Учебник: Алгебра и начала анализа 10 – 11. Колмогоров А.Н. М. Просвещение, 2005г. § 7, пункт 26, 27, 28, § 8, пункт 29.
ТЕМА: «ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ».
План лекции.
Корень n – степени и его свойства.
Иррациональные уравнения.
Степень с рациональным показателем.
Показательная функция.
Решение показательных уравнений.
Решение показательных неравенств.
Контрольные вопросы для самоподготовки.
Учебник: Алгебра и начала анализа 10 – 11. Колмогоров А.Н. М. Просвещение, 2005г. Вопросы № 1 – 5, страница 261 – 262.
Литературные источники.
Учебник: Алгебра и начала анализа 10 – 11. Колмогоров А.Н. М. Просвещение, 2005г. § 9, пункт 32, 33, 34, § 10, пункт 35, 36.
ТЕМА: «ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ».
План лекции.
Основные свойства логарифмов.
Логарифмическая функция.
Решение логарифмических уравнений.
Решение логарифмических неравенств.
Контрольные вопросы для самоподготовки.
Учебник: Алгебра и начала анализа 10 – 11. Колмогоров А.Н. М. Просвещение, 2005г. Вопросы № 6 – 9, страница 262 – 263.
Литературные источники.
Учебник: Алгебра и начала анализа 10 – 11. Колмогоров А.Н. М. Просвещение, 2005г. § 10, пункт 37, 38, 39.
ТЕМА: «ПРОИЗВОДНАЯ ПОКАЗАТЕЛЬНОЙ, ЛОГАРИФМИЧЕСКОЙ И СТЕПЕННОЙ ФУНКЦИИ».
План лекции.
Производная показательной функции.
Первообразная показательной функции.
Производная логарифмической функции.
Степенная функция и ее производная.
Контрольные вопросы для самоподготовки.
Учебник: Алгебра и начала анализа 10 – 11. Колмогоров А.Н. М. Просвещение, 2005г. Вопросы № 10 – 12, страница 263 – 264.
Литературные источники.
Учебник: Алгебра и начала анализа 10 – 11. Колмогоров А.Н. М. Просвещение, 2005г. § 11, пункт 41, 42, 43.
ТЕМА: «ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ».
План лекции.
Аксиомы стереометрии.
Следствия из аксиом стереометрии.
Параллельные и скрещивающие прямые в пространстве.
Параллельность прямых и плоскостей.
Изображение пространственных фигур на плоскости.
Контрольные вопросы для самоподготовки.
Учебник Геометрия 7 – 11. Погорелов А.В. М. Просвещение. 2005 г.
Вопросы 1 – 5, страница 237. Вопросы 1, 2, 5, 7, 12.
Литературные источники.
Учебник Геометрия 7 – 11. Погорелов А.В. М. Просвещение. 2005 г.
§ 15, пункт 130 – 133, § 16, пункт 136 – 139, 142.
ТЕМА: «ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ».
План лекции.
Перпендикулярность прямых.
Перпендикулярность прямых и плоскостей.
Перпендикуляр и наклонная.
Перпендикулярность плоскостей.
Расстояние между скрещивающимися прямыми.
Контрольные вопросы для самоподготовки.
Учебник Геометрия 7 – 11. Погорелов А.В. М. Просвещение. 2005 г.
Вопросы 1, 3, 7, 8, 9, 11, 15, страница 263.
Литературные источники.
Учебник Геометрия 7 – 11. Погорелов А.В. М. Просвещение. 2005 г.
§ 17, пункт 143 – 150.
ТЕМА: «МНОГОГРАННИКИ».
План лекции.
Многогранники.
Призма. Прямая призма
Изображение призмы и построение ее сечений.
Параллелепипед.
Прямоугольный параллелепипед.
Пирамида. Правильная пирамида.
Правильные многогранники.
Контрольные вопросы для самоподготовки.
Учебник Геометрия 7 – 11. Погорелов А.В. М. Просвещение. 2005 г.
Вопросы 1 – 9, 11 – 12, 15 – 17, 19, 23, 24, 27, 32, 33, 34, 36, стр 311.
Литературные источники.
Учебник Геометрия 7 – 11. Погорелов А.В. М. Просвещение. 2005 г.
§ 19, пункт 166 – 172, 174, 176, 178 – 180.
ТЕМА: «ТЕЛА ВРАЩЕНИЯ».
План лекции.
Цилиндр.
Конус.
Шар.
Контрольные вопросы для самоподготовки.
Учебник Геометрия 7 – 11. Погорелов А.В. М. Просвещение. 2005 г.
Вопросы 1 – 3, 6 – 8, 10, 12 – 13, страница 333.
Литературные источники.
Учебник Геометрия 7 – 11. Погорелов А.В. М. Просвещение. 2005 г.
§ 20, пункт 181, 184, 187.
ТЕМА: «ОБЪЕМЫ МНОГОГРАННИКОВ».
План лекции.
Понятие объема.
Объем прямоугольного параллелепипеда.
Объем наклонного параллелепипеда.
Объем призмы.
Объем пирамиды.
Контрольные вопросы для самоподготовки.
Учебник Геометрия 7 – 11. Погорелов А.В. М. Просвещение. 2005 г.
Вопросы 1 – 9, страница 349.
Литературные источники.
Учебник Геометрия 7 – 11. Погорелов А.В. М. Просвещение. 2005 г.
§ 21, пункт 194 – 200, 174.
ТЕМА: «ОБЪЕМЫ И ПОВЕРХНОСТИ ТЕЛ ВРАЩЕНИЯ».
План лекции.
Объем цилиндра.
Объем конуса.
Общая формула для объемов тел вращения.
Объем шара.
Объем шарового сегмента и сектора.
Площадь боковой поверхности цилиндра.
Площадь боковой поверхности конуса.
Площадь сферы.
Контрольные вопросы для самоподготовки.
Учебник Геометрия 7 – 11. Погорелов А.В. М. Просвещение. 2005 г.
Вопросы 1 – 9, страница 360.
Литературные источники.
Учебник Геометрия 7 – 11. Погорелов А.В. М. Просвещение. 2005 г.
§ 22, пункт 202 – 210.
infourok.ru

Проект по алгебре (11 класс) по теме: Социальный проект «Краткий справочный материал по математике для студентов 1 курса колледжа (теория и практика)»

Департамент образования города Москвы

Государственное бюджетное образовательное учреждение

среднего профессионального образования

Педагогический колледж №18 «Митино»

Социальный проект
Краткий справочный материал

по математике

для студентов 1 курса

( теория и практика )

Руководитель и автор проекта: Юнанова Ю.В.

Москва, 2012

Паспорт проектной работы

1. Название проекта: Краткий справочный материал по математике для студентов 1 курса ( теория и практика)

2. Руководитель проекта: Юнанова Ю.В., ГБОУ СПО ПК №18 «Митино»

3. Консультанты проекта: Шевченко А.Е., заслуженный учитель РФ, доцент

4. Учебный предмет, в рамках которого проводится работа по проекту: математика.

5. Учебные дисциплины, близкие к теме проекта : математика.

6. Возраст студентов, на который рассчитан проект: 15-21 лет

7. Состав проектной группы :

№ п\п	ФИО студента	№ группы	Предполагаемая роль
1	Петрова Мария	11	Представление проекта
2	Ким Анжела	11	Составление краткого справочного материала
3	Анисимова Тамара	11	Презентация
4	Прянишникова Ксения	11	Составление краткого справочного материала
5	Рагузина Ирина	11	Презентация
6	Соколова Анастасия	11	Представление проекта
7	Куракина Евгения	11	Составление краткого справочного материала
8	Погорелова Екатерина	11	Составление краткого справочного материала

8. Тип проекта: практико-ориентированный, информационный, творческий .

9. Заказчик проекта: ГБОУ СПО Педагогический колледж №18 «Митино»

10. Проблема проекта: программа по математике 1 курса очень насыщенная: изучаются разделы алгебры, геометрии, начала математического анализа, комбинаторики, статистики и теории вероятности. На изучение некоторых тем отводится небольшой объем часов. Для слабоуспевающих студентов, для студентов, пропустивших занятия, нет кратного изложения теоретического материала с примерами решения типовых заданий, который помог бы им овладеть необходимыми знаниями , умениями и навыками по математике.

11. Цель проекта: улучшение качества формирования математической компетенции — знаний, умений и навыков с использованием краткого теоретического материала по математике 1 курса с примерами решения типовых заданий.

12. Задачи проекта:

— оказание помощи студентам при изучении курса математики 1 курса,

— поддержка и создание психолого-педагогических условий и среды для развития и реализации творческого потенциала студентов,

— организация совместной коллективно – творческой деятельности студентов.

13. Вопросы проекта:

— какие ключевые темы изучаются к каждом разделе;

— что должны знать и уметь студенты в результате изучения ключевых тем;

— какой краткий теоретический материал выделить по каждой выбранной теме;

— какие привести примеры типовых заданий с решениями по каждой выбранной теме;

— какие задания подобрать по каждой теме для самостоятельной работы студентов;

— как скомпоновать и оформить материалы проектной деятельности.

14. Необходимое оборудование:

— Учебные издания : 1. Алимов Ш.А. Алгебра и начала анализа. 10-11 кл.- М., 2010

2. Башмаков М.И.Алгебра и начала математического анализа(базовый уровень). 10 кл. М. 2010

3. Погорелов А.В. Геометрия 10-11 “Базовый уровень” — М. 2011

4. Тюрин Ю.Н. Теория вероятностей и статистика- М. 2010

— ПК;

— Принтер.

15. Аннотация:

Настоящий проект предназначен для студентов 1 курса и может быть также использован в работе преподавателей математики. Он поможет систематизировать имеющиеся знания по математике и ликвидировать пробелы в них, если такие окажутся. Особенно он может быть полезным при подготовке к контрольным работам и экзамену. Проект включает краткий теоретический материал по основным темам математики 1 курса; примеры решения типовых заданий с подробными комментариями ; упражнения для самостоятельной работы.

В состав проектной группы входят студенты, хорошо успевающие по дисциплине. Работа над проектом поможет студенту — будущему преподавателю и в общении, и в профессиональной деятельности. В связи с этим творческое развитие становится явной необходимостью.

Новизна проекта заключается в том, что нами предпринята попытка кратко изложить теоретический и практический материал по математике 1 курса, привлекая для работы над проектом студентов 1 курса. Основная идея нашей работы – использование творческого потенциала студентов, раскрытие их талантов, предоставление возможности поделиться своими знаниями и опытом друг с другом, развитие интереса к математике, нахождение занятий, приносящих удовлетворение.

16. Предполагаемый продукт проекта:

— Планируется создать краткий справочный материал-«шпаргалку» для студентов по основным темам математики 1 курса.

17. Этапы работы над проектом:

Название этапа	Содержание работы	Сроки реализации
Организационный	Определение темы проекта, постановка цели и задач	Сентябрь — ноябрь 2012 г.
Основной	Сбор и оформление информации по темам проекта:
	1. «Корни»	Ноябрь 2012 г.
	2. «Степени»	Ноябрь 2012 г.
	3. «Логарифмы»	Ноябрь 2012 г.
	4. «Элементы комбинаторики»	Ноябрь 2012 г.
	5. «Координаты и векторы»	Декабрь 2012 г.
	6. «Основы тригонометрии»	Декабрь 2012 г. — январь 2013 г.
	7. «Функции, их свойства (четность/нечетность)»	Февраль — март 2013 г.
	8. «Преобразование графиков функции»	Март 2013 г.
	9. «Иррациональные уравнения»	Апрель 2013 г.
	10. «Рациональные уравнения»	Май 2013 г.
	11. «Решение простейших тригонометрических уравнений»	Май 2013 г.

Продукт проекта

Краткий

справочный материал – «шпаргалки»

по математике

для студентов 1 курса

ПРЕЗЕНТАЦИЯ ПРОЕКТА

Достижения участников проекта:

Приняли активное участие в конкурсе проектов МПК №18 «Митино», были награждены Дипломом 2-ой степени;

Приняли участие в Межрегиональной научно-практической конференции преподавателей и студентов «Пространство детства: современность и будущее» — подготовили стенд-доклад.

nsportal.ru

Программа по математике для I-го курса профессионального колледжа

Коммунальное государственное учреждение

«Рузаевский аграрно-технический колледж»

акимата Северо-Казахстанской области

Министерства образования и науки Республики Казахстан

Утверждаю

Зам.директора по УПР

________А.Потехин

«____» ___________2015г.

РАБОЧАЯ УЧЕБНАЯ ПРОГРАММА

МАТЕМАТИКА

Специальность: «Фермерское хозяйство (по профилю)»

Квалификация:

1504062 – тракторист-машинист с/х производства

1504012 – бухгалтер

Преподаватель: Ельжанова Г.С.

Рассмотрено и одобрено на заседании МО общеобразовательных дисциплин

Протокол № ____ от «_____» ________________ 2015 г.

Руководитель МО: Вышинская Ю.Ю. ___________

с.Рузаевка

2015

Қазақстан Республикасы Білім және ғылым министрлігі

Солтүстік Қазақстан облысы әкімдігінің

«Рузаевка аграрлы-техникалық колледжі»

коммуналдық мемлекеттік мекемесі

Бекітемін

Директордың ОӨЖ жөн. орынб.

________ А.Потехин

2015ж. «____» __________

ЖҰМЫС ОҚУ БАҒДАРЛАМАСЫ

МАТЕМАТИКА

Мамандық: «Ферма шаруашылығы (бейін бойынша)»

Біліктілік: 1504062 – а/ш өндірісінің тракторшы-машинисі

1504012 – бухгалтер

Әзірледі оқытушы: Ельжанова Г.С.

Жалпы білім пәндері ӘБ отырысында қаралды және мақұлданды

2015 ж. «_____» ________________ № ____ хаттама

ӘБ жетекшісі: Вышинская Ю.Ю. ___________

Рузаевка с.

2015

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Курс математики для студентов профессионального колледжа дает представление о самых основных математических понятиях, идеях и методах математики, знание которых является элементом общей культуры человека.

В рамках этого направления предполагается изучение одного предмета – математики, в котором чередуются относительно самостоятельные алгебраические и геометрические темы.

Для данного курса математики характерна разгрузка на основе отказа от рассмотрения большинства теоретических фактов с доказательствами, строгие доказательства теорем даются в очень малом количестве, в основном как образцы точных рассуждений, объяснения в значительной степени основываются на наглядных представлениях, а сложность упражнений ограничивается уровнем простейших. Некоторые традиционные разделы курса изучаются в более обобщенном виде (на уровне представлений, без доказательств).

Задачи курса математики в колледже:

— формирование и развитие личностных качеств учащихся, адекватных полноценной математической деятельности;

— формирование математического языка как средства описания и исследования окружающего мира, его закономерностей;

— формирование умений, навыков, необходимых для полноценного функционирования в современном обществе.

Объем учебной нагрузки по предмету «Математика» составляет: 1 курс — 144 часа.

ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ СТУДЕНТОВ

В результате изучения курса все студенты должны овладеть следующими умениями, задающими уровень обязательной подготовки:

находить область определения и область значений заданной числовой функции;
определять промежутки возрастания и убывания функции;
определять является ли заданная функция четной, нечетной;
строить графики элементарных функций, опираясь на изученные свойства этих функций;
определять знаки тригонометрических функций по четвертям;
использовать свойства периодичности, четности и нечетности при нахождении значений тригонометрических функций для значений аргумента, сводимых к перечисленным выше;
строить графики тригонометрических функций с учетом их свойств;
решать простейшие тригонометрические уравнения на основе использования основных тригонометрических тождеств;
понимать механический и геометрический смысл производной;
вычислять производную степенной функции с натуральным показателем;
выносить постоянный множитель за знак производной;
находить производную многочлена;
применять производную к нахождению промежутков возрастания и убывания исследуемых функций;
с помощью производной находить экстремумы исследуемых функций, их наибольшие и наименьшие значения;
применять производную к построению графиков исследуемых функций.
находить на рисунке заданные точки, прямые и плоскости;
иллюстрировать на моделях названные фигуры в заданном взаимном расположении;
характеризовать пересекающиеся, параллельные и скрещивающиеся прямые;
находить на моделях и рисунках пересекающиеся, параллельные и скрещивающиеся прямые;
характеризовать случаи взаимного расположения прямой и плоскости;
находить на моделях и рисунках прямые, пересекающие плоскость и параллельные, перпендикулярные ей;
правильно изображать на рисунках пересечение прямой и плоскости, параллельность, перпендикулярность прямой и плоскости;
определять отрезок, длина которого задает расстояние от данной точки до данной плоскости;
определять полупрямые, задающие угол между прямой и плоскостью;
характеризовать случаи взаимного расположения плоскостей;
находить на моделях и рисунках пересекающиеся и параллельные плоскости;
задавать линейный угол двугранного угла и изображать его на рисунке.

Проверять является ли функция первообразной для данной;
находить первообразную степенной функции;
находить первообразную многочлена;
исследовать свойства степенной функции с натуральным показателем по заданному графику;
проверять, является ли целое число корнем n-ой степени (n=3, 4, 5 ) из данного числа;
использовать свойства корней для упрощения вычислений;
представлять степень с рациональным показателем в виде корня;
строить график показательной функции;
на основе графика описывать свойства показательной функции;
решать простейшие показательные уравнения и неравенства;
в простейших случаях определять логарифм числа по данному основанию;
применять свойства логарифмов для упрощения несложных логарифмических выражений;
решать простейшие логарифмические уравнения и неравенства.
различать и показывать на моделях прямую и правильную призмы, прямоугольный параллелепипед, куб, пирамиду, правильную пирамиду, указывает их основные элементы;
изображать на рисунках треугольные и четырехугольные призмы и пирамиды и их элементы;
решать простейшие задачи на нахождение элементов, вычисление площадей поверхностей, объемов параллелепипеда, прямой и правильной призмы, правильной пирамиды;
различать и показывает на моделях цилиндр и конус;
вычислять площади поверхностей и объемы цилиндра и конуса;
различать сферу и шар;
использовать соответствующие формулы для вычисления площади поверхности сферы и объема шара.

ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА

№

Наименование разделов и тем

Количество часов

Повторение

Функция, ее свойства и график

Тригонометрические функции

Параллельность прямых и плоскостей

Перпендикулярность прямых и плоскостей

Производная

Применение производной

Первообразная и интеграл

Многогранники

Тела вращения

Корни и степени. Степенная функция

Показательная и логарифмическая функция

Комбинаторика. Вероятность.

Повторение

СОДЕРЖАНИЕ УЧЕБНОГО МАТЕРИАЛА

Функция, ее свойства и график.

Функция. Числовая функция: область определения, область значений. Способы задания функции. График функции. (Простейшие преобразования графиков функций). Свойства функции: периодичность, возрастание и убывание, четность, нечетность, экстремумы, ограниченность, сохранение знака.

Тригонометрические функции.

Свойства и графики функций синус, косинус, тангенс. Обратные тригонометрические функции: арксинус, арккосинус, арктангенс. Простейшие тригонометрические уравнения вида sin x=а, cos x=а, tg x=а.

Параллельность прямых и плоскостей.

Точки, прямые и плоскости в пространстве. Понятие о принадлежности точек и прямых плоскостям.

Взаимное расположение прямых и плоскостей в пространстве.

Пересекающиеся, параллельные и скрещивающиеся прямые.

Пересекающиеся и параллельные прямая и плоскость. Признак параллельности прямой и плоскости.

Параллельные и пересекающиеся плоскости. Равенство отрезков параллельных прямых, заключенных между параллельными плоскостями. Параллельность линий пересечения двух параллельных плоскостей третьей плоскостью.

Перпендикулярность прямых и плоскостей.

Перпендикулярность прямой и плоскости. Перпендикуляр и наклонная к плоскости, проекция наклонной на плоскость. Расстояние от точки до плоскости. Расстояние между параллельными плоскостями. Теорема о трех перпендикулярах. Перпендикулярные плоскости.

Угол между прямыми. Угол между прямой и плоскостью. Линейный угол двугранного угла.

Производная.

Производная, ее механический и геометрический смысл. Производная функции у= х (n єN). Производные суммы и произведения двух функций. Производная тригонометрических функций. Признаки знакопостоянства, возрастания и убывания, экстремума функции.

Применение производной.

Применение производной к исследованию функций. Наибольшее и наименьшее значения функции на промежутке.

Первообразная и интеграл.

Первообразная. Основное свойство первообразной. Таблица первообразных (первообразные степенной функции с целым показателем (n-1), синуса, косинуса). Простейшие правила нахождения первообразных. Понятие о площади криволинейной трапеции.

Многогранники.

Понятие о многограннике. Ребра, грани, вершины. Плоские углы при вершинах. Теорема о сумме плоских углов. Параллелепипед: прямой, прямоугольный, куб. Свойства параллелепипеда.

Призма, ее элементы. Сечения призмы, проходящей через два боковых ребра.. Прямая и правильная призмы. Прямоугольный параллелепипед. Пирамида, ее элементы. Сечения пмрамиды, параллельные ее основанию. Правильная пирамида. Усеченная пирамида. Площади боковой и полной поверхностей многогранников. Понятие об объеме многогранника. Объемы многогранников: прямой призмы, прямоугольного параллелепипеда, пирамиды.

Тела вращения.

Прямой круговой цилиндр, его элементы. Осевые сечения цилиндра. Прямой круговой конус, его элементы. Осевые сечения конуса. Сечения конуса плоскостью, параллельной основанию. Шар и сфера. Сечение шара. Касательная плоскость к сфере, ее свойства. Формулы для нахождения площадей боковых поверхностей цилиндра и конуса, площади поверхности сферы. Формулы объемов цилиндра, конуса, шара.

Корни и степени. Степенная функция.

Свойства и график степенной функции с натуральным показателем. Корень n-ой степени. Степень с рациональным показателем и ее свойства.

Показательная и логарифмическая функции.

Показательная функция, ее свойства и график. Решение простейших показательных уравнений и неравенств.

Логарифм числа. Свойства логарифмов. Логарифмическая функция, ее свойства и график. Десятичные и натуральные логарифмы. Решение простейших логарифмических уравнений и неравенств.

Производная показательной и логарифмической функций.

Комбинаторика. Вероятность.

Основные понятия комбинаторики (размещения, перестановки, сочетания). Применение комбинаторики и бинома Ньютона в теории вероятностей. Случайная величина и ее виды. Закон распределения случайной величины. Числовые характеристики случайной величины.

ЛИТЕРАТУРА

Алгебра и начала анализа. Учебник для 10 классов общественно-гуманитарного направления общеобразовательных школ. А.Е.Абылкасымова, К.Д. Шойынбеков, М.И.Есенова, З.А.Жумагулова. – Алматы: Изд-во «Мектеп», 2006.
Алгебра и начала анализа. Учебник для 11 классов общественно-гуманитарного направления общеобразовательных школ. А.Е.Абылкасымова, К.Д. Шойынбеков, З.А.Жумагулова. – Алматы: Изд-во «Мектеп», 2007.
Геометрия. Учебник для 10 классов общественно-гуманитарного направления общеобразовательных школ. В.Гусев, Ж.Кайдасов, А.Кагазбаева. – Алматы: Изд-во «Мектеп», 2010.
Геометрия. Учебник для 11 классов общественно-гуманитарного направления общеобразовательных школ. В.Гусев, Ж.Кайдасов, А.Кагазбаева. – Алматы: Изд-во «Мектеп», 2007.
Алгебра и начала анализа. Сборник задач. Учебное пособие для 10 кл. общественно-гуманитарного направления общеобразовательных школ. А.Е.Абылкасымова, К.Д. Шойынбеков, М.И.Есенова, С.К.Тулеубаева. – Алматы: Мектеп, 2010.
Алгебра и начала анализа. Дидактические материалы: Учебное пособие для 10 классов общественно-гуманитарного направления общеобразовательных школ. А.Е.Абылкасымова, К.Д. Шойынбеков, М.И.Есенова, З.А.Жумагулова. – Алматы: Мектеп, 2010.
Геометрия. Сборник задач. Учебное пособие для 10 классов общественно-гуманитарного направления общеобразовательных школ. В.Гусев, А.Еден. – Алматы: Мектеп, 2010.
Геометрия. Сборник задач. Учебное пособие для 11 классов общественно-гуманитарного направления общеобразовательных школ. В.Гусев, Ж.Кайдасов, Е.Есенгазин. – Алматы: Мектеп, 2011.
Геометрия. Дидактические материалы: Учебное пособие для 10 классов общественно-гуманитарного направления общеобразовательных школ. В.Гусев, Ж.Кайдасов. – Алматы: Мектеп, 2010.
Геометрия. Методическое руководство: Пособие для учителей 10 кл. общественно-гуманитарного направления общеобразовательных школ. Кайдасов Ж. и др. – Алматы: Мектеп, 2010.

infourok.ru

Пакет заданий по математике для студентов 1 курса Башкирского строительно-архитектурного колледжа

Содержание

Пояснительная записка -2-

2. Проверочные задания по темам:

2.1 Вычисление пределов. Раскрытие неопределенностей. -3-

2.2 Линейные уравнения и неравенства -7-

2.3 Преобразование выражений, содержащих радикалы и степени с дробными показателями. -11-

2.4 Иррациональные уравнения -12-

2.5 Корень п-ой степени и его свойства -13-

2.6 Определение и свойства логарифма -17-

2.7 Логарифмические уравнения -18-

2.8 Практикум решения показательных уравнений -23-

2.9 Показательные уравнения -26

2.10 Правильная пирамида -30-

2.11. Индивидуальная контролирующая проверочная работа по теме: «Пирамида» -31-

2.12 Цилиндр. Конус. Шар. -35-

Пояснительная записка.

В результате решения практических заданий студент должен иметь представление:

о роли и месте математики в современном мире, общности ее понятий и представлений;

о методах решения некоторых практических задач с использованием элементов математического анализа.

Знать:

базовые понятия дифференциального исчисления;

способы решения простейших видов показательных и логарифмических уравнений;

способы решения простейших и иррациональных уравнений;

способы раскрытия неопределенностей при вычислении пределов;

2. Проверочные задания по темам:

2.1 Вычисление пределов. Раскрытие неопределенностей

Н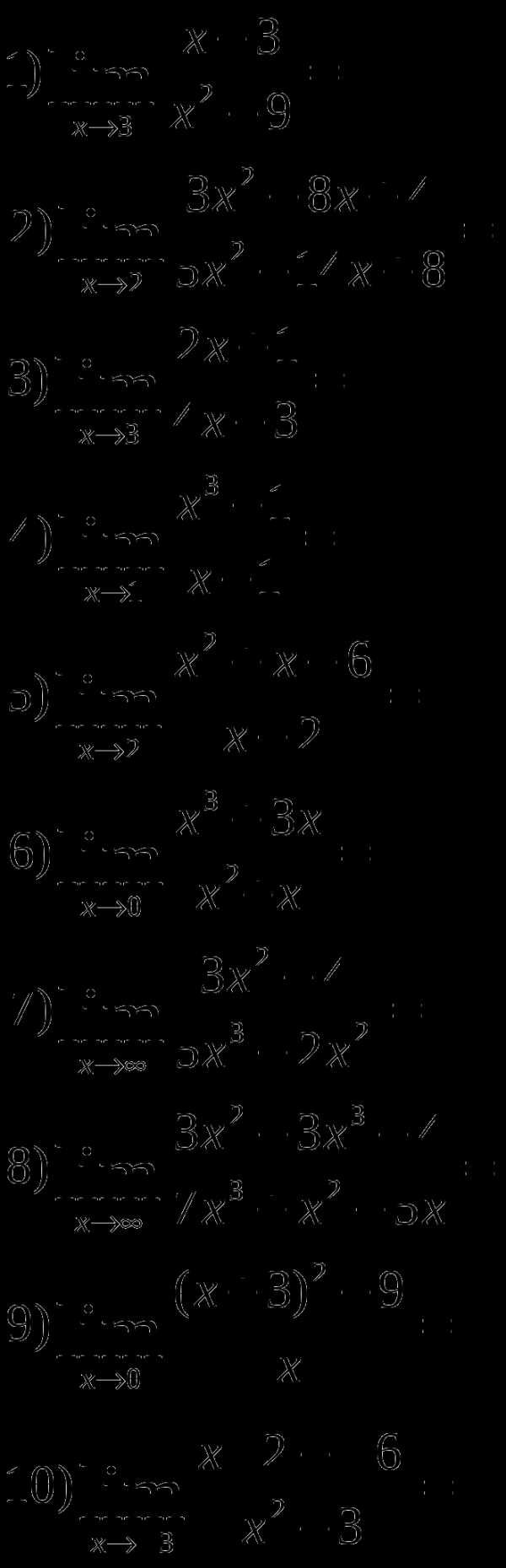
айти пределы функций

вариант 1.

2.1 Вычисление пределов. Раскрытие неопределенностей

Найти пределы функций

вариант 2.

2.1 Вычисление пределов. Раскрытие неопределенностей.

Н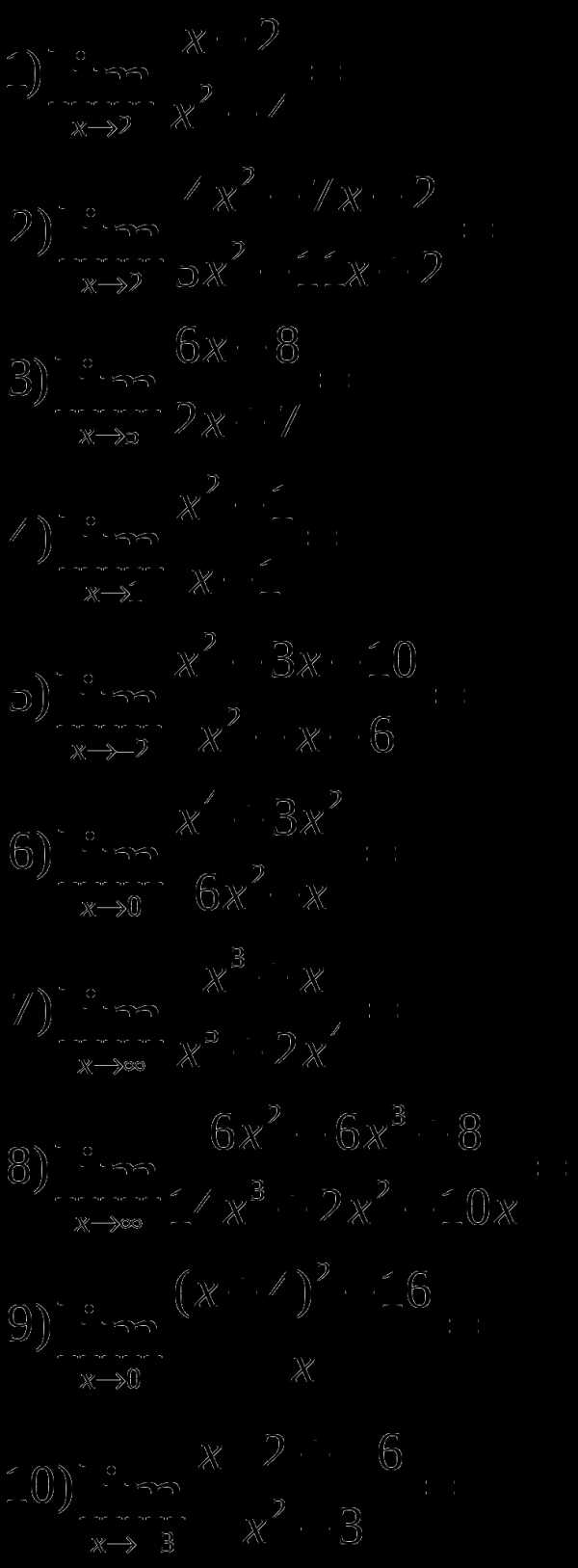
айти пределы функций

вариант 3.

2.1 Вычисление пределов. Раскрытие неопределенностей.

Н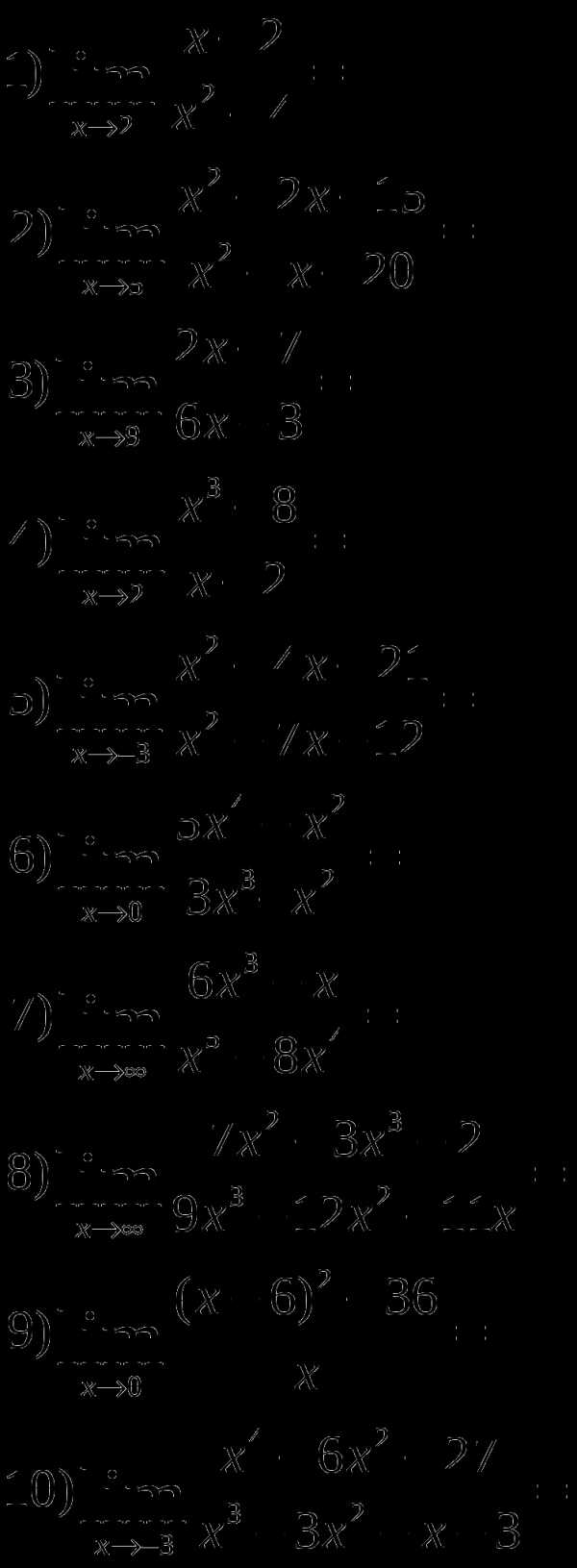
айти пределы функций

вариант 4.

2. 2 Линейные уравнения и неравенства

Р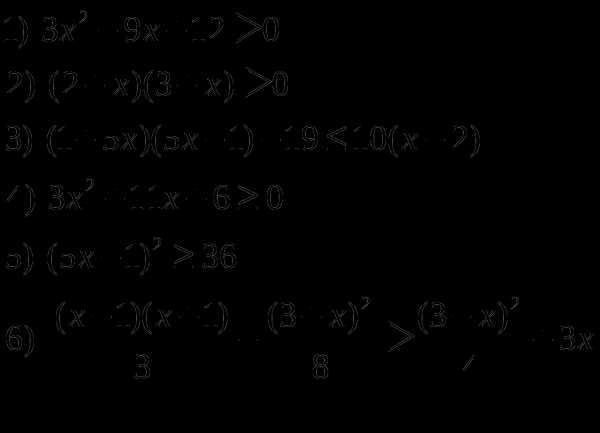
ешить неравенства:

Решить уравнения:

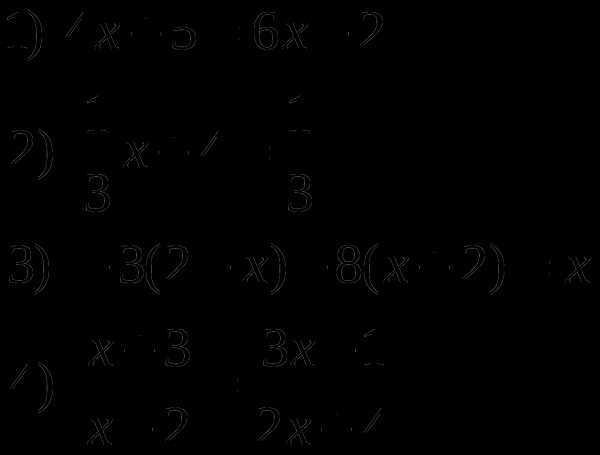
2.2 Линейные уравнения и неравенства

Р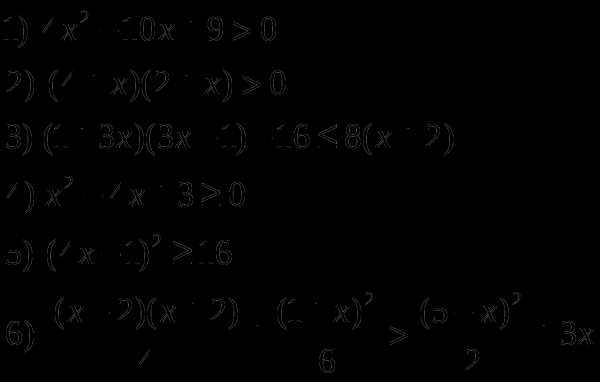
ешить неравенства:

Р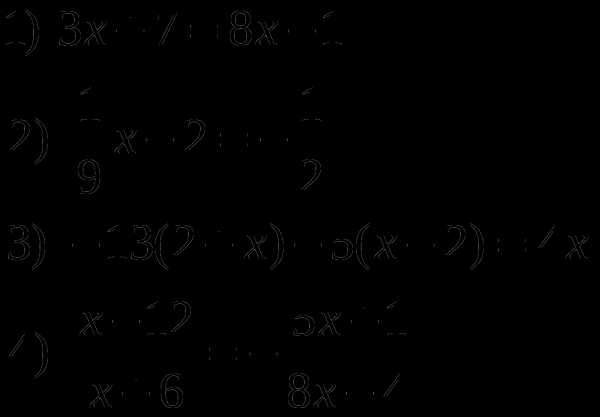
ешить уравнения:

2.2 Линейные уравнения и неравенства

Р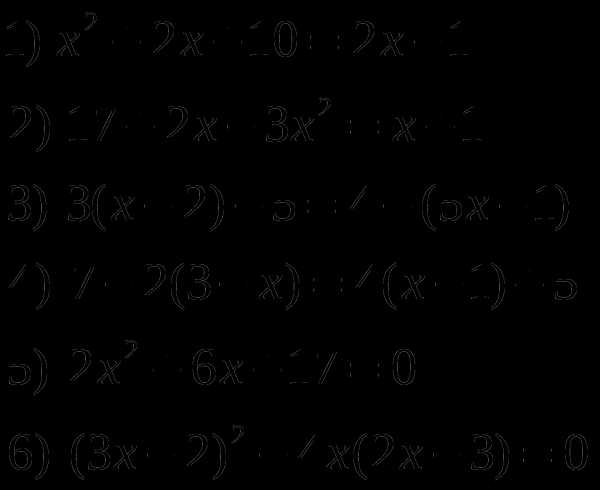
ешить уравнения:

Решите неравенства:

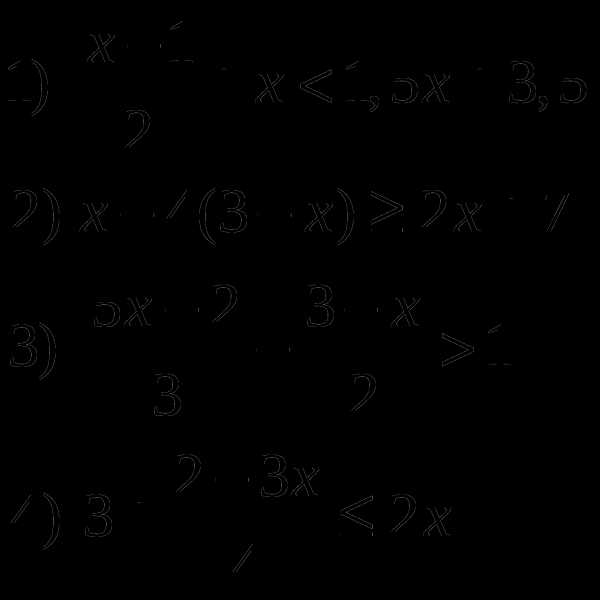
2.2 Линейные уравнения и неравенства

Р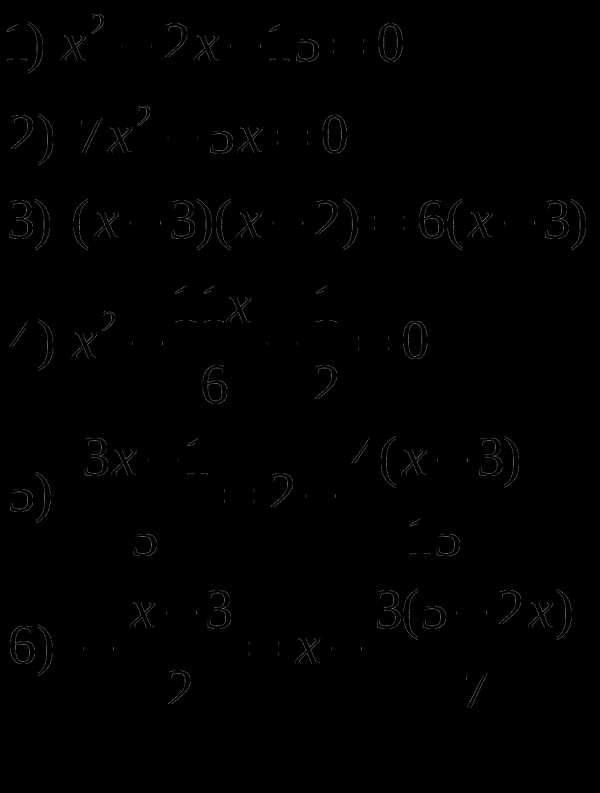
ешить уравнения:

Решить неравенства:

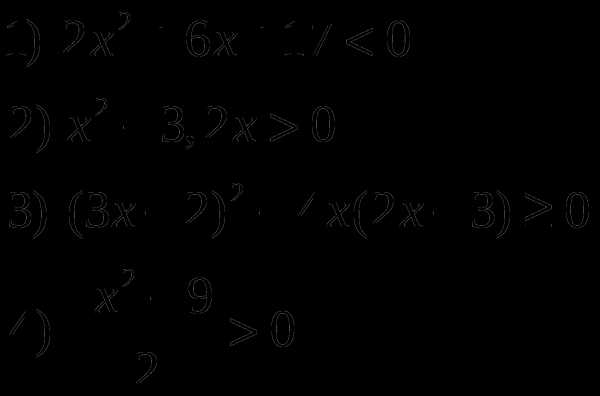
2.3 Преобразование выражений, содержащих радикалы

и степени с дробными показателями.

У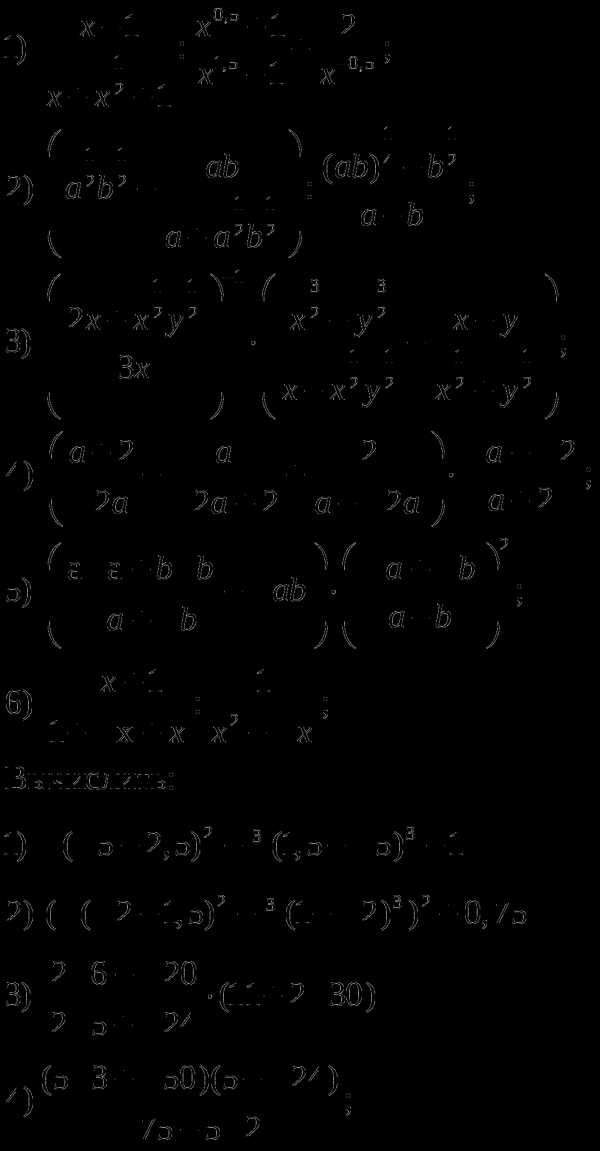
простите выражения:

2.4 Иррациональные уравнения

Р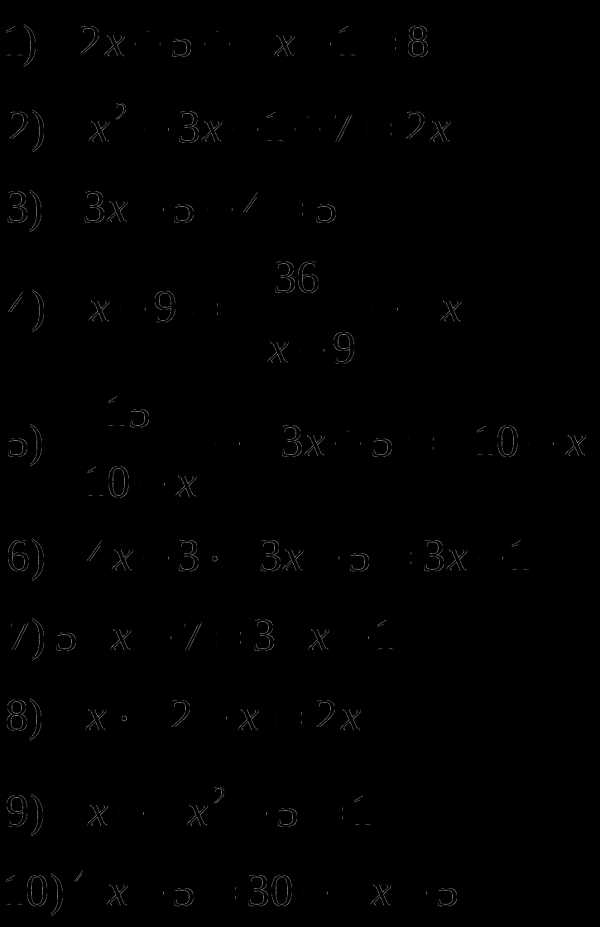

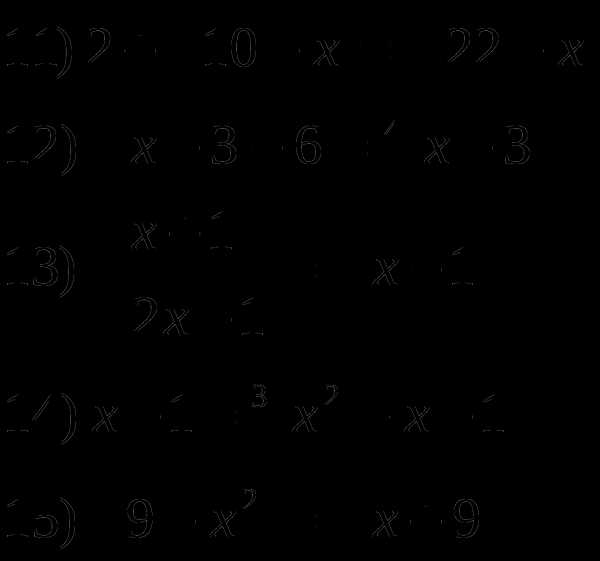
ешить уравнения:

2.5 Корень п-ой степени и его свойства

1 вариант.

В
ычислить:
Н
айдите значение числового выражения:

П
редставьте выражение в виде дроби, знаменатель которой не содержит знака корня:

Н
айдите значение выражения:

В
ыполнить действия:
Р
ешить уравнения:

2.5 Корень п-ой степени и его свойства

2 вариант.

В
ычислить:
Н
айдите значение числового выражения:

П
редставьте выражение в виде дроби, знаменатель которой не содержит знака корня:

Н
айдите значение выражения:

В
ыполнить действия:
Р
ешить уравнения:

2.5 Корень п-ой степени и его свойства

3 вариант.

В
ычислить:
Н
айдите значение числового выражения:

П
редставьте выражение в виде дроби, знаменатель которой не содержит знака корня:

Н
айдите значение выражения:

В
ыполнить действия:
Решить уравнения:

2.5 Корень п-ой степени и его свойства

4 вариант.

В
ычислить:
Н
айдите значение числового выражения:

П
редставьте выражение в виде дроби, знаменатель которой не содержит знака корня:

Н
айдите значение выражения:

В
ыполнить действия:
Решить уравнения:

2.6 Определение и свойства логарифма

В
ычислить логарифмы:

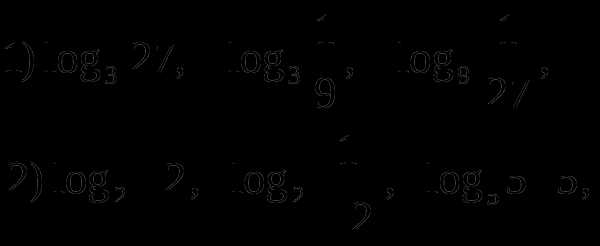
Вычислите:

Найдите А по его логарифму:

2.7 Логарифмические уравнения

Решите уравнения:

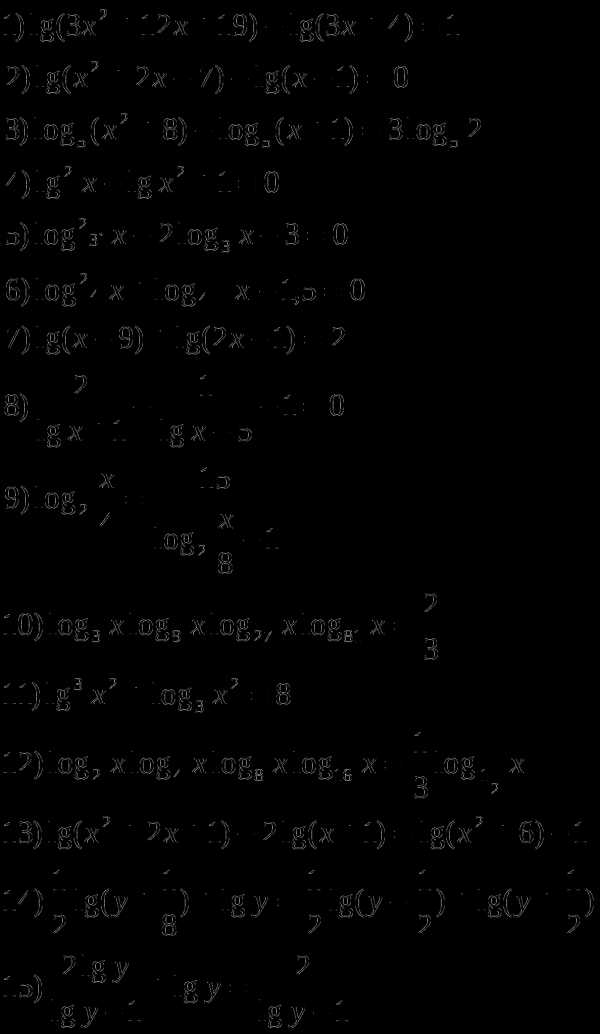
2.7. Логарифмические уравнения

В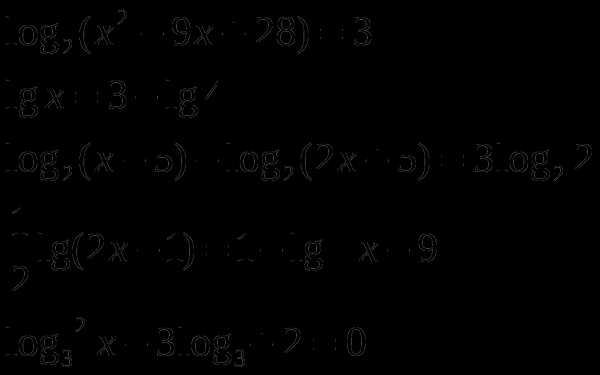
ариант 1

Решить уравнение:

Д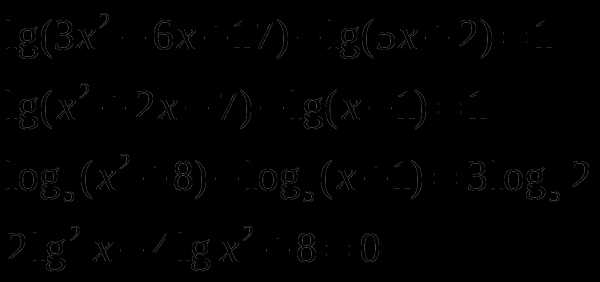
ополнительные задания:

2.7. Логарифмические уравнения

Вариант 2

Р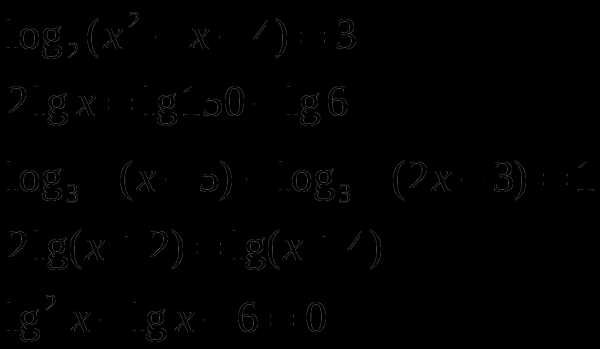
ешить уравнение:

Дополнительные задания:

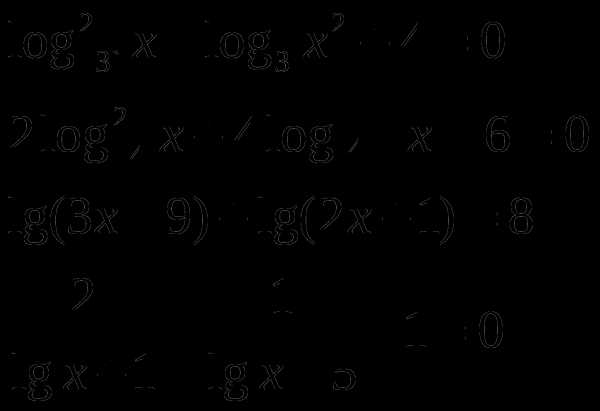
2.7. Логарифмические уравнения

Вариант 3

Решить уравнение:

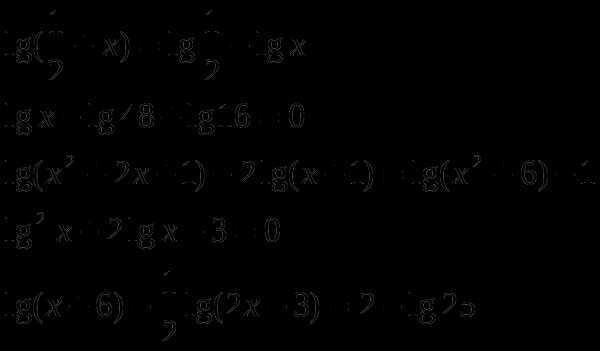
Дополнительные задания:

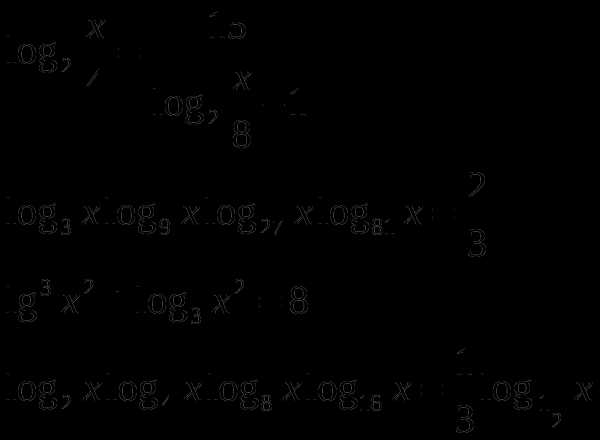
2.7. Логарифмические уравнения

Вариант 4

Решить уравнение:

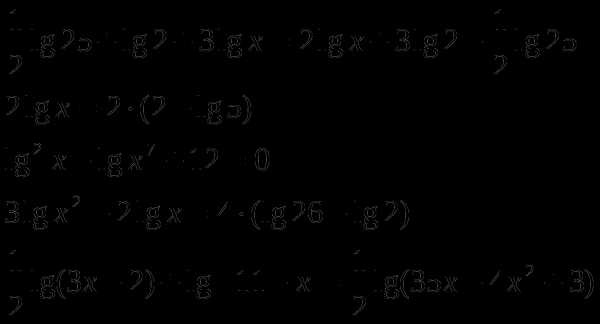
Дополнительные задания:

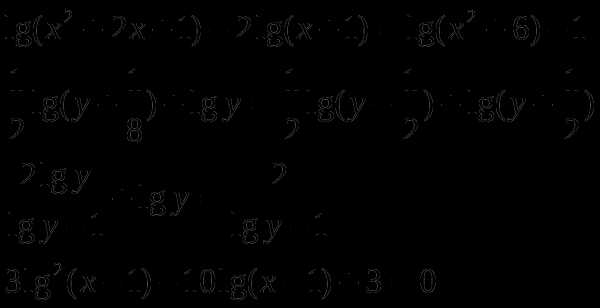
2. 8. Практикум по решению показательных уравнений

Вариант №1

Решите уравнения

2^х=4
3^х=81
4^х=2

5^х= ;
=4;
7^х=1

=25;
7^–х= –;

=1
2^6–х=2^3х–2
2^х– 2^х–2 =3

3^х+3– 2•3^х–1–4•3^х–2 =17

Решите уравнение вынесением за скобки

2^х+2^х–1 +2^х–2 56

10^х+10^х–1=1100

3^х+3^3–х=12

Решите уравнение графически

2^х=х–1

2.8. Практикум по решению показательных уравнений

Вариант №2

9^х=27
3^х=9
4^х=64

6^х= ;
=27;
8^х=1

=36;
8^–х= –;

=1
3^5–х=3^2х–1
5^х+1– 5 =500

2•3^х+1 +2•3^2–х =56

Решите уравнение вынесением за скобки

2•3^3х–1+27^х–2/3=^{9^х–1+2•3^2х–1}

6^х+6^х+2=222

Решите уравнение графически

0,5^х =2х

2.8. Практикум по решению показательных уравнений

Вариант №3

5^х=25
6^х=216
100^х=10000

8^х= ;
=125;
5^х=1

=16;
5^–х= –;

=1
4^9–х=4^2х–7
3^х–2– 3^х–3 =36

2^х+ 2^х–1 +2^х–2 =3^х–3^х–1+3^х–2

Решите уравнение вынесением за скобки

3^х+1–4:3^х–1=45

2^х+2^х+2=40

2^2х+6+2^х+7=17

Решите уравнение графически

х =3^х–2

2.9. Показательные уравнения

вариант 1

Р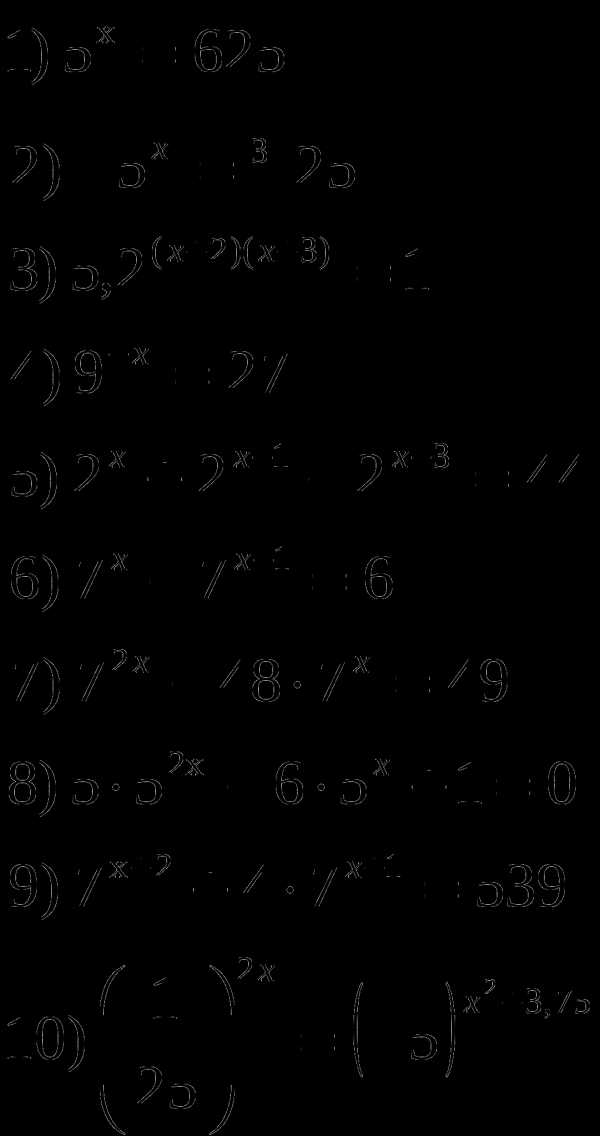
ешить показательные уравнения:

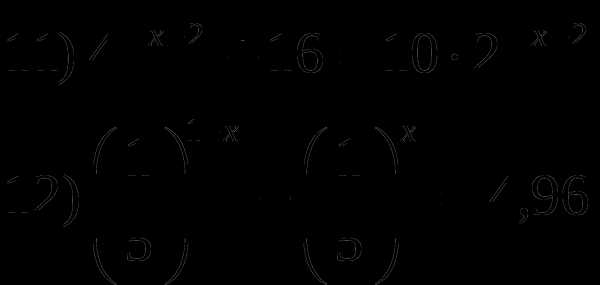
2.9. Показательные уравнения

вариант 2

Р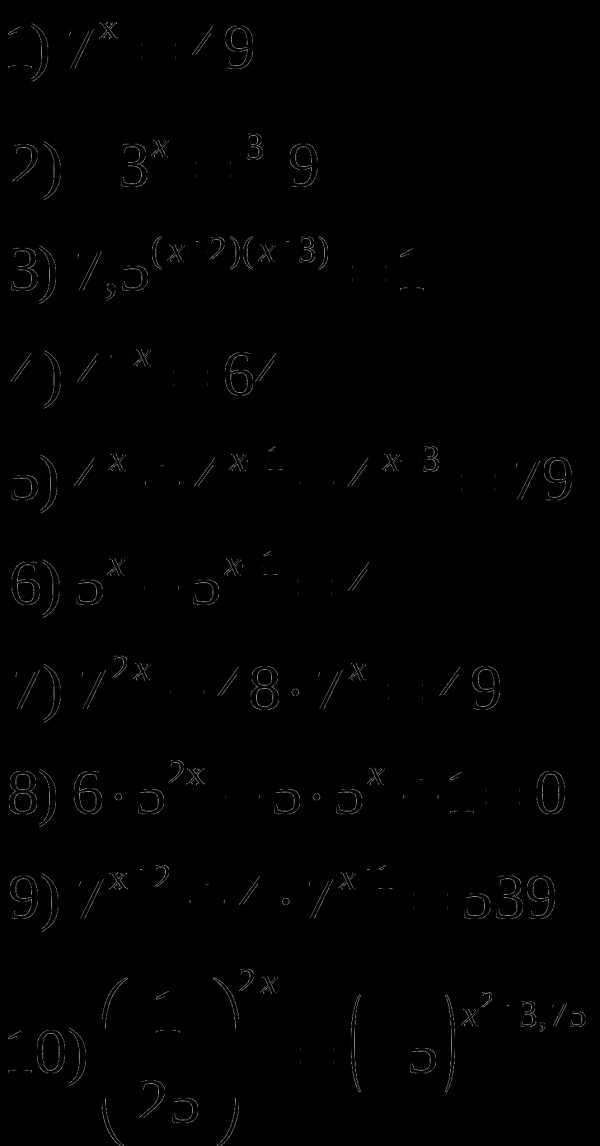

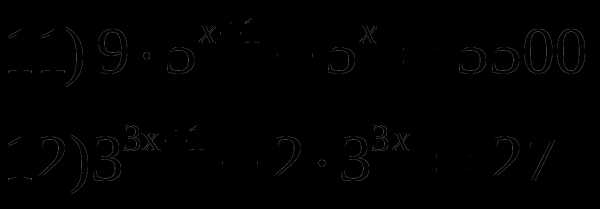
ешить показательные уравнения:

2.9. Показательные уравнения

вариант 3

Р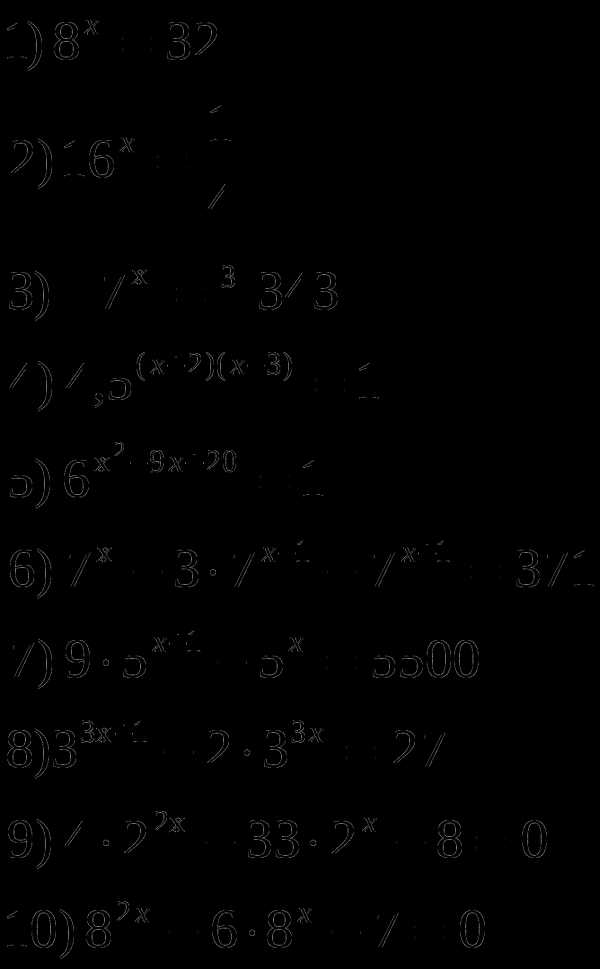
ешить показательные уравнения:

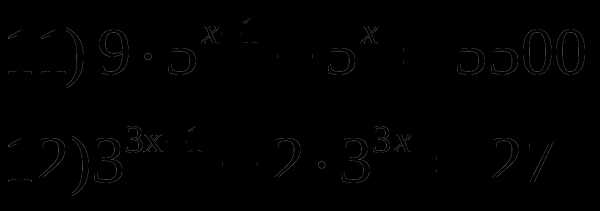
2.9. Показательные уравнения

вариант 4

Решить показательные уравнения:

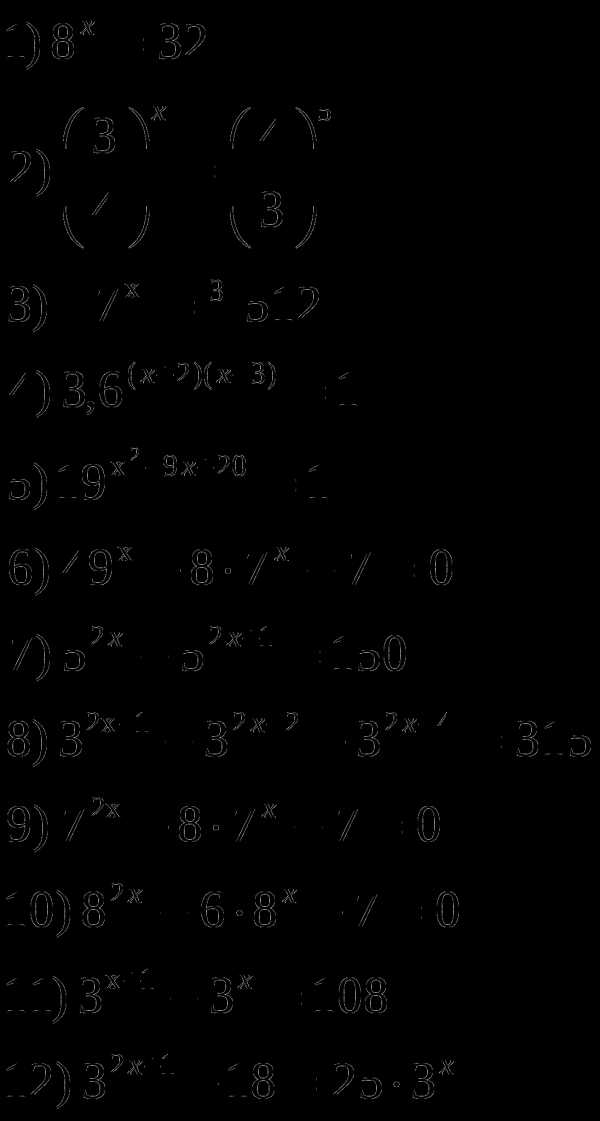
2.10. Правильная пирамида

Задача № 1

Задача № 2

Апофема правильной шестиугольной пирамиды равна 5 см, а высота – 4 см. Найдите площадь боковой поверхности.

Задача № 3.

Задачи № 4

2.11. Индивидуальная контролирующая проверочная работа.

Вариант 1

Найдите высоту правильной шестиугольной пирамиды, если сторона ее основания равна а, апофема h

Сторона основания правильной четырехугольной пирамиды равна а, а высота h. Определить полную поверхность пирамиды.

Найдите высоту правильной треугольной пирамиды, у которой боковая поверхность равна
60 см², а полная поверхность 108 см².

2.11. Индивидуальная контролирующая проверочная работа по теме: «Пирамида»

Вариант 2

Найдите высоту правильной треугольной пирамиды, если сторона ее основания равна а, а апофема h.

Боковое ребро правильной четырехугольной пирамиды, равное 12 см, образует с плоскостью основания угол в 60⁰. Найдите боковую поверхность^{пирамиды.}

Найдите высоту правильной треугольной пирамиды, у которой площадь основания равна
27см², а полная поверхность 72см^2.

2.11. Индивидуальная контролирующая проверочная работа по теме: «Пирамида»

Вариант 3

Сторона основания правильной четырехугольной пирамиды равна а. Двугранные углы при основании равны . Определите полную поверхность.

Найдите величину двугранного угла при основании правильной четырехугольной пирамиды, если ее боковые ребра наклонены к плоскости основания под углом 30⁰.

Найдите высоту правильной треугольной пирамиды, у которой площадь основания равна
27см², а полная поверхность 72см².

2.11. Индивидуальная контролирующая

проверочная работа по теме: «Пирамида»

Вариант 4

Найдите величину двугранного угла при основании правильной четырехугольной пирамиды, если ее боковые ребра наклонены к плоскости основания под углом 60⁰.

Высота боковой грани правильной четырехугольной пирамиды равна 10 см. Определите полную поверхность пирамиды, если боковая грань наклонна к плоскости основания под углом 60^0.

Найдите высоту правильной треугольной пирамиды, у которой боковая поверхность равна
60см², а полная поверхность 108см².

2.12. Задания по теме: «Цилиндр. Конус. Шар».

Вариант 1

1. Длина окружности основания цилиндра равна 12, высота 10 см. Найти объем цилиндра.

3. Через середину радиуса шара проведено сечение, найти площадь, если радиус шара равен 6 см.

2.12. Задания по теме: «Цилиндр. Конус. Шар».

Вариант 2

1. Осевым сечением цилиндра является квадрат, площадь которого 8 см². Вычислите боковую поверхность цилиндра.

2. Осевым сечением конуса является правильный треугольник, площадь которого 64 см² . Найти объем цилиндра.

3. Осевым сечением цилиндра является квадрат, площадь которого 64 см² . Найти объем цилиндра.

2.12. Задания по теме: «Цилиндр. Конус. Шар».

Вариант 3

1. Длина окружности основания цилиндра равна 12, высота 10 см. Найти объем цилиндра.

3. Через середину радиуса шара проведено сечение, найти площадь, если радиус шара равен 6 см.

2.12. Задания по теме: «Цилиндр. Конус. Шар».

Вариант 4

1. Осевым сечением цилиндра является квадрат, площадь которого 8 см². Вычислите боковую поверхность цилиндра.

2. Осевым сечением конуса является правильный треугольник, площадь которого 64 см² . Найти объем цилиндра.

Осевым сечением цилиндра является квадрат, площадь которого 64 см² . Найти объем цилиндра.

Список литературы:

1. Лисичкин В.Т., Соловейчик И.Л.

Математика: Учеб. Пособие для техникумов.- М.:

Высшая школа, 2005

3. Апанасов П.Т., Орлов М.И.

Сборник задач по математике: Учебное пособие для техникумов.- М.: Высшая школа, 1987.

4. М.И.Башмаков.

Математика.- 2-е издание- М.: «Высшая школа». Учебное пособие для профессионально- технических училищ, 2001

infourok.ru