Кто первым решил произвести измерения земли – Как впервые измерили окружность Земли » Детская энциклопедия (первое издание)
Как впервые измерили окружность Земли » Детская энциклопедия (первое издание)
Представления древних народов о Земле Как уточнялись знания о форме и величине ЗемлиБолее точное определение размеров земного шара сделал древнегреческий ученый Эратосфен Киренский, живший за 200 лет до н. э.
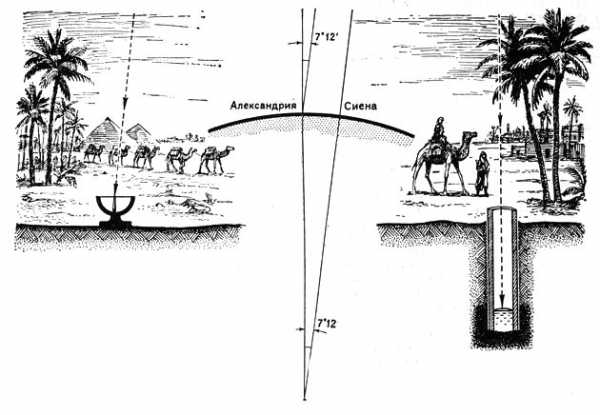
Слева — определение высоты Солнца скафисом. В центре — схема направления солнечных лучей: в Сиене они падают вертикально, в Александрии — под углом в 7° 12′. Справа — направление луча солнца в Сиене в момент летнего солнцестояния.
Совершая путешествия из г. Александрии на юг, в г. Сиену (теперь Асуан), люди замечали, что там летом, в тот день, когда солнце бывает всего выше на небе (день летнего солнцестояния — 22 июня), в полдень оно освещает дно глубоких колодцев, т. е. бывает как раз над головой, в зените. Предметы в этот момент не дают тени. В Александрии же и в этот день солнце в полдень не доходит до зенита, не освещает дна колодцев, предметы дают тень.
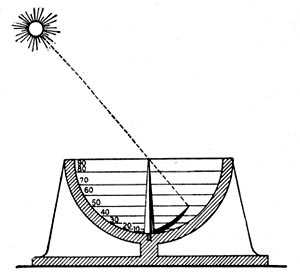
Скафис — прибор для определения высоты Солнца над горизонтом.
Эратосфен измерил, насколько полуденное солнце в Александрии отклонено от зенита, и получил величину, равную 7°12′, что составляет 1/50 окружности. Это ему удалось сделать с помощью прибора, называемого скафисом. Скафис представлял собой чашу в форме полушария. В центре ее отвесно укреплялась игла. Тень от иглы падала на внутреннюю поверхность скафиса. Для измерения отклонения солнца от зенита (в градусах) на внутренней поверхности скафиса проводились окружности, помеченные цифрами. Если, например, тень доходила до окружности, помеченной цифрой 50, солнце стояло на 50° ниже зенита. Построив чертеж, Эратосфен совершенно правильно заключил, что Александрия отстоит от Сиены на 1/50 окружности Земли. Чтобы узнать окружность Земли, оставалось измерить расстояние между Александрией и Сиеной и умножить его на 50. Это расстояние было известно по времени, которое тратили караваны верблюдов на переход между городами. В единицах мер того времени оно равнялось 5000 стадий. Если 1/50 окружности Земли равняется 5000 стадии, то вся окружность Земли равна 5000 X 50 = = 250 000 стадий. В переводе на наши меры это расстояние приблизительно равно 39 500 км.
Зная длину окружности, можно вычислить и величину радиуса Земли.
Известно, что радиус всякой окружности в 6,283 раза меньше ее длины. Поэтому средний радиус Земли, по Эратосфену, оказался равным круглым числом 6290 км, а диаметр — 12 580 км.
Так Эратосфен нашел приблизительно размеры Земли, близкие к тем, которые определены точными приборами в наше время.
Эратосфен — Греческий математик, астроном, географ и поэт. Ученик Каллимаха, с 235 г. до н. э. — глава Александрийской библиотеки.
Скафис представляет собой чашу в форме полушария, в центре которой укрепляется игла. При ярком свете солнца тень от иглы падала на внутреннюю поверхность скафиса, на которой были нанесены окружности с цифрами, которые соответствовали значениям угла наклона солнца.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Представления древних народов о Земле Как уточнялись знания о форме и величине Земли.
de-ussr.ru
История измерения радиуса Земли — Мегаобучалка
Впервые идея о шарообразности Земли была выдвинута, вероятно, халлейскими жрецами в VI в. до н.э. С таким же утверждением выступал грек Филолай (V в. до н.э.). Ту же мысль высказывал Аристотель в IV в. до н.э. В качестве доказательств они ссылались на то обстоятельство, что шар-это самая «совершенная» из геометрических форм. Наблюдения за уходящими за горизонт кораблями также наталкивали на мысль о том, что Земля круглая.
Попытки измерить Землю, вероятно, делались в древние времена не один раз. Однако первое исторически достоверное измерение земли проделал древнегреческий учёный Эратосфен в III в. до н.э. Он заметил, что в двух египетских городах, расположенных на Ниле, в одно и то же время солнце стоит в Сиене (нынешнем Асуане) почти в зените ,тогда как в Александрии светит под углом. Зная расстояние между городами и измерив с помощью гномона, закреплённого в полусферической чаше, угол ɀ (зенитное расстояние), Эратосфен вычислил радиус Земли.
Поскольку расстояние между городами в то время измерялось в стадиях, мы не можем сейчас сказать, насколько точен был результат измерений Эратосфена. Стадией греки называли расстояние, которое проходил человек спокойным шагом от момента появления края солнца над горизонтом до момента появления всего его диска, что составляет примерно 158-185м. Современные расчеты, выполненные при этих приблизительно значениях, дали результат R=6311-6320 км, который следует признать вполне удовлетворительным, поскольку сейчас мы принимаем радиус Земли равным 6371 км.
Первые попытки измерения радиуса Земли
Эратосфен Кирены, был греческий математик, географ, поэт, астроном и музыкальный теоретик. Он был человеком изучения, становясь директором библиотеки в Библиотеке Александрии. Он изобрел дисциплину географии, включая терминологию, используемую сегодня.
Он известен прежде всего тем, что был первым человеком, который вычислит окружность Земли, которую он сделал, применив систему измерения, используя стадионы или длину стадионов во время того периода времени. Его вычисление было удивительно точно. Он был также первым, чтобы вычислить наклон оси Земли (снова с замечательной точностью). Кроме того, он, возможно, точно вычислил расстояние от Земли до Солнца и изобрел день прыжка. Он создал первую карту параллелей слияния мира и меридианов, основанных на доступном географическом знании эры.
Эратосфен был основателем научной хронологии; он пытался пересматривать даты главных литературных и политических событий от завоевания Троя. В теории чисел он ввел решето Эратосфена, эффективный метод идентификации простых чисел.
Он был фигурой влияния, которая отказалась специализироваться только на одной области. Согласно входу в Suda, его критики презирали его, называя его Бетой, из второго письма от греческого алфавита, потому что он всегда входил второй во всех его усилиях. Тем не менее, его приверженцы назвали его Pentathlos после олимпийцев, которые были хорошо округленными конкурентами, поскольку он оказался, чтобы быть хорошо осведомленным в каждой области относительно изучения. Эратосфен очень хотел понимать сложности всего мира.
В 1528 г. Жан Фернель путем подсчета числа оборотов колеса экипажа измерил расстояние от Парижа до Амьена. Величина 10 дуги меридиана у него составила 110,6 км.
Через 4 года после возвращения спутников Магеланна в изучении Земли был сделан первый шаг. Парижанин Фернель пришел к мысли провести измерение радиуса Земли. Он решил измерить длину дуги величиной 1 градус. Он измерил полуденную высоту Солнца в Париже 26 августа.
Далее ему нужно было найти место, где в то же время высота Солнца была ровно на 1 градус меньше.
Для этого он потратил несколько дней. Но так как наступала осень, разница была меньше 1 градуса. Фернель, чтобы обойти это препятствие рассчитал высоту Солнца в Париже на несколько дней вперед.
Двигаясь на север, он мог сравнивать полученные данные каждый день в этот же самый день.
Каждый день в полдень он останавливался и производил наблюдения. 29 августа он обнаружил, что высота Солнца на 1 градус меньше чем в Париже в то же время.
Фернель измерил длину колеса (20 футов), а затем повернул обратно в Париж и считал обороты колеса (17024 об.). Потом он вычислил градусную меру дуги меридиана в туазах (1 туаз = 6 футов = 1.949 м), потом умножив на 360 и переведя туазы в метры можно найти длину меридиана:
1.949*20*17024*360/1000=39815 км
Еще век спустя, в 1614-1617 гг. голландский астроном Виллеброрд Снеллиус впервые применил метод триангуляции, когда линейная протяженность большой дуги на поверхности Земли измеряется через систему последовательно сопряженных треугольников. Его измерение 1градуса дало 107335 м. Наконец, в 1671 г. член Парижской академии Жан Пикар (1620-1682) опубликовал свой труд «Измерение Земли», в котором не только сообщил результаты высокоточных триангуляционных измерений в 1669-1670 гг. дуги Париж-Амьен (1градус = 111210 м, истинное значение 111180 м), но и высказал предположение о том, что истинная форма Земли — не шар!
Это открытие вновь заострило бурный спор, имевший место в то время в европейской науке. Дело в том, что в соответствии с теорией всемирного тяготения Ньютона, вращающиеся тела (в том числе наша Земля) должны принимать форму сплюснутого эллипсоида, а по теории эфирных вихрей Декарта, напротив, вытянутого сфероида. Поэтому вопрос об истинной форме Земли для ньютонианцев и картезианцев был принципиально важен. Дыня или тыква, огурец или помидор, мандарин или лимон — эта дилемма имела воистину вселенское значение. Директор Парижской обсерватории Джованни Доменико Кассини (1625-1712) с 1683 г. начал проводить новые обширные работы по градусным измерениям уже на длинной дуге — от нормандских берегов Франции на севере до испанской границы на юге. К сожалению, из-за смерти Кольбера (министр финансов Людовика 14) и самого Кассини работы прерывались и были завершены его сыном Жаком Кассини (1677-1756) только в 1718 г., а результаты опубликованы в 1720 г. Кассини также был картезианцем по своим взглядам и даже вступил в спор с Ньютоном, утверждая, что земной шар имеет вытянутую форму. Сам Ньютон давал теоретическую оценку сжатия Земли в 1/230.
Чтобы окончательно разобраться с «дынями», «помидорами» и прочими «лимонами», Французская академия наук в 1735 г. организовала две грандиозные по тому времени экспедиции к экватору и полярному кругу. В Лапландию (66о с.ш.) отправились Пьер Мопертюи и Алексис Клеро, где измерили дугу протяженностью 57’30» и получили длину 1о равной 57422 туаз (111,9 км). В Перу под руководством академика Пьера Бугера (1698-1758) методом триангуляции была измерена дуга от +0о2’30» с. ш. до -3о04’30» ю. ш., по которой длина 1о составила 56748 туаз (110,6 км). Результат этой экспедиции стал первым опытным подтверждением сплюснутости Земли, что могло иметь место в случае, когда Земля имеет форму эллипсоида вращения. В честь этого события была даже выбита медаль, на которой изображенный Бугер слегка опирался на земной шар и слегка его сплющивал. Первую теорию фигуры Земли предложил в 1743 г. Алексис Клод Клеро (1713-1765). Теоремы Клеро устанавливают связь между формой Земли, ее вращением и распределением силы тяжести на ее поверхности, тем самым были заложены основы нового направления науки — гравиметрии. В 1841 г. Фридрих Бессель (1784-1846) установил для Земли форму сфероида со сжатием в 1/299,15 , а в 1909 г. Джон Хейфорд получил эллипсоид с экваториальным радиусом 6378,388 м и сжатием 1/297,0 , который использовался в качестве стандарта до 1964 г.
Фундаментальные определения были выполнены в 1940 г. Ф. Н. Красовским и А. А. Изотовым и опубликованы в 1950 г. Эллипсоид Красовского очень близок к современной системе астрономических постоянных, принятых Международным астрономическим союзом: экваториальный радиус Земли 6378160+3 м, полярный радиус 6356779 м, сжатие 0,0033529=1/298,25. При этом было введено и экваториальное сжатие 1/30000. Таким образом, некоторым промежуточным приближением формы Земли служит трехосный эллипсоид, у которого разница между экваториальным и полярным радиусами составляет 21381 м, а экваториальные радиусы в направлении Африки и Бразилии отличаются на 200 м.
На самом деле, истинная форма Земли на уровне точности в сотни метров уже не может быть представлена ни одной из математических фигур, и для ее представления применяется понятие геоида. Геоид — условная поверхность равного потенциала (поверхность равновесия), совпадающая с поверхностью свободно покоящейся воды в открытом океане. Отклонения геоида от эллипсоида не превышают, как правило, 100 м. Тем не менее, при условном представлении отклонений реальной формы Земли от аналитической фигуры, эти отклонения напоминают по форме грушу: «шишка» на северном полюсе и «провал» в Антарктиде. С помощью современных методов определения координат, в том числе и высоты над уровнем моря (спутниковые навигационные системы GPS, радиоинтерферометрические измерения и т. д.) реальная поверхность Земли описывается огромным массивом данных, при этом положение любого репера в трехмерном пространстве может быть определено с точностью до сантиметров.
Не надо путать форму Земли (геоид) с ее реальной твердой поверхностью. Очевидно, что рельеф литосферы в океанах располагается ниже поверхности геоида, а на материках — выше . Самая глубокая (относительно геоида) точка литосферы расположена в Марианском желобе (-11022 м), а самая высокая — г. Джомолунгма (8848 м). Наибольший перепад высот рельефа находится около Южной Америки, где разница высоты Анд (г. Аконкагуа — 6960 м) и прилегающего Чилийского желоба (максимальная глубина — 8180 м) составляет 15140 м.
Интересно напомнить, что форма Земли изменяется во времени. На ранних этапах существования Земли, как планетного тела, она вращалась вокруг своей оси значительно быстрее; предполагается, что древние земные сутки могли составлять 4-5 часов. Очевидно, что сжатие Земли в ту эпоху было значительно больше современного. С течением времени скорость вращения Земли замедляется (примерно на 15% за полмиллиарда лет), а ее форма, соответственно, «округляется».
На меньших отрезках времени и меньших масштабах по высоте существенную роль играет геотектоника плит. Как известно, материки «плавают» по поверхности магмы, как льдины по воде, и, перемещаясь, искажают при этом форму геоида на величины ~100 м за времена ~200*106 лет.
Наиболее «быстрыми» искажениями формы Земли являются приливы — гравитационные возмущения от Луны и Солнца. Наиболее известны эти возмущения в водной оболочке Земли, хотя присутствуют они и в атмосфере, и в литосфере. Теоретическая высота прилива (т. е. искажение формы геоида вследствие гравитационного возмущения от Луны) составляет около 50 см. Однако «приподнимание» «твердой» земной поверхности из-за упругости тела Земли существенно меньше (10-20 см). Наибольшую величину имеют водные приливы, связанные с воздействием на океаническую приливную волну мелкого дна и узостей береговой линии (до 18 м в заливе Фанди).
Глава 2. . Изучение показателей радиуса Земли отечественных и зарубежных исследователей.
2.1. Геодезические работы по измерению радиуса Земли в России.
В области геодезии в начале XIX в., так же как и в области астрономических исследований, произошел важный организационный перелом. В XVIII в. преимущественно трудами ученых из Академии наук была выполнена огромная работа по определению астропунктов, как основы для точных геодезических работ. Однако Отечественная война 1812 г. и последующий заграничный поход русской армии через Европу показали военному ведомству и правительству, что отечественная картография далеко еще не удовлетворительна. В частности, это было вызвано тем, что съемки территорий производились геодезистами часто без применения метода триангуляций и не было достаточного числа астрономических пунктов, определенных с достаточной точностью.
Для практических целей физическую поверхность Земли проектируют на вспомогательную поверхность, имеющую простую форму. Эта поверхность называется поверхностью относимости. Поверхность относимости должна
незначительно отличаться от поверхности квазигеоида в пределах какой либо территории, например, Европы, Азии, либо отдельного государства. В масштабах всей Земли удобно использовать общий земной эллипсоид, а в масштабах ограниченной территории за поверхность относимости удобно принимать другой эллипсоид (референц -эллипсоид),ориентировка которого в теле Земли может отличаться от ориентировки общего земного эллипсоида, при этом малая ось референц-эллипсоида может и не совпадать с осью вращения Земли, а быть ей параллельной. В табл. 1.1 приведена историческая справка по определению параметров земного эллипсоида(референц-эллипсоидов).
До настоящего времени используются различные референц-эллипсоиды:в Германии – эллипсоид Бесселя (1841 г.), в Великобритании – эллипсоид Кларка (1880 г.), в США – эллипсоид Хейфорда (1909 г.). В России до 1942 г. использовался эллипсоид Бесселя. При детальном исследовании этого референц-эллипсоида оказалось, что он дает весьма большие погрешности в положении точек на поверхности Земли в пределах России. Под руководством русского ученого Ф.Н.Красовского (1878 – 1948 гг.) выполнены расчеты по определению параметров референц-эллипсоида для России. С 1946 г. параметры полученного референц-эллипсоида приняты для использования в геодезических расчетах: большая полуось а = 6378245 м, полярное сжатие α = 1 : 298,3. При этом следует отметить, что полученный референц эллипсоид(референц-эллипсоид Красовского) в наибольшей степени определяет параметры общего земного эллипсоида. Это подтверждают и современные спутниковые измерения.
| Таблица 1.1 | |||
| Государство(ученый) | Год | Большая полуось, | Полярное сжатие |
| Франция (Деламбер) | м | ||
| 6 375 653 | 1 : 334,0 | ||
| Германия (Бессель) | 6 377 397 | 1 : 299,2 | |
| Великобритания (Кларк) | 6 378 206 | 1 : 295,0 | |
| Россия (Слудский) | 6 377 494 | 1 : 297,1 | |
| Россия (Жданов) | 6 377 717 | 1 : 299,0 | |
| С Ш А (Хейфорд) | 6 378 388 | 1 : 297,0 | |
| Россия (Красовский) | 6 378 210 | 1 : 298,6 | |
| Россия (Красовский) | 6 378 245 | 1 : 298,3 | |
| Спутниковые данные | Совр. | 6 378 137 | 1 : 298,257 |
megaobuchalka.ru
Как измерили Землю и узнали ее форму | Архив
Теперь вы знаете, что в сказочной Вселенной наших далеких предков Земля даже не напоминала шар. Жители Древнего Вавилона представляли ее в виде острова в океане. Египтянам она виделась вытянутой с севера на юг долиной, в центре которой был Египет. А древние китайцы одно время изображали Землю в виде прямоугольника… Вы улыбаетесь, представляя себе такую Землю, но часто ли вы задумывались о том, как люди догадались, что Земля — не безграничная плоскость или диск, плавающий в океане? Когда я спрашивал об этом ребят, то одни говорили, что о шарообразности Земли люди узнали после первых кругосветных путешествий, а другие вспоминали, что при появлении из-за горизонта корабля мы сначала видим мачты, а потом палубу. Доказывают ли такие и некоторые подобные им примеры, что Земля — шар? Вряд ли. Ведь объехать можно и вокруг… чемодана, а верхние части корабля появлялись бы и в том случае, если бы Земля имела форму полушария или была похожа, скажем, на… бревно. Подумайте об этом и постарайтесь изобразить сказанное на своих рисунках. Тогда вы поймете: приведенные примеры свидетельствуют лишь о том, что Земля изолирована в пространстве и, возможно, шарообразна.
Как же узнали, что Земля — шар? Помогла, как я уже вам рассказал, Луна, а точнее — лунные затмения, во время которых на Луне всегда видна круглая тень Земли. Устройте небольшой «театр теней»: освещайте в темной комнате предметы разной формы (треугольник, тарелку, картофелину, мяч и т. д.) и замечайте, какая тень от них получается на экране или просто на стене. Убедитесь, что только мячик всегда образует на экране тень в виде круга. Итак, Луна помогла людям узнать, что Земля — это шар. К такому выводу ученые в Древней Греции (например, великий Аристотель) пришли еще в IV веке до нашей эры. Но еще очень долго «здравый смысл» человека не мог смириться с тем, что люди обитают на шаре. Даже представить себе не могли, как можно жить на «другой стороне» шара, ведь находящимся там «антиподам» пришлось бы все время ходить вниз головой… Но где бы ни находился человек на земном шаре, всюду брошенный вверх камень будет под действием силы притяжения Земли падать вниз, то есть на земную поверхность, а если бы было возможно, то и к центру Земли. На самом деле, людям, конечно, нигде, кроме цирков и спортивных залов, не приходится ходить вверх ногами и вниз головой. Они в любом месте Земли ходят нормально: земная поверхность у них под ногами, а небо над головой.
Около 250 года до нашей эры греческий ученый Эратосфен впервые довольно точно измерил земной шар. Эратосфен жил в Египте в городе Александрия. Он догадался сравнить высоту Солнца (или его угловое расстояние от точки над головой, зенита, которое так и называется — зенитное расстояние) в один и тот же момент времени в двух городах — Александрии (на севере Египта) и Сиене (ныне Асуан, на юге Египта). Эратосфену было известно, что в день летнего солнцестояния (22 июня) Солнце в полдень освещает дно глубоких колодцев. Следовательно, в это время Солнце находится в зените. Но в Александрии в этот момент Солнце не бывает в зените, а отстоит от него на 7,2°. Такой результат Эратосфен получил, изменяя зенитное расстояние Солнца с помощью своего несложного угломерного инструмента — скафиса. Это просто вертикальный шест — гномон, укрепленный на дне чаши (полусферы). Скафис устанавливают так, чтобы гномон принимал строго вертикальное положение (направлен в зенит) Освещенный солнцем шест отбрасывает тень на разделенную на градусы внутреннюю поверхность скафиса. Так вот в полдень 22 июня в Сиене гномон тень не отбрасывает (Солнце в зените, его зенитное расстояние равно 0°), а в Александрии тень от гномона, как видно по шкале скафиса, отмечала деление 7,2°. Во времена Эратосфена расстояние от Александрии до Сиена считали равным 5000 греческих стадий (примерно 800 км). Зная все это, Эратосфен сопоставил дугу в 7,2° со всей окружностью в 360° градусов, а расстояние 5000 стадий — со всей окружностью земного шара (обозначим ее буквой X) в километрах. Тогда из пропорции
получилось, что Х = 250 000 стадий, или примерно 40 000 км (представьте себе, это так и есть!).
Если вам известно, что длина окружности равна 2πR, где R — радиус окружности (а π ~ 3,14), зная длину окружности земного шара, легко найти его радиус (R):
Замечательно, что Эратосфену удалось очень точно измерить Землю (ведь и сегодня считают, что средний радиус Земли 6371 км!).
Но почему здесь упомянут средний радиус Земли, разве у шара не все радиусы одинаковы? Дело в том, что фигура Земли отличается от шара. Об этом ученые стали догадываться еще в XVIII веке, но какова в действительности Земля — сжата она у полюсов или у экватора — выяснить было трудно. Чтобы разобраться в этом, Французской академии наук пришлось снарядить две экспедиции. В 1735 году одна из них отправилась проводить астрономические и геодезические работы в Перу и занималась этим в экваториальном районе Земли около 10 лет, а другая, лапландская, трудилась в 1736-1737 годах вблизи Северного полярного круга. В результате выяснилось, что длина дуги одного градуса меридиана неодинакова у полюсов Земли и у ее экватора. Градус меридиана оказался у экватора длиннее, чем в высоких широтах (111,9 км и 110,6 км). Так может быть лишь в том случае, если Земля сжата у полюсов и представляет собой не шар, а тело, близкое по форме к сфероиду. У сфероида полярный радиус меньше экваториального (у земного сфероида полярный радиус короче экваториального почти на 21 км).
Полезно знать, что великий Исаак Ньютон (1643-1727) предвосхитил результаты экспедиций: он сделал правильный вывод о том, что Земля сжата, потому наша планета вращается вокруг оси. Вообще, чем быстрее вращается планета, тем больше должно быть ее сжатие. Поэтому, например, сжатие Юпитера больше, чем Земли (Юпитер успевает сделать оборот вокруг оси по отношению к звездам за 9 ч 50 мин, а Земля только за 23 ч 56 мин).
И еще. Истинная фигура Земли очень сложна и отличается не только от шара, но и от сфероида вращения. Правда, в данном случае речь идет о разнице не в километры, а …метры! Подобным тщательным уточнением фигуры Земли ученые занимаются по сей день, используя для этой цели специально проводимые наблюдения с искусственных спутников Земли. Так что вполне возможно, что в решении задачи, за которую давным-давно взялся Эратосфен, когда-нибудь и вам придется принять участие. Это очень нужное людям дело.
Какой же лучше всего запомнить вам фигуру нашей планеты? Думаю, что пока достаточно, если вы будете представлять Землю в виде шара с надетым на него «дополнительным поясом», своего рода «нашлепкой» на область экватора. Такое искажение фигуры Земли, превращающее ее из шара в сфероид, имеет немалые последствия. В частности, из-за притяжения Луной «дополнительного пояса» земная ось примерно за 26 000 лет описывает в пространстве конус. Это движение земной оси называется прецессионным. В результате роль Полярной звезды, которая сейчас принадлежит α Малой Медведицы, поочередно играют некоторые другие звезды (ею в будущем станет, например, α Лиры — Вега). Кроме того, из-за такого (прецессионного) движения земной оси знаки Зодиака все больше и больше не совпадают с соответствующими созвездиями. Другими словами, через 2000 лет после эпохи Птолемея «знак Рака», например, уже не совпадает с «созвездием Рака» и т. д. Впрочем, современные астрологи стараются не обращать на это внимания…
Смотрите также:
www.aif.ru
А вы знаете кто определил первым радиус Земли?
Эратосфен — молодец, при помощи элементарных математических вычислений 2251 лет назад определил радиус Земли с ошибкой от определенного на сегодняшний день 5%. Это очень точный результат для того времени и тех возможностей.Солнце при своем годичном движении среди звёзд по эклиптике достигает максимального склонения в точке летнего солнцестояния, находящейся в созвездии Тельца, и вступает в знак Рака. В этот момент наступает астрономическое лето.
Интересно, что 21 июня Солнце в пунктах с широтой φ = 23°27′ в полдень находится в зените. В следующие дни склонение Солнца уменьшается, и оно будет проходить через зенит только южнее. Таким образом, параллель с φ = 23°27′ определяет северную границу мест, где Солнце хотя бы раз в году бывает в зените. Эта граница называется северным тропиком или тропиком Рака. Южная граница или тропик Козерога проходит по параллели φ = — 23°27′. Если Вы посмотрите на географическую карту, то увидите, что египетский город Асуан, где с нашей помощью построена гигантская асуанская плотина на реке Нил, расположен почти на Северном тропике. В древности этот город назывался Сиена. С измерением высоты Солнца в Сиене и Александрии, проведённого великим древнегреческим астрономом Эратосфеном, связано не только первое доказательство шарообразности Земли, но и первое прямое измерение длины земного меридиана.
Греческий астроном Эратосфен жил в III в. до нашей эры в городе Александрии. Он был очень разносторонне образованном человеком, его увлекали подчас очень далёкие друг от друга области науки, его даже в шутку на спортивный манер называли «пятиборцем», он, словно спортсмен, принимающий участие в пяти разных видах соревнований, всегда готов был ринуться в любую новую область знаний. В математике достаточно вспомнить знаменитое «решето Эратосфена», позволяющее определять простые числа.
Эратосфен знал, что в полдень в день летнего солнцестояния Солнце над Сиеной бывает настолько высоко, что его отражение видно на дне даже очень глубокого колодца. Отсюда Эратосфен сделал вывод, что Солнце в этот день в Сиене находится в зените и его высота равна точно 90°. Кроме того, Сиена лежит строго на юге от Александрии, т.е. эти города расположены на одном меридиане. Но в Александрии Солнце в этот день не в зените, что, как считал Эратосфен, указывает на шарообразность Земли – вывод, который в те времена противоречил общепризнанной точке зрения. Исходя из шарообразности Земли, он решил путём точных измерений определить длину земного меридиана. Для своих измерений в Александрии он воспользовался скафисом – чашеобразными солнечными часами со штырьком и делениями внутри них (более сложная разновидность гномона). Установленные вертикально, эти солнечные часы по тени от штырька дают возможность измерить высоту Солнца над горизонтом. И вот в полдень, в день летнего солнцестояния, когда в Сиене все предметы перестали отбрасывать тени, Эратосфен измерил его высоту на городской площади Александрии.
Солнце в Александрии, по измерениям Эратосфена, отстояло от зенита на 1/50 часть окружности. Следовательно, разность широт Александрии и Сиены равно этой величине, что в градусной мере составляет 7°12′. Так как наблюдения проводились в плодороднейшей долине Нила, где искусные шагатели-бематисты неоднократно проводили тщательные межевание земель, а бесчисленные караваны двигались друг другу навстречу, то расстояние между Александрией и Сиеной было известно в эпоху Эратосфена довольно точно по сравнению с другими местами. Это расстояние было равно 5000 греческих стадиев, следовательно, длина окружности земного меридиана была в 50 раз больше и равнялась 250 000 стадиям. При длине стадии в 158,5 м это соответствовало 39 600 км, всего на 400 км меньше современного точного значения. Зная длину окружности Земного меридиана легко вычислить радиус. Это конечно же принимая фигуру Земли за сферу, а не эллипсоид.
P.S. А Ватикан только в 1992 году признал, что Земля круглая и вращается вокруг своей оси:-)
evgris.livejournal.com
Кто первым измерил Землю — ПОЧИТАЙ-КА
Еще не было на земле Москвы, еще не крестил Владимир Русь огнем и мечом, когда в 973 году родился в городе Кят, столице древнего Хорезма, мальчик Мухаммад-ибн-Ахмед, названный позже Бируни — «человек из предместья».
Он интересовался всем. Спрашивал у заезжего грека, как называются на его языке плоды и травы, от каких болезней они лечат. Допытывался у своего приемного отца и учителя, зачем измеряют высоту солнца над горизонтом, как пользоваться древним прибором астролябией, как называются звезды.
Ему не было и двадцати, а он уже сумел вычислить широту своей обсерватории. В 22 года Бируни построил глобус Земли, вернее, северного ее полушария, «чтобы определять на нем долготы и широты». Глобус был таким большим, что нужно было встать на скамейку, чтоб дотянуться до неведомых Бируни городов, координаты которых он определил только по звездам!
В те времена многие правители держали при дворе ученого-звездочета, составлявшего гороскопы. Стал таким мудрецом и Бируни. Но султаны больше любили слушать лесть и воевать, чем смотреть на звезды. От набега войска соседнего султана Бируни пришлось бежать. Глобус его был разрушен, работа не закончена.
Султан Махмуд Газневийский, разоривший Хорезм, сказал ученому: «Если хочешь, чтоб при мне счастье было с тобой, говори не о своей науке, а говори то, что мне по желанию». Священные книги писали, что мир был сотворен за шесть дней, предания гласили, что Земля плоская, а упрямый Бируни твердил, что «опыт превыше всего», что Земля — шар и можно определить ее величину. «Я в Индии нашел большую гору над равниной. Я искал на вершине горы слияния земли и неба и определил угол, определил затем высоту горы…» Когда Бируни вычислил радиус Земли, он ошибся всего на 266 метров!
Точные измерения, опыты, изучение истории и сравнение свидетельств многих людей — вот основа любой науки: астрономии, математики, геодезии, минералогии, истории, географии. А Бируни много сделал для всех этих наук.
Он составил точные тригонометрические таблицы для математиков.
Он доказывал: не Солнце вращается вокруг Земли, а наоборот!
Бируни называют «отцом геодезии» — науки об измерении расстояний и углов на Земле. Он научился изображать на плоской карте круглую Землю, связал приливы и отливы с действием Луны. Он говорил, что звезды — это не сверкающая пыль, а огромные Солнца.
Ученый доказал, что между Азией и другой землей, которую мы теперь называем Америкой, есть пролив, и через семьсот лет Витус Беринг открыл этот пролив!
Бируни описал многие растения и их целительное действие.
Его книга «Минералогия» описывает минералы по твердости, цвету и впервые — по удельному весу. Только одно не интересовало Бируни в металлах: ценность, которую приписывали им люди. Когда султан Масуд прислал старому ученому в награду вьюк серебра, Бируни отослал его обратно со словами: «Когда мне это тратить?»
«Геодезия», «Хронология», «Вразумление начаткам искусства звездочета» — вот настоящие сокровища, оставленные Бируни людям.
- 01.06.2003
read-ka.cofe.ru
Первые измерения размеров Земли
Совершая путешествия из г. Александрии на юг, в г. Сиену (теперь Асуан), люди замечали, что там летом в тот день, когда солнце бывает всего выше на небе (день летнего солнцестояния — 21 или 22 июня), в полдень оно освещает дно глубоких колодцев, т. е. бывает как раз над головой, в зените. Вертикально стоящие столбы в этот момент не дают тени. В Александрии же и в этот день солнце в полдень не доходит до зенита, не освещает дна колодцев, предметы дают тень.
Эратосфен измерил, насколько полуденное солнце в Александрии отклонено от зенита, и получил величину, равную 7°12′, что составляет 1/50 окружности. Это ему удалось сделать при помощи прибора, называемого скафисом. Скафис представлял собой чашу в форме полушария. В центре ее отвесно укреплялась
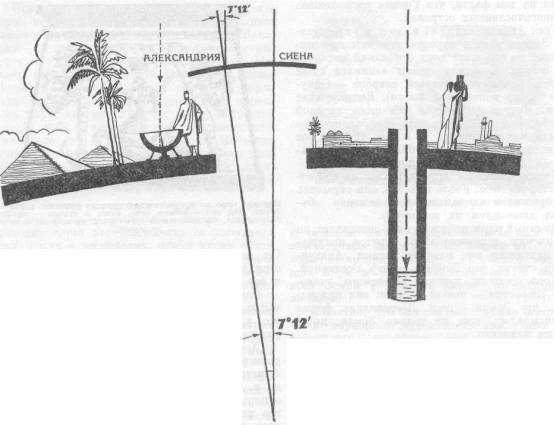
Слева — определение высоты солнца скафисом. В центре — схема направления солнечных лучей: в Сиене они падают вертикально, в Александрии — под углом в 7°12′. Справа — направление солнечного луча в Сиене в момент летнего солнцестояния.
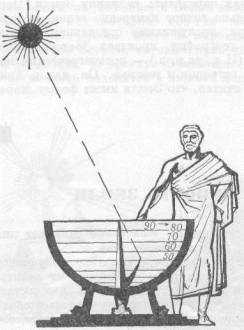
Скафис — древний прибор для определения высоты солнца над горизонтом (в разрезе).
игла. Тень от иглы падала на внутреннюю поверхность скафиса. Для измерения отклонения солнца от зенита (в градусах) на внутренней поверхности скафиса проводились окружности, помеченные цифрами. Если, например, тень доходила до окружности, помеченной цифрой 50, солнце стояло на 50° ниже зенита. Построив чертеж, Эратосфен совершенно правильно заключил, что Александрия отстоит от Сиены на 1/50 окружности Земли. Чтобы узнать окружность Земли, оставалось измерить расстояние между Александрией и Сиеной и умножить его на 50. Это расстояние было определено по числу дней, которое тратили караваны верблюдов на переход между городами. В единицах того времени оно равнялось 5 тыс. стадий. Если 1/50 окружности Земли равняется 5000 стадий, то вся окружность Земли равна 5000х50 = 250 000 стадий. В переводе на наши меры это расстояние приблизительно равно 39 500 км. Зная длину окружности, можно вычислить и величину радиуса Земли. Радиус всякой окружности в 6,283 раза меньше ее длины. Поэтому средний радиус Земли, по Эратосфену, оказался равным круглому числу — 6290 км, а диаметр — 12 580 км. Так Эратосфен нашел приблизительно размеры Земли, близкие к тем, которые определены точными приборами в наше время.
Как проверялась информация о форме и величине земли
После Эратосфена Киренского на протяжении многих столетий никто из ученых не пытался вновь измерить земную окружность. В XVII в. был изобретен надежный способ измерения больших расстояний на поверхности Земли — способ триангуляции (названный так от латинского слова «триангулюм» — треугольник). Этот способ удобен тем, что встречающиеся на пути препятствия — леса, реки, болота и т. п.— не мешают точному измерению больших расстояний. Измерение производится следующим образом: непосредственно на поверхности Земли очень точно измеряют расстояние между двумя близко расположенными точками А и В, из которых видны удаленные высокие предметы — холмы, башни, колокольни и т. п. Если из А и В через зрительную трубу можно разглядеть предмет, находящийся в точке С, то нетрудно измерить в точке А угол между направлениями АВ и АС, а в точке В— угол между ВА и ВС.
После этого по измеренной стороне АВ и двум углам при вершинах А и В можно построить треугольник АBС и, следовательно, найти длины сторон АС и ВС, т. е. расстояния от А до С и от Вдо С. Такое построение можно выполнить на бумаге, уменьшив все размеры в несколько раз или с помощью вычисления по правилам тригонометрии. Зная расстояние от В до С и наводя из этих точек зрительную трубу измерительного инструмента (теодолита) на предмет в какой-либо новой точке D, тем же путем измеряют расстояния от В до D и от С до D. Продолжая измерения, как бы покрывают часть поверхности Земли сетью треугольников: ABC, BCD и т. д. В каждом из них можно последовательно определить все стороны и углы (см. рис.). После того как измерена сторона АВпервого треугольника (базис), все дело сводится к измерению углов между двумя направлениями. Построив сеть треугольников, можно вычислить по правилам тригонометрии расстояние от вершины одного треугольника до вершины любого другого, как бы далеко друг от друга они ни находились. Так решается вопрос об измерении больших расстояний на поверхности Земли. Практическое применение способа триангуляции — дело далеко не простое. Эту работу могут выполнять только опытные наблюдатели, вооруженные очень точными угломерными инструментами. Обычно для наблюдений приходится сооружать специальные вышки. Работы такого рода поручаются особым экспедициям, которые продолжаются по нескольку месяцев и даже лет.
Способ триангуляции помог ученым уточнить знания о форме и величине Земли. Произошло это при следующих обстоятельствах.
Знаменитый английский ученый Ньютон (1643—1727) высказал мнение, что Земля не может иметь форму точного шара, потому что она вращается вокруг своей оси. Все частицы Земли находятся под влиянием центробежной силы (силы инерции), которая особенно велика
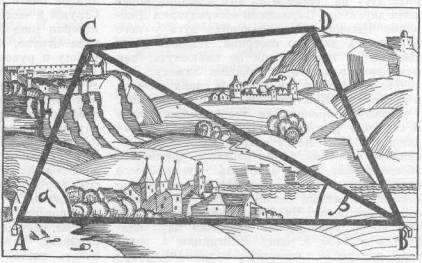
Если нам нужно измерить расстояние от А до D (при этом точку В не видно из точки А), то мы измеряем базис АВ и в треугольнике AВС измеряем углы, прилегающие к базису (a и b). По одной стороне и прилегающим к ней двум углам определяем расстояние АС и BС. Далее из точки С мы с помощью зрительной трубы измерительного инструмента находим точку D, видимую из точки С и точки B. В треугольнике CUB нам известна сторона СВ. Остается измерить прилегающие к пей углы, а затем определить расстояние DB. Зная расстояния DB u AB и угол между этими линиями, можно определить расстояние от А до D.
Схема триангуляции: АB — базис; BE — измеряемое расстояние.
у экватора и отсутствует у полюсов. Центробежная сила у экватора действует против силы тяжести и ослабляет ее. Равновесие между силой тяжести и центробежной силой было достигнуто тогда, когда земной шар у экватора «раздулся», а у полюсов «сплющился» и постепенно приобрел форму мандарина, или, выражаясь научным языком, сфероида. Интересное открытие, сделанное в то же время, подтвердило предположение Ньютона.
В 1672 г. один французский астроном установил, что если точные часы перевезти из Парижа в Кайенну (в Южной Америке, вблизи экватора), то они начинают отставать на 2,5 минуты в сутки. Это отставание происходит потому, что маятник часов около экватора качается медленнее. Стало очевидно, что сила тяжести, которая заставляет маятник качаться, в Кайенне меньше, чем в Париже. Ньютон объяснил это тем, что на экваторе поверхность Земли находится дальше от ее центра, чем в Париже.
Французская академия наук решила проверить правильность рассуждений Ньютона. Если Земля имеет форму мандарина, то дуга меридиана размером в 1° должна удлиняться при приближении к полюсам. Оставалось при помощи триангуляции измерить длину дуги в 1° на разном расстоянии от экватора. Измерить дугу на севере и на юге Франции поручили директору Парижской обсерватории Джованни Кассини. Однако южная дуга у него получилась длиннее северной. Казалось, что Ньютон не прав: Земля не сплюснута, как мандарин, а вытянута подобно лимону.
Но Ньютон не отказался от своих выводов и уверял, что Кассини ошибся при измерениях. Между сторонниками теории «мандарина» и «лимона» разгорелся ученый спор, который длился 50 лет. После смерти Джованни Кассини его сын Жак, также директор Парижской обсерватории, чтобы защитить мнение своего отца, написал книгу, где доказывал, что по законам механики Земля должна быть вытянута, как лимон. Чтобы окончательно решить этот спор, Французская академия наук снарядила в 1735 г. одну экспедицию к экватору, другую — к северному полярному кругу.
Южная экспедиция проводила измерения в Перу. Для измерения была выбрана дуга меридиана длиной около 3° (330 км). Она пересекала экватор и проходила через ряд горных долин и высочайших горных хребтов Америки.
Работа экспедиции продолжалась восемь лет и была сопряжена с большими трудностями и опасностями. Однако ученые выполнили свою задачу: градус меридиана у экватора был измерен с очень большой точностью.
Северная экспедиция работала в Лапландии (так до начала XX в. называлась северная часть Скандинавского и западная часть Кольского полуостровов).
После сравнения результатов работы экспедиций выяснилось, что полярный градус длиннее экваториального. Следовательно, Кассини действительно ошибался, а Ньютон был прав, утверждая, что Земля имеет форму мандарина. Так кончился этот затянувшийся спор, и ученые признали правильность утверждений Ньютона.
В наше время существует особая наука — геодезия, которая занимается определением величины Земли при помощи точнейших измерений ее поверхности. Данные этих измерений позволили достаточно точно определить действительную фигуру Земли.
Геодезические работы по измерению Земли проводились и проводятся в различных странах. Такие работы выполнены и в нашей стране. Еще в прошлом веке русскими геодезистами была проделана очень точная работа по измерению «русско-скандинавской дуги меридиана» протяжением более 25°, т. е. длиной почти в 3 тыс. км. Ее назвали «дугой Струве» в честь основателя Пулковской обсерватории (под Ленинградом) Василия Яковлевича Струве, который задумал эту огромную работу и руководил ею.
Градусные измерения имеют большое практическое значение прежде всего для составления точных карт. Как на карте, так и на глобусе вы видите сеть меридианов — кругов, идущих через полюсы, и параллелей — кругов, параллельных плоскости земного экватора. Карта Земли не могла быть составлена без длительной и кропотливой работы геодезистов, определявших шаг за шагом на протяжении многих лет положение разных мест на земной поверхности и затем наносивших полученные результаты на сеть меридианов и параллелей. Чтобы иметь точные карты, требовалось знать действительную форму Земли.
Результаты измерений Струве и его сотрудников оказались очень важным вкладом в эту работу.
Впоследствии другие геодезисты с большой точностью измерили длины дуг меридианов и параллелей в разных местах земной поверхности. По этим дугам при помощи вычислений удалось определить длину поперечников Земли в плоскости экватора (экваториальный диаметр) и в направлении земной оси (полярный диаметр). Оказалось, что экваториальный диаметр длиннее полярного примерно на 42,8 км. Это еще раз подтвердило, что Земля сжата с полюсов. По последним данным советских ученых, полярная ось на 1/298,3 короче экваториальной.
Допустим, мы хотели бы изобразить отклонение формы Земли от шара на глобусе с поперечником в 1 м. Если шар по экватору имеет поперечник точно 1 м, то его полярная ось должна быть всего лишь на 3,35 мм короче! Это столь малая величина, что на глаз ее нельзя обнаружить. Форма Земли, таким образом, очень мало отличается от шара.
Можно подумать, что неровности земной поверхности, и особенно горные вершины, высочайшая из которых Джомолунгма (Эверест) достигает почти 9 км, должны сильно искажать форму Земли. Однако это не так. В масштабе глобуса диаметром в 1 м девятикилометровая гора изобразится в виде прилипшей к нему песчинки диаметром около 3/4 мм. Разве только на ощупь, да и то с трудом, можно обнаружить этот выступ. А с той высоты, на которой летают наши корабли-спутники, его можно различить разве по черному пятнышку тени, отбрасываемой им при низком стоянии Солнца.
В наше время размеры и форма Земли очень точно определены учеными Ф. Н. Красовским, А. А. Изотовым и др. Вот числа, показывающие размер земного шара по измерениям этих ученых: длина экваториального диаметра — 12 756,5 км, длина полярного диаметра — 12 713,7 км.
Изучение пути, пройденного искусственными спутниками Земли, позволит определить величину силы тяжести в разных местах над поверхностью земного шара с такой точностью, которой нельзя было достигнуть никаким другим способом. Это в свою очередь позволит внести дальнейшее уточнение в наши знания о размерах и форме Земли.
Постепенное изменение формы земли
Однако, как удалось выяснить при помощи все тех же космических наблюдений и сделанных на их базе специальных вычислений, геоид имеет сложный вид вследствие вращения Земли и неравномерного распределения масс в земной коре, но достаточно хорошо ( с точностью до нескольких сотен метров) представляется эллипсоидом вращения, имеющим полярное сжатие 1:293,3 (эллипсоид Красовского).
Тем не менее до самого недавнего времени считалось вполне установленным фактом, что этот небольшой дефект медленно, но верно нивелируется из-за так называемого процесса восстановления гравитационного (изостатического) равновесия, начавшегося примерно восемнадцать тысяч лет назад. Но совсем недавно Земля опять начала сплющиваться.
Геомагнитные измерения, которые с конца 70-х годов стали неотъемлемым атрибутом научно-исследовательских программ спутникового наблюдения, стабильно фиксировали выравнивание гравитационного поля планеты. В общем, с точки зрения мейнстримовских геофизических теорий гравитационная динамика Земли представлялась вполне прогнозируемой, хотя, разумеется, как внутри мейнстрима, так и за его рамками существовали многочисленные гипотезы, по-разному интерпретирующие средне- и долгосрочные перспективы этого процесса, а равно и то, что происходило в прошлой жизни нашей планеты. Довольно большой популярностью пользуется сегодня, скажем, так называемая пульсационная гипотеза, согласно которой Земля периодически то сжимается, то расширяется; есть сторонники и у «контракционной» гипотезы, постулирующей, что в долгосрочном плане размеры Земли будут уменьшаться. Нет единства у геофизиков и по части того, в какой фазе находится сегодня процесс послеледникового восстановления гравитационного равновесия: большинство специалистов полагают, что он довольно близок к завершению, но имеются и теории, утверждающие, что до его конца еще далеко или что он уже прекратился.
Тем не менее, несмотря на обилие разночтений, до конца 90-х годов прошлого века
у ученых все-таки не было сколько-нибудь веских причин сомневаться в том, что
процесс послеледникового гравитационного выравнивания живет и здравствует. Конец
научному благодушию пришел довольно внезапно: потратив несколько лет на проверку
и перепроверку результатов, полученных с девяти различных спутников, двое
американских ученых, Кристофер Кокс из компании Raytheon и Бенджамен Чао,
геофизик Годдардовского центра управления космическими полетами NASA, пришли к
удивительному выводу: начиная с 1998 года, «экваториальный охват» Земли (или,
как окрестили эту размерность многие западные СМИ, ее «толщина») вновь стал
увеличиваться.
Зловещая роль течений океана.
Статья Кокса и Чао, в которой декларируется «обнаружение крупномасштабного перераспределения массы Земли», была опубликована в журнале Science в начале августа 2002 года. Как отмечают авторы исследования, «длительные наблюдения за поведением гравитационного поля Земли показали, что у выравнивавшего его послеледникового эффекта в последние несколько лет неожиданно возник более мощный противник, примерно вдвое превосходящий его по силе гравитационного воздействия». Благодаря этому «таинственному противнику» Земля вновь, как и в последнюю «эпоху Великого Обледенения», начала сплющиваться, то есть с 1998 года в районе экватора происходит нарастание массы вещества, тогда как из полярных зон идет его отток.
Прямых измерительных методик, позволяющих обнаружить этот феномен, у земных геофизиков пока нет, поэтому в своей работе им приходится пользоваться косвенными данными, прежде всего результатами сверхточных лазерных замеров изменений траекторий орбит спутников, происходящих под влиянием колебаний гравитационного поля Земли. Соответственно, говоря о «наблюдаемых перемещениях масс земного вещества», ученые исходят из предположения о том, что именно они ответственны за эти локальные гравитационные колебания. Первые попытки объяснения этого странного явления и предприняты Коксом и Чао.
Версия о каких-либо подземных явлениях, например перетекании вещества в земной магме или ядре, выглядит, по мнению авторов статьи, довольно сомнительной: для того, чтобы подобные процессы возымели хоть сколько-нибудь значимый гравитационный эффект, якобы требуется куда более длительное время, чем смехотворные по научным меркам четыре года. В качестве возможных причин, обусловивших утолщение Земли по экватору, они называют три основных: океаническое воздействие, таяние полярных и высокогорных льдов и некие «процессы в атмосфере». Впрочем, последняя группа факторов ими также сразу отметается — регулярные замеры веса атмосферного столба не дают никаких оснований для подозрений в причастности тех или иных воздушных явлений к возникновению обнаруженного гравитационного феномена.
Далеко не столь однозначной представляется Коксу и Чао гипотеза о возможном влиянии на экваториальное вздутие процесса таяния льда в арктической и антарктической зонах. Этот процесс как важнейший элемент пресловутого глобального потепления мирового климата, безусловно, в той или иной степени может быть ответственен за перенос значительных масс вещества (прежде всего воды) от полюсов к экватору, но сделанные американскими исследователями теоретические расчеты показывают: для того, чтобы он оказался определяющим фактором (в частности, «перекрыл» последствия тысячелетнего «роста положительного рельефа»), размерность ежегодно растапливаемой с 1997 года «виртуальной глыбы льда» должна была бы составлять 10х10х5 километров! Никаких эмпирических свидетельств того, что процесс таяния льда в Арктике и Антарктике за последние годы мог принять подобные масштабы, у геофизиков и метеорологов не имеется. Согласно самым оптимистическим оценкам, совокупный объем растаявших льдин как минимум на порядок меньше этого «суперайсберга», следовательно, даже если он и оказал какое-то влияние на прирост экваториальной массы Земли, едва ли это влияние могло быть столь существенным.
В качестве наиболее вероятной причины, обусловившей внезапное изменение гравитационного поля Земли, Кокс и Чао рассматривают сегодня океаническое воздействие, то есть все тот же перенос больших объемов водной массы Мирового океана от полюсов к экватору, который, однако, связан не столько с быстрым таянием льда, сколько с некими не вполне объяснимыми резкими флуктуациями океанических течений, происходящими в последние годы. Причем, как полагают специалисты, главный кандидат на роль возмутителя гравитационного спокойствия — Тихий океан, точнее, циклические перемещения огромных водных масс из его северных регионов в южные.
Если данная гипотеза окажется верной, человечество в весьма скором будущем может столкнуться с очень серьезными изменениями мирового климата: зловещая роль океанических течений хорошо известна всем мало-мальски знакомым с основами современной метеорологии (чего стоит один Эль-Ниньо). Правда, вполне логичным выглядит и предположение, что внезапное разбухание Земли по экватору — следствие уже идущей полным ходом климатической революции. Но, по большому счету, толком разобраться по свежим следам в этом клубке причинно-следственных взаимосвязей пока едва ли представляется возможным.
Очевидную нехватку понимания происходящих «гравитационных безобразий» прекрасно иллюстрирует небольшой фрагмент интервью самого Кристофера Кокса корреспонденту службы новостей журнала Nature Тому Кларку: «По моему мнению, сейчас можно с высокой степенью определенности (здесь и далее выделено нами. — ‘Эксперт’) говорить лишь об одном: ‘проблемы с весом’ нашей планеты, вероятно, носят временный характер и не являются прямым результатом человеческой деятельности». Однако, продолжая эту словесную эквилибристику, американский ученый тут же еще раз предусмотрительно оговаривается: «Постровидимому, рано или поздно все вернется ‘к норме’, но, возможно, мы заблуждаемся на сей счет».
biofile.ru
Какова история измерения радиуса Земли?
Полярный радиус Земли — малая полуось эллипсоида Красовского, равная 6 356 863 м.
Экваториальный радиус Земли — большая полуось эллипсоида Красовского, равная 6 378 245 м.
Средний радиус Земли — 6 371 302 м.
История измерения радиуса Земли
Эраторсфен. Еще древнейшие египтяне увидели, что во время летнего солнцестояния Солнце освещает дно глубочайших колодцев в Сиене (сейчас Асуан), а в Александрии — нет. У Эратосфена Киренского (276 год до н. э.-194 год до н. э.) появилась превосходный мысль — применять данный факт для измерения окружности и радиуса Земли. В день летнего солнцестояния в Александрии он использовал скафис — чашу с длинноватой иглой, с помощью которого есть возможность было найти под каким углом Солнце находится на небе.
Итак, после измерения угол оказался 7 градусов 12 минут, другими словами 1/50 окружности. Стало быть Сиена отстоит от Александрии на 1/50 окружности Земли. Расстояние меж городами числилось равным 5 тыс. стадиев, как следует окружность Земли равнялась 250 тыс. стадиев, а радиус тогда 39,8 тыс. стадиев.
Непонятно каким стадием воспользовался Эратосфен. В том случае греческим (178 метров), то его радиус Земли выходил 7,08 тыс. км, в том случае египетским, то 6,3 тыс. км. Современные измерения предоставляют для усреднённого радиуса Земли величину 6,371 км. В любом случае, точность для тех времён потрясающая.
Фернель. В 1528 г. Жан Фернель методом подсчета числа оборотов колеса экипажа измерил расстояние от Парижа до Амьена. Величина 1ой дуги меридиана у него составила 110,6 км. Через 4 года после возвращения спутников Магеланна в исследовании Земли был изготовлен 1-ый шаг. Парижанин Фернель пришел к мысли провести измерение радиуса Земли. Он решил измерить длину дуги величиной 1 градус. Он измерил полуденную высоту Солнца в Париже 26 августа. Дальше ему необходимо было отыскать место, где тогда же высота Солнца была ровно на 1 градус меньше. Для этого он издержал некоторое количество дней. Однако потому что наступала осень, разница была меньше 1 градуса. Фернель, чтоб обойти это препятствие высчитал высоту Солнца в Париже на неколько дней вперед.
Двигаясь на север, он имел возможность ассоциировать приобретенные данные каждый день в тот же самый день. Каждый день в полдень он останавливался и создавал наблюдения. 29 августа он нашел, что высота Солнца на 1 градус меньше чем в Париже тогда же. Фернель измерил длину колеса (20 футов), а потом повернул назад в Париж и считал обороты колеса (17024 об.). Позже он вычислил градусную меру дуги меридиана в туазах (1 туаз = 6 футов = 1,949 м), позже умножив на 360 и переведя туазы в метры есть возможность отыскать длину меридиана:
1,949/6-20-17024-360/1000=39815 км.
Другие пробы
Еще век спустя, в 1614-1617 гг. голландский астролог Виллеброрд Снеллиус в первый раз применил способ триангуляции, когда линейная протяженность большой дуги на поверхности Земли измеряется через систему поочередно сопряженных треугольников. Его измерение 1 градуса отдало 107 335 м.
В 1671 г. член Парижской академии Жан Пикар (1620-1682) опубликовал собственный труд «Измерение Земли», в каком не только лишь сказал результаты высокоточных триангуляционных измерений в 1669-1670 гг. дуги Париж-Амьен (1° = 111 210 м, настоящее значение 111 180 м), да и высказал предположение о том, что настоящая форма Земли — не шар.
Практически через год, в 1672 г. Жан Рише, проводя наблюдения Марса в Кайенне (Гвиана в Южной Америке, широта +5°), нашел замедление периода секундного маятника по сопоставлению с его периодом в Париже. Это было 1-ое инструментальное свидетельство уменьшения силы тяжести на экваторе. Это открытие вновь заострило бурный спор, имевший место в то время в европейской науке. Дело в том, что в согласовании с теорией глобального тяготения Ньютона, крутящиеся тела (в том числе наша Земля) должны принимать форму сплюснутого эллипсоида, а по теории эфирных вихрей Декарта, напротив, вытянутого сфероида. Потому вопрос об настоящей форме Земли для ньютонианцев и картезианцев был принципно важен.
Директор Парижской обсерватории Джованни Доменико Кассини (1625-1712) с 1683 г. начал проводить новые необъятные работы по градусным измерениям уже на длинноватой дуге — от нормандских берегов Франции на севере до испанской границы на юге. К огорчению, из-за погибели Кольбера (министра денег Людовика XIV) и самого Кассини работы прерывались и были завершены его отпрыском Жаком Кассини (1677-1756) исключительно в 1718 г., а результаты размещены в 1720 г. Кассини также был картезианцем по своим взорам и даже вступил в спор с Ньютоном, утверждая, что земной шар имеет вытянутую форму. Сам Ньютон давал теоретическую оценку сжатия Земли в 1/230.
Чтоб совсем разобраться с формой Земли, Французская академия в 1735 г. организовала две превосходные по тому времени экспедиции к экватору и полярному кругу. В Лапландию (66° с.ш.) направились Пьер Мопертюи и Алексис Клеро, где измерили дугу протяженностью 57’30» и получили длину 1° равной 57 422 туаз (111,9 км). В Перу под управлением академика Пьера Бугера (1698-1758) способом триангуляции была измерена дуга от +0°02’30» с. ш. до -3°04’30» ю. ш., по которой длина 1° составила 56 748 туаз (110,6 км). Итог этой экспедиции стал первым опытным доказательством сплюснутости Земли, что она имеет форму эллипсоида вращения. В честь этого действия была даже выбита медаль, на которой изображенный Бугер опирался на земной шар и немного его сплющивал.
Самое потрясающее градусное измерение XIX века возглавил основоположник Пулковской обсерватории В. Я. Струве. Под управлением Струве российские геодезисты вместе с норвежскими измерили дугу, простиравшуюся от Дуная по западным областям Рф в Финляндию и Норвегию до побережья Северного Ледовитого океана. Общая протяженность этой дуги превысила 2800 км. Она обхватывала более 25 градусов, что составляет практически 1/14 часть земной окружности. В историю науки она вошла под заглавием «дуги Струве». Создателю этой книжки в послевоенные годы довелось работать на наблюдениях (измерениях углов) на пт гос триангуляции, примыкавших прямо к известной «дуге».
Первую теорию фигуры Земли предложил в 1743 г. Алексис Клод Клеро (1713-1765). Аксиомы Клеро устанавливают связь меж формой Земли, ее вращением и рассредотачиванием силы тяжести на ее поверхности, тем были заложены базы нового направления науки — гравиметрии. В 1841 г. Фридрих Бессель (1784-1846) установил для Земли форму сфероида со сжатием в 1/299,15, а в 1909 г. Джон Хейфорд получил эллипсоид с экваториальным радиусом 6378,388 м и сжатием 1/297,0, который употреблялся в качестве эталона до 1964 г.
Фундаментальные определения были выполнены в 1940 г. Ф. Н. Красовским и А. А. Изотовым и размещены в 1950 г. Эллипсоид Красовского очень близок к современной системе астрономических неизменных, принятых Интернациональным астрономическим союзом:
При всем этом было введено и экваториальное сжатие 1/30000. Следовательно, неким промежным приближением формы Земли служит трехосный эллипсоид, у которого разница меж экваториальным и полярным радиусами составляет 21381 м, а экваториальные радиусы в направлении Африки и Бразилии отличаются на 200 м.
По сути, настоящая форма Земли на уровне точности в сотки метров уже не может быть представлена ни одной из математических фигур, и для ее представления применяется понятие геоида. Геоид — условная поверхность равного потенциала (поверхность равновесия), совпадающая с поверхностью свободно покоящейся воды в открытом океане. Отличия геоида от эллипсоида не превосходят, чаше всего, 100 м. Все же, при условном представлении отклонений реальной формы Земли от аналитической фигуры, эти отличия напоминают по форме грушу: «шишка» на северном полюсе и «провал» в Антарктиде. При помощи современных способов определения координат, в том числе и высоты над уровнем моря (спутниковые навигационные системы GPS, радиоинтерферометрические измерения и т. д.) настоящая поверхность Земли описывается большущим массивом данных, при всем этом положение хоть какого репера в трехмерном пространстве может быть определено с точностью до см.
Не нужно путать форму Земли (геоид) с ее реальной жесткой поверхностью. Явно, что рельеф литосферы в океанах размещается ниже поверхности геоида, а на континентах — выше (говорят: «высота над уровнем моря»). Самая глубочайшая (относительно геоида) точка литосферы размещена в Марианском желобе (-11022 м), а самая высочайшая — г. Джомолунгма (8848 м). Больший перепад высот рельефа находится около Южной Америки, где разница высоты Анд (г. Аконкагуа — 6960 м) и прилегающего Чилийского желоба (наибольшая глубина — 8180 м) составляет 15140 м.
Любопытно напомнить, что форма Земли меняется во времени. На ранешних шагах существования Земли, как планетного тела, она крутилась вокруг собственной оси существенно резвее; подразумевается, что древнейшие земные день имели возможность составлять 4-5 часов. Явно, что сжатие Земли в ту эру было существенно больше современного. Со временем скорость вращения Земли замедляется (приблизительно на 15% за полмиллиарда лет), а ее форма, соответственно, «округляется». На наименьших отрезках времени и в наименьших масштабах по высоте существенную роль играет геотектоника плит. Как понятно, континенты «плавают» по поверхности магмы, как льдины по воде, и, перемещаясь, искажают при всем этом форму геоида на величины ~100 м за периоды ~200 млн лет.
Более «быстрыми» искажениями формы Земли являются приливы — гравитационные возмущения от Луны и Солнца. Более известны эти возмущения в аква оболочке Земли, хотя находятся они и в атмосфере, и в литосфере. Теоретическая высота прилива (т.е. искажение формы геоида вследствие гравитационного возмущения от Луны) составляет около 50 см. Но «приподнимание» «твердой» земной поверхности из-за упругости тела Земли значительно меньше (10-20 см). Самую большую величину имеют водные приливы, связанные с воздействием на океаническую приливную волну маленького дна и узостей береговой полосы (до 18 м в заливе Фанди).
Первоисточники:
Дополнительно на New-Best.com:
Источник материала Интернет-сайт www.genon.ru
new-best.com

