Формирование математических навыков у детей с тнр – . , — .

Содержание

Структура и содержание математического образования дошкольников с тяжелыми нарушениями речи Текст научной статьи по специальности «Народное образование. Педагогика»

Казанский педагогический журнал. 2015. №6

УДК 376

СТРУКТУРА И СОДЕРЖАНИЕ МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ

ДОШКОЛЬНИКОВ С ТЯЖЕЛЫМИ НАРУШЕНИЯМИ РЕЧИ

Л.Б. Баряева

Аннотация. В статье рассматриваются вопросы математического образования дошкольников с тяжелыми нарушениями речи (ТНР). Выделяются основные компоненты факторной модели математического развития дошкольников с нормальным речевым развитием и детей с ТНР. Определены основные направления формирования математических представлений у дошкольников с ТНР на основе выделения содержательных компонентов факторной модели и современных подходов к математическому образованию дошкольников с ТНР в условиях реализации ФГОС ДО.

Ключевые слова: знаково-символические способности, факторы, тяжелые нарушения речи, речевые функции, математическое образование, математическая деятельность.

STRUCTURE AND DETAILS OF MATHEMATICS EDUCATION

OF PRESCHOOL CHILDREN WITH HEAVY SPEECH PATHOLOGY

L. Baryaeva

Abstract. In article we considered questions of mathematical formation at preschool children with heavy speech pathology (HSP). There are allocated basic components of factorial model of mathematical development of preschool children with normal speech children with HSP. We defined basic directions of formation of mathematical representations of preschool children with HSP on the basis of allocation of substantial components of factorial model and modern approaches to mathematical formation of preschool children with HSP in the conditions of realization of state educational standards.

Keywords: sign-symbolical abilities, factors, heavy speech pathology, speech functions, mathematical formation, mathematical activity.

Теоретически и экспериментально доказана не только возможность, но и необходимость раннего ознакомления детей с логикой математики. Это позволяет уже в дошкольном возрасте организовать работу по формированию знаково-символической способности как инструментария мыслительной деятельности [2, 4, 5, 9, 11 и др.]. Поэтому математическое образование имеет такое большое значение для целостного, в том числе когнитивного, развития дошкольников с тяжелыми нарушениями речи (ТНР).

Исходя из требований ФГОС ДО и примерной адаптированной программы для детей с ТНР, выделены следующие задачи математического образования дошкольников: общеинтеллектуальное развитие; развитие познавательных интересов и способностей, мышления; формирование представлений о величине, форме, пространстве и времени, множестве, числе, пространственных, временных, количественных отношениях; формирование навыков и умений счета, вычислений; моделирование; понимание математической терминологии [13]. Анализ исследований, направленных на формирование у дошкольников физической и социальной

картины мира («модели мира»), показал, что наиболее значимым для их математического образования является формирование

опосредующих символических структур [1, 8, 12, 13, 14, 15, 16 и др.].

Математическая деятельность дошкольников рассматривается нами как деятельность, направленная на формирование и преобразование математического опыта путем активного, преднамеренного, осознанного овладения детьми физической и социальной картиной мира. Математическая деятельность в нашем понимании базируется на предметнопрактической, игровой, трудовой, речевой деятельности, а также на зарождающейся в старшем дошкольном возрасте учебной деятельности [2].

Проведенные нами исследования свидетельствуют о том, что математические представления у детей с ТНР и дошкольников с нормальным речевым развитием совпадают по основным показателям. В тоже время в ряде показателей они имеют отличие [3, 13 и др.]. Это является значимым для определения путей коррекционно-развивающей работы с детьми с нарушением речи. Не останавливаясь подробно на всех показателях математического развития

125

Казанский педагогический журнал. 2015. №6

детей, обратим внимание на наиболее значимые для определения направлений

общеразвивающей и коррекционной работы с детьми с ТНР.

Установлено, что основным компонентом факторной модели математического развития детей с нормальным интеллектуальным развитием, в том числе и детей с ТНР (первый фактор), выступает: «Вербализованные

пространственно-количественные отношения» (31,07% дисперсии). Среди показателей, составляющих данный фактор, наиболее значимым для понимания структуры математического развития детей является показатель «Умение составлять арифметические задачи по наглядной ситуации» (0,71). Эксперимент показал, что старшим дошкольникам с нормальным интеллектуальным развитием, но разным уровнем речевого развития, было доступно понимание элементарного психологического содержания задачи, логических и математических отношений, которые необходимо иметь в виду, формулируя условие задачи. У большинства из них в старшем дошкольном возрасте уже сформирована ориентировочная основа действий для решения или составления арифметических задач. Основное отличие в показателях наблюдалось у дошкольников с нормальным речевым развитием и детей с ТНР в способах вербального выражения текста задачи, его полноты и цельности.

Второй фактор, условно обозначенный нами как «Понимание знаково-символической функции числа» (21,11% дисперсии) детьми старшего дошкольного возраста, включал показатели, отражающие освоение детьми знаково-символических средств

интеллектуальной деятельности. Нами

выявлено, что несформированность понимания некоторых общих принципов счета у детей с ТНР соотносится с особенностями понимания ими речи взрослого. Именно неполное понимание речевой инструкции затрудняла выполнение детьми заданий, а в целом и процесс овладения речевыми компонентами счетной

деятельности.

Проведенный факторный анализ

математического развития детей с нормальным интеллектуальным развитием, но разным уровнем речевого развития, дал основание выделить также фактор «Вербальное

обоснование конкретных математических операций» (12,31% дисперсии), который позволяет судить о способности нормально развивающихся детей осуществлять переход от

восприятия математических операций к речевому суждению, их обоснованию. Анализ показателей данного фактора позволил сделать вывод о том, что дети овладевают зрительнопространственной ориентировкой и используют ее в счетной деятельности уже в среднем дошкольном возрасте. В то же время для детей с ТНР по сравнению со сверстниками с нормальным речевым развитием сложнее было выполнять задания в двухмерном малом пространстве. Это свидетельствовало о недостаточной сформированности зрительнопространственных гностических функций у детей с ТНР (дети с дизартрией).

Таким образом, факторная структура математического развития нормально развивающихся детей с различным уровнем речевого развития в целом отражает понятийносмысловую сущность, динамику формирования математических представлений в предметнопрактической, игровой деятельности и в речи.

Нами были определены основные направления математического образования дошкольников с ТНР в виде трех ступеней обучения. В статье даны краткие рекомендации по содержанию формируемых математических представлений [13].

На первой ступени обучения дошкольников с ТНР основное внимание уделяется дидактическим играм и игровым упражнениям с математическим содержанием: играм с водой, песком и другими природными материалами (плодами, крупой и т.п.), бумагой, рукотворными материалами, объемными и плоскостными моделями предметов.

Математическое развитие детей с ТНР осуществляется воспитателями в процессе непосредственно образовательной деятельности, а учитель-логопед включает в индивидуальную логопедическую работу с детьми игры и упражнения с элементами материала математического содержания.

Материал с математическим содержанием используется учителем-логопедом в процессе формирования предметного, предикативного, адъективного словаря экспрессивной речи детей, в ходе развития импрессивной речи, в процессе формирования слухо-зрительного и слухомоторного взаимодействия в процессе восприятия и воспроизведения ритмических структур, а также в процессе формирования произвольного слухового и зрительного восприятия, внимания, памяти. Счетный материал, природный и рукотворный, активно используется для развития движений кистей рук и совершенствования межанализаторного

126

Казанский педагогический журнал. 2015. №6

взаимодействия зрительного, слухового и тактильного анализаторов.

На второй ступени обучения рекомендуется активно развивать у детей с ТНР аналитикосинтетическую деятельность, значимую для их математического развития. Дети с ТНР, как и их сверстники с нормальным речевым развитием, осваивают правила счета, овладевают общепринятыми эталонами форм, величины, осваивают навыки измерения. Особое внимание специалистов в работе с детьми с ТНР обращается на оречевление действий, связанных с математическими операциями, на их словесное обозначение, в ходе которого необходимо изменять имена существительные по родам, числам и падежам, глаголы по временам.

В процессе экспериментов, проводимых на основе опытов Ж. Пиаже [12, 16], мы

установили, что для детей с ТНР характерны трудности в овладении простейшими топологическими представлениями, играющими важную роль в формировании речевой деятельности. Нарушения в овладении ими приводят к нарушениям в овладении счетной деятельностью (предрасположенность к дискалькулии) [3, 9, 10 и др.]. Поэтому

формирование элементарных математических представлений на второй ступени обучения проводится комплексно на основе широкого использования разнообразных видов

деятельности и включения в процесс формирования данных представлений не только воспитателей, но и учителей-логопедов. Детей учат показывать различные действия, направленные на воспроизведение величины, формы предметов, протяженности, удаленности с помощью пантомимических средств. Наряду с этим у них формируются представления о независимости количества элементов множества от пространственного расположения и качественных признаков предметов,

составляющих множество, в процессе игр и игровых упражнений. Дети с ТНР осваивают элементарные счетные действия с множествами предметов на основе слухового, тактильного и зрительного восприятия, в ходе чего у них развивается сенсорно-перцептивная

способность: узнавание количества предметов, формы, величины на ощупь, зрительно, узнавание количества звуков на слух. Важным на этой ступени обучения является формирование у детей операциональнотехнической стороны деятельности: они учатся действовать двумя руками, одной рукой (удерживать, приближать, поворачивать, расставлять фигурки в ряд, брать по одной

игрушке, картинке и т.п., убирать счетный материал, геометрические фигуры и т.п.). У детей развивается зрительно-двигательная координация. Они учатся прослеживать взглядом за движением руки, игрушками, расположением картинок и т.п. В ходе обучения у детей формируется умение определять пространственное расположение предметов относительно себя (впереди — сзади, рядом со мной, надо мной, подо мной). Среди значимых достижений детей в формировании математических представлений, которая выделяется как важный компонент математического развития, является

развивающаяся на этой ступени обучения способность детей вычленять анализируемый объект, видеть его во всем его многообразии свойств, определять элементарные отношения сходства и отличия.

Формирование элементарных

математических представлений на третьей ступени обучения проводится также на комплексной основе с обеспечением самых разнообразных видов деятельности. В процессе предматематической подготовки детей педагогам рекомендуется учитывать то, что у детей с ТНР в старшем дошкольном возрасте на фоне сравнительно развернутой речи часто еще наблюдается неточное знание и неточное употребление многих слов, в том числе и элементарных математических терминов. Дети затрудняются в употреблении слов, характеризующих качества, признаки, состояния предметов и действий, а также способы действий, затрудняются в использовании сложных предлогов, что важно для обучения решению арифметических задач, словесного обозначения пространственных отношений.

На третьей ступени обучения по формированию элементарных математических представлений большое внимание уделяется созданию условий для игровой (дидактические, сюжетно-дидактические, театрализованные и подвижные игры), трудовой (ручной труд и хозяйственно-бытовой труд), конструктивной и изобразительной деятельности детей, направленной на расширение, уточнение и закрепление полученных представлений. В ходе непосредственно образовательной деятельности с детьми внимание уделяется формированию произвольного слухового и зрительного восприятия, целенаправленного развития внимания, памяти, зрительно-пространственных представлений, увеличению объема зрительной, слуховой и слухоречевой памяти детей в ходе овладения математическими представлениями.

127

Казанский педагогический журнал. 2015. №6

В процессе предметно-практических действий детей обращается внимание на формирование кинестетической и кинетической основы движений с материалами с математическим содержанием.

Важным на этой ступени обучения является совершенствование основных компонентов мыслительной деятельности детей,

формирование у них логического мышления на математическом материале. В процессе математического развития детей с ТНР ведется обучение планированию математической деятельности, контроля за ней при участии речи детей.

Задачей обучения дошкольников с ТНР на третьей ступени обучения является не только передача им определенных знаний и способов решения задач, но и формирование психологических механизмов, обеспечивающих успешность развития и обучения, самостоятельность детей в дальнейшей учебной деятельности, и применение математического опыта в практической жизни. На этой ступени обучения дети овладевают наиболее сложным психологическим действием при овладении математикой — решением арифметических задач. Наряду с этим большое внимание уделяется совершенствованию пространственного

восприятия детей. Так как у детей с ТНР (дети с дизартрией) выполнение математических заданий, связанных с развитием ручной моторики, затруднено и в старшем дошкольном возрасте, в ходе непосредственно образовательной и коррекционной работы по развитию элементарных математических представлений используются схемы, таблицы, фигуры, рисунки, которые дети должны составить или изобразить самостоятельно. Это требует высокого уровня развития моторики рук. Затруднения, связанные с практическими действиями, отвлекают ребенка от основной цели математической деятельности и препятствуют достижению ее, снижают темп и качество выполнения задания. Необходимо учитывать то, что нарушение четкости движений рук, точности восприятия, а также низкий уровень зрительно-двигательной координации оказывают отрицательное влияние на процесс овладения математикой.

На этой ступени обучения внимание обращается на овладение детьми символическими средствами математического словаря. Детям предлагаются упражнения на отношения равенства и неравенства с обозначением знаками, зависимости между величинами, числами, выраженными в знаках

«больше»,«меньше». Счетные операции с использованием «записи» решения примеров, задач с помощью цифр и математических символов и называнием их с опорой на символы.

Детей учат пользоваться стрелкой-вектором, знаками, указывающими отношения между величиной и направлениями объектов, количеством и т.п. Наряду с уточнением геометрических представлений о

пространственных телах и плоскостных фигурах у детей формируют представления о внутренней и внешней части геометрической фигуры, границе фигуры. Дети знакомятся с понятиями «точка», «прямая», «кривая», «извилистая», «ломаная линия», «замкнутая и незамкнутая линия», «отрезок» и взаимоотношением точек и линий. Они учатся моделировать линии из различных материалов (шнуров, ниток, мягкой цветной проволоки, лент, геометрических фигур и т.п.). Эти представления закрепляются в практических видах деятельности.

Особое внимание в процессе математического образования детей с ТНР к обучению в школе обращается на использование ими в речи математических терминов, обозначающих величину, форму, количество и т.п., называние всех свойств, присущих объектам, а не присущих им — с использованием отрицания «не». В ходе речевой работы на занятиях по формированию математических представлений у детей развивают речевые умения, необходимые для определения и отражения в речи оснований группировок, классификаций по ведущему признаку (форма, величина, количество и т.п.), выделению связей и зависимостей различных проводимых группировок в зависимости от основания классификаций.

Для расширения представлений о «картине мира» детям с ТНР предлагаются познавательные сведения из истории арифметики: как люди учились считать, от зарубок через символы к цифрам, цифры у разных народов, малый счет у славян, абак и счеты и другая доступная и интересная дошкольникам информация. Эти представления уточняются и закрепляются в процессе театрализованных игр по сюжетам рассказов, сказок, бесед с детьми. Например, театрализованные игры «Древние математики»: возведение пирамид, «чтение» древних папирусов («папирус Ринда») и измерения участков древних египтян, имеющих форму квадрата, треугольника, прямоугольников, строительство домов круглой, квадратной и т.п. формы с использованием полифункциональных

128

Казанский педагогический журнал. 2015. №6

модульных наборов, например, «Радуга», «Гномик», «Фантазия», «Часики» и т.п.

В ходе обучения дети с ТНР знакомятся с современными техническими интерактивными средствами: калькулятором, компьютером,

мобильным телефоном и т.п. Им предлагаются компьютерные математические развивающие игры.

Все вышепредставленные содержательные компоненты обучения детей с ТНР ведутся в структуре совместной образовательной

деятельности взрослых с детьми, а также в процессе коррекционно-развивающей работы, направленной на профилактику дискалькулии у детей. Ведь предрасположенность к дискалькулии обнаруживается у детей с ТНР именно в старшем дошкольном возрасте, то есть на этапе подготовки к обучению в школе. Поэтому педагоги (учитель-логопед,

воспитатели) на данной ступени обучения выявляют факторы риска возникновения дискалькулии и используют адекватные профилактические меры для оказания помощи каждому ребенку с ТНР [13].

По результатам факторного анализа экспериментального исследования определены основные этапы, отражающие формирование структуры математических знаний у

дошкольников с тяжелыми нарушениями речи. Установлено, что эти этапы каждый ребенок с ТНР может проходить в разном темпе. Чаще всего, как показал наш научный и практический опыт, первый этап соотносится с первой ступенью обучения, второй и третий этап соотносятся со второй ступенью обучения, а четвертый и пятый этап — это третья ступень в обучении. В то же время могут наблюдаться и индивидуальные различия, связанные с индивидуальными особенностями ребенка, периодом включения его в коррекционноразвивающее обучение и особенностями речевого развития. Исходя из этого, возрастает роль индивидуальных занятий различных специалистов с ребенком ТНР для гармонизации его продвижения в математическом развитии. Содержание основных этапов, отражающих формирование структуры математических знаний у дошкольников с тяжелыми нарушениями речи в обобщенном виде можно представить следующим образом.

Напервом этапедети овладевают навыками математических действий на основе овладения чувственным опытом, путем повторения и многократного воспроизведения различных игровых, трудовых действий с природным и рукотворным материалом. В играх и

упражнениях с детьми обращается внимание на пространственно-временные характеристики объектов, с которыми они взаимодействуют. В процессе экспериментирования с реальными объектами дети усваивают характеристики формы и движения, а затем количественные характеристики. Этот этап можно назвать этапом приобретения навыков, знаний и умений, основанных на взаимодействии и воспроизведении субъектом обучения действий другого (взрослого, сверстника, имеющего определенный математический опыт). В этот период ребенок лишь эксплицитно осваивает систему правил, на основе которой формируются и понимаются математические действия. Данный этап является предматематическим, направленным на формирование сенсорно-перцептивных,

моторных, интеллектуальных предпосылок овладения математической деятельностью.

Второй этап — формирование перцептивных, двигательных и мыслительных навыков, реализуемых во внешнем предметном плане, опирающихся на предварительное осознание компонентов действия и усвоение критериев-индикаторов

(правильности/ошибочности) математических действий с последующим переходом от автоматизированных навыков математических действий к навыкам вторично

автоматизированным, то есть предварительно закрепленным и осознанным. У детей формируется совокупность внутренних и внешних условий освоения математических представлений и действий: от формирования навыка как результата выполнения конкретного правила до автоматизированного,

интериоризированного действия, не требующего повторения правил и развернутого контроля.

Третий этап — освоение логических операций, необходимых для счета, с опорой на сенсорно-перцептивный опыт; объединение математических действий в операциональные схемы на основе сенсорных эталонов; синтез теоретических и практических составляющих математического развития в результате освоения конструктивного компонента пространственновеличинных представлений. В ходе обучения у ребенка формируются устойчивые

математические паттерны. Его референтами выступают простые действия и более сложные умения, характеризующие определенную

компетентность в математической деятельности.

Четвертый этап — целостное освоение счета, включающее: знание числовой

последовательности; взаимосвязи между

129

Казанский педагогический журнал. 2015. №6

числами и объектами; понимание итогового числа; позиционных связей в пространстве и времени; способность к выявлению связей и отношений между реальными совокупностями множеств. На данном этапе формируется понимание элементарных математических отношений и зависимостей, взаимосвязей, устанавливаются причинно-следственные

отношения между ними.

Пятый этап предполагает сформированную понятийно-смысловую сущность

математических действий. На данном этапе усваиваются вербализованные,

пространственно-величинно-количественные и временные отношения, опирающиеся на понятийную базу практических умений и навыков. У детей формируется вербальное обоснование конкретных математических операций. Содержание этого этапа отражает

Литература:

1. Ахутина Т.В., Обухова Л.Ф., Обухова О.Б. Трудности усвоения начального курса математики детьми младшего школьного возраста и их причины // Психологическая наука и образование. -2001. — № 1. — С. 65-78.

2. Баряева Л.Б. Математическое образование дошкольников с задержкой психического развития: диагностика и коррекция. — СПб.: ЦДК проф. Л.Б. Баряевой, 2013. — 320 с.

3. Баряева Л.Б., Кондратьева С.Ю., Лопатина Л.В. Профилактика и коррекция дискалькулии у детей. — СПб.: ЦДК проф. Л.Б. Баряевой, 2015. -127 с.

4. Белошистая А.В. Формирование и развитие математических способностей дошкольников. — М.: ВЛАДОС, 2003. — 400 с.

5. Вахрушева Л.Н. Современные требования к математическому развитию детей дошкольного возраста / Перспективы развития дошкольного и начального образования. — СПб.: Изд. РГПУ им.

А.И. Герцена, 2002. — С. 30-31.

6. Венгер Л.А. О качественном подходе к динамике умственного развития ребенка // Вопросы психологии. — 1974. — № 1. — С. 116-122.

7. Гальперин П.Я. Методы обучения и умственное развитие ребенка. — М.: Изд-во МГУ, 1985. — 45 с.

8. Зинченко В.П. От классической к органической психологии // Вопросы психологии. -1996. — № 6. — С. 6-25.

9. Кондратьева С.Ю. Познаем математику в игре. — СПб.: ЦДК проф. Л.Б. Баряевой, 2011. — 255 с.

10. Лалаева Р.И., Гермаковска А. Дискалькулии у детей // Дети с проблемами в развитии. — 2004. — № 2. — С. 7-9.

11. Леушина А.М. Формирование

элементарных математических представлений у

сдвиг от перцептивной достоверности к опоре на логику, возможность выражать собственные математические представления, в основном вербальными средствами. Ребенок постигает смысл и значение совершаемых математических действий, убеждается в логической упорядоченности усвоенных им математических представлений, переходит от восприятия математических операций к речевому суждению о них, обоснованию их в практическом и речевом плане.

Общим для всех этапов фактором выступают математические представления, связанные с систематизацией знаний об окружающем предметном и социальном мире, позволяющие эффективно с ним взаимодействовать, раскрывающие адаптационный смысл математического развития, направленного на формирование у ребенка с ТНР «картины мира».

детей дошкольного возраста. — М.: Просвещение, 1974. — 368 с.

12. Пиаже Ж. Генезис числа у ребенка: Пер. с франц. — М.: Международная педагогическая академия. — 1994. — С. 237-582.

13. Примерная адаптированная основная образовательная программа для дошкольников с тяжелыми нарушениями речи / Л.Б. Баряева, Т.В. Волосовец, О.П. Гаврилушкина, Г.Г. Голубева и др.; под. ред. проф. Л.В. Лопатиной. — СПб., 2014. -386 с.

14. Салмина Н.Г. Знак и символ в обучении. -М.: МГУ, 1988. — 288 с.

15. Gelman R., Meck E. Prescholer’s counting: principles before skill // Cognition. 1983. — V. 13. — P.

343-359.

16. Inhelder B., Piaget J. The growth of logical thinking from childhood to adolescence. — N.Y. -Basic books, 1958. — 326 pp.

References:

1. Ahutina T.V., Obuhova L.F., Obuhova O.B. Trudnosti usvoenija nachal’nogo kursa matematiki det’mi mladshego shkol’nogo vozrasta i ih prichiny // Psihologicheskaja nauka i obrazovanie. — 2001. — № 1. — S. 65-78.

2. Baryaeva L.B. Matematicheskoe obrazovanie doshkol’nikov s zaderzhkoj psihicheskogo razvitija: diagnostika i korrekcija. — SPb.: CDK prof. L.B. Baryaevoj, 2013. — 320 s.

3. Baryaeva L.B., Kondrat’eva S.Ju., Lopatina L.V. Profilaktika i korrekcija diskal’kulii u detej. -SPb.: CDK prof. L.B. Baryaevoj, 2015. — 127 s.

4. Beloshistaya A.V. Formirovanie i razvitie matematicheskih sposobnostej doshkol’nikov. — M.: VLADOS, 2003. — 400 s.

5. Vahrusheva L.N. Sovremennye trebovanija k matematicheskomu razvitiju detej doshkol’nogo vozrasta / Perspektivy razvitija doshkol’nogo i

130

Казанский педагогический журнал. 2015. №6

nachal’nogo obrazovanija. — SPb.: Izd. RGPU im. A.I. Gercena, 2002. — S. 30-31.

6. Venger L.A. O kachestvennom podhode k dinamike umstvennogo razvitija rebenka // Voprosy psihologii. — 1974. — № 1. — S. 116-122.

7. Gal’perin P.Ja. Metody obuchenija i umstvennoe razvitie rebenka. — M.: Izd-vo MGU, 1985. — 45 s.

8. Zinchenko V.P. Ot klassicheskoj k organicheskoj psihologii // Voprosy psihologii. — 1996.

— № 6. — S. 6-25.

9. Kondrat’eva S.Ju. Poznaem matematiku v igre.

— SPb.: CDK prof. L.B. Baryaevoj, 2011. — 255 s.

10. Lalaeva R.I., Germakovska A. Diskal’kulii u detej // Deti s problemami v razvitii. — 2004. — № 2. —

S. 7-9.

11. Leushina A.M. Formirovanie jelementarnyh matematicheskih predstavlenij u detej doshkol’nogo vozrasta. — M.: Prosveshhenie, 1974. — 368 s.

12. Piazhe Zh. Genezis chisla u rebenka: Per. s franc. — M.: Mezhdunarodnaja pedagogicheskaja akademija. — 1994. — S. 237-582.

13. Primernaja adaptirovannaja osnovnaja obrazovatel’naja programma dlja doshkol’nikov s tjazhelymi narushenijami rechi / L.B. Baryaeva, T.V. Volosovec, O.P. Gavrilushkina, G.G. Golubeva i dr.; Pod. red. prof. L.V. Lopatinoj. — SPb., 2014. — 386 s.

14. Salmina N.G. Znak i simvol v obuchenii. -M.: MGU, 1988. — 288 s.

15. Gelman R., Meck E. Prescholer’s counting: principles before skill // Cognition. 1983. — V. 13. — P. 343-359.

16. Inhelder B., Piaget J. The growth of logical thinking from childhood to adolescence. — N.Y. -Basic books, 1958. — 326 pp.

Сведения об авторе:

Баряева Людмила Борисовна (г. Москва, Россия), доктор педагогических наук, профессор, профессор кафедры логопедии Института специального образования и комплексной реабилитации ГБОУ ВПО «Московский городской педагогический университет», e-mail: [email protected]

Data about the author:

L. Baryaeva (Moscow, Russia), doctor of education, full professor, Department of Speech-Language Pathology of the Institute of Special Education and Complex Rehabilitation “The State Budget Educational Institution of Higher Professional Education “Moscow City Pedagogical University”, e-mail: alesej @yandex.ru

131

cyberleninka.ru

Тема 4.4. Методика формирования представлений о числе и отношениях между числами у детей с тяжелыми нарушениями речи

Число – основное понятие начального курса математики. Это самое используемое в повседневной жизни математическое понятие. Без него не обходится ни один день нашей жизни, ни один вид профессиональной деятельности. Число – единственное математическое понятие, которое образует «свою» особую часть речи в русском и во многих других языках — числительные. Понятие числа – одно из древнейших математических понятий. Оно является предметом исследований не только математики, но и философии, истории науки. С числом связано множество мифов и легенд. Число является продуктом интеллектуальной деятельности людей. Оно не исчерпывается только математическим содержанием. Число – это феномен культуры.

Задача профессиональной деятельности учителя начальных классов, независимо от того, каких педагогических взглядов он придерживается, учебники каких авторов использует – создать условия для овладения младшими школьниками понятием числа и способами действий с числами на уровне, достаточном для продолжения математического образования в основной школе и использования чисел в повседневной жизни.

Начать готовиться к решению этой задачи можно и нужно с осознания, обобщения и обогащения собственных представлений о числе, отношениях между числами, операциях с числами.

В формировании представлений о числе есть несколько аспектов, которые условно можно назвать смысловой, знаниевый и процедурный. Эти аспекты отражают три характеристики качества владения понятием числа – понимание, знание и умение.

Первая характеристика – понимание смыслов числа. Такое понимание проявляется при представлении того, что обозначает, может обозначать число, при самостоятельном использовании чисел, отношений и операций с ними для выражения утверждений о каких-либо объектах, при выборе арифметических действий в решении текстовых сюжетных задач, при переходе от одних средств представления чисел, отношений и действий с ними к другим. Характер, глубина, уровень понимания школьником понятия числа зависят как от индивидуальных психологических особенностей и субъектного опыта познания, не связанного со специальным изучением чисел, так и от педагогической, методической системы школьного обучения математике, в особенности от обучения математике в начальной школе в целом и, в частности, в первом классе – именно в первом классе закладываются основные смысловые установки.

Вторая характеристика – знание, знание способов обозначения чисел в речи и на письме, в том числе в виде математических выражений; знание способов чтения, свойств чисел, отношений между ними, свойств арифметических действий, знание определений отношений между числами, способов сравнения чисел, способов выполнения арифметических действий и т.д. Знание может строиться на понимании и (или) на запоминании. Знание, построенное на понимании более гибкое, более действенное и более прочное: запоминание на основе понимания обычно более эффективное. Знание, строящееся на понимании, образуется с опорой на смысловую и логическую память. Знание, построенное только на запоминании, в особенности на запоминании механическом, может быть прочным. Оно может быть и действенным, однако только в ситуациях, в которых показывались образцы соответствующих действий. Знание может быть структурированным, системным, а может быть разрозненным, фрагментарным. Системное знание всегда строится на понимании – понимании смыслов основных понятий, понимание связей между ними. Действенное знание чисел – это знание, проявляющееся во владении способами действий с числами, т.е. в умениях.

Третья характеристика качества наших числовых представлений – это ответ на вопрос, что мы умеем делать с числами. Умения – один из важнейших показателей содержания и уровня числовых представлений. Это умения называть, читать и записывать числа, сравнивать их, выполнять арифметические действия, применять при решении текстовых сюжетных задач, представлять свое знание о числах в устной и письменной речи.

Данные характеристики тесно связаны друг с другом, они взаимно дополняют и усиливают друг друга. Понимание обеспечивает более прочное и уверенное знание, более свободное владение умением действовать с числами. Знание некоторых фактов, свойств, версий происхождения способствует более глубокому пониманию и служит основой соответствующих умений. Умение действовать с числами позволяет создать основу для наблюдений, для построения выводов, обеспечивающих понимание и знание. Сочетание названных характеристик у каждого учащегося индивидуально.

В методике обучения математике существует несколько подходов к формированию понятия числа у младших школьников. Один из них сформировался в середине прошлого века, когда в отечественной методике обучения математике велись споры относительно теории числа, которая может быть положена в основу изучения чисел в начальной школе. Мы уже отмечали, что в этот период широкое распространение получило мнение: успех в изучении чисел будет тогда, когда учебный материал о числах будет представлен в учебниках и на уроках в строгом соответствии с одной из теорий числа. Предполагалось, что в этом случае все сведения о числах, которые необходимо знать учащимся, будут представать перед ними в единой логической структуре соответствующей математической теории, и потому будут легче осваиваться. Математическими теориями числа, которые в адаптированном виде могли, по мнению исследователей, выполнять названную выше функцию являлись две теории: основанная на теории множеств и основанная на теории величин. Поэтому споры велись в основном по поводу выбора одной из них. Порядковая теория, выстраиваемая в математике в виде формальной аксиоматической теории, в качестве основной теории отклонялась как недоступная детям из-за ее формализации.

Построение учебного материала о числах с явным использованием языка теории множеств было реализовано в ряде экспериментальных учебников, в частности в уже упоминавшихся учебниках, разработанных под руководством А. И. Маркушевича, с использованием теории величин – в трех комплектах учебников методической системы Д. Б. Эльконина – В. В. Давыдова разных авторов и авторских коллективов. В учебниках других направлений подход к числу в основном соответствует его теоретико-множественной трактовке, но изложение учебного материала строится на предметных и условно-предметных действиях (действиях с изображениями предметов, в том числе условными), при этом активно используются порядковые свойства числа.

Однако практика показала, что строгое следование какой-либо одной теории при изучении чисел неизбежно приводит к необходимости ограничивать привлечение субъектного опыта познания учащихся, игнорировать имеющийся у детей запас числовых представлений. Опыт же познания количественных и порядковых отношений, числовые представления, с которыми дети приходят в первый класс, как было показано в предыдущем параграфе, таковы, что в них можно найти корни всех теорий натурального и целого неотрицательного числа. Поэтому современный и эффективный подход к формированию понятия числа у младших школьников состоит в том, чтобы идти от имеющихся у детей числовых представлений и опыта предметной деятельности во всем их многообразии. Число при таком подходе выступает в единстве всех своих свойств. Оно предстает перед детьми многопланово: как обозначение количества предметов в группе и как выражение длины, площади, массы, температуры и т. п. конкретных объектов, как признак некоторых объектов и ситуаций и как элемент упорядоченного множества, как средство упорядочивания и как группа слов родного языка, используемых, как и любые другие слова, в основных и переносных своих значениях. Причем, на начальном этапе обучения знание учащимися последовательности имен чисел – последовательности числительных «один, два, три, четыре, …», отражающей порядковые свойства натуральных чисел, является той необходимой базой, на которой могут строиться другие смыслы числа – теоретико-множественный и «величинный».

Формирование понятия числа у младших школьников условно можно разделить на несколько блоков.

Первый этап. Обобщение и систематизация числовых представлений, полученных в дошкольный период. Обучение умению (или его развитие) последовательно называть числа начального отрезка натурального ряда, а также любой части начального отрезка натурального ряда в прямом и обратном порядке. Обучение последовательному называнию чисел через одно, через два числа, например, «один, три, пять, семь …», «два, четыре, шесть, …», «один, четыре, семь, десять, …». Обучение количественному и порядковому счету предметов, частей предметов и мерок. Формирование смыслов числа, отношений между числами, действий сложения и вычитания: обучение умению обозначать числом группы (множества) предметов, звуков, слов, знаков и т. д., мерок, составляющих измеряемый предмет, место предмета в ряду; накопление опыта представления числа множеством предметов, звуков, слов, знаков и т.д., мерок, места предмета в ряду других предметов; обучение умению переходить от сравнения предметов, групп предметов к сравнению чисел и, наоборот, от сравнения чисел к сравнению предметов, групп предметов; обучение умению переходить от действий с предметами, их изображениями, с отрезками и другими геометрическими фигурами к сложению и вычитанию чисел и наоборот, от сложения и вычитания чисел к соответствующим действиям с предметами, с группами предметов, последовательностями предметов и знаков, с отрезками и другими геометрическими фигурами. Различение понятий числа и цифры. Обучение письму цифр. Обучение умению обозначать число цифрами, рисунками, отрезками и т. п.

Задача освоения содержания первого блока – обеспечить понимание смыслов числа, отношений между числами, арифметических действий, а также овладение техникой счета предметов в группе, техникой письма. Работа учащихся в первом блоке должна обеспечить элементарную числовую грамотность. В нее входит свободное, прочное знание последовательности чисел начального отрезка натурального ряда (наибольшее число этого отрезка может быть различным для разных учащихся, но не меньшим того минимума, который учитель запланировал в соответствии с возможностями учащихся.

Второй. Обеспечение знания особенностей количественных и порядковых числительных, знания цифр, знаков отношений и знаков арифметических действий, знания названий компонентов действий и выражений, знания свойств и алгоритмов сложения, вычитания, умножения и деления нацело и деления с остатком, правил порядка действий в выражении, знания принципов построения названий чисел в десятичной системе счисления. Формирование умения читать числа, записанные в десятичной системе, записывать многозначные числа при восприятии числительных на слух вначале в простейших случаях (без пропусков разрядов), а затем и любых чисел. Формирование вычислительных навыков, навыков нахождения значений числовых выражений. Формирование умений решать основные типы сюжетных текстовых задач на сложение, вычитание, умножение, деление нацело и деление с остатком на основе понимания смысла действий, формирование общего умения решать задачи и умения решать задачи некоторых видов с помощью арифметических действий. Задача второго этапа – развить элементарную числовую грамотность в свободное владение

studfiles.net

Методика формирования у дошкольников с ТНР элементарных математических представлений.

Счет и вычисление вошли в наш быт так, что мы не можем себе представить взрослого человека, который не умеет считать и выполнять простейшие вычисления. Точно неизвестно, когда появились у того или другого народа начальные математические понятия о счете, но с уверенностью можно сказать, что бурное развитие математики тесно связано с тем, что сначала практика, а потом и теория выдвигали перед ней все новые и новые задачи.

Придерживаясь схемы, предложенной академиком А.М. Колмогоровым, всю историю развития математики можно разделить на три основных этапа.
Первый этап – самый продолжительный. Он охватывает тысячелетия – от начала человеческого общества до XVII в. В этот период формировались и разрабатывались понятия действительного числа, величины, геометрические фигуры.
Становление математики как науки началось в Древней Греции, где появились значительные достижения в области геометрии. Именно в Греции разрабатывается математическая теория. Из науки практической математика превращается в логическую, дедуктивную.

Второй этап охватывает XVI — начало XIX в. С XVI в. Начинается расцвет математики в Европе. Возникновение новых математических теорий связано с именами великих ученых XVII в. Декарта, Ферма, Ньютона, Лейбница.
В 1755 году благодаря заботам выдающегося российского ученого М.В. Ломоносова был основан первый российский университет в Москве.

Третий этап развития математики – с XIX в. До наших дней. Он характеризуется интенсивным развитием классической высшей математики.
Большой вклад в развитие математики внесли российские ученые (М.И. Лобачевский, П.Л. Колмогоров и др.) Современная математика достигла очень высокого уровня развития. Теперь насчитывается несколько десятков разных областей математики, каждая из которых имеет свое содержание, свои методы исследования и сферы применения.
Самыми древними приборами для облегчения счета были человеческая рука и камешки. Вопросы математического развития детей дошкольного возраста уходят своими корнями в классическую и народную педагогику. Различные считалки, пословицы, поговорки, загадки, потешки были хорошим материалом в обучении детей счету, позволяли сформировать у ребенка понятия о числах, форме, величине, пространстве и времени.
Первая печатная учебная книжка И. Федорова «Букварь» (1574 г.) включала мысли о необходимости обучения детей счету в процессе различных упражнений.
В классических системах сенсорного обучения Ф. Фребеля (1782-1852) и М.Монтессори (1870 – 1952) представлена методика ознакомления детей с геометрическими фигурами, величинами, измерением и счетом.

Методика формирования элементарных математических представлений у детей дошкольного возраста прошла длительный путь своего развития. В ΧVΙΙ – ΧΙΧ вв. вопросы содержания и методов обучения детей дошкольного возраста арифметике и формирования представлений о размерах, мерах измерения, времени и пространстве нашли отражение в передовых педагогических системах воспитания, разработанных Я.А. Коменским, И.Г. Песталоцци, К.Д. Ушинским, Л.Н. Толстым и др. Современниками методики математического развития являются такие ученые как Р.Л. Березина, З.А. Михайлова, Р.Л.Рихтерман, А.А. Столяр, А.С. Метлина и др

Развивающий эффект обучения достигается лишь тогда, когда оно, (по словам Л.С. Выготскому и Г.С. Костюку) сориентировано на «зону ближайшего развития». Воспитатель должен помнить, что «зона ближайшего развития» зависит не только от возраста, но и от индивидуальных особенностей детей.
В учебном процессе вся система дидактических принципов реализуется одновременно, широким фронтом. Это – воспитывающий и развивающий характер обучения, научность, наглядность, последовательность и систематичность, учет возрастных и индивидуальных особенностей детей, осознанность и активность, доступность. При этом следует помнить, что основным, главным является принцип развивающего и воспитывающего обучения.
Г.С. Костюк доказал, что в процессе обучения у детей развивается способность точнее и полнее воспринимать окружающий мир, выделять признаки предметов и явлений, раскрывать их связи, замечать свойства, интерпретировать наблюдаемое; формируются мыслительные действия, приемы умственной деятельности, создаются внутренние условия для перехода к новым формам памяти, мышления и воображения.
Воспитатель проводит занятия в соответствии с планом. Организационная целостность и завершенность занятия заключается в том, что оно начинается и заканчивается в одно и то же время.

При выборе методов учитываются: цели, задачи обучения; содержание формируемых знаний на данном этапе; возрастные и индивидуальные особенности детей; наличие необходимых дидактических средств; личное отношение воспитателя к тем или иным методам; конкретные условия, в которых протекает процесс обучения, и др.

Успешное обучение детей в начальной школе зависит от уровня развития мышления ребёнка, умения обобщать и систематизировать свои знания, творчески решать различные проблемы. Развитое математическое мышление не только помогает ребёнку ориентироваться и уверенно себя чувствовать в окружающем его современном мире, но и способствует его общему умственному развитию. Отсюда вытекает основное требование к форме организации обучения и воспитания- сделать занятия по формированию элементарных математических представлений максимально эффективными для того, чтобы на каждом возрастном этапе обеспечить ребёнку максимально доступный ему объём знаний и стимулировать поступательное интеллектуальное развитие.

Основные задачи:

1. Формирование мотиваций учебной деятельности, ориентированной на активизацию познавательных интересов.

2. Развития восприятия и представления детей через накопление и расширение сенсорного опыта.

3. Увеличение объёма внимания и памяти.

4. Развитие наглядно-действенного и наглядно-образного мышления за счёт обучения приёмам умственных действий (анализ, синтез, сравнение, обобщение, группировка, установление причинно-следственных связей).

5. Обучение элементарным математическим представлениям в объёме программы старшей группы.

6. Развития речи, введение в активную речь математических терминов, активное использование знаний и умений, полученных на занятии.

Занятия состоит из нескольких частей, объединенных одной темой. На каждом занятии дети выполняют различные виды деятельности: игровые, с предметами, с счётным материалом т. д.

Игровые виды деятельности: имитационные игры и игры-упражнения с предметами, сюжетно-ролевые игры, игры с правилами без сюжета, игры-упражнения с ориентировкой на определённые достижения.

Продолжительность и интенсивность занятий на протяжении всего года увеличивается постепенно. В структуру каждого занятия предусмотрен перерыв для снятия умственного и физического напряжения продолжительностью 1-3 минуты. Это может быть динамическое упражнение с речевым сопровождением или «пальчиковая гимнастика», упражнения для глаз или упражнение на релаксацию. В конце каждого занятия необходимо подвести итог. Детям необходимо задать вопросы: Что нового узнали ?..Чему сегодня научились?

Комплексное использование всех приёмов, методов, форм обучения поможет решить одну из главных задач- осуществить математическую подготовку дошкольников и вывести развитие их мышления на уровень, достаточный для успешного усвоения математики в школе.

Важной составляющей программного материала по развитию элементарных математических представлений у дошкольников является специально разработанная совокупность заданий содержательно-логического характера, направленных как на более осмысленное усвоение математического содержания, так и на развитие у детей основных познавательных процессов и интереса к математике.
Успешное обучение детей в школе зависит от уровня развития познавательных процессов (мышление, память, внимание, воображение).

Особое внимание уделяется работе, направленной на развитиепроизвольного внимания, так как от уровня его развития зависит успешность и чёткость работы сознания, а следовательно, и осознанного восприятия изучаемого математического материала. Естественно, что все задания и их последовательность подчинены дидактическому требованию постепенного усложнения и в итоге подводят к успешному развитию произвольного внимания, которое служит основой развития других познавательных процессов. Ребёнок должен находить отличия между предметами, выполнять самостоятельно задания по предложенному образцу, находить несколько пар одинаковых предметов.

Среди заданий на развитие памятив дошкольном возрасте предпочтение отдаётся зрительным и слуховым диктантам и упражнениям, в содержании которых используются математические символы, записи, термины, геометрические фигуры и их расположение на листе бумаги. Большое значение в развитии словесно-логической памяти имеют дидактические игры, предполагающие развитие у детей приёмов смысловой группировки представленных слов или словосочетаний.

Таким образом, ведущей методической линией является организация разнообразной математической деятельности, в результате которой идёт накопление элементарных математических представлений и активное развитие основных познавательных процессов у детей,приоритетныхсреди которых являются воображение и мышление. Именно поэтому большое внимание уделяется развитию таких мыслительных операций, как сравнение, анализ и синтез, обобщение, классификация, аналогия.

Анализ-это процесс, расчленения целого не части, а также установление связей, отношений между ними.

Синтез— это процесс мысленного соединения в единое целое частей предмета или его признаков, полученных в процессе анализа. Анализ и синтез неразрывно связаны друг с другом и являются одним из основных мыслительных операций.

Сравнение— мысленное установление сходства и различия предметов по существенным или несущественным признакам.

Обобщение-процессмысленного объединения в одну группу предметов и явлений по их основным свойствам.

Классификация-это распределение предметов по группам, обычно по существенным признакам.

Учитывая, что запас математических знаний у дошкольников ещё не так велик, задания содержательно- логического блока не всегда будут иметь ярко выраженное математическое содержание, что, однако, не снижает их развивающей ценности и значимости для развития познавательных способностей детей. Постепенно с ростом математической базы у ребёнка, такие задания всё более обогащаются разнообразным математическим содержанием и выполняют уже одновременно несколько функций.
Большинство заданий даются в игровой занимательной форме, что способствует наиболее успешному развитию познавательных процессов у детей.

Основные требования к заданиям содержательно-логического характера:

— задания должны иметь яркую целевую направленность на развитие одного или одновременно нескольких познавательных процессов, среди которых отдаётся приоритет математическому мышлению, но присутствуют и такие познавательные процессы как внимание, восприятие, память.

-задания должны иметь математическое содержание и нести определённую интеллектуальную нагрузку для детей, расширять их представления или знакомить с простейшими методами познания действительности.

— задания должны быть представлены в интересной форме и построены на близком детям материале.

Программа по развитию ЭМП.Старший возраст. (25 мин каждое ???)

Количество и счёт

Числа и цифры 1,2,3,4,5,6,:.9. Число и цифра 0.

Названия чисел по порядку от 1до 10. Образование чисел путём присчитывания 1. Прямой и обратный счёт. Состав числа первого десятка (практический способ)
Арифметические знаки: ( +,-,=,). Особенности первого элемента в ряду натуральных чисел. Таблица сложения и вычитания в пределах 10. Десяток — новая счётная единица. Счёт десятками.

Величины

Сравнение предметов по размеру. Обучение способам сравнения предметов. Обучение способам приложения и наложения. Обучению сравнению по: длине, высоте, ширине, толщине, массе. Введение в активный словарь понятий : больше, меньше, длиннее, корче, одинаковые (равные) по длине, выше, ниже, равные по высоте, шире, уже, толще, тоньше, легче, тяжелее.

Геометрические фигуры.

Основные геометрические фигуры: круг, треугольник, овал, прямоугольник (квадрат). Деление фигур. Построение композиций из геометрических фигур одинаковой и разной формы, одинаковых и разных размеров. Узор . Выявление его построения и продолжения. Преобразования одной фигуры в другую. Знакомство с пространственными телами : шар, брусок, куб. Конструирование из пространственных тел.

cyberpedia.su

2. психпед особенности усвоения математики детьми с ТНР

Психолого-педагогические особенности усвоения математики детьми с ТНР.

В научных исследованиях отмечаются такие характерные затруднения в усвоении математического материала детьми с ТНР, как недостаточная сформированность понятия о числе и нарушения счетных операций по типу акалькулии и дискалькулии (Р.Е.Левина, Л.А.Дмитриева, А. Гермаковска и др.), недоразвитие пространственно-временных представлений (И.Н.Садовникова, Р.И. Лалаева, А.Н.Корнев и др.), нарушение понимания логико-грамматических отношений арифметических задач (Л.С.Цветкова и др.).
Проблемы усвоения математики детьми с ТНР могут быть связаны с воздействием нескольких факторов:
Недостаточное развитие речевых функций, ограничивающее возможности приобретения математических знаний и умений. Характерные для детей с тяжелыми нарушениями речи низкий уровень понимания словесных инструкций, бедность словаря и недоразвитие грамматического строя препятствует пониманию и выполнению математических действий.
Низкий уровень самоорганизации психической деятельности — целостной направленности психики на активацию познавательной деятельности и на ее управление, что создает необходимые условия для протекания мыслительной деятельности.
Недоразвитие некоторых психических функций, составляющих основу математических понятий: логических операций анализа, синтеза, сравнения, обобщения, абстрагирования, пространственной и временной ориентировки, перцептивно-моторных функций.
Наличие специфических нарушений счетных операций (дискалькулии)

1. Недостаточное развитие речевых функций. У ребенка с ТНР недоразвитие речи вызывает большие затруднения при усвоении математики. Отмечается бедность математического словаря, трудности в обозначении количественных, пространственных, временных отношений при помощи языковых средств, так как многие слова для ребенка с ТНР незнакомы. К началу обучения в школе математический словарь у ребенка с ТНР очень ограничен, при усвоении математической терминологии наблюдаются все характерные особенности словаря при недоразвитии речи: названия числительных, арифметических действий и т.д. усваиваются ребенком в более долгие сроки, наблюдаются искажения звукового, слогового состава (двенадцать – двецать, треугольник – трегольник и др.) терминов.
Из-за несформированности грамматического строя речи изменение формы числительного (от двух отнять– к двум прибавить – два плюс) либо не воспринимается ребенком, либо приводит к тому, что грамматическую форму одного и того же числительного ребенок воспринимает как новое слово. Ребенок затрудняется в понимании грамматических отношений в математических выражениях типа «от семи отнять , к пяти прибавить, в 2 раза больше – на 2 больше»: он слабо различает значение предлогов, как следствие возникают трудности в подборе правильного арифметического действия.
Наибольшие трудности вызывает у ребенка с ТНР реше

edudocs.net

Формирование мыслительных процессов у детей дошкольного возраста с тяжелыми нарушениями речи (ТНР) в процессе организации интеллектуально-математических игр

Библиографическое описание:

Сокольникова Н. М., Матухнова С. В. Формирование мыслительных процессов у детей дошкольного возраста с тяжелыми нарушениями речи (ТНР) в процессе организации интеллектуально-математических игр // Образование и воспитание. 2018. №5. С. 20-22. URL https://moluch.ru/th/4/archive/108/3632/ (дата обращения: 06.06.2019).

Авторы представили опыт работы, который заключается в систематизации и комбинировании имеющихся в отечественной педагогике, коррекционной педагогике и психологии технологий, направленных на формирование мыслительных процессов у детей старшего дошкольного возраста с тяжелыми нарушениями речи. В создании системы работы, построенной на основе комплексно-тематического подхода и направленной на формирование и развитие мыслительной деятельности.

Ключевые слова: система работы, мыслительная деятельность, игровые технологии, комплексный подход.

Проблема состояния мыслительной деятельности детей с тяжёлыми нарушениями речи (ТНР) является на сегодняшний день очень значимой. Ведь именно речь и мышление являются непременным условием развития всех остальных человеческих способностей. Логическое мышление у детей формируется к старшему дошкольному возрасту. Вот почему вопросы развития мыслительных операций являются основными в подготовке дошкольников к школе.

Однако, в настоящее время в большинстве своем, дети, поступающие в школу, не подготовлены в этом плане, у них слабо сформированы мыслительные операции, необходимые для успешного усвоения знаний в школе. В связи с этим, мы считаем необходимым осуществить подбор и комбинирование имеющихся в практике игровых технологий с целью создания системы интеллектуально-математических игр, направленных на формирование мыслительных процессов у дошкольников с тяжелыми нарушениями речи.

Ведущая педагогическая идея опыта заключается в организации целенаправленной работы с использованием игровых технологий, направленных на формирование у детей старшего дошкольного возраста с тяжелыми нарушениями речи (ТНР) мыслительных процессов. В создании игровых ситуаций, стимулирующих развитие представлений у детей о существенных свойствах, связях и отношениях объективной реальности.

Учитывая специфику данного возраста, мы делаем акцент на использование разнообразных наглядных и демонстрационных материалов в процессе игровой деятельности, которые будут способствовать наиболее успешному формированию мыслительных процессов у детей. Формирование математических представлений является мощным средством интеллектуального развития дошкольника, его познавательных сил и творческих способностей.

В своей работе мы опирались на методические разработки и практический материал следующих авторов: Р. С. Немов, Е. В. Колесникова, З. А. Михайлова, М. М. Безруких, Т. А. Филиппова.

Цель: подбор и систематизация интеллектуально-математических игр, направленных на формирование мыслительных процессов у детей старшего дошкольного возраста с тяжелыми нарушениями речи.

Задачи:

Изучить научно-методическую литературу по организации работы с детьми с ТНР в процессе формирования мыслительных процессов.
Подобрать диагностический материал, разработать диагностическую карту по данному разделу, осуществить диагностическую работу.
Провести отбор и систематизацию игр и игровых упражнений по данному направлению и внедрить ее в работу с детьми с тяжелыми нарушениями речи.
Провести итоговый мониторинг по окончании формирующего этапа работы по формированию мыслительных процессов с целью отслеживания эффективности работы.

Детальное изучение психических особенностей детей старшего дошкольного возраста, а также анализ и обобщение научной и методической литературы, помогли выстроить систему развивающей работы по формированию мыслительных процессов дошкольников с тяжелыми нарушениями речи.

Работа по данному направлению началась с подбора и изучения методической литературы. Были составлены диагностические карты обследования уровня сформированности мыслительных процессов для детей старшего дошкольного возраста, разработаны диагностические задания, критерии и показатели оценки умений детей.

Затем был проведен первоначальный мониторинг, который показал, что у детей недостаточно сформирована речемыслительная деятельность.

Высокий уровень в результате первоначальной диагностики показал один ребенок — 10 %, средний уровень — 20 %, а низкий уровень — 70 % детей.

Учитывая данные обследования, была осуществлена разработка развивающих мероприятий с детьми данного возраста. Проведена систематизация игр и игровых упражнений по комплексно-тематическому принципу. Составлен перспективный план работы на два учебных года, который включил в себя игры, игровые упражнения на формирование элементарных математических представлений.

Одной из труднейших и важнейших задач дидактики как была, так и остается проблема воспитания интереса к обучению. В связи с этим педагогами ведется поиск эффективных форм и методов обучения математике, которые способствовали бы активизации учебной деятельности, формированию познавательного интереса. Одной из таких форм является математическая игра. Для того, чтобы правильно и грамотно управлять детской игрой, была подобрана методика проведения математических игр.

Для развития интереса детей к элементарной математической деятельности и непосредственно формирования мышления детей были созданы определенные условия. Уголок занимательной математики «Для умников и умниц» тематически оснащен играми, пособиями и материалом математического содержания, к которым дети имеют свободный доступ. Эти игры способствовали развитию интереса детей к математике. Благодаря этой игротеке у детей воспитывается потребность занимать свое свободное время не только развлекательными, но и требующими умственного напряжения играми.

Работа по решению поставленных задач велась поэтапно:

I этап — развитие у дошкольников психических процессов через использование математических игр;

II этап — развитие основных мыслительных операций через использование игр математического содержания;

В результате целенаправленной работы у детей повысился уровень сформированности мыслительных операций, уровень развития сенсорных и умственных способностей. Можно было наблюдать следующую динамику: высокий уровень сформированности мыслительных процессов увеличился по сравнению с первоначальным на 30 %, средний повысился с с 20 % до 60 %, низкого не стало вообще. Интеллектуальные игры математического содержания воспитывали у детей познавательный интерес, способность к творческому поиску, желание и умение учиться. У них сформировалась способность к обобщению и классификации. Дети овладели умением группировать предметы по определенному признаку, свойству, назначению, сравнивать предметы по пространственным признакам, хорошо владеют количественными операциями. Дети умеют применять знания и умения в решении проблемно-игровых и практических задач, у них достаточно хорошо сформированы представления о математических свойствах и закономерностях; умеют сравнивать предметы по величине, хорошо устанавливают логические связи и закономерности. Наблюдая за ростом мыслительной деятельности, которая очевидна при многоразовом использовании логических операций, можно смело утверждать, что:

а) все дети знакомы с приёмами сравнения, анализа, синтеза, классификации. Почти всем понятны способы использования логических игр и применение их на практике;

б) примерно 70 % детей испытывает устойчивый интерес к развивающим играм. Возросла степень их активности в самостоятельной деятельности;

в) дети достигают нужного результата;

г) работа по развитию мышления на основе логических игр принесла свои плоды: дети стали более активными и интеллектуальными.

Кроме того, данная деятельность оказала огромное положительное влияние на развитие речи ребенка: обогащение словаря, согласование слов в единственном и множественном числе, формулировка ответов полным предложением, логические рассуждения.

Таким образом, на основании данных мониторинга, полученных после проведенной работы с детьми с тяжелыми нарушениями речи, можно говорить о том, что применение данной системы мероприятий оказывает положительное влияние на формирование у детей данной категории мыслительных процессов в процессе интеллектуально-математических игр.

Литература:

1. Венгер Л. А., Дьяченко О. М., Говорова Р. И., Цеханская Л. И. Игры и упражнения по развитию умственных способностей у детей дошкольного возраста-М., 1999

2. Венгер Л. А. Овладение опосредованным решением познавательных задач и развитие когнитивных способностей ребенка//Вопросы психологии. — 1983. — № 2.

3. Волонина В. В. Занимательная математика С-Петербург, 1996г.1

4. А. З. Зак «Развитие интеллектуальных способностей у детей 6–7 лет» — М.,1996г.

5. Ковалев В. И. Развивающие игры: 10 шагов к успеху-М., 2004г.

Основные термины (генерируются автоматически): тяжелое нарушение речи, ребенок, старший дошкольный возраст, игра, процесс, формирование, математическое содержание, мыслительная деятельность, высокий уровень, методическая литература.

Тема 3. Содержание обучения учения математике детей с тяжелыми нарушениями речи

Понятие содержания обучения математике. Учебный материал и содержание обучения. Компоненты содержания обучения математике: ключевые идеи математики и математических теорий, способы математической деятельности; математические понятия и математический язык, математические действия и операции и способы их представления в языке, смыслы математических понятий и утверждений, системы взглядов на познание вообще и математическое в частности, версии (история) происхождения математических понятий, утверждений, правил, символов, способов действий. Разделы начального курса обучения математике в школе для детей с ТНР.

Гуманитарные аспекты разделов курса математики начальной школы как необходимый элемент эффективной методической системы обучения математике. Прикладные аспекты содержания математики в обучении младших школьников: способы вычислений, методы и способы решения задач и т. п. Приоритет психологического, гуманитарного, смыслового компонента над формально-логическим. Связи содержания обучения с другими компонентами методической системы обучения математике: целями, методами и приемами, формами и средствами обучения. Содержание обучения математике и индивидуально-психологические особенности каждого учащегося. Особенности представления содержания в обучении детей с тяжелыми нарушениями речи. Развитие речи на уроках математики, ее коррекция. Место логопедической работы на уроках математики детей с ТНР.

Тема 4. Организация обучения математичке детей с тяжелыми нарушениями речи

Организация обучения математике детей с ТНР. Подготовительный период обучения математике. Причины, обуславливающие необходимость длительного подготовительного периода в обучении математике детей с ТНР. Содержание и организация занятий в подготовительный период. Диагностика уровня подготовленности учащихся с ТНР к обучению математике. Система работы в подготовительный период обучения математике. Коррекция и развитие ВПФ и моторики учащихся речевой школы в период пропедевтического периода, предупреждение «зеркальности», формирование навыков учебной деятельности, работа по развитию и коррекции речи.

Типы уроков. Структура уроков. Современные требования к уроку. Урок и система уроков математики. Учебная деятельность и умение учиться. Формирование учебной деятельности. Анализ урока математики (психолого-педагогический, методический). Планирование учебного материала: тематические и поурочные планы. Требования к содержанию урока. Контроль и учет уровня математической подготовки и математического развития учащихся. Оценка знаний учащихся по математике. Виды текущей проверки знаний. Роль самоконтроля в овладении требуемыми компетенциями в области математики.

Использование дидактического материала на уроках математики в речевой школе. Разнообразие форм организации учебной работы по математике (экскурсии, измерительные работы на местности, самостоятельные, индивидуальные и групповые занятия учащихся в классе).

Домашняя самостоятельная работа. Формирование у учащихся умения самостоятельно выполнять математические задания. Роль занимательных математических заданий в школе для детей с ТНР. Дидактические игры и упражнения.

Значение внеклассных занятий по математике для развития и коррекции познавательной деятельности учащихся с ТНР. Особенности внеклассной работы по математике в речевой школе. Разнообразие форм и видов внеклассной работы.

Модуль 2. Частные вопросы методики обучения математике детей с тяжелыми нарушениями речи

studfiles.net

формирование алгебраических представлений у детей с тяжелыми нарушениями речи

Понятие о математическом языке, его связь с естественным языком. Буквенная символика — алфавит «математической письменности». Математические выражения как элементы математической речи. Математические выражения как математические объекты. Числовые равенства и неравенства, буквенные равенства и неравенства, уравнения как элементы математического языка. Проблема изучения и использования математического языка в начальной школе.

Математические выражения: определение, виды, способы и формы чтения и называния, операции над выражениями, сравнение выражений — установление сходства и различий, установление отношений равенства и неравенства, виды выражений, способы чтения. Математические выражения как способ записи чисел и действий с ними. Числовые и буквенные выражения в начальной школе как способ обобщения знаний о числах и действиях с ними. Равенство выражений, тождественные преобразования выражений, нахождение значений выражений, правила порядка действий.

Методика формирования понятия о математических выражениях, умений использовать их для записи чисел, действий и их свойств. Обучение использованию выражений при решении задач. Смыслы выражений. Формирование умения читать и записывать математические выражения, составлять выражения по словесному описанию ситуаций, отношений, по текстам условий задач, по текстам задач.

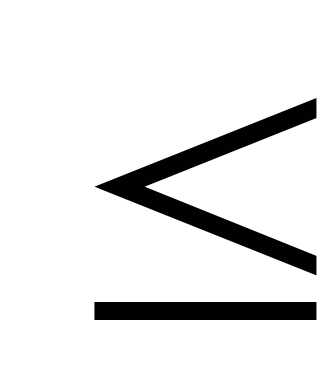
Числовые равенства и неравенства как математические записи определенного вида (записи вида a = b, a < b, a > b, a b, А = В, А < В, А > В, А В, АВ, где a и b — числа, записанные буквами или цифрами, А и В — числовые («цифровые») или буквенные выражения). Связь отношений равенства и неравенства между числами с числовыми и буквенными равенствами и неравенствами. Верные и неверные равенства и неравенства. Свойства верных (истинных) числовых равенств и неравенств на разных числовых множествах. Методика изучения равенств и неравенств в начальной школе в разных системах обучения.

Буквы в математических записях как обозначение неизвестных чисел и переменных. Понятие переменной. Выражения с переменной, область определения, множество значений. Уравнения как равенства с переменной (равенства с неизвестным числом). Область определения. Множество значений переменной, при которых уравнение или неравенство обращается в верное равенство или неравенство. Понятие о решении уравнений и неравенств с переменной (с неизвестным числом). Корни уравнения, множество решений неравенства. Равносильные уравнения, равносильные неравенства. Различие вопросов и ответов на вопросы: “Что значит решить уравнение (неравенство)?” и «Как решить уравнение (неравенство)?». Однозначность ответа на первый вопрос и бесконечность множества ответов на второй вопрос (бесконечность путей и способов решения уравнений и неравенств, в той или иной мере отличающихся друг от друга; многообразие математических способов решения). Формирование у учащихся представлений о переменных, об использовании букв для построения общих суждений о числах и действиях с ними, о выражениях, равенствах и неравенствах с переменными как способе записи этих общих суждений. Решение уравнений методом подбора как средство понимания учащимися смысла понятий уравнение, неравенство, решение уравнений, решение неравенств.

Способы получения равносильных уравнений и неравенств. Решение уравнений и неравенств на основе смысла того, что значит решить уравнение, что значит решить неравенство. Обучение учащихся такому решению уравнений и неравенств. Решение уравнений и неравенств на основе преобразования уравнений и неравенств в равносильные им и приведения их к простейшим вида х = a, x < a, x > a, x 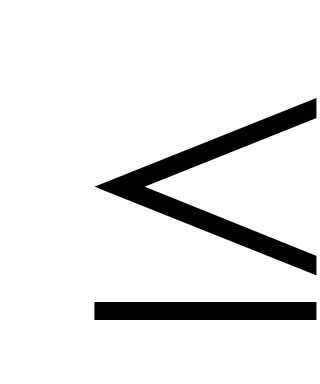а, xa. Теоремы о равносильных уравнениях и неравенствах (о равносильности уравнений и неравенств). Уравнения и неравенства с переменными как способ записи отношений между числами и величинами. Решение уравнений на основе смысла уравнения — подбором, зависимости между компонентами и результатами арифметических действий. Использование уравнений и неравенств с переменными как инструмента решения задач. Возможная роль уравнений и неравенств с переменной в математическом образовании младших школьников.

История методики изучения уравнений и неравенств с переменной в начальной школе. (Споры о преимуществах арифметических и «алгебраических» задач в XVIII—XIX веках, о способности учащихся овладеть буквенной символикой. Работы В. В. Давыдова и других исследователей, доказавших, что дети способны к обобщениям, в частности, к овладению буквенной символикой, к изучению уравнений и неравенств, способов их решения, к использованию уравнений для решения задач.) История развития понятий уравнения и неравенства. Уравнения и неравенства с переменными в математике, в школьном обучении математике.

Обучение учащихся умению решать задачи с помощью уравнений и неравенств с переменной. Особенности процесса решения задач с помощью уравнений. Приемы перевода текста задачи на язык математических выражений. «Словарь», слова «синонимы» как условие равенства выражений и основа записи уравнения. Система заданий по формированию и развитию умения решать задачи составлением уравнения.

Методические указания. Великий Исаак Ньютон называл алгебру «всеобщей арифметикой». Действительно, то что в арифметике утверждается для конкретных чисел, то в алгебре исследуется и обозначается относительно некоторого числового множества. Если это помнить, то знания чисел, действий с ними, свойств помогут при изучении алгебраического материала, и наоборот, изучение алгебраического материала поможет глубже понять числа. В обучении учащихся начальных классов алгебраический материал также должен служить способом выражения обобщенных знаний о числах. Рассмотрение этого обобщенного знания может предшествовать в школьном обучении рассмотрению конкретных чисел (система Д.Б. Эльконина – В.В. Давыдова), а может служить средством обобщения ранее изученного о числах. В любом случае нужно помнить об обобщающем характере алгебраического знания и обеспечить понимание этого учащимися.

studfiles.net