ЕГЭ физика 2019 формулы по заданиям

В помощь ученику и студенту мы подготовили краткую шпаргалку “ЕГЭ физика 2019 формулы по заданиям”. Разъяснение формул можно найти на сайте через форму поиска или в “Архиве”. Удачи!

xn—-ctbjzeloexg6f.xn--p1ai

Все формулы для ЕГЭ по физике 2019

В помощь ученику и студенту мы подготовили краткую шпаргалку “Все формулы для ЕГЭ по физике 2019”. Разъяснение формул можно найти на сайте через форму поиска или в “Архиве”. Удачи!

xn—-ctbjzeloexg6f.xn--p1ai

19 обязательных формул для успешной сдачи ЕГЭ по физике

Как правило, именно математику, а не физику принято считать королевой точных наук. Мы полагаем, что это утверждение спорно, ведь технический прогресс невозможен без знания физики и её развития. Из-за своей сложности она вряд ли когда-либо будет включена в список обязательных государственных экзаменов, но, так или иначе, абитуриентам технических специальностей приходится сдавать её в обязательном порядке. Труднее всего запомнить многочисленные законы и формулы по физике для ЕГЭ, именно о них мы расскажем в этой статье.

Секреты подготовки

Возможно, это связано с кажущейся сложностью предмета или популярностью профессий гуманитарного и управленческого профиля, но в 2016 году только 24 % всех абитуриентов приняли решение сдавать физику, в 2017 – лишь 16 %. Такие статистические данные невольно заставляют задуматься, не слишком ли завышены требования или просто уровень интеллекта в стране падает. Почему-то не верится, что так мало школьников 11 класса желают стать:

• инженерами;
• ювелирами;
• авиаконструкторами;                                              
• геологами;
• пиротехниками;
• экологами,
• технологами на производстве и т.д.

Знание формул и законов физики в равной степени необходимо для разработчиков интеллектуальных систем, вычислительной техники, оборудования и вооружения. При этом всё взаимосвязано. Так, например, специалисты, производящие медицинское оборудование, в своё время изучали углубленный курс атомной физики, ведь без разделения изотопов, у нас не будет ни рентгенологической аппаратуры, ни лучевой терапии. Поэтому создатели ЕГЭ постарались учесть все темы школьного курса и, кажется, не пропустили ни одной.

Те ученики, которые исправно посещали все уроки физики вплоть до последнего звонка, знают, что в период с 5 по 11 класс изучается около 450 формул. Выделить из этих четырех с половиной сотен хотя бы 50 крайне сложно, поскольку все они важны. Подобного мнения, очевидно, также придерживаются разработчики Кодификатора. Тем не менее, если вы одарены необыкновенно и не ограничены во времени, вам хватит 19 формул, ведь при желании из них можно вывести все остальные. За основу мы решили взять главные разделы:

• механику;
• физику молекулярную;
• электромагнетизм и электричество;
• оптику;
• физику атомную.

Очевидно, что подготовка к ЕГЭ должна быть ежедневной, но если по каким-то причинам вы приступили к изучению всего материала лишь сейчас, настоящее чудо может совершить экспресс-курс, предлагаемый нашим центром. Надеемся, эти 19 формул также будут вам полезны:

Вы, наверное, заметили, что некоторые формулы по физике для сдачи ЕГЭ остались без пояснений? Мы предоставляем вам самим их изучить и открыть для себя законы, по которым абсолютно всё вершится в этом мире.

ege-merlin.ru

Материал для подготовки к ЕГЭ (ГИА) по физике (11 класс) по теме: Подготовка к ЕГЭ. Формулы.

Первый закон Ньютона. Масса. Сила

При движении тела по траектории его скорость v может изменяться по модулю и направлению. Это означает, что тело двигается с некоторым ускорением a. В кинематике не ставится вопрос о физической причине, вызвавшей ускорение движения тела. Как показывает опыт, любое изменение скорости тела возникает под влиянием других тел. Динамика рассматривает действие одних тел на другие как причину, определяющую характер движения тел.

Взаимодействием тел принято называть взаимное влияние тел на движение каждого из них.

Раздел механики, изучающий законы взаимодействия тел, называется динамикой.

Законы динамики были открыты великим ученым И. Ньютоном (1687 г.). Три закона динамики, сформулированные Ньютоном, лежат в основе так называемой классической механики. Законы Ньютона следует рассматривать как обобщение опытных фактов. Выводы классической механики справедливы только при движении тел с малыми скоростями, значительно меньшими скорости света c.

Самой простой механической системой является изолированное тело, на которое не действуют никакие тела. Так как движение и покой относительны, в различных системах отсчета движение изолированного тела будет разным. В одной системе отсчета тело может находиться в покое или двигаться с постоянной скоростью, в другой системе это же тело может двигаться с ускорением.

Первый закон Ньютона (или закон инерции) из всего многообразия систем отсчета выделяет класс так называемых инерциальных систем.

Существуют такие системы отсчета, относительно которых изолированные поступательно движущиеся тела сохраняют свою скорость неизменной по модулю и направлению.

Свойство тел сохранять свою скорость при отсутствии действия на него других тел называется инерцией. Поэтому первый закон Ньютона называют законом инерции.

Впервые закон инерции был сформулирован Г. Галилеем (1632 г.). Ньютон обобщил выводы Галилея и включил их в число основных законов движения.

В механике Ньютона законы взаимодействия тел формулируются для класса инерциальных систем отсчета.

При описании движения тел вблизи поверхности Земли системы отсчета, связанные с Землей, приближенно можно считать инерциальными. Однако, при повышении точности экспериментов, обнаруживаются отклонения от закона инерции, обусловленные вращением Земли вокруг своей оси.

Примером тонкого механического эксперимента, в котором проявляется неинерциальность системы, связанной с Землей, служит поведение маятника Фуко. Так называется массивный шар, подвешенный на достаточно длинной нити и совершающий малые колебания около положения равновесия. Если бы система, связанная с Землей, была инерциальной, плоскость качаний маятника Фуко оставалась бы неизменной относительно Земли. На самом деле плоскость качаний маятника вследствие вращения Земли поворачивается, и проекция траектории маятника на поверхность Земли имеет вид розетки (рис. 1.7.1).

Рисунок 1.7.1. Поворот плоскости качаний маятника Фуко.

С высокой степенью точности инерциальной является гелиоцентрическая система отсчета (или система Коперника), начало которой помещено в центр Солнца, а оси направлены на далекие звезды. Эту систему использовал Ньютон при открытии закона всемирного тяготения (1682 г.).

Инерциальных систем существует бесконечное множество. Система отсчета, связанная с поездом, идущим с постоянной скоростью по прямолинейному участку пути, – тоже инерциальная система (приближенно), как и система, связанная с Землей. Все инерциальные системы отсчета образуют класс систем, которые движутся друг относительно друга равномерно и прямолинейно. Ускорения какого-либо тела в разных инерциальных системах одинаковы.

Итак, причиной изменения скорости движения тела в инерциальной системе отсчета всегда является его взаимодействие с другими телами. Для количественного описания движения тела под воздействием других тел необходимо ввести две новые физические величины – инертную массу тела и силу.

Масса – это свойство тела, характеризующее его инертность. При одинаковом воздействии со стороны окружающих тел одно тело может быстро изменять свою скорость, а другое в тех же условиях – значительно медленнее. Принято говорить, что второе из этих двух тел обладает большей инертностью, или, другими словами, второе тело обладает большей массой.

Если два тела взаимодействуют друг с другом, то в результате изменяется скорость обоих тел, т. е. в процессе взаимодействия оба тела приобретают ускорения. Отношение ускорений двух данных тел оказывается постоянным при любых воздействиях. В физике принято, что массы взаимодействующих тел обратно пропорциональны ускорениям:

В этом соотношении величины и следует рассматривать как проекции векторов a1  и a2 на ось OX (рис. 1.7.2). Знак «минус» в правой части формулы означает, что ускорения взаимодействующих тел направлены в противоположные стороны.

В Международной системе единиц (СИ) масса тела измеряется в килограммах (кг).

Масса любого тела может быть определена на опыте путем сравнения с массой эталона (mэт = 1 кг). Пусть m1 = mэт = 1 кг. Тогда

Масса тела – скалярная величина. Опыт показывает, что если два тела с массами m1 и m2 соединить в одно, то масса m составного тела оказывается равной сумме масс m1 и m2 этих тел:

Это свойство масс называют аддитивностью.

Рисунок 1.7.2. Сравнение масс двух тел.

Сила – это количественная мера взаимодействия тел. Сила является причиной изменения скорости тела. В механике Ньютона силы могут иметь различную физическую причину: сила трения, сила тяжести, упругая сила и т. д. Сила является векторной величиной. Векторная сумма всех сил, действующих на тело, называется равнодействующей силой.

Для измерения сил необходимо установить эталон силы и способ сравнения других тел с этим эталоном.

В качестве эталона силы можно взять пружину, растянутую до некоторой заданной длины. Модуль силы F0, с которой эта пружина при фиксированном растяжении действует на прикрепленное к ее концу тело, называют эталоном силы. Способ сравнения других тел с эталоном состоит в следующем: если тело под действием измеряемой силы F и эталонной силы F0 остается в покое (или движется равномерно и прямолинейно), то силы равны по модулю F = F0 (рис. 1.7.3).

Рисунок 1.7.3. Сравнение силы F с эталоном F = F0.

Если измеряемая сила F больше (по модулю) эталонной силы, то можно соединить две эталонные пружины параллельно (рис. 1.7.4). В этом случае измеряемая сила равна 2F0. Аналогично могут быть измерены силы 3F0, 4F0 и т. д.

Рисунок 1.7.4. Сравнение силы F с эталоном. F = 2F0.

Измерение сил, меньших 2F0, может быть выполнено по схеме, показанной на рис. 1.7.5.

Рисунок 1.7.5. Сравнение силы F с эталоном. 2Fcosα.

Эталонная сила в Международной системе единиц называется ньютон (Н).

На практике нет необходимости все измеряемые силы сравнивать с эталоном силы. Для измерения сил используют пружины, откалиброванные описанным выше способом. Такие откалиброванные пружины называются динамометрами. Сила измеряется по растяжению динамометра (рис. 1.7.6).

Рисунок 1.7.6. Измерение силы по растяжению пружины. При равновесии

1.8. Второй закон Ньютона

Второй закон Ньютона – основной закон динамики. Этот закон выполняется только в инерциальных системах отсчета.

Приступая к формулировке второго закона, следует вспомнить, что в динамике (см. §1.7) вводятся две новые физические величины – масса тела m и сила F, а также способы их измерения. Первая из этих величин – масса m – является количественной характеристикой инертных свойств тела. Она показывает, как тело реагирует на внешнее воздействие. Вторая – сила F– является количественной мерой действия одного тела на другое.

Второй закон Ньютона – это фундаментальный закон природы; он является обобщением опытных фактов, которые можно разделить на две категории:

1. Если на тела разной массы подействовать одинаковой силой, то ускорения, приобретаемые телами, оказываются обратно пропорциональны массам:

2. Если силами разной величины подействовать на одно и то же тело, то ускорения тела оказываются прямо пропорциональными приложенным силам:

Обобщая подобные наблюдения, Ньютон сформулировал основной закон динамики:

Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение:

Это и есть второй закон Ньютона. Он позволяет вычислить ускорение тела, если известна его масса m и действующая на тело сила F:

В Международной системе единиц (СИ) за единицу силы принимается сила, которая сообщает телу массой 1 кг ускорение 1 м/с2. Эта единица называется ньютоном (Н). Ее принимают в СИ за эталон силы  

Если на тело одновременно действуют несколько сил (например, F1, F2, F3 ) и то под силой F в формуле, выражающей второй закон Ньютона, нужно понимать равнодействующую всех сил:

Если равнодействующая сила F0 =0 то тело будет оставаться в состоянии покоя или равномерного прямолинейного движения. Таким образом, формально второй закон Ньютона включает как частный случай первый закон Ньютона, однако первый закон Ньютона имеет более глубокое физическое содержание – он постулирует существование инерциальных систем отсчета.

Модель. Движение тел на легком блоке.

1.9. Третий закон Ньютона

В §1.7 понятие массы тела было введено на основе опытов по измерению ускорений двух взаимодействующих тел: массы взаимодействующих тел обратно пропорциональны численным значениям ускорений

В векторной форме это соотношение принимает вид

Знак «минус» выражает здесь тот опытный факт, что ускорения взаимодействующих тел всегда направлены в противоположные стороны. Согласно второму закону Ньютона, ускорения тел вызваны силами и возникающими при взаимодействии тел. Отсюда следует:

Это равенство называется третьим законом Ньютона.

Тела действуют друг на друга с силами, равными по модулю и противоположными по направлению.

Силы, возникающие при взаимодействии тел, всегда имеют одинаковую природу. Они приложены к разным телам и поэтому не могут уравновешивать друг друга. Складывать по правилам векторного сложения можно только силы, приложенные к одному телу.

Рис. 1.9.1 иллюстрирует третий закон Ньютона. Человек действует на груз с такой же по модулю силой, с какой груз действует на человека. Эти силы направлены в противоположные стороны. Они имеют одну и ту же физическую природу – это упругие силы каната. Сообщаемые обоим телам ускорения обратно пропорциональны массам тел.

Рисунок 1.9.1. Третий закон Ньютона.

Силы, действующие между частями одного и того же тела, называются внутренними. Если тело движется как целое, то его ускорение определяется только внешней силой. Внутренние силы исключаются из второго закона Ньютона, так как их векторная сумма равна нулю. В качестве примера рассмотрим рис. 1.9.2, н

nsportal.ru

Формулы по физике для подготовки к ЕГЭ

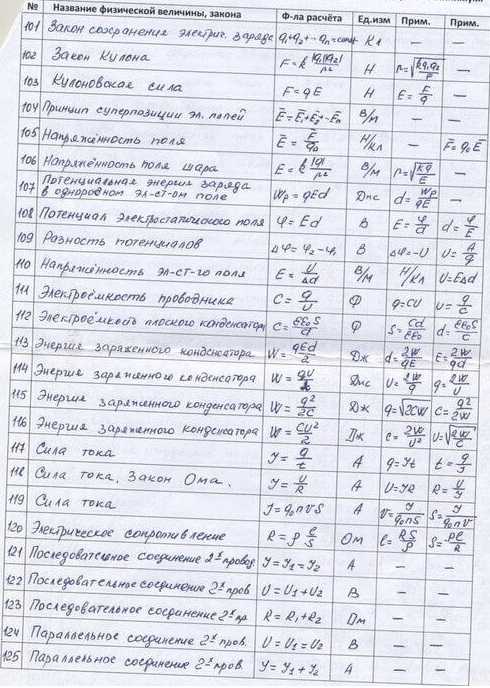
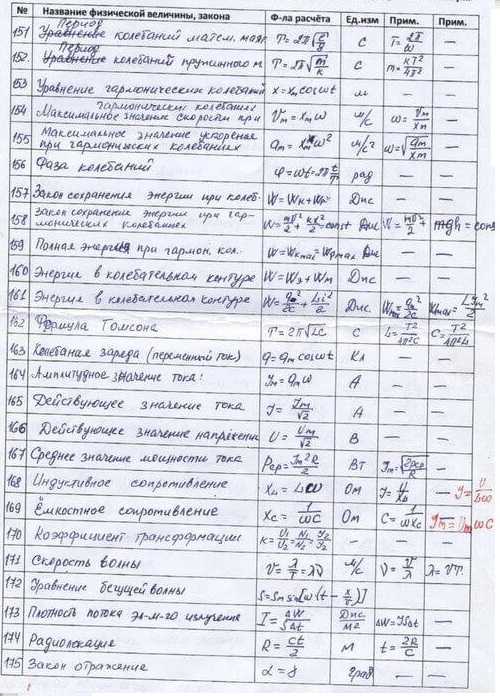
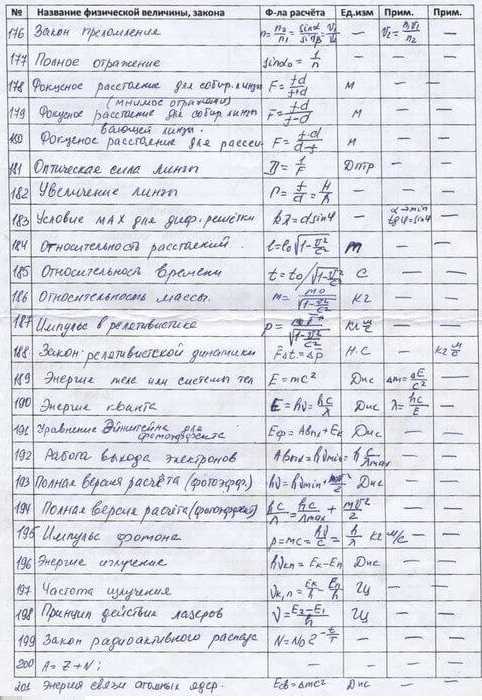
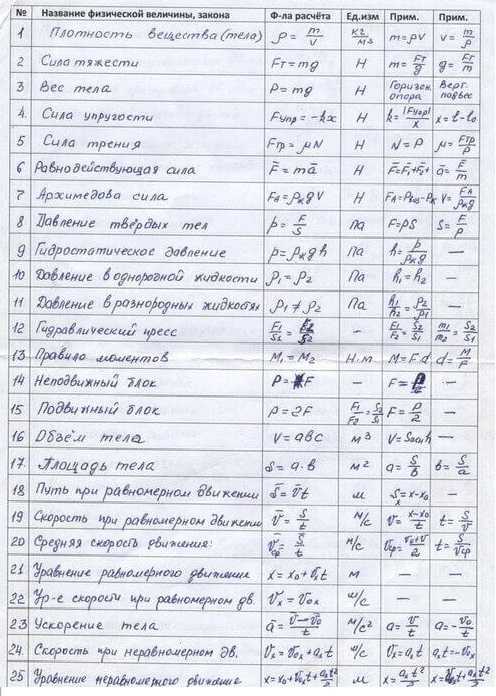
1	v=s/t скор. при равном. движ.	47	I=q/t сила тока, А I=qnvs	93	Q= A+∆U кол.тепл.,получен.двигателем	139	sinαo= n2/n1 пред. угол полн. отр.
2	ρ=m/V плотность, кг/м	48	U=A/q напряжение, В	94	η=(Q1-Q2)/Q1 КПД тепл. двиг.	140	n=c/v показ.прел. v=с/n скор.в среде
3	P=mg вес тела, Н P=m(g±a)	49	I=U/R закон Ома	95	η =(Т1-Т2)/Т1 КПД тепл. двиг.	141	D=1/F оптич. сила, дптр (м!!!)
4	F=mg сила тяжести, Н	50	R= ρℓ/s сопротивление проводника, Ом	96	F=kq1q2/εR2 закон Кулона	142	1/F=1/d+1/f формула линзы
5	p=F/S давление, Па	51	Q=I2Rt закон Джоуля-Ленца, Дж	97	E=F/q навряж. эл. поля, В/м	143	Г=f/d=H/h увелич. линзы
6	p=ρgh давлен. внутри жидк., Па	52	P=IU=I2R=U2/R мощн. тока, Вт	98	A=qU работа электр. поля	144	dsinφ =kλ формула дифр. решетки
7	F1/F2=S1/S2 гидравл. пресс	53	A=IUt=Pt работа тока, Дж	99	φ=A/q потенциал, В	145	Е=hv энергия фотона, Дж
8	h1/h2= ρ2/ρ1 сообщ.сосуды	54	I=I1=I2	100	φ1-φ2=U=A/q разность потенц., В	146	m=hv/c2 масса фотона
9	FA=gρжVп Архимедова сила (Vвыт.ж.)	55	R=R1+R2 Последоват.соединен.	101	E=kq/εR2 напряж.точечн.заряда,В/м	147	p=mc=hv/c=h/λ имрульс фотона
10	A=Fscosα мех. работа, Дж	56	U=U1+U2	102	φ=kq/εR потенц точечн. заряда,В	148	hv=A+mv2/2 ур. для фотоэффек.
11	η=Ап/А КПД 0,8 (80%)	57	U=U1=U2	103	Е=U/d связь Е и U, В/м.	149	A=hvm работа выхода, Дж
12	N=A/t мех. мощность, Вт	58	I=I1+I2 Параллельн.соединен.	104	W= kq1q2/εR энергия зарядов	150	mv2/2=eU задерж. разность потенц.,В
13	N=Fv мех. мощность, Вт	59	1/R=1/R1+1/R2	105	C=q/U ёмкость, Ф	151	v=(v1+v2)/(1+ v1* v2/ c2) рел.слож.ск.
14	M=Fd момент силы, Нм, М1+М2=М3+М4+…	60	Т=t/n период колебаний, Гц	106	W=qU/2=CU2/2= q2/2C энерг. конденс.	152	∆m=∆E/c2 измен.массы, энерг.
15	vср=s/t, vср=(vo+v)/2 при равноуск. движ.	61	ν=n/t частота колебаний, Гц	107	C=εε0S/d ёмкость плоск. конд.	153	m= m0/√1-(v/c) 2 масса движ. тела
16	vx=vox+axt скор. при равноуск.движ., м/с	62	ν =1/T частота, Гц	108	С=С1+С2 Параллельн.соединен.	154	Rc=1/2πνC емкостное сопротивл
17	vy=voy+gyt скор. при равноуск.движ., м/с	63	Т=1/ν период, с	109	q=q1+q1	155	RL=2πνL индуктивное сопротивл
18	sx=voxt + axt2/2 перем.при равноуск.дв., м	64	Т=2π√m/k период. кол. груза	110	U=U1=U2	156	√1-(v/c) 2 релятив. корень
19	hy=voyt+gyt2/2 перемещение по высоте	65	Т=2π√ℓ/g период. кол. маятн.	111	1/С=1/С1+1/С2 Послед.соединен.	157	N=N02^(-t/T) закон радиоактивн распада
20	s=(v2-v02)/2a путь при равноус.движ., м	66	v=νλ скорость волны	112	q=q1=q2
21	aц= v2/R= ω2R центростр. ускор.	67	ω =2πν циклич. частота (за 2πс)	113	U=U1+U2		Это может пригодиться:
22	aц=4π2R/T2=4π2Rn2 центростр. ускор	68	x=Acosωt=Acos2πνt координ.колебл.тела	114	I=E/(R+r) зак Ома полн. цепи	158	P=m(g±a) вес ускор вверх, вниз.
23	Fцс=mv2/R сила, сооб. центростр.уск.	69	v=Aωsinωt=A2πνsinωt	115	Iкз=E/r	159	При R=r P максимальна
24	φ=ωt=2πνt угол поворота	70	H=gt2/2 выс падения из сост.покоя	116	Ei=Aст/q ЭДС	160	P*=IE мощн. во всей цепи
25	v=2πRn. v=ωR	71	vx=v0cosα гориз.сост.скор.	117	U=E – Ir напряжение	161	η=R/(R+r) кпд эл. цепи
26	F=ma R=ma 2-й закон Ньютона, Н	72	vy=v0sinα вертик.сост.скор.	118	P=IE-I2r мощн. тока, Вт	162	η=U/E кпд эл. цепи
27	Fтр=μN сила трения	73	tmax=vosinα/g время подъёма до максим.выс.	119	m=kIt масса при электролизе	163	η=Р/P* кпд эл.цепи
28	F упр=-kx сила упругости, Н	74	S=v0хt= (v0cosα)t дальность полёта	120	i=I/S плотность тока, А/м2	164	mgsinα «скат.» сила
29	F=Gm1m2/R2 зак. всем. тягот.	75	S=vo2sin2α/g дальн. полёта	121	W=LI2/2 эн. магн. поля (тока), Дж	165	mgcosα сила реакц. на накл.пл. (след.строч.)
30	g= GM/R2 ускорение своб.пад.	76	H= vo2sin2α/2g макс.выс.подъёма	122	Ф=ВScos α магн. поток	166	mg-Fsinα на гориз., mgcosα-Fsinα на накл.пл.
31	gh=GM/(R+h)2 ускор. своб. пад. на h	77	p=1/3monv2 давл. газа, Па	123	Ф=LI ∆Ф=L∆I	167	sinα против.кат./гипотен.
32	v=√gR 1 косм скор h=0	78	mo=μ/NAмасса молекулы	124	B=Fm/Iℓ индукция	168	cosα прил.кат./гипот.
33	v=√GM/(R+h) 1 косм скор h>0	79	p=nkT давл. газа, Па	125	Ei=-∆Ф/∆t (Ei=S∆B/∆t) закон эл.магн.инд.	169	tgα прот.кат./прил.кат.
34	v2(R+h)=g0R2 соотношение	80	n=N/V концентр. молек.,1/м3	126	Ei=-(∆Ф/∆t )n зак. эл. маг. инд. для катуш.,В	170	S= πR2 площадь круга
35	p=mv импульс, кг·м/с (→!!!)	81	p=(2/3)nĒ давл. газа, Па	127	Еsi=L∆I/∆t ЭДС самоинд., В	171	C=2πR длина окружности
36	m1v1+m2v2=m1u1+m2u2 зак.сохр. имп. (→!!!)	82	E=(3/2)kT кин. энерг. мол., Дж	128	Fa=IBℓsinα сила Ампера лев рука	172	1м3=1000 л=1000 дм3
37	Ft=mv-mv0=m∆v=∆ p импульс силы	83	T=t+273 абсол. темп., К	129	Fл=qBvsinα сила Лоренца	173	54 км/ч=54/3,6=15 м/с
38	E=mv2/2 кинетич. энерг., Дж	84	ν =m/μ= N/NA колич. вещества, моль	130	Е= Bvℓsinα эдс в движ. проводн.	174	I=q/∆t и I=S∆B/∆tr (тогда q/∆t= S∆B/∆tr)
39	E=mgh потенц. энергия, Дж	85	v=√(3kT/m0)скор. молек.	131	e=BSωsinωt=Emsinωt эдс во вращ рамке в мп	175	Работа газа в осях (pV) равна площади фиг.
40	E=kx2/2 потенц. энергия, Дж	86	PV=mRT/M=νRT ур. Менд-Клайп.	132	qBR=mv вращ.зар.част.в МП	176	2см=2·10-2м, 2см2=2·10-4м2, 2см3=2·10-6м3
41	σ=F/s=Eε механич. напряжение, Па	87	p1V1/T1 = p2V2/T2 ур-е сост-я идеальн.газа	133	T=2πR/v=2πm/qB период вращ.зар.част.в мп	177	v =x’= — xmωsinωt a= v’= xmω2cosωt
42	ε=∆ℓ/ℓ0 относительное удлинение	88	U=(3/2) mRT/M вн.эн.одноат.ид.г.	134	T=2π√LC период кол. в КК	178	Eim=BSωn максим. эдс инд. во вращ. рамке
43	Q=mc∆t кол. тепл. НАГР. ОХЛ, Дж	89	U=(3/2)pV внутр. энерг. одноат. ид. газа	135	E=mc2 взаимос массы и энерг.,Дж	179	Fоткл=mgtgα (нить, электр.сила …)
44	Q=mλ кол. тепл. ПЛАВЛ. ОТВЕРД.	90	A=p∆V=mR∆T/M работа газа при р=const	136	α=β закон отр. света (\ п / в одной плоск.)	180	sinα≈tgα прималых α
45	Q=mL кол. тепл. ПАРООБР. КОНД.	91	A=Q1-Q2 работа двигателя	137	sinα/sinγ=n2/n1 зак прел. света (\ п / в одн.пл.)	181	Ускорение-изменение скорости за 1 с.
46	Q=mq кол. тепл. СГОРАНИЕ	92	∆U=Q+A изменен. внутр. энергии	138	q =∆Ф/R	182	d=√2а в квадрате
			Q=0 Адиабатн процесс				ЮрВас

infourok.ru

Основные формулы по физике — Физика — Теория, тесты, формулы и задачи

Знание формул по физике является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по физике. Формулы по физике, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении физических задач. На этой странице сайта представлены основные формулы по школьной физике в двух частях. В первой части Вы найдете самые важные физические формулы, а во второй — дополнительный набор полезных формул по физике.

 

Оглавление:

 

Основные формулы по школьной физике (Часть I)

К оглавлению…

 

Основные формулы по школьной физике (Часть II)

К оглавлению…

 

Как успешно подготовиться к ЦТ по физике и математике?

Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:

1. Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
2. Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
3. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.

Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.

 

Нашли ошибку?

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (адрес электронной почты и ссылки в социальных сетях здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.

educon.by

Формулы по физике для подготовки к ЕГЭ.

Уравнение скорости при равноускоренном движении υ=υ₀+a∙t

Ускорение a=(υ—υ ₀)/t

Скорость при движении по окружности υ=2πR/Т ; υ= ω R

Центростремительное ускорение a=υ²/R

Связь периода с частотой ν=1/T=ω/2π ; ω=2πν

II закон Ньютона F=ma

Закон Гука (сила упругости) Fy=-kx

Закон Всемирного тяготения F=G∙M∙m/R²

Первая космическая скорость V=√ G∙M/R ; =√gR

Вес тела, движущегося с ускорением а↑ Р=m(g+a)

Вес тела, движущегося с ускорением а↓ Р=m(g-a)

Сила трения Fтр=µN

Импульс тела p=mυ

Импульс силы p = Ft

Момент силы M=F∙ℓ

Потенциальная энергия тела, поднятого над землей Eп=mgh

Потенциальная энергия упруго деформированного тела Eп=kx²/2

Кинетическая энергия тела Ek=mυ²/2 = p²/2m

Работа A=F∙S∙cosα

Работа А= mυ²/2 — mυ_о ²/2

Работа А= mgh₁ — mgh₂

Мощность N=A/t=F∙υ

Коэффициент полезного действия η=Aп/Аз

Период колебаний математического маятника T=2π√ℓ/g

Период колебаний пружинного маятника T=2 π √m/k

Связь длины волны, ее скорости и периода λ= υТ

Закон сохранения импульса:

Закон Кулона F=k∙q₁∙q₂/R²

Напряженность электрического поля E=F/q

Напряженность эл. поля точечного заряда E=k∙q/R²

Поверхностная плотность зарядов σ = q/S

Напряженность эл. поля бесконечной плоскости E=2πkσ

Диэлектрическая проницаемость ε=E₀/E

Потенциальная энергия взаимод. зарядов W= k∙q₁q₂/R

Потенциал φ=W_p/q

Потенциал точечного заряда φ=k∙q/R

Напряжение U=A/q ; U= Ed

Для однородного электрического поля U=E∙d

Электроемкость C=q/U

Электроемкость плоского конденсатора C=S∙ε∙

ε₀/d

Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2

Сила тока I=q/t

Сопротивление проводника R=ρ∙ℓ/S

Закон Ома для участка цепи I=U/R

Мощность электрического тока P=I∙U

Работа тока A= IUt

Масса вещества выделившаяся на электроде m=kIt ; m= kq

Радиус движения заряженной частицы r= mv/qB

Закон Джоуля-Ленца Q=I²Rt

Закон Ома для полной цепи I=ε/(R+r)

Ток короткого замыкания (R=0) I=ε/r

Вектор магнитной индукции B=Fmax/ℓ∙I

Сила Ампера Fa=IBℓsin α

Сила Лоренца Fл=Bqυsin α

Магнитный поток Ф=BSсos α ; Ф=LI

Закон электромагнитной индукции Ei=ΔФ/Δt

ЭДС максимальное E_max = BSω

ЭДС индукции в движ проводнике Ei=Вℓυsinα

ЭДС самоиндукции Esi=-L∙ΔI/Δt

Энергия магнитного поля катушки Wм=LI²/2

Период колебаний кол. контура T=2π ∙√LC

Индуктивное сопротивление X_L=ωL=2πLν

Емкостное сопротивление Xc=1/ωC

Полное сопротивление Z=√(Xc-X_L)²+R²

Параллельное соединение: I_об = I₁ + I₂ ; U_об = U₁=U₂ ;

multiurok.ru