Задачи на кинетическую энергию с решением: Задачи на кинетическую и потенциальную энергия с решением

Содержание

Задачи на кинетическую и потенциальную энергия с решением

А почему-бы и нет? У нас уже были задачи на свободное падение, законы Ньютона, силу трения и проч. и проч. Сегодня решаем задачи на кинетическую и потенциальную энергию.

А вообще, помните, что мы занимаемся далеко не только решением задач. Наш телеграм – это полезная информация для студентов всех специальностей, новости, лайфхаки, акции и скидки.

Задачи на кинетическую и потенциальную энергию

Приведем примеры задач на нахождение кинетической и потенциальной энергии с решением. Прежде чем приступать к практике, почитайте теорию по теме, повторите общую памятку по решению задач по физике и на всякий случай держите под рукой полезные формулы.

Задача №1 на кинетическую энергию

Условие

Максимальная высота, на которую поднимается тело массой 1 кг, подброшенное вертикально вверх, составляет 20 м. Найдите, чему была равна кинетическая энергия сразу же после броска.

Решение

Потенциальная энергия тела над поверхностью Земли составляет:

Здесь m – масса тела, g – ускорение свободного падения, h – высота. Согласно закону сохранения энергии, потенциальная энергия тела в наивысшей точке должна равняться кинетической энергии тела в начальный момент, то есть:

Принимая ускорение свободного падения равным 10 м/с2, находим кинетическую энергию тела сразу же после броска:

Ответ: 200 Дж.

Задача №2 на потенциальную энергию

Условие

Чему равна потенциальная энергия трех кубических дециметров воды на высоте 10 м?

Решение

По определению, потенциальная энергия равна в поле силы тяжести равна:

Масса трех кубических дециметров воды (трех литров) легко находится из формулы для плотности воды:

Осталось вычислить потенциальную энергию:

Ответ: 300 Дж.

При решении задач не забывайте переводить все размерности величин в систему СИ.

Задача №3 на полную механическую энергию

Условие

Какова полная механическая энергия дирижабля массой 5 тонн, если он летит на высоте 2 км со скоростью 60 км/ч?

Решение

Полная механическая энергия состоит из кинетической и потенциальной энергий:

Вычислим:

Ответ: 100,7 МДж.

Задача №4 на кинетическую и потенциальную энергию

Условие

Шарик массой 200 г падает с высоты 20 м с начальной скоростью, равной нулю. Какова его кинетическая энергия в момент перед ударом о землю, если потеря энергии за счет сопротивления воздуха составила 4 Дж? (Ответ дайте в джоулях.) Ускорение свободного падения принять равным 10 м/с2.

Решение

Перед началом падения потенциальная энергия шарика составляет:

По закону сохранения энергии, эта энергия должна перейти в кинетическую энергию Ек за вычетом потери за счет сопротивления воздуха дельта Е. Таким образом, можем найти кинетическую энергию:

Ответ: 36 Дж.

Задача №5 кинетическую и потенциальную энергию

Условие

Шарик висит на нити. В нем застревает пуля, летящая горизонтально, в результате чего нить отклоняется на некоторый угол. Как изменятся при увеличении массы шарика следующие величины: импульс, полученный шариком в результате попадания в него пули; скорость, которая будет у шарика тотчас после удара; угол отклонения нити?

Решение

Согласно закону сохранения импульса, скорость шарика с застрявшей в нем пулей равна

Здесь M и m – массы шарика и пули соответственно, v – скорость пули перед ударом. Таким образом, при увеличении массы шарика его скорость после удара уменьшится.

Найдем импульс, переданный шарику при попадании пули:

Следовательно, с увеличением массы шарика переданный ему импульс увеличивается.

Согласно закону сохранения энергии, кинетическая энергия пули перейдет в потенциальную энергию шарика с пулей:

Таким образом, при увеличении массы шарика угол отклонения нити уменьшится, поскольку уменьшится скорость u.

Ответ: см решение выше.

Вопросы на потенциальную и кинетическую энергию

Вопрос 1. Что такое энергия? Что такое механическая энергия?

Ответ. Для энергии существует множество определений. В наиболее общем смысле:

Энергия – мера способности тела совершать работу.

Механическая энергия – это энергия, связанная с движением тела или его положением в пространстве. Механическая энергия в механике описывается суммой кинетической и потенциальной энергии.

Вопрос 2. Сформулируйте закон сохранения энергии

Ответ. Закон сохранения энергии является фундаментальным физическим принципом. Для каждого вида энергии он имеет свою формулировку. Для механической энергии:

Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остается неизменной.

Вопрос 3. Какие силы называются консервативными?

Ответ. Консервативные, или потенциальные силы – это силы, работа которых не зависит от формы траектории. В качестве примера такой силы можно привести силу тяжести.

Вопрос 4. Какую энергию называют кинетической?

Ответ. Кинетическая энергия является энергией движения. Ею обладают только движущиеся тела, она зависит от массы тела и его скорости.

Вопрос 5. Какую энергию называют потенциальной?

Ответ. Потенциальная энергия является энергией взаимодействия в поле консервативных сил. 2}{2} \)

\( v= \sqrt { \dfrac{2E_{к}}{m} } \)

\( v= \sqrt { \dfrac{2 \cdot 243}{6} } =9 м/с \)

Ответ: \( v=9 м/с \)

6. Кинетическая энергия моторной лодки массой \( m_л=176 кг \; \), движущейся со скоростью \(v_л=8 м/с \) равна кинетической энергии радиоуправляемого квадрокоптера, который движется со скоростью \(v_к=32 м/с . \; \) Вычислить массу квадрокоптера .
Показать ответ Показать решение Видеорешение

Ответ: \( m_к= 11 кг \)

Каждый выбирает для себя то решение, которое ему понятнее
Решение номер 1 (для тех, кто сдает ЕГЭ и хочет научиться решать трудные задачи)
Решение номер 2 (для тех кто любит попроще)

Дано:
\( m_л=176 кг\)

\( v_л=8 м/с \)

\( v_к=32 м/с \)

\(m_к-?\)

\(\dfrac{m_лv_л^2}{2}=\dfrac{m_к v_к^2}{2} \)

\(m_{л} v_{л}^2=m_{к} v_{к}^2 \)

\( m_к= \dfrac{m_лv_л^2}{v_к^2} \)

\( m_к= \dfrac{176 \cdot 8^2 }{32^2}=11 кг \)

Ответ: \( m_к= 11 кг \)

Решение номер 2 (для тех, кому тяжело понять)

Дано:
\( m_л=176 кг\)

\( v_л=8 м/с \)

\( v_к=32 м/с \)

\(m_к-?\)

Вычислим кинетическую энергию лодки:

\( E_л=\dfrac{m_лv_л^2}{2}=5632 Дж \)

По условию \( E_л=E_к \) , поэтому :

\(E_л=\dfrac{m_к v_к^2}{2} \)

\(m_к= \dfrac{2E_{л}}{v_к^2} \)

\(m_к= \dfrac{2 \cdot 5632}{32^2}=11 кг \)

Ответ: \(m_к= 11 кг \)

7. Кинетическая энергия моторной лодки массой \( m_л=176 кг \; \), движущейся со скоростью \(v_л=8 м/с \) равна кинетической энергии радиоуправляемого квадрокоптера массой \( m_к= 11 кг \; . \) Вычислить скорость квадрокоптера .
Показать ответ Показать решение Видеорешение

Ответ: \( v_к= 32 м/с \)

Дано:
\( m_л=176 кг\)

\( v_л=8 м/с \)

\( m_к=11 кг \)

\(v_к-?\)

\(\dfrac{m_лv_л^2}{2}=\dfrac{m_к v_к^2}{2} \)

\(m_{л} v_{л}^2=m_{к} v_{к}^2 \)

\( v_{к}^2= \dfrac{m_лv_л^2}{m_{к}} \)

\( v_{к}= \sqrt { \dfrac{m_лv_л^2}{m_{к}} } \)

\( v_{к}= \sqrt { \dfrac{m_л}{m_{к}} } \cdot v_л \)

\( v_{к}= \sqrt { \dfrac{176}{11} } \cdot 8=32 м/с \)

Ответ: \( v_{к}=32 м/с \)

Решение номер 2 (для тех, кому тяжело понять)

Дано:
\( m_л=176 кг\)

\( v_л=8 м/с \)

\( m_к=11 кг \)

\(v_к-?\)

Вычислим кинетическую энергию лодки:

\( E_л=\dfrac{m_лv_л^2}{2}=5632 Дж \)

По условию \( E_л=E_к \) , поэтому :

\(E_л=\dfrac{m_к v_к^2}{2} \)

\(v_к^2= \dfrac{2E_{л}}{m_к} \)

\(v_к= \sqrt{ \dfrac{2E_{л}}{m_к} } \)

\(v_к= \sqrt{ \dfrac{2 \cdot 5632}{11} } = 32 м/с \)

Ответ: \(v_к= 32 м/с \)

8. Кинетическая энергия моторной лодки массой \( m_л=98 кг \; \), движущейся со скоростью \(v_л=5 м/с \) равна кинетической энергии игрушечного радиоуправляемого катера, который движется со скоростью \(v_к=35 м/с . \; \) Вычислить массу игрушечного радиоуправляемого катера.
Показать ответ Показать решение Видеорешение

Ответ: \( m_к= 2 кг \)

Дано:
\( m_л=98 кг\)

\( v_л=5 м/с \)

\( v_к=35 м/с \)

\(m_к-?\)

\(\dfrac{m_лv_л^2}{2}=\dfrac{m_к v_к^2}{2} \)

\(m_{л} v_{л}^2=m_{к} v_{к}^2 \)

\( m_к= \dfrac{m_лv_л^2}{v_к^2} \)

\( m_к= \dfrac{98 \cdot 5^2 }{35^2}=2 кг \)

Ответ: \( m_к= 2 кг \)

Решение номер 2 (для тех, кому тяжело понять)

Дано:
\( m_л=98 кг\)

\( v_л=5 м/с \)

\( v_к=35 м/с \)

\(m_к-?\)

Вычислим кинетическую энергию лодки:

\( E_л=\dfrac{m_лv_л^2}{2}=1225 Дж \)

По условию \( E_л=E_к \) , поэтому :

\(E_л=\dfrac{m_к v_к^2}{2} \)

\(m_к= \dfrac{2E_{л}}{v_к^2} \)

\(m_к= \dfrac{2 \cdot 1225}{35^2}=2 кг \)

Ответ: \(m_к= 2 кг \)

9. 2= \dfrac{2E_{л}}{m_к} \)

\(v_к= \sqrt{ \dfrac{2E_{л}}{m_к} } \)

\(v_к= \sqrt{ \dfrac{2 \cdot 1225}{2} } = 35 м/с \)

Ответ: \(v_к= 35 м/с \)

11. Кинетическая энергия тела \(E_к=8 Дж \; \), а импульс \(p=4 кг \cdot м/с \). Найти скорость тела.
Показать ответ Показать решение Видеорешение

Ответ: \( v=4 м/с \)

Дано:
\(p=4 кг \cdot м/с\)

\( E_к=8 Дж \)

\(v-?\)

\(E_{к}=\dfrac{mv^2}{2} \)

\(p=mv \)

разделим первое уравнение на второе:

\( \dfrac{E_{к}}{p}=\dfrac{mv^2}{2}:(mv) \)

\( \dfrac{E_{к}}{p}=\dfrac{mv^2}{2}:\dfrac{mv}{1} \)

\( \dfrac{E_{к}}{p}=\dfrac{mv^2}{2} \cdot \dfrac{1}{mv} \)

\( \dfrac{E_{к}}{p}=\dfrac{v}{2} \)

\(v= \dfrac{2E_{к}}{p} \)

\(v= \dfrac{2\cdot 8}{4}=4м/с \)

Ответ: \( v=4 м/с \)

Решение номер 2 (для тех, кому тяжело понять)

Дано:
\(p=4 кг \cdot м/с\)

\( E_к=8 Дж \)

\(v-?\)

\(E_{к}=\dfrac{mv^2}{2} \)

\(p=mv =4 \)

\(E_{к}=\dfrac{mv\cdot v}{2} \)

\(8=\dfrac{4\cdot v}{2} \)

\(v=4 м/с \)
Ответ: \(v=4 м/с \)

12. 2}{2} \)

\(p=mv =5000 \)

\(E_{к}=\dfrac{mv\cdot v}{2} \)

\(12500=\dfrac{5000\cdot v}{2} \)

\(v=5 м/с \)
Ответ: \(v=5 м/с \)

13. Кинетическая энергия пули при вылете из ружья равна \(1125 Дж \; \), а импульс \(p=4,5 кг \cdot м/с \). Найти скорость пули.
Показать ответ Показать решение Видеорешение

Ответ: \( v=500 м/с \)

Дано:
\(p=4,5 кг \cdot м/с\)

\( E_к=1125 Дж \)

\(v-?\)

\(E_{к}=\dfrac{mv^2}{2} \)

\(p=mv \)

разделим первое уравнение на второе:

\( \dfrac{E_{к}}{p}=\dfrac{mv^2}{2}:(mv) \)

\( \dfrac{E_{к}}{p}=\dfrac{mv^2}{2}:\dfrac{mv}{1} \)

\( \dfrac{E_{к}}{p}=\dfrac{mv^2}{2} \cdot \dfrac{1}{mv} \)

\( \dfrac{E_{к}}{p}=\dfrac{v}{2} \)

\(v= \dfrac{2E_{к}}{p} \)

\(v= \dfrac{2\cdot 1125Дж}{4,5}=500м/с \)

Ответ: \( v=500 м/с \)

Решение номер 2 (для тех, кому тяжело понять)

Дано:
\(p=4,5 кг \cdot м/с\)

\( E_к=1125 Дж \)

\(v-?\)

\(E_{к}=\dfrac{mv^2}{2} \)

\(p=mv =4,5 \)

\(E_{к}=\dfrac{mv\cdot v}{2} \)

\(1125=\dfrac{4,5\cdot v}{2} \)

\(v=500 м/с \)
Ответ: \(v=500 м/с \)

Практические задачи на кинетическую энергию

Когда работа совершается силой над объектом.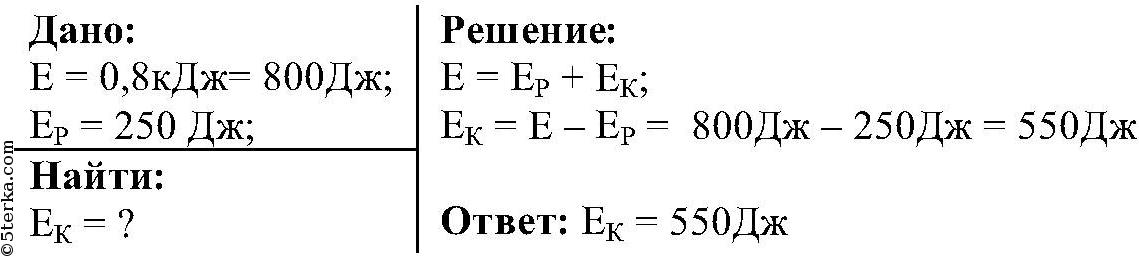 Он приобретает энергию, он может быть любой формы. Энергия может принимать различные формы и может быть преобразована из одной формы в другую. Потенциальная энергия, электрическая потенциальная энергия, кинетическая энергия и т. д. являются некоторыми примерами различных типов энергии. Кинетическая энергия возникает, когда объект начинает двигаться. Эта энергия обусловлена движением. Хотя эта энергия обусловлена движением, эта энергия не создается. Обычно она преобразуется из одного вида энергии в другой вид. Рассмотрим это понятие подробнее.

Кинетическая энергия

Если объект неподвижен, и мы хотим привести этот объект в движение. Нам нужно применить силу. Любой тип ускорения требует некоторой силы. При приложении этой силы над телом совершается работа. Когда над объектом совершается работа, это означает, что энергия передается объекту в той или иной форме. Силу можно снять, когда объект находится в движении, но до момента, когда к объекту была приложена сила. Работа, совершенная за это время, превращается в энергию.

Кинетическая энергия — это энергия, которую объект приобретает благодаря своему движению.

Эта энергия может передаваться от одного объекта к другому. Например, удар движущегося мяча по неподвижному мячу может привести к движению другого мяча. В этой ситуации часть кинетической энергии мяча передается другому мячу.

Формула кинетической энергии
Для расчета кинетической энергии объекта рассмотрим сценарий, в котором сила F действует на объект массой M. В этом случае объект начинает двигаться с ускорением «a ” и преодолевает расстояние “d”.
В этом случае работа будет равна
W = F.d
⇒ W = m.a.d
Ускорение «a» можно заменить уравнением движения.
v ² = u ² + 2a.d
⇒v ² – u ² = 2a.d
⇒ = d
Подставив значение «d» в уравнение,
W = m.a.d
⇒ W =
⇒ W =
⇒ W =
Итак, вся эта проделанная работа преобразуется в КЭ объекта.
В случае, если начальная скорость u = 0,
K.E =
Можно также сказать, что сетевая работа, совершаемая над системой, равна изменению кинетической энергии объекта.
Примечание:
1. Кинетическая энергия зависит от квадрата скорости объекта. Это означает, что при удвоении скорости объекта его кинетическая энергия увеличивается в четыре раза.
2. K.E всегда должен иметь нулевое или положительное значение.
3. Кинетическая энергия является скалярной величиной и выражается в джоулях.
Примеры задач
Вопрос 1. Мяч массой 2 кг предположим, что он движется со скоростью 10 м/с. Найдите кинетическую энергию, которой он обладает.
Ответ:
Дано: m = 2 кг и v = 10 м/с =
⇒ К.Э =
⇒ К.Э = 100 Дж
Вопрос 2: Мяч массой 10 кг, предположим, что он движется со скоростью 100 м/с. Найдите кинетическую энергию, которой он обладает.
Ответ:
Дано: m = 10 кг и v = 100 м/с. E =
⇒ K.E =
⇒ K.E = 50000J
Вопрос 3: Космический корабль имеет массу 20000 кг, предположим, что он движется со скоростью 10 м/с. Найдите кинетическую энергию, которой он обладает.
Ответ:
Дано: m = 20000 кг и v = 10 м/с0002 K.E =
K.E =
⇒ K.E =
⇒ K.E = 10 ⁶ J
Вопрос 4. Работа силы при движении объект 100Дж. Он двигался со скоростью 2 м/с. Найдите новую скорость тела, если масса тела 2 кг.
Ответ:
Дано: W = 100 Дж
Работа, совершаемая силой, равна изменению кинетической энергии.
W =
Дано, u = 2 м/с и v = ?, m = 2 кг.
Подставляя значения в данное уравнение,
Вт =
⇒
⇒
Вопрос 5: Работа, совершаемая силой над движущимся объектом, равна -50 Дж. Он двигался со скоростью 10 м/с. Найдите новую скорость тела, если масса тела 2 кг.
Ответ:
Дано: W = -50 Дж
Работа, совершаемая силой, равна изменению кинетической энергии.
W =
Дано, u = 10 м/с и v = ? . м = 2 кг.
Подставляя значения в данное уравнение,
W =
⇒
⇒
Скорость уменьшается, потому что проделанная работа была отрицательной. Это означает, что сила действовала противоположно блоку и скорость уменьшалась.
Вопрос 6: Предположим, что 1000 кг движется со скоростью 10 м/с. Теперь эта масса передает всю свою энергию массе 10 кг. Какова будет скорость тела массой 10 кг после удара о него?
Ответ:
КЭ определяется по формуле
КЭ =
КЭ более тяжелого объекта =
⇒ К.Э =
⇒К.Э = 50 000 Дж
Теперь эта энергия передается другому шару.
м = 10 кг и v = ?
50 000 =
⇒ 10 000 = v ²
⇒ v = 100 м/с
со скоростью 100 м/с. Теперь эта масса передает всю свою энергию массе 20 кг. Какова будет скорость тела массой 20 кг после удара о него?
Ответ:
KE определяется по формуле
KE =
KE более тяжелого объекта s
К.Э =
⇒ К.Э =
⇒K.E = 50 000 Дж
Теперь эта энергия передается другому шару.
м = 20 кг и v = ?
50 000 =
⇒ 5000 = v ²
⇒ v = 50√2 м/с
Вопрос 8. Предположим, двигаясь со скоростью 100 м/с. Теперь эта масса передает всю свою энергию массе 20 кг. Какова будет скорость тела массой 20 кг после удара о него?
Ответ:
KE определяется по формуле
KE =
KE более тяжелого объекта s
К. Э =
⇒ К.Э =
⇒K.E = 50 000 Дж
Теперь эта энергия передается другому шару.
м = 20 кг и v = ?
50 000 =
⇒ 5000 = v ²
⇒ v = 50√2 м/с
Вопрос 9. Предположим, держится на высоте 20 м. Теперь этот блок снят. Найдите скорость шарика непосредственно перед тем, как он упадет на землю.
Ответ:
Блок массой 10 кг находится на высоте 20 м.
Потенциальная энергия блока будет равна
P.E = mgh
Здесь m = 10, g = 10 м/с ² и h = 20 м.
ЛЭ = mgh
⇒ ЛЭ = (10)(10)(20)
⇒ ЛЭ = 2000 Дж
Теперь эта энергия полностью преобразуется в КЭ.
KE = PE
⇒ 2000 =
Учитывая m = 10 кг,
⇒ 2000 =
⇒ 400 = v ²
v = 20 м/с
Вопрос 10: Предположим, что камень весом 100 кг находится на высоте 80 м. Теперь этот блок снят. Найдите скорость шарика непосредственно перед тем, как он упадет на землю.
Ответ:
Блок массой 10 кг находится на высоте 20 м.
Потенциальная энергия блока будет равна
P.E = mgh
Здесь m = 100, g = 10 м/с ² и h = 80 м.
ЛЭ = mgh
⇒ ЛЭ = (100)(10)(80)
⇒ ЛЭ = 80000 Дж
Теперь эта энергия полностью преобразуется в КЭ.
KE = PE
⇒ 80000 =
Учитывая m = 100 кг,
⇒ 80000 =
⇒ 1600 = v ^{2 9003 2}
v = 40 м/с

Работа, энергия и мощность
Кинетическая энергия — это энергия движения. Объект, который движется — будь то вертикальное или горизонтальное движение — обладает кинетической энергией. Существует много форм кинетической энергии: колебательная (энергия колебательного движения), вращательная (энергия вращательного движения) и поступательная (энергия движения из одного места в другое). Для простоты сосредоточимся на поступательной кинетической энергии. Количество поступательной кинетической энергии (далее фраза «кинетическая энергия» будет относиться к поступательной кинетической энергии), которой обладает объект, зависит от двух переменных: массы (m) объекта и скорости (v) объекта. Следующее уравнение используется для представления кинетической энергии (KE) объекта.
KE = 0,5 • m • v ²
где м = масса объекта
v = скорость объекта
Это уравнение показывает, что кинетическая энергия объекта прямо пропорциональна квадрату его скорости. Это означает, что при двукратном увеличении скорости кинетическая энергия увеличится в четыре раза. При трехкратном увеличении скорости кинетическая энергия увеличится в девять раз. А при четырехкратном увеличении скорости кинетическая энергия увеличится в шестнадцать раз. Кинетическая энергия зависит от квадрата скорости. Как часто говорят, уравнение — это не только рецепт решения алгебраических задач, но и руководство к размышлению о связи между величинами. 92.

1 Джоуль = 1 кг • м ² /с ²

Мы хотели бы предложить…
Как скорость автомобиля (и, следовательно, его кинетическая энергия) влияет на расстояние, необходимое для его торможения до полной остановки? Взаимодействуйте, исследуйте и узнавайте ответ на этот вопрос с помощью нашего интерактива Stopping Distance. Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивное приложение Stopping Distance позволяет учащимся исследовать влияние скорости на тормозной путь игрушечной машинки.

Посетите: Stopping Distance Interactive

Проверьте свое понимание
Используйте свое понимание кинетической энергии, чтобы ответить на следующие вопросы.