Теория по геометрии для егэ: Геометрия на ЕГЭ по математике. Что нужно знать?
Геометрия на ЕГЭ по математике. Что нужно знать?
Геометрия на профильном ЕГЭ по математике — одна из сложных тем для абитуриентов. Дело в том, что когда-то экзамен по геометрии в школе был обязательным, а сейчас — нет. В результате у большинства абитуриентов знания по геометрии близки к нулю.
Геометрия на профильном ЕГЭ — это три задачи в части 1 (сюда входит и планиметрия, и стереометрия), а также задача 14 (стереометрия) и для многих недосягаемая задача 16 (геометрия) из второй части. Как же научиться их решать?
Начнем с планиметрии. Прежде всего, выучите основные формулы геометрии.
На нашем сайте вы найдете курс геометрии с нуля — основные определения, формулы и теоремы, а также разбор множества экзаменационных задач по геометрии из части 1.
Для решения задач по геометрии из части 2 нужна более серьезная подготовка.
Первый этап — теория. Необходимый материал есть в учебнике по геометрии за 7-9 класс (автор — А. В. Погорелов или Л. С. Атанасян). Выпишите в тетрадь определения и формулировки теорем. Сделайте чертежи. Доказывать теоремы старайтесь самостоятельно.
Выпишите в тетрадь определения и формулировки теорем. Сделайте чертежи. Доказывать теоремы старайтесь самостоятельно.
Программа по геометрии.
1. Треугольники. Элементы треугольника. Вершины и стороны. Высоты, медианы, биссектрисы (определения).
2. Построение треугольника: практические задания.
а) Три стороны треугольника равны и сантиметров соответственно. Постройте треугольник с помощью циркуля и линейки.
б) В треугольнике угол равен градусов, сторона равна , равна . Постройте треугольник .
в) В треугольнике сторона равна , угол равен , угол равен . Постройте треугольник .
3. Три признака равенства треугольников. Неравенство треугольника.
4. Постройте с помощью циркуля и линейки:
а) серединный перпендикуляр к отрезку;
б) биссектрису угла.
5. Углы при параллельных прямых и секущей. Вертикальные, смежные, соответственные, односторонние и накрест лежащие углы. Их определение и свойства.
6. Теорема о сумме углов треугольника.
7. Внешний угол треугольника.
8. Постройте в одном и том же треугольнике
а) Три высоты. Рассмотрите также случаи тупоугольного и прямоугольного треугольника.
б) Три биссектрисы.
в) Три медианы.
9. Равнобедренный треугольник. Определение и свойства. Высота в равнобедренном треугольнике.
10. Средняя линия треугольника и ее свойства.
11. Прямоугольный треугольник. Теорема Пифагора.
12. Определения синуса, косинуса и тангенса:
— для острого угла прямоугольного треугольника;
— для произвольного угла.
13. Четырехугольники. Сумма углов четырехугольника.
14. Параллелограмм. Определение и свойства. Площадь параллелограмма.
15. Виды параллелограммов и их свойства (ромб, прямоугольник, квадрат).
16. Трапеция. Средняя линия трапеции. Площадь трапеции.
17. Подобные треугольники. Три признака подобия треугольников.
18. Площадь треугольника. Формулы и .
19. Теоремы синусов и косинусов.
20. Чему равно отношение площадей подобных фигур.
21. Свойство медианы (в каком отношении делятся медианы в точке пересечения?)
22. Свойство биссектрисы (в каком отношении биссектриса делит противоположную сторону?)
23. Окружность и круг. Длина окружности. Площадь круга. Длина дуги и площадь сектора.
24. Теорема о радиусе, проведенном в точку касания.
25. Центральный и вписанный углы. Связь между ними.
26. Теоремы о вписанных углах.
27. Теорема о пересекающихся хордах.
28. Теорема об отрезках длин касательных, проведенных из одной точки.
29. Теорема о секущей и касательной.
30. Дан треугольник . Постройте:
а) окружность, вписанную в данный треугольник;
б) окружность, описанную вокруг данного треугольника.
31. Еще три формулы площади треугольника (через радиус вписанной окружности, через радиус описанной окружности и формула Герона).
32. Когда можно вписать окружность в четырехугольник? Когда — описать вокруг четырехугольника?
Программа по стереометрии
Разбирая и решая задания ЕГЭ по геометрии, вы заметите очень интересную вещь.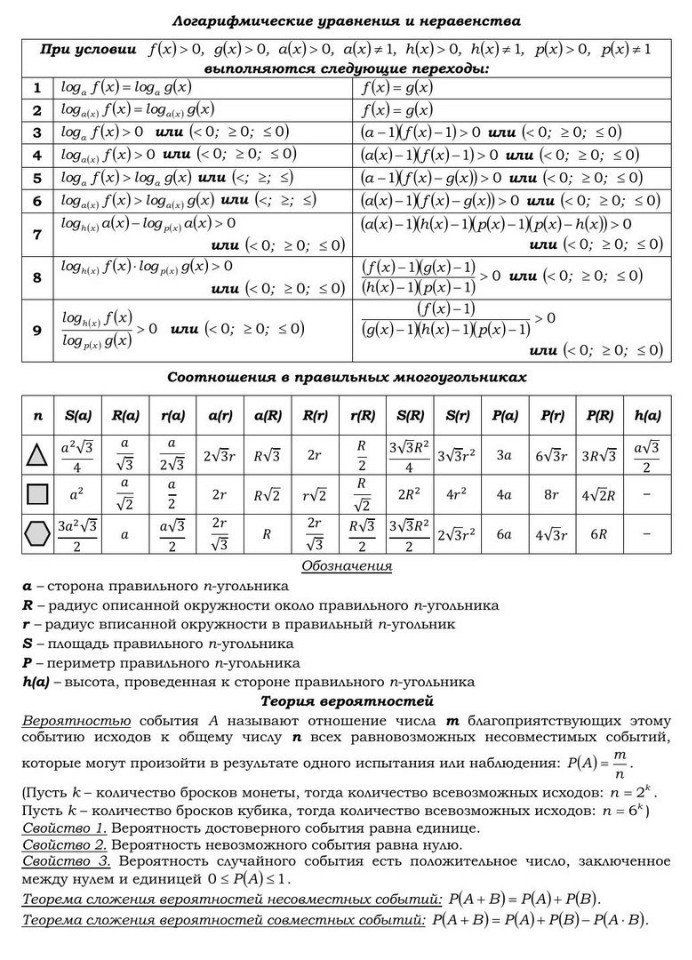 Простые задачи из части 1, разобранные на нашем сайте, часто оказываются базовыми схемами, на которых строятся сложные задачи из части 2 профильного ЕГЭ.
Простые задачи из части 1, разобранные на нашем сайте, часто оказываются базовыми схемами, на которых строятся сложные задачи из части 2 профильного ЕГЭ.
Решая на ЕГЭ задачи по геометрии, обращайте особое внимание на оформление. Помните совет, который дал абитуриентам автор бестселлера «Математика — абитуриенту» В. В. Ткачук. Вот он, этот ценнейший совет:
«Подробность решения должна быть такова, чтобы его мог понять человек в 10 (десять) раз глупее вас».
Спасибо за то, что пользуйтесь нашими публикациями. Информация на странице «Геометрия на ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08. 01.2023
01.2023
Подготовка к ЕГЭ и ОГЭ (справочник по математике для школьников — Геометрия
Подготовка к ЕГЭ и ОГЭ (справочник по математике для школьников — Геометрия — Планиметрия)Поиск по сайту:
К. Л. САМАРОВ, С.С.САМАРОВА
Справочник по математике для школьников
Тематическое содержание
Основные фигуры планиметрии | ||
| Фигуры, составляющие основу планиметрии | ||
Углы | ||
| Углы на плоскости | ||
| Теорема Фалеса | ||
| Углы, связанные с окружностью | ||
| Вписанные и центральные углы | ||
| Углы, образованные хордами, касательными и секущими | ||
| Доказательства теорем об углах, связанных с окружностью | ||
Параллельность прямых | ||
| Признаки параллельности прямых | ||
Треугольники | ||
Типы треугольников.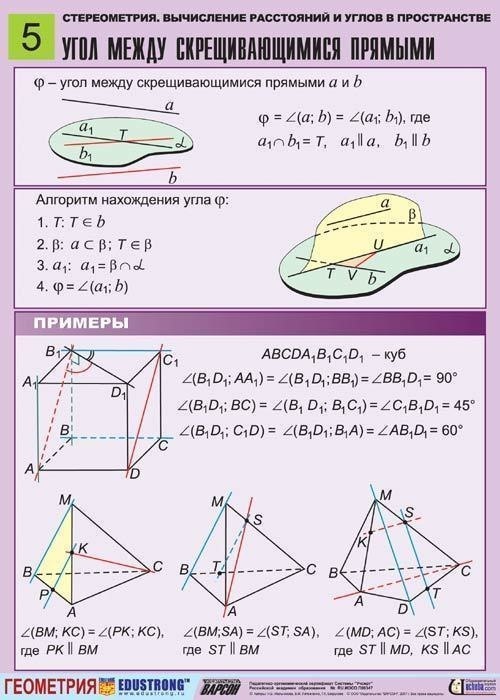 Признаки равенства треугольников Признаки равенства треугольников | ||
| Типы треугольников | ||
| Признаки равенства треугольников | ||
| Признаки равенства прямоугольных треугольников | ||
| Свойства и признаки равнобедренного треугольника | ||
| Свойства прямоугольного треугольника | ||
| Свойства сторон и углов треугольника | ||
| Подобные треугольники. Признаки подобия треугольников | ||
| Подобные треугольники | ||
| Признаки подобия треугольников | ||
| Признаки подобия прямоугольных треугольников | ||
| Теорема Пифагора. Теорема косинусов | ||
| Теорема Пифагора | ||
| Теорема косинусов | ||
Биссектриса треугольника. Свойства биссектрисы. Вычисление длины биссектрисы Свойства биссектрисы. Вычисление длины биссектрисы | ||
| Медиана треугольника. Свойства медианы. Вычисление длины медианы | ||
| Высота треугольника. Задача Фаньяно | ||
| Высота треугольника. Свойство высоты прямоугольного треугольника | ||
| Расположение высот у треугольников различных типов | ||
| Ортоцентр треугольника | ||
| Расположение ортоцентров у треугольников различных типов | ||
| Ортоцентрический треугольник | ||
| Задача Фаньяно | ||
| Средние линии треугольника | ||
| Теорема Чевы | ||
| Теорема Чевы 1 | ||
| Теорема Чевы 2 | ||
| Применения теоремы Чевы | ||
| Теорема Менелая | ||
Окружность, описанная около треугольника. Треугольник, вписанный в окружность. Теорема синусов Треугольник, вписанный в окружность. Теорема синусов | ||
| Серединный перпендикуляр к отрезку | ||
| Окружность описанная около треугольника | ||
| Свойства описанной около треугольника окружности. Теорема синусов | ||
| Доказательства теорем о свойствах описанной около треугольника окружности | ||
| Формулы для стороны, периметра и площади правильного треугольника | ||
| Площадь треугольника | ||
| Формулы для площади треугольника | ||
| Вывод формул для площади произвольного треугольника | ||
| Вывод формул для площади равностороннего (правильного) треугольника | ||
| Вывод формул для площади прямоугольного треугольника | ||
| Вывод формулы Герона для площади треугольника | ||
 Основное свойство биссектрисы угла Основное свойство биссектрисы угла | ||
| Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла | ||
| Формулы для радиуса окружности, вписанной в треугольник | ||
| Вывод формул для радиуса окружности, вписанной в треугольник | ||
| Вневписанные окружности | ||
Четырехугольники | ||
| Четырехугольники | ||
| Типы четырехугольников | ||
| Типы параллелограмов | ||
| Типы трапеций | ||
| Параллелограммы | ||
| Свойства и признаки параллелограмма | ||
| Свойства и признаки прямоугольника | ||
| Свойства и признаки ромба | ||
| Свойства и признаки квадрата | ||
| Трапеции | ||
| Основные определения и свойства трапеций | ||
| Свойства и признаки равнобедренных трапеций | ||
Четырехугольники, вписанные в окружность. Теорема Птолемея Теорема Птолемея | ||
| Вписанные четырехугольники и их свойства | ||
| Теорема Птолемея | ||
| Описанные четырехугольники | ||
| Средние линии четырехугольников | ||
| Средняя линия трапеции | ||
| Средние линии четырехугольников. Теорема Вариньона | ||
| Формулы для стороны, периметра и площади квадрата | ||
| Площади четырехугольников | ||
| Формулы для площадей четырехугольников | ||
| Вывод формул для площадей четырехугольников | ||
| Вывод формулы Брахмагупты для площади вписанного четырехугольника | ||
Многоугольники | ||
| Многоугольники | ||
| Определение многоугольника | ||
| Диагонали n – угольника | ||
| Внешний угол многоугольника | ||
| Свойства углов треугольника | ||
| Свойства углов многоугольника | ||
| Свойства углов правильного n – угольника | ||
| Доказательства теорем о свойствах углов многоугольника | ||
| Правильные многоугольники | ||
| Формулы для стороны, периметра и площади правильного n – угольника | ||
| Формулы для стороны, периметра и площади правильного треугольника | ||
| Формулы для стороны, периметра и площади правильного шестиугольника | ||
| Формулы для стороны, периметра и площади квадрата | ||
Окружность и круг | ||
| Углы, связанные с окружностью | ||
| Вписанные и центральные углы | ||
| Углы, образованные хордами, касательными и секущими | ||
| Доказательства теорем об углах, связанных с окружностью | ||
Отрезки и прямые, связанные с окружностью. Теорема о бабочке Теорема о бабочке | ||
| Отрезки и прямые, связанные с окружностью | ||
| Свойства хорд и дуг окружности | ||
| Теоремы о длинах хорд, касательных и секущих | ||
| Доказательства теорем о длинах хорд, касательных и секущих | ||
| Теорема о бабочке | ||
| Две окружности на плоскости. Общие касательные к двум окружностям | ||
| Взаимное расположение двух окружностей | ||
| Общие касательные к двум окружностям | ||
| Формулы для длин общих касательных и общей хорды | ||
| Доказательства формул для длин общих касательных и общей хорды | ||
| Длина окружности и ее дуг. Площадь круга и его частей | ||
| Основные определения и свойства. Число π | ||
| Формулы для площади круга | ||
| Формулы для длины окружности и ее дуг | ||
| Площадь круга | ||
| Длина окружности | ||
| Длина дуги | ||
| Площадь сектора | ||
| Площадь сегмента | ||
Окружность, описанная около треугольника.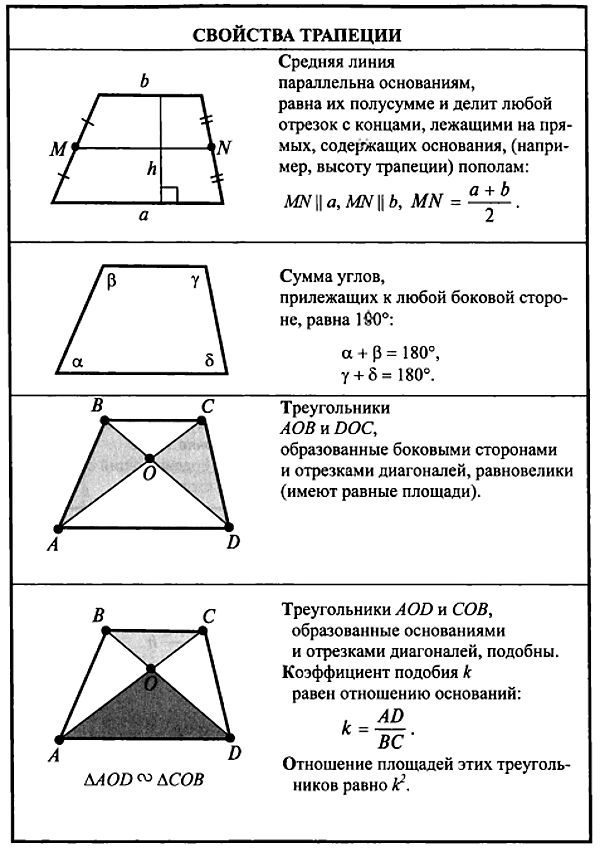 Треугольник, вписанный в окружность. Теорема синусов Треугольник, вписанный в окружность. Теорема синусов | ||
| Серединный перпендикуляр к отрезку | ||
| Окружность описанная около треугольника | ||
| Свойства описанной около треугольника окружности. Теорема синусов | ||
| Доказательства теорем о свойствах описанной около треугольника окружности | ||
| Окружность, вписанная в треугольник. Основное свойство биссектрисы угла | ||
| Существование окружности, вписанной в треугольник | ||
| Формулы для радиуса окружности, вписанной в треугольник | ||
| Вывод формул для радиуса окружности, вписанной в треугольник | ||
| Вневписанные окружности | ||
| Четырехугольники, вписанные в окружность. Теорема Птолемея | ||
| Вписанные четырехугольники и их свойства | ||
| Теорема Птолемея | ||
| Вывод формулы Брахмагупты для площади вписанного четырехугольника | ||
| Описанные четырехугольники | ||
Площади | ||
| Площади четырехугольников | ||
| Формулы для площадей четырехугольников | ||
| Вывод формул для площадей четырехугольников | ||
| Площадь треугольника | ||
| Формулы для площади треугольника | ||
| Вывод формул для площади произвольного треугольника | ||
| Вывод формул для площади равностороннего (правильного) треугольника | ||
| Вывод формул для площади прямоугольного треугольника | ||
| Вывод формул Герона и Брахмагупты | ||
| Вывод формулы Герона для площади треугольника | ||
| Вывод формулы Брахмагупты для площади вписанного четырехугольника | ||
Средние линии | ||
| Средние линии | ||
| Средние линии треугольника | ||
| Средняя линия трапеции | ||
Средние линии четырехугольников.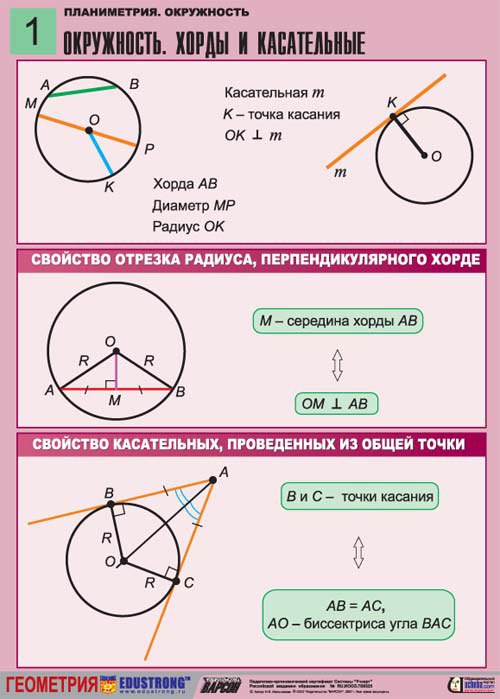 Теорема Вариньона Теорема Вариньона | ||
| Средние линии тетраэдра | ||
Геометрические места точек на плоскости | ||
| Геометрические места точек на плоскости | ||
Преобразования плоскости | ||
| Движения плоскости. Теорема Шаля. Афинные преобразования плоскости | ||
| Преобразования плоскости | ||
| Движения плоскости | ||
| Теорема Шаля | ||
| Афинные преобразования плоскости | ||
| Классификация афинных преобразований плоскости | ||
С демонстрационными вариантами ЕГЭ и ОГЭ, опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.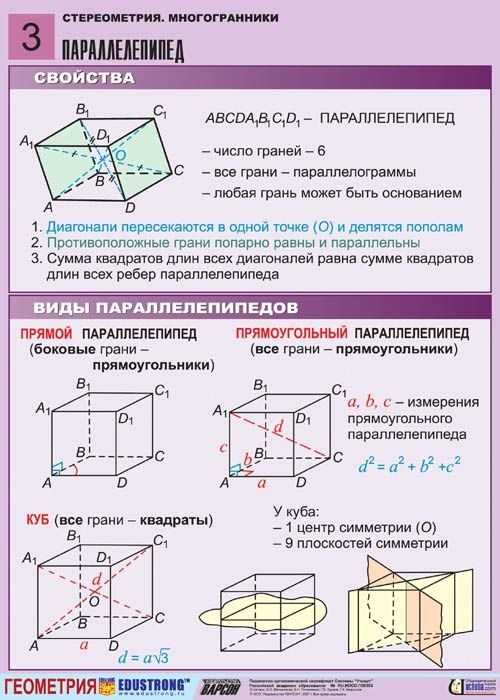
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
|
Заметки по изучению геометрии: треугольники, линии и углы
В этой статье мы приводим важные факты, связанные с геометрией. Прочтите подробную статью, чтобы получить дополнительную информацию о примечаниях к изучению геометрии.
Автор:Amit Pundir
Последнее обновление: 24 сентября 2022 г., 14:02
Оставить комментарий к заметкам об изучении геометрии, треугольникам, линиям и углам
Table of Contents
Математика является одним из самых важных предметов, сдаваемых на государственных экзаменах. Как правило, задаются вопросы, связанные с основными понятиями и формулами тригонометрии. Чтобы вы могли максимально использовать раздел математики, , мы предоставляем важные факты, связанные с геометрией. Кроме того, RRB NTPC, CGL и государственные экзамены находятся рядом с кучей должностей для заинтересованных кандидатов, в которых математика является основной частью. Мы рассмотрели важные примечания и вопросы, касающиеся этих престижных экзаменов. Желаем вам удачи в преодолении страха перед математическим отделением.
Как правило, задаются вопросы, связанные с основными понятиями и формулами тригонометрии. Чтобы вы могли максимально использовать раздел математики, , мы предоставляем важные факты, связанные с геометрией. Кроме того, RRB NTPC, CGL и государственные экзамены находятся рядом с кучей должностей для заинтересованных кандидатов, в которых математика является основной частью. Мы рассмотрели важные примечания и вопросы, касающиеся этих престижных экзаменов. Желаем вам удачи в преодолении страха перед математическим отделением.
- Заметки о времени и работе: краткие советы по решению вопросов
- Формула простых процентов, концепция и примечания к исследованию
Основные понятия геометрии
- Точка : Это точное местоположение. Это тонкая точка, которая не имеет ни длины, ни ширины, ни толщины, но имеет положение, т. е. не имеет величины.
- Отрезок: Прямой путь, соединяющий две точки A и B, называется отрезком AB.
 Он имеет точки и определенную длину.
Он имеет точки и определенную длину. - Луч : Отрезок линии, который можно продолжить только в одном направлении, называется лучом .
- Пересекающиеся прямые: Две прямые, имеющие общую точку, называются пересекающимися прямыми. Общая точка называется точкой пересечения.
- Параллельные линии: Если две или более линий пересекаются в одной и той же точке, они называются параллельными линиями.
- Углы: Когда две прямые пересекаются в одной точке, они образуют угол.
- Прямой угол: Угол, градусная мера которого равна 90°, называется прямым углом.
- Острый угол: Угол, градусная мера которого меньше одного прямого угла (т. е. меньше 90°), называется острым углом.
- Тупой угол: Угол, градусная мера которого больше одного прямого угла и меньше двух прямых углов (т. е. меньше 180° и больше 90°), называется тупым углом.

- Угол рефлекса: Угол, величина которого больше 180° и меньше 360°, называется углом рефлекса.
- Дополнительные углы: Если сумма двух углов составляет один прямой угол (т. е. 90°), они называются дополнительными углами. Следовательно, дополнение угла θ равно 90° – θ.
- Дополнительные углы: Два угла называются дополнительными, если сумма их мер равна 180°. Пример: Углы, равные 130° и 50°, являются дополнительными углами. Два дополнительных угла дополняют друг друга. Следовательно, дополнение угла θ. равен 180° – θ.
- Вертикально противоположные углы: Когда две прямые пересекаются друг с другом в точке, образующиеся при этом пары противоположных углов называются вертикально противоположными углами.
- Биссектриса угла: Если луч или прямая, проходящая через вершину этого угла, делит угол на два равных угла, то эта линия называется биссектрисой этого угла.

- Параллельные прямые: Две прямые параллельны, если они лежат в одной плоскости и не пересекаются друг с другом, даже если они продолжены в обе стороны.
- Сечение: Сечение — это линия, которая пересекает (или пересекает) две или более копланарных линий в разных точках.
Треугольники: часть 1
- Центроид делит медиану в отношении 2:1. Центроид – это точка пересечения трех медиан.
- Отношение двух смежных сторон треугольника равно двум частям третьей стороны, которые составляют биссектрису внутреннего угла.
- В равностороннем треугольнике биссектриса внутреннего угла и медиана равны.
- Любые два из четырех треугольников, образованных соединением середины сторон данного треугольника, конгруэнтны.
- Два треугольника имеют одинаковую площадь, если они имеют одинаковое основание и лежат между двумя параллельными прямыми.
- В треугольнике сторона, противолежащая меньшему углу, меньше по сравнению со стороной, противолежащей большему углу.

- Если соответствующие стороны двух треугольников пропорциональны, то соответствующие углы также пропорциональны.
- Если два треугольника подобны, то мы имеем следующие результаты –
Отношение площадей двух треугольников = отношение квадратов соответствующих сторон
Отношение сторон двух треугольников = отношение высот (высот)
= Отношение медиан
= Отношение биссектрисы угла
= Отношение радиусов в радиусе к радиусу окружности
= Отношение периметра
- Некоторые важные термины:
- Ортоцентр → Точка пересечения трех высот.
- Центр → Точка пересечения биссектрис треугольника
- Центр окружности → Точка пересечения серединных перпендикуляров к сторонам.
- Медиана → Линия, соединяющая середину стороны с вершиной, противоположной сторонам
- В прямоугольном треугольнике треугольник с каждой стороны высоты, проведенной из вершины прямого угла к гипотенузе, подобен исходному треугольнику и друг другу тоже.

1 . На приведенном ниже рисунке PQ и RS — две параллельные прямые, а AB — поперечная. AC и BC — биссектрисы углов ∠BAQ и ∠ABS соответственно. Если ∠BAC = 30°, найдите ∠ABC и ∠ACB.
A. 60° и 90°
B. 30° и 120°
C. 60° и 30°
D. 30° и 90°
2. Если дуга 45° окружности A имеет той же длины, что и 60-градусная дуга окружности B, найдите отношение площадей окружности A и окружности B.
A. 16/8
B. 16/9
C. 8/16
D. 9/16
3. На приведенном ниже рисунке прямые AB и DE параллельны. Каково значение ∠CDE?
A. 60°
B. 120°
C. 30°
D. 150°
4. Найдите значение a + b на приведенном ниже рисунке:
A. 60°
4 B . 120°
C. 80°
D. 150°
5. Точки D, E и F делят стороны треугольника ABC в отношении 1:3, 1:4 и 1:1, как показано на рис. фигура. Какую часть площади треугольника ABC составляет площадь треугольника DEF? 92 = 16/9
3(D): Проводим линию CF//DE в точке C, как показано на рисунке ниже.
∠BCF = ∠ABC = 55° ⇒ ∠DCF = 30°.
⇒ CDE = 180° − 30° = 150°.
4.(C) На приведенном выше рисунке ∠CED = 180° − 125° = 55°. ∠ACD — это
внешний угол ΔABC. Следовательно, ∠ACD = a + 45°. В ΔCED a + 45° + 55° + b = 180° ⇒ a + b = 80°
5.(B) Площадь Δ ADE/площадь ΔABC = (1×3)/(4×5)=3/20 ,
Площадь Δ BDF/Площадь ΔABC = (1×1)/(4×2)=1/8,
Площадь Δ CFE/Площадь ΔABC = (4×1)/(5×2)=2/5,
Следовательно, площадь Δ DEF/площадь ΔABC = 1-(3/20+1/8+2/5)=13/40
ОпубликованоAmit Pundir Опубликовано вЗаметки по математике, ЗаметкиМетки: предварительные математические заметки, математические заметкиЗагрузите бесплатный контент прямо сейчас!
Чтобы скачать капсулу General Awareness & Science Capsule в формате PDF, пожалуйста, заполните форму.
Пожалуйста, заполните правильное имя, телефон и адрес электронной почты.
Отправить
Загрузите бесплатный контент прямо сейчас!
Поздравляем!
Общая информация и научная капсула PDF
Загрузите бесплатный контент прямо сейчас!
Мы уже получили ваши данные!
Нажмите «Загрузить», чтобы получить Премиум-контент Adda247 на ваш электронный адрес
Неправильные данные? Заполните форму еще раз здесь.
Популярные сообщения
SSC CHSL
SSC CGL
SSC GD Constable
Последние сообщения
- Набор водителей CISF 2023, подайте заявку онлайн 451 вакансия констебля 24 января 2023 г.
- IB Recruitment 2023, подать заявку онлайн 1675 SA и MTS Posts 24 января 2023 г.
- Приемная карточка CISF 2023 вышла, скачать прямую ссылку констебля ASI 24 января 2023 г.
- SSC GD Admit Card 2023 для всех регионов, прямая ссылка для скачивания, билет в зал 24 января 2023 г.
- Карта допуска SSC CPO PET 2023, ссылка на карту допуска
24 января 2023 г.

- Научный ассистент SSC IMD за предыдущий год PDF с решениями 24 января 2023 г.
- Подать заявку онлайн UP BC Sakhi Recruitment 2023 24 января 2023 г.
- SSC MTS Recruitment, Уведомление 2023 Out, 12523 Вакансия 24 января 2023 г.
РСК МТС
РРБ НТПК
AFCAT
- AFCAT 2023
Справка по геометрии, примечания и уравнения | CourseNotes
You are here
Home » Class Notes » Math
Версия для печати
Геометрия — это раздел математики, который, как следует из названия, сочетает абстрактную алгебру, особенно коммутативную алгебру, с геометрией. Его можно рассматривать как изучение множеств решений систем многочленов. Когда имеется более одной переменной, вступают геометрические соображения, которые важны для понимания явления. Можно сказать, что предмет начинается там, где заканчивается решение уравнений, и становится не менее важным понять совокупность решений системы уравнений, чем найти какое-то решение; это действительно ведет к одним из самых глубоких вод во всей математике, как с концептуальной, так и с точки зрения техники.
Математику должен знать каждый хороший ученик, но геометрию не все изучают регулярно. Однако существует несколько стандартизированных тестов, которые могут потребовать от учащихся достаточного знания геометрии. Существует также несколько тестов, созданных различными учебными заведениями, таких как ACT и SAT, которые могут проверить способность учащегося мыслить быстро и эффективно. Колледжи обычно смотрят на эти баллы, чтобы определить, каких студентов они хотят видеть в своих студенческих кругах. Поскольку старшая школа — это очень важный шаг на пути к поступлению в колледж, очень важно изучать вещи, которые больше всего помогут вам, например, геометрию.
Подготовка к экзаменам
Поскольку существует так много стандартизированных тестов, которые требуют от вас хорошего знания математики, включая геометрию, важно знать свой предмет. Однако важно не только знать геометрию, но и очень важно сделать все возможное, чтобы подготовиться к тесту другими способами. Поскольку тесты обычно рассчитаны по времени, очень важно научиться готовиться к тестам, прежде чем приступать к ним. Вот несколько советов, которые помогут вам начать:
Поскольку тесты обычно рассчитаны по времени, очень важно научиться готовиться к тестам, прежде чем приступать к ним. Вот несколько советов, которые помогут вам начать:
- Первое, что вы должны сделать, когда готовитесь к тесту, — это убедиться, что вы знаете, чего ожидать, когда впервые пойдете на тест. Это тест на время? Если да, то сколько времени у вас будет? Разделы есть или это только тест по геометрии? Большинство тестов, которые будут рассматривать колледжи, такие как SAT и ACT, будут рассчитаны по времени. Для временных тестов лучшее, что вы можете сделать, — это попрактиковаться, чтобы убедиться, что вы можете решать задачи достаточно быстро. Чем больше вы что-то делаете, тем легче вам пройти через процесс выполнения этого. Чем больше вы практикуете геометрические задачи, тем быстрее вы научитесь их решать.
- Убедитесь, что вы практикуете все, что может быть на вашем тесте. На контрольной по геометрии может появиться множество вещей, поэтому обязательно ознакомьтесь со всем, что может быть на ней.
 Вы никогда не знаете, что может быть на тесте, поэтому вы должны убедиться, что вы охватили все свои базы и знаете все, что может быть на нем. Убедитесь, что вы можете найти высоту, ширину, окружность и т. д. Проведите небольшое исследование и ознакомьтесь с видами геометрии, которые могут содержать тесты для поступления в колледж, а затем найдите соответствующие книги и попрактикуйтесь.
Вы никогда не знаете, что может быть на тесте, поэтому вы должны убедиться, что вы охватили все свои базы и знаете все, что может быть на нем. Убедитесь, что вы можете найти высоту, ширину, окружность и т. д. Проведите небольшое исследование и ознакомьтесь с видами геометрии, которые могут содержать тесты для поступления в колледж, а затем найдите соответствующие книги и попрактикуйтесь. - Обязательно выспитесь в ночь перед тестом. Если вы устали, ваш мозг вряд ли будет работать так быстро, а скорость жизненно важна, когда речь идет о тестах на время. Кроме того, не забудьте хорошо поужинать накануне теста и хорошо позавтракать в день теста. Если вы голодны, ваши мысли вряд ли будут заняты проблемами, над которыми вы пытаетесь справиться; это, вероятно, будет на вашем урчащем желудке.
- Если вы проходите стандартизированный тест, который прошли многие люди, пройдите тренировочные тесты, которые познакомят вас с материалом и типами вопросов по геометрии, которые будут в тесте.
 Зачем вам идти на холодную индейку, когда вы можете точно знать, чего ожидать, еще до того, как откроете свой тестовый пакет? Для таких тестов, как ACT и SAT, существуют тренировочные тесты, специально разработанные для того, чтобы подготовить вас к реальному тесту. Глупо не воспользоваться такими тренировочными тестами, потому что чем больше вы будете с ними практиковаться, тем больше вы будете знать, когда действительно пойдете сдавать тест.
Зачем вам идти на холодную индейку, когда вы можете точно знать, чего ожидать, еще до того, как откроете свой тестовый пакет? Для таких тестов, как ACT и SAT, существуют тренировочные тесты, специально разработанные для того, чтобы подготовить вас к реальному тесту. Глупо не воспользоваться такими тренировочными тестами, потому что чем больше вы будете с ними практиковаться, тем больше вы будете знать, когда действительно пойдете сдавать тест. - Когда вы начнете сдавать тест, обратите внимание на то, сколько времени у вас есть. Если есть проблема, которую вы не можете решить, пропустите ее и перейдите к следующей. Не тратьте слишком много времени на какую-то одну проблему; вы можете потратить свое время и в конечном итоге либо оставить это поле пустым, либо угадать. Если вы не знаете ответа, вернитесь к нему в конце, если у вас есть время. Вы можете либо пропустить один вопрос, либо не решить половину задач теста.
- Это может показаться таким простым советом, но обязательно внимательно прочитайте каждый вопрос.
 Иногда создателям тестов нравится обманывать учащихся; вы можете легко не попасться на удочку, внимательно читая вопросы. Кроме того, убедитесь, что вы прочитали инструкции, чтобы убедиться, что вы решаете задачи правильно. Не хочется возвращаться и что-то исправлять.
Иногда создателям тестов нравится обманывать учащихся; вы можете легко не попасться на удочку, внимательно читая вопросы. Кроме того, убедитесь, что вы прочитали инструкции, чтобы убедиться, что вы решаете задачи правильно. Не хочется возвращаться и что-то исправлять. - Убедитесь, что вы знакомы со всеми материалами, которые вам разрешено использовать в тесте. Иногда калькуляторы не допускаются на экзаменах по геометрии, но обязательно ознакомьтесь с вашим калькулятором, если они разрешены. Не тратьте время во время теста на то, что вы могли бы сделать до того, как вошли в тест.
Что нужно знать о геометрии?
Когда вы идете на тест, иногда это немного сложнее, чем просто знать материал, по которому, по словам учителя, вы будете тестироваться. Когда вы проходите стандартизированные тесты, вы не всегда можете быть уверены, какие уравнения вам придется решать. Вот несколько вещей, которые вы, возможно, захотите узнать:
- Убедитесь, что вы делаете свою домашнюю работу каждый вечер.
 Большинство учителей дают тесты, очень похожие на домашнее задание. Домашняя работа может показаться повторяющейся и отнимающей много времени, но легче всего научиться чему-то, когда вы вынуждены делать это снова и снова. Большинство учителей будут основывать свои тесты на том, что вы уже практиковали заранее.
Большинство учителей дают тесты, очень похожие на домашнее задание. Домашняя работа может показаться повторяющейся и отнимающей много времени, но легче всего научиться чему-то, когда вы вынуждены делать это снова и снова. Большинство учителей будут основывать свои тесты на том, что вы уже практиковали заранее. - Для стандартизированных тестов убедитесь, что вы ищете именно то, что вы должны знать. Возможно, вам не удастся найти настоящие вопросы, но вы сможете найти практические вопросы, основанные на тех же принципах и уравнениях.
Темы на сайте:
Тема:
Геометрия
Тема X2:
Геометрия
Основы геометрии ›
Нужна помощь?
Мы надеемся, что ваш визит был продуктивным. Если у вас возникли проблемы или вы хотите оставить отзыв, мы будем рады услышать от вас.
Для получения общей помощи, вопросов и предложений посетите наши специализированные форумы поддержки.
Если вам нужно связаться с командой веб-опыта Course-Notes.


 Он имеет точки и определенную длину.
Он имеет точки и определенную длину.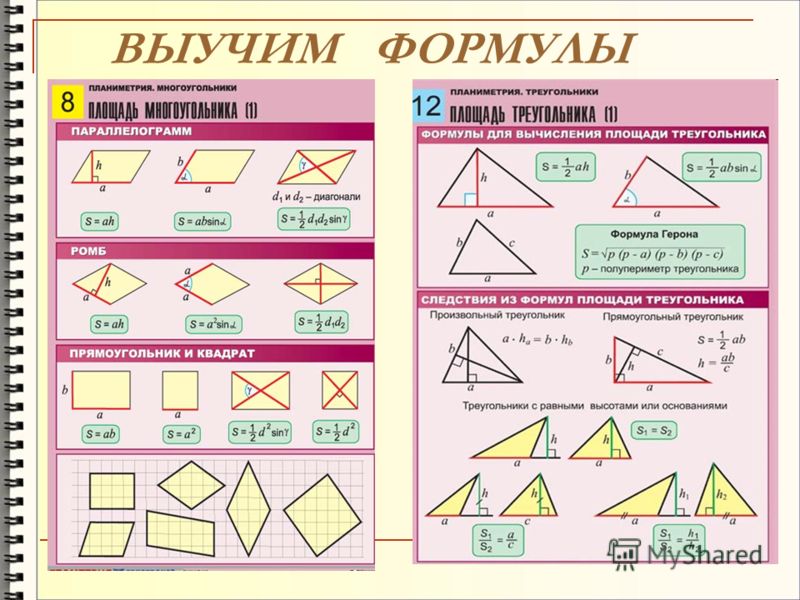


 Вы никогда не знаете, что может быть на тесте, поэтому вы должны убедиться, что вы охватили все свои базы и знаете все, что может быть на нем. Убедитесь, что вы можете найти высоту, ширину, окружность и т. д. Проведите небольшое исследование и ознакомьтесь с видами геометрии, которые могут содержать тесты для поступления в колледж, а затем найдите соответствующие книги и попрактикуйтесь.
Вы никогда не знаете, что может быть на тесте, поэтому вы должны убедиться, что вы охватили все свои базы и знаете все, что может быть на нем. Убедитесь, что вы можете найти высоту, ширину, окружность и т. д. Проведите небольшое исследование и ознакомьтесь с видами геометрии, которые могут содержать тесты для поступления в колледж, а затем найдите соответствующие книги и попрактикуйтесь. Зачем вам идти на холодную индейку, когда вы можете точно знать, чего ожидать, еще до того, как откроете свой тестовый пакет? Для таких тестов, как ACT и SAT, существуют тренировочные тесты, специально разработанные для того, чтобы подготовить вас к реальному тесту. Глупо не воспользоваться такими тренировочными тестами, потому что чем больше вы будете с ними практиковаться, тем больше вы будете знать, когда действительно пойдете сдавать тест.
Зачем вам идти на холодную индейку, когда вы можете точно знать, чего ожидать, еще до того, как откроете свой тестовый пакет? Для таких тестов, как ACT и SAT, существуют тренировочные тесты, специально разработанные для того, чтобы подготовить вас к реальному тесту. Глупо не воспользоваться такими тренировочными тестами, потому что чем больше вы будете с ними практиковаться, тем больше вы будете знать, когда действительно пойдете сдавать тест. Иногда создателям тестов нравится обманывать учащихся; вы можете легко не попасться на удочку, внимательно читая вопросы. Кроме того, убедитесь, что вы прочитали инструкции, чтобы убедиться, что вы решаете задачи правильно. Не хочется возвращаться и что-то исправлять.
Иногда создателям тестов нравится обманывать учащихся; вы можете легко не попасться на удочку, внимательно читая вопросы. Кроме того, убедитесь, что вы прочитали инструкции, чтобы убедиться, что вы решаете задачи правильно. Не хочется возвращаться и что-то исправлять. Большинство учителей дают тесты, очень похожие на домашнее задание. Домашняя работа может показаться повторяющейся и отнимающей много времени, но легче всего научиться чему-то, когда вы вынуждены делать это снова и снова. Большинство учителей будут основывать свои тесты на том, что вы уже практиковали заранее.
Большинство учителей дают тесты, очень похожие на домашнее задание. Домашняя работа может показаться повторяющейся и отнимающей много времени, но легче всего научиться чему-то, когда вы вынуждены делать это снова и снова. Большинство учителей будут основывать свои тесты на том, что вы уже практиковали заранее.