Свойства биссектрисы параллелограмма: Параллелограмм – свойства, признаки, определение
Параллелограмм – свойства, признаки, определение
Научим решать сложные задачи о параллелограммах
Начать учиться
425.6K
Геометрические фигуры изучают не только восьмиклассники и технари, но и представители творческих специальностей. Нестандартные четырехугольные формы можно встретить как в дизайне обуви, так и в современных зданиях. В этой статье расскажем о параллелограмме и его отличительных особенностях.
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны и равны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
- В параллелограмме точка пересечения диагоналей делит их пополам.

- Любая диагональ параллелограмма делит его на два равных треугольника.
- Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.
Биссектриса угла параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
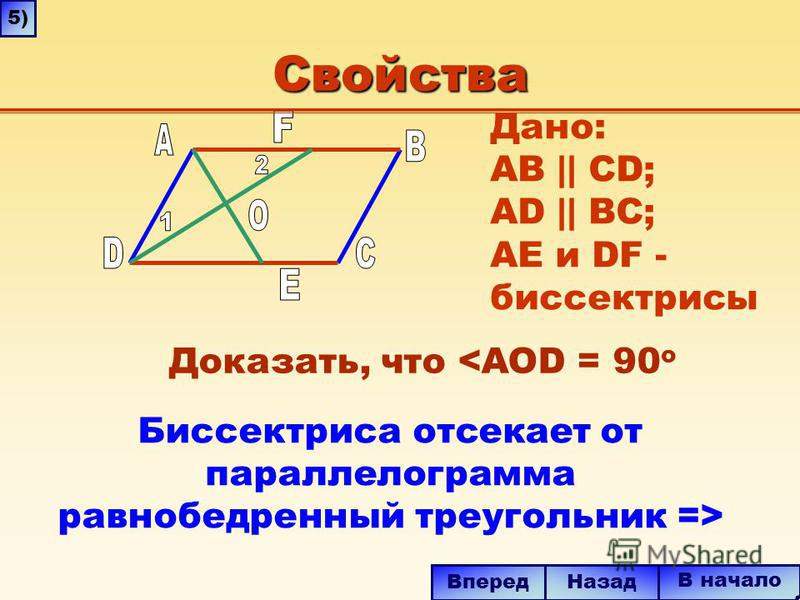
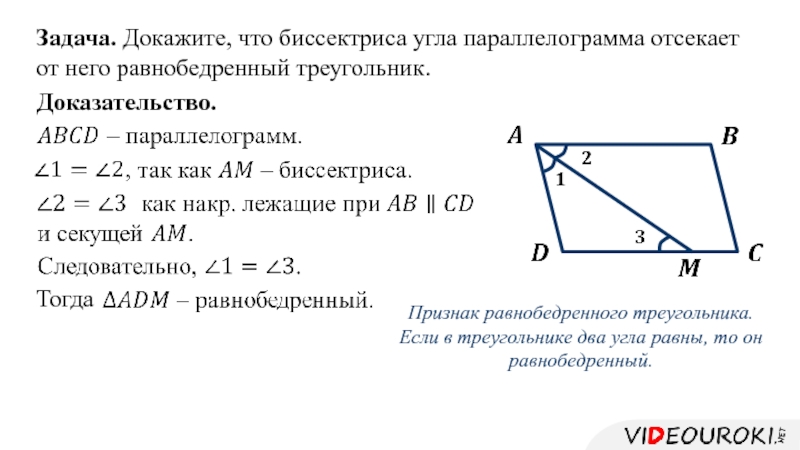
- Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
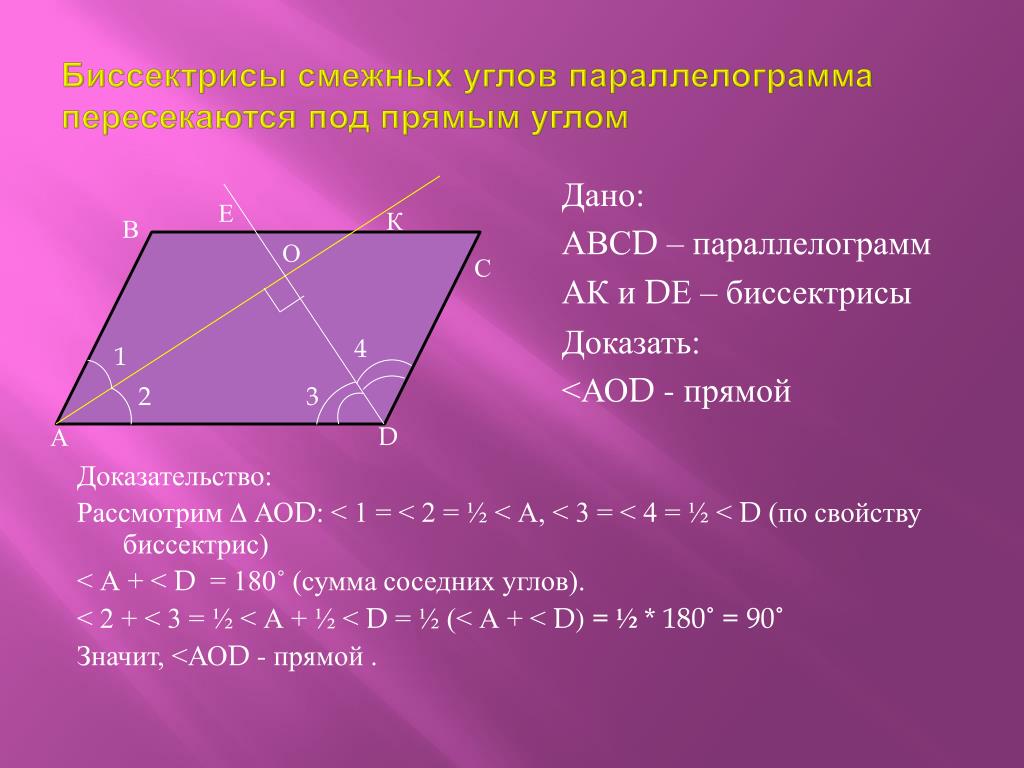
- Биссектрисы углов, прилежащих к одной стороне параллелограмма пересекаются под прямым углом.
- Отрезки биссектрис противоположных углов равны и параллельны.
Как найти площадь параллелограмма:
- S = a × h, где a — сторона, h — высота.

- S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. Для ромба формула примет вид S = a2 × sinα.
- Для ромба: S = 0,5 × (d1 × d2), где d1 и d2 — две диагонали.
Для параллелограмма: S = 0,5 × (d1 × d2) × sinβ, где β — угол между диагоналями.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
- Противоположные стороны параллелограмма равны.
ABCD — параллелограмм, значит, AB = DC, BC = AD. - Противоположные углы параллелограмма равны.
ABCD — параллелограмм, значит, ∠A = ∠C, ∠B = ∠D. - Диагонали параллелограмма точкой пересечения делятся пополам.
ABCD — параллелограмм, AC и BD — диагонали, AC∩BD=O, значит, BO = OD, AO = OC. - Диагональ делит параллелограмм на два равных треугольника.
ABCD — параллелограмм, AC — диагональ, значит, △ABC = △CDA. - Сумма углов в параллелограмме, прилежащих к одной стороне, равна 180 градусам.
ABCD — параллелограмм, значит, ∠A + ∠D = 180°. - В параллелограмме диагонали d1, d2 и стороны a, b связаны следующим соотношением: d12 + d22 = 2 × (a2 + b2 ).

А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
- AB = CD как противоположные стороны параллелограмма.
- ∠1 = ∠2 как накрест лежащие углы при пересечении секущей AC параллельных прямых AB и CD; ∠3 = ∠4 как накрест лежащие углы при пересечении секущей BD параллельных прямых AB и CD.
- Следовательно, треугольник AOB равен треугольнику COD по второму признаку равенства треугольников, то есть по стороне и прилежащим к ней углам, из чего следует:
- CO = AO
- BO = DO
Теорема доказана. Наше предположение верно.
Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
- AB || CD
- AB = CD
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
- AC — общая сторона;
- По условию AB = CD;
- ∠1 = ∠2 как внутренние накрест лежащие углы при пересечении параллельных прямых AB и CD секущей АС.

Шаг 3. Из равенства треугольников также следует:
- ∠3 = ∠4
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
- AB = CD
- BC = AD
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:
- AC — общая сторона;
- AB = CD по условию;
- BC = AD по условию.

Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
- ∠ DCA = ∠BAC
А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
- ∠DAC = ∠BCA
Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Третий признак параллелограмма.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
- CO = OA;
- DO = BO;
- углы между ними равны, как вертикальные, то есть угол AOB равен углу COD.

Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
416.7K
Натуральные числа
К следующей статье
305. 5K
5K
Обыкновенные дроби
Получите план обучения, который поможет понять и полюбить геометрию
ПремиумНа вводном уроке с методистом
Проверим знание геометрии и других разделов математики, выявим пробелы
Подберём курс
Познакомим с интерактивной платформой
Свойства биссектрис параллелограмма (геометрия, 8-й класс)
Разделы: Математика, Мастер-класс
Класс: 8
Цель: доказать свойства биссектрис параллелограмма и рассмотреть их применение к решению задач.
Презентация к уроку
I. Повторение (устно)1. Сформулируйте определение параллелограмма.
2. Сформулируйте свойства параллелограмма.
3. Сформулируйте признаки параллелограмма.
4. Сформулируйте свойства параллельных прямых.
5. Решите задачу:
Дано: a || b , МЕ – секущая, МО и ЕО – биссектрисы. Найти: MOE.
6. Решите задачу:
Дано: ABCD – параллелограмм, AK – биссектриса, AKB = 15o. Найти: BAD.
II. Изучение нового материалаУчащиеся самостоятельно по парам решают задачи на доказательство (3-5 мин) с последующей проверкой на доске и формулируют свойства биссектрис параллелограмма (каждый ряд решает по одной задаче). Оформление доказательств к задачам записывает учитель на доске под диктовку учеников.
Задача № 1. Биссектриса угла параллелограмма пересекает противоположную сторону. Определите вид полученного треугольника.
Биссектриса угла параллелограмма пересекает противоположную сторону. Определите вид полученного треугольника.
Задача № 2. Найдите угол образованный биссектрисами углов параллелограмма, прилежащих к одной стороне.
Задача № 3. Определите взаимное расположение прямых на которых лежат биссектрисы противоположных углов.
Свойства биссектрис параллелограмма:
1). Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
2). Биссектрисы углов параллелограмма, прилежащих к одной стороне, перпендикулярны.
3). Биссектрисы противоположных углов параллелограмма параллельны или лежат на одной прямой.
III. Закрепление изученного материала Учащиеся решают задачи на применение свойств биссектрис параллелограмма. (Тексты задач и чертежи к ним выдаются каждому ученику.) Оформление решений к задачам записывают ученики на доске.
- Биссектрисы углов А и B параллелограмма ABCD пересекаются в точке K. Найдите длину BK, если B = 120o, AB = 19 см.
- Биссектрисы углов А и D параллелограмма ABCD пересекаются в точке, лежащей на стороне ВС. Найдите периметр параллелограмма, если ВС = 34 см.
- Впараллелограмме ABCD биссектрисы углов В и D пересекают диагональ АС в точках К и Р соответственно. Доказать, что четырёхугольник BРDК — параллелограмм.
- Докажите, что при пересечении биссектрис параллелограмма образуется прямоугольник.
Конспект (свойства биссектрис параллелограмма), задачи:
1. Дано: TPLK – параллелограмм, РТ = РL, TF – биссектриса LTK, TFL= 120o. Найти углы параллелограмма.
Найти углы параллелограмма.
2. Дано: ABCD – параллелограмм, AM – биссектриса BAD, AM : MC = 5 : 3, POBC > POCD на 6 см. Найти стороны и периметр параллелограмма.
Приложения к уроку. Раздаточный материал.
СВОЙСТВА БИССЕКТРИС ПАРАЛЛЕЛОГРАММАЗадача № 1. Биссектриса угла параллелограмма пересекает противоположную сторону. Определите вид полученного треугольника.
Свойство 1.
Задача № 2.Найдите угол образованный биссектрисами углов параллелограмма, прилежащих к одной стороне.
Свойство 2.
Задача № 3.Определите взаимное расположение прямых на которых лежат биссектрисы противоположных углов.
Свойство 3.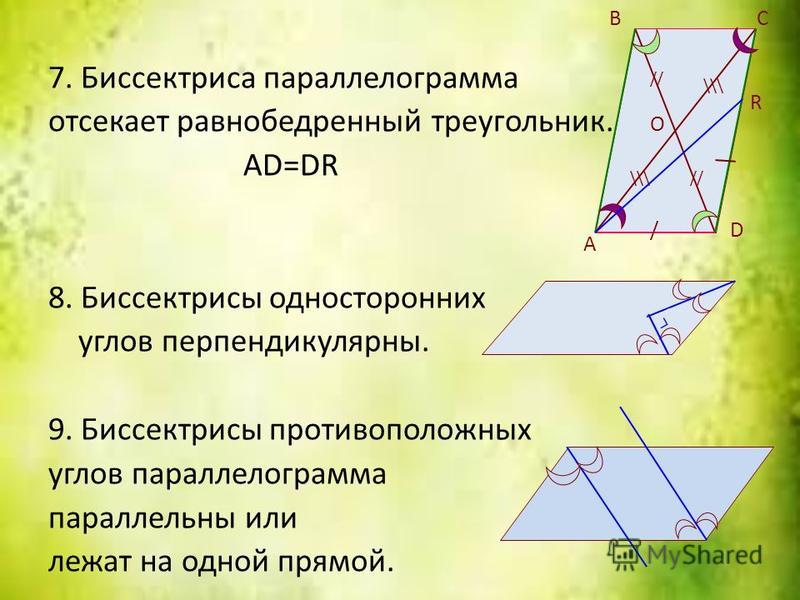
ПРИМЕНЕНИЕ СВОЙСТВ БИССЕКТРИС ПАРАЛЛЕЛОГРАММА
Биссектрисы углов А и B параллелограмма ABCD пересекаются в точке K. Найдите длину BK, если B, AB = 19 см.
Биссектрисы углов А и D параллелограмма ABCD пересекаются в точке, лежащей на стороне ВС. Найдите периметр параллелограмма, если ВС = 34 см.
Впараллелограмме ABCD биссектрисы углов В и D пересекают диагональ АС в точках К и Р соответственно. Доказать, что четырёхугольник BРDК — параллелограмм.
Докажите, что при пересечении биссектрис параллелограмма образуется прямоугольник.
V. Домашнее задание.Конспект (свойства биссектрис параллелограмма), задачи:
3. Дано: TPLK – параллелограмм, РТ = РL, TF – биссектриса LTK, TFL= 120o. Найти углы параллелограмма.
Найти углы параллелограмма.
4. Дано: ABCD – параллелограмм, AM – биссектриса BAD, AM : MC = 5 : 3, POBC > POCD на 6 см. Найти стороны и периметр параллелограмма.
Свойства параллелограмма — теоремы, доказательства, примеры
свойства параллелограмма помогают нам легко и быстро идентифицировать параллелограмм из заданного набора фигур. Прежде чем мы узнаем о свойствах, давайте сначала узнаем о параллелограммах. Это четырехсторонняя замкнутая фигура с равными и параллельными противоположными сторонами и равными противоположными углами. Давайте узнаем больше о свойствах параллелограммов подробно в этой статье.
1. | Каковы свойства параллелограмма? |
| 2. | Свойства диагоналей параллелограмма |
| 3. | Теоремы о свойствах параллелограмма |
| 4. | Часто задаваемые вопросы о свойствах параллелограмма |
Каковы свойства параллелограмма?
Параллелограмм — это тип четырехугольника, в котором противоположные стороны параллельны и равны. В параллелограмме при вершинах четыре угла. Понимание свойств параллелограмма помогает легко связать его углы и стороны. Кроме того, свойства полезны для вычислений в задачах, касающихся сторон и углов параллелограмма.
Свойства углов параллелограмма
Важными свойствами параллелограммов, связанными с углами, являются следующие:
- Противоположные углы параллелограмма равны, т. е. ∠A = ∠C и ∠B = ∠D.
- Сумма всех углов параллелограмма составляет 360°, т. е. ∠A + ∠B + ∠C + ∠D = 360°.
- Последовательные углы параллелограмма являются дополнительными, т.
 е.
е.
∠А + ∠В = 180°
∠В + ∠С = 180°
∠С + ∠D = 180°
∠D + ∠А = 180°
Свойства сторон параллелограмма
Противоположные стороны параллелограмма равны и параллельны друг другу.
Обратите внимание на следующий рисунок, чтобы понять свойства параллелограмма.
Все вышеперечисленные свойства справедливы для всех типов параллелограммов, но теперь давайте также узнаем об индивидуальных свойствах некоторых специальных параллелограммов. Три разных параллелограмма — квадрат, прямоугольник и ромб, которые отличаются друг от друга из-за своих свойств, но все они подпадают под категорию параллелограммов.
Свойства квадрата
- Все четыре стороны квадрата равны.
- Все четыре угла равны и по 90 градусов каждый.
- Диагонали квадрата делят его углы пополам.
- Обе диагонали квадрата имеют одинаковую длину.
- Противоположные стороны квадрата равны и параллельны друг другу.

Свойства прямоугольника
- Противоположные стороны прямоугольника равны и параллельны.
- Все четыре угла прямоугольника равны и равны 90° каждый.
- Обе диагонали прямоугольника имеют одинаковую длину.
Свойства ромба
- Все стороны ромба равны по длине.
- Диагонали ромба пересекаются под углом 90°.
- Сумма любых двух смежных внутренних углов равна 180°.
- Противоположные стороны ромба равны и параллельны друг другу.
Теперь давайте расширим наши знания, изучив свойства диагоналей параллелограммов в следующем разделе.
Свойства диагоналей параллелограмма
Сначала вспомним значение диагонали. Диагонали — это отрезки, соединяющие несмежные вершины любого многоугольника. В параллелограмме ABCD (см. рисунок выше) диагонали AC и BD. Предположим, что O — точка пересечения диагоналей AC и BD. Свойства диагоналей параллелограмма следующие:
- Диагонали параллелограмма делят друг друга пополам, т.
 е. OB = OD и OA = OC.
е. OB = OD и OA = OC. - Каждая диагональ делит параллелограмм на два конгруэнтных треугольника, т. е. ΔCDA ≅ ΔABC и ΔBAD ≅ ΔDCB.
- Parallelogram Law: The sum of the squares of the sides is equal to the sum of the squares of the diagonals, i.e., AB 2 + BC 2 + CD 2 + DA 2 = AC 2 + БД 2
Теоремы о свойствах параллелограмма
Теоремы о свойствах параллелограмма помогают определить правила решения задач на параллелограммы. Свойства, относящиеся к сторонам и углам параллелограмма, легко понять и применить для решения различных задач. Кроме того, эти теоремы также поддерживают понимание концепций других четырехугольников. Ниже приведены четыре важные теоремы, относящиеся к свойствам параллелограмма:
- Противоположные стороны параллелограмма равны.
- Противоположные углы параллелограмма равны.
- Диагонали параллелограмма делятся пополам.

- Если в четырехугольнике одна пара противоположных сторон равна и параллельна, то это параллелограмм.
Теорема 1: В параллелограмме противоположные стороны равны.
Доказательство:
Дано: ABCD — параллелограмм.
Доказать: Противоположные стороны равны, AB = CD и BC = AD.
В параллелограмме ABCD сравните треугольники ABC и CDA. В этих треугольниках:
- AC = CA (общая сторона)
- ∠BAC = ∠DCA (альтернативные внутренние углы)
- ∠BCA = ∠DAC (альтернативные внутренние углы)
Следовательно, по критерию ASA оба треугольника конгруэнтны и соответствующие стороны равны. Следовательно, мы имеем AB = CD и BC = AD.
Обратное к теореме 1: если в четырехугольнике противоположные стороны равны, то это параллелограмм.
Доказательство:
Дано: В четырехугольнике ABCD противоположные стороны равны, AB = CD и BC = AD.
Доказать: ABCD — параллелограмм.
В четырехугольнике ABCD дано, что AB = CD и AD = BC. Теперь сравните два треугольника ABC и CDA. Здесь мы имеем
- AC = AC (общие стороны)
- AB = CD (поскольку внутренние углы равны)
- г. н.э. = до н.э. (дано).
Таким образом, по критерию SSS оба треугольника равны и соответствующие углы равны. Отсюда можно сделать вывод, что ∠BAC = ∠DCA, а ∠BCA = ∠DAC.
Поэтому AB || CD, Британская Колумбия || AD, ABCD — параллелограмм.
Теорема 2. В параллелограмме противоположные углы равны.
Доказательство:
Дано: ABCD — параллелограмм, а ∠A, ∠B, ∠C, ∠D — четыре угла.
Доказать: ∠A = ∠C и ∠B = ∠D
Предположим, что ABCD — параллелограмм. Теперь сравните треугольники ABC и CDA. Здесь у нас есть,
- AC = CA (общая сторона)
- ∠1 = ∠4 (чередующиеся внутренние углы)
- ∠2 = ∠3 (чередующиеся внутренние углы)
Таким образом, согласно ASA, два треугольника конгруэнтны, а это означает, что ∠B = ∠D. Точно так же мы можем показать, что ∠A = ∠C. Это доказывает, что противоположные углы в любом параллелограмме равны.
Точно так же мы можем показать, что ∠A = ∠C. Это доказывает, что противоположные углы в любом параллелограмме равны.
Обратное к теореме 2: Если в четырехугольнике противоположные углы равны, то это параллелограмм.
Доказательство:
Дано: ∠A = ∠C и ∠B = ∠D в четырехугольнике ABCD.
Доказать: ABCD — параллелограмм.
Предположим, что ∠A = ∠C и ∠B = ∠D в приведенном выше параллелограмме ABCD. Нам нужно доказать, что ABCD — параллелограмм. Имеем:
∠A + ∠B + ∠C + ∠D = 360º
2(∠A + ∠B) =360º
∠А + ∠В = 180º.
Это должно означать, что AD || ДО Н.Э. Аналогично можно показать, что AB || CD. Следовательно, АД || до н.э. и АВ || CD. Следовательно, ABCD — параллелограмм.
Теорема 3. Диагонали параллелограмма делят друг друга пополам.
Доказательство:
Дано: PQTR — параллелограмм. PT и QR — диагонали параллелограмма.
PT и QR — диагонали параллелограмма.
Доказать: Диагонали PT и RQ делят друг друга пополам, т. е. PE = ET и ER = EQ.
Во-первых, предположим, что PQTR — параллелограмм. Сравните треугольники TER и треугольник PEQ. Имеем,
- PQ = RT (противоположные стороны параллелограмма PQTR)
- ∠QRT = ∠PQR (альтернативные внутренние углы)
- ∠PTR = ∠QPT (альтернативные внутренние углы).
По критерию ASA два треугольника конгруэнтны, что означает по CPCTC, PE = ET и RE = EQ. Таким образом, две диагонали PT и RQ делят друг друга пополам, а PE = ET и ER = EQ.
Обратное к теореме 3: Если диагонали в четырехугольнике делят друг друга пополам, то это параллелограмм. В четырехугольнике PQTR, если PE=ET и ER=EQ, то это параллелограмм.
Дано: Диагонали PT и QR делят друг друга пополам.
Доказать: PQRT — параллелограмм.
Доказательство: Предположим, что диагонали PT и QR делят друг друга пополам.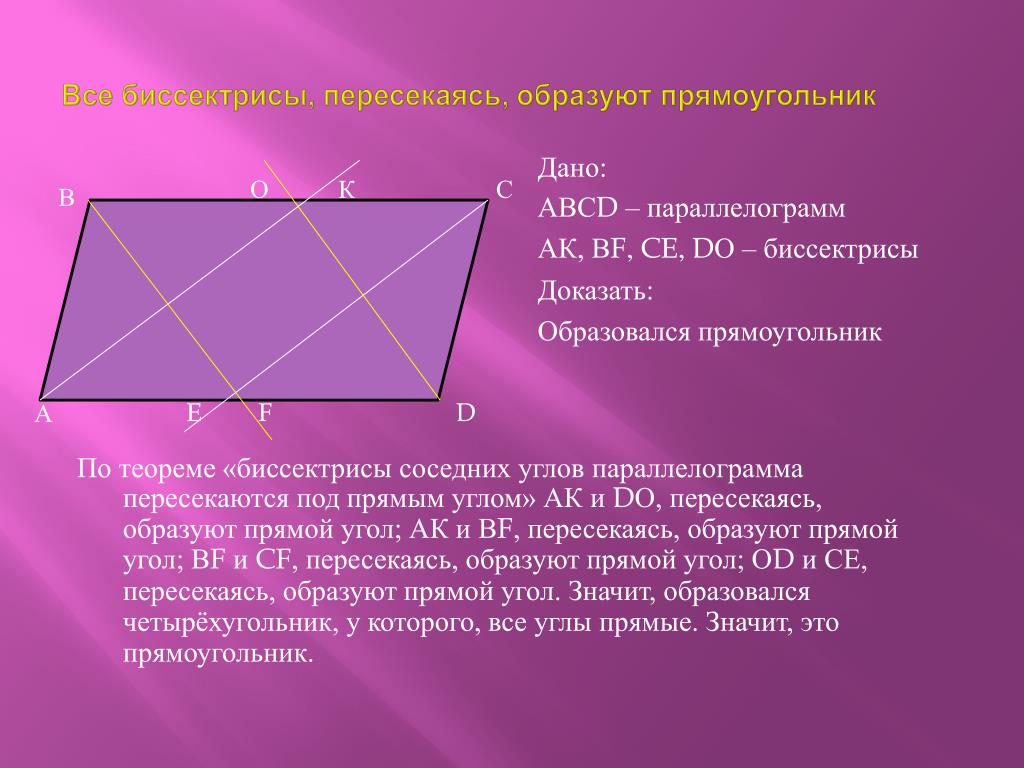 Еще раз сравните треугольник RET и треугольник PEQ. У нас есть:
Еще раз сравните треугольник RET и треугольник PEQ. У нас есть:
- RE = EQ
- ET = PE (диагонали делят друг друга пополам)
- ∠RET =∠PEQ (вертикально противоположные углы).
Следовательно, по критерию SAS два треугольника конгруэнтны. Это означает, что ∠QRT = ∠PQR и ∠PRT = ∠QPT. Следовательно, PQ || РТ и РТ || КТ. Таким образом, PQRT является параллелограммом.
Теорема 4: Если одна пара противоположных сторон равна и параллельна в четырехугольнике, то это параллелограмм.
Доказательство:
Дано: Дано, что AB = CD и AB || CD.
Доказать: ABCD — параллелограмм.
Сравним треугольник AEB и треугольник CED. Имеем,
- AB = CD (дано)
- ∠1 = ∠3 (чередующиеся внутренние углы)
- ∠2 = ∠4 (чередующиеся внутренние углы)
Таким образом, по критерию ASA два треугольника конгруэнтны. Отсюда можно сделать вывод, что по CPCTC AE = EC, а BE = ED. Следовательно, диагонали AC и BD делят друг друга пополам, а это в дальнейшем означает, что ABCD — параллелограмм.
Следовательно, диагонали AC и BD делят друг друга пополам, а это в дальнейшем означает, что ABCD — параллелограмм.
Важные примечания:
Четырехугольник является параллелограммом, если:
- Противоположные стороны четырехугольника равны и параллельны.
- Противоположные углы четырехугольника равны.
- Диагонали делятся пополам.
- Одна пара противоположных сторон равна и параллельна.
☛ Статьи по теме
- Формула параллелограмма
- Площадь параллелограмма
- Свойства прямоугольника
- Разница между прямоугольником и параллелограммом
Часто задаваемые вопросы о свойствах параллелограмма
Каковы 7 свойств параллелограмма?
Семь свойств параллелограмма таковы:
- Противоположные стороны параллелограмма равны.
- Противоположные углы параллелограмма равны.

- Последовательные углы параллелограмма являются дополнительными.
- Если один угол параллелограмма прямой, то все углы прямые.
- Диагонали параллелограмма делятся пополам.
- Каждая диагональ параллелограмма делит его пополам на два равных треугольника.
- Если одна пара противоположных сторон четырехугольника равна и параллельна, то четырехугольник является параллелограммом.
Каковы свойства диагоналей параллелограмма?
Диагонали параллелограмма обладают двумя важными свойствами. Диагональ параллелограмма делит параллелограмм на два равных треугольника. А диагонали параллелограмма делят друг друга пополам.
Диагонали параллелограмма равны?
Диагонали параллелограмма НЕ равны. Противоположные стороны и противоположные углы параллелограмма равны. Диагонали квадрата и прямоугольника равны, что является особым типом параллелограмма.
Запись свойств параллелограмма.
Параллелограмм – это четырехугольник, у которого противоположные стороны равны и параллельны. Противоположные углы параллелограмма также равны. Короче говоря, параллелограмм можно рассматривать как скрученный прямоугольник. Это скорее прямоугольник, но углы при вершинах не обязательно должны быть прямыми. Четыре важных свойства параллелограмма таковы:
Противоположные углы параллелограмма также равны. Короче говоря, параллелограмм можно рассматривать как скрученный прямоугольник. Это скорее прямоугольник, но углы при вершинах не обязательно должны быть прямыми. Четыре важных свойства параллелограмма таковы:
- Противоположные стороны параллелограмма равны.
- Противоположные углы параллелограмма равны.
- Смежные углы параллелограмма дополнительные.
- Диагонали параллелограмма делятся пополам.
Можно ли прямоугольник назвать параллелограммом?
Противоположные стороны прямоугольника равны и параллельны. Таким образом, прямоугольник удовлетворяет всем свойствам параллелограмма, поэтому его можно назвать параллелограммом.
Каковы уникальные свойства параллелограммов?
Уникальные характеристики параллелограмма, отличающие его от других четырехугольников, приведены ниже:
- Противоположные стороны каждого параллелограмма равны и параллельны.
- Противоположные углы всегда равны.

- Сумма последовательных внутренних углов всегда равна 180°.
Каковы различные свойства каждого специального параллелограмма?
Существует три особых типа параллелограммов — квадрат, прямоугольник и ромб. Квадрат – это четырехугольник, у которого все стороны и углы равны. У прямоугольника противоположные стороны равны и параллельны. Все углы квадрата и прямоугольника равны и равны 90° каждый. Ромб — это параллелограмм с четырьмя равными сторонами, но его углы не обязательно должны быть прямыми.
Как отличить параллелограмм от четырехугольника по свойствам параллелограмма?
Каждый параллелограмм можно назвать четырехугольником, но не каждый четырехугольник можно назвать параллелограммом. Трапецию и воздушного змея можно назвать четырехугольниками, но они не полностью удовлетворяют свойствам параллелограмма и, следовательно, не могут быть названы параллелограммом.
Что составляют противоположные углы параллелограмма?
Противоположные углы параллелограмма всегда равны. Однако следует отметить, что сумма последовательных внутренних углов параллелограмма всегда составляет 180°.
Однако следует отметить, что сумма последовательных внутренних углов параллелограмма всегда составляет 180°.
Каковы правила параллелограмма?
Правила параллелограмма — это характеристики параллелограмма, которые отличают его от других многоугольников. Другими словами, это все свойства параллелограмма, которые помогают нам его идентифицировать. Основные характеристики параллелограмма приведены ниже:
- Противоположные стороны параллелограмма равны.
- Противоположные углы параллелограмма равны.
- Последовательные углы параллелограмма являются дополнительными.
- Диагонали параллелограмма делятся пополам.
- Каждая диагональ параллелограмма делит его пополам на два равных треугольника.
Свойства параллелограмма
Свойства параллелограмма перечислены ниже. Мы будем использовать параллелограмм ABCD, чтобы показать эти свойства.
Свойство №1
Противоположные стороны параллелограмма равны.
Длина AB равна длине DC.
Длина BC равна длине AD.
Вот как доказать, что противоположные стороны параллелограмма равны.
Свойство №2
Противоположные углы параллелограмма равны.
Угол A равен углу C
Угол B равен углу D
Как доказать, что противоположные углы параллелограмма равны
Для заданного параллелограмма ABCD нам нужно доказать, что ∠A ≅ ∠C; ∠B ≅ ∠D
1. Даны
ABCD — параллелограмм
2. Смежные углы являются дополнительными углами в параллелограмме ( свойство #4 90 482)
∠А + ∠В = 180 градусов
∠B + ∠C = 180 градусов
3. Свойство переходности в свойствах равенства 1 4. Свойство вычитания в свойствах равенства
∠A + ∠B — ∠B = ∠B — ∠B + ∠C
5. ∠A = ∠C
Используя аналогичные рассуждения, можно показать, что ∠B ≅ ∠D
Свойство # 3
Диагонали параллелограмма делятся пополам.
Диагональ AC (красная линия) пересекает и делит пополам диагональ BD (зеленая линия) в точке E.
Как доказать, что диагонали параллелограмма делят друг друга пополам
Для заданного параллелограмма ABCD нам нужно доказать, что отрезок AC и отрезок BD делят друг друга пополам в E.
1. Дано
ABCD — параллелограмм
2. Определение параллелограмма
Отрезок AB || отрезок DC
3. Параллельные прямые, разделенные секущей, образуют конгруэнтные параллельные внутренние углы
∠1 ≅ ∠4; ∠2 ≅ ∠3
4. Противоположные стороны параллелограмма равны
Отрезок AB ≅ отрезок DC
5. Треугольник ABE равен треугольнику CDE по ASA (угол -боковой угол)
6. Отрезок AE ≅ отрезок CE и отрезок BE ≅ отрезок DE по CPCTC (соответствующие части конгруэнтных треугольников конгруэнтны)
7. Определение биссектрисы
Отрезок AC и отрезок BD делят друг друга пополам в точке E.
Свойство № 4
Смежные углы являются дополнительными или в сумме составляют 180 градусов.
Угол A + угол B = 180 градусов
Угол B + угол C = 180 градусов
Угол C + угол D = 180 градусов
Угол D + угол A = 180 градусов
Свойство №5
Каждая диагональ параллелограмма превращает параллелограмм в 2 конгруэнтных треугольника.
Треугольник ABC равен или идентичен треугольнику ADC.
Треугольник BCD равен или идентичен треугольнику BAD.
Использование свойств параллелограмма для решения математических задач
Пример #1 : Используйте приведенный ниже параллелограмм, чтобы найти длину отрезка BC и отрезка AD.
Поскольку противоположные стороны параллелограмма равны, длина отрезка BC равна длине отрезка AD.
4x — 10 = 3x + 5.
Вычесть 3x с каждой стороны
4x — 3x — 10 = 3x — 3x + 5
Упростить каждую сторону
x — 10 = 5 900 05
Добавьте 10 к обеим сторонам уравнение.
x — 10 + 10 = 5 + 10
Упрощение
x = 15
BC = AD = 4x — 10 = 4 x 15 — 10 = 60 — 10 = 50
Пример #2 : Используйте приведенный ниже параллелограмм, чтобы найти длину отрезка AC и отрезка BD.
Поскольку диагонали параллелограмма делят друг друга пополам, получаем следующие результаты:
- Длина отрезка AI равна длине отрезка CI
- Длина отрезка BI равна длине отрезок DI
Это приводит к системе линейных уравнений для решения
2y — 4 = 4x
y = x + 4
Заменить x + 4 на y в 2y — 4 = 4x
2(x + 4) — 4 = 4x
Распределить
2x + 8 — 4 = 4x
Упростить
90 002 2x + 4 = 4x4 = 2x
x = 4/2 = 2
y = x + 4 = 2 + 4 = 6 9 0005
АС = AI + CI = 2y — 4 + 4x = 2×6 — 4 + 4×2 = 12 — 4 + 8 = 16
BD = BI + DI = x + 4 + y = 2 + 4 + 6 = 12
Посмотрите также урок о параллелограмме, чтобы узнать кое-что интересное о параллелограмме, например:
- Что такое параллелограмм?
- Типы параллелограмма, такие как ромб и прямоугольник
- Периметр параллелограмма
- Площадь параллелограмма
Треугольник 45-45-90
01, 23 мая 07:00
Что такое треугольник 45-45-90? Определение, доказательство, площадь и простые примеры из реальной жизни.








 е.
е. 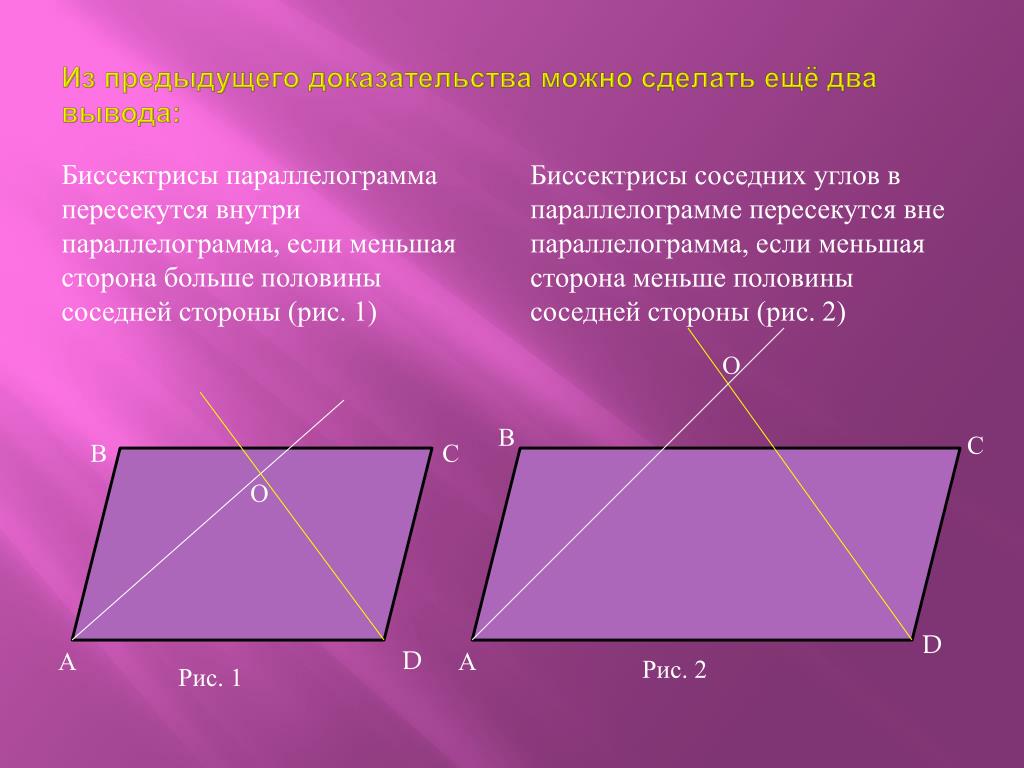
 е. OB = OD и OA = OC.
е. OB = OD и OA = OC.