Подготовка школьников к ЕГЭ (Справочник по математике — Стереометрия

Сечения призмы

     Определение 1.Сечением тела некоторой плоскостью α называют фигуру, состоящую из всех точек этого тела, лежащих в плоскости  α.

      В качестве примера рассмотрим сечение куба куба   ABCDA₁B₁C₁D₁   плоскостью, проходящей через точку   D  и середины ребер   A₁B₁   и   B₁C₁ . Рассмотрим процесс построения сечения подробно.

      Обозначим буквами   E   и   F середины ребер   A₁B₁   и   B₁C₁ (рис. 1).

Рис.1

      Поскольку точки   E   и   F   лежат на ребрах одной грани куба   A₁B₁C₁D₁ , то проведем прямую   EF   до пересечения с продолжениями двух других ребер этой грани. Обозначим буквой   G   точку пересечения прямой   EF   с продолжением отрезка   D₁C₁   за точку   C₁,   а буквой   Н   – точку пересечения прямой   EF   с продолжением отрезка   D₁A₁  за точку  A₁ . Эти точки пересечения существуют, поскольку все указанные прямые лежат в одной плоскости   A₁B₁C₁D₁   и не параллельны параллельны попарно (рис. 2).

Рис.2

      Точки   G   и   D   принадлежат плоскости сечения, а, значит, и вся прямая   DG   лежит в плоскости сечения. С другой стороны, эти точки лежат на ребрах (или их продолжениях) одной грани куба   DD₁C₁C.   Значит, точка пересечения   DG   с ребром куба   C₁C (точка   N ) будет принадлежать сечению.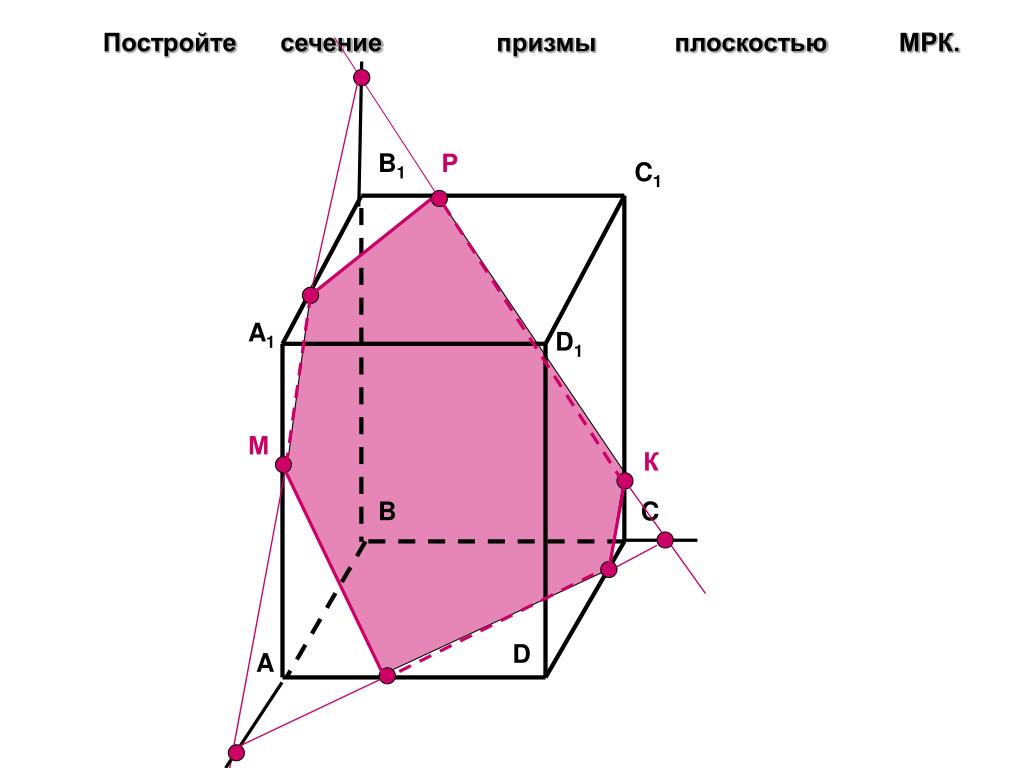 Таким образом, мы получаем еще два отрезка сечения:   FN  и   DN   (рис. 3).

Рис.3

      Теперь, действуя аналогичным образом, проводим прямую   HD,   обозначаем точку перечения этой прямой с ребром   AA₁ буквой   M   и проводим линии сечения   ME   и   MD   в плоскостях граней   AA₁B₁B   и   AA₁D₁D   (рис. 4).

Рис.4

      В результате, как и показано на рисунке 4, получаем, что искомое сечение – пятиугольник   DMEFN.

      Предлагаем посетителю нашего сайта решить в качестве полезного упражнения следующую задачу.

     Задача. Найти площадь сечения   DMEFN, если ребро куба равно 6.

     Указание к решению. Треугольники   HA₁E,   EB₁F и   FC₁G равны.

Перпендикулярные сечения призмы

      Определение 2. Перпендикулярным сечением призмы называют такое сечение, плоскость которого пересекает все боковые ребра призмы и перпендикулярна к ним.

     На рисунке 5 построено перпендикулярное сечение наклонной треугольной призмы – треугольник   KLM.   Хотим обратить Ваше внимание на то, что призма на рисунке 5 изображена лежащей на одной из своих боковых граней. Такой способ представления призмы на чертеже часто очень удобен при решении задач.

Рис.5

      Замечание 1. Все перпендикулярные сечения призмы равны между собой.

     Замечание 2. С понятием призмы и различными видами призм можно ознакомиться в разделе «Призмы».

     Замечание 3. С различными формулами для вычисления объема призмы и площадей боковой и полной поверхности призмы можно ознакомиться в разделе «Формулы для объема, площади боковой поверхности и площади полной поверхности призмы».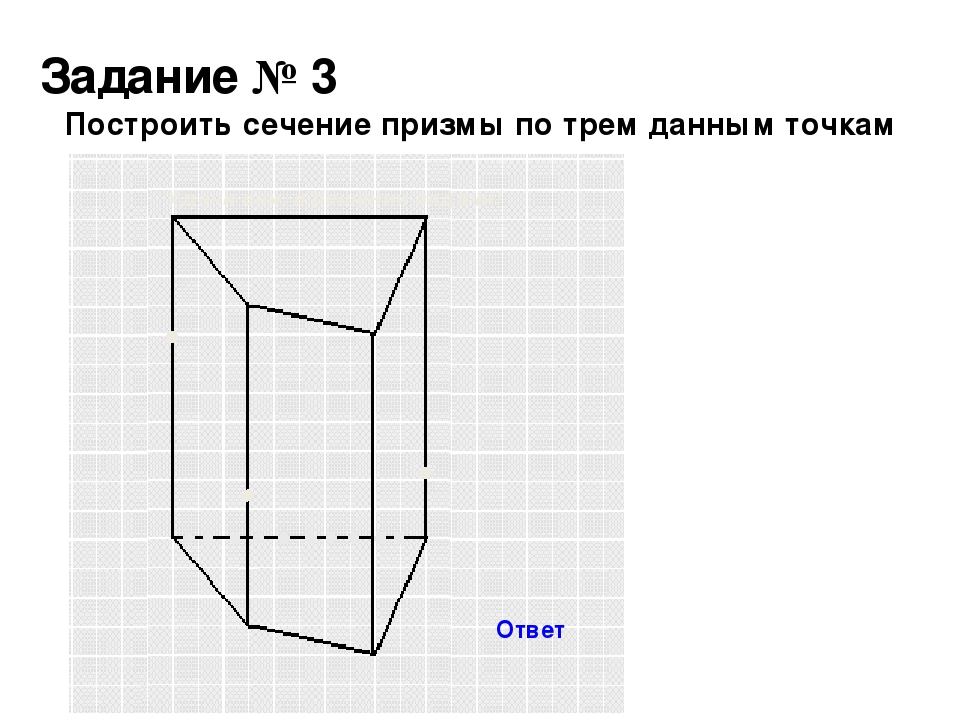

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

Задача по математике — 1151

2015-11-02   
Правильная треугольная призма $ABCA_{1}B_{1}C_{1}$ пересечена плоскостью, проходящей через середины ребер $AB, A_{1}C_{1}, BB_{1}$. Построить сечение призмы, найти площадь сечения и вычислить угол между плоскостью основания $ABC$ и плоскостью сечения, если сторона основания равна 4, а высота призмы равна $\frac{ \sqrt{42}}{7}$.

Решение:

$arccos \sqrt{\frac{2}{3}}, \frac{13 \sqrt{2}}{4}$.
Решение.
а) Построение сечения. Пусть $E, F$ и $K$ — середина ребер $AB, A_{1}C_{1}$ и $BB_{1}$ соответственно. Проведем:
а) прямые $KE$ и $AA_{1}$ пересекающиеся в точке $M$;
б) прямую $FM$, пересекающую отрезок $AC$ в точке $P$;
в) прямую $A_{1}B_{1}$, пересекающую прямую $KE$ в точке $L$;
г) прямую $FL$, пересекающую ребро $B_{1}C_{1}$ в точке $N$ (рис. ).
Тогда $EPFNK$ — пятиугольник, получаемый в сечении призмы плоскостью, проходящей через точки $E, P$ и $K$.

б) Вычисление угла между плоскостью основания и плоскостью сечения $\alpha$.
Пусть $F_{1}$ — середина $AC, G$ — основание перпендикуляра опущенного из точки $F_{1}$ на $PE$. Так $FF_{1}$ — перпендикуляр к плоскости $ABC$, а прямая $PE$ перпендикулярна проекции $F_{1}G$ наклонной $FG$, то $FG \perp PE$ (теорема о трех перпендикулярах). Итак, прямые $GF$ и $GF_{1}$ лежащие в плоскостях $\alpha$ и $ABC$ соответственно, перпендикулярные $PE$ — линия пересечения этих плоскостей. Поэтому $\angle FGF_{1} = \phi$ — линейный угол двугранного угла между плоскостями $\alpha$ и $ABC$, a $tg \phi = \frac{FF_{1}}{F_{1}G}$.
Найдем $F_{1}G$.
Пусть $AB = a, BB_{1} = h$. Тогда из равенства треугольников $AME$ и $KBE$ следует, что $AM = \frac{h}{2}$, а из подобия треугольников $MAP$ и $MA_{1}F$ находим: $\frac{AP}{A_{1}F} = \frac{MA}{MA_{1}} = \frac{1}{3}$, откуда $AP = \frac{1}{3}A_{1}F = \frac{a}{6}$. {2} \sqrt{3}}{4}}{ \frac{a \sqrt{7}}{6}} = 2 \sqrt{\frac{3}{7}}$,
$tg \phi = \frac{h}{F_{1}G} = \frac{ \frac{ \sqrt{42}}{7}}{ 2 \sqrt{ \frac{3}{7}}} = \frac{1}{ \sqrt{2}}, \cos \phi = \sqrt { \frac{2}{3}}, \phi = arccos \sqrt{ \frac{2}{3}}$.
в) Вычисление площади сечения.
Пусть $\sigma$ и $\sigma_{1}$ — площади соответственно сечения и его проекции на плоскости $ABC$. Тогда $\sigma = \frac{ \sigma_{1}}{ \cos \phi}$.
Заметим, что проекцией сечения на плоскость $ABC$ является пятиугольник $PF_{1}N_{1}BE$ ($N_{1}$ — проекция точки $N$ на плоскость $ABC$), в котором $F_{1}N_{1} \parallel PE$, так как $F_{1}N_{1} \parallel FN$, a $FN \parallel PE$.
Если $Q$ — середина $PF_{1}$, то $PQ = QF_{1} = AP = \frac{a}{6}, PE$ — средняя линия в треугольнике $ABQ$ и поэтому $PE \parallel BQ$, откуда следует, что $F_{1}N_{1} \parallel BQ$, так как $F_{1}N_{1} \parallel PE$.
Из подобия треугольников $CF_{1}N_{1}$ и $CQB$ следует, что
$\frac{CN_{1}}{CB} = \frac{CF_{1}}{CQ}$, где $CB = a, CF_{1} = \frac{a}{2}, CQ = \frac{2}{3}$,
откуда находим $CN_{1} = \frac{3}{4}a$. {2} \sqrt{3}}{4} = \frac{13 \sqrt{3}}{6}$;
откуда $\sigma = \sigma_{1} \sqrt{ \frac{3}{2}} = \frac{13 \sqrt{2}}{4}$.

Начертательная геометрия

12.5.2. Способ нормального сечения

Способ нормального сечения заключается в том, что цилиндр или призма пересекаются плоскостью, перпендикулярной образующим цилиндра или ребрам призмы.

Способ нормального сечения применяется в том случае, если основание призмы не является плоскостью уровня, а основание цилиндра – окружностью.

Строится сечение цилиндра или призмы этой плоскостью и определяется его натуральная величина. Затем сечение спрямляется, и перпендикулярно спрямленному нормальному сечению проводятся прямые, соответствующие образующим цилиндра или ребрам призмы, и на этих прямых откладываются натуральные величины образующих или ребер.

Соединив концы образующих или ребер плавной кривой или ломаной линией, получают развертку боковой поверхности цилиндра или призмы.

Рассмотрим применение этого способа для призматических поверхностей на примере треугольной призмы, ребра которой являются фронтальными линиями уровня (рис. 155).

Так как боковые ребра призмы являются фронтальными линиями уровня, они проецируются на фронтальную плоскость проекций в натуральную величину. Тогда фронтально – проецирующая плоскость δ(δ₂), перпендикулярная к боковым ребрам, определит нормальное сечение I–II–III призмы. Способом плоскопараллельного движения определена его натуральная величина I’₁–II’₁–III’₁.

Для построения развертки призмы строится спрямленное нормальное сечение I₀–II

0–III₀. Для этого нужно отложить на произвольной прямой натуральные величины сторон нормального сечения, а затем через точки I₀, II₀ и III₀ нужно провести прямые, перпендикулярные к этой прямой. На этих прямых откладываются натуральные величины ребер:

Затем точки A₀, B₀, C₀, A₀ и точки A’₀, B’₀, C’₀, A’₀ соединяются прямыми линиями. К полученной развертке боковой поверхности призмы пристраиваются натуральные величины двух ее оснований:

Если боковые ребра данной призмы занимают произвольное расположение относительно плоскостей проекций, то нужно предварительно преобразовать их в линии уровня.

Рассмотрим построение разверток цилиндрических поверхностей на примере построения развертки боковой поверхности кругового цилиндра, ось i которого является фронтальной линией уровня (рис. 156).

Так же, как и в случае призмы, построено нормальное сечение цилиндра фронтально — проецирующей плоскостью α(α₂), перпендикулярной оси цилиндра и определена его натуральная величина – окружность радиусом r. Эта окружность разбита на шесть равных частей точками I, II, III, IV, V и VI. Далее строится спрямленное нормальное сечение I₀-II₀-III₀-IV₀-V₀-VI₀-I₀, длина которого равна 2πr. Через точки I₀,II₀,III₀,IV₀,V₀,VI₀ и I₀ проводятся прямые, перпендикулярные спрямленному нормальному сечению, и на них откладываются натуральные величины образующих цилиндра:

Точки A₀, B₀, C₀…и точки A’₀, B’₀, C’₀…соединяются плавными кривыми линиями, которые будут развертками верхнего и нижнего оснований цилиндра.

Если образующие цилиндра являются прямыми общего положения, то следует преобразовать их так, чтобы они стали линиями уровня.

Рис. 155. Построение развертки треугольной наклонной призмы способом нормального сечения

Рис. 156. Построение развертки боковой поверхности кругового цилиндра способом нормального сечения

Построение сечений многогранника на примере призмы

Слайд 1

Построение сечений многогранников на примере пр измы ® Создатели : Антон Дмитриев, Киреев Александр. При содействии: Гудковой Ольги Викторовны

Слайд 2

План урока Алгоритмы построения сечений Самопроверка Демонстрационные задачи Задачи для закрепления материала

Слайд 3

Алгоритмы построения сечений следов параллельных прямых параллельного переноса секущей плоскости внутреннего проектирования комбинированный метод дополнения n -угольной призмы до треугольной призмы Построение сечения методом :

Слайд 4

Построение сечения методом следов Основные понятия и умения Построение следа прямой на плоскости Построение следа секущей плоскости Построение сечения

Слайд 5

Алгоритм построения сечения методом следов Выяснить имеются ли в одной грани две точки сечения (если да, то через них можно провести сторону сечения). Построить след сечения на плоскости основания многогранника. Найти дополнительную точку сечения на ребре многогранника (продолжить сторону основания той грани, в которой есть точка сечения, до пересечения со следом). Через полученную дополнительную точку на следе и точку сечения в выбранной грани провести прямую, отметить точки пересечения её с рёбрами грани. Выполнить п.1.

Слайд 6

Построение сечения призмы Двух точек принадлежащих одной грани нет. Точка R лежит в плоскости основания. Найдем след прямой KQ на плоскости основания: — KQ ∩K1Q1=T1, T1R- след сечения. 3. T1R ∩CD=E. 4. Проведем EQ. EQ∩DD1=N. 5. Проведем NK. NK ∩AA1=M. 6. Соединяем M и R . Построить сечение плоскостью α , проходящей через точки K,Q,R; K є ADD1, Q є CDD1, R є AB.

Слайд 7

Метод параллельных прямых В основу метода положено свойство параллельных плоскостей: «Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Основные умения и понятия Построение плоскости параллельной данной Построение линии пересечения плоскостей Построение сечения

Слайд 8

Алгоритм построения сечения методом параллельных прямых. Строим проекции точек, определяющих сечение. Через две данные точки (например P и Q ) и их проекции проводим плоскость. Через третью точку (например R) строим параллельную ей плоскость α . Находим линии пересечения (например m и n) плоскости α с гранями многогранника содержащими точки P и Q . Через точку R проводим прямую а параллельную PQ . Находим точки пересечения прямой а с прямыми m и n. Находим точки пересечения с ребрами соответствующей грани.

Слайд 9

(ПРИЗМА) Строим проекции точек P и Q на плоскости верхнего и нижнего оснований. Проводим плоскость P1Q1Q2P2. Через ребро, содержащее точку R, проводим плоскость α параллельную P1Q1Q2. Находим линии пересечения плоскостей ABB1 и CDD1 с плоскость α . Через точку R проводим прямую a||PQ . a∩n=X, a∩m=Y. XP∩AA1=K, XP∩BB1=L; YQ∩CC1=M, YQ∩DD1=N. KLMNR – искомое сечение. Построить сечение плоскостью α , проходящей через точки P,Q,R; P є ABB1, Q є CDD1, R є EE1.

Слайд 10

Метод параллельного переноса секущей плоскости Строим вспомогательное сечение данного многогранника, которое удовлетворяет следующим требованиям: оно параллельно секущей плоскости; в пересечении с поверхностью данного многогранника образует треугольник. Соединяем проекцию вершины треугольника с вершинами той грани многогранника, которую пересекает вспомогательное сечение, и находим точки пересечения со стороной треугольника, лежащей в этой грани. Соединяем вершину треугольника с этими точками. Через точку искомого сечения проводим прямые параллельные построенным отрезкам в предыдущем пункте и находим точки пересечения с ребрами многогранника.

Слайд 11

ПРИЗМА R є AA1, P є EDD1, Q є CDD1. Построим вспомогательное сечение AMQ1 ||RPQ. Проведем AM||RP, MQ1||PQ, AMQ1∩ABC=AQ1. P1- проекция точек Р и М на АВС. Проведем Р1В и Р1С. Р1В∩ AQ1=O1, P1C ∩ AQ1=O2. Через точку Р проведем прямые m и n соответственно параллельные МО1 и МО2. m∩BB1=K, n∩CC1=L. LQ∩DD1=T, TP∩EE1=S. RKLTS – искомое сечение Построить сечение призмы плоскостью α , проходящей через точки P,Q,R; P є EDD1, Q є CDD1, R є AA1 .

Слайд 12

Алгоритм построения сечения методом внутреннего проектирования. Построить вспомогательные сечения и найти линию их пересечения. Построить след сечения на ребре многогранника. Если точек сечения не хватает для построения самого сечения повторить пп.1-2.

Слайд 13

Построение вспомогательных сечений. ПРИЗМА Параллельное проектирование .

Слайд 14

Построение следа сечения на ребре

Слайд 15

Комбинированный метод. Через вторую прямую q и какую-нибудь точку W первой прямой р провести плоскость β . В плоскости β через точку W провести прямую q‘ параллельную q . Пересекающимися прямыми p и q‘ определяется плоскость α . Непосредственное построение сечения многогранника плоскостью α Суть метода состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом. Применяется для построения сечения многогранника с условием параллельности. 1. Построение сечения многогранника плоскостью α , проходящей через заданную прямую p параллельно другой заданной прямой q .

Слайд 16

ПРИЗМА Построить сечение призмы плоскостью α , проходящей через прямую PQ параллельно AE1; P є BE, Q є E1C1. 1. Проведем плоскость через прямую AE1 и точку P. 2. В плоскости AE1P через точку P проведем прямую q’ параллельную AE1. q’∩E1S’=K. 3. Пересекающимися прямыми PQ и PK определяется искомая плоскость α. 4. P1 и K1- проекции точек Р и К на А1В1С1. P1K1∩PK=S”. S”Q∩E1D1=N, S”Q∩B1C1=M, NK∩EE1=L; MN∩A1E1=S”’, S”’L∩AE=T, TP∩BC=V. TVMNL-искомое сечение.

Слайд 17

Метод дополнения n -угольной призмы(пирамиды) до треугольной призмы(пирамиды). Данная призма(пирамида) достраивается до треугольной призмы(пирамиды) из тех граней на боковых ребрах или гранях которой лежат точки, определяющие искомое сечение. Строится сечение полученной треугольной призмы(пирамиды). Искомое сечение получается как часть сечения треугольной призмы(пирамиды).

Слайд 18

Основные понятия и умения Построение вспомогатель- ных сечений Построение следа сечения на ребре Построение сечения Центральное проектирование Параллельное проектирование

Слайд 19

ПРИЗМА Q є BB1C1C, P є AA1, R є EDD1E1. Достраиваем призму до треугольной. Для этого продлим стороны нижнего основания: AE, BC, ED и верхнего основания: A 1 E 1 , B 1 C 1 , E 1 D 1. AE ∩BC=K, ED∩BC=L, A1E1∩B1C1=K1, E1D1∩B1C1=L1. Строим сечение полученной призмы KLEK1L1E1 плоскостью PQR , используя метод внутреннего проектирования. Это сечение является частью искомого. Строим искомое сечение.

Слайд 20

Правило для самоконтроля Если многогранник выпуклый, то сечение выпуклый многоугольник. Вершины многоугольника всегда лежат на ребрах многогранника. Если точки сечения лежат на ребрах многогранника, то они являются вершинами многоугольника, который получится в сечении. Если точки сечения лежат на гранях многогранника, то они лежат на сторонах многоугольника, который получится в сечении. Две стороны многоугольника, который получится в сечении, не могут принадлежать одной грани многогранника. Если сечение пересекает две параллельные грани, то и отрезки (стороны многоугольника, который получится в сечении) будут параллельны.

Слайд 21

Базовые задачи на построение сечений многогранников Если две плоскости имеют две общие точки, то прямая, проведенная через эти точки, является линией пересечения этих плоскостей. M є AD, N є DCC1, D1 ; ABCDA1B1C1D1- куб M є ADD1, D1 є ADD1, MD1. D1 є D1DC, N є D1DC, D1N ∩ DC=Q. M є ABC, Q є ABC, MQ. II. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. M є CC1, AD1; ABCDA1B1C1D1- куб. MK||AD1, K є BC. M є DCC1, D1 є DCC1, MD1. A є ABC, K є ABC, AK.

Слайд 22

III. Общая точка трех плоскостей (вершина трехгранного угла) является общей точкой линий их парного пересечения (ребер трехгранного угла). M є AB, N є AA1, K є A1D1; ABCDA1B1C1D1- куб. NK∩AD=F1 — вершина трехгранного угла образованного плоскостями α , ABC, ADD1. F1M∩CD=F2 — вершина трехгранного угла образованного плоскостями α , ABC, CDD1. F1M ∩BC=P. NK∩DD1=F3 — вершина трехгранного угла образованного плоскостями α , D1DC, ADD1. F3F2∩D1C1=Q, F3F2∩CC1=L. IV. Если плоскость проходит через прямую, параллельную другой плоскости и пересекает ее, то линия пересечения параллельна данной прямой. A1, C, α ||BC1; ABCA1B1C1- призма. α∩ BCC1=n, n||BC1, n∩BB1=S. SA1∩AB=P. Соединяем A1,P и C.

Слайд 23

V. Если прямая лежит в плоскости сечения, то точка ее пересечения с плоскостью грани многогранника является вершиной трехгранного угла, образованного сечением, гранью и вспомогательной плоскостью, содержащей данную прямую. M є A1B1C1, K є BCC1, N є ABC; ABCDA1B1C1- параллелепипед. 1 . Вспомогательная плоскость MKK1: MKK1∩ABC=M1K1, MK∩M1K1=S, MK∩ABC=S, S- вершина трехгранного угла образованного плоскостями : α , ABC, MKK1. 2. SN∩BC=P, SN∩AD=Q, PK∩B1C1=R, RM∩A1D1=L.

Слайд 24

Задачи . На каком рисунке изображено сечение куба плоскостью ABC ? Сколько плоскостей можно провести через выделенные элементы? Какие аксиомы и теоремы вы применяли? Сделайте вывод, как построить сечение в кубе? Давайте вспомним этапы построения сечений тетраэдра (параллелепипеда, куба). Какие многоугольники могут при этом получиться?

Сечение призмы. Задачи на 3 уровня сложности

Через вершины A₁, C₁ и середину ребра ВВ₁, правильной треугольной призмы ABCA₁B₁C₁ проведено сечение. Найдите его периметр, если каждое ребро призмы равно а.

Через вершину А₁ и середины боковых ребер ВВ₁, СС₁ прямой треугольной призмы ABCA₁B₁C₁ проведено сечение. Вычислите его периметр, если АА₁ = 6 см, АВ = АС = 4 см, ВС = 3 см.

Через вершину А, и середины ребер АВ и АС правильной треугольной призмы ABCA₁B₁C₁ проведено сечение. Вычислите его периметр, если ВС = 16 см, АА₁= 6 см.

Проведите сечение правильной треугольной призмы ABCA₁B₁C₁, содержащее ребро СС₁ и середину ребра АВ. Какой фигурой является это сечение?

Проведите сечение правильной треугольной призмы ABCA₁B₁C₁, содержащее ребро ВС и середину ребра A₁B₁. Какой фигурой является это сечение?

6-9 Lost

Проведите сечение куба ABCDA₁B₁C₁D₁ плоскостью, содержащей прямую A₁C₁ и точку К — середину ребра ВС. Найдите периметр этого сечения, если ребро куба равно а.

Проведите сечение правильной треугольной призмы ABCA₁B₁C₁ плоскостью, содержащей середины ребер AA₁, CC₁ и ВС. Найдите периметр сечения, если все ребра призмы равны а.

Проведите сечение куба ABCDA₁B₁C₁D₁, содержащее точки А, С и середину ребра A₁D₁. Какой фигурой является сечение? Найдите его периметр, если ребро куба равно а.

Основание прямой призмы — прямоугольный треугольник, катеты которого равны 6 см и 8 см. Высота призмы равна 5 см. Через больший катет нижнего основания и середину гипотенузы верхнего основания проведена плоскость. Вычислите площадь сечения призмы этой плоскостью.

Через концы трех ребер, выходящих из одной вершины прямоугольного параллелепипеда, проведено сечение. Косинус угла между плоскостями сечения и основания равен 1/8. Стороны основания параллелепипеда равны 3 дм и 5 дм. Вычислите площадь сечения.

Диагональ основания прямоугольного параллелепипеда равна 5 см. Косинус угла между этой диагональю и большей стороной основания — 0,8. Через противоположные большие стороны верхнего и нижнего оснований проведено сечение. Косинус угла между плоскостями сечения и основания равен 0,3. Вычислите площадь сечения призмы.

Через сторону нижнего основания правильной треугольной призмы проведена плоскость, пересекающая противоположное боковое ребро. Косинус угла между этой плоскостью и плоскостью основания равен – 0,6. Вычислите площадь сечения призмы данной плоскостью, если сторона основания равна 6 см.

Проведите сечение куба ABCDA₁B₁C₁D₁ плоскостью, параллельной прямой A₁C₁ и проходящей через точку А и середину ребра A₁B₁. Какой фигурой является это сечение? Вычислите площадь сечения, если ребро куба равно 24 см.

Основанием прямой призмы является ромб, сторона которого равна а, угол — 60°. Высота призмы равна Н. Проведите сечение призмы плоскостью, которая содержит середину одной из сторон основания, параллельна боковому ребру и плоскости меньшего диагонального сечения. Найдите периметр и площадь сечения призмы.

Через боковое ребро правильной треугольной призмы проведено сечение, плоскость которого перпендикулярна плоскости противоположной боковой грани. Найдите его площадь, если боковое ребро призмы равно b, сторона основания — а.

Один из двугранных углов при боковых ребрах прямой треугольной призмы равен 90°. Проведите сечение призмы плоскостью, содержащей ребро данного двугранного угла и перпендикулярной противоположной боковой грани. Вычислите площадь сечения призмы, если ее боковое ребро равно 15 см, а плоскость сечения делит большую сторону основания на отрезки длиной 12 см и 27 см.

Проведите сечение наклонной четырехугольной призмы ABCDA₁B₁C₁D₁ плоскостью, содержащей вершину D₁ и середины ребер AD и СС₁.

Проведите сечение наклонной треугольной призмы ABCA₁B₁C₁ плоскостью, содержащей вершину А₁ и середины ребер CC₁ и АВ.

Проведите сечение наклонной треугольной призмы ABCA₁B₁C₁ плоскостью, содержащей вершину В и середины ребер CC₁ и АС.

Проведите сечение наклонной четырехугольной призмы ABCDA₁B₁C₁D₁ плоскостью, содержащей вершину В и середины ребер АА₁ и В₁С₁. Какой фигурой является это сечение?

Проведите сечение наклонной треугольной призмы ABCA₁B₁C₁ плоскостью, содержащей середины ребер АА₁, АВ и A₁C₁.

Проведите сечение правильной треугольной призмы ABCA₁B₁C₁ плоскостью, содержащей вершину А₁ и середины ребер CC₁ и ВС. Вычислите периметр сечения призмы, если высота ее равна 6 см, а сторона основания — 8 см.

Проведите сечение куба ABCDA₁B₁C₁D₁ плоскостью, содержащей середины ребер АА₁, A₁D₁ и CC₁.

Проведите сечение правильной четырехугольной призмы ABCDA₁B₁C₁D₁ плоскостью, содержащей вершину D, и середины ребер АВ и ВС. Вычислите его периметр и площадь, если высота призмы равна 14 см, а сторона основания — 16 см.

Проведите сечение куба ABCDA₁B₁C₁D₁ плоскостью, проходящей через вершины D₁ и В, параллельной прямой A₁C₁. Какой фигурой является это сечение? Найдите площадь сечения, если ребро куба равно а.

Проведите сечение куба ABCDA₁B₁C₁D₁ плоскостью, проходящей через середины ребер D₁C₁, C₁C и АВ. Какой фигурой является это сечение? Найдите его периметр, если ребро куба равно а.

Проведите сечение правильной треугольной призмы ABCA₁B₁C₁ плоскостью, содержащей вершину А, перпендикулярной плоскости сечения А₁ВС и параллельной прямой ВС.

Проведите сечение куба ABCDA₁B₁C₁D₁ плоскостью, проходящей через вершины А и С, перпендикулярной диагонали D₁B. Найдите площадь сечения, если ребро куба равно а.

Пошаговое построение сечения: треугольная пирамида.

В этой статье мы построим несколько сечений треугольной пирамиды, будем при этом использовать метод следов. Сначала мы рассмотрим самые простые случаи: когда точки, через которые должно пройти сечение, принадлежат ребрам пирамиды. Потом – случаи сложнее, когда одна или две из точек плоскости сечения принадлежат граням пирамиды. Поехали!

Задача 1. Построить сечение пирамиды, проходящее через точки P, Q, R.

Дано

Сначала надо попробовать отыскать такие точки, которые принадлежат одной плоскости. У нас это точки P и Q – они принадлежат грани ASC, а также пара P и R – они принадлежат грани ABC. Их можно сразу соединять:

Шаг 1

Теперь, чтобы понять, как плоскость рассечет грань SBC, нужно заполучить точку в этой грани, или в плоскости, которой принадлежит грань. Но нужна нам не любая, а особенная точка, которая также будет принадлежать и плоскости сечения. Чтобы точка принадлежала плоскости нужно, чтобы она принадлежала прямой этой плоскости. Заметим, что прямая PR лежит в плоскости основания и принадлежит искомому сечению. Прямая CB тоже лежит в плоскости основания, но не только. Она еще лежит в плоскости грани SBC, где нам необходима точка, чтобы построить сечение.  Воспользуемся случаем: найдем точку, где прямые PR и CB пересекутся. Такая точка принадлежит сечению, а также плоскостям боковой (SBC) и нижней (ABC)  граней пирамиды.

Шаг 2

Так как построенная точка T и точка Q лежат в одной плоскости, то можем соединить их прямой:

Шаг 3

Эта прямая пересечет ребро SB в точке F – это и есть еще одна нужная нам точка для построения сечения. Соединяем R и F – они лежат в одной плоскости (SAB). Теперь смотрим: можно ли пройти по линиям сечения, принадлежащим граням пирамиды,  от точки P и снова попасть в нее непрерывным маршрутом? Если да, то построение окончено. У нас такой маршрут замкнутый: P-Q-F-R-P. Это и есть сечение.

Шаг 4

Задача 2. Построить сечение пирамиды, проходящее через точки P, Q, R.

Дано

Видим, что точки R и Q принадлежат одной грани пирамиды – SCB – и соединяем их.

Шаг 1

Можно, конечно, было бы сразу и точки P и Q соединить – они тоже лежат в одной плоскости – плоскости грани SAB.

Но это успеется, пока что нам нужна точка в плоскости грани SAC, да такая, чтобы принадлежала и сечению. Поэтому она должна принадлежать прямой искомого сечения, и прямой, принадлежащей плоскости SAB, то есть быть пересечением таких прямых. Продлим SC до пересечения с прямой QR  -и получим такую точку.

Шаг 2

Точка X и точка P принадлежат одной плоскости, можем их соединить и получить точку пересечения данной прямой с ребром AC:

Шаг 3

 

Соединяем E  с R, P с Q, и получаем сечение.

Шаг 4

 

Задача 3. Построить сечение пирамиды, проходящее через точки P, Q, R.

Дано

Теперь, уже имея опыт, первый шаг выполняем без проблем:

Шаг 1

Понимаем, что нет точки в задней грани. Вернее, одна есть – P – но второй не хватает. Аналогично, есть одна точка в нижней грани – в плоскости основания, а второй точки нет. Определим такую точку: пересечем AC и PQ. Обе прямые лежат в плоскости SAC, PQ принадлежит плоскости сечения, поэтому их пересечение будет принадлежать обеим плоскостям:

Шаг 2

Теперь имеем две точки в плоскости основания – U и R, и можем смело соединять их:

Шаг 3

Прямая UR пересечет ребро AB в точке Z.  Теперь маршрут Q-R-Z-P-Q замкнут, можем достраивать сечение:

Шаг 4

Задача 4. Построить сечение пирамиды, проходящее через точки P, Q, R, причем точка P принадлежит грани ASC.

Дано

Тут уже задача сложнее. Но пока метод следов позволяет ее решить.

Имеем две точки в одной плоскости – Q и R, и можем их сразу же соединять.  AS так же, как и QR, принадлежит плоскости задней грани, поэтому продолжение AS пересечет QR в точке L, также принадлежащей плоскости задней грани.

Шаг 1

Но, так как AS принадлежит также и плоскости боковой грани SAC, то точка L лежит  с точкой P  в одной плоскости и их можно соединять:

Шаг 2

LP пересечет ребро AC в точке M, а ребро SC – в точке N, и можно восстанавливать четырехугольник сечения:

Шаг 3

Треугольная призма все формулы и примеры задач

Треугольная призма — это трехмерное тело, образованное соединением прямоугольников и треугольников.  В этом уроке вы узнаете, как найти размер внутри (объем) и снаружи (площадь поверхности) треугольной призмы.

Определение

Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.

Элементы треугольной призмы

Треугольники ABC и A₁B₁C₁ являются основаниями призмы.

Четырехугольники A₁B₁BA, B₁BCC₁ и A₁C₁CA являются боковыми гранями призмы.

Стороны граней являются ребрами призмы (A₁B₁, A₁C₁, C₁B₁, AA₁, CC₁, BB₁, AB, BC, AC), всего у треугольной призмы 9 граней.

Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).

Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.

Площадь основания — это площадь треугольной грани призмы.

Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.

Виды треугольных призм

Треугольная призма бывает двух видов: прямая и наклонная.

У прямой призмы боковые грани прямоугольники, а у наклонной боковые грани — параллелограммы (см. рис.)

Прямая треугольная призма

Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой.

Наклонная треугольная призма

Призма, боковые ребра которой являются наклонными к плоскостям оснований, называется наклонной.

Основные формулы для расчета треугольной призмы

Объем треугольной призмы

Чтобы найти объем треугольной призмы, надо площадь ее основания умножить на высоту призмы.

 Объем призмы = площадь основания х высота

или

V=S_осн ^. h

Площадь боковой поверхности призмы

Чтобы найти площадь боковой поверхности треугольной призмы, надо периметр ее основания умножить на высоту.

Площадь боковой поверхности треугольной призмы = периметр основания х высота

или

S_бок=P_осн^.h 

Площадь полной поверхности призмы

Чтобы найти площадь полной поверхности призмы, надо сложить ее площади оснований и площадь боковой поверхности.

так как S_бок=P_осн^.h, то получим:

S_{полн.пов.}=P_осн^.h+2S_осн

Правильная призма — прямая призма, основанием которой является правильный многоугольник.

Свойства призмы:

Верхнее и нижнее основания призмы – это равные многоугольники.
Боковые грани призмы имеют вид параллелограмма.
Боковые ребра призмы параллельные и равны.

Совет: при расчете треугольной призмы вы должны обратить внимание на используемые единицы. Например, если площадь основания указана в см², то высота должна быть выражена в сантиметрах, а объем — в см³ . Если площадь основания в мм², то высота должна быть выражена в мм, а объем в мм³ и т. д.

Пример призмы

В этом примере:
— ABC и DEF составляют треугольные основания призмы
— ABED, BCFE и ACFD являются прямоугольными боковыми гранями
— Боковые края DA, EB и FC соответствуют высоте призмы.
— Точки A, B, C, D, E, F являются вершинами призмы.

Задачи на расчет треугольной призмы

Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:

V = 1/2  · 6 · 8 · 5 = 120.

Задача 2.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.

Решение: 

Объём призмы равен произведению площади основания на высоту: V = S_осн ·h.

Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S₂ = S₁k² = S₁2² = 4S₁.

Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.

Таким образом, искомый объём равен 20.

Призмы с примерами

Перейти к площади или объему поверхности.

Призма — это твердый объект с:

• одинаковые концы
• плоские поверхности
• и тот же сечение по всей длине!

Поперечное сечение — это форма, полученная прямым разрезом по объекту.

Поперечное сечение этого объекта — треугольник …

.. одинаковое поперечное сечение по всей длине …

… значит, это треугольная призма .

изображения / prism-grow.js

Попробуйте нарисовать фигуру на листе бумаги (используя прямые линии) А теперь представьте, что он выходит из листа бумаги . .. … это призма!

Без кривых!

Призма — это многогранник, а это значит, что все грани плоские!

Например, цилиндр не является призмой , потому что у него изогнутые стороны.

Базы

Концы призмы параллельны
, и каждый из них называется основанием.

Стороны

Боковые грани призмы — параллелограммы
(четырехсторонние формы с параллельными противоположными сторонами)

Это все призмы:

и более!

Пример: гексагональный кристалл льда.

Похоже на шестиугольник, но из-за некоторой толщины на самом деле это шестиугольная призма!

Фотография НАСА / Алексей Клятов.

Обычная и неправильная призмы

Все предыдущие примеры — это призмы Regular , потому что поперечное сечение является правильным (другими словами, это форма с равными длинами кромок и равными углами).

Вот пример неправильной призмы :

Неправильная пятиугольная призма:
		Поперечное сечение
Он «неправильный», потому что поперечное сечение не имеет «правильной» формы.

Правая и наклонная призма

Когда два конца идеально выровнены, это правая призма, в противном случае — наклонная призма:

Площадь призмы

Площадь поверхности = 2 × площадь основания
+ периметр основания × длина

Пример: Какова площадь поверхности призмы, у которой площадь основания 25 м

² , периметр основания 24 м, а длина 12 м:

Площадь поверхности = 2 × Площадь основания + Периметр основания × Длина

= 2 × 25 м ² + 24 м × 12 м

= 50 м ² + 288 м ²

= 338 м ²

(Примечание: у нас есть инструмент для расчета площади)

Объем призмы

Объем призмы — это площадь одного конца, умноженная на длину призмы.

Объем = Базовая площадь × длина

Пример: каков объем призмы с площадью основания 25 м

² и длиной 12 м:

Объем = Площадь × Длина

= 25 м ² × 12 м

= 300 м ³

Поиграй с этим здесь. Формула также работает, когда он «наклоняется» ( наклон ), но помните, что высота находится под прямым углом к ​​основанию:

И вот почему:

Стек может наклоняться, но имеет тот же объем

Подробнее о боковых гранях

Боковые грани призмы — параллелограммы (четырехсторонняя форма с параллельными противоположными сторонами)

Призма может наклоняться в одну сторону, что делает ее наклонной призмой , но два конца по-прежнему параллельны, а боковые грани по-прежнему параллелограммы!

Но если два конца не параллельны , это не призма .

639 640 863, 1826, 1827 864, 3379, 3377, 3378, 7649

Треугольная призма

Треугольная призма — это призма с треугольным основанием. На рисунке ниже представлены три типа треугольных призм.

Свойства треугольной призмы

Треугольная призма — это многогранник, состоящий из двух параллельных и совпадающих треугольников, называемых основаниями. Боковые грани (стороны, не являющиеся основанием) представляют собой параллелограммы, прямоугольники или квадраты. У треугольной призмы три боковые грани.Ребро — это отрезок прямой, образованный пересечением двух смежных граней. Вершина — это точка пересечения трех ребер.

Треугольные призмы, подобные приведенной выше, имеют в общей сложности 5 граней, 2 основания и 3 боковые грани. У него также 9 ребер и 6 вершин.

Любое поперечное сечение треугольной призмы, параллельное основаниям, образует треугольник, соответствующий основаниям.

Два треугольных поперечных сечения треугольной призмы показаны зеленым цветом выше.Они совпадают с двумя треугольными основаниями треугольной призмы, поскольку они образованы поперечными сечениями, расположенными в плоскостях, параллельных основаниям.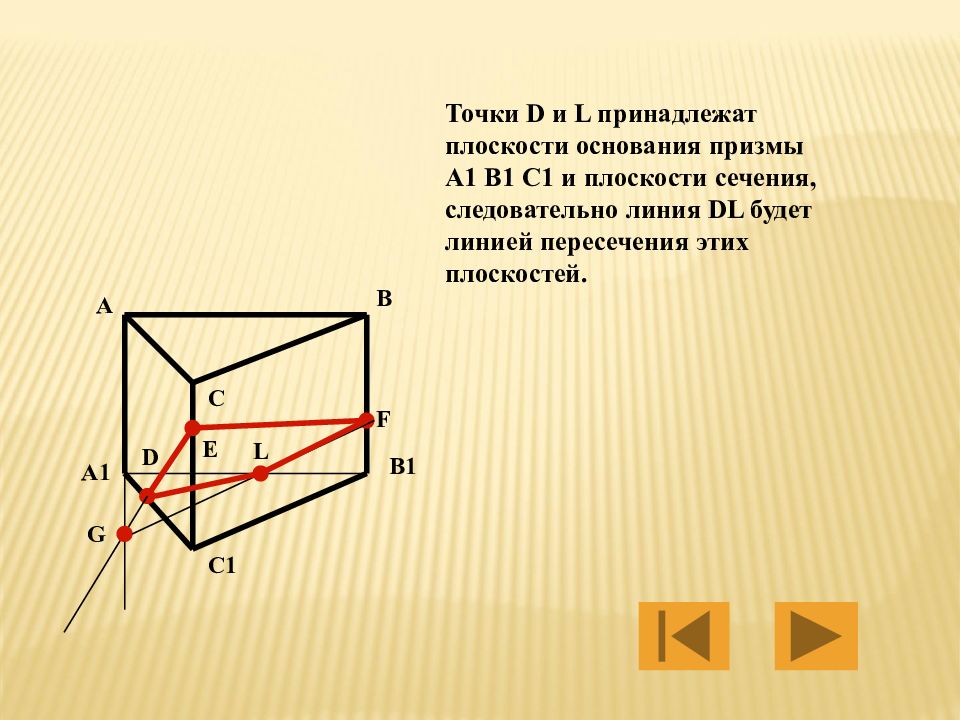 Это верно для любого параллельного сечения треугольной призмы.

Классификация треугольных призм по их пересекающимся граням

Треугольные призмы можно классифицировать в зависимости от того, как их основания и боковые грани пересекаются или встречаются. Если основания перпендикулярны боковым граням, то есть встречаются под прямым углом, это прямоугольная призма.В противном случае это наклонная треугольная призма.

Прямоугольная призма	Косая треугольная призма

Треугольные призмы правильной и неправильной формы

Треугольные призмы также можно классифицировать по типу треугольника, образующего его основание. Правильная призма определяется призмой, основания которой являются правильными многоугольниками. Следовательно, если основания треугольной призмы представляют собой равносторонние треугольники, это правильная треугольная призма.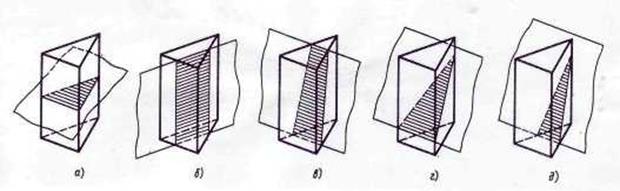 В противном случае это нерегулярно. Часто под правильной треугольной призмой подразумевают прямоугольную призму.

Правильная треугольная призма	Неправильная треугольная призма

Объем треугольной призмы

Объем V треугольной призмы равен площади одного из ее оснований, умноженной на ее высоту:

S = B · ч

, где B — площадь треугольного основания, а h — высота (расстояние между двумя параллельными основаниями) треугольной призмы.

Калькулятор треугольной призмы

Если вы когда-нибудь задумывались, как определить объем треугольной призмы, этот калькулятор треугольной призмы — это то, что вы ищете. Он не только может рассчитать объем, но также может быть полезен, если вам нужно определить площадь поверхности треугольной призмы. Выберите вариант, соответствующий вашим потребностям, и поэкспериментируйте с инструментом! Если вас интересуют формулы треугольной призмы за калькулятором, прокрутите вниз, чтобы узнать больше.

Треугольная призма — что это?

Что такое призма? Это твердый объект с:

• идентичные две базы
• три прямоугольных грани (правая призма) или в форме параллелограмма (наклонная призма)
• То же сечение по всей длине

Мы используем термин треугольная призма для описания правой треугольной призмы , что является довольно распространенной практикой.Если вы ищете призму другого типа, воспользуйтесь нашим калькулятором прямоугольной призмы.

Формулы треугольной призмы

Обычно вам нужно рассчитать объем треугольной призмы и площадь ее поверхности. Два основных уравнения:

• объем = 0,5 * b * h * длина , где b — длина основания треугольника, h — высота треугольника и длина — длина призмы

• площадь = длина * (a + b + c) + (2 * base_area) , где a, b, c — стороны треугольника, а base_area — площадь основания треугольника

Но что, если у нас нет высоты и основания треугольника? А как найти площадь поверхности треугольной призмы без всех сторон треугольного основания? Ознакомьтесь с другими формулами треугольной призмы!

Объем треугольной призмы

В калькуляторе треугольной призмы вы можете легко определить объем этого твердого тела. Общая формула: объем = длина * base_area ; один параметр, который вам всегда нужно указывать, — это длина призмы, и есть четыре способа рассчитать площадь основания треугольника. Все они реализованы в нашем калькуляторе треугольной призмы, разве это не круто?

Конкретные формулы выглядят следующим образом:

• Длина * Площадь основания треугольника с учетом основания и высоты треугольника

  Это известная формула, о которой говорилось ранее:

  объем = длина * 0.5 * ш * в

• Длина * Треугольное основание с трех сторон (SSS)

  Если вам известны длины всех сторон, используйте формулу Герона , чтобы найти площадь основания треугольника:

  объем = длина * 0,25 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c))

• Длина * Треугольное основание с учетом двух сторон и угла между ними (SAS)

  Вы можете легко вычислить площадь треугольника по тригонометрии:

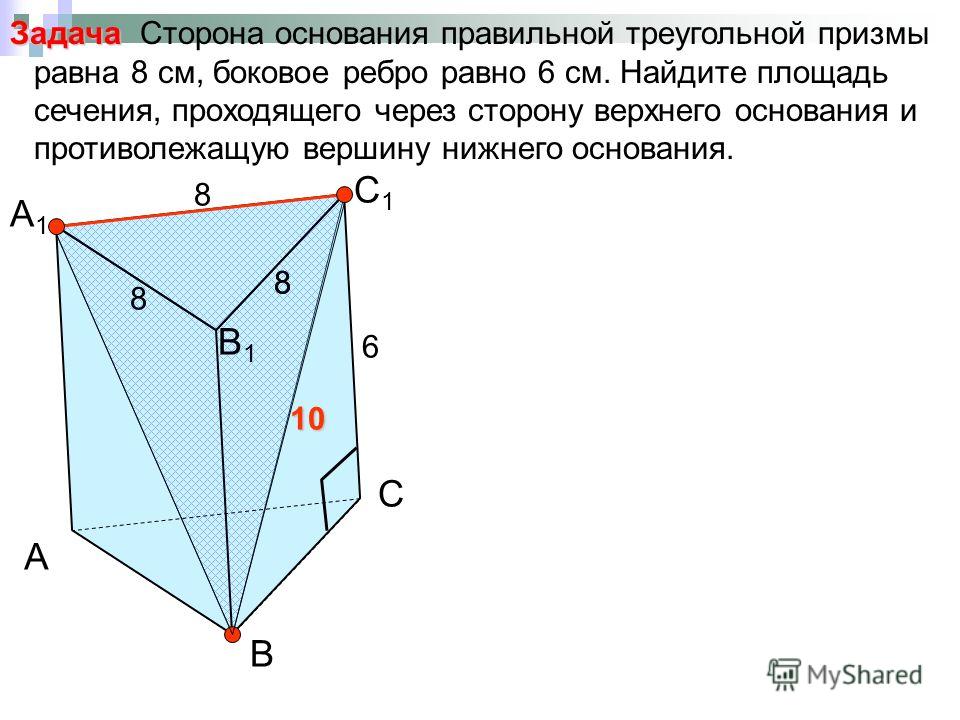
  объем = длина * 0. 5 * а * б * sin (γ)

• Длина * Треугольное основание с учетом двух углов и стороны между ними (ASA)

  Вы можете рассчитать это с помощью тригонометрии:

  объем = = длина * a² * sin (β) * sin (γ) / (2 * sin (β + γ))

Площадь поверхности треугольной призмы

Если вы хотите вычислить площадь поверхности твердого тела, наиболее известная формула — это формула с учетом трех сторон треугольного основания:

• площадь = длина * (a + b + c) + (2 * base_area) = длина * base_perimeter + (2 * base_area)

Однако у нас не всегда есть три стороны.Что тогда?

• Треугольное основание: заданы две стороны и угол между ними (SAS)

  Используя закон косинусов, мы можем найти третью сторону треугольника:

  площадь = длина * (a + b + √ (b² + a² - (2 * b * a * cos (угол)))) + a * b * sin (угол)

• Треугольное основание: заданы два угла и сторона между ними (ASA)

  Используя закон синусов, мы можем найти две стороны треугольного основания:

  площадь = (длина * (a + a * (sin (angle1) / sin (angle1 + angle2)) + a * (sin (angle2) / sin (angle1 + angle2)))) + a * ((a * грех (угол1)) / грех (угол1 + угол2)) * грех (угол2)

Единственный вариант, когда вы не можете рассчитать объем треугольной призмы, — это задать основание треугольника и его высоту (знаете почему? Задумайтесь на минутку). Все другие версии могут быть рассчитаны с помощью нашего калькулятора треугольной призмы.

Давайте проверим, каков объем и площадь поверхности палатки в виде треугольной призмы:

1. Узнайте, какова длина треугольной призмы . Предположим, что оно равно 80 дюймам, введите это значение в первое поле калькулятора треугольной призмы.
2. Выберите вариант с заданными вами параметрами . Например, даны три стороны нашей базы.
3. Введите стороны основания .Наша палатка имеет a = 60 дюймов, b = 50 дюймов и c = 50 дюймов.
4. Площадь поверхности и объем треугольной призмы появляются мгновенно . Это 96 000 куб. Дюймов (55,56 куб. Футов) и 15 200 кв. Дюймов (105,56 кв. Футов).

Призмы

Если концы твердого тела (т. Е. Трехмерного объекта) не являются правильным многоугольником, но имеют идентичные поперечные сечения при разрезе плоскостью, параллельной один из концов, то твердое тело называется неправильной призмой .

Объем призмы

В этом разделе мы рассмотрим объем куба, кубоида, цилиндра и треугольной призмы.

Если бы прямоугольная коробка была заполнена кубиками размером 1 см, то было бы:

Так как есть 3 слоя,

Теперь обратите внимание, что площадь основания коробки определяется по формуле:

Из приведенного выше обсуждения мы можем вывести формулу для объема прямоугольной коробки следующим образом:

Всего:

Объем призмы V равен

, где A — площадь основания (или поперечного сечения) призмы. h — высота.

Объем следующих твердых веществ часто требуется для решения реальных мировые проблемы, связанные с количеством, вместимостью, массой и силой материалы, включая жидкости.

Куб с длиной стороны л шт. Имеет объем В куб. единиц от

Кубоид длиной л единиц, шириной w единиц и высотой h единиц имеет объем V кубических единиц, определяемый

Цилиндр радиусом r единиц и высотой h единиц имеет объем В куб. из

Треугольная призма длиной л шт., Треугольная призма которой поперечное сечение имеет основание б шт. и высоту х шт., имеет объем В куб. из

Пример 2

Найдите объем куба со стороной 5 см.

Поперечные сечения прямоугольной призмы

Пересечение — это точка или набор точек, общих для двух или более геометрических фигур. Плоскость — это плоская поверхность, которая простирается во всех направлениях.

Поперечное сечение — это пересечение трехмерной фигуры и плоскости. Представьте себе плоскость, пересекающую показанную пирамиду, конус или призму.

На приведенном ниже рисунке показано пересечение конуса и плоскости. Поперечное сечение — круг.

На приведенном ниже рисунке показано пересечение треугольной призмы и плоскости. Поперечное сечение — треугольник.

Трехмерная фигура может иметь несколько различных поперечных сечений в зависимости от положения и направления среза.

Например, если пересечение плоскости и конуса было вертикальным, поперечное сечение образовало бы треугольник.

Практические вопросы

Вопрос 1:

Опишите поперечное сечение правой прямоугольной призмы, приведенное ниже, с названием ее формы.

Ответ:

Поперечное сечение правой прямоугольной призмы выше треугольное.

Вопрос 2:

Опишите поперечное сечение правой прямоугольной призмы, приведенное ниже, с названием ее формы.

Ответ:

Поперечное сечение правой прямоугольной призмы выше представляет собой прямоугольник.

Вопрос 3:

Опишите поперечное сечение правой прямоугольной призмы, приведенное ниже, с названием ее формы.

Ответ:

Поперечное сечение правой прямоугольной призмы выше представляет собой параллелограмм.

Вопрос 4:

Опишите поперечное сечение правой прямоугольной призмы, приведенное ниже, с названием ее формы.

Ответ:

Поперечное сечение правой прямоугольной призмы выше представляет собой прямоугольник.

Вопрос 5:

Опишите поперечное сечение правой прямоугольной призмы, приведенное ниже, с названием ее формы.

Ответ:

Поперечное сечение указанной выше правой прямоугольной призмы представляет собой треугольник или равносторонний треугольник.

Вопрос 6:

Опишите поперечное сечение правой прямоугольной призмы, приведенной ниже, с названием ее формы.

Ответ:

Поперечное сечение правой прямоугольной призмы выше представляет собой прямоугольник.

Вопрос 7:

Опишите поперечное сечение правой прямоугольной призмы, приведенной ниже, с названием ее формы.

Ответ:

Поперечное сечение правой прямоугольной призмы выше треугольное.

Вопрос 8:

Опишите поперечное сечение правой прямоугольной призмы, приведенное ниже, с названием ее формы.

Ответ:

Поперечное сечение правой прямоугольной призмы выше представляет собой кривую в форме радуги.

Вопрос 9:

Возможно ли круглое сечение в правой прямоугольной призме?

Ответ:

Нет, в правой прямоугольной призме нет кривых.

Вопрос 10:

Показана правая прямоугольная пирамида с неквадратным основанием.

(В правой пирамиде точка, где встречаются треугольные стороны, центрирована над основанием.)

Какова форма основания и каждой стороны пирамиды?

Ответ:

Форма основания — прямоугольник, а форма каждой стороны — треугольник.

Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.

Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:

[email protected]

Мы всегда ценим ваши отзывы.

Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.

ЗАДАЧИ СО СЛОВАМИ

Задачи со словами HCF и LCM

Задачи со словами на простых уравнениях

Задачи со словами на линейных уравнениях

Задачи со словами на квадратных уравнениях

Алгебраные задачи со словами

Проблемы со словами в поездах

Проблемы со словами по площади и периметру

Проблемы со словами по прямой и обратной вариациям

Проблемы со словами по цене за единицу

Проблемы со словами по цене за единицу

Word Задачи по сравнению ставок

Преобразование обычных единиц в текстовые задачи

Преобразование в метрические единицы в словесных задачах

Словесные задачи по простому проценту

Словесные задачи по сложным процентам

Текстовые задачи по типам ngles

Проблемы с дополнительными и дополнительными углами в словах

Проблемы со словами с двойными фактами

Проблемы со словами тригонометрии

Проблемы со словами в процентах

Проблемы со словами о прибылях и убытках

Разметка и разметка Задачи

Задачи с десятичными словами

Задачи со словами о дробях

Задачи со словами о смешанных фракциях

Одношаговые задачи с уравнениями со словами

Проблемы со словами о линейных неравенствах

задачи

Проблемы со временем и рабочими словами

Задачи со словами на множествах и диаграммах Венна

Задачи со словами на возрастах

Проблемы со словами по теореме Пифагора

Процент числового слова pr проблемы

Проблемы со словами при постоянной скорости

Проблемы со словами при средней скорости

Проблемы со словами на сумме углов треугольника 180 градусов

ДРУГИЕ ТЕМЫ

Сокращения прибылей и убытков

Сокращения в процентах

Сокращения в таблице времен

Сокращения времени, скорости и расстояния

Сокращения соотношения и пропорции

Домен и диапазон рациональных функций

Домен и диапазон рациональных функций функции с отверстиями

График рациональных функций

График рациональных функций с отверстиями

Преобразование повторяющихся десятичных знаков в дроби

Десятичное представление рациональных чисел

Поиск квадратного корня с помощью длинного di видение

L.Метод CM для решения временных и рабочих задач

Преобразование задач со словами в алгебраические выражения

Остаток при делении 2 в степени 256 на 17

Остаток при делении 17 в степени 23 на 16

Сумма всех трехзначных чисел, делимых на 6

Сумма всех трехзначных чисел, делимых на 7

Сумма всех трехзначных чисел, делимых на 8

Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4

Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами

Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3

Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6

Объем призм — пояснения и примеры

Объем призмы — это общая площадь, занимаемая призмой.В этой статье вы узнаете, как найти объем призмы, используя формулу объема призмы.

Прежде чем мы начнем, давайте сначала обсудим, что такое призма. По определению призма — это геометрическая сплошная фигура с двумя одинаковыми концами, плоскими гранями и одинаковым поперечным сечением по всей длине .

Призмы названы в честь формы их поперечного сечения . Например, призма с треугольным поперечным сечением известна как треугольная призма. Другие примеры призм включают прямоугольную призму.пятиугольная призма, шестиугольная призма, трапецеидальная призма и т. д.

Как определить объем призмы?

Чтобы определить объем призмы, вам потребуется площадь и высота призмы. Объем призмы рассчитывается путем умножения площади основания и высоты. Объем призмы также измеряется в кубических единицах, то есть в кубических метрах, кубических сантиметрах и т. Д.

Формула объема призмы

Формула для расчета объема призмы зависит от поперечного сечения или основания призмы .Поскольку мы уже знаем формулу для вычисления площади многоугольников, определить объем призмы так же просто, как круговой.

Общая формула объема призмы имеет вид;

Объем призмы = площадь основания × длина

Где основание — это форма многоугольника, который выдавливается для образования призмы.

Обсудим объем различных типов призм.

Объем треугольной призмы

Треугольная призма — это призма, поперечное сечение которой представляет собой треугольник.

Формула объема треугольной призмы имеет вид;

Объем треугольной призмы = ½ abh

, где

a = апофема треугольной призмы.

Апофема многоугольника — это линия, соединяющая центр многоугольника с серединой одной из сторон многоугольника. Апофема треугольника — это высота треугольника.

b = длина основания треугольника

h = высота призмы.

Пример 1

Найдите объем треугольной призмы, апофема которой равна 12 см, длина основания — 16 см, а высота — 25 см.

Решение

По формуле треугольной призмы

объем = ½ abh

= ½ x 12 x 16 x 25

= 150 см ³

Пример 2

Найти объем призмы высотой 10 см, а в поперечном сечении равносторонний треугольник со стороной 12 см.

Решение

Найдите апофему треугольной призмы.

По теореме Пифагора,

h ² + 6 ² = 12 ²

h ² + 36 = 144

h ² = 108

h = 108

h =4 см

Следовательно, апофема призмы составляет 10,4 см

Объем = ½ abh

= ½ x 10,4 x 12 x 10

= 624 см ³

Объем пятиугольной призмы

Для пятиугольной призмы объем определяется по формуле:

Объем пятиугольной призмы = (5/2) abh

Где,

a = апофема пятиугольника

b = длина основания пятиугольной призмы

h = высота призмы.

Пример 3

Найдите объем пятиугольной призмы с апофемой 10 см, длиной основания 20 см и высотой 16 см.

Раствор

Объем пятиугольной призмы = (5/2) abh

= (5/2) x 10 x 20 x 16

= 8000 см ³

Объем шестиугольной призмы

Шестиугольная призма имеет шестиугольник в качестве основания или поперечного сечения. Объем шестиугольной призмы определяется как:

Объем шестиугольной призмы = 3abh

, где

a = апофема длина шестиугольника

b = базовая длина шестиугольной призмы

h = высота призма.

Пример 4

Рассчитайте объем шестиугольной призмы с апофемой 5 м, длиной основания 12 м и высотой 6 м.

Решение

Объем шестиугольной призмы = 3abh

= 3 x 5 x 12 x 6

= 1080 м ³ .

В качестве альтернативы, если апофема призмы неизвестна, объем любой призмы рассчитывается следующим образом;

Объем призмы = (h) (n) (s ² ) / [4 tan (180 / n)]

Где h = высота призмы

s = длина стороны экструдированного стержня многоугольник.

n = количество сторон многоугольника

tan = касательная:

ПРИМЕЧАНИЕ: Эта формула применяется только тогда, когда основание или поперечное сечение призмы является правильным многоугольником.

Пример 5

Найдите объем пятиугольной призмы с высотой 0,3 м и длиной стороны 0,1 м.

Решение

В данном случае n = 5,

h = 0,3 м и s = 0,1 м

При подстановке

Объем пятиугольной призмы = (0.3) (5) (0,1 ² ) / [4 tan (180/5)]

= 0,015 / 4 tan 36

= 0,015 / 2,906

= 0,00516 м ³ .

Предыдущий урок | Главная страница | Следующий урок

Поперечное сечение, типы, свойства, формулы, решенные проблемы и часто задаваемые вопросы

Призма имеет очень прочную форму, которая состоит из двух одинаковых концов (например, треугольника, квадрата, прямоугольника и т. Д.), Плоских граней или поверхностей и однородного поперечного сечения по всей длине.Поперечное сечение выглядит как треугольник, отсюда и название треугольных призм. Форма призмы не имеет кривой. Таким образом, призма также может иметь квадратную, прямоугольную, пятиугольную и многие другие формы многоугольника, но не круглую.

Поперечное сечение призмы

Поперечное сечение — это точка, в которой форма получается пересечением объекта плоскостью вдоль его оси. Это также называют вырезанием трехмерного объекта плоскостью для получения другой формы.

Если призму пересекает плоскость, параллельная основанию, то форма поперечного сечения будет такой же, как у основания.Например, квадратная пирамида разрезается плоскостью, параллельной основанию, тогда форма поперечного сечения пирамиды также будет квадратной.

Типы призм

В зависимости от поперечного сечения призмам присваиваются названия. Он бывает двух типов, а именно;

• Обычная призма

• Неправильная призма

Обычная призма

Если основание призмы имеет форму правильного многоугольника, она называется правильной призмой.

Неправильная призма

Если основание призмы имеет форму неправильного многоугольника, то призма называется неправильной призмой.

Призма на основе формы оснований

На основании формы оснований она подразделяется на различные типы, а именно;

• Призма треугольная (с треугольным основанием).

• Квадратная призма (с квадратным основанием).

• Прямоугольная призма (с прямоугольным основанием).

• Пятиугольная призма (с пятиугольным основанием).

• Призма шестигранная (с шестиугольным основанием).

Правая призма и наклонная призма

Помимо обычной и неправильной призмы часто подразделяют еще на два типа;

Различия между призмами для треугольных оснований приведены ниже;

Разница между правой и наклонной призмой

Правая призма	Наклонная призма
Если грани и, следовательно, соединяющиеся кромки перпендикулярны нижним граням, то это относится как правая призма	Если грани и соединяемые кромки не перпендикулярны нижним граням, то это называется наклонной призмой
В правой призме боковые грани представляют собой прямоугольники	В наклонной призме боковые грани представляют собой параллелограммы
Площадь поверхности равна сумме [Базовая длина × высота] + 2 [длина призмы × длина стороны] + [длина призмы × длина основания]	Площадь поверхности равна [Длина основания × высота] + 2 [длина призмы × длина стороны] + [длина призмы × длина основания]
Объем равен ½ [длина основания × высота × длина призмы]	Объем равен ½ [длина основания × высота × длина призмы]

Свойства призмы

1. Призма может быть своего рода трехмерной (3D) форма с плоскими сторонами.

2. Он имеет два конца эквивалентной формы и размера (и выглядит как двумерная форма).

3. Имеет эквивалентное поперечное сечение по форме от конца до конца; это означает, что если вы сузите его, вы увидите эквивалентную 2D-форму на обоих концах.

Формулы (площадь поверхности и объем)

Формулы определены для площади и объема призмы. Поскольку призма может иметь трехмерную форму, поэтому оба свойства, т.е.е., площадь поверхности и объем.

Объем призмы

Объем призмы определяется произведением площади дна и, следовательно, высоты призмы.

Следовательно,

Например, если вы хотите найти объем квадратной призмы, то важно знать площадь квадрата, тогда его объем можно рассчитать следующим образом:

Объем квадратной призмы равняется площади для квадрата × высота.

V = s ² × h кубических единиц

Где «s» — сторона квадрата.

Площадь поверхности призмы

Площадь поверхности призмы равна общей площади, покрытой гранями призмы.

Для любого типа призмы площадь поверхности может быть найдена по указанной формуле;

Решенные задачи

Пример 1. Найдите объем заданной треугольной призмы, площадь которой задана равной 60 см2, а заданная высота равна 7 см.

Решение: Дано,

Площадь основания = 60 см2

Высота = 7 см

Мы знаем, что

Объем призмы равен (Площадь основания × Высота) кубических единиц

Следовательно, V = 60 × 7 = 420

Следовательно, объем треугольной призмы = 420 см3.

Пример 2: Найдите высоту квадратной призмы, объем которой равен 360 см ³ , а площадь основания 60 см ² .