Реферат по математике система счисления: Реферат по математике на тему: » Системы счисления»
Доклад по математике «Системы счисления»
Доклад на тему:
Системы счисления
(позиционная и непозиционная)
СИСТЕМЫ СЧИСЛЕНИЯ
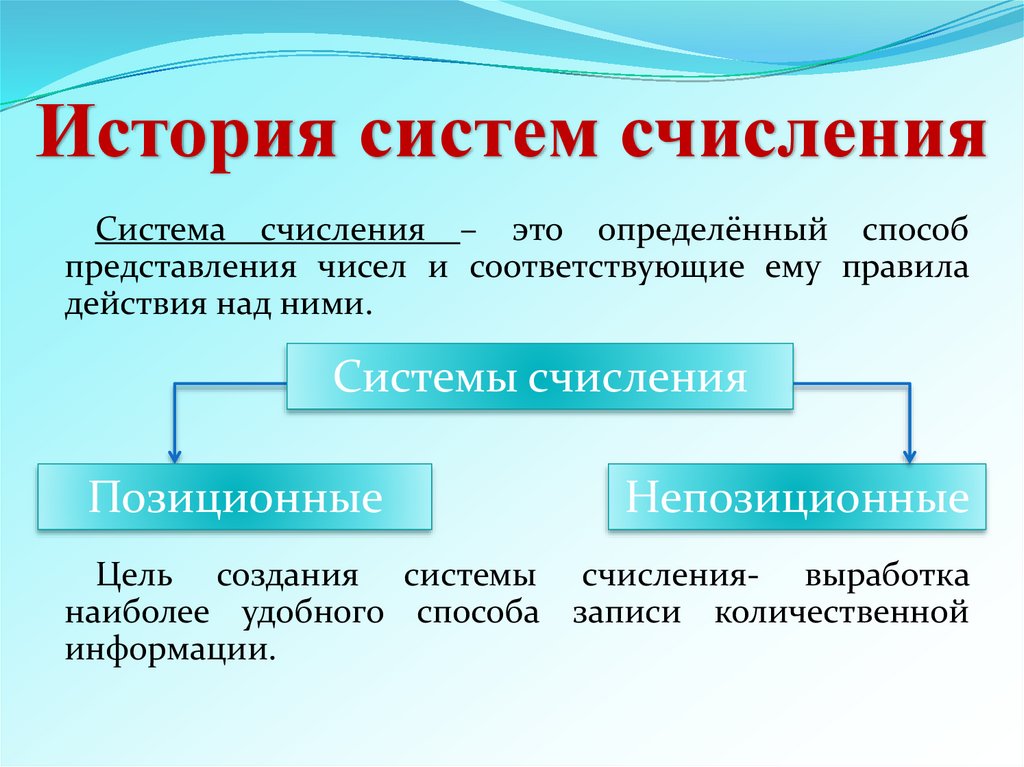
СИСТЕМЫ СЧИСЛЕНИЯ (нумерация) – совокупность способов обозначения натуральных чисел.
На
ранних ступенях развития общества люди почти не умели считать. Они различали
совокупности двух и трех предметов; всякая совокупность, содержавшая бóльшее
число предметов, объединялась в понятии «много». Предметы при счете
сопоставлялись обычно с пальцами рук и ног. По мере развития цивилизации
потребность человека в счете стала необходимой. Первоначально натуральные числа
изображались с помощью некоторого количества черточек или палочек, затем для их
изображения стали использовать буквы или специальные знаки. В древнем Новгороде
использовалась славянская система, где применялись буквы славянского алфавита;
при изображении чисел над ними ставился знак ~ (титло).
Древние римляне пользовались нумерацией, сохраняющейся до настоящего времени под именем «римской нумерации», в которой числа изображаются буквами латинского алфавита. Сейчас ею пользуются для обозначения юбилейных дат, нумерации некоторых страниц книги (например, страниц предисловия), глав в книгах, строф в стихотворениях и т.д. В позднейшем своем виде римские цифры выглядят так:
I = 1; V = 5; X = 10; L = 50; С = 100; D = 500; M = 1000.
О
происхождении римских цифр достоверных сведений нет. Цифра V могла
первоначально служить изображением кисти руки, а цифра Х могла составиться из
двух пятерок. В римской нумерации явственно сказываются следы пятеричной
системы счисления. Все целые числа (до 5000) записываются с помощью повторения
вышеприведенных цифр. При этом, если бóльшая цифра стоит перед меньшей, то они
складываются, если же меньшая стоит перед бóльшей (в этом случае она не может
повторяться), то меньшая вычитается из бóльшей). Например, VI = 6, т.е. 5 + 1,
IV = 4, т.
Первые 12 чисел записываются в римских цифрах так:
I, II, III, IV, V, VI, VII, VIII. IX, X, XI, XII.
Другие же числа записываются, например, как:
XXVIII = 28; ХХХIХ = 39; CCCXCVII = 397; MDCCCXVIII = 1818.
Выполнение арифметических действий над многозначными числами в этой записи очень трудно. Тем не менее, римская нумерация преобладала в Италии до 13 в., а в других странах Западной Европы – до 16 в.
В славянской системе нумерации для записи чисел использовались все буквы алфавита, правда, с некоторым нарушением алфавитного порядка. Различные буквы означали различное количество единиц, десятков и сотен. Например, число 231 записывалось в виде ~ СЛА (C – 200, Л – 30, А – 1).
Этим
системам свойственны два недостатка, которые привели к их вытеснению другими:
необходимость большого числа различных знаков, особенно для изображения больших
чисел, и, что еще важнее неудобство выполнения арифметических операций.
Более удобной и общепринятой и наиболее распространенной является десятичная система счисления, которая была изобретена в Индии, заимствована там арабами и затем через некоторое время пришла в Европу. В десятичной системе счисления основанием является число 10.
Существовали системы исчисления и с другими основаниями. В Древнем Вавилоне, например, применялась шестидесятеричная система счисления. Остатки ее мы находим в сохранившемся до сих пор делении часа или градуса на 60 минут, а минуты – на 60 секунд.
Широкое
распространение имела в древности и двенадцатеричная система, происхождение
которой, вероятно, связано, как и десятичной системы, со счетом на пальцах: за
единицу счета принимались фаланги (отдельные суставы) четырех пальцев одной
руки, которые при счете перебирались большим пальцем той же руки. Остатки этой
системы счисления сохранились и до наших дней и в устной речи, и в обычаях.
Хорошо известно, например, название единицы второго разряда – числа 12 –
«дюжина».
Самой молодой системой счисления по праву можно считать двоичную. Эта система обладает рядом качеств, делающей ее очень выгодной для использования в вычислительных машинах и в современных компьютерах.
Позиционные
и непозиционные системы счисления.
Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить на непозиционные и позиционные. Знаки, используемые при записи чисел, называются цифрами.
В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает. Примером непозиционной системы счисления является римская система, в которой в качестве цифр используются латинские буквы.
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количество используемых цифр называется основанием системы счисления. Место каждой цифры в числе называется позицией. Первая известная нам система, основанная на позиционном принципе – шестидесятeричная вавилонская. Цифры в ней были двух видов, одним из которых обозначались единицы, другим – десятки.
Однако
наиболее употребительной оказалась индо-арабская десятичная система. Индийцы
первыми использовали ноль для указания позиционной значимости величины в строке
цифр.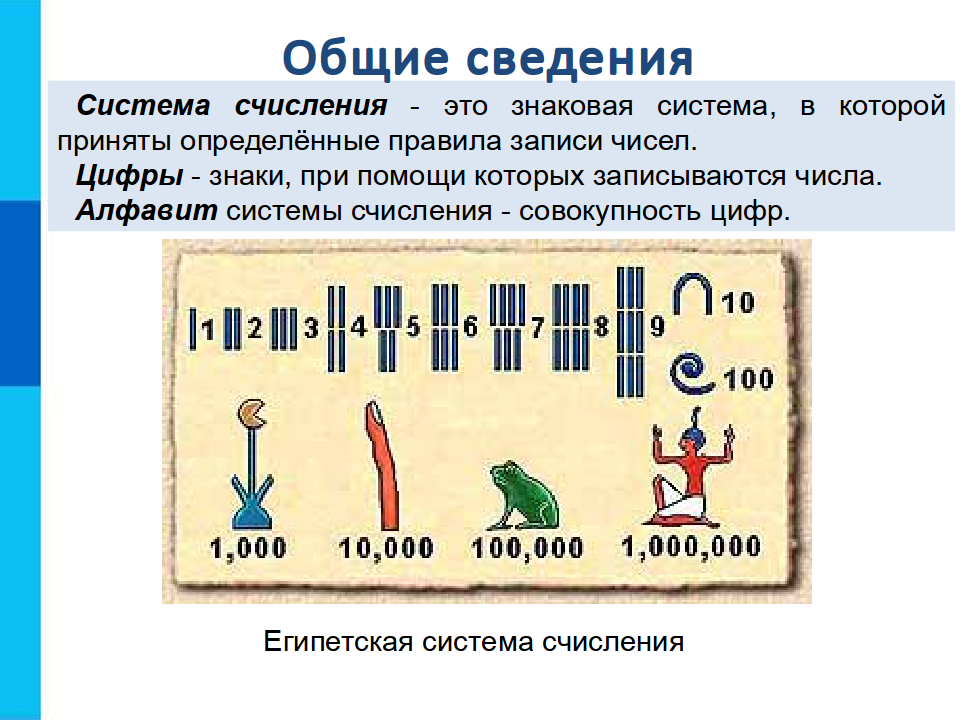 Эта система получила название десятичной, так
как в ней десять цифр.
Эта система получила название десятичной, так
как в ней десять цифр.
Различие между позиционой и непозиционной систем счисления легче всего понять на примере сравнения двух чисел. В позиционной системе счисления сравнение двух чисел происходит следующим образом: в рассматриваемых числах слева направо сравниваются цифры, стоящие в одинаковых позициях. Бóльшая цифра соответствует бóльшему значению числа. Например, для чисел 123 и 234, 1 меньше 2, поэтому число 234 больше, чем число 123. В непозиционной системе счисления это правило не действует. Примером этого может служить сравнение двух чисел IX и VI. Несмотря на то, что I меньше, чем V, число IX больше, чем число VI.
Позиционные системы счисления.
Основание
системы счисления, в которой записано число, обычно обозначается нижним
индексом. Например, 5557 –
число, записанное в семеричной системе счисления. Если число записано в десятичной
системе, то основание, как правило, не указывается. Основание системы – это
тоже число, и его мы будем указывать в обычной десятичной системе.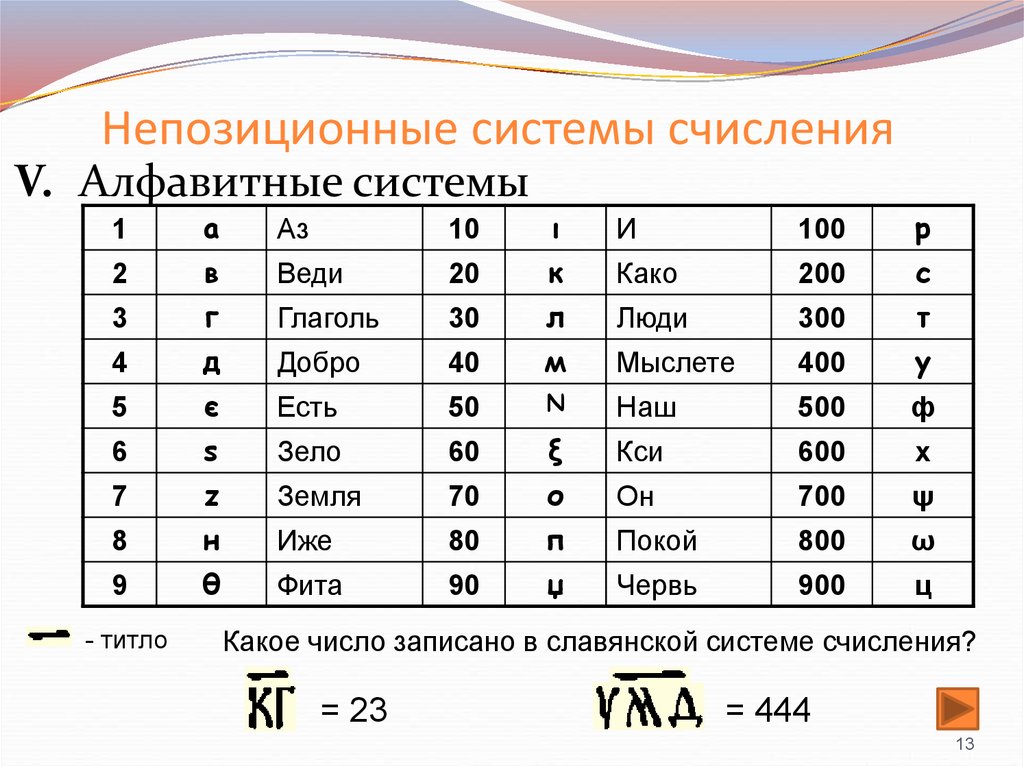
103510=1·103 + 0·102 + 3·101 + 5·100;
10102 = 1·23 + 0·22 + 1·21 + 0·20 = 10.
Наибольший интерес при работе на ЭВМ представляют системы счисления с основаниями 2, 8 и 16. Вообще говоря, этих систем счисления обычно хватает для полноценной работы как человека, так и вычислительной машины, однако иногда в силу различных обстоятельств все-таки приходится обращаться к другим системам счисления, например к троичной, семеричной или системе счисления по основанию 32.
Чтобы
оперировать с числами, записанными в таких нетрадиционных системах, нужно иметь
в виду, что принципиально они ничем не отличаются от привычной десятичной. Сложение, вычитание, умножение в них осуществляется по одной и той же схеме.
Сложение, вычитание, умножение в них осуществляется по одной и той же схеме.
Почему же не используются другие системы счисления? В основном, потому, что в повседневной жизни люди привыкли пользоваться десятичной системой счисления, и не требуется никакая другая. В вычислительных же машинах используется двоичная система счисления, так как оперировать числами, записанными в двоичном виде, довольно просто.
Часто в информатике используют шестнадцатеричную систему, так как запись чисел в ней значительно короче записи чисел в двоичной системе. Может возникнуть вопрос: почему бы не использовать для записи очень больших чисел систему счисления, например по основанию 50? Для такой системы счисления необходимы 10 обычных цифр плюс 40 знаков, которые соответствовали бы числам от 10 до 49 и вряд ли кому-нибудь понравится работать с этими сорока знаками. Поэтому в реальной жизни системы счисления по основанию, большему 16, практически не используются.
Наиболее часто встречающиеся системы счисления – это двоичная,
шестнадцатеричная и десятичная. Как же связаны между собой представления числа
в различных системах счисления? Есть различные способы перевода чисел из одной
системы счисления в другую на конкретных примерах.
Как же связаны между собой представления числа
в различных системах счисления? Есть различные способы перевода чисел из одной
системы счисления в другую на конкретных примерах.
Пусть нужно перевести число 567 из десятичной в двоичную систему. Сначала определяется максимальная степень двойки, такая, чтобы два в этой степени было меньше или равно исходному числу. В данном случае это 9, т.к. 29 = 512, а 210

Седьмой разряд также оказывается нулевым. Искомая двоичная запись числа принимает вид 1000хххххх. 25 = 32 < 55, поэтому шестой разряд равен 1 (результат 10001ххххх). Для остатка 55 – 32 = 23 справедливо неравенство 24 = 16 < 23, что означает равенство единице пятого разряда. Аналогично получается в результате число 1000110111. Это число разлагается по степеням двойки:
567 = 1·29 + 0·28 + 0·27 + 0·26 + 1·25 + 1·24 + 0·23 + 1·22 + 1·21 + 1·20
При другом способе перевода чисел используется операция деления
в столбик. Если взять то же число 567 и разделить его на 2, получается частное
283 и остаток 1. Та же операция производится и с числом 283. Частное – 141,
остаток – 1. Опять полученное частное делится на 2 и так до тех пор, пока
частное не станет меньше делителя. Теперь, чтобы получить число в двоичной
системе счисления, достаточно записать последнее частное, т.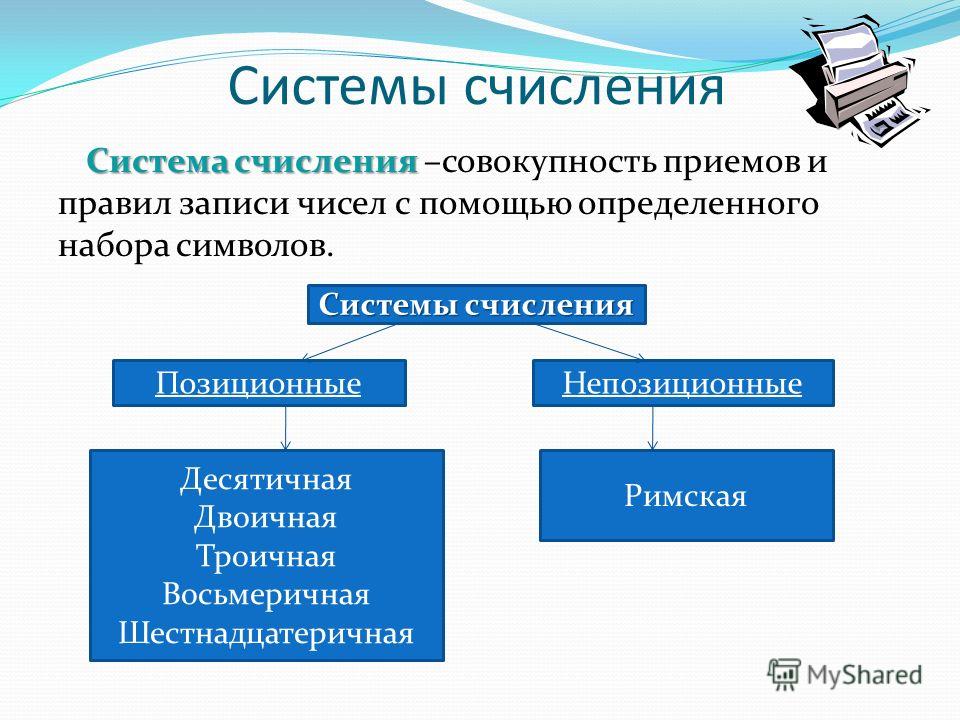 е. 1, и приписать к
нему в обратном порядке все полученные в процессе деления остатки.
е. 1, и приписать к
нему в обратном порядке все полученные в процессе деления остатки.
Результат, естественно, не изменился: 567 в двоичной системе счисления записывается как 1 000 110 111.
Эти два способа применимы при переводе числа из десятичной системы в систему с любым основанием. Например, при переводе числа 567 в систему счисления с основанием 16 число сначала разлагается по степеням основания. Искомое число состоит из трех цифр, т.к. 162 = 256 < 567 < 163 = 4096. Определяется цифра старшего разряда. 2·162 = 512 < 567 < 3·162 = 768, следовательно, искомое число имеет вид 2хх, где вместо х могут стоять любые шестнадцатеричные цифры. Остается распределить по следующим разрядам число 55 (567 – 512). 3·16 = 48 < 55 < 4·16 = 64, значит во втором разряде находится цифра 3. Последняя цифра равна 7 (55 – 48). Искомое шестнадцатеричное число равно 237.
Второй способ состоит в последовательном делении в столбик, с
единственным отличием в том, что делить надо не на 2, а на 16, и процесс
деления заканчивается, когда частное становится строго меньше 16.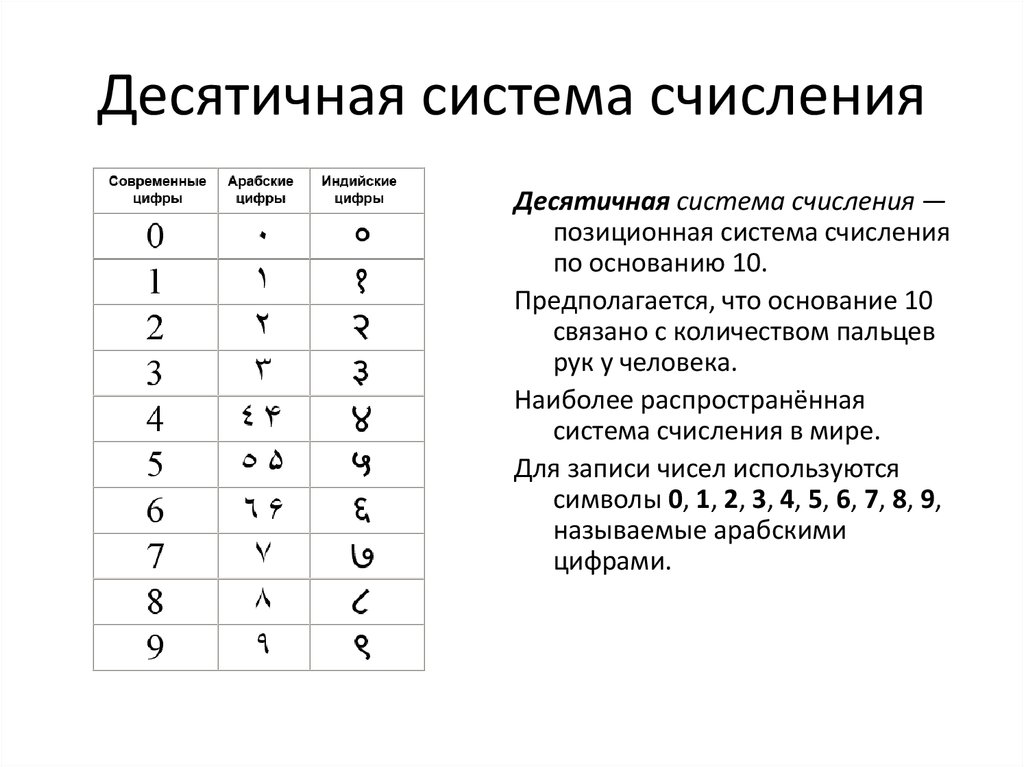
Конечно, для записи числа в шестнадцатеричной системе счисления, необходимо заменить 10 на A, 11 на B и так далее.
Операция перевода в десятичную систему выглядит гораздо проще, так как любое десятичное число можно представить в виде x = a0·pn + a1·pn–1 +… + an–1·p1 + an·p0, где a0 … an – это цифры данного числа в системе счисления с основанием p.
Например,так можно перевести число 4A3F в десятичную систему. По определению, 4A3F= 4·163 + A·162 + 3·16 + F. При замене A на 10, а F на 15, получается 4·163 + 10·162 + 3·16 + 15= 19007.
Проще всего переводить числа из двоичной системы в системы с
основанием, равным степеням двойки (8 и 16), и наоборот. Для того чтобы целое
двоичное число записать в системе счисления с основанием 2n,
нужно данное двоичное число разбить справа налево на группы по n-цифр в каждой; если в
последней левой группе окажется меньше n разрядов, то дополнить ее нулями до
нужного числа разрядов; рассмотреть каждую группу, как n-разрядное двоичное число, и
заменить ее соответствующей цифрой в системе счисления с основанием 2n.
Таблица 1. Двоично-шестнадцатеричная таблица | ||||||||
Таблица 1. ДВОИЧНО-ШЕСТНАДЦАТЕРИЧНАЯ ТАБЛИЦА | ||||||||
2-ная | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
16-ная | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
2-ная | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
16-ная | 8 | 9 | A | B | C | D | E | F |
Таблица
2. | ||||||||
Таблица 2. ДВОИЧНО-ВОСЬМЕРИЧНАЯ ТАБЛИЦА | ||||||||
2-ная | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
8-ная | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Известный французский астроном, математик и физик Пьер Симон
Лаплас(1749–1827) писал об историческом развитии систем счисления, что
«Мысль выражать все числа девятью знаками, придавая им, кроме значения по
форме, еще значение по месту, настолько проста, что именно из-за этой простоты
трудно понять, насколько она удивительна. Как нелегко было прийти к этому
методу, мы видим на примере величайших гениев греческой учености Архимеда и
Аполлония, от которых эта мысль осталась скрытой.»
Как нелегко было прийти к этому
методу, мы видим на примере величайших гениев греческой учености Архимеда и
Аполлония, от которых эта мысль осталась скрытой.»
Сравнение десятичной системы исчисления с иными позиционными системами позволило математикам и инженерам-конструкторам раскрыть удивительные возможности современных недесятичных систем счисления, обеспечившие развитие компьютерной техники.
Реферат на тему: Система счисления
Оглавление:
У вас нет времени на реферат или вам не удаётся написать реферат? Напишите мне в whatsapp — согласуем сроки и я вам помогу!
В статье «Как научиться правильно писать реферат», я написала о правилах и советах написания лучших рефератов, прочитайте пожалуйста.
Собрала для вас похожие темы рефератов, посмотрите, почитайте:
- Реферат на тему: Источники права
- Реферат на тему: Инфаркт миокарда
- Реферат на тему: Мировые религии
- Реферат на тему: Гепатиты
Введение
На
протяжении всей жизни мы сталкиваемся с числами и выполняем с ними
арифметические операции. Это нас не удивляет. Мы принимаем это как факт. И
откуда взялись цифры и результат? Что такое цифровая система? Где мы теперь с
ними встретимся? Мне было очень интересно, поэтому я решил изучить этот
предмет.
Это нас не удивляет. Мы принимаем это как факт. И
откуда взялись цифры и результат? Что такое цифровая система? Где мы теперь с
ними встретимся? Мне было очень интересно, поэтому я решил изучить этот
предмет.
Эта тема интересна и для меня, так как двоичная система счисления в настоящее время стала очень важной в связи с ее использованием в электронных компьютерах. Численные системы с базами 8 и 16 используются в программировании различных процессов на компьютерах.
Я поставил перед собой цель: познакомиться с историей возникновения счетных и числовых систем, изучить числовые системы, используемые в вычислениях, позиционные и непозиционные числовые системы, а также арифметические действия в различных системах. В данной диссертации рассматриваются различные вычислительные системы.
История происхождения систем счисления
В
древние времена людям приходилось рассчитывать на пальцы. Кроме пальцев, нужно
было сосчитать много испытуемых, на счету было больше участников. Один считал
единицы, второй — дюжины, третий — сотни. Очевидно, что такой расчет лег в
основу принятой почти всеми народами системы вычислений, называемой десятичной
системой. Расчет с базовой десяткой также применим к восточным славянам.
Один считал
единицы, второй — дюжины, третий — сотни. Очевидно, что такой расчет лег в
основу принятой почти всеми народами системы вычислений, называемой десятичной
системой. Расчет с базовой десяткой также применим к восточным славянам.
Там, где люди ходили босиком, их пальцы легко сосчитать до 20. Следы использования при подсчете до 20, например, во французском число 80 в буквальном переводе на русский звучит как «четырежды двадцать».
Были также распределены десятки аккаунтов, т.е. аккаунт, на котором использовалась система базы 12. Его происхождение связано с 12 фалангами на четырех пальцах (кроме большого). Даже сейчас некоторые пункты все еще считаются десятками. Столовые приборы состоят из полдюжины или дюжины комплектов.
В древнем Вавилоне, где математика была очень высоко развита, существовала очень сложная шестнадцатеричная система счисления. В настоящее время мы также используем эту систему. Например: 1 час=60 минут; 1 минута=60 секунд.
Самой
старой из систем пальцев считается система с пятью пальцами. Эта система
родилась и наиболее широко используется в Америке. Его происхождение восходит к
эпохе, когда человек считал на пальцах одной руки. До недавнего времени
некоторые племена сохранили пятипальцевую систему счисления в чистом виде.
Эта система
родилась и наиболее широко используется в Америке. Его происхождение восходит к
эпохе, когда человек считал на пальцах одной руки. До недавнего времени
некоторые племена сохранили пятипальцевую систему счисления в чистом виде.
Таким образом, все системы (пятикратные, двенадцатикратные, двадцати четырехкратные) соединены одним или другим способом счета пальцев ног (или рук и ног). Переход человека к счету пальцев привел к созданию различных систем подсчета. /1/
Численные системы, используемые в компьютерных технологиях
Система счисления — это система методов и правил, позволяющих установить взаимосогласованную связь между любым числом и его представлением в виде набора конечного числа символов. Многие символы, используемые для этого представления, называются цифрами.
В зависимости от того, как отображаются номера, они делятся на номера элементов и номера без элементов.
В
непозиционных системах каждое число определяется как особая функция числовых
значений набора чисел, представляющих это число. Числа в непозиционных системах
счисления соответствуют некоторым фиксированным числам. Исторически сложилось
так, что первыми вычислительными системами были непозиционные системы. Одним из
главных недостатков является сложность написания больших чисел. Написание
больших чисел в таких системах либо очень громоздко, либо системный алфавит
чрезвычайно велик. Не-позиционные системы не используются в компьютерных
технологиях.
Числа в непозиционных системах
счисления соответствуют некоторым фиксированным числам. Исторически сложилось
так, что первыми вычислительными системами были непозиционные системы. Одним из
главных недостатков является сложность написания больших чисел. Написание
больших чисел в таких системах либо очень громоздко, либо системный алфавит
чрезвычайно велик. Не-позиционные системы не используются в компьютерных
технологиях.
Система счисления называется позиционной, когда одна и та же цифра может принимать различные числовые значения в зависимости от того, какая позиция цифры присутствует в наборе цифр, представляющих определенное число. Примером такой системы является арабская десятичная система счисления.
Фактические количества и количественные пропорции могут быть отображены различными способами. Основа системы нумерации элементов определяет их название. В вычислениях используются двоичная, восьмеричная, десятичная и шестнадцатеричная системы. Чтобы явно указать используемую систему счисления, заключим номер в скобки и укажем основу системы счисления в нижнем индексе. Каждая числовая позиция соответствует коэффициенту положения (цифра) или весу.
Каждая числовая позиция соответствует коэффициенту положения (цифра) или весу.
В настоящее время позиционные системы охлаждения встречаются чаще, чем непозиционные. Это связано с тем, что они позволяют писать большие числа относительно небольшим количеством символов. Еще более важным преимуществом систем позиционирования является простота и легкость арифметических операций по сравнению с числами, написанными в этих системах.
Преобразование чисел в десятичную систему осуществляется путем суммирования последовательностей степеней, основанных на системе, из которой переводится число. Затем вычисляется суммарное значение.
Как правило, вычислительные машины могут быть встроены в любую систему счисления. Но такая общая десятичная система крайне непрактична для нас. Если в механических вычислительных машинах с десятичной системой достаточно использовать только один элемент с множеством состояний (колесо с десятью зубцами), то в электронных машинах в цепях необходимо иметь 10 различных потенциалов.
Системы без номеров позиций
В настоящее время как позиционные, так и непозиционные системы расчета широко используются как в технологии, так и в быту.
В системах без вычисления позиции вес фигуры не зависит от позиции, которую она занимает в номере. Примером непозиционной системы счисления является римская система счисления. Он появился в Древнем Риме и существует по сей день. Традиционно используется для нумерации веков или для создания оглавления печатных произведений. Римские цифры можно найти на циферблатах часов.
В
современной жизни наиболее показательным вариантом использования системы
непозиционного учета являются денежные отношения. Мы сталкиваемся с ними каждый
день. Никому не приходит в голову, что сумма, которую мы тратим на еду в
магазине, может зависеть от того, в каком порядке мы поставим монеты на стол.
Номинальная стоимость монеты не зависит от порядка, в котором она была взята из
кошелька. Это классический пример непозиционной системы подсчета.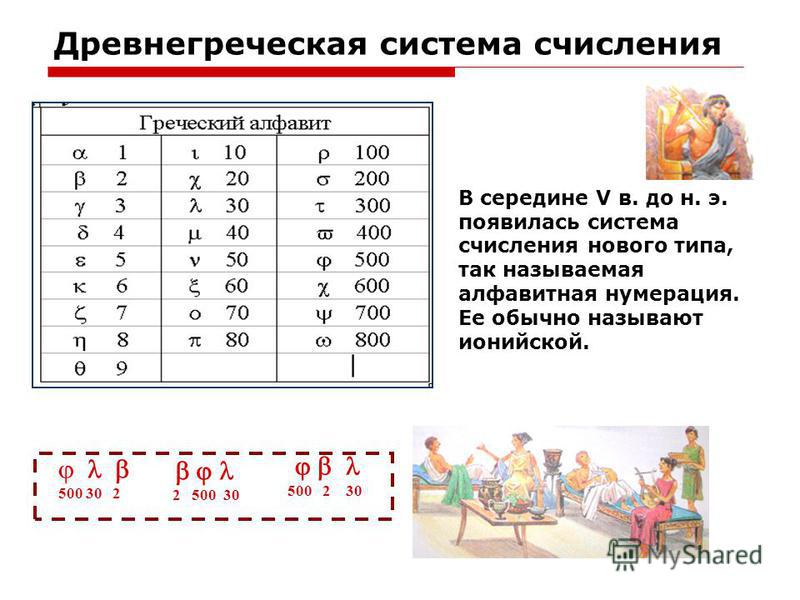
Это означает, что в настоящее время наиболее широко используется система позиционирования чисел.
Позиционные номера
В системах подсчета позиций вес каждой цифры изменяется в зависимости от ее положения в последовательности цифр, представляющих число. Каждая система позиций характеризуется своей базой. Основой системы нумерации элементов является количество различных символов или символов, используемых для представления цифр в этой системе. Любое натуральное число — два, три, четыре, шестнадцать и т.д. — может быть принято за основу. Следовательно, возможны бесконечные системы позиций: двоичные, состоящие из чисел 0 и 1; троичные, состоящие из чисел 0,1,2; и так далее.
Системы позиционирования удобны тем, что позволяют захватывать большие числа с небольшим количеством символов при выполнении простых и легко выполняемых арифметических операций.
Десятичная система счисления
Основой
десятичной системы числа 10 является число 10, которое является единицей второй
цифры, единицей третьей цифры будет 100 = 102, в общем случае единица каждой
следующей цифры в десять раз больше, чем единица предыдущей цифры
(предполагается, что выбор в качестве основы D. S. числа 10 связан с подсчетом
на пальцах).
S. числа 10 связан с подсчетом
на пальцах).
Д.С. С. основывается на принципе положения, т.е. один и тот же знак (число) имеет разное значение в зависимости от места его расположения. Поэтому только первые 10 цифр нуждаются в специальных символах, чтобы покрыть все цифры. Эти символы, которые обозначаются символами 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называются цифрами. Для захвата числа вы определяете, сколько единиц наибольшей цифры в нем содержится; остальное определяется как количество единиц наибольшей цифры, на единицу меньше, и т.д. Полученные цифры записываются бок о бок: например, 4×102 + 7×101 + 3×100 = 473.
При этом действия выполняются над числами в цифрах, т.е. отдельно над числами каждой цифры; если при этом числа складываются более чем до 10 (в случае сложения, умножения), то к следующей, более высокой цифре прибавляется одна или несколько единиц; в случае деления и вычитания, цифры должны быть разбиты на более мелкие.
Двоичная система счисления
Двоичная
система счисления, система счисления, основанная на позиционном принципе записи
чисел, с основой 2 Двоичная система счисления использует только два символа,
цифры 0 и 1, и, как и в любой позиционной системе, значение цифры также зависит
от ее позиции.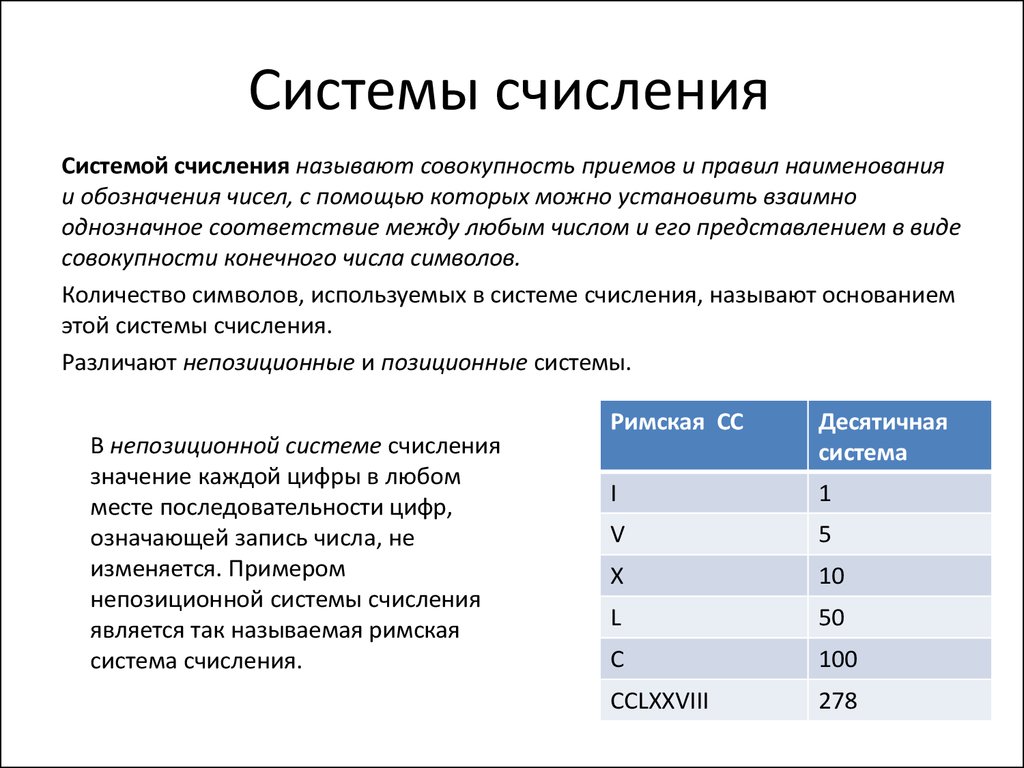 Цифра 2 считается единицей 2-й цифры и записывается следующим
образом: 10 (читать: «один, ноль»). Каждая единица следующей цифры в
два раза больше предыдущей, т.е. эти единицы образуют последовательность цифр
2, 4, 8, 16, … , 2n.
Цифра 2 считается единицей 2-й цифры и записывается следующим
образом: 10 (читать: «один, ноль»). Каждая единица следующей цифры в
два раза больше предыдущей, т.е. эти единицы образуют последовательность цифр
2, 4, 8, 16, … , 2n.
По числу, записанному в десятичной системе в D. S., он поочередно делится на 2, а получившиеся остатки 0 и 1 записываются в порядке от последнего к первому, например: 43 = 21-2 +1; 21 = 10-2 +1; 10 = 5-2 +0; 5 = 2-2 +1; 2 = 1-2 + 0; 1 = 0-2 + 1; таким образом, двоичный вход числа 43 равен 101011. Таким образом, в EPS 101011 обозначает 1-20+1-21 + 0×22 +1×23 + 0-24 + 1-25.
В D. S. все арифметические операции особенно просты: например, таблица умножения сводится к равенству 1-1 = 1. Однако, запись в D.S. очень громоздка: например, число 9000 будет иметь 14 цифр.
В связи с тем, что двоичная система счисления использует только две цифры, она часто полезна в теоретических вопросах и для вычислений на ДЦК.
Восьмикратная числовая система
Восьмая система счисления — это система позиционных целых чисел с базой 8.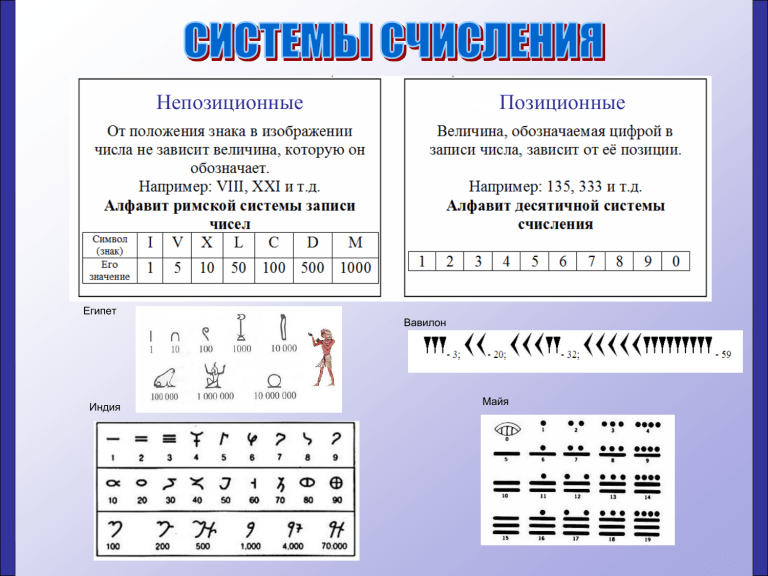 Для представления чисел используются 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Число 1 в нижней цифре означает только одну, как и в десятичной системе счисления. То же число 1 в следующей цифре означает 8, следующие 64 и так далее. Число 100 (восьмеричное) не более 64 (десятичное). Например, чтобы перевести число 611 (восьмеричное) в двоичную систему, каждая цифра должна быть заменена соответствующей двоичной триадой (три цифры). Легко догадаться, что для перевода многозначного двоичного числа в восьмеричной системе необходимо разделить его на триады справа налево и заменить каждую триаду соответствующим восьмеричным числом.
Для представления чисел используются 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Число 1 в нижней цифре означает только одну, как и в десятичной системе счисления. То же число 1 в следующей цифре означает 8, следующие 64 и так далее. Число 100 (восьмеричное) не более 64 (десятичное). Например, чтобы перевести число 611 (восьмеричное) в двоичную систему, каждая цифра должна быть заменена соответствующей двоичной триадой (три цифры). Легко догадаться, что для перевода многозначного двоичного числа в восьмеричной системе необходимо разделить его на триады справа налево и заменить каждую триаду соответствующим восьмеричным числом.
Восьмая система наиболее часто используется в областях, связанных с цифровым оборудованием. Например, восьмеричная система счисления служит самым простым языком общения человека с компьютером.
Шестнадцатеричная система счисления
Шестнадцатеричная
система счисления (шестнадцатеричные числа) — Позиционная система счисления на
целочисленном базисе 16 Запись чисел в восьмеричной системе счисления
достаточно компактна, но еще более компактна в шестнадцатеричной системе. В
качестве первых 10 из 16 шестнадцати десятичных цифр берутся обычные цифры 0,
1, 2, 3, 4, 5, 6, 7, 8, 9, а в качестве остальных 6 цифр используются первые
буквы латинского алфавита: A, B, C, D, E, F. Номер 1, написанный нижней цифрой,
означает только один. Одна и та же цифра 1 в следующей — 16 (после запятой),
следующая — 256 (после запятой) и т.д. Цифра F, записанная внизу цифры,
означает 15 (десятичная).
В
качестве первых 10 из 16 шестнадцати десятичных цифр берутся обычные цифры 0,
1, 2, 3, 4, 5, 6, 7, 8, 9, а в качестве остальных 6 цифр используются первые
буквы латинского алфавита: A, B, C, D, E, F. Номер 1, написанный нижней цифрой,
означает только один. Одна и та же цифра 1 в следующей — 16 (после запятой),
следующая — 256 (после запятой) и т.д. Цифра F, записанная внизу цифры,
означает 15 (десятичная).
Преобразование из шестнадцатеричной системы в двоичную и наоборот осуществляется таким же образом, как и для восьмеричной системы.
Шестнадцатеричная система счисления на сегодняшний день является самой популярной компактной программой записи двоичных чисел. Он широко использовался при разработке и проектировании цифровых технологий и, как восьмеричная система счисления, является простейшим языком для общения человека с компьютером.
Заключение
В
соответствии с целью исследований в работе я ознакомился с историей зарождения
исчисления и систем нотации, изучил системы нотации, используемые в
компьютерной технике, позиционные и непозиционные системы нотации, а также
арифметические действия в различных системах нотации.
После знакомства с компьютерными системами я узнал много нового и полезного, и считаю, что эта наука необходима для развития общества. Трудно представить мир без компьютеров. Это связано с тем, что именно бинарная система получила широкое распространение в различных областях техники, особенно в современных компьютерах и калькуляторах.
Система позиционирования номера состоит в использовании ограниченного числа цифр, но положение каждой цифры в номере обеспечивает значение (вес) этой цифры Положение цифры в числе называется цифрой в математическом языке.
Основой системы нумерации элементов является количество различных символов или символов (чисел), используемых для представления чисел в определенной системе.
Двоичная система счисления — наиболее широко используемая в компьютерах, так как одна цифра двоичного числа соответствует одному биту — минимальной единице информации в компьютерной технике
Для того, чтобы двоичные числа, которые достаточно сильно отличаются друг от друга по длине, более воспринимаемые и легче представляемые, сжимаются в восьмеричные и шестнадцатеричные числа.
В компьютерных технологиях все виды информации кодируются только числами, точнее числами, представленными в двоичной системе счисления — метод представления любого числа двумя символами (числами) по позиционному принципу.
Шестнадцатеричная система счисления широко используется как в низкоуровневом программировании, так и в компьютерной документации. Система восьмеричных чисел также иногда используется в компьютерах — по-видимому, чаще всего в определении прав в Unix-подобных операционных системах. Когда-то были компьютеры, которые использовали 24-битные и 36-битные слова. Шестизначная система счисления широко используется для подсчета минут и секунд. /4/. В целом, восьмеричная и шестнадцатеричная системы счисления являются самым простым языком общения человека с компьютером.
Я
думаю, что у моей работы есть перспективы, потому что тема числовых систем
достаточно сложна и обширна и может быть использована в реальной жизни. В моей
работе собраны и систематизированы все материалы на эту тему.
Надеюсь, что мою работу будут применять не только учителя, но и студенты.
Список литературы
- ФоминС.В. Числовые системы, издание 1987 г. Главная редакцияфизико-математической литературыиздательства»Наука».
- ГашковС.Б. Вычислительные системы и их применение, 2014 . Публикация: ICNSM.
- КовриженкоГ.А. Числовые системы и двоичная арифметика, 1983.
- Базовыекомпьютерные системы/Хабрахабр.
- Фринландский университет. Вычислительная техника. М., 2003.
- Сидоров В.К. Численные системы // Наука и жизнь 2000. №2.
- Радюк Л. алгоритм трансляции в двоичную систему счисления и из нее // Наука и жизнь. 2003. №1.
- РасселДжесси — Система двоичных чисел, 2014-е издание: Книгаспроса.
- КолмогоровА.Н. Система чисел, 1973 Издатель «Академия наук СССР
- Алексеев Е.Г., Богатырев С.Д. Информатика. Мультимедийный электронный учебник.
Числа и абстракция | Математика: очень краткое введение
Фильтр поиска панели навигации Oxford AcademicМатематика: очень краткое введениеОчень краткое введениеФилософия математики и логикиЧистая математикаКнигиЖурналы Мобильный телефон Введите поисковый запрос
Закрыть
Фильтр поиска панели навигации Oxford AcademicМатематика: очень краткое введениеОчень краткое введениеФилософия математики и логикиЧистая математикаКнигиЖурналы Введите поисковый запрос
Расширенный поиск
Иконка Цитировать Цитировать
Разрешения
- Делиться
- Твиттер
- Подробнее
Укажите
Гауэрс, Тимоти, «Числа и абстракция», Mathematics: A Very Short Introduction , Very Short Introductions (
Oxford, 2002; онлайн-издание, Oxford Academic, 24 сентября 2013 г. ), https://doi.org/10.1093 /actrade/9780192853615.003.0002, по состоянию на 23 марта 2023 г.
), https://doi.org/10.1093 /actrade/9780192853615.003.0002, по состоянию на 23 марта 2023 г.
Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Фильтр поиска панели навигации Oxford AcademicМатематика: очень краткое введениеОчень краткое введениеФилософия математики и логикиЧистая математикаКнигиЖурналы Мобильный телефон Введите поисковый запрос
Закрыть
Фильтр поиска панели навигации Oxford AcademicМатематика: очень краткое введениеОчень краткое введениеФилософия математики и логикиЧистая математикаКнигиЖурналы Введите поисковый запрос
Advanced Search
Abstract
«Числа и абстракция» объясняет абстрактный метод математики, который можно выразить в лозунге: математический объект есть то, что он делает , используя графовую модель шахмат. Затем он переходит к описанию натуральных чисел; понятие числа, тесно связанное с арифметическими действиями сложения и умножения; и коммутативные, ассоциативные и дистрибутивные законы сложения и умножения. Описаны также свойства числа ноль, отрицательные числа и дроби, действительные и комплексные числа, бесконечность, возведение чисел в отрицательные и дробные степени.
Затем он переходит к описанию натуральных чисел; понятие числа, тесно связанное с арифметическими действиями сложения и умножения; и коммутативные, ассоциативные и дистрибутивные законы сложения и умножения. Описаны также свойства числа ноль, отрицательные числа и дроби, действительные и комплексные числа, бесконечность, возведение чисел в отрицательные и дробные степени.
Ключевые слова: абстракция, ассоциативная, коммутативная, дистрибутивная, бесконечность, негативная абстракция, ассоциативная, коммутативная, дистрибутивная, бесконечность, негативная
Тема
Чистая математикаФилософия математики и логики
СерияКраткие введения
В настоящее время у вас нет доступа к этой главе.
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Нажмите Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением.
 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. - После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом.
 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. - После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. См. ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.

- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
Покупка
Наши книги можно приобрести по подписке или купить в библиотеках и учреждениях.
Информация о покупке
Математика: очень краткое введение
Иконка Цитировать Цитировать
Разрешения
- Делиться
- Твиттер
- Подробнее
Укажите
Гауэрс, Тимоти, Mathematics: A Very Short Introduction , Very Short Introductions (
Oxford, 2002; онлайн-издание, Oxford Academic, 24 сентября 2013 г. ), https://doi.org/10.1093/actrade/9780192853615.001.0001 , по состоянию на 16 марта 2023 г.
), https://doi.org/10.1093/actrade/9780192853615.001.0001 , по состоянию на 16 марта 2023 г.
Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Фильтр поиска панели навигации Oxford AcademicМатематика: очень краткое введениеОчень краткое введениеФилософия математики и логикиЧистая математикаКнигиЖурналы Мобильный телефон Введите поисковый запрос
Закрыть
Фильтр поиска панели навигации Oxford AcademicМатематика: очень краткое введениеОчень краткое введениеФилософия математики и логикиЧистая математикаКнигиЖурналы Введите поисковый запрос
Расширенный поиск
Abstract
Цель Математика: очень краткое введение состоит в том, чтобы объяснить, тщательно, но не технически, различия между высшей математикой исследовательского уровня и той математикой, которую мы изучаем в школе. Он предлагает читателям ознакомиться с такими, казалось бы, парадоксальными понятиями, как бесконечность, мнимые числа и искривленное пространство. Первые несколько глав посвящены общим аспектам математической мысли, за ними следуют главы по более конкретным темам, таким как пределы и бесконечность, размерность, геометрия, оценки и приближения. Он завершается некоторыми ответами на распространенные социологические вопросы о математическом сообществе.
Он предлагает читателям ознакомиться с такими, казалось бы, парадоксальными понятиями, как бесконечность, мнимые числа и искривленное пространство. Первые несколько глав посвящены общим аспектам математической мысли, за ними следуют главы по более конкретным темам, таким как пределы и бесконечность, размерность, геометрия, оценки и приближения. Он завершается некоторыми ответами на распространенные социологические вопросы о математическом сообществе.
Ключевые слова: абстракция, площадь, ассоциативный, коммутативный, Евклид, геометрия, бесконечность, математика, пространство, квадратный корень
Предмет
Чистая математикаФилософия математики и логики
Серия
Очень краткое знакомство
Содержание
Передний вопрос
- Страница авторского права
- Предисловие
- Список диаграмм
- Расширять 1
Модели
- Расширять 2
Числа и абстракция
- Расширять 3
Доказательства
- Расширять 4
Пределы и бесконечность
- Расширять 5
Измерение
- Расширять 6
Геометрия
- Расширять 7
Оценки и приближения
- Расширять 8
Некоторые часто задаваемые вопросы
Конечная Материя
- дальнейшее чтение
- Индекс
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Нажмите Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением.
 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. - После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом.
 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. - После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. См. ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.



 Двоично-восьмеричная таблица
Двоично-восьмеричная таблица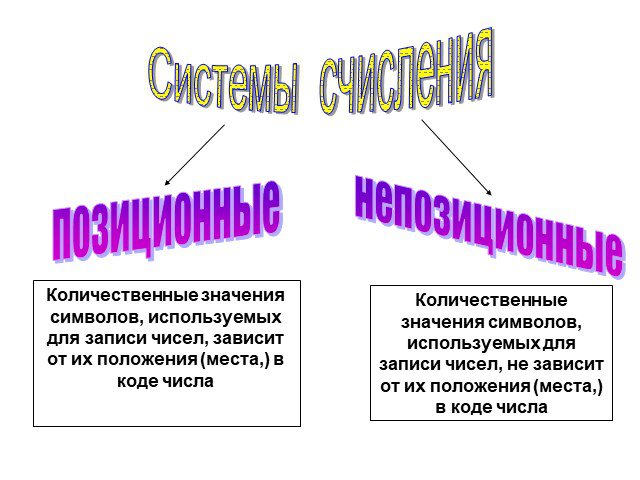 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic.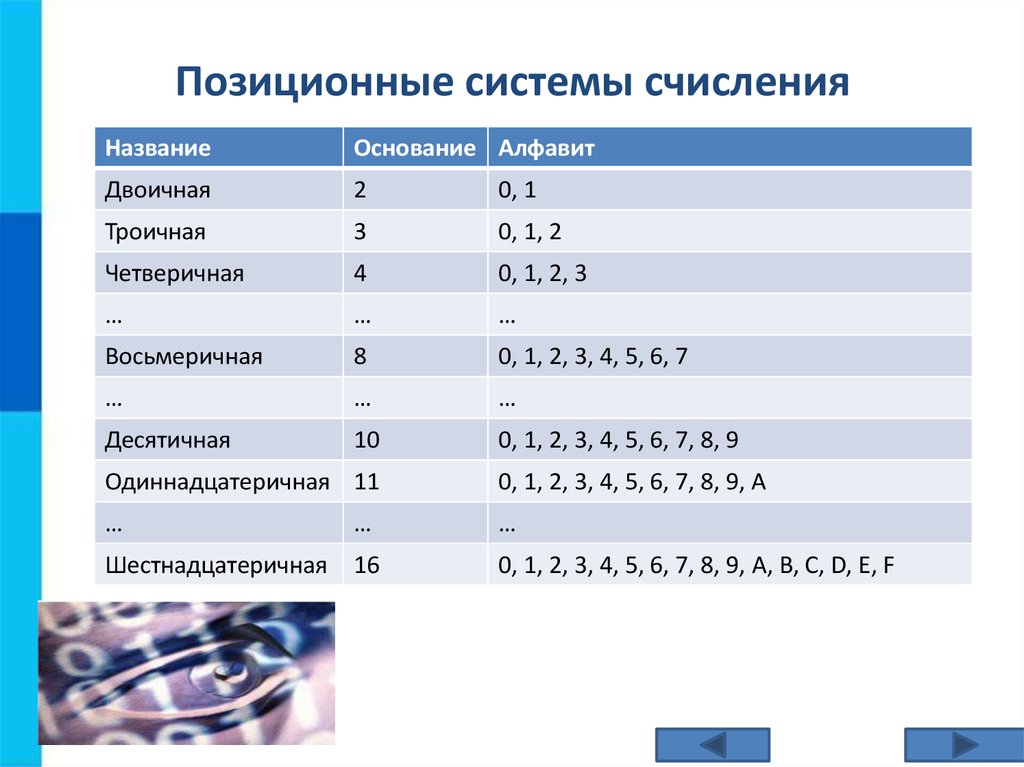 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic.
 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic.