Презентация числа от 1 до 5 закрепление изученного материала: «Числа от 1 до 5. Закрепление» Презентация к уроку математики 1 класс
Презентация «Закрепление знаний. Нумерация. Числа от 1 до 10 и число 0» 1 класс УМК «Школа России»
Урок математики в 1классе Тема урока: «Закрепление знаний. Числа от 1 до 10 и число 0.» (УМК «Школа России)
Учитель начальных классов
Лушавина И.Н.
Прочитай ряд чисел
1,2,3,6,5,4,7,8,9,10
10,9,8,7,6,5,4,3,2,1
1,2,3,4,5,6,7,8,9,10
Работа с веером
4
Сравните Сколько треугольников? Работа по учебнику с. 785 — 1
2 + 1
4 — 3
Проверим Работа в тетрадиУ Сашки в кармашке
Конфеты в бумажке.
Он дал по конфете Свете и Пете,
Ирине, Галине, Марине и Нине,
И сам съел конфету.
А больше и нету.
Сколько было конфет?
7
Пошла курочка гулять,
Собрала своих цыплят.
6 — бежали впереди,
3 – остались позади.
Беспокоится их мать
и не может сосчитать.
Посчитайте-ка, ребята,
Сколько было всех цыпляток?
9
Семь малюсеньких котят-
Что дают им –всё едят.
А один сметаны просит.
Сколько же котяток?
8
8 зайчат по дорожке идут.
За ними вдогонку двое бегут.
Так сколько ж всего
По дорожке лесной
Торопится в школу Зайчишек зимой?
10
Работа
по учебнику
С. 78
Работа в тетради на печатной основе с.28
Молодцы!
Источники- 1. М.И. Моро, С.И. Волкова. Математика. Учебник для 1 класса (1 часть) Учебник для общеобразовательных учреждений.- М.Просвещение 2018 г.
- 2. Учебно-методическое пособие. Поурочные разработки по математике. 1 класс. Е.П.Фефилова, О.А.Мокрушина. — Москва, «ВАКО», 2014
- 3.М.И. Моро, С.И. Волкова. Математика. Рабочая тетрадь. 1 часть.
- 4.О.В.Узорова, Е.А.Нефёдова. 3000 примеров по математике. Счёт в пределах 10. Устный счёт.
- 5. http://www.youloveit.ru/gallery/fixiki_kartinki/111336-fixiki-9.html
- 6. http://www.youloveit.
 ru/gallery/fixiki_kartinki/111328-fixiki-1.html
ru/gallery/fixiki_kartinki/111328-fixiki-1.html - 7. https://fb.ru/article/243052/lyubimyiy-multfilm-fiksiki-osnovnyie-geroi-kak-fiksikov-zovut
Урок по математике » Числа от 1 до 5 . Состав числа 5″.
Тема урока: Закрепление пройденного материала по теме «Числа от 1 до 5. Состав числа 5».
Тип урока: закрепление пройденного материала.
Формируемые УУД
*Регулятивные УУД
-уметь организовывать свое рабочее место и работу;
-принимать и сохранять учебную задачу через постановку темы, целей урока, через самостоятельную формулировку заданий для одноклассников
-планировать учебные действия с помощью плана, определять пути решения.
— оценивать результаты действия, через проверку выполненных заданий;
*Коммуникативные УУД
— ставить учебные задачи в сотрудничестве с учителем в совместной постановке целей и темы урока;
— уметь задавать вопросы, договариваться, уступать
*Познавательные УУД
— осуществлять поиск необходимой информации для выполнения учебных заданий;
— строить речевое высказывание в устной и в письменной форме;
Планируемые результаты:
— учащиеся научатся определять место чисел в натуральном ряду;
— определять состав чисел 2,3,4 5;
— соотносить цифру и число;
— образовывать следующее число прибавлением числа к предыдущему числу или вычитанием числа 1 из следующего за ним числа;
Цель: повторить и систематизировать материал, изученный ранее.
Ход урока
1.Мотивация. — А сейчас прикоснитесь друг к другу ладошечками и подарите друг другу чувство уверенности в том, что сегодня у вас все получится, поддержите друг друга перед предстоящей работой! Улыбнитесь друг другу, чтобы наш класс наполнился светом!
2.Актуализация знаний
1. — А сейчас послушайте занимательные задачки и постарайтесь ответить на вопросы.
Четыре сороки пришли на уроки.
Одна из сорок не знала урок.
Сколько прилежно
Три пушистых кошечки
Улеглись в лукошечке.
Тут одна к ним подбежала.
Сколько кошек вместе стало? (Четыре. 3 + 1)
Два мяча у Ани,
Два мяча у Вани.
Два мяча да два. Малыш!
Сколько их? Сообразишь? (Четыре. 2 + 2)
2 + 2)
2.Устный счет
— Посчитайте:
от 1 до 10 и обратно;
-Посчитайте от1 до 9 через один, начиная с 1.
-Как называются эти числа?( нечетные)
-Посчитайте от2 до 10, через один.
-Как называются эти числа? (четные).
- Назови соседей числа 3. (2 и 4.)
- Какое число стоит за числом 5? (6.)
- Назови число, стоящее перед числом 9.
3.Практическая работа
-Выложите числа, которые мы изучили, по порядку, начиная с самого большого.
-Назовите их, начиная с самого маленького.
-Так чем мы будем заниматься на уроке? Какую цель мы поставим?
III.Работа по теме урока
1. Работа по учебнику
-Рассмотрите рисунки на с. 44. Кто изображен на первом рисунке? {Котята.)
-Сколько всего котят? (5.)
-Какие записи подойдут к рисунку? (5 — 2 = 5 — всего 5 котят, 3 котенка пьют молоко, а 2 еще не пьют. 3 + 2 = 5 — молоко пьют 3 котенка, к ним идут еще 2 котенка. Всего котят пять.)
-Кто изображен на втором рисунке? {Поросята.)
-Сколько всего поросят? (5.)
-Какая запись подойдет к рисунку? (5 — 1 = 4 — из корыта ели 5 поросят, 1 поросенок убежал. Осталось 4 поросенка.)
-Сравните отрезки.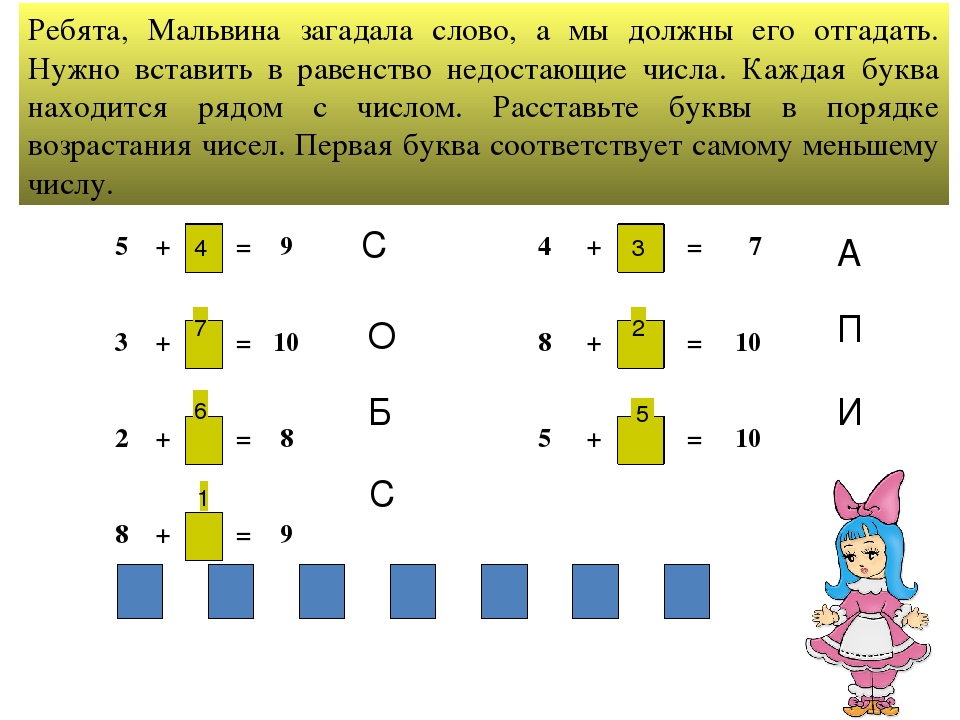 Какой из них длиннее и почему? (Зеленый отрезок состоит из 4 мерок. Красный отрезок состоит из 3мерок, значит, зеленый отрезок длиннее красного, а красный отрезок короче зеленого.)
Какой из них длиннее и почему? (Зеленый отрезок состоит из 4 мерок. Красный отрезок состоит из 3мерок, значит, зеленый отрезок длиннее красного, а красный отрезок короче зеленого.)
-Что изображено на первом рисунке на с. 45? (Игрушки: 2машинки, мишка и жираф.)
-Что обозначает схема? (Было 4 игрушки, 2 игрушки убрали.)
-Какую запись нужно составить к этой схеме? (4 — 2 = 2.)
-Что изображено на втором рисунке? (Тоже игрушки: 4 куклы и кораблик.)
-Что обозначает схема? (Было 4 игрушки, добавили еще 1 игрушку.)
-Какая запись должна быть? (4 + 1=5.)
-Рассмотрите линии, данные ниже. Почему линии на первом рисунке называются ломаными? (Они состоят из отрезков, конец одного служит началом другого, никакие два звена не лежат на одной прямой. )
)
-Почему линии на втором рисунке не являются ломаными? (У первой линии конец одного отрезка не служит началом другого, у второй соседние звенья лежат на одной прямой.)
2. Работа в тетради с печатной основой
-Откройте тетрадь на с. 17. Объясните, что нужно сделать в первом задании. (Соединить рамку с числом, которое показывает, сколько там предметов.)
(Самостоятельное выполнение. Фронтальная проверка.)
-Что нужно сделать в следующем задании? (Соединить точки по линейке, чтобы получилась ломаная линия.)
(Самостоятельное выполнение. Проверка.)
-Ломаная из скольких звеньев у вас получилась? (Из 4.)
-Прочитайте следующее задание. По какому признаку составим пары? (По длине.)
(Самостоятельное выполнение. Проверка.)
-С карандашом какого цвета соединили самый длинный отрезок? (Синего. )
)
-С каким отрезком соединили красный карандаш? (С самым коротким.)
-Какая фигура изображена на следующем рисунке? (Луч.)
-Что нужно сделать, чтобы получился отрезок? (Отметить конец отрезка.)
IV. Физкультминутка
Воробьишка потянулся,
Распрямился, встрепенулся.
Головой кивнул три раза,
Подмигнул нам черным глазом,
Лапки в стороны развел
И по жердочке пошел.
Прогулялся и присел,
Свою песенку запел:
Чик-чирик-чирик-чирик…
- Проверка знаний
(Выполнение заданий в тетради для проверочных работ (с.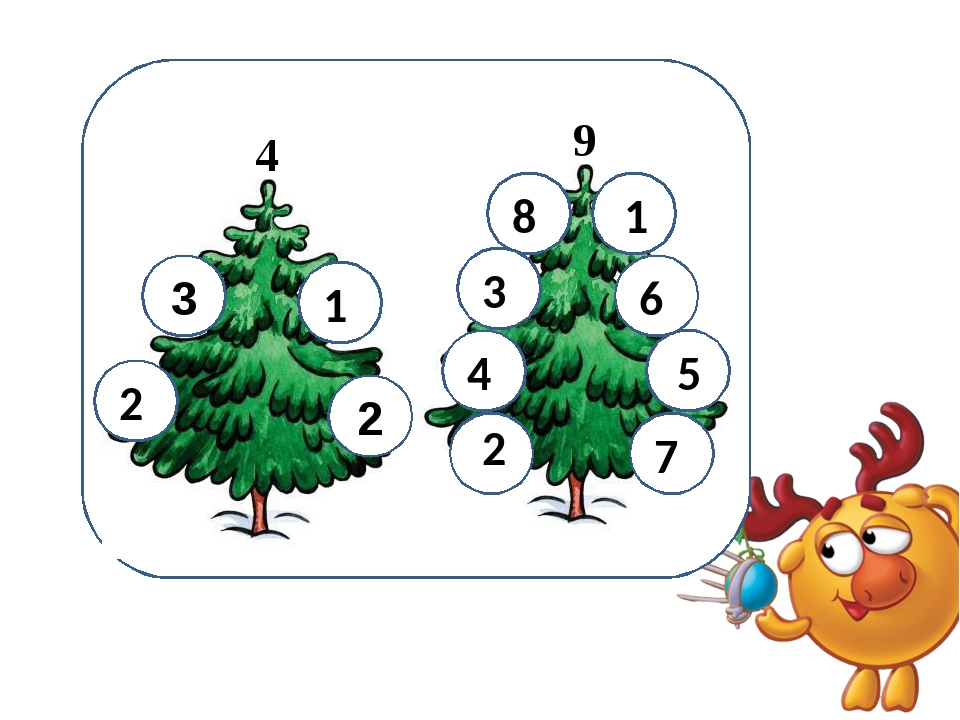
- Рефлексия
-Оцените свою работу.
-Кто считает, что все задания проверочной работы выполнил правильно?
-Кто не уверен в том, что хорошо справился с работой?
«Повторение и обобщение по теме «Числа от 1 до 10»
Конспект №30
Ф.И.О. педагога: Ляшко Елена Николаевна 23.10.18г.
Предмет: математика
Класс: 1-Б
Тип урока: Закрепление и обобщение пройденного материала.
Тема: «Повторение и обобщение по теме «Числа от 1 до 10»
Цель: Повторить, закрепить и обобщить изученный материал: закрепление знаний нумерации чисел от 1 до 10.
Планируемые результаты:
Личностные: определяют и высказывают под руководством педагога самые простые общие для всех людей правила поведения при сотрудничестве (этические нормы)
Метапредметные :
Регулятивные- уметь осуществлять самоконтроль по результату, контроль результата по просьбе учителя; отличать верно выполненное задание от неверного.
Коммуникативные- уметь слушать и вступать в диалог, участвовать в коллективном обсуждении.
Познавательные-уметь выполнять универсальные логические действия: анализ, синтез, выбирать основания для сравнения.
Предметные:
Знать устную нумерацию и состав чисел в пределах 10, математическую терминологию при сложении, признаки и различия геометрических фигур
Уметь решать примеры.
Оборудование: презентация, проектор, ноутбук, абак, цветочки-примеры, картинка букет, перекидные цифры, 2 карандаша желтого и красного цвета, карточки «Найди пару», цветочки шаблоны и стаканчики с водой, картинки цифр «1» и «4».
Ход урока
I. Организационный момент.
— Улыбнитесь друг другу. Подарите и мне свои улыбки. Спасибо. Ваши улыбки располагают к приятому общению, создают хорошее настроение.
II. Актуализация знаний.
1. Устный счет. Разминка.
Работа с абаком.
-Покажите 5 кружочков вверху и 5 кружочков внизу. Сколько это? Какой состав числа мы повторили?
— Покажите 3 кружочка вверху и 4 кружочка внизу. Сколько это? Какой состав числа мы повторили?
Сколько это? Какой состав числа мы повторили?
— Покажите 4 кружочка вверху и 4 кружочка внизу. Сколько это? Какой состав числа мы повторили? Правильно, молодцы.
2. Сообщение темы и целей урока.
Глядя, какие мы разные решали примеры кто мне скажет, какая у нас тема урока?
Правильно, сегодня на уроке мы с вами будем закреплять те знания, которые вы получили, изучая числа от 1 до 10.
Мы будем решать примеры, весёлые задачи и выполнять много интересных заданий.
Целеполагания.
Но не просто будем считать и решать — мы отправимся в путешествие. А вот кого мы возьмём в путешествие, вы узнаете,
отгадав загадку.
Из муки его слепили,
После в печку посадили,
По дорожке он катился.
Был он весел, был он смел,
Съесть хотел его зайчишка,
Серый волк и бурый мишка.
А когда малыш в лесу
Встретил рыжую лису,
От неё уйти не смог.
Кто же это?
Дети: Колобок.
Учитель: А как начинается сказка?
Дети вспоминают.
Учитель: И привела его дорожка в сказочный лес (математический).
Учитель: Ребята, а вы помните, как закончилась сказка?
Дети: Лиса съела Колобка.
Учитель: — А вам нравится такой конец сказки? (Нет.)
Сегодня мы с вами выручим Колобка из беды. Это в наших силах. Но для этого вам нужно помочь Колобку пройти испытания. Итак, отправляемся вместе с нашим героем в путешествие по сказочному лесу.
III. Устный счёт.
Учитель: Катится Колобок по дороге. А навстречу ему Заяц. Слайд 1
— Сосчитайте:
* 1 ряд от1 до 10 и обратно.
* 2 ряд- от 8 до 4,
* 3 ряд- от 5 до 9,
Возьмите перекидные цифры.
— Покажите число, которое:
* следует за числом 6;
* стоит между числами 6 и 8;
* предшествует числу 5;
* соседей числа 2.
Учитель: Молодцы! Справились с Зайкиными заданиями. Можно путешествовать дальше. Катится Колобок по лесу, а ему навстречу Серый Волк. В Колобках он знает толк. Слайд 2
Серый Волк: Решишь мои задачи, отпущу тебя на волю.
Учитель: Поможем Колобку, ребята?
Четыре зайца шли из школы,
И вдруг на них напали пчёлы.
Два зайчика спаслись едва,
А сколько не успело? Слайд 3
Дети: 2
Учитель: Как вы это узнали?
Дети: 4-2=2
Из норки выглянул барсук,
Уселась белочка на сук,
Вспорхнул на ветку воробей,
На тропку выполз муравей-
Все улыбнулись солнцу!
Сколько всего животных улыбнулись солнцу?
Дети: 1+1+1+1=4 Слайд 4
Три зелёные лягушки
Сидели на опушке.
Одна им подмигнула
И в озеро нырнула.
Сколько лягушек осталось на опушке?
Дети: 3-1=2 Слайд 5
IV. Закрепление пройденного материала.
Учитель: Молодцы! А теперь снова в путь. Катится Колобок по тропинке в лесу, а навстречу ему Медведь. Слайд 6
-Найдите отрезок, луч, прямую? Слайд 7
— Чем отличается луч от прямой?
Физкультминутка «Найди пару» Слайд 8
Геометрия.
Учитель: Продолжим путешествие по математическому лесу. Покатился наш герой по дорожке и чуть не столкнулся вот с таким человечком. Слайд 9
— Скажите из каких геометрических фигур он состоит? Так вот этот геометрический мальчик тоже приготовил Колобку задания.
Давайте запишем цифру 1 и 4 чередуя через клетку и запишем примеры.
3+3= 7-1=
3+2= 3+4=
4+6= 4-2=
Проверим правильно ли вы записали и решили, сколько клеточек между столбиками вы пропустили?
Молодцы!
VI. Работа по учебнику. (с. 62 учебника)
1.Составьте рассказ по 1 рисунку. (На одной тарелке было 5 зелёных груш, а на другой- 2 жёлтые груши. Сколько всего груш? )
На доске запись: 5+2=7.
И какой будет ответ?
7 груш.
VII. Учитель: Молодцы! Катится колобок. А на встречу ему…как вы думаете кто?
Дети: Лиса. Слайд 10
— Уж от меня-то, Колобок, ты не уйдёшь. И ребята тебе не помогут.
Учитель: Поможем, ребята? Будьте внимательней. Потому что задачи на смекалку.
Улитка на танцы спешила
И выйти пораньше решила.
Кокетливо выставив рожки,
Улитка ползла по дорожке.
Час лезла вдоль зарослей мха
И два- по листу лопуха.
Час кочку она штурмовала.
А жаль, ведь проделала путь не простой.
Как долго придётся ползти ей домой?
(Домой ей ползти не надо, потому что домик у неё на спине. )
)
Слон на обед съел корзину бананов,
Пару корзинок грибов со сметаной,
Яблок корзинку, корзинку галет.
Сколько корзинок он съел на обед?
(Ни одной. Потому что корзины несъедобные.)
Чтоб лиса точно отпустила колобка мы ей подарим букет из цветов, а цветы не простые, на них написаны примеры, надо их решить и закрасить в соответствующий цвет. Слайд 11
VIII. Итог урока. Рефлексия. Слайд 12
Учитель: Ну что же, придётся Лисе отпустить Колобка, ведь все задания он выполнил правильно. И мы подарили ей такой прекрасный букет. А помогли вы Колобку, ребята. Как вы ему помогли?
Дети: Решали, считали, отгадывали. Слайд 13
Учитель: Колобку очень понравилось у вас, ведь вы такие добрые, умные, смекалистые.
Что повторили? Что больше всего понравилось на уроке? Если вы хорошо работали, то ваши цветочки все распустятся в стаканчиках с водой. Слайд 14
Урок математики в 1 классе «Числа от 1 до 9. Письмо цифры 9»
Технологическая карта урока
Технологическая карта урока Вводная часть Ф. И.О. Заславская Татьяна Николаевна, учитель МОУ Зебляковская средняя общеобразовательная школа. Предмет: математика Класс: 1 Наименование учебно-методического
И.О. Заславская Татьяна Николаевна, учитель МОУ Зебляковская средняя общеобразовательная школа. Предмет: математика Класс: 1 Наименование учебно-методического
Тема: Равнобедренные треугольники.
Конспект урока по учебнику И. И. Аргинской «Математика. 2 класс» (1-4) Учитель Шульженко Ольга Игоревна г. Москва ГБОУ «Школа с углублённым изучением иностранных языков 1900» Тема: Равнобедренные треугольники.
ПодробнееУрок 29 ( 3.19) Число пять. Цифра 5
Урок 29 ( 3.19) Число пять. Цифра 5 Помочь детям усвоить: получение числа 5 прибавлением 1 к числу 4 и обозначение его цифрой 5; построение натурального ряда чисел; написание цифры 5; состав числа 5, все
Подробнее7* : :2 31 4*
Открытый урок математики в 3в классе Тема: «Умножение числа на произведение» урок закрепления материала Цели урока: Образовательные: Обобщить материал по темам «Умножение многозначных чисел на однозначное»,
ПодробнееТехнологическая карта урока
Технологическая карта урока Приложение 2. Тема: Конкретный смысл действия умножения. Тип урока: урок первичного предъявления знаний Цель: создать условия для организации совместной деятельности учащихся
Тема: Конкретный смысл действия умножения. Тип урока: урок первичного предъявления знаний Цель: создать условия для организации совместной деятельности учащихся
Открытый урок по математике в 1 классе.
Автор: Матющенко М.А., учитель начальных классов Предмет: Математика Класс: 1 класс Тип урока: урок изучения новой темы Открытый урок по математике в 1 классе. Оборудование: учебник «Математика» (Дорофеев
ПодробнееСложение и вычитание смешанных чисел
Предмет: Математика Класс: 5 «Б» класс Сложение и вычитание смешанных чисел Учебник: Математика: 5 класс: учебник для учащихся общеобразовательных учреждений / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.
ПодробнееКромского района Орловской области
Муниципальное бюджетное общеобразовательное учреждение Кромского района Орловской области «Черкасская средняя общеобразовательная школа» Конспект урока математики по теме: «Порядок выполнения действий.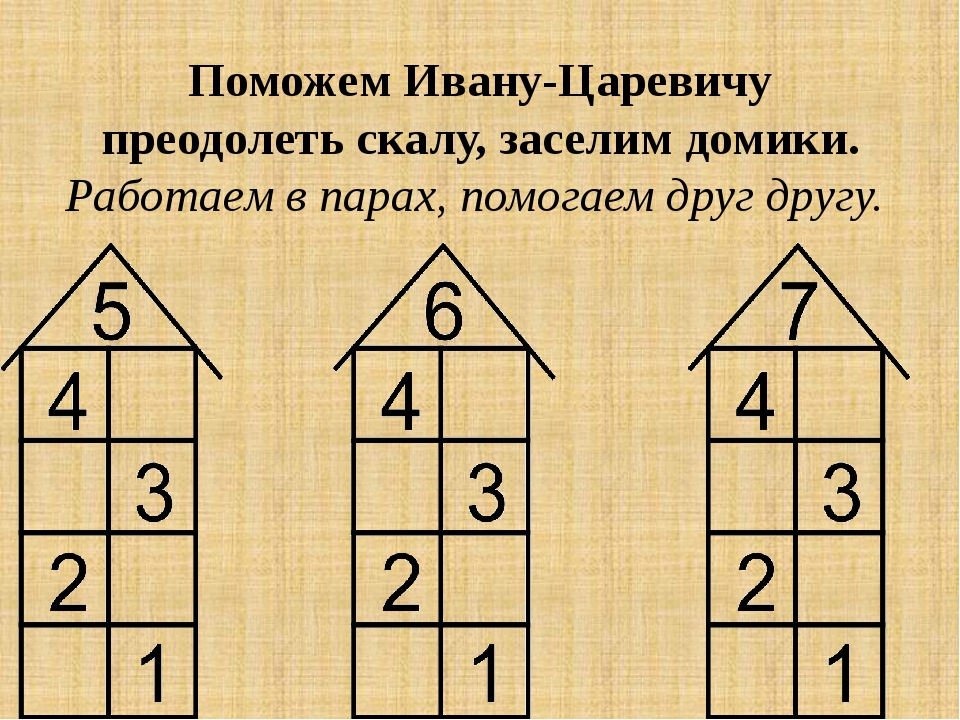
Конспект урока математики в 1 классе.
Конспект урока математики в 1 классе. Учебник «Математика». Авторы Т.Е.Демидова, С. А. Козлова. Тема урока: «Число 8. Цифра 8» Составила конспект учитель МАОУ «СОШ 96» Оборина Светлана Геннадьевна Основные
ПодробнееТема: «Сложение дробей с одинаковыми
Урок по математике. 4 класс. Программа «Школа 2100». по учебнику Л.Г.Петерсон (4 класс, 2 часть, урок 3) Тема: «Сложение дробей с знаменателями». Урок открытия новых знаний. Подготовила: Моисеева Е.Р.
ПодробнееУчитель начальных классов: Левыкина А. В
Конспект открытого урока по математике на тему «Сложение и вычитание трехзначных чисел на основе знания их разрядного состава». 2 «А» класс Учитель начальных классов: Левыкина А. В. 15.03. 12. Цели: формирование
12. Цели: формирование
Урок математики в 1 классе
Учитель: Бажутова С.Г. Тема: Единица длины сантиметр. Урок математики в 1 классе Цель урока: формирование представлений о единице длины (сантиметре) как единой принятой мерке, путем сравнения различных
ПодробнееТема: «Больше. Меньше. Столько же»
Технологическая карта урока по математике 1 класс «Планета знаний» Тема: «Больше. Меньше. Столько же» Галецкая Виктория Александровна ГБОУ гимназия 426 учитель начальных классов Тема: «Больше. Меньше.
ПодробнееОткрытый урок по математике во 2 классе
МКС(К) ОУ для обучающихся воспитанников с ограниченными возможностями здоровья Старогородковской специальной (коррекционной) общеобразовательной школы-интерната VIII вида им. Заслуженного учителя РФ Фурагиной
ПодробнееУрок математики во 2 классе
Урок математики во 2 классе Автор: Матвеева С. А., учитель начальных классов Тема: Приемы вычислений для случаев вида 36-2, 36-20 Цели урока: 1. Познакомить детей с приемами устных вычислений вида 36-2,
А., учитель начальных классов Тема: Приемы вычислений для случаев вида 36-2, 36-20 Цели урока: 1. Познакомить детей с приемами устных вычислений вида 36-2,
Русский язык (письмо) 1 класс
Русский язык (письмо) 1 класс Тема: Письмо заглавной буквы Ц. (УМК Развивающая система Л.В.Занкова) Подготовила Романенко Е. Н. Планируемые результаты (универсальные учебные действия) Личнoстные: — знать
ПодробнееУрок математики в 1Б классе по программе «Школа России» по теме: «Задачи в два действия». Первый урок в теме, когда дети переходят от решения задач-цепочек к решению задач в два действия. Цели деятельности
Подробнеепо предмету математика 3 класс
Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа 27 с углубленным изучением отдельных предметов» г. Балаково Саратовской области АВТОРСКИЙ ПРОДУКТ МЕТОДИЧЕСКАЯ
Балаково Саратовской области АВТОРСКИЙ ПРОДУКТ МЕТОДИЧЕСКАЯ
План- конспект урока
План- конспект урока Тема: Число девять. Цифра 9. Предмет: Математика. Класс: 1 класс Тип урока: Изучение нового материала. Дата проведения: 28 ноября 2017г. Присутствующие: заместитель директора по УВЧ
ПодробнееВершинина Анна Владимировна
МБОУ «СОШ 76» Урок математики ( 27) Сложение и вычитание в пределах 100. Образовательная программа: Материально-техническое обеспечение: Тип урока: Цель: Задачи: Формируемые УУД: Вершинина Анна Владимировна
ПодробнееТема «Прибавить и вычесть число 3»
Муниципальное бюджетное общеобразовательное учреждение «Центр образования г. Певек» Конспект урока математики в 1 классе (УМК «Перспектива») Тема «Прибавить и вычесть число 3» Семеева Нина Семёновна, высшая
Подробнее8 1 (1 ) , 2 ( 7) 10 2 (1 ) — 10
3. 1.Конспект урока (в таблице). III. Содержательная часть: Деятельность учителя с указанием Деятельность ученика номера слайда (при наличии презентации) Этап 1 урока Организационный момент. 3 мин Цель
1.Конспект урока (в таблице). III. Содержательная часть: Деятельность учителя с указанием Деятельность ученика номера слайда (при наличии презентации) Этап 1 урока Организационный момент. 3 мин Цель
Технологическая карта урока
Технологическая карта урока Ф.И.О. Ковалева Юлия Сергеевна Предмет: Математика Класс: 5 класс Автор УМК: Математика 5 класс: учебник для общеобразовательных учреждений А. Г. Мерзляк и др. Тема урока: Сложение
Подробнее«Число и цифра 8» (1 класс)
государственное бюджетное специальное (коррекционное) образовательное учреждение для обучающихся, воспитанников с ограниченными возможностями здоровья общеобразовательная школа 9 VIII вида г. Туапсе Краснодарского
ПодробнееУрок «Число 7. Письмо цифры 7»
Муниципальное казенное общеобразовательное учреждение
«Лахденпохская средняя общеобразовательная школа»
Тема: «Число 7. Письмо цифры 7»
Письмо цифры 7»
УМК «Школа России»
Составила
учитель начальных классов
Степаненко В. И.
г. Лахденпохья
2016/2017
Тема: «Число 7. Письмо цифры 7»
Тип урока: Урок изучения и первичного закрепления новых знаний.
Цель:
— сформировать представление о числе 7 с опорой на числовой луч;
— научиться с помощью сложения получать число 7, зная предыдущее 6;
— научиться писать цифру 7.
УУД:
Регулятивные – Научиться принимать задачу по рисунку в учебнике и сохранять ее до конца урока. Выполнять учебные действия из учебника, в тетради как под руководством учителя, так и самостоятельно. Познавательные — ориентироваться в материале учебника; осуществлять поиск информации как самостоятельно, так и совместно с учителем, учиться простым рассуждениям.
Коммуникативные – использовать простую речь; вести диалог с одноклассниками и с учителем при коллективном обсуждении, отвечать на вопросы учителя.
Личностные: — осознавать значение предмета «Математика», проявлять положительное отношение к предмету, проявлять интерес к новому учебному материалу.
Оборудование: мультимедиа проектор, презентация, рабочая тетрадь по математике 1 класс, числовой луч.
Ход урока.
I. Организационный момент.
Долгожданный дан звонок
Начинается урок!
Мы пришли сюда учиться,
Не лениться, а трудиться.
Работаем старательно,
Слушаем внимательно!
II. Актуализация знаний.
2 слайд. У вас на парте лежит у каждого числовой луч, возьмите простой карандаш, и внимательно выполняйте задание.
1 2 3 4 5 6 7 8 9 10
— Обведи в кружок самое большое число ( 10 )
— Найдите самое маленькое и зачеркните его ( 1 )
— В треугольник возьмите число, которое указывает сколько углов в треугольнике ( 3 )
— Одной чертой подчеркните число, которое стоит справа от числа 3 ( 4 )
— Двумя черточками подчеркните число, которое стоит слева от числа 3 ( 2 )
— В квадрат возьмите число 9
— Поставьте точку под числом, которое стоит между числами 4 и 6 ( 5 )
— Число, которое стоит слева от 9, подчеркните тремя черточками ( 8 )
— Подчеркните волнистой линией то число с которым работали вчера ( 6 )
III. Самоопределение к деятельности.
Самоопределение к деятельности.
Постановка проблемы. Сообщение темы и цели урока.
— Посмотрите внимательно на числовой луч и скажите, какое число осталось без задания?
— Кто может определить тему урока?
Тема урока «Число 7. Письмо цифры 7.
— Чему вы должны будете научиться? (Узнать всё о числе 7, научиться писать цифру 7).
— Рассмотрите рисунки снизу страница 54, где мы можем встретиться с числом 7? (домино, на часах.)
Открытие нового знания.
Проблема: Как из 6 получить 7?
— Подумайте! (6 + 1 = 7)
IV. Работа по теме урока.
3 слайд. 1. Рассмотрите верхнюю картинку на стр. 54 .
— Кто на ней изображён? (Рыбак ловит рыбу на озере)
— Как вы думаете, какое будет задание? (Объяснить записи по рисунку, поставить недостающие числа.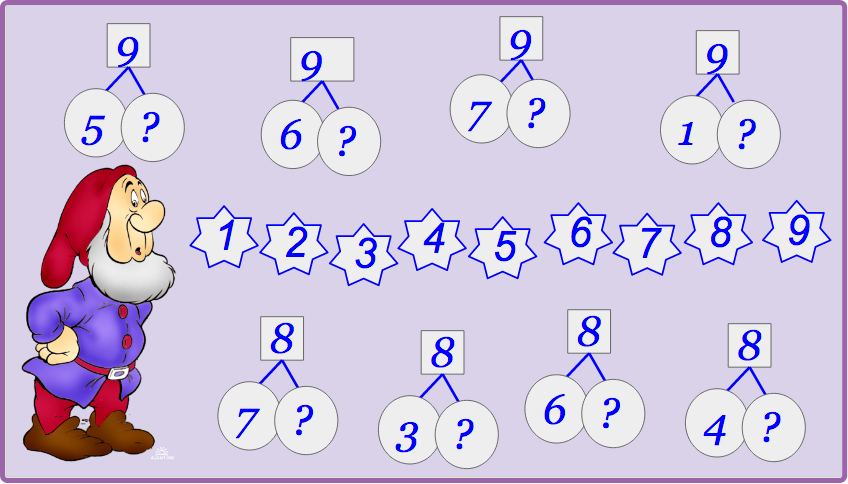 )
)
— Объясните записи слева.
5+1= 6 – рыбак уже поймал 5 рыб, ещё 1 рыба у него на крючке. Всего у рыбака 6 рыб.
6+1=7 – у рыбака 6 рыб, ещё 1 рыбу утащил кот. Сколько рыб было у рыбака?
— Чем отличаются равенства справа от равенств слева? (Они со знаком «минус».)
— Объясните их.
6 – 1 = 5 — у рыбака 6 рыб, 1 из них ещё на крючке. На траве лежат 5 рыб.
7 – 1 = 6 — рыбак поймал 7 рыб, 1 утащил кот. Осталось 6 рыб.
4 слайд. 2. — Чем отличаются поезда? (цветом и количеством вагонов)
— Сколько вагонов в первом поезде? (6)
— Сколько вагонов во втором поезде? (7)
— Как получили 7 вагонов?
— Кто запишет мне это выражение?
— Это равенство или неравенство? Почему?
— В каком поезде вагонов больше и на сколько?
— В каком поезде вагонов меньше и на сколько?
— Возьмите простые карандаши и заполните пропуски в примерах ( по цепочке)
V. Физкультминутка.
Физкультминутка.
VI. Закрепление изученного материала
5 слайд. 1. — Рассмотрите рисунки на 55 странице.
— Какие записи подходят к рисунку слева, справа?
— Сравните отрезки. (Они равны)
— Почему? (В них укладываются по шесть мерок)
6 слайд. 2. Работа с геометрическим материалом.
— Как называются изображённые линии? (Отрезки.)
— Как вы узнали, что это отрезки?
— Как вы думаете, есть ли среди отрезков, изображённых на рисунке, отрезки, имеющие одинаковую длину? Как это проверить? (Необходимо измерить длины отрезков при помощи мерки.)
7 слайд. 3. Посчитайте треугольники и квадраты. Работа в парах.
— Помочь может только дружная пара.
— Назовите правила дружной работы в паре:
Выскажи своё мнение
Выслушай мнение соседа
Придите к единому мнению
Действуйте!
— О готовности скажут руки: вот так!
— А сейчас проверим, как вы справились с этим заданием (Треугольников — 7, квадратов – 4).
8 слайд. VII. Работа в тетради с печатной основой
— Откройте тетрадь на 21 странице. Сейчас будем учиться писать цифру 7.
— Рассмотрите внимательно цифру 7.
— Сколько элементов в написании цифры? (3) (Волнистая, наклонная прямая палочка и маленькая горизонтальная палочка)
— Откуда начинаем писать? (Начинаем писать волнистую линию чуть ниже середины верхней стороны клетки, доводя ее до верхнего правого угла клетки. Из верхнего правого угла проводим наклонную палочку к середине нижней стороны клетки. Маленькая горизонтальная палочка должна перечеркивать длинную палочку примерно по середине).
— Пробуем в воздухе
9 слайд. Начинаем работу в тетрадке, обведите цифру 7 и допишите до конца строки, соблюдая закономерность.
— Сравните каждую цифру с образцом и те, которые получились правильно «зажгите огоньком». (Под цифрой красным карандашом поставить точку).
— Обведите и напишите недостающие цифры во второй строке.
VIII. Итог урока. Рефлексия.
10 слайд. — В названии каких сказок встречается цифра 7. («Белоснежка и семь гномов», «Семеро храбрецов» авторы Братья Гримм, русская народная сказка «Волк и семеро козлят», А. С. Пушкин «Сказка о мёртвой царевне и семи богатырях»))
— Как называется эта сказка? («Цветик-семицветик»)
— Кто автор? (Валентин Катаев)
— Вспомните, что загадала девочка Женя на последний лепесток? (Здоровья своему другу.)
— Я тоже загадаю очень хорошее желание.
Лети, лети, лепесток,
Через запад на восток,
Через север, через юг,
Возвращайся, сделав круг.
Лишь коснёшься ты земли –
Быть по-моему вели.
Желаю, чтобы вы, ребята, были здоровыми и счастливыми.
И цветик-семицветик загадает своё желание. Он хочет, чтобы вы запомнили написание цифры 7 и выучили состав числа 7.
— Спасибо за работу!
— Урок окончен.
11 слайд. Домашнее задание (раскраска)
Закрепление изученного материала по математике во 2 классе
Слайды и текст этой онлайн презентации
Слайд 1
Математика
Закрепление изученного материала во 2 классе
Слайд 2
План урока
Математический диктант
Посчитаем, поиграем
Решение задач
Проверочная работа
Слайд 3
Математический диктант
Увеличьте 7 на 4
Уменьшите 36 на 20
Из какого числа надо вычесть 8, чтобы получить 22
Израсходовали 10 л молока и осталось еще 30 л. Сколько литров молока было
Уменьшаемое 80, вычитаемое 2. Найди разность.
На сколько 7 меньше 40?
К какому числу надо прибавить4, чтобы получить 30?
11 16 30 40 78 33 26
Слайд 4
Реши удобным способом
50 + ( 20 + 4 )=
67 + (3 + 5 ) =
60 – ( 10 + 8 ) =
42
75
74
Слайд 5
Решим задачу
В одном ящике 30 кг масла, а в другом на 5 кг больше, чем в первом. Сколько килограммов масла в двух ящиках?
Слайд 6
Проверь решение!
Сколько килограммов масла во втором ящике?
30 + 5 = 35(кг)
2) Сколько килограммов масла в двух ящиках?
30 + 35 = 65(кг)
Ответ: 65 килограммов.
Слайд 7
Вспомним умножение и деление!
27 : 3 (И)
18 : 3 (А)
4 · 3 (У)
3 · 7 (Ы)
2 · 8 (Л)
24 : 8 (К)
14 : 2 (Н)
9
6
12
21
16
3
7
Слайд 8
Выполни действия
(70 – 46 ) : 3 = 8
(36 – 27 ) : 3 = 3
12 : 12 + 39 = 40
18 · 1 + 42 = 60
14 : 2 + 53 = 60
3 · 6 + 3 = 21
(72 – 64 ) · 10 = 80
Слайд 9
Проверочная работа
В доме 5 комнат. В каждой комнате 3 окна. Сколько окон в доме?
х – 36 = 70
14 : 2 24 : 3
18 : 2 6 · 2
7 · 2 5 · 3
В классе 15 парт. В одном ряду 5 парт. Сколько рядов в классе?
25 + х = 60
5 · 2 16 : 8
3 · 7 16 : 2
21 : 3 6 · 3
В доме 5 комнат. В каждой комнате 3 окна. Сколько окон в доме?
х – 36 = 70
14 : 2 24 : 3
18 : 2 6 · 2
7 · 2 5 · 3
В классе 15 парт. В одном ряду 5 парт. Сколько рядов в классе?
25 + х = 60
5 · 2 16 : 8
3 · 7 16 : 2
21 : 3 6 · 3
Слайд 10
Вы лучшие
«Числа от 1 до 10. Закрепление изученного материала»
ТЕХНОЛОГИЧЕСКАЯ КАРТА
урока математики,
проведенного 20.10.2016 г. в 1«В» классе
учителем начальных классов
Тема урока «Числа от 1 до 10. Закрепление изученного материала»
Цели:создать условия для закрепления прибавления и вычитания чисел от 1 до 10; решение задачи.
Учебные задачи:
Направленные на достижение предметных результатов:
Учащиеся закрепят:
1)название чисел при сложении и вычитании;
2) прибавление и вычитание чисел;
3) умения решать простые задачи;
Направленные на достижение метапредметных результатов
Учащиеся научатся:
принимать учебную задачу, соответствующую этапу обучения; (П)
с помощью учителя выполнять сравнения изучаемых математических объектов и формулировать выводы;(Р)
использовать простые речевые средства для передачи своего мнения. (К)
Направленные на достижение личностных результатов
У обучающего будут сформированы:
ориентация на понимание предложений и оценок учителей и одноклассников;
начальная стадия внутренней позиции школьника, положительного отношения к урокам математики;
представления о значении математики для познания окружающего мира.
Материалы для учителя:
Презентация, карточки.
Материалы для учащихся:
1. Учебник;
2.Карточки с математическими выражениями для контроля умения прибавления и вычитания от1 до 10.
3.Рабочие тетради.
Ход занятия
Этап занятия | Деятельность учителя | Деятельность учащихся | Формируемые УУД |
Этап мотивации (самоопределения) к учебной деятельности | Организует психологический настрой. Приветствует учащихся. Организует запись в тетрадях. — Громко прозвенел звонок – Начинается урок. Наши ушки на макушке, Глазки широко открыты. Слушаем, запоминаем, Ни минуты не теряем. | Приветствуют учителя, проверяют готовность к уроку. —Присаживаются на свои места. | Личностные: учебно-познавательный интерес к новому учебному материалу и способам решения новой задачи. |
Этап актуализации пробного действия | Организует работу по повторению состава числа 10. — .Сегодня на уроке мы попадем к героям К.И.Чуковского «Телефон». — Сколько животных перед вами? — Что вы можете рассказать о числе 9? — Как получить число 10? Ребята, давайте откроем тетради. Отступим от последней работы четыре строчки вниз и в строчку до конца строки запишем цифру 10. — Какие 2 числа нужно сложить чтобы получить 10? | Устно отвечают на вопросы. — 9 — Ответы детей -К числу 9 прибавить 1. -Записывают в строчку число 10. — 9 и 1; 5 и 5; 4 и 6….. | Познавательные: строить рассуждения в форме связи простых суждения об объекте, его строении, свойствах и связях; произвольно и осознанно владеть общими приемами решения задач; коммуникативные: аргументировать свою позицию и координировать ее с позициями партнеров в сотрудничестве при выработке общего решения в совместной деятельности; формулировать собственное мнение и позицию. |
3. Этап выявления места и причины затруднения | Организует решение неравенств. Организует работу по учебнику, решение задач по картинкам. — « — У меня зазвонил телефон. — Кто говорит? — Слон. -Откуда? — От верблюда. — Что вам надо? — Шоколада. — Для кого? — Для сына моего». Шоколад, чтоб нам достать, нужно очень быстро устно решить неравенства. — Хорошо ребята вы справились с заданием и заработали для слона шоколада. — «А потом позвонил Крокодил И со слезами просил: — Мой милый, хороший, Пришли мне калоши, И мне, и жене, и Тотоше.» Калоши Крокодил получит, если мы с вами решим задачи по картинкам, данным в учебнике на странице 62; — Что изображено на первой картинке? — Сколько зеленых груш на 1тарелке? — Сколько желтых груш на 2 тарелке? — Какой вопрос нужно поставить, чтобы подошел первый вариант решения со знаком плюс? — Предположим, что все груши были на одной тарелке. -Сколько было груш? -Потом 2 груши переложили в другую тарелку. -Какой вопрос можно сформулировать? Молодцы ребята, а теперь давайте посмотрим на вторую картинку. -Сколько птиц вы видите на картинке? — Сколько улетело? — Какой вопрос можно задать? А какую задачу можно придумать со знаком плюс. — Сколько сидит на верхней веточке птиц? — Сколько сидит на нижней веточке? — Какой вопрос можно сформулировать? | -Дети устно решают неравенства. 7 6 7 6 1 6 — Ребята открывают учебник на странице 62. — Груши -В первой тарелке 5 зеленых груш. — Во второй тарелке 2 желтые груши. — Сколько всего груш на двух тарелках? (5+2=7) Всего было 6 груш, две груши переложили в другую тарелку. Сколько осталось груш в тарелке? 6-2 = 4 — 5 — 1 — Сколько птиц осталось сидеть на ветках? — 3 -1 — Сколько всего птичек сидело на двух веточках. | Познавательные: осуществлять запись (фиксацию) выборочной информации об окружающем мире и о себе самом, в том числе с помощью инструментов ИКТ; ориентироваться на разнообразие способов решения задач. Личностные: учебно-познавательный интерес к новому учебному материалу и способам решения новой задачи; внутренней позиции обучающегося на уровне положительного отношения к образовательному учреждению, понимания необходимости учения, выраженного в преобладании учебно-познавательных мотивов и предпочтении социального опыта оценки знаний. Регулятивные: планировать свои действия в соответствии с поставленной задачей и условиями ее реализации, в том числе во внутреннем плане; самостоятельно учитывать выделенные учителем ориентиры действия в новом учебном материале; |
Физминутка | «А потом позвонили зайчата: — Нельзя ли прислать перчатки?» Зайчикам доставят перчатки. Если вы выполните упражнения физминутки. | — дети выполняют упражнения. | |
7. Этап самостоятельной работы с проверкой по эталону | Предлагает детям решить самостоятельно примеры на карточках. «А потом позвонил медведь Да как начал, как начал реветь. — Погодите, медведь, не ревите, Объясните, чего вы хотите?» — К мудрой сове в гости хочу. Просила она примеры решить. А у меня зубы разболелись. Как быть? Ну, что ж, ребята, поможем медведю? . Нужно самостоятельно решить примеры. 2+3 = 10-1= 7+2= 8+2= 5-3= 9-8= Выполняется проверка выполнения самостоятельной работы. «А потом позвонили цапли. — Пришлите, пожалуйста, капли: Мы лягушками нынче объелись, И у нас животы разболелись!» Отдохните цапли. Посмотрите, как работают ребята. Как они правильно и аккуратно выполняют задание, на странице 62 даны отрезки. Начертите такие отрезки и найдите равные. | Ученики самостоятельно решают примеры на карточках. -Решают примеры самостоятельно. 2+3 = 5 10-1=9 7+2= 9 8+2=10 5-3= 2 9-8=1 Ребята открывают книги на странице 62, чертят отрезки, находят равные отрезки. | Коммуникативные: аргументировать свою позицию и координировать ее с позициями партнеров в сотрудничестве при выработке общего решения в совместной деятельности; формулировать собственное мнение и позицию. Регулятивные: осуществлять итоговый и пошаговый контроль по результату. |
9. Этап рефлексии учебной деятельности | Раздает карточки с изображением бегемота. -Пора заканчивать урок. Но тут опять звонок! «- Кто говорит? — Носорог. — Что такое? — Беда! Беда! Бегите скорее сюда! — В чем дело? — Спасите. — Кого? — Бегемота. Наш бегемот провалился в болото» Если вам было сложно сегодня работать на уроке, раскрасьте бегемота красным цветом. А если задания не вызвали затруднения и всё было понятно – зеленым. Мальчишки и девчонки героям К.Чуковского помогла. Были все молодцы. Немало вспомнить пришлось, чтобы всем им помочь. | Раскрашивают карточки. |
Самоанализ урока математики.
Урок по математике проведен в 1 «В» классе 20.10.2016 г. по теме: «Числа от 1 до 10. Закрепление изученного материала».Данная тема запланирована по программе «Школа России».
На уроке работает определенная масса детей. Вступают в диалог с учителем легко. Могут поддержать и завести беседу. Хорошо сформированы учебные действия. Все дети проявляли интерес к уроку. Учебный материал осваивают лучше на практическом уровне.
Данный урок является обобщающим.
Цель урока: закреплять создать условия для закрепления прибавления и вычитания чисел от 1 до 10; решение задачи.
Для реализации цели сформулировала задачи, направленные на достижение предметных результатов
Направленные на достижение предметных результатов:
Учащиеся закрепят:
1)название чисел при сложении и вычитании;
2) прибавление и вычитание чисел;
3) умения решать простые задачи;
Направленные на достижение метапредметных результатов
Учащиеся научатся:
принимать учебную задачу, соответствующую этапу обучения; (П)
с помощью учителя выполнять сравнения изучаемых математических объектов и формулировать выводы;(Р)
использовать простые речевые средства для передачи своего мнения. (К)
Направленные на достижение личностных результатов
У обучающего будут сформированы:
ориентация на понимание предложений и оценок учителей и одноклассников;
начальная стадия внутренней позиции школьника, положительного отношения к урокам математики;
представления о значении математики для познания окружающего мира.
Личностные результаты решались на протяжении всего урока, на всех этапах. Метапредметные результаты решались на этапе актуализации знаний, работы по теме урока, закрепления изученного, рефлексивного этапа урока. Предметные результаты решали на этапе актуализации знаний, работы по теме урока, на этапе закрепления изученного.
Класс удалось включить в запланированную деятельность. Этому способствовало, использование занимательного материала, диалога с учителем, работа у доски с комментариями, самостоятельная работа.
Запланированное, удалось реализовать с высокой степенью эффективности, с помощью практической работы, беседы с учащимися по теме урока.
Личностные УУД на занятии формировались на этапе организационного момента, работы по теме урока, закрепления изученного, с помощью беседы с детьми по теме урока. Познавательные УУД формировались на этапе актуализации знаний и на работе по теме этапах занятия, с помощью работы над темой урока. Регулятивные УУД формируются на этапе закрепления изученного и работе по теме этапах занятия, с помощью выполнения заданий по теме, ответов на вопросы, рефлексии. Коммуникативные УУД формировались на этапе актуализации знаний, на рефлексии этапах занятия, с помощью беседы с детьми по теме урока.
Я считаю, что урок достиг поставленной цели, критерием таковой оценки является полное подведение урока.
Проверка уплотнения почвы и одометра
Что такое уплотнение почвы?
Уплотнение почвы относится к процессу, при котором объем насыщенной (частично или полностью) почвы уменьшается из-за приложенного напряжения. Термин был введен Карлом фон Терзаги, также известным как «отец механики грунтов и геотехнической инженерии». Терзаги установил теорию одномерной консолидации и изменил определение этого термина, поскольку ранее он ассоциировался (и до сих пор ассоциируется в геолого-геофизических исследованиях) с уплотнением глинистых отложений, которые образовывали сланцы.
Когда нагрузка прикладывается к грунту с низкой проницаемостью, она первоначально переносится водой, которая существует в пористой части насыщенного грунта, что приводит к быстрому увеличению порового давления воды. Это избыточное давление поровой воды рассеивается, когда вода стекает из пустот почвы, и давление передается на скелет почвы, который постепенно сжимается, что приводит к оседанию. Процедура консолидации длится до тех пор, пока не исчезнет избыточное давление поровой воды.
Увеличение приложенного напряжения, вызывающее уплотнение, может быть вызвано либо естественными нагрузками (например,грамм. процессы седиментации), или антропогенные нагрузки (например, строительство здания или насыпи над массивом почвы), или даже снижение уровня грунтовых вод.
Продолжительность консолидации
Продолжительность процесса консолидации является критическим вопросом и в значительной степени зависит от проницаемости почвы, подверженной нагрузке, и от дренажных путей. В целом, уплотнение песчаных грунтов — это быстрый процесс (происходящий, возможно, сразу во время строительства), тогда как в глинистых грунтах этот процесс может длиться многие годы или даже десятилетия.
Процедура уплотнения обычно разделяется на 3 этапа:
- Начальное уплотнение: быстрая потеря объема массы почвы, связанная с приложением внешнего напряжения, которое сжимает воздух внутри пустот почвы.
- Первичное уплотнение: оседание почвы, во время которого избыточное давление поровой воды передается на каркас почвы
- Вторичное уплотнение: последующая процедура оседания, которая происходит после первичного уплотнения и связана с внутренними изменениями в структуре почвы при почти постоянной нагрузке .Этот процесс обычно называют ползучестью.
Тест одометра
Простейшим рассмотренным случаем консолидации является одномерная консолидация. При этом не учитывается поперечная деформация грунтового массива. Процедура тестирования для количественной оценки критических свойств почвы, связанных с консолидацией почвы, — это тест одометра. Термин «одометр» происходит от древнегреческого языка и означает «набухать». Тест является одним из наиболее часто проводимых и важных лабораторных тестов в геотехнической инженерии.Одометрический тест направлен на измерение вертикального смещения цилиндрического насыщенного образца грунта, подвергнутого вертикальной нагрузке, когда он ограничен в радиальном направлении. В последующем тесте описывается тест консолидации добавочной нагрузки. Обратите внимание, что существует также испытание с постоянной скоростью деформации (CRS), которое в настоящее время становится все более популярным.
Компоненты испытательной установки
Типичная испытательная установка одометра, показанная на рис. 1 , состоит из: i ) — ячейка консолидации , ii) — нагружающая рама , и iii) — механизм измерения деформации .
Ячейка консолидации состоит из следующих компонентов:
- Ограничивающее кольцо, расположенное по окружности вокруг образца для ограничения бокового смещения
- Нагрузочная крышка для передачи нагрузки на образец грунта
- Резервуар, заполненный водой до обеспечить, чтобы почва оставалась по существу насыщенной.
- Пористые камни, которые на несколько порядков более проницаемы, чем типичные образцы мелкозернистого грунта.Эти камни позволяют отводить воду сверху и снизу образца.
- Фильтровальная бумага, помещаемая между камнем и образцом почвы, чтобы предотвратить закупорку поры камня.
Типичный диаметр ( D ) до высоты ( H ) соотношения образцов грунта составляют D / H = 3 — 4 . Площадь поперечного сечения образца грунта может составлять 20, 35 или 50 см 2 ( D = 5-8 см ), а его высота составляет H = 2-2,5 см .
Нагрузочная рама Конфигурация состоит из грузовой балки и собственных грузов. Конфигурация позволяет поддерживать постоянную нагрузку неограниченное время. Приложение нагрузки вызывает деформацию погрузочной рамы, пористых камней и образца грунта. Поскольку испытание предназначено для измерения только деформации почвы, необходимо измерить другие движения (прогиб машины), а затем вычесть их из общей деформации. Это достигается путем измерения прогиба установки с использованием алюминиевого образца, который характеризуется линейно-упругим и, следовательно, известным откликом.
Измерение вертикальной деформации образца грунта выполняется с помощью индикатора часового типа (чаще всего) или электронного прибора.
Рис. 1: Типичная испытательная установка одометра (фото из Афинского национального технического университета)
Процедура испытания
Типичная процедура испытания состоит из следующих шагов:
- Размещение индикатора часового типа (или электронный прибор)
- Измерьте вес, высоту и диаметр ограничивающего кольца
- Измерьте высоту (H) и диаметр (D) алюминиевого образца
- Поднесите образец к ограничивающему кольцу
- Измерьте содержание воды с обрезков
- Взвешивание образца грунта и ограничивающее кольцо
- Замачивание пористых камней и фильтровальной бумаги
- Поместите ячейку уплотнения в загрузочную раму и отрегулируйте высоту.Загрузочная балка должна быть почти горизонтальной.
- Снимите начальные показания ( R i — показания будут вычтены из всех измерений)
- Установите нагрузку на сиденье
- Добавьте воды в резервуар
Нагрузка поддерживается в течение 24 часов (в для некоторых глин необходимое время составляет 48 часов), в течение которого почва уплотняется дренажем из пористых камней.После этого прилагаемая нагрузка постепенно увеличивается, удваивая прилагаемое напряжение на каждом этапе. Количество ступеней нагрузки и максимальное прикладываемое напряжение зависит от интересующего диапазона напряжений. Во время процесса загрузки в ячейку подается вода, так что образец остается полностью насыщенным. На каждом этапе нагружения систематически снимаются показания деформации для построения кривой времени оседания. То есть после приложения каждой нагрузки деформация измеряется через 6, 15, 30 секунд, затем через 1, 2, 4, 8, 16, 30 минут и через 1, 2, 4, 8 и 24 часа соответственно. .Когда достигается максимальная нагрузка и, возможно, с промежуточным приращением нагрузки, вводится этап разгрузки, который может проводиться в один или несколько этапов; обычно нагрузка уменьшается в 4 раза на каждом этапе. Когда испытание завершено, измеряется окончательная высота образца и содержание в нем воды.
Результаты и параметры, полученные в ходе одометрического теста
Следующие свойства почвы получены из одометрического теста:
- Давление предварительного уплотнения : Максимальное эффективное напряжение, которое образец грунта выдержал за свою геологическую историю.
- Индекс сжатия C C : C C — это индекс, связанный с сжимаемостью почвы. В частности, он измеряется как наклон кривой между коэффициентом пустотности и эффективным напряжением. Коэффициент пустотности отображается в нормальном масштабе, а эффективное напряжение — в логарифмическом масштабе. Типичная кривая сжатия с точки зрения коэффициента пустотности — эффективного напряжения представлена на рис. , рис. 2 . Наклон «девственной» части кривой обозначает индекс сжатия C C .
Рис. 2: Типичная диаграмма соотношения пустот — корреляция между эффективными напряжениями, полученная с помощью теста Oedometer. Также представлены индексы сжатия C C и рекомпрессии C r .
Следовательно, C C :
C C = Δe / Δlog (σ ‘)
C C обычно находится в диапазоне от 0,1 до 10 и не имеет единиц измерения. Для нормально консолидированных глин индекс обычно находится в диапазоне от 0,20 до 0,50, а для илов — от 0,16 до 0.24. Для песков индекс находится в диапазоне от 0,01 до 0,06, хотя для песка это не особенно значимый параметр.
Вот некоторые эмпирические выражения, которые связывают индекс сжатия C C с пределом жидкости (LL) и индексом пластичности (PI) почвы:
- C c = 0,007 (LL-10 ), (Skempton, 1944)
- C c = 0,009 (LL-10), (Terzaghi and Peck, 1967)
- C c = 0,50 × PI × G s , (Wroth and Wood, 1978 )
- Индекс рекомпрессии C r : C r используется для определения сжимаемости переуплотненного грунта и рассчитывается с использованием наклона кривой отскока-рекомпрессии (Рисунок 2).Для неорганических почв C r составляет 0,1-0,2 от значения C C .
- Коэффициент консолидации C V : C V — это параметр, который описывает скорость, с которой процесс консолидации развивается во время теста. Типовые значения коэффициента уплотнения приведены в Табл. 1 .
Таблица 1: Типичные значения коэффициента C v
ПОЧВА
C v (см 2 / сек) x 10 -4
Мягкая голубая глина (CL-CH)
(Wallace & Otto, 1964)
1.6-26
Chicago Silty Clay (CL)
(Terzaghi & Peck, 1967)
8-11
Mexico City Clay (MH)
(Леонардс и Леонардс 1961)
0,9-1,5
Органические илы и глины (OH)
(Сивакуган, 1990)
1-10
C
VКоэффициент консолидации C V можно легко оценить по кривой зависимости от времени с помощью графических методов.Наиболее часто используются две методологии:
Метод подгонки логарифма Касагранде (Casagrande and Fadum, 1940):
Коэффициент консолидации, C V , определяется путем оценки времени на уровне 50. % консолидации ( t 50 ), как показано в короткой анимации / презентации ниже. Тогда C V можно оценить как:
C V = 0,917 * (H 2 dr / t 50 )
, где H dr — дренаж. дорожка.Учитывая начальную высоту образца ( H i ) и сжатие образца почвы при 50% консолидации ( ΔΗ ), рассчитывается путь дренажа (для двойного дренажа), H dr . как:
H dr = ( H i — ΔΗ ) / 2
Квадратный корень Тейлора метода подгонки времени (Taylor, 1948):
В этом методе показания шкалы откладываются от квадратного корня из времени.Коэффициент консолидации, C V , определяется путем оценки времени при 90% консолидации ( t 90 ), как показано в короткой анимации / презентации ниже. Тогда C V можно оценить как:
C = 0,848 * (H 2 dr / t 90 )
, где H dr — средний путь дренажа ( обычно половина высоты образца).
Источники
Леонардс, Г.А. и Жиро П. (1961). Исследование теста одномерной консолидации, Proc. Пятый Int. Конф. по механике грунтов и найденному. Eng., Paris, Vol. 1, 116-130.
Сивакуган Н., (1990). Развитие заболоченных территорий в Коломбо, Шри-Ланка, Proc. Десятый Геот Юго-Восточной Азии. Конф., Тайбэй, т. 1, 469-472.
Скемптон, А. У. (1944). Замечания о сжимаемости глин. Q. J. Geol. Soc. Лондон, 100 (1-4), 119-135.
Терзаги К. и Пек Р. Б. (1967). Механика грунтов в инженерной практике, John Wiley & Sons, Нью-Йорк, 729 стр.
Уоллес, Дж. Б. и Отто, В. К. (1964). Дифференциальный расчет на базе ВВС Селфридж, Jnl. Почвенная механика и найдено. Div., ASCE, Vol. 90, № SM5, 197-220.
Рот, К. П. и Вуд, Д. М. (1978). Связь индексных свойств с некоторыми основными инженерными свойствами почв. Канадский геотехнический журнал, 15, 137-145.
Сводное определение
Что означает консолидация?
Консолидация (консолидация) — это объединение активов, обязательств и других финансовых статей двух или более организаций в одну.В контексте финансового учета термин консолидировать часто относится к консолидации финансовой отчетности, в которой все дочерние компании представляют отчетность под эгидой материнской компании. Консолидация также относится к объединению небольших компаний в более крупные компании посредством слияний и поглощений (M&A).
Ключевые выводы
- Консолидация (консолидация) — это объединение активов, обязательств и других финансовых статей двух или более организаций в одну.
- В финансовом учете термин консолидировать часто относится к консолидации финансовой отчетности, в которой все дочерние компании представляют отчетность под эгидой материнской компании.
- Консолидация также относится к объединению небольших компаний в более крупные компании посредством слияний и поглощений.
Консолидация: Слово на улице
Как работает консолидация
Термин «консолидировать» происходит от латинского Consolidatus, , что означает «объединяться в одно тело».«Независимо от контекста, консолидация предполагает объединение большего количества предметов в единое меньшее количество. Например, путешественник может объединить весь свой багаж в одну большую сумку. В сфере финансов и бухгалтерского учета консолидация имеет более специфический нюанс. .
Консолидация в финансах
Консолидация включает в себя создание нескольких учетных записей или предприятий и объединение информации в единую точку. В финансовой отчетности консолидированная финансовая отчетность дает исчерпывающее представление о финансовом положении как материнской компании, так и ее дочерних компаний, а не обособленной позиции одной компании.
В консолидированном бухгалтерском учете информация материнской компании и ее дочерних предприятий трактуется так, как если бы она была получена от одного предприятия. Совокупные активы от бизнеса, а также любые доходы или расходы отражаются в балансе материнской компании. Эта информация также указывается в отчете о прибылях и убытках материнской компании.
Консолидированная финансовая отчетность используется, когда материнская компания владеет контрольным пакетом акций, контролируя более 50% дочернего бизнеса.Материнские компании, владеющие более 20%, имеют право использовать консолидированный бухгалтерский учет. Если материнская компания владеет менее 20% акций, она должна использовать метод долевого участия.
Консолидация предприятий
В бизнесе консолидация происходит, когда два или более предприятий объединяются в одну новую организацию с ожиданием увеличения доли рынка и прибыльности, а также выгоды от объединения талантов, отраслевых знаний или технологий. Консолидация, также называемая слиянием, может привести к созданию совершенно нового предприятия или дочерней компании более крупной фирмы.Такой подход может объединить конкурирующие фирмы в один совместный бизнес.
Например, в 2015 году Target Corp. перешла на продажу аптечной части своего бизнеса CVS Health, крупной сети аптек. В рамках соглашения CVS Health намеревалась провести ребрендинг аптек, работающих в магазинах Target, изменив название на MinuteClinic. Консолидация носила дружественный характер и снизила общую конкуренцию на фармацевтическом рынке.
Консолидация на практике отличается от слияния тем, что объединенные компании также могут привести к созданию нового юридического лица, тогда как при слиянии одна компания поглощает другую и продолжает существовать, в то время как другая распадается.
Консолидация потребительского долга
На потребительском рынке консолидация включает использование одной ссуды для погашения всех долгов, которые являются частью консолидации. Это переводит задолженность нескольких кредиторов, позволяя потребителю иметь единую точку платежа для выплаты всей суммы.
Часто консолидация долга позволяет добиться более управляемых ежемесячных платежей и может привести к более низкой общей процентной ставке. Например, он может превратить платеж по кредитной карте с высоким процентом в более разумную кредитную линию для собственного капитала.
Консолидация в техническом анализе и торговле
Консолидация — это также термин технического анализа, относящийся к колебаниям цен на ценные бумаги в пределах коридора и обычно интерпретируемый как нерешительность рынка. Другими словами, консолидация используется в техническом анализе для описания движения цены акции в рамках четко определенной модели торговых уровней.
Консолидация обычно рассматривается как период нерешительности, который заканчивается, когда цена актива движется выше или ниже цен в торговой схеме.Модель консолидации ценовых движений нарушается после выхода крупных новостей, которые существенно влияют на производительность ценных бумаг или срабатывание последовательности лимитных ордеров. Консолидация также определяется как набор финансовых отчетов, в которых материнская и дочерняя компании представлены как одна компания.
Консолидация памяти — обзор
3 Современная молекулярная биология памяти
Процессы памяти очень сложны. Их можно разложить на ряд различных процессов, от чрезвычайно кратковременной памяти (миллисекунды) до кратковременной памяти (часы) и, наконец, до долговременной памяти (дни) или очень долговременной памяти (десятилетия). 4
Известно, что консолидация памяти является непрерывным процессом. Marra et al. 2 изучали восприимчивость к консолидации памяти во время провалов в припоминании. Известно, что воспоминания, которые можно вспомнить через несколько часов после обучения, могут парадоксальным образом стать недоступными на короткие периоды после их формирования. Это поднимает основные вопросы о функции этих ранних провалов памяти в структуре консолидации памяти. Эти вопросы трудно исследовать из-за отсутствия информации о точном времени упущений.Marra et al. 2 использовали электрофизиологические и поведенческие эксперименты в Lymnaea для решения этой проблемы, которые выявили провалы в воспроизведении памяти через 30 минут и 2 часа после кондиционирования. Эти авторы демонстрируют, что только во время этих провалов консолидация LTM может быть прервана внешним воздействием. Они показывают, что эти общие временные точки провала памяти и восприимчивости соответствуют основным переходам между отдельными фазами памяти, которые имеют разные и специфические изменения в молекулярных механизмах только на ранних стадиях формирования памяти.Таким образом, кажется, что восстановление памяти становится более трудным, когда есть изменения в молекулярных зависимостях, указывающие на то, что различные молекулярные пути ответственны за различные фазы формирования памяти. 18 Их предыдущие эксперименты показали, что эти существенные изменения в молекулярных потребностях начинаются после единственного тренировочного испытания на ранней стадии консолидации памяти. 19,20 Последующие нижестоящие механизмы вызывают отзыв между STM и ранним ITM (через 30 минут), а также между ранним и поздним ITM (через 2 часа), что по своей природе становится более слабым и восприимчивым.Marra et al. 2 использовали тренировочную парадигму, ведущую к непрерывной памяти, чтобы проверить механизмы отказа в памяти в критические моменты в своих экспериментах по фармакологической блокировке. Это вызвало вопрос, приводят ли две тренировочные парадигмы к воспоминаниям с использованием сходных или различных молекулярных процессов. Они продемонстрировали, что обе обучающие парадигмы индуцировали одну и ту же трансляцию, но не зависимую от транскрипции ITM через 3 часа, а LTM, зависимую от синтеза белка и РНК, через 4 и 24 часа.Во время идентификации различных фаз памяти они продемонстрировали, что 2 :
- •
память на 10 минут является STM, поскольку характеризуется отсутствием потребности в синтезе белка и РНК;
- •
память на 1 час — это ITM, которая характеризуется потребностью в синтезе белка и отсутствием потребности в синтезе новой РНК;
- •
4-часовой график памяти — это LTM, потому что он требует синтеза как белка, так и РНК.
Они предположили, что во время периодов молекулярных переходов воспоминания ослабевают, что позволяет новым сенсорным сигналам блокировать консолидацию LTM.
В обзоре, посвященном молекулярной биологии памяти, Кандел 21 заявил, что вклад в синаптическую пластичность и память потребовал усилий многих лабораторий по всему миру. Существует шесть ключевых шагов в молекулярно-биологическом разграничении STM и его преобразовании в LTM как для неявной (процедурной), так и для явной (декларативной) памяти: цАМФ (циклический аденозинмонофосфат), PKA (протеинкиназа A), CRE (элемент ответа цАМФ). , CREB-1 (белок-1, связывающий элемент ответа цАМФ), CREB-2 (белок-2, связывающий элемент ответа цАМФ) и CPEB (белок, связывающий элемент цитоплазматического полиаденилирования).
В этом крупном обзоре 21 Kandel вспоминает появление молекулярной биологии связанной с памятью синаптической пластичности и разграничение cAMP и PKA в хранении STM; и что классическая обусловленность включает как пре-, так и постсинаптические механизмы пластичности. Затем он разработал молекулярную биологию долговременной синаптической пластичности, связанной с обучением. Как указывалось ранее, образование LTM требует синтеза нового белка. Повышение уровня цАМФ приводит к более длительным формам синаптической пластичности.Этот более устойчивый паттерн стимуляции заставляет каталитическую субъединицу PKA рекрутировать p42 MAPK (митоген-активированная протеинкиназа), а затем обе они перемещаются в ядро, где они фосфорилируют факторы транскрипции и активируют экспрессию генов, необходимую для индукции LTM. Различные синаптические протеинфосфатазы действуют как ингибиторы формирования памяти, поскольку они локально противодействуют активности PKA, а равновесие между активностями киназы и фосфорилазы может регулировать как хранение, так и восстановление памяти. 22 В этом обзоре Кандел 21 объясняет активацию факторов ядерной транскрипции, то, как долгосрочные синаптические изменения регулируются как положительными, так и отрицательными регуляторами, и что переход от краткосрочного содействия (STF) к долгосрочному фасилитация (LTF) требует одновременного удаления репрессоров транскрипции и активации активаторов транскрипции. Эти репрессоры и активаторы транскрипции могут взаимодействовать друг с другом как физически, так и функционально.
Для Кандела, 21 , вероятно, что переход представляет собой сложный процесс, включающий в себя отдельные во времени фазы активации, репрессии и регуляции передачи сигнала. Как сообщается в литературе, CREB-опосредованный ответ на внеклеточные стимулы может модулироваться киназами (PKA, CaMKII или кальмодулин-зависимые протеинкиназы II, MAPK, PKC и т. Д.) И фосфатазами (фосфопротеинфосфатаза 1 или PP1 и кальциневрин). . Таким образом, регуляторный блок CREB может служить для интеграции сигналов от различных путей передачи сигналов.Эта способность интегрировать передачу сигналов, а также опосредовать активацию или репрессию может объяснить, почему CREB так важен для хранения в памяти. Изменение хроматина и эпигенетические изменения в экспрессии генов наблюдались при хранении в памяти: интеграция LTM-связанной синаптической пластичности включает двунаправленную регуляцию экспрессии генов и структуры хроматина. 23 Хотя широко известно, что эпигенетические механизмы участвуют в формировании и долгосрочном хранении клеточной информации в ответ на временные сигналы окружающей среды, открытие их предполагаемой значимости для функционирования мозга взрослых людей произошло сравнительно недавно. 23,24
Эпигенетическая маркировка хроматина, такая как модификация гистонов, ремоделирование хроматина и активность ретротранспозонов, может, таким образом, иметь долгосрочные последствия в регуляции транскрипции конкретных локусов, участвующих в долговременных синаптических изменениях. 25 LTM принципиально отличается от краткосрочного процесса тем, что вовлекает рост новых синаптических связей. Для Kandel 21 рост новых синапсов может представлять последнюю и, возможно, наиболее стабильную фазу хранения LTM, повышая вероятность того, что устойчивость долгосрочного процесса может быть достигнута, по крайней мере частично, из-за относительной стабильности синаптическая структура.Принципиальное различие между хранением LTM и краткосрочными изменениями заключается в необходимости активации экспрессии генов. LTF и связанные с ним синаптические изменения специфичны для синапсов и требуют CREB-1. Для синаптического захвата существует не только ретроградная передача сигналов от синапса обратно к ядру, но также антероградная передача сигналов от ядра к синапсу. Молекулярный механизм синаптического захвата включает множество факторов, таких как PKA, CPEB, который активирует мРНК и CRE. 21
Примечания к финансовой отчетности — Обзор, компоненты
Что такое примечания к финансовой отчетности?
Примечания к финансовой отчетности — это дополнительные примечания, которые включаются в публикуемую финансовую отчетность компании.Примечания используются для объяснения допущений, использованных при составлении чисел в финансовой отчетности, а также учетной политики, принятой компанией. Они помогают разным типам пользователей, например финансовым аналитикам, финансовым аналитикам и инвесторам, интерпретировать все числа, указанные в финансовых отчетах.
Источник: Amazon.com Годовой отчет за 2018 год
При проведении аудита финансовой отчетности аудитор тщательно исследует всю информацию, содержащуюся в финансовой отчетности, включая примечания к финансовой отчетности.Аудиторы используют примечания, чтобы определить, является ли используемая учетная политика подходящей, применяемой должным образом и отражена ли в отчетных результатах компании.
В примечаниях также может содержаться информация по основным вопросам, касающимся общего финансового состояния компании. Аудитор основывает свое аудиторское заключение на номерах финансовой отчетности, а также примечаниях к финансовой отчетности.
Резюме- Примечания к финансовой отчетности относятся к дополнительным примечаниям, включенным в финансовую отчетность компании,
- Примечания используются для раскрытия важной информации, объясняющей допущения, использованные при подготовке финансовой отчетности компании.
- Общие примечания к финансовой отчетности включают учетную политику, амортизацию активов, оценку запасов, события после отчетной даты и т. Д.
Общие примечания к финансовой отчетности
Ниже приведены общие статьи, которые появляются в примечания к финансовой отчетности:
1. Принципы представления
В первом разделе примечаний к финансовой отчетности объясняются основы подготовки и представления ключевой финансовой отчетности.
2. Учетная политика
В разделе учетной политики представлена информация об учетной политике, принятой руководством при подготовке финансовой отчетности. Раскрытие учетной политики помогает пользователям лучше интерпретировать и понимать финансовую отчетность.
Некоторые из представленных здесь раскрытий — это используемый метод амортизации, то, как компания оценивает запасы, учет нематериальных активов Нематериальные активы Согласно МСФО нематериальные активы являются идентифицируемыми немонетарными активами, не имеющими физического содержания.Как и все активы, нематериальные активы и т. Д. Все важные принципы учетной политики, принятые в финансовой отчетности, должны быть раскрыты в этом разделе.
3. Амортизация активов
Амортизация относится к снижению стоимости основных средств с течением времени из-за нормального износа. В разделе «Амортизация активов» представлена информация о методе, принятом компанией при начислении амортизации активов.
В зависимости от используемого метода амортизации могут быть значительные колебания между чистой прибылью в отчете о прибылях и убытках и значением, указанным в балансе.Информация о методе начисления амортизации в примечаниях информирует пользователей о разнице в чистой прибыли, отраженной в финансовой отчетности.
4. Оценка товарно-материальных запасов
Оценка товарно-материальных запасов информирует пользователей о том, как компания оценила свои товарные запасы, что позволяет им легко сравнивать показатели запасов за один период или с другими конкурирующими организациями. В разделе представлена информация по двум основным вопросам инвентаризации, а именно, как указывается сумма инвентаря и метод, используемый для определения стоимости инвентаря.
ПравилаGAAP требуют, чтобы компании указывали свои запасы по наименьшей стоимости или рыночной (LCM) Низкой стоимости или рыночной (LCM) Низкой стоимости или рыночной (LCM) — это метод оценки запасов, необходимый для компаний, которые следуют US GAAP. По более низкой цене или по рынку. Это означает, что компания будет оценивать запасы по самой низкой восстановительной стоимости, которая может быть либо оптовой стоимостью запасов, либо стоимостью запасов на рынке. Для определения стоимости запасов GAAP позволяет использовать три различных метода, которые включают средневзвешенное значение, конкретную идентификацию и метод «первым пришел — первым обслужен» (FIFO), первым пришел — первым обслужен (FIFO), первым пришел — первым обслужен (FIFO). ) Методика учета товарно-материальных ценностей основана на практике реализации метода продажи или использования товаров.
5. События после отчетной даты
Информацию о любых событиях после отчетной даты также можно найти в разделе примечаний к финансовой отчетности. Под последующими событиями понимаются события, которые происходят после отчетной даты, но до выпуска финансовой отчетности. То, как компания обрабатывает события, зависит от того, изменяют ли они условия, существующие на отчетную дату.
Два типа событий после отчетной даты:
Дополнительная информация: Событие, которое предоставляет информацию об условиях, существующих на дату баланса, включая дополнительную информацию, которая влияет на оценки, используемые для подготовки финансовой отчетности.Примером может служить объединение бизнеса после отчетной даты.
Новые события: Событие, которое предоставляет новую информацию об условиях, которые не существовали на дату баланса. Примером может служить повреждение или кража машины на заводе.
Согласно общепринятым принципам бухгалтерского учета, финансовая отчетность должна включать влияние всех событий после отчетной даты, которые предоставляют дополнительную информацию об условиях, существующих на дату составления баланса.Однако последующие события, которые являются новыми, не должны отражаться в финансовой отчетности, но, если они существенны, должны раскрываться в примечаниях к финансовой отчетности.
6. Нематериальные активы
Примечания к финансовой отчетности также включают информацию о любых нематериальных активах, принадлежащих компании. Нематериальные активы — это активы, не имеющие физической формы, включая товарные знаки и патенты. В разделе подробно описаны все нематериальные активы, которыми владеет компания, и то, как она определяла стоимость нематериальных активов, отраженных в балансе.
7. Консолидация финансовой отчетности
Консолидация раздела финансовой отчетности подтверждает, что выпускаемая отчетность содержит финансовую отчетность всех дочерних компаний компании и их учет. В нем подробно описывается основа консолидации финансовой отчетности, и необходимо объяснять любые отклонения от дочерних компаний.
8. Вознаграждения сотрудникам
В разделе примечаний о вознаграждениях сотрудникам упоминаются льготы, которые компания предоставляет своим сотрудникам, включая медицинское страхование, сберегательные счета для здоровья, пенсионные планы и т. Д.
Типичная информация, которую компания раскрывает в примечаниях, включает планы здравоохранения и социального обеспечения для своих сотрудников, такие как медицинские, отпускные и дополнительные льготы. Он также предоставляет информацию об оплаченных и неоплаченных расходах и обязательствах по пенсионным планам сотрудников Пенсионный фонд Пенсионный фонд — это фонд, который накапливает капитал, который будет выплачиваться в качестве пенсии для сотрудников, когда они выходят на пенсию в конце своей карьеры.
9 Условное обязательство
Условное обязательство относится к обязательству, которое может возникнуть, но зависит от результата неопределенного будущего события.Примером условного обязательства является неурегулированный судебный процесс против компании или спор о подоходном налоге. Раскрытие условных обязательств информирует пользователей о том, что компания может понести убытки в будущем, если надвигающееся событие закончится против компании.
Дополнительные ресурсы
CFI является официальным поставщиком сертификации коммерческого банковского и кредитного аналитика (CBCA) ™ CBCA®. Аккредитация коммерческого банковского и кредитного аналитика (CBCA) ™ является мировым стандартом для кредитных аналитиков, охватывающим финансы, бухгалтерский учет и т.д. кредитный анализ, анализ денежных потоков, моделирование ковенантов, погашение ссуд и многое другое.программа сертификации, призванная превратить любого в финансового аналитика мирового уровня.
Чтобы помочь вам стать финансовым аналитиком мирового уровня и продвинуть свою карьеру в полной мере, вам будут очень полезны следующие дополнительные ресурсы:
- Анализ финансовой отчетности Анализ финансовой отчетности Как проводить анализ финансовой отчетности. Это руководство научит вас выполнять анализ финансовой отчетности отчета о прибылях и убытках.
- Руководство по судебному аудиту Руководство по судебному аудиту Судебный аудит — это подробный аудит документации компании, которая будет использоваться в суде в ходе судебного разбирательства.Бухгалтеры, юристы и
- Методы начисления амортизации Методы амортизации Наиболее распространенные типы методов амортизации включают прямолинейный, двойной уменьшающийся баланс, единицы производства и цифры суммы лет. Существуют различные формулы для расчета амортизации актива. Расходы на амортизацию используются в бухгалтерском учете для распределения стоимости материального актива на протяжении срока его полезного использования.
- МСФО, ОПБУ США и ОПБУ США МСФО и ОПБУ США относятся к двум стандартам бухгалтерского учета и принципам, которых придерживаются страны мира в отношении финансовой отчетности
Часть II МАТЕМАТИКА-5 Понимание математики: Введение | Как студенты учатся: история, математика и естественные науки в классе
Фусон, К.К. и Смит Т. (1997). Поддержка нескольких двузначных концептуальных структур и методов расчета в классе: вопросы концептуальной поддержки, учебного дизайна и языка. В M. Beishuizen, K.P.E. Гравемейер и E.C.D.M. van Lieshout (Eds.), Роль контекстов и моделей в разработке математических стратегий и процедур (стр. 163-198). Утрехт, Нидерланды: CD-B Press / Институт Фройденталя.
Фусон, К.С., Стиглер, Дж., И Бартч, К.(1988). Размещение оценок по темам сложения и вычитания в Японии, материковом Китае, Советском Союзе, Тайване и США. Журнал исследований в области математического образования , 19 (5), 449-456.
Фусон, К.С., Перри, Т., и Квон, Ю. (1994). Латиноамериканские, англоязычные и корейские детские методы сложения пальцев. В J.E.H. van Luit (Ed.), Исследование по изучению и преподаванию математики в детском саду и начальной школе , (стр. 220-228).Doetinchem / Rapallo, Нидерланды: Graviant.
Fuson, K.C., Perry, T., and Ron, P. (1996). Уровни развития в различающихся в культурном отношении пальцевых приемах: англоязычные и латиноамериканские детские методы сложения пальцев В E. Jakubowski, D. Watkins и H. Biske (Eds.), Proceedings 18-го ежегодного собрания Североамериканского отделения психологии математического образования (2-е издание, стр. 347-352). Колумбус, Огайо: Информационный центр ERIC по естествознанию, математике и экологическому образованию.
Фусон, К.С., Ло Цицеро, А., Хадсон, К., и Смит, С.Т. (1997). Снимки двух лет из жизни городского латиноамериканского класса. В J. Hiebert, T. Carpenter, E. Fennema, K.C. Фьюсон, Д. Вирн, Х. Мюррей, А. Оливье и П. Хуман (ред.), Осмысление смысла: преподавание и изучение математики с пониманием (стр. 129-159). Портсмут, Нью-Хэмпшир: Хайнеманн.
Фусон, К.С., Смит, Т., и Ло Цицеро, А. (1997). Поддержка десятиструктурированного мышления латиноамериканских первоклассников в городских классах. Журнал исследований в области математического образования , 28 , 738-760.
Фусон, К.С., Вирн, Д., Хиберт, Дж., Мюррей, Х., Хьюман, П., Оливье, А., Карпентер, Т., и Феннема, Э. (1997). Детские концептуальные конструкции для многозначных чисел и методы сложения и вычитания многозначных чисел. Журнал исследований в области математического образования , 28 , 130-162.
Фусон, К.С., Де Ла Крус, Ю., Смит, С., Ло Цицеро, А., Хадсон, К., Рон, П., и Стиби, Р. (2000). Объединение лучших достижений 20-го века для достижения математической педагогики равенства в 21-м веке. В книге M.J. Burke и F.R. Curcio (Eds.), Изучение математики для нового века (стр. 197-212). Рестон, Вирджиния: Национальный совет учителей математики.
Гири, округ Колумбия (1994). Математическое развитие детей: исследования и практическое применение . Вашингтон, округ Колумбия: Американская психологическая ассоциация.
Гельман Р.(1990). Первые принципы организуют внимание и изучение соответствующих данных: число и различие между живым и неодушевленным в качестве примеров. Когнитивная наука , 14 , 79-106.
Гинзбург, Г. (1984). Детская арифметика: процесс обучения. Нью-Йорк: Ван Ностранд.
Ginsburg, H.P., and Allardice, B.S. (1984). Проблемы детей с школьной математикой. В B. Rogoff and J. Lave (Eds.), Повседневное познание: его развитие в социальных контекстах (стр.194-219). Кембридж, Массачусетс: Издательство Гарвардского университета.
5 Знания и рассуждения | Как люди учатся II: учащиеся, контексты и культуры
ПоясненияПоощрение учащихся к объяснению того, что они изучают, является многообещающим методом поддержки понимания. Были изучены три техники для этого: уточняющий допрос, самообъяснение и обучение.
Подробный допрос — это стратегия, в которой учащимся задают или побуждают задавать себе вопросы, требующие глубоких рассуждений, например, почему, как, что, если и что, если нет (в отличие от поверхностных вопросов, таких как кто, что, когда и где) (Gholson et al., 2009). Любопытная ученица, применяющая интеллектуальный уточняющий допрос, задает вопросы с глубоким рассуждением, пытаясь понять сложный материал и решить проблемы. Однако подробный допрос не является естественным для большинства детей и взрослых; Было показано, что обучение людей использованию этого навыка — и особенно обучение заданию глубоких вопросов — оказывает положительное влияние на понимание, обучение и память (Gholson et al., 2009; Graesser and Lehman, 2012; Graesser and Olde, 2003; Rosenshine et al., 1996). Например, в раннем исследовании людей просили либо дать объяснения «почему» для нескольких несвязанных предложений, либо прочитать и изучить предложения. Затем обе группы тестировались на запоминание предложений. Те, кто задавал вопросы, работали лучше, чем группа, которая только что изучала предложения (Pressley et al., 1987). Исследования с детьми также показали преимущества уточняющего допроса (Woloshyn et al., 1994), и преимущества уточняющего допроса могут сохраняться с течением времени (например,g., через 1 или 2 недели после обучения), хотя мало исследований изучали влияние подробного допроса на долгосрочное удержание.
В большинстве исследований, проведенных исследователями экспериментальной психологии, отдельные факты использовались в качестве материалов для изучения эффектов обработки и оценки дословного запоминания, но исследователи в области педагогической психологии также изучали более сложное текстовое содержание и оценивали умение делать выводы (Дорниш и Сперлинг, 2006 ; Озгунгор, Гатри, 2004).Например, Макдэниел и Доннелли (1996) попросили студентов колледжа изучить краткие описания физических понятий, таких как сохранение углового момента, а затем ответить на вопрос, почему это понятие (например, «Почему объект ускоряется по мере увеличения его радиуса»). стать меньше, как при сохранении момента импульса? »). Окончательная оценка включала как фактические вопросы, так и вопросы вывода, которые затрагивали более глубокие уровни понимания. Авторы обнаружили преимущества уточняющего допроса для сложных материалов и оценок, а также обнаружили, что те, кто участвовал в уточняющем допросе, превосходили учащихся, создававших маркированные диаграммы понятий в каждом кратком тексте.
Самообъяснение — это стратегия, при которой учащиеся объясняют материал или свои мыслительные процессы во время чтения, ответа на вопросы или решения проблем. В самом общем случае учащихся можно просто попросить объяснить каждый шаг, который они делают при решении задачи (Chi et al., 1989b; McNamara, 2004), или объяснять текст предложение за предложением, когда они его читают (Chi
).Что такое вмешательство в психологии?
Интерференция — это одна из теорий, объясняющих, как и почему в долговременной памяти происходит забывание.Интерференция — это явление памяти, при котором одни воспоминания мешают восстановлению других воспоминаний.
По сути, интерференция возникает, когда некоторая информация затрудняет вспоминание аналогичного материала. Подобные воспоминания конкурируют друг с другом, из-за чего некоторые из них труднее запомнить или даже полностью забыть. Из-за этого некоторые долговременные воспоминания не могут быть восстановлены в кратковременной памяти.
Обзор
Вы когда-нибудь путали воспоминания об одном событии с другим? Этот опыт может быть на удивление обычным, особенно если вы столкнулись с рядом очень похожих воспоминаний.Например, если кто-то попросил вас вспомнить, что вы ели на завтрак в прошлый понедельник, вам может быть сложно вспомнить, потому что у вас так много похожих воспоминаний о других блюдах.
Есть много разных, но похожих воспоминаний, закодированных в долговременной памяти, из-за чего сложно вспомнить конкретное событие и перенести его в кратковременную память.
Истоки
Что вызывает забывание? Исследователи давно интересовались не только тем, как работает память, но и тем, почему люди иногда забывают.Теория интерференции — лишь одно из нескольких предлагаемых объяснений.
Некоторые важные исследования внесли свой вклад в развитие теории интерференции. В одном из первых исследований феномена интерференции исследователь Джон А. Бергстром попросил участников разделить карточки на две разные стопки.
Он обнаружил, что изменение местоположения второй стопки приводит к снижению производительности, предполагая, что изучение правил для первой задачи мешает запоминанию правил для второй задачи.
В 1900 году исследователи Мюллер и Пильцекер провели важные исследования ретроактивного вмешательства. Они обнаружили, что люди с меньшей вероятностью будут вспоминать бессмысленные слоги, если промежуточный материал был представлен через 10 минут или раньше после первоначального учебного задания.
Они предположили, что это указывает на то, что новым воспоминаниям требуется период времени, чтобы они стабилизировались в памяти, и этот процесс они назвали «консолидацией».
Теория распада
В конце 1950-х годов психолог Бентон Дж.Андервуд посмотрел на знаменитую кривую забывания Эббингауза и пришел к выводу, что на забывание влияет не только время, но и ранее усвоенная информация.
Теория распада развивает исследования Эббингауза и предполагает, что воспоминания со временем распадаются, что приводит к забыванию. Однако память также может быть подвержена ряду других влияний, которые влияют на то, насколько хорошо вещи вспоминаются и почему они иногда забываются.
Хотя исследователи могут контролировать другие факторы в лабораторных условиях, реальный мир наполнен множеством событий, которые также могут иметь влияние на память.
Многие события могут иметь место между моментом кодирования памяти и моментом ее вызова. Насколько редко (если вообще когда-либо) вы формируете воспоминание, а затем не узнаете ничего нового между формированием этого воспоминания и потребностью вспомнить эту информацию?
Такие условия обычно создаются искусственно только в экспериментальных лабораториях.
Однако в вашей повседневной жизни может произойти любое количество событий, переживаний и нового обучения между фактическим формированием одного воспоминания и необходимостью вспомнить это воспоминание.
Исследователи обнаружили, что когда промежутки между кодированием и воспроизведением заполняются другой информацией, это оказывает соответствующее негативное влияние на память.
Из-за этого явления может быть сложно определить, связано ли забывание с течением времени или это следствие одного из этих промежуточных факторов. Исследования показывают, например, что мешающие воспоминания являются одним из факторов, которые также могут способствовать забыванию.
Существует два различных типа помех: проактивное вмешательство и обратное вмешательство.
Упреждающее вмешательство
Проактивное вмешательство — это когда старые воспоминания мешают восстановлению новых воспоминаний. Поскольку старые воспоминания часто лучше репетируются и более прочно закрепляются в долговременной памяти, часто легче вспомнить ранее усвоенную информацию, чем более недавнее обучение.
Проактивное вмешательство иногда может затруднить изучение нового. Например, если вы переезжаете в новый дом, вы можете случайно записать свой старый адрес при заполнении форм.Более старая память о вашем предыдущем адресе затрудняет вспоминание вашего нового адреса.
Обратное вмешательство
Ретроактивное вмешательство — это когда новые воспоминания мешают восстановлению старых воспоминаний. По сути, этот тип вмешательства создает обратный эффект, затрудняя вспоминание вещей, которые были ранее изучены.
В случае ретроактивного вмешательства изучение новых вещей может затруднить вспоминание того, что мы уже знаем.Например, музыкант может выучить новую пьесу только для того, чтобы обнаружить, что новая песня затрудняет вспомнить старую, ранее выученную пьесу.
Исследования показали, что около 70% информации забывается за 24 часа первоначального изучения.
Хотя ретроактивное вмешательство может иметь огромное влияние на сохранение новых знаний, есть несколько эффективных стратегий, которые могут быть реализованы для минимизации этих эффектов.
Изучение
Избыточное обучение — один из эффективных подходов, который можно использовать для уменьшения обратного вмешательства.Переучивание включает в себя повторение нового материала после момента его приобретения.
Это значит изучать и практиковать то, чему вы научились, снова и снова, даже после того, как вы достигли достаточного уровня владения предметом или навыком. Эта практика помогает обеспечить более стабильную информацию в долговременной памяти и улучшить запоминание и производительность.
Примеры помех
Есть много разных примеров того, как вмешательство может влиять на повседневную жизнь.Подумайте, что произойдет, когда вы научитесь делать что-то новое. Если вы приобретете привычку делать что-то неправильно, вам, вероятно, будет намного сложнее исправить поведение и правильно выполнять действия в будущем.
Согласно теории интерференции, трудности с изменением прошлого неправильного поведения, скорее всего, являются результатом вашего предыдущего обучения, препятствующего вашей способности запоминать более свежий материал, что является примером упреждающего вмешательства.
Представьте себе студента, готовящегося к экзамену по истории.Между изучением информации и прохождением реального теста может происходить многое. Студент может посещать другие занятия, работать, смотреть телевизор, читать книги, участвовать в беседах и выполнять многие другие действия в течение этого промежуточного периода.
В дополнение к общему разложению, вызванному истекшим временем, могут образоваться другие воспоминания, которые потенциально могут конкурировать с материалом, который студент изучил для своего экзамена. Если бы этот студент был специалистом по истории, он мог бы даже выучить и изучить материал по аналогичным предметам, что могло бы вызвать еще большие помехи.
Поэтому, когда студент идет на экзамен, ему может быть сложно вспомнить некоторую информацию. Если они усвоили последующий материал, который очень похож на исходную информацию, вспомнить факты и детали для экзамена будет сложнее. Они могут обнаружить, что смешивают обновления исторических сражений или даже не могут вспомнить важные детали о том, как и почему произошли определенные события.
Воспоминания, сформированные в промежутке между обучением и тестом, мешают старым воспоминаниям, что значительно затрудняет их воспроизведение.
Есть много других примеров вмешательства и его влияния на нашу память:
- После смены номера мобильного телефона вам трудно запомнить новый номер, поэтому вы продолжаете случайно сообщать людям свой старый номер. Память о вашем старом номере мешает вам вспомнить новый номер.
- Вы пытаетесь запомнить список вещей, которые вам нужно забрать в продуктовом магазине. За это время вы также случайно прочитали новый рецепт на своем любимом кулинарном веб-сайте.Позже в продуктовом магазине вы обнаруживаете, что изо всех сил пытаетесь вспомнить товары из своего списка покупок. Конкурирующая память об ингредиентах нового рецепта мешает вам вспомнить, что вам нужно в магазине.
- Студенты часто более склонны вспоминать информацию, которую они усвоили незадолго до экзамена, чем материал, который они усвоили ранее в семестре. В этом случае более новая информация конкурирует со старым обучением.
- Носитель английского языка, который пытается выучить французский, может обнаружить, что он продолжает пытаться применить правила своего родного языка к новому языку, который он пытается выучить.Старые воспоминания мешают воспоминаниям о новой информации, затрудняя запоминание грамматических правил нового языка.
- Учитель может с трудом выучить имена новых учеников каждый год, потому что они продолжают путать их с именами учеников прошлых лет.
Что говорят исследования
Исследователи смогли продемонстрировать эффекты вмешательства в многочисленных исследованиях. Часто они делают это, увеличивая схожесть представленной информации.Например, участникам может быть представлена исходная информация, а затем, через некоторое время, представлена дополнительная информация.
При проверке того, что они помнят, интерференция наблюдается чаще, когда вторичная информация содержит больше сходства с исходным материалом.
Чем больше схожих двух запоминающих устройств, тем больше вероятность возникновения помех.
В одном из самых ранних исследований интерференционной теории забывания исследователи просили испытуемых запомнить список двухсложных прилагательных.Позже испытуемых просили запомнить один из пяти разных списков. Некоторые из этих списков были очень похожи на исходный тестовый материал, в то время как другие сильно отличались.
Например, некоторые списки содержали синонимы оригинальных слов, некоторые антонимы, а некоторые были просто бессмысленными слогами. Более позднее тестирование показало, что запоминание улучшается по мере увеличения различий между двумя списками. Чем более похожи были списки, тем больше было помех, что затрудняло их вспоминание.
В одном исследовании 2018 года исследователи обнаружили, что ретроактивное вмешательство оказывает негативное влияние на обучение и консолидацию памяти. После учебного задания некоторым участникам было предложено последующее задание вмешательства в различные моменты времени. У некоторых было второе обучающее задание через три минуты после изучения первой информации, а у других — через девять минут.
Исследователи обнаружили, что задача вмешательства снижает производительность памяти на целых 20%.
Интересно, что вмешательство, как правило, оказывало более сильное негативное влияние на тех, кто идентифицировался как «быстро обучающиеся», чем на тех, кто был идентифицирован как «медленно обучающиеся».
Помехи могут играть заметную роль в процессе обучения. Исследования показывают, что ранее изученный материал может повлиять на будущее обучение, и, наоборот, новая информация может повлиять на прошлое обучение. Одно исследование показало, что эффекты ретроактивного вмешательства более выражены у детей младшего возраста, но эти эффекты могут уменьшаться с возрастом.Взаимодействие с другими людьми
Приложения
Теория интерференции может иметь множество реальных приложений. С практической, повседневной точки зрения теория интерференции предполагает, что один из лучших способов улучшить вашу память о чем-то — это выделить его.
Если вы пытаетесь что-то запомнить и хотите избежать воздействия помех, ищите способ добавить новизны. Составление песни, рифмы или мнемоники — один из способов помочь выделить то, что вы изучаете, в вашей памяти.Взаимодействие с другими людьми
Сделав материал запоминающимся и менее похожим на другие воспоминания, его будет легче вспомнить. Регулярные практические занятия также могут быть полезны для стимулирования избыточного обучения и снижения вероятности того, что новые воспоминания будут мешать тому, что вы изучаете сейчас.
Слово от Verywell
Хотя вмешательство — лишь одно из объяснений того, почему мы забываем, оно очень важно. Конкуренция между похожими воспоминаниями может значительно затруднить вспоминание того, что вы узнали в прошлом.Это вмешательство также может затруднить вспоминание недавних воспоминаний, что может затруднить обучение.
Исследования в лабораторных условиях подтверждают существование и влияние помех, но в реальных условиях гораздо труднее установить, насколько забвение может быть связано с эффектами помех.


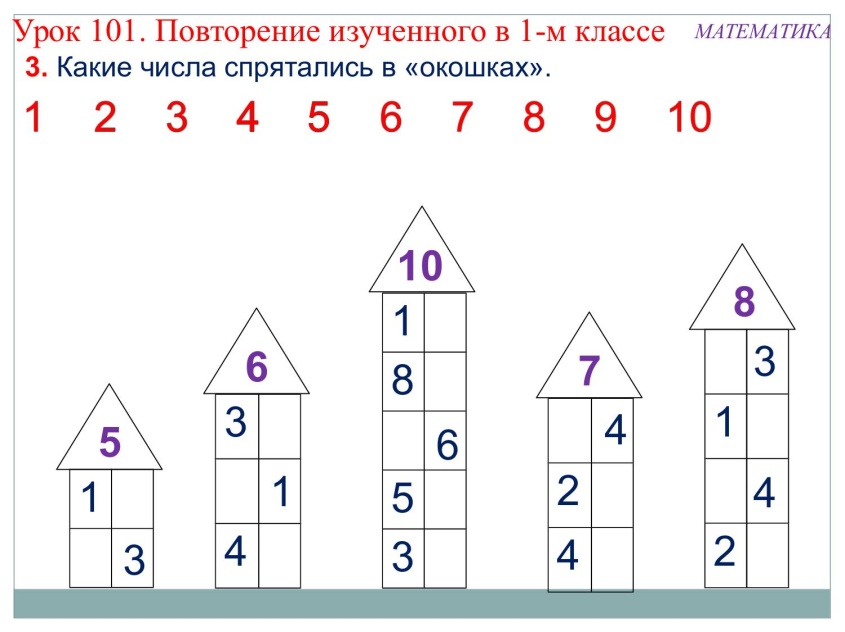 ru/gallery/fixiki_kartinki/111328-fixiki-1.html
ru/gallery/fixiki_kartinki/111328-fixiki-1.html