Пифагор и музыка: Немного о том, какими узами связаны Пифагор и музыка. – Пифагорейская теория музыки — Символизм древних культур
 Все слышали о Пифагоре и его теореме, но далеко не все знают о том, что это был великий мудрец, который повлиял на древнегреческую и древнеримскую культуру, оставив неизгладимый след в мировой истории. Пифагор считался первым философом, еще он сделал множество открытий в музыке, геометрии и астрономии; также, он был непобедим в кулачных боях.
Все слышали о Пифагоре и его теореме, но далеко не все знают о том, что это был великий мудрец, который повлиял на древнегреческую и древнеримскую культуру, оставив неизгладимый след в мировой истории. Пифагор считался первым философом, еще он сделал множество открытий в музыке, геометрии и астрономии; также, он был непобедим в кулачных боях.
Философ сначала учился у своих соотечественников и был посвящен в Элевсинские мистерии. Потом он много путешествовал и собирал по крупицам истину у разных учителей, например, он побывал в Египте, в Сирии, в Финикии, учился у халдеев, проходил через вавилонские мистерии и есть даже свидетельства, что Пифагор получал знания у браминов в Индии.
Собрав паззлы разных учений, философ вывел учение о Гармонии, которой подчинено все. Потом Пифагор создал свое общество, которое было своего рода аристократией духа, где люди обучались искусствам и наукам, тренировали свое тело различными упражнениями и воспитывали свой дух с помощью различных практик и предписаний.
Учение Пифагора показывало единство всего во множестве, а главная цель человека была выражена в том, что путем саморазвития человек достигал соединения с Космосом, избегая дальнейшего перерождения.
Легенды, которые связаны с Пифагором и Музыкой
Музыкальная гармония в учении Пифагора является моделью вселенской гармонии, которая состоит из нот – различных аспектов Мироздания. Считалось, что Пифагор слышал музыку сфер, которая была определенными звуковыми колебаниями, что исходили от звезд и планет и вместе сплетались в божественную гармонию – Мнемосину. Также, Пифагор и его ученики использовали определенные песнопения и звуки лиры, чтобы успокоить свой ум либо исцелиться от определенных болезней.
По легенде именно Пифагор открыл законы музыкальной гармонии и свойства гармонических отношений между звуками. Легенда гласит, что учитель однажды прогуливался и услышал звуки молотов из кузницы, которые ковали железо; прислушавшись к ним, он понял, что их стук создает гармонию.
Позже, опытным путем Пифагор установил, что различие звуков зависит только от массы молотка, а не от других характеристик. Потом философ сделал из струн устройство с различным количеством гирек; струны крепились к гвоздю, который был вбит в стену его дома. Ударяя по струнам, он вывел понятие октавы, и то, что её соотношение равно 2:1, открыл квинту и кварту.
Затем Пифагор сделал устройство с параллельными струнами, которые натягивались колками. С помощью этого инструмента он установил, что определенные созвучия и законы есть во многих инструментах: флейтах, цимбалах, лирах и других устройствах, с помощью которых можно производить ритм и мелодию.
Есть легенда, которая повествует о том, что однажды гуляя, Пифагор увидел неистовую пьяную толпу, которая вела себя неподобающим образом, а впереди толпы шел флейтист. Философ приказал этому музыканту, сопровождавшему толпу, играть в спондаическом размере – тот заиграл, и вмиг все протрезвели и успокоились. Так с помощью музыки можно управлять людьми.
Современные научные теории и практическое подтверждение пифагорийских взглядов на музыку
Звуки могут, как исцелить, так и убить. Лечение музыкой, например, арфотерапия, в некоторых странах была признаётся и изучается (например, в Британском институте арфовые мелодии используют для облегчения прохождения курса химиотерапии). Пифагорийское учение о музыке сфер подтверждается современной теорией суперструн: колебаниями, которыми пронизано все космическое пространство.
Автор – Артур Витер

Пифагоров строй — Википедия
Материал из Википедии — свободной энциклопедии
Пифагоров строй — музыкальный строй, теорию которого связывают с пифагорейской школой гармоники. Со времён поздней Античности видные теоретики музыки (Никомах, Ямвлих, Боэций и другие) приписывали его непосредственно Пифагору.
Абстрактно-математическое представление о пифагоровом строе (как квинтовой цепи) сложилось в эпоху западноевропейского барокко.
В некоторых научных статьях именуется также «пифагорейским строем»[источник не указан 2680 дней].
Обычно представляется в виде последовательности квинт (или кварт), например так (цепь из 6 квинт от звука фа):
F — C — G — D — A — E — H
или в виде диатонической гаммы:
В западной музыке пифагорову строю приписывается роль основы не только для античной монодии, но также и для полифонической музыки Средневековья. Музыкальные теоретики всё ещё продолжают описывать интервалы, опираясь на пифагоров строй[источник не указан 2779 дней], хотя певческая, а затем инструментальная многоголосная тональная музыка не позже XVI века начала осваивать чистый строй. В сравнении с последним, пифагоров является октавно-квинтовым строем, порождаемым натуральными интервалами чистой октавы (1:2) и чистой квинты (2:3)[1]. У всех занятых в интервальных соотношениях пифагорова строя чисел факторизации основаны на простых числах величиной не более 3. По этой причине, преимущественно в англоязычной среде, пифагоров строй ещё называют
Таблица интервалов пифагорова строя[править | править код]
В следующей таблице показаны интервалы пифагорова строя, не превосходящие октаву и получаемые не более чем 18 квинтовыми шагами. Диатонические интервалы (то есть возникающие в пифагоровой 7-ступенной диатонике и получаемые не более чем 6 квинтовыми шагами) выделены жирным шрифтом. Обычным шрифтом отмечены хроматические интервалы (возникающие, наряду с диатоническими интервалами, в 12-ступенном пифагоровом октавном звукоряде, и получаемые 7—11 квинтовыми шагами). Остальные, «дихроматические» (или «энармонические»), интервалы, получаемые 12—18 квинтовыми шагами, выделены курсивом. Эти последние (за исключением пифагоровой коммы, соответствующей увеличенной септиме без октавы, и уменьшённой ноны) соответствуют дважды увеличенным и уменьшенным интервалам диатоники.
Сокращения: «м.» — малая; «б.» — большая; «ум.» — уменьшённая; «ув.» — увеличенная.
В колонках Q и O таблицы показаны соответственно количества квинт и октав, откладыванием которых получается данный интервал (при этом положительным числам соответствует откладывание вверх, а отрицательным — вниз). Например, уменьшённой септиме соответствуют значения Q = −9 и O = 6, то есть уменьшенная септима получается откладыванием от данного звука (высоты) 9 квинт вниз и 6 октав вверх; таким образом, она имеет отношение частот звуков, равное
- (32)−9×(21)6=215⋅3−9=3276819683.{\displaystyle \left({\frac {3}{2}}\right)^{-9}\times \left({\frac {2}{1}}\right)^{6}=2^{15}\cdot 3^{-9}={\frac {32768}{19683}}.}
При этом число О (для интервалов, меньших октавы) однозначно определяется числом Q, находясь от него в функциональной зависимости, определяемой формулой:
- O=−⌊Q×(log23−1)⌋,{\displaystyle \mathrm {O} =-\lfloor \mathrm {Q} \times (\log _{2}{3}-1)\rfloor ,}
где ⌊x⌋{\displaystyle \lfloor x\rfloor } — целая часть числа x{\displaystyle x}[2].
Далее, каждый из интервалов, указанных в таблице, однозначно представляется как сложенный из T целых тонов (указанных в колонке T), L лимм (колонка L) и K пифагоровых комм (колонка K), при ограничениях
- 0⩽T⩽6,0⩽L⩽1,−2⩽K⩽1{\displaystyle 0\leqslant T\leqslant 6,\qquad 0\leqslant L\leqslant 1,\qquad -2\leqslant K\leqslant 1}.
Как видно из таблицы, для диатонических интервалов имеет место одно из трёх пар равенств: L=0{\displaystyle L=0} и K=0{\displaystyle K=0}, либо L=1{\displaystyle L=1} и K=0{\displaystyle K=0}, либо L=0{\displaystyle L=0} и K=−1{\displaystyle K={-1}} (то есть диатонический интервал всегда равен либо целому числу тонов, либо целому числу тонов с прибавленной лиммой, либо меньше целого числа тонов на пифагорову комму). Для хроматических интервалов сверх того могут иметь место соотношения L=1{\displaystyle L=1} и K=1{\displaystyle K=1}, либо L=1{\displaystyle L=1} и K=−1{\displaystyle K={-1}}, а «дихроматических» (выделенных курсивом) — также L=0{\displaystyle L=0} и K=1{\displaystyle K=1}, либо L=0{\displaystyle L=0} и K=−2{\displaystyle K={-2}}.
| Название | Q | O | T | L | K | Отношение | Величина в центах | Ступень от c | Дополнительные примеры |
|---|---|---|---|---|---|---|---|---|---|
| унисон, прима | 0 | 0 | 0 | 0 | 0 | 1:1 | 0,00 | c | |
| Пифагорова комма (ув. септима без октавы)[3] | 12 | -7 | 0 | 0 | 1 | 531441:524288 | 23,46 | His | des—cis, fes—e, a—gisis |
| дважды ум. терция | -17 | 10 | 0 | 1 | -1 | 134217728:129140163 | 66,76 | eseses[4] | cis—eses, eis—ges |
| лимма, м. секунда, меньший (диатонический) полутон | -5 | 3 | 0 | 1 | 0 | 256:243 | 90,22 | des | e—f, cis—d, des—eses |
| апотома, ув. прима, больший (хроматический) полутон | 7 | -4 | 0 | 1 | 1 | 2187:2048 | 113,69 | cis | cis—cisis, des—d, eses—es |
| ум. терция | -10 | 6 | 1 | 0 | -1 | 65536:59049 | 180,45 | eses | cis—es, e—ges |
| целый тон, б. секунда | 2 | -1 | 1 | 0 | 0 | 9:8 | 203,91 | d | d—e, e—fis, B—c, des—es, cis—dis |
| дважды ув. прима | 14 | -8 | 1 | 0 | 1 | 4782969:4194304 | 227,37 | cisis | ces—cis, deses—d |
| дважды ум. кварта | -15 | 9 | 1 | 1 | -1 | 16777216:14348907 | 270,67 | feses | cis—fes, fis-b, cisis—f |
| полудитон, м. терция | -3 | 2 | 1 | 1 | 0 | 32:27 | 294,13 | es | d—f, es—ges |
| ув. секунда | 9 | -5 | 1 | 1 | 1 | 19683:16384 | 317,60 | dis | des—e, es—fis |
| ум. кварта | -8 | 5 | 2 | 0 | -1 | 8192:6561 | 384,36 | fes | cis—f, fis—b, dis—ges |
| дитон, б. терция | 4 | -2 | 2 | 0 | 0 | 81:64 | 407,82 | e | d—fis, eis-gisis |
| дважды ув. секунда | 16 | -9 | 2 | 0 | 1 | 43046721:33554432 | 431,28 | disis | ces—dis, es—fisis |
| дважды ум. квинта | -13 | 8 | 2 | 1 | -1 | 2097152:1594323 | 474,58 | geses | cis—ges, disis—a |
| кварта | -1 | 1 | 2 | 1 | 0 | 4:3 | 498,04 | f | d—g, ces—fes |
| ув. терция | 11 | -6 | 2 | 1 | 1 | 177147:131072 | 521,51 | eis | des—fis, deses—f |
| дважды ум. секста | -18 | 11 | 3 | 0 | -2 | 536870912:387420489 | 564,81 | aseses[4] | cisis—as, cis—ases |
| ум. квинта (комматический тритон | -6 | 4 | 3 | 0 | -1 | 1024:729 | 588,27 | ges | cis—g, H—f, e—b |
| тритон, ув. кварта | 6 | -3 | 3 | 0 | 0 | 729:512 | 611,73 | fis | f—b, des—g |
| дважды ув. терция | 18 | -10 | 3 | 0 | 1 | 387420489:268435456 | 635,19 | eisis | des—fisis, eses—gis |
| ум. секста (волчья квинта пифагорова строя) | -11 | 7 | 3 | 1 | -1 | 262144:177147 | 678,49 | ases | cis—as, Gis—es |
| квинта | 1 | 0 | 3 | 1 | 0 | 3:2 | 701,96 | g | d—a, dis—ais |
| дважды ув. кварта | 13 | -7 | 3 | 1 | 1 | 1594323:1048576 | 725,42 | fisis | des—gis, deses—a |
| дважды ум. септима | -16 | 10 | 4 | 0 | -2 | 67108864:43046721 | 768,72 | heseses[4] | cis—heses, cisis—b |
| м. секста | -4 | 3 | 4 | 0 | -1 | 128:81 | 792,18 | as | d—b, dis-h |
| ув. квинта (тетратон) | 8 | -4 | 4 | 0 | 0 | 6561:4096 | 815,64 | gis | des—a, eses—b |
| ум. септима | -9 | 6 | 4 | 1 | -1 | 32768:19683 | 882,40 | heses | cis—b, Gis—f |
| б. секста | 3 | -1 | 4 | 1 | 0 | 27:16 | 905,87 | a | d—h, Es—c |
| дважды ув. квинта | 15 | -8 | 4 | 1 | 1 | 14348907:8388608 | 929,33 | gisis | des—ais, deses—a |
| дважды ум. октава | -14 | 9 | 5 | 0 | -2 | 8388608:4782969 | 972,63 | ceses1 | Dis—des, Disis—d |
| м. септима | -2 | 2 | 5 | 0 | -1 | 16:9 | 996,09 | b | G—f, Des—ces |
| ув. секста (пентатон) | 10 | -5 | 5 | 0 | 0 | 59049:32768 | 1019,55 | ais | des—h, deses—b |
| ум. октава | -7 | 5 | 5 | 1 | -1 | 4096:2187 | 1086,31 | ces1 | Cis—c, Des—deses |
| б. септима | 5 | -2 | 5 | 1 | 0 | 243:128 | 1109,78 | h | cis—his |
| дважды ув. секста | 17 | -9 | 5 | 1 | 1 | 129140163:67108864 | 1133,24 | aisis | ces—ais, Eses—cis |
| ум. нона | -12 | 8 | 6 | 0 | -2 | 1048576:531441 | 1176,54 | deses1 | Dis—es, Eis—f |
| октава | 0 | 1 | 6 | 0 | -1 | 2:1 | 1200,00 | c1 |
- ↑ Натуральные интервалы, или интервалы натурального звукоряда, между 1-м и 2-м, 2-м и 3-м обертонами обозначены соотношениями 1:2 и 2:3 соответственно.
- ↑ Указанная формула получается логарифмированием неравенства 1⩽(32)Q⋅2O<2{\displaystyle 1\leqslant \left({\frac {3}{2}}\right)^{\mathrm {Q} }\cdot 2^{\mathrm {O} }<2}, однозначно определяющего зависимость величины O от величины Q.
- ↑ Увеличенная септима пифагорова строя (например, c—his) шире октавы (c—c1) на пифагорову комму.
- ↑ 1 2 3 Орфография буквенного обозначения ступени, отстоящей от с на данный интервал (дважды уменьшенная терция, секста или септима) требует указания «тройного бемоля» (-eseses), обозначающего понижение соответствующей диатонической ступени (в данном случае соответственно e, a и h) на три хроматических полутона; примеры тех же интервалов между другими ступенями, не требующими «тройных знаков альтерации», см. в колонке «Дополнительные примеры».
- ↑ То есть тритон, уменьшенный на (пифагорову) комму.
«Связь Пифагора с музыкой».
4 класс
Составитель : Мерзликина Наталья Петровна.
Урок музыки в 4-м классе по теме «Связь Пифагора с музыкой».
Музыка обладает сильным воздействием на внутренний мир человека. Она может доставлять наслаждение или, напротив, вызывать сильное душевное беспокойство, побуждать слушателя к размышлениям и открывать перед ним неизвестные ранее стороны жизни. Именно музыке дано выразить чувства столь сложные, что их порой невозможно описать словами.
Тема урока: «Связь Пифагора с музыкой»
Цель урока: Дать первоначальные знания о Пифагоре и его значимости к музыке, а также как возникла древнее нотное письмо.
Задачи: изучить необходимую литературу и интернет – источники для ознакомления с новым материалом для учеников.
ОБУЧАЮЩАЯ: Учить детей слушать и анализировать музыку, сопоставлять различные виды искусства;
ВОСПИТАТЕЛЬНАЯ: Видеть взаимовлияние истории жизни и музыки;
РАЗВИВАЮЩАЯ: Учить детей формировать и высказывать свое мнение о музыке.
План урока: Организационный момент. Этап подготовки учащихся к активному усвоению знаний. Этап усвоения новых знаний. Этап закрепления новых знаний.
Тип урока: Интегрированный урок.
Оборудование: Компьютер с колонками, «Портрет Пифагора».
ХОД УРОКА: Организационный момент. Музыкальное приветствие.
Учитель. Здравствуйте ребята! Мы с вами уже не раз убеждались в том, насколько многообразен мир музыки. Музыка обладает сильным воздействием на внутренний мир человека. Она может доставлять наслаждение или, напротив, вызывать сильное душевное беспокойство, побуждать слушателя к размышлениям и открывать перед ним неизвестные ранее стороны жизни.
Легенды, которые связаны с Пифагором и Музыкой.
Музыкальная гармония в учении Пифагора является моделью вселенской гармонии, которая состоит из нот – различных аспектов Мироздания. Считалось, что Пифагор слышал музыку сфер, которая была определенными звуковыми колебаниями, что исходили от звезд и планет и вместе сплетались в божественную гармонию — Мнемосину. Также, Пифагор и его ученики использовали определенные песнопения и звуки лиры, чтобы успокоить свой ум либо исцелиться от определенных болезней.
Пифагор родился примерно в 570 до н. э. По легенде, рождение ребёнка будто бы предсказала Пифия (жрица –прорицательница Древней Греции), поэтому Пифагор и получил своё имя, которое значит «тот, о ком объявила Пифия». Она сообщила, что Пифагор принесет столько пользы и добра людям, сколько не приносил и не принесет в будущем никто другой. С ранних лет он отличался удивительным стремлением к познанию мира. Помимо любви к науке и искусству, юный Пифагор уделял время и своей физической подготовке (как и все древнегреческие юноши). Ряд источников указывает, что Пифагор стал чемпионом одной из первых Олимпиад по кулачному бою.
В юном возрасте Пифагор отправился в Египет, чтобы набраться мудрости и тайных знаний у египетских жрецов. Диоген и Порфирий пишут, что самосский тиран Поликрат снабдил Пифагора рекомендательным письмом к фараону Амасису, благодаря чему он был допущен к обучению и посвящён в таинства, запретные для прочих чужеземцев. Ямвлих пишет, что Пифагор в 18-летнем возрасте покинул родной остров и, объехав мудрецов в разных краях света, добрался до Египта. Там он пробыл 22 года, приобщаясь к математике и занимаясь созданием из центра своей философской системы. Эти занятия были прерваны – он был пленён персидским царем Камбизом, завоевавшим Египет в 525 до н. э. и уведён в Вавилон в числе пленников. В Вавилоне Пифагор пробыл ещё 12 лет, общаясь с магами, пока наконец не смог вернуться на остров Самос, где соотечественники признали его мудрым человеком. Пифагор покинул родной остров в знак протеста против тирании Поликрата.
Примерно на сороковом году жизни, философ основал строго закрытое общество своих последователей, уже при жизни почитавших его как высшее существо. Это было этико-религиозное братство – пифагорейский союз. Пифагорейцы занимаются геометрией, математикой, гармонией, астрономией. Примерно в 500 году до нашей эры в Сибарисе вспыхивает восстание против правления аристократической партии.
Не исключено, что поводом послужил отказ Пифагора принять в свою школу некого богатого, но недостойного гражданина, а тот из мести спровоцировал бунт. После восстания начинаются жестокие преследования и гонения на пифагорейцев. По сохранившимся данным, Пифагор прожил около 100 лет. Воспоминания о Пифагоре дошли до нас благодаря его ученикам.
По легенде именно Пифагор открыл законы музыкальной гармонии и свойства гармонических отношений между звуками. Легенда гласит, что учитель однажды прогуливался и услышал звуки молотов из кузницы, которые ковали железо; прислушавшись к ним, он понял, что их стук создает гармонию.
Позже, опытным путем Пифагор установил, что различие звуков зависит только от массы молотка, а не от других характеристик. Потом философ сделал из струн устройство с различным количеством гирек; струны крепились к гвоздю, который был вбит в стену его дома. Ударяя по струнам, он вывел понятие октавы, и то, что её соотношение равно 2:1, открыл квинту и кварту.
Затем Пифагор сделал устройство с параллельными струнами, которые натягивались колками. С помощью этого инструмента он установил, что определенные созвучия и законы есть во многих инструментах: флейтах, цимбалах, лирах и других устройствах, с помощью которых можно производить ритм и мелодию.
Есть легенда, которая повествует о том, что однажды гуляя, Пифагор увидел неистовую пьяную толпу, которая вела себя неподобающим образом, а впереди толпы шел флейтист. Философ приказал этому музыканту, сопровождавшему толпу, играть в спондаическом размере – тот заиграл, и вмиг все протрезвели и успокоились. Так с помощью музыки можно управлять людьми.
Но сегодня мы с вами поговорим об основоположнике теории музыки, то есть о Пифагоре который родился в Сидоне Финикийском примерно в 570 до н. э. По легенде, рождение ребёнка будто бы предсказала Пифия в Дельфах, поэтому Пифагор и получил своё имя, которое значит «тот, о ком объявила Пифия». Пифия сообщила Мнерсарху, что Пифагор принесет столько пользы и добра людям, сколько не приносил и не принесет в будущем никто другой. Поэтому Мнесарх дал жене новое имя Пифаида, а ребенку дал имя Пифагор.
Для Пифагора музыка была производной от науки математики, и ее гармонии жестко контролировалась математическими пропорциями.
Пифагор разработал свою теорию гармонии, работая с монохордом (изобретение, состоящее из одной струны, натянутой между зажимами и снабженное подвижными ладами). Когда Пифагор передвигал перекладины, прижимая их к заранее размеченным точкам, звучали различные музыкальные интервалы.
Сравнив высоту звучания целой струны и ее половинки, он был поражен: струна, которая была вдвое короче, звучала значительно выше, но тем же тоном, что и целая струна. При этом тон целой струны и тон ее половинки как бы сливались воедино, издавая чистое согласное созвучие.
Если и дальше половинку большой струны тоже разделить на два, новая половинка струны дала тот же звук, сливающийся с предыдущим, только еще более высокий.
Пифагор обнаружил, что приятные слуху созвучия – консонансы, т. е. созвучия, получаются лишь в том случае, когда длины струн относятся как целые числа первой четверки, т. е. как 1:2, 2:3, 3:4.
Пифагор разделил струну на три, четыре, пять равных частей. При этом он получал разные по высоте звуки.
Эти звуки тоны Пифагор расположил по высоте этакими ступеньками звуковой лесенки. И у древнего математика получилось, что внутри октавы, между ее верхним и нижним звуками, уместилось 8 звуков ступенек.
Гораздо позднее расстояние между нижним и верхним тонами этого абсолютного созвучия стали называть октавой, что на латинском языке означает «восьмая».
Эти 8 звуков, получившие впоследствии «имена» ДО-РЕ-МИ-ФА-СОЛЬ-ЛЯ-СИ и снова ДО, обязательно повторяются внутри каждой октавы. Этот ряд – звукоряд – позже стал называться Пифагоровым строем, или Пифагоровым звукорядом.
Закон 1. Две звучащие струны дают консонанс лишь тогда, когда их длины относятся как целые числа 1:2, 2:3, 3:4.
Закон 2. Пифагор обнаружил приятные слуху созвучия: квинта – пятая ступень, кварта – четвертая, октава – восьмая. Основа всей музыки – тризвучие.
Шло время…Музыкант-ученый Веркхмейстер немного подправил Пифагоров звукоряд. Он чуть повысил одни звуки, понизил другие, получив тем самым темперированный строй.
Величайший немецкий композитор Иоганн Себастьян Бах первым продемонстрировал достоинства темперированного строя. Бах сочинил 48 прелюдий и фуг во всех возможных тональностях, помещенных в два сборника, которые называются «Хорошо темперированный клавир» (клавир – старинное название клавесина)
Вывод:
Математическая теория музыки Пифагора явилась вообще первой теорией музыки. Иоганн Себастьян Бах первым продемонстрировал достоинства темперированного строя. х порой невозможно описать словами.
(короткая музыкальная физ.разминка)
2. Невозможно представить, что было время, когда на свете не существовало нотной записи, и музыка передавалась только устно. Настоятельная потребность найти способ сохранения музыкальных напевов привела к созданию нотной записи. Усилиями многих поколений создавались все более совершенные системы перевода «живого» звучания музыки на язык условной графической записи — нотации. Сравнивая образцы нотного текста разных времен и народов, можно увидеть, что они не похожи. Но при всем различии в них есть и общее: музыка фиксируется с помощью специальных условных знаков. Они менялись на протяжении многовекового развития музыкальной культуры, и прошло много времени, прежде чем люди привыкли к той форме нотной записи, которая используется сейчас.
— Древнее нотное письмо.
Из всех известных способов самым древним является обозначение мелодий, передаваемых по слуху, с помощью рисунков. Образцы такой записи обнаружены при изучении древнеегипетских памятников. К древнейшим способам относится также слоговая запись музыкальных звуков с помощью клинописи, применявшаяся, как предполагают ученые, в Древнем Вавилоне. До сих пор считалось, что первая система нотного письма, включавшая семь нот, была разработана Пифагором в VI веке до нашей эры. Однако, по словам итальянских исследователей, им удалось доказать, что аналогичная система существовала на берегах Нила уже в середине IV тысячелетия до нашей эры! Для записи нот использовались иероглифы, обозначавшие небесные светила. Среди них — Солнце, Луна и звезды: Сириус, посвященный богине Изиде, и Венера, которая в мифологии древних египтян служила олицетворением божества времени.
Нотная грамота могла зародиться и на территории современной Сирии.
С таким утверждением выступили сирийские ученые, завершив на днях исследования записей, обнаруженных в древнем городе Угарит на северо-западе Сирии в 50-х годах прошлого века. Тогда археологам удалось найти записанные музыкальные символы, относящиеся к середине второго тысячелетия до нашей эры. Завершенное на днях исследование подтвердила сделанная в Угарите находка — первая запись музыкального произведения в истории человечества.
Таким образом, возникновение нот приблизительно можно датировать 3500 годом до нашей эры.
Дальнейшее развитие музыкальной письменности связано с буквенным обозначением звуков, указывающих на их высоту. Зародившись в Древней Греции, эта система получает все более широкое распространение. Со временем буквы греческого алфавита заменяются латинскими. И сейчас можно встретить обозначение звука «до» латинской буквой «c», звука «ре» — д.
Пифагор исследовал не только половинки струны. Он делил струну на три, четыре, пять равных частей. При этом он получал разные по высоте звуки. Не будем углубляться в расчеты древнего ученого. Скажем только, что эти звуки, эти тоны и расположил по высоте Пифагор. Как ступеньки звуковой, лесенки. При этом внутри октавы между ее верхним и нижним звуками выстроились по порядку восемь звуков-ступенек. Эти восемь звуков, получивших, впоследствии имена ДО РЕ-МИ-ФА-СОЛЬ-ЛЯ-СИ-ДО, повторяются внутри каждой октавы. Этот ряд звуков, звукоряд, получил название Пифагорейский, или Пифагоров звукоряд.
Согласно преданию, сам Пифагор обнаружил, что приятные слуху созвучия — консонансы, т. е. созвучия, получаются лишь в том случае., когда длины струн относятся как целые числа первой четверки, т. е. как 1:2, 2: 3, 3 : 4. Именно это открытие впервые указывало на существование числовых закономерностей в природе.

(ноты писались именно так в середине IV тысячелетия )
Исполнение песни «Школьный РЭП» и «Мне сегодня скучно».
3. Подведение итогов урока. Оценка работы всего класса и отдельных учащихся.
4. Домашнее задание: сколько считалось, включала первая система нотного письма Пифагором в VI веке до нашей эры? (запишите в тетради по музыке).
5. Спасибо за урок. До свидания!
Почтенный Пифагор отвергал оценку музыки, основанную на свидетельстве чувств. Он утверждал, что достоинства ее должны восприниматься умом, и потому судил о музыке не по слуху, а на основании математической гармонии и находил достаточным ограничить изучение музыки пределами одной октавы.
Плутарх
Строго говоря, речь здесь пойдет о пифагоровом строе. Что же такое гамма и строй в музыке?
Гаммой, или звукорядом, называется последовательность звуков (ступеней) некоторой музыкальной системы (лада), расположенных, начиная от основного звука (основного тона), в восходящем или нисходящем порядке. Название «гамма» происходит от греческой буквы Гγ (гамма), которой в средние века обозначали крайний нижний тон звукоряда, а затем и весь звукоряд.
Важнейшей характеристикой музыкального звука является его высота, представляющая отражение в сознании частоты колебания звучащего тела, например струны. Чем больше частота колебаний струны, тем «выше» представляется нам звук.
Каждый отдельно взятый звук не образует музыкальной системы и, если он не слишком громкий, не вызывает у нас особой реакции. Однако уже сочетание двух звуков в иных случаях получается приятным и благозвучным, а в других, наоборот «режет» ухо. Согласованное сочетание двух звуков называется консонансом, несогласованное — диссонансом. Ясно, что консонанс или диссонанс двух тонов определяются высотным расстоянием между этими тонами или интервалом.
Интервалом между двумя тонами назовем порядковый номер ступени верхнего тона относительно нижнего в данном звукоряде, а интервальным коэффициентом I21 двух тонов — отношение частоты колебаний верхнего тона к частоте нижнего*:
(6.1)
* (В теории музыки понятия интервала и интервального коэффициента строго не разграничены. Следуя традиции, мы часто для краткости будем называть интервальный коэффициент интервалом. )
Рассмотрим теперь некоторую совокупность звуков, нажав, например, на фортепиано последовательно несколько клавиш. Скорее всего, у нас получится бессвязный набор звуков, как говорится, ни складу ни ладу. В других случаях звуки вроде бы подходят, ладятся между собой, но их совокупность покажется оборванной, незаконченной. Эту последовательность так и хочется продолжить до определенной ноты, которая в данной системе звуков кажется наиболее устойчивой, основной и называется тоникой. Итак, звуки в музыкальной системе связаны между собой определенными зависимостями, одни из них являются неустойчивыми и тяготеют к другим — устойчивым.
Но не только тоника и совокупность устойчивых и неустойчивых звуков определяют характер музыкальной системы. Легко убедиться, нажав подряд восемь белых клавиш от ноты до (гамма до мажор натуральный) и от ноты ля (ля минор натуральный), что эти гаммы звучат по-разному: первая — мажор — звучит бодро и светло, а вторая — минор — грустно и пасмурно*. Следовательно, существует и другая характеристика системы звуков — наклонение: мажорное или минорное. Таким образом, мы приходим к одному из самых сложных понятий в теории музыки — понятию лада.
* (Характер звучания лада, конечно, не определяется столь грубо и однозначно. Вопрос этот очень деликатный, и о нем мы еще поговорим в конце главы. )
Ладом называется приятная для слуха взаимосвязь музыкальных звуков, определяемая зависимостью неустойчивых звуков от устойчивых, и прежде всего от основного устойчивого звука — тоники, и имеющая определенный характер звучания — наклонение. История музыкальной культуры знает множество ладов, свойственных разным народам и разным временам. Древние греки знали с десяток ладов, а лады некоторых восточных стран и Индии чрезвычайно сложны, своеобразны и непривычны для европейского слуха. Наиболее распространенные современные лады состоят из семи основных ступеней, каждая из которых может повышаться или понижаться, что дает еще пять дополнительных звуков. Таким образом, диатоническая (7-ступенная) гамма лада превращается в хроматическую (12-звуковую). Первой ступенью лада является тоника. Законы строения лада — это целая наука, краеугольный камень музыкознания, а изучению этих законов многие ученые и композиторы посвятили всю свою жизнь.
Нас же будут в первую очередь интересовать математические закономерности, описывающие строение лада, т. е. музыкальный строй. Музыкальным строем называется математическое выражение определенной системы звуковысотных отношений. Помимо чисто теоретического интереса строй находит применение при настройке музыкальных инструментов с фиксированной высотой звуков, таких, как фортепиано или орган.
В заключение заметим, что наши эксперименты с нажатием клавиш на фортепиано могут закончиться самым редким и самым приятным феноменом, когда взятая система звуков будет не только принадлежать к какому-либо ладу, но и будет носить осмысленный характер. Такой художественно осмысленный последовательный ряд звуков разной высоты называется мелодией. Это как раз то, что мы так любим напевать в зависимости от нашего настроения — бодрого, грустного, веселого…
После такого кратчайшего экскурса в теоретическое музыкознание мы можем вернуться на берега солнечной Эллады во времена мудрого Пифагора. Попытаемся восстановить рассуждения Пифагора и его учеников при построении пифагорова строя, ибо именно этот строй определил на тысячелетия, если не навечно, все развитие музыкальной культуры, не только европейской, но и восточной. Сам Пифагор не оставил никаких письменных работ, да и наследие пифагорейцев представляется безнадежной грудой развалин, т. е. собранием случайно уцелевших фрагментов и более поздних цитат. Бесспорно, развалины эти прекрасны и поныне поражают воображение, как развалины знаменитого Парфенона, однако многое в этих обломках бесследно утеряно и о целом часто можно только догадываться. И все-таки…
Монохорд — однострунный — был одним из первых музыкальных инструментов древних греков. Это был длинный ящик, необходимый для усиления звука, над которым натягивалась струна. Снизу струна поджималась передвижной подставкой для деления струны на две отдельно звучащие части. На деревянном ящике под струной имелась шкала делений, позволявшая точно установить, какая часть струны звучит. Конечно, как музыкальный инструмент монохорд покажется нам слишком примитивным, однако он был прекрасным физическим прибором и учебным пособием, на котором античные созерцатели постигали премудрости музыкальной грамоты.
Древние уверяли, что уже Пифагор знал законы колебания струны монохорда и построения музыкальных созвучий (консонансов), однако запись об этих законах мы находим у пифагорейца Архита из Тарента (428-365 гг. до н. э.), жившего На полтора столетия позже Пифагора. Архит был, безусловно, самым выдающимся представителем пифагорейской школы, другом философа Платона и учителем математика Евдокса (ок. 408 — ок. 355 гг. до н. э.), государственным деятелем и полководцем. Многосторонность Архита поразительна: он решил знаменитую де-лосскую задачу об удвоении куба, заслуженно считался крупнейшим пифагорейским теоретиком музыки, первым упорядочил механику на основе математики и свел движения механизмов к геометрическим чертежам, работал над деревянной моделью летающего голубя. По мнению Ван дер Вардена, Архит является автором VIII книги «Начал» Евклида, в которой изложена арифметическая теория пропорций. Как государственный деятель Архит пользовался исключительным уважением: он семь лет подряд избирался стратегом*, хотя по закону стратеги выбирались лишь на один год. Путем искусных дипломатических маневров Архит вызволил из плена Платона и тем самым спас жизнь великому философу. «Славный Архит, земель, и морей, и песков исчислитель…» — писал Гораций.
* (Стратег — в древнегреческих городах-государствах военачальник, облеченный ши-кими военными и политическими полномочиями. )
«Законы Пифагора — Архита», на которых основывалась вся пифагорейская теория музыки, можно сформулировать так:
1- Высота тона (частота колебаний f) звучащей струны обратно пропорциональна ее длине l:
(6.2)
здесь а — коэффициент пропорциональности, зависящий от физических свойств струны (толщины, материала и т. п.).
2. Две звучащие струны дают консонанс лишь тогда, когда их длины относятся как целые числа, составляющие треугольное число 10 = 1 + 2 + 3 + 4, т. е. как 1:2, 2:3, 3:4.
Эти интервалы — «совершенные консонансы», и их интервальные коэффициенты позже получили латинские названия*:
* (Названиями интервалов в музыке служат латинские числительные, которые указывают порядковый номер ступени звукоряда, составляющей интервал с исходной ступенью: октава — восьмая, квинта — пятая, кварта — четвертая и т. д.)
октава
квинт
кварта
Треугольное число 10
Было замечено также, что наиболее полное слияние тонов дает октава (2/1), затем идут квинта (3/2) и кварта (4/3), т. е. чем меньше число п в отношении вида тем созвучнее интервал.
«Второй закон Пифагора — Архита» и сейчас кажется удивительным. Что же говорить о пифагорейцах, которых он просто привел в восторг! Здесь они нашли подтверждение всей своей философии: целые числа, более того, числа тетрактиса правят всем, даже музыкой! Пифагорейцы не заставили себя долго ждать и распространили закон музыкальных отношений всюду, где это возможно, в том числе и на строение вселенной.
Итак, если в качестве цены деления шкалы монохорда взять отрезок l, равный 1/12 длины струны монохорда l1, то вместе со всей струной монохорда длины l1 = 12l будут созвучны ее части длины l2 = 6l — звук на октаву выше (l2/l1 = l/2), l3 = 9l — звук на квинту выше (l3/l1 = 2/3) и l4 = 8l — звук на кварту выше (l4/l1 = 3/4). Это созвучие и определяющие его числа 6, 8, 9, 12 назывались тетрада (четверка). Пифагорейцы считали, что тетрада — это «та гамма, по которой поют сирены». При настройке античной лиры, ставшей символом музыки, четыре ее струны обязательно настраивались по правилу тетрады, а настройка остальных струн зависела от лада, в котором предстояло на ней играть.
Но для античного мыслителя было мало установить численные значения изучаемых величин. Пифагорейский глаз и ум привыкли не только измерять, но и соизмерять, т. е. раскрывать внутренние связи между изучаемыми предметами, другими словами, устанавливать пропорциональные отношения. Архит был истинным пифагорейцем, и он установил пропорциональные отношения между основным совершенным консонансом — октавой, квинтой и квартой. Решение это было получено Архитом в связи с желанием разделить октаву на благозвучные интервалы. Вероятно, Архит исходил из того интуитивно очевидного предположения, что вместе с тонами f1 и f2 = 2f1, дающими основной консонанс — октаву, должно дать консонанс и их среднее арифметическое f3 = (f1 + f2)/2. Но тогда длина струны l3 выразится через длины струн l1 и l2 согласно (6.2) следующим образом:
т. е. l3 есть среднее гармоническое l1 и l2 (см. 5.1). Легко обнаружить и обратное: среднее гармоническое для частот f1 и f2 переходит в среднее арифметическое для длин l1 и l2:
Вспоминая, что мы вместе с Архитом приходим к важному выводу:
(6.3)
(6.4)
т. е. квинта есть среднее гармоническое длин струн основного тона l1 и октавы l2, а кварта — среднее арифметическое l1 и l2.
Но произведение среднего арифметического на среднее гармоническое равно произведению исходных чисел:
(6.5)
откуда, разделив обе части на l12, получаем второй важный вывод:
(6.6)
или
т. е. октава есть произведение квинты на кварту.
Разделив же (6.5) на l1l3, Архит получает и третью из основных пропорций -геометрическую:
(6.7)
которую называли «музыкальной»: октава так относится к квинте, как кварта к основному тону.
Деление струны монохорда (l1) на части, образующие с ней совершенные консонансы: октаву (l2), квинту (l3) и кварту (l4) и соотношения между ними. Интервалы, которые целая струна монохорда образует со своими частями, показаны красными стрелками
Легко получить еще два соотношения:
(6.8)
т. е. октава делится на два неравных консонансных интервала — квинту и кварту. Интервал, дополняющий данный интервал до октавы, называется его обращением. Таким образом, квинта есть обращение кварты и наоборот.
Наконец, найдем интервальный коэффициент между струнами квинты l3 и кварты l4, который вместе со своим интервалом называется тоном (не нужно путать тон-интервал и тон-звук данной высоты):
(6.9)
т. е. тон-интервал равен отношению квинты к кварте.
Заметим, что в отличие от обычного расстояния на прямой r21 = х2 — x1 определяемого как разность координат конца и начала, интервальный коэффициент — высотное расстояние — определен как отношение составляющих его тонов Тогда три тона f1 <f2 <f3, расположенных на равных расстояниях r и образующих арифметическую прогрессию x1, х2 = x1 + r, x3 = x1 + 2r. Поэтому интервальные коэффициенты складываются и вычитаются «геометрически», а сами интервалы — «арифметически», как обычные расстояния, а именно:
сумма двух интервалов равна произведению их интервальных коэффициентов:
(6.10)
разность двух интервалов равна частному их интервальных коэффициентов:
(6.11)
разделить интервал на n равных частей означает извлечь корень степени n из его интервального коэффициента:
(6.12)
и т. д.
Чтобы перейти от интервальных коэффициентов к интервалам-расстояниям, достаточно ввести логарифмический интервал L = loga I и логарифмическую частоту F = loga f. Тогда, логарифмируя определение (6.1) и равенства (6.10) — (6.12) получаем привычное определение и правила действия с расстояниями:
(6.13)
Решение проблемы деления октавы подсказало Архиту сразу два доказательства иррациональности . В самом деле, если попытаться разделить октаву на два равных интервала I, то, полагая в (6.8) I23 = I31 = I, имеем
Но при таком соотношении длин струн прослушивается явный диссонанс. Поскольку же консонанс определяется отношением целых чисел вида (n+1):2, то напрашивается мысль, что число не может быть выражено отношением двух целых чисел, т. е. является иррациональным.
Второе доказательство иррациональности менее музыкально, но более математично. Чтобы найти квадратный корень числа, не являющегося полным квадратом, Архит разлагает его на два неравных сомножителя (2 = 1*2), затем образует из этих сомножителей среднее арифметическое 3/2 и среднее гармоническое 4/3 и составляет из этих чисел музыкальную пропорцию (6.7):
Произведение средних членов этой пропорции равно данному числу 2, а их разность меньше, чем разность нулевого приближения 2 — 1 = 1. Следовательно, можно рассматривать как приближенные значения .
(3/2 с избытком, 4/3 с недостатком ].
Проделав ту же процедуру над первыми приближениями, получим вторые приближения:
причем
а затем — и третьи приближения:
причем
1,414216-1,414211=0,000005.
Поскольку данную процедуру можно повторять неограниченно, то ясно, что число иррациональное. Попутно мы убеждаемся в справедливости пифагорейской мысли о том, что чем больше целые числа в отношении, тем точнее они выражают иррациональное число (см. с. 96). Наконец, вспоминая, что значение равно 1,414213…, мы видим, что «музыкальный» метод Архита очень быстро сходится к точному значению и уже третье приближение дает пять верных знаков после запятой!
Но вернемся к нашим интервалам. Итак, октава делится на два неравных консонанса квинту и кварту, а квинта — на консонанс кварту и диссонанс тон. Тон-интервал и был принят за интервал между соседними по высоте звуками (ступенями) при построении пифагоровой гаммы. Здесь и находится ключ к построению лада. По мнению советского музыковеда Л. А. Мазеля, интервал квинты, разделенный на кварту и тон, является основным музыкальным элементом. Выбрав тон в качестве основной ладообразующей ступеньки, античным теоретикам осталось только отложить от основного звука , затем — еще один тон , а оставшийся интервал между вторым тоном и тоном кварты назвать полутоном Название это вполне оправдано, так как деление тона-интервала пополам по формуле (6.12) дает т. е. полутон практически равен половине тона*. Так была получена основа всей древнегреческой музыки — тетрахорд — четырехструнный звукоряд в пределах кварты.
* (Интервал тона (полутона) в теории музыки принят в качестве единицы арифметического измерения интервалов, а сами интервалы тона и полутона в отличие от их интервальных коэффициентов называют большой и малой секундами.)
Ясно, что имеется только три возможности для положения полутона в пределах тетрахорда, что и определяло характер и название тетрахорда:
дорийский: полутон — тон — тон;
фригийский: тон — полутон — тон;
лидийский: тон — тон — полутон.
Названия тетрахордов указывают на соответствующие области Греции и Малой Азии, каждая из которых пела в своем ладу.
Конечно, четырех струн в пределах кварты было мало для ведения мелодии, поэтому тетрахорды соединялись. Мы уже выяснили, что октава состоит из двух кварт и тона; следовательно, в пределах октавы можно расположить два тетрахорда, разделенных интервалом в тон. Объединяя с помощью разделительного тона два одноименных тетрахорда, получили октаву, которую греки называли «гармония». Именно в античной теории музыки слово «гармония» обрело свое современное значение — согласие разногласного. Таких основных видов гармонии по числу тетрахордов получалось три:
Здесь 1 обозначает тон, 1/2 — полутон, разделительный тон обведен кружком. Эти античные гармонии сопоставимы с современными гаммами. В самом деле, каждый, знакомый с азами музыкальной грамоты, узнает в лидийской гармонии обычный натуральный мажор (2 тона — полутон, 3 тона — полутон, или на белых клавишах фортепиано до—ре—ми—фа—соль—ля—cи—дo), а в дорийской и фригийской — почти натуральный минор*.
* («Почти» потому, что в сравнении с натуральным минором (1 — 1/2 — 1 — 1 — 1/2 — 1 — 1) у дорийской гаммы понижена вторая ступень, а у фригийской — повышена шестая.)
Пифагоров строй лидийской гаммы и его математические характеристики
Зная размеры интервалов, образующих, например, лидийскую гармонию и правила действия с ними, легко получить математическое выражение этой гаммы, т. е. построить ее пифагоров строй. Приняв частоту нижнего тона за единицу f1 = 1, oнаходим первый тетрахорд: f1 = 1, f2 = 9/8, f3 = 9/8*9/8=81/64, f4=4/3. Второй тетрахорд получается сдвигом первого на квинту: f5 = 3/2fl = 3/2, f6 = 3/2f2 = 27/16, f7 = 3/2f3 = 243/128, f8 = 3/2f4 = 2. Окончательно для интервальных коэффициентов имеем
(6.14)
Это и есть канон Пифагора. По преданию, канон Пифагора впервые нашел практическое применение при настройке лиры легендарного Орфея.
Существовал и другой способ расположения тетрахордов в октаве. Античные теоретики «склеивали» тетрахорды так, что верхний звук одного тетрахорда являлся нижним звуком второго. Тогда дополняющий до октавы тон помещали внизу или наверху такой системы. Если этот тон помещался внизу, то к названию тетрахорда прибавляли приставку гипо-(под-), а если наверху — приставку гипер- (над-). Так получалось еще 6 гармоний, среди которых две пары (гипо-фригийская — гиперлидийская и гиподорийская — гиперфригийская) оказывались совершенно одинаковыми. Отбросив две лишние гаммы, оставалось семь основных ладов. Эти лады имели огромное значение не только в античной музыке, но и через тысячу лет продолжали жить в средневековых ладах, а через две тысячи лет живут в современных натуральных ладах. Правда, средневековые монахи перепутали названия своих ладов в сравнении с античными, что часто порождает различные недоразумения. В таблице 1 собраны все основные античные лады, указан порядок следования в них интервалов, считая, что нижний звук расположен слева, а верхний — справа, приведены их древнегреческие и средневековые названия и указано их наклонение. Разделительный тон обведен кружком.
Таблица 1. Порядок следования интервалов тон (1) и полутон (1/2) в античных ладах (снизу вверх), древнегреческие и средневековые названия ладов и их наклонения
Если вспомнить, что сейчас господствуют только два лада — мажор и минор, то остается только удивляться, насколько утонченным было античное музыкальное сознание. Каждый лад греки наполняли определенным этико-эстетическим содержанием, его «этосом», устанавливая ясную связь между музыкальными образами и состояниями души. Музыке приписывали магические и даже врачебные Функции, но особенное значение придавалось музыке как средству воспитания.
Пляшущая менада. Рельеф
Так, развивая в работе «Государство» теорию идеального государства, Платон исключительное значение придает воспитательной роли музыки. Примечательно, что здесь Платон перекликается с другим выдающимся мыслителем, жившим на другом конце Земли за двести лет до Платона,- древнекитайским философом Конфуцием (ок. 551-479 гг. до н. э.), сказавшим: «Если хотите знать, как страна управляется и какова ее нравственность — прислушайтесь к ее музыке». Платон для мирной жизни оставляет один строгий дорийский лад, считая его подлинно греческим, мужественным, деятельным. Для чрезвычайного события, каковым, например, является война, Платон оставляет фригийский лад как наиболее страстный. Лидийский же лад он называет печальным, погребальным, соответствующим женской, а не мужской психике и потому неуместным в идеальном государстве. Остальные лады как слишком утонченные Платон также отбрасывает, неукоснительно проводя в воспитании принцип строгости и простоты. Безусловно, это не означает, что Платон плохо разбирался в музыке. Напротив, в музыке он находил чистый и возвышенный, «платонический» идеал прекрасного, идеал, лишенный вычурности, размягченности, грубых и разнузданных страстей.
Аристотель в «Политике» судит о ладах, пожалуй, еще строже Платона, признавая только дорийский лад как лад, способный тренировать психику. Тем не менее Аристотель делает подробную «этическую» классификацию ладов, различая лады, которые вызывают психическое равновесие (дорийский), напротив, нарушают его (гипофригийский — «застольный» лад), возбуждают волю и стремление к действию (гиподорийский — лад греческой трагедии), вызывают восторженное и экстатическое состояние (фригийский, гиполидийский).
Прекрасное описание «этоса» греческих ладов мы находим в книге древнеримского писателя Апулея (ок. 124 — ?) «Флориды»: «Жил когда-то флейтист по имени Антигенид. Сладостен был каждый звук в игре этого музыканта, все лады были знакомы ему, и он мог воссоздать для тебя, по твоему выбору, и простоту эолийского лада, и богатство ионийского, и грусть лидийского, и приподнятость фригийского, и воинственность дорийского».
Впрочем, стоп! Нет ли здесь противоречия? Дорийский лад называется воинственным, а ведь это, по существу, наш минор! Поскольку именно дорийский лад считался истинно греческим, то получается, что основной характер греческой музыки печальный, минорный. Для греков же дорийский лад является выражением бодрости, жизнерадостности и даже воинственности. Вот как объясняет это кажущееся противоречие выдающийся современный знаток античности, последний философ русского «серебряного века» профессор А. Ф. Лосев (1893-1988)*: «Греческое искусство — неизменное жизнеут-верждение. Благородная сдержанность и даже печаль не оставляют грека и тогда, когда он веселится, когда он бодро строит жизнь, когда он воюет и погибает. „Веселые“ же лады так или иначе тяготеют к этому прекрасному, благородному, бодрому, важному и в то же время величественно-печальному ладу — дорийскому. Дорийский лад — это скульптурный стиль греческой музыки… Так задумчива, печальна и благородна вся греческая скульптура».
* (Судьба Алексея Федоровича Лосева счастлива и трагична. Счастлива, потому что до последнего дня своей 95-летней жизни Лосев сохранил поразительную работоспособность и успел завершить главный труд — восьмитомную «Историю античной эстетики». Трагична, потому что другие восемь томов его сочинений, написанных на полвека ранее (1927 — 1930), были преданы анафеме, а сам автор, будучи незаконно репрессирован, продолжил свои философские изыскания на строительстве Беломорско-Балтийского канала, откуда он писал: «Я закован в цепи, когда в душе бурлят непочатые и неистощимые силы». Одна из этих работ Лосева — «Музыка как предмет логики» — могла бы служить путеводной звездой к этой книге. И все-таки судьба А. Ф. Лосева счастлива, ибо рукописи не горят. Сегодня огромное философское наследие А. Ф. Лосева обретает свое второе рождение. )
Ну а лидийский лад? Ведь это в точности наш мажор, тогда как Апулей называет его грустным, а Платон — погребальным! Что ж, в оценке лидийского лада с Платоном не соглашался уже Аристотель, находя в лидийском ладу наивную детскость и прелесть и относя его к ладам, вызывающим психическое равновесие. С течением времени лидийский лад утратил плачевный характер, и античные теоретики стали чаще говорить о «сладкой лидийской мелодии» или о «разнообразной лидийской мелодии».
Таким образом, мы видим, что вопрос об «этосе» ладов не решается однозначно и во многом определяется традицией применения того или иного лада. И в наше время слушатель, воспитанный, например, на тонкой и своеобразной индийской музыке, вообще не отличит мажора от минора, не говоря уж об их «этосе». Конечно, мажорный лад отличается более светлыми и радостными тонами и тому есть объективные причины, о которых мы расскажем в главе 10. Но реализация этих возможностей зависит от массы других факторов (темп, ритм, мелодический рисунок и т. д.), и поэтому есть много веселых, энергичных произведений в миноре и грустных, задумчивых — в мажоре. Вспомним хотя бы «Патетическую сонату» до минор Бетховена, этот огненно-страстный монолог Героя, зовущего на яростную схватку и даже на смерть. Многие художники подобрали многие эпитеты к этой сонате (хотя, пожалуй, лучший из них — патетическая — принадлежит самому Бетховену), но только грустной — минорной — ее назвать никак нельзя. Напротив, Ноктюрн № 2 соч. 9 ми бемоль мажор Шопена пронизан настроением нежной мечтательности. Это подернутые дымкой грусти воспоминания автора, но отнюдь не веселая — мажорная — пьеса. В заключение попытаемся сказать несколько слов об «этосе интервалов», ибо именно анализу музыкальных интервалов и посвящена настоящая глава. Попытаемся, потому что данный вопрос еще более спорный и неразработанный, чем «этос ладов». И все-таки…
До сих пор мы ничего не говорили о «самом совершенном консонансе» — приме (унисоне) (l2/l1 = 1, т. е. две струны издают звук одинаковой высоты), ибо с точки зрения математики этот интервал не представляет интереса. Однако в оркестре этот простейший интервал играет огромную роль, придавая данному звуку объемность и яркость.
Следующий совершенный консонанс — октава. При одновременном звучании октава также дает впечатление объемности звука, а при последовательном — ощущение простора и широты. Прекрасной тому иллюстрацией является «Песня о Родине» композитора И. О. Дунаевского (1900-1955). В ее запеве («От Москвы до самых до окраин…») дважды звучит восходящая октава (l1/l2 = 2), рисуя необъятные просторы нашей Родины. Здесь же после двух октав идет восходящая квинта. Квинта (l1/l2 = 3/2) также звучит широко, но более рельефно и динамично, чем октава.
Мелодии многих революционных песен и гимнов начинаются интервалом восходящей кварты (l1/l2 = 4/3), например «Интернационал», «Гимн Советского Союза», «Марсельеза». Здесь интервал кварты звучит решительно и активно, как призыв к действию.
Особый «этос» у интервала секунды: при одновременном звучании он диссонирует и неприятен, но при последовательном предыдущий звук как бы переливается в последующий, образуя естественное течение мелодии от одного звука к другому. В мелодии интервалы между двумя опорными звуками часто заполняются последовательными секундовыми интервалами. Например, песня «Во поле береза стояла» начинается интервалом квинты, заполненным последовательными секундами, что создает впечатление спокойного и величавого течения мелодии, как величавы и спокойны картины русской природы.
А наиболее неприятным и неблагозвучным является интервал тритон или полуоктава (l1/l2 = ). Своей неблагозвучностью этот интервал «подсказал» Архиту «музыкальное доказательство» иррациональности .
Благодарность «Библиотеке по математике» за оцифровку книги.
Мысли о музыке. Пифагор: barucaba — LiveJournal
Первые научные принципы музыкальной эстетики были заложены Пифагором и его последователями. До Пифагора эстетика базировалась на основе мифологии, то есть на фантастическом представлении о природе и обществе. С Пифагора начинается история научной эстетики, опирающейся на законы естественно-научного познания. Пифагорейцы считали, что в основе всех вещей лежит число. Этим самым была высказана догадка о закономерности природы и мира в целом.
Пифагор на фреске Рафаэля (1509 г.)
До нас не дошли достоверные сведения о Пифагоре и его школе. Большинство сведений о пифагорействе содержится в поздних источниках и часто носит полулегендарный, полумифалогический характер. Пифагорейское учение о музыке излагается в трактате «О пифагорейской жизни» философа Ямвлиха IV века н.э., о нём сообщают в своих музыкальных трактатах Плутарх, Квинтилиан, Марциан Капелла, а также математик Теон из Смирны, историк Страбон и другие.
Время жизни Пифагора обычно относят к VI веку до н.э. Ему приписывается открытие математических отношений, лежащих в основе музыкальных интервалов. Его последователи — Гиппас, Филолай, Архит из Тарена разрабатывали, наряду с этим, вопросы музыкальной акустики.
В трактате «О пифагорейской жизни» Ямвлих выдвигает на первый план учение Пифагора о музыкальном катарсисе, о нравственном и практически-медицинском значении музыки. Об этом Ямвлих говорит наиболее подробно. По его словам, Пифагор «установил в качестве первого — воспитание при помощи музыки, тех или иных мелодий и ритмов, откуда происходитт врачевание человеческих нравов и страстей и восстанавливается гармония душевных способностей… Он ещё полагал, что музыка многому способствует в смысле здоровья, если кто пользуется ею надлежащим образом. И, действительно, у него было обыкновение пользоваться подобным очищением не мимоходом. Этим наименованием он, очевидно, и называл музыкальное врачевание, существовали те или иные мелодии, созданные против страстей души, против уныния и внутренних язв. Другие в свою очередь — против раздражения, против гнева, против всякой душевной перемены. Ещё иной род песнетворчества был найден против вожделений«.МЫСЛИ ВЕЛИКИХ ЛЮДЕЙ: Пифагор
Ямвлих иллюстрирует пифагорейскую концепцию музыкального катарсиса знаменитой историей о некоем разбушевавшемся юноше, которого Пифагору удалось утихомирить, сменив фригийский лад на размеренный дорийский. Этой истории суждено было в течение более, чем десяти веков странствовать по страницам музыкальных трактатов Западной Европы. Идея музыкального катарсиса — постоянный мотив всех античных авторов, излагающих пифагорейское учение о музыке.
Бюст Пифагора в Капитолийском музее в Риме
Другая характерная для пифагорейской музыкальной эстетики особенность — убеждение в космическом значении музыки, которое содержится в учении о гармонии сфер. Согласно представлениям пифагорейцев, движение небесных тел создаёт прекрасную музыку. Весь космос представляет гармонически устроенное и музыкально звучащее тело. В одном из источников это учение излагается следующим образом: «Когда же несутся солнце, луна и ещё столь великое множество таких огромных светил со столь великою быстротою, невозможно, чтобы не возникал некоторый необыкновенный по силе звук. Предположив это и приняв, что скорости движения их, зависящие от расстояний, имеют отношения созвучий, они говорят, что от кругового движения светил возникает гармонический звук. А так как казалось странным, что мы не слышим этого звука, то в объяснении этого они говорят, что причиной этого является то, что тотчас по рождении имеется этот звук, так что он вовсе не отличается от противоположной ему тишины… Таким образом, подобно тому, как медникам, вследствие привычки, кажется, что нет никакого различия между тишиной и стуком при работе их, так и со всеми людьми бывает то же самое при восприятии гармонии сфер».
Фёдор Бронников. Гимн пифагорейцев солнцу
Пифагорейскому пониманию гармонии свойственны элементы диалектики: «Гармония вообще возникает из противоположностей. Ибо «гармония есть соединение разнообразной смеси и согласие разногласного».
При характеристике музыкальной эстетики пифагорейцев нельзя пройти мимо их открытий в области музыкальной акустики и теории звука. Именно пифагорейцам принадлежит идея о связи высоты тона с быстротой движения и частотой колебаний. Об этом мы читаем у Архита в его трактате «Гармоника»: «…из звуков, которые нами ощущаются, те кажутся высокими, которые получаются от ударов с быстротой и силой, а те, которые идут медленно и слабо, кажутся нам низкими…» Так Архит закладывает основы музыкальной акустики. Архит связывает качество музыкального звука, его высоту или низкость, — именно с движением, причем, это движение он понимает не механически, как результат столкновения различных тел, но как удар этих тел по воздуху и как движение самого ударяемого воздуха. Тем самым он создаёт динамическую картину движения звука.Архиту принадлежит также учение о гармонической пропорции, которое он применил к характеристике музыкальных тонов и измерению интервалов. По его заключению, октава делится не арифметически — на два равных интервала, а гармонически — на два неравных, на кварту 3/4 и квинту 3/2. Пытаясь определить числовую величину интервала, Архит приходил к учению о трёх типах пропорции — арифметической, геометрической и гармонической. Таким образом, пифагорейцы заложили эмпирические основы музыкальной акустики и впервые сформулировали некоторые понятия и принципы музыкальной теории.
Лит.: Шестаков В.П. История музыкальной эстетикиПрименение произведений музыкального искусства с лечебной целью является одним из самых древних методов благотворного воздействия на человека. Такие великие античные философы как Пифагор, Платон, Аристотель и другие обращали внимание на целебную силу музыки, считая, что она восстанавливает нарушенный порядок и утраченную гармонию начиная с отдельного человека и заканчивая всей Вселенной. Было замечено, что музыка и некоторые её элементы – сочетания и отношения звуков – мелодия, ритм, темп способны изменять настроение человека, влиять на его эмоциональное состояние. Музыка помогает находить верный ритм во многих проявлениях жизненных процессов – речи, жестах, мыслях, поступках, способствует гармонизации взаимоотношений между человеком и окружающим его миром.
Все дошедшие до нашего времени сведения о возникновении в древней Греции учения о музыкальной гармонии определённо связывают его с именем Пифагора Самосского (570 — 497 до н.э.). Пифагором и его последователями были заложены первые научные принципы музыкальной эстетики. С него начинается история научной эстетики, опирающейся на законы естественно-научного познания. До Пифагора эстетика главным образом базировалась на основе мифологии, но уже тогда был очевиден резкий разрыв эстетики с мифологией и имела место рационально разработанная система моральных предписаний и наукообразное учение о катартическом, очистительном воздействии музыки на человека.
Книга философа Ямвлиха (ок.250 – ок.330 гг.) посвящена жизни и учению Пифагора – одного из самых загадочных философов и мудрецов Древней Греции. Ямвлих подробно останавливается в ней на описании учения Пифагора, касающегося музыки, об особенностях и способах её воздействия на человека. В трактате «О пифагорейской жизни» Ямвлих выдвигает на первый план учение Пифагора о музыкальном катарсисе, о нравственном и практически-медицинском значении музыки. И хотя сочинение Ямвлиха написано через 800 лет после смерти Пифагора и является одной из наиболее приукрашенных его биографий, нет оснований подвергать его полному отрицанию, к тому же это самое большое по объёму и наиболее сложное из всех сохранившихся трудов о древнем философе.
Итак, Пифагор полагал, что музыка очень благотворно действует на здоровье, если заниматься ею соответствующим, «надлежащим» образом. Он часто прибегал к этому важному виду избавления от недугов, душевных или телесных. И действительно, этот вид оздоровления он называл «лечением музыкой». Весной он устраивал такое исполнение песен: усаживал посередине кого-нибудь с лирой, а вокруг садились те, кто был способен петь, и под его аккомпанемент хором пели какие-нибудь пеаны (хоровые лирические песни), и таким образом собравшиеся поднимали себе настроение, веселились и учились петь стройно и ритмично, сами становясь при этом «благозвучными и эвритмичными». Эвритмия – термин, которым древние греки обозначали взаимное соответствие, взаимную соразмерность отдельных частей и их уравновешенное соединение в одном целом.
В других случаях музыка использовалась непосредственно в медицинских целях. У Пифагора были специальные мелодии, сочиненные для разных душевных состояний. Одни мелодии предназначались как самое эффективное средство для воздействия против уныния и переживаний, другие против раздражения, гнева и против «всякого умственного помрачения разгневанной души»; был также и еще один род музыкального творчества, предназначенный для ограничения желаний. Пение в таких случаях сопровождалось плясками. Из всех музыкальных инструментов предпочтение отдавалось лире, поскольку Пифагор считал, что флейты имеют резкое звучание, напыщенное и совершенно не благородное. Для исправления изъянов и пороков души пифагорейцы применяли также чтение избранных стихов Гомера и Гесиода.
Paul Jourdy, Homère chantant ses vers
Интересные рассуждения о практически-жизненном значении поэзии и музыки можно встретить у Страбона в его «Географии», где он также упоминает пифагорейцев и указывает на то, что ещё сам Гомер в «Одиссее» называл певцов блюстителями нравственности. Согласно утверждению Страбона, древние греки считали, что поэзия – словно первая философия, которая вводит нас в жизнь с детства и, доставляя удовольствие, учит понимать характеры, страсти и действия человека. По их мнению, единственный мудрец – это поэт, вследствие чего жители эллинских городов воспитывали своих детей прежде всего на поэзии, не ради пустого развлечения, а «для развития в них благоразумия». Точно так же и музыканты, обучающие петь под звуки инструментов или играть на флейте и лире, считались воспитателями и исправителями характеров.
На страницах многих музыкальных трактатов, начиная с Ямвлиха и далее в течение более десяти веков, приводится в пример случай, когда Пифагор унял однажды спондеической мелодией, исполняемой флейтистом, ярость нетрезвого юноши, который ночью домогался своей возлюбленной перед воротами соперника и намеревался их поджечь. Юноша был возбужден и распален фригийским напевом флейты, который Пифагор посчитал нужным остановить как можно скорее (сам он в этот поздний час занимался астрономией). Философ убедил флейтиста перейти на спондеическую мелодию, благодаря чему юноша, сразу успокоившись, в пристойном виде отправился домой, хотя только что не воспринимал ничего и просто не хотел слышать обращенных к нему доводов, более того, безрассудно отвергал участие Пифагора. Кроме самого Ямвлиха о подобных случаях очищения аффектов при помощи музыки упоминали Квинтилиан, Марциан Капелла и другие.
Известна также история о том, как древнегреческий философ, врач – Эмпедокл, автор поэмы «О природе», однажды спас своего хорошего знакомого Анхита, когда один юноша поднял против того меч, потому что Анхит, будучи судьей, приговорил отца юноши к смерти. Юноша в гневе безрассудно бросился, чтобы поразить мечом приговорившего к смерти его отца. Эмпедокл же, имея под рукой лиру, и, исполнив какой-то успокаивающий и умиротворяющий напев, тотчас, как сказал поэт, влил «соку гореусладного, миротворящего, сердцу забвенье бедствий дающего» и спас своего друга от смерти, а юношу от совершения убийства. После этого юноша стал самым верным учеником Эмпедокла.
Кроме того, Ямвлих довольно подробно описывает некоторые обычаи, принятые у пифагорейцев, например – вся пифагорейская школа осуществляла то, что они называли «настройкой», «музыкальным сочетанием» и «прикосновением», соответствующими мелодиями сообщая душе эмоции, противоположные ее состоянию. Отходя ко сну, пифагорейцы очищали разум от дневного смятения и шума определенными песнями и особого рода мелодиями и этим обеспечивали себе спокойный сон с немногими и приятными сновидениями. Встав с постели, они вновь снимали вялость и оцепенение песнями другого рода, иногда это были песни без слов. Были случаи, когда они излечивали чувства и некоторые болезни «настоящим пением». Таким образом, Пифагор ввел в употребление исключительно полезный и безвредный способ исправления человеческих нравов и образа жизни с помощью музыки.

Francesco Hayez
Поскольку зашла речь о мастерстве Пифагора-воспитателя, то далее следует рассказать и об одном связанном с этим событием, а именно – как он открыл знание гармонии и гармонические законы.
Очень популярна легенда о том, как Пифагор открыл закон целочисленных отношений в консонансах. Эта легенда впоследствии получила название «кузнечной легенды». Действительно, пифагорейцам удалось опытным путём верно установить пропорциональные выражения симфонных[1] интервалов – кварты, квинты и октавы. Одним из первых источников, в котором эта легенда содержится, является «Руководство по гармонике» Никомаха. О ней упоминают также его современник – Теон Смирнский, римский писатель Цензорин, большое внимание уделил открытию Пифагора и Боэций. Содержание легенды заключается в том, что однажды Пифагор пребывал в напряженном размышлении над проблемой, можно ли придумать для слуха какой-нибудь вспомогательный инструмент, надежный и не вводящий в заблуждение, каким для глаза является циркуль, отвес и, разумеется, диоптры, а для осязания – весы и изобретение мер. По счастливой случайности проходя мимо кузницы, Пифагор услышал, как на наковальне ковали железо, и одновременные удары молотов издавали очень гармоничные звуки, кроме одного сочетания. Он различил в них октаву и созвучия, построенные на квинте и кварте, а интервал между квартой и квинтой он видел как не образующий гармонии сам по себе, но заполняющий расстояние между ними. Радуясь, как будто он получил эту идею от богов, он вбежал в кузницу и методом проб выяснил, что звучание зависит от тяжести молота, а не от силы удара, формы молота или изменения положения железа, которое ковали. Узнав точный вес молотов, и установив, что их наклон при ударе одинаков, он удалился к себе домой. На один колышек, вбитый между углами стен (чтобы не внести в эксперимент никаких различных данных и чтобы вообще не было разницы между колышками), он повесил четыре струны из одного и того же материала, сплетенные из равного числа нитей, с одинаковой толщиной и одинаково скрученные. Он подвесил к ним разные грузы и сохранил равную их длину. Затем, ударяя поочередно по паре струн, он нашел созвучия, о которых говорилось выше, в разных сочетаниях струн. Он установил, что струна, к которой прикреплен самый большой груз, и струна, к которой прикреплен наименьший груз, образуют октаву. Так как к первой было подвешено 12 гирек, а ко второй – шесть, то он открыл, что октаве свойственно отношение 2:1, что подтверждало и весовое соотношение гирек. С другой стороны, он открыл, что между струной с самым большим весом и ближайшей к самой легкой, имевшей восемь гирек, был интервал в квинту и, следовательно, полуторное отношение, и в полуторном отношении находились и подвешенные к ним грузы. Между струной с самым большим весом и следующей, которая была с большим грузом, чем другие, – к которой были подвешены девять гирек, – был интервал в кварту соответственно подвешенным грузам. Он выяснил, что эта струна (с девятью грузами) находится в отношении 3:4 к струне с самым большим грузом и что одновременно эта струна находится в полуторном отношении к струне с наименьшим весом, поскольку девять именно так относится к шести. Равным образом струна, следующая за струной с наименьшим весом, к которой было прикреплено восемь гирек, образовывала со струной, имевшей шесть гирек, отношение 4:3, а со струной, которая имела 12 гирек, находилась в полуторном отношении. Следовательно, интервал между квинтой и квартой, на который квинта превосходит кварту, был установлен в отношении 9:8. Звукоряд в октаве раскрывался двояко, либо с сочетанием квинты с квартой, как трехчленная пропорция 12:8:6, либо, в обратном порядке, с сочетанием кварты с квинтой, как трехчленная пропорция 12:9:6. Набив руку и изощрив слух на опытах с весами, а также открыв их пропорции, Пифагор искусно перенес общее крепление струн с вбитого на углу стены колышка на подставку под струны в лире, которую он назвал орудием натяжения струн, а натяжение струн в повороте колков в верхней части инструмента было аналогично подвешенным грузам.
Благодаря этому эксперименту, словно с помощью точного инструмента, он распространил свой опыт на различные инструменты: цимбалы, флейты, свирели, монохорды, тригон и подобные им и нашел, что во всех них арифметическое отношение было одинаково гармоничным. Он назвал звук, соответствующий числу 6, гипатой, звук, соответствующий числу 8 и находящийся в отношении 4:3 к гипате, – месой, звук, следующий за месой, выражающийся числом 9 и звучащий тоном выше, чем меса, и находящийся к ней в отношении 9:8, – парамесой, а звук, соответствующий числу 12, – нэтой. Заполнив интервалы соответственно диатоническому роду пропорциональными звуками, он подчинил, таким образом октахорд числовой гармонии, существующей в отношениях 2:1, 3:2, 4:3 и отличном от них отношении 9:8. Таким образом, он обнаружил в диатоническом ладу необходимую и естественную прогрессию тонов от самого низкого звука к самому высокому.
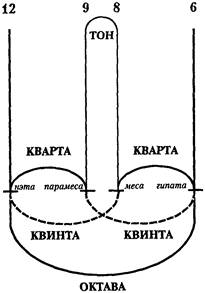
Диатонический же лад являет следующие ступени и такое естественное движение: полутон, тон, затем еще тон, и это есть кварта, соединение двух тонов и так называемого полутона. Затем, с прибавлением другого тона, вставленного в середину, образуется квинта, соединение трех тонов и полутона. Затем следуют полутон, тон и еще тон – другая кварта, то есть еще одно отношение 4:3. Поэтому в более древнем гептахорде каждый четвертый звук, начиная с самого низкого звука, образовывал созвучие кварты во всем звукоряде, причем полутон занимал поочередно первое, среднее и третье места тетрахорда. В пифагорейском октахорде, представлял ли он сочетание тетрахорда с пентахордом или два несовпадающих тетрахорда, отделенные друг от друга целым тоном, мелодическое движение начиналось от самого низкого звука, так что каждый пятый звук образовывал созвучие квинты, а полутон здесь последовательно занимал четыре места: первое, второе, третье и четвертое. Так, по описаниям, Пифагор открыл искусство музыки и, изложив систематически, передал его ученикам для самых благородных целей. Кроме того, именно в музыке впервые была обнаружена направляющая роль чисел и заложен её фундамент – методы построения музыкальной гаммы, фундамент, на котором и было затем возведено прекрасное здание искусства музыки (замечательное сравнение А.В. Волошинова, автора книги о Пифагоре[2]). За два с половиной тысячелетия этот математический фундамент музыки, заложенный пифагорейцами, настолько глубоко «врос в землю», что о его существовании почти забыли. А ведь без него рухнуло бы всё здание музыки.
Пифагор советовал воздвигнуть храм Музам, дабы они охраняли установленное гражданское согласие, поскольку эти богини одинаково все называются музами, предание всегда говорит о них вместе, и они особенно радуются общим для всех них почестям. Вообще хоровод Муз всегда один и тот же, охватывающий звук, гармонию, ритм – все, что ведет к согласию. Пифагор указывал, что власть Муз распространяется не только на самые прекрасные учения, но также и на созвучие и гармонию существующих вещей.

Муза играющая на кифаре
Пифагор считал, что «воздействие на людей в первую очередь осуществляется посредством чувств: если кто-либо видит прекрасные образы и формы или слушает прекрасные ритмы и песни, то такой человек начинает музыкальное образование с мелодий и ритмов, от которых излечиваются человеческие нравы и страсти и устанавливается первоначальная гармония душевных сил». Он также придумал средства, способные, по его мнению, сдерживать и исцелять болезни души и тела. И еще более интересно и заслуживает упоминания то, что он для своих учеников упорядочил и привел в систему так называемые настройки и аранжировки, придумав сочетания диатонических, хроматических и энгармонических созвучий. По словам Ямвлиха, с их помощью Пифагор легко изменял и приводил в противоположное состояние страстные движения души, если они только что беспорядочно возникли и усилились (печаль, гнев, отчаяние, зависть, страх, различные влечения, приступы ярости, желания, чувство превосходства, приступы лени, горячность). Пифагор также считал возможным направить каждую из этих страстей к добродетели с помощью соответствующих мелодий, словно с помощью правильно подобранных лекарств. В своём трактате Ямвлих повествует о том, что Пифагор избавлял своих учеников от дневных волнений и впечатлений, «очищая» их ум, и они спали спокойно и хорошо. А когда они просыпались, помогал им взбодриться, освободиться от сонного состояния, расслабленности и вялости особыми напевами и простыми мелодиями, исполняемыми на лире, либо сопровождая игру на лире пением. Однако для самого себя он не предназначал и не устраивал такой процедуры с помощью инструментов или голоса, но, используя, как считал сам Пифагор, редкую и труднодостижимую способность, напрягал слух и пытался уловить высшие созвучия космоса. Он, по его словам, слышал и понимал всеобщую гармонию и созвучие сфер и движущихся по ним светил, которые издают пение более насыщенное и полнозвучное, чем любые земные источники, более мелодичного и прекрасного в своем разнообразии, и это движение он определял как состоящее из их неодинаковых и разнообразных шумов, скоростей, величин и констелляций, которые расставлены в некой исключительно музыкальной пропорции. Вдохновляясь этим движением и утвердившись в своих принципах, он решил открыть ученикам, насколько возможно, подобия этих звуков, воспроизводя их инструментами или одним пением. Он думал, что ему одному на земле понятны и слышны космические звуки, и от этого природного источника и корня он считал себя способным учиться и учить других. Он верил, что и другие люди могут получать пользу и исправляться посредством образов и знаков, если они не способны правильно воспринимать первичные и чистые первообразы.
Эмпедокл, скорее всего, намекает на Пифагора, на его исключительные способности, данные от бога и превышающие обычные человеческие, когда говорит:
Жил среди них некий муж, умудренный безмерным познаньем,
Подлинно мыслей высоких владевший сокровищем ценным,
В разных искусствах премудрых свой ум глубоко изощривший,
Ибо как скоро всю силу ума напрягал он к познанью,
То без труда созерцал любое, что есть и что было,
За десять или за двадцать провидя людских поколений.
Слова «безмерное познание», «созерцал любое, что есть и что было», «сокровище мыслей высоких» и тому подобные выразительно указывают на исключительную остроту зрения, слуха и ума Пифагора, превосходящую способности большинства других людей.
Для более полного и правильного понимания пифагорейского учения об использовании музыки нужно учесть следующее: в нём не было никакого чисто эстетического элемента, ни о каком эстетическом удовольствии не было и речи, как не было никакого намёка на понимание эстетического в музыке как чего-то исключительно субъективного. Нельзя отождествлять его и с чистой моралью. Катарсис у пифагорейцев охватывал всего человека, а не только его нравственность. По словам А.Ф. Лосева, это был «такой глубокий синтез, в котором уже нельзя отделить душу от тела, мораль от инстинкта и красоту от здоровья».
Пояснения:
Чистая кварта — интервал в четыре ступени (два с половиной тона). Является совершенным консонансом.
Чистая квинта — интервал в пять ступеней (три с половиной тона). Является устойчивым интервалом и совершенным консонансом.
Консонанс и диссонанс (от лат. consonantia – созвучие, согласное звучание, и от лат. dissonantia – неблагозвучие, нестройное звучание; названные латинские термины – переводы, соответственно, др.-греч. συμφωνία и др.-греч. διαφωνία) в теории музыки – категории гармонии, характеризующие слияние или неслияние в восприятии одновременно звучащих тонов, а также сами созвучия (интервалы, аккорды), воспринимаемые как «слитные» и «неслитные».
Гептахорд — (греч.) – семь струн в лире, которые дают звукоряд из семи звуков, отстоящих друг от друга так же, как и ступени в диатонической мажорной гамме.
Тетрахорд (др.-греч. τετράχορδον, букв. четырёхструнник; лат. tetrachordum) – четырёхступенный звукоряд в диапазоне кварты. Тетрахорд лежал в основе всех древнегреческих звукорядов. Тетрахорд – важнейший конструктивный элемент модальных ладов. Октавные ладовые звукоряды («гармонии», «тоны») античная и средневековая ладовые теории представляли как сцепление структурных разновидностей (т.наз. «видов» – др.-греч. εἶδη, σχήματα, лат. species) кварты и квинты.
Диатоника – семиступенная интервальная система, все звуки которой могут быть расположены по чистым квинтам и/или квартам. Служит основой диатонического звукоряда со специфическим чередованием идущих подряд 2-3 целых тонов и полутона (в отличие от хроматической гаммы из одних полутонов, целотоновой гаммы и других).
Интервал в музыке – соотношение между двумя звуками определённой высоты.
[1] Интервалы, полученные пифагорейцами экспериментально на монохорде (октава, кварта, квинта), именовались симфониями (в переводе с греческого – «созвучия»), а все остальные – диафониями (букв.: «разнозвучия»)
[2] А.В. Волошинов – кандидат физико-математических наук, доктор философских наук, автор книги «Пифагор: Союз истины, добра и красоты».
Пифагор: музыкотерапия и искусство музыки
Цитата сообщения BarucabaПифагор: музыкотерапия и искусство музыки
Пифагор полагал, что музыка очень благотворно действует на здоровье, если заниматься ею подобающим образом. Он часто прибегал к этому важному виду очищения, и действительно этот вид очищения он называл«лечением музыкой». Весной он устраивал такое исполнение песен: усаживал посередине кого-нибудь с лирой, а вокруг садились те, кто был способен петь, и так под его аккомпанемент они хором пели какие-нибудь пеаны, и они полагали, что таким образом веселились и учились петь стройно и ритмично. В других случаях они использовали музыку в медицинских целях. У них были мелодии, сочиненные для разных душевных состояний. Одни мелодии предназначались как самое действенное средство против уныния и терзаний, а другие также против раздражения, гнева и против всякого умственного помрачения разгневанной души; был также и еще один род музыкального творчества, предназначенный для ограждения желаний. Они также сопровождали пение плясками. Музыкальным инструментом у них была лира, потому что Пифагор считал, что флейты имеют звучание резкое, напыщенное и совершенно не благородное. Для исправления души они применяли также избранные стихи Гомера и Гесиода.
Paul Jourdy, Homère chantant ses vers
Что касается его дел, то про Пифагора среди прочего говорили, что он унял однажды спондеической мелодией, исполняемой флейтистом, ярость пьяного юноши из Тавромения, который ночью домогался своей любовницы перед воротами соперника и намеревался их поджечь. Юноша был возбужден и распален фригийским напевом флейты, который Пифагор остановил как можно скорее (он в поздний час занимался астрономией). Он убедил флейтиста перейти на спондеический ритм, благодаря чему юноша, сразу успокоившись, в пристойном виде отправился домой, хотя только что он не воспринимал его и просто не хотел слышать обращенных к нему доводов, более того, безрассудно отвергал участие Пифагора. Также Эмпедокл однажды спас своего гостеприимца Анхита, когда один юноша поднял против него меч, потому что тот, будучи судьей, приговорил отца юноши к смерти. Юноша бросился, в помрачении рассудка и в гневе, чтобы поразить мечом приговорившего к смерти его отца, как будто Анхит был убийцей. Эмпедокл же, имея под рукой лиру, изменил мотив и, исполнив какой-то успокаивающий и умиротворяющий напев, тотчас, как сказал поэт, влил «соку гореусладного, миротворящего, сердцу забвенье бедствий дающего» и спас своего гостеприимца Анхита от смерти, а юношу от убийства. Рассказывают, что после этого юноша стал самым верным учеником Эмпедокла.
Кроме того, вся пифагорейская школа осуществляла то, что они называли «настройкой», «музыкальным сочетанием» и «прикосновением», соответствующими мелодиями с пользой сообщая душе эмоции, противоположные ее состоянию. Отходя ко сну, они очищали разум от дневного смятения и шума определенными песнями и особого рода мелодиями и этим обеспечивали себе спокойный сон с немногими и приятными сновидениями. Встав с постели, они вновь снимали вялость и оцепенение песнями другого рода, иногда это были песни без слов. Были случаи, когда они излечивали чувства и некоторые болезни, как говорят, настоящим пением (то есть заклинанием), и, вероятно, отсюда и вошло в употребление это понятие «заклинание». Так Пифагор ввел в употребление исключительно полезный способ исправления человеческих нравов и образа жизни с помощью музыки.
Раз у нас зашла здесь речь о мастерстве Пифагора-воспитателя, то дальше можно рассказать и о том, что связано с этим: как он открыл знание гармонии и гармонические законы. Начнем несколько издалека.
Однажды он пребывал в напряженном размышлении над проблемой, можно ли придумать для слуха какой-нибудь вспомогательный инструмент, надежный и не вводящий в заблуждение, каким для глаза является циркуль, отвес и, разумеется, диоптры, а для осязания – весы и изобретение мер. По счастливой случайности проходя мимо кузницы, Пифагор услышал, как на наковальне ковали железо и одновременные удары молотов издавали очень гармоничные звуки, кроме одного сочетания. Он различил в них октаву и созвучия, построенные на квинте и кварте, а интервал между квартой и квинтой он видел как не образующий гармонии сам по себе, но заполняющий расстояние между ними. Радуясь, как будто он получил эту идею от богов, он вбежал в кузницу и методом проб выяснил, что звучание зависит от тяжести молота, а не от силы удара, формы молота или изменения положения железа, которое ковали. Узнав точный вес молотов и установив, что их наклон при ударе одинаков, он удалился к себе домой. На один колышек, вбитый между углами стен (чтобы не внести в эксперимент никаких различных данных и чтобы вообще не было разницы между колышками), он повесил четыре струны из одного и того же материала, сплетенные из равного числа нитей, с одинаковой толщиной и одинаково скрученные. Он подвесил к ним разные грузы и сохранил равную их длину. Затем, ударяя поочередно по паре струн, он нашел созвучия, о которых говорилось выше, в разных сочетаниях струн. Он установил, что струна, к которой прикреплен самый большой груз, и струна, к которой прикреплен наименьший груз, образуют октаву. Так как к первой было подвешено 12 гирек, а ко второй – шесть, то он открыл, что октаве свойственно отношение 2:1, что подтверждало и весовое соотношение гирек. С другой стороны, он открыл, что между струной с самым большим весом и ближайшей к самой легкой, имевшей восемь гирек, был интервал в квинту и, следовательно, полуторное отношение, и в полуторном отношении находились и подвешенные к ним грузы. Между струной с самым большим весом и следующей, которая была с большим грузом, чем другие, – к которой были подвешены девять гирек, – был интервал в кварту соответственно подвешенным грузам. Он выяснил, что эта струна (с девятью грузами) находится в отношении 3:4 к струне с самым большим грузом и что одновременно эта струна находится в полуторном отношении к струне с наименьшим весом, поскольку девять именно так относится к шести. Равным образом струна, следующая за струной с наименьшим весом, к которой было прикреплено восемь гирек, образовывала со струной, имевшей шесть гирек, отношение 4:3, а со струной, которая имела 12 гирек, находилась в полуторном отношении. Следовательно, интервал между квинтой и квартой, на который квинта превосходит кварту, был установлен в отношении 9:8. Звукоряд в октаве раскрывался двояко, либо с сочетанием квинты с квартой, как трехчленная пропорция 12:8:6, либо, в обратном порядке, с сочетанием кварты с квинтой, как трехчленная пропорция 12:9:6. Набив руку и изощрив слух на опытах с весами и открыв их пропорции, он искусно перенес общее крепление струн с вбитого на углу стены колышка на подставку под струны в лире, которую он назвал орудием натяжения струн, а натяжение струн в повороте колков в верхней части инструмента было аналогично подвешенным грузам.
Francesco Hayez
Благодаря этому эксперименту, словно с помощью точного инструмента, он распространил наконец свой опыт на различные инструменты: цимбалы, флейты, свирели, монохорды, тригон и подобные им и нашел, что во всех них арифметическое отношение было одинаково гармоничным. Он назвал звук, соответствующий числу 6, гипатой, звук, соответствующий числу 8 и находящийся в отношении 4:3 к гипате, –месой, звук, следующий за месой, выражающийся числом 9 и звучащий тоном выше, чем меса, и находящийся к ней в отношении 9:8, –парамесой, а звук, соответствующий числу 12, – нэтой. Заполнив интервалы соответственно диатоническому роду пропорциональными звуками, он подчинил таким образом октахорд числовой гармонии, существующей в отношениях 2:1, 3:2, 4:3 и отличном от них отношении 9:8. Таким образом он обнаружил в диатоническом роде необходимую и естественную прогрессию тонов от самого низкого звука к самому высокому.
Диатонический же род являет следующие ступени и такое естественное движение: полутон, тон, затем еще тон, и это есть кварта, соединение двух тонов и так называемого полутона. Затем, с прибавлением другого тона, вставленного в середину, образуется квинта, соединение трех тонов и полутона. Затем следуют полутон, тон и еще тон – другая кварта, то есть еще одно отношение 4:3. Поэтому в более древнем гептахордекаждый четвертый звук, начиная с самого низкого звука, образовывал созвучие кварты во всем звукоряде, причем полутон занимал поочередно первое, среднее и третье места тетрахорда. В пифагорейском октахорде, представлял ли он сочетание тетрахорда с пентахордомили два несовпадающих тетрахорда, отделенные друг от друга целым тоном, мелодическое движение начиналось от самого низкого звука, так что каждый пятый звук образовывал созвучие квинты, а полутон здесь последовательно занимал четыре места: первое, второе, третье и четвертое. Вот так, рассказывают, открыл он искусство музыки и, изложив систематически, передал его ученикам для всех самых прекрасных целей.
Муза играющая на кифаре
Он советовал воздвигнуть храм Музам, дабы они охраняли царящее гражданское согласие, ведь эти богини одинаково называются музами, предание всегда говорит о них вместе, и они особенно радуются общим для всех них почестям. Вообще хоровод Муз всегда один и тот же, охватывающий звук, гармонию, ритм – все, что ведет к согласию. Он показал, что власть Муз распространяется не только на прекраснейшие учения, но также и на созвучие и гармонию существующих вещей.
Filippos Margaritis. Эвтерпа (муза лирической поэзии и музыки)
Он считал, что воздействие на людей сначала осуществляется посредством чувств: если кто-либо видит прекрасные образы и формы или слушает прекрасные ритмы и песни, то такой человек начинает музыкальное образование с мелодий и ритмов, от которых излечиваются человеческие нравы и страсти и устанавливается первоначальная гармония душевных сил. Он также придумал средства сдерживать и исцелять болезни души и тела. И еще более достойно упоминания то, что он для своих учеников упорядочил и привел в систему так называемые настройки и аранжировки, с божественным искусством придумав сочетания диатонических, хроматических и энгармонических созвучий. С их помощью он легко изменял и приводил в противоположное состояние страсти души, если они только что беспорядочно возникли и усилились (печаль, гнев, жалость, глупую зависть, страх, различные влечения, приступы ярости, желания, чувство превосходства, приступы лени, горячность). Он направлял каждую из этих страстей к добродетели с помощью соответствующих мелодий, словно с помощью правильно подобранных лекарств. Когда его ученики вечером засыпали, он освобождал их от дневных волнений и впечатлений, очищал смятенный ум, и они спали спокойно и хорошо, их сны становились вещими. Когда они просыпались, он освобождал их от сонного оцепенения, расслабленности и вялости особыми напевами и простыми мелодиями, исполняемыми на лире, либо сопровождая игру на лире пением. Но для самого себя он не предназначал и не устраивал такой процедуры с помощью инструментов или голоса, но, используя некую невыразимую и трудно постижимую божественную способность, напрягал слух и вперял ум в высшие созвучия космоса. Он один, по его словам, слышал и понимал всеобщую гармонию и созвучие сфер и движущихся по ним светил, которые издают пение более насыщенное и полнозвучное, чем любые смертные, происходящее от движения и обращения светил, мелодичного и прекрасного в своем разнообразии, и это движение слагается из их неодинаковых и разнообразных шумов, скоростей, величин и констелляций, которые расставлены в некой исключительно музыкальной пропорции. Вдохновляясь этим движением, утвердившись в своих принципах и, если так можно выразиться, укрепив свое тело, он задумал открыть ученикам, насколько возможно, подобия этих звуков, воспроизводя их инструментами или одним пением. Он думал, что ему одному на земле понятны и слышны космические звуки, и от этого природного источника и корня он считал себя способным учиться и учить других и уподобиться небесным существам соответственно стремлению и способности подражания, поскольку он один был так счастливо наделен породившим его божественным началом. Он верил, что другим людям достаточно получать пользу и исправляться посредством образов и знаков, если они не способны правильно воспринимать первичные и чистые первообразы. Он придумал все это точно так же, как мы для тех, кто не может прямо смотреть на солнце из-за слишком яркого света его лучей, придумываем показывать затмение солнца через толщу воды или через расплавленную смолу или с помощью темного зеркала, щадя слабость зрения этих людей и изобретая возможность равносильного восприятия для тех, кто должен довольствоваться им, даже если оно и не достоверно. Эмпедокл, как представляется, намекает на Пифагора, на его исключительные способности, данные от бога и превышающие обычные человеческие, когда говорит:
Жил среди них некий муж, умудренный безмерным
познаньем,
Подлинно мыслей высоких владевший сокровищем
ценным,
В разных искусствах премудрых свой ум глубоко
изощривший,
Ибо как скоро всю силу ума напрягал он к познанью,
То без труда созерцал любое, что есть и что было,
За десять или за двадцать провидя людских поколений.
Слова «безмерное познание», «созерцал любое, что есть и что было», «сокровище мыслей высоких» и тому подобные выразительно указывают на исключительную остроту зрения, слуха и ума Пифагора, превосходящую способности других людей.
Ямвлих. О Пифагоровой жизни
Книга знаменитого философа-неоплатоника Ямвлиха (ок. 242–306 гг.) посвящена жизни и учению Пифагора – одного из самых загадочных философов, мистиков и мудрецов Древней Греции. Ямвлих – автор трактата «О египетских мистериях», многих трудов, посвященных символике богов, и комментариев к работам Платона и Аристотеля.
Сами числа, которыми можно выразить тоны, имеют неразрешимые иррациональности.Артур Шопенгауэр, Мир как воля и представление, том I, §52 [Dover Publications, 1966, E.F.J. Перевод Пейна, с.266]

Одно из самых известных открытий Пифагора из Самоса, Πυθαγόρας ὁ Σάμιος, или из пифагорейской школы (часто трудно отличить разницу), по словам Г.С. Кирка и Дж.
Интервалы вызова «четвертый», «пятый» или «октава» (то есть «восьмой»), когда они являются частью системы из семи тонов, немного сбивают с толку. Добавление четырех к пяти даже не равно восьми, гораздо меньше семи, но девяти. Однако, что происходит, это устройство «инклюзивного» подсчета порядковых номеров, где мы начинаем новый цикл нумерации (первый) с конца предыдущего цикла (octava, восьмой). Эта форма подсчета обсуждается в другом месте в отношении календарей.«Средняя С» — это точка отсчета для всех клавиш на пианино и для музыкальной гаммы в целом. «A выше среднего C» — это эталонная отметка, для которой есть определение с точки зрения физики, при этом звук часто устанавливается точно на 440 Гц (герц). Затем таблица заполняет «простые математические отношения», которые традиционно присваиваются всем интервалам. Это уже создает некоторые проблемы. В то время как четвертый и пятый складываются в октаву, если мы попытаемся сделать то же самое с третьим (5/4) и шестым (5/3) или вторым (9/8) и седьмым (15/8) отношения не умножаются до 2, но до 25/12 и 135/64 или до 2.08 и 2.11 соответственно. Возможно, это не то, чего ожидал Пифагор. Мы слышим, что это всего лишь «полшага» от E до F и от B до C, в то время как это «целый шаг» между другими нотами. Что это должно означать, мы можем видеть на пианино, где между белыми клавишами есть черные клавиши, но нет черных клавиш между E и F или между B и C. Это может запутать математику отношений.Шаблон выглядит нерегулярно. Между E и F есть только два 24-х, и это половина следующих двух интервалов, но это больше половины предыдущих, и интервал между B и C фактически равен (трем) интервалу между C и D. Здесь нет «простых математических соотношений».
Я мог бы тогда спросить, как бы выглядел масштаб, если бы мы отдали от масштаба до , чтобы разделить Как это происходит, большинство традиционных соотношений не используются. Почему это так, мы можем видеть из следующей таблицы, где мы берем интервал пятого (3/2) и начинаем его последовательно добавлять — где это теперь делается по шкале -двенадцатью нот, «хроматической» шкале, где черные клавиши пианино добавляются к белым (различаются как «острые», # или «плоские», Следующая таблица описывает этот процесс. Коэффициенты синего цвета являются нашими эталонными значениями для октав (первые и восьмые, включительно). В красном мы следуем дополнениям (умножением) пятых. Как только мы получим красное значение для любой клавиши, мы разделим его на октаву на октаву до первого. Это дает нам значения для всех интервалов и всех примечаний, хотя большинство из них сейчас очень далеки от «простых математических соотношений». Но, к сожалению, проблема несоответствия, обнаруженная в предыдущей таблице, возникает снова.[Мир как воля и представление, том I, §52, E.F.J. Перевод Пейна, Dover Publications, 1966, p.266] Это создает дилемму для настоящих музыкантов, которая заключается в том, как вообще построить весы. Безусловно, музыку можно воспроизводить с использованием интервалов, полученных путем добавления пятых, или даже с использованием исходных соотношений, и ухо может не возражать — несмотря на использование нот, созданных системами, которые в конечном итоге противоречивы. Различия, в конце концов, довольно малы даже для оригинальных и традиционных соотношений.Но это раздражает. Существует своего рода пифагорейский зуд, который заставляет нас думать, что должно быть правильное математическое решение вопроса. Это не будет так просто, как ожидал Пифагор, но продолжает верить, что фундаментальное соотношение, октава, 2: 1, может быть согласовано с делением шкалы на другие интервалы. Хотя Шопенгауэр, с его характерным пессимизмом, похоже, этого не оценил, с этой проблемой можно что-то сделать. Pythagoras Пифагора часто называют первым чистым математиком. Он родился на острове Самос, в Греции в 569 году до нашей эры. Различные писания помещают его смерть между 500 до н.э и 475 до н.э в Metapontum, Лукания, Италия.Его отец, Мнесарх, был торговцем драгоценными камнями. Имя его матери было Пифайс. У Пифагора было два или три брата. Некоторые историки говорят, что Пифагор был женат на женщине по имени Феано и имел дочь Дамо и сына по имени Телог, который сменил Пифагора в качестве учителя и, возможно, преподавал Эмпедокла. Другие говорят, что Теано был одним из его учеников, а не его женой, и говорят, что Пифагор никогда не был женат и не имел детей. Пифагор был хорошо образован, он всю жизнь играл на лире, знал поэзию и читал Гомера.Он интересовался математикой, философией, астрономией и музыкой и находился под сильным влиянием Ферекидеса (философия),
Фалес (математика и астрономия) и Анаксимандр (философия, геометрия). Пифагор уехал с Самоса в Египет примерно в 535 году до нашей эры. учиться у священников в храмах. Многие из практик общества, созданного им позже в Италии, можно отнести к убеждениям египетских священников, таким как кодексы секретности, стремление к чистоте и отказ от употребления в пищу бобов или ношения шкур животных в качестве одежды.Его методы обучения не были популярны у лидеров Самоса,
и их желание, чтобы он занялся политикой, не привлекло его, поэтому он ушел. Пифагор поселился в Кротоне, греческой колонии на юге Италии, около 518 г. до н.э.
и основал философскую и религиозную школу, где жили и работали его многочисленные последователи.
Пифагорейцы жили по правилам поведения, в том числе, когда они говорили, что они носили и что они ели.
Пифагор был Владыкой общества, и последователи, как мужчины, так и женщины, которые также жили там, были известны как mathematikoi.Он движется от одного существа к
другой, иногда от человека к животному, через серию
реинкарнации называются переселением, пока оно не станет чистым. Пифагор
считал, что и математика, и музыка могут очистить. Из-за строгой секретности среди членов общества Пифагора и того факта, что они делились идеями и интеллектуальными открытиями внутри группы и не давали людям индивидуальности, трудно быть уверенным, были ли все теоремы, приписываемые Пифагору, изначально его, или пришли ли они из общинного общества пифагорейцев. Некоторые из учеников Пифагора в конце концов записали теории, учения и открытия группы, но пифагорейцы всегда отдают должное Пифагору как Мастеру за: Пифагор изучал нечетные и четные числа, треугольные числа и совершенные числа.
Пифагорейцы внесли свой вклад в наше понимание углов, треугольников, площадей, пропорций, многоугольников и многогранников. Пифагор также связывал музыку с математикой. Он долго играл семиструнную лиру и узнал, как гармонично звучат вибрирующие струны, когда длины струн были пропорциональны целым числам, таким как 2: 1, 3: 2, 4: 3. Пифагорейцы также поняли, что эти знания могут быть применены к другим музыкальным инструментам. Сообщения о смерти Пифагора разнообразны. Говорят, что он был убит разъяренной толпой, пойман на войне между Агриджентумом и сиракузанцами и убит сиракузанцами, или был сожжен в своей школе в Кротоне, а затем отправился в Метапонтум, где он голодал сам до смерти. По крайней мере, две из этих историй включают сцену, в которой Пифагор отказывается растоптать урожай бобовых растений, чтобы сбежать, и из-за этого его поймали. Теорема Пифагора является краеугольным камнем математики и продолжает быть настолько интересной для математиков, что существует более 400 различных доказательств этой теоремы, включая оригинальное доказательство президента Гарфилда.
и умножив на 24, мы получим значения в прилагаемой таблице по сравнению с традиционными коэффициентами и нашей предыдущей шкалой 24-х. Как это происходит, каждое значение находится в пределах единицы традиционных значений, за исключением шестого (B), что больше, чем на единицу не по ступеням. Интервал между этими значениями неуклонно растет вверх по шкале, но мы можем оправдать это как артефакт основного умножения.Это объясняет сходную общую тенденцию в традиционных ценностях. В результате получается, что исходные отношения для интервалов we выглядят как попытка дажеC D E F G A B C 1 / 1 9 / 8 5/4 4 / 3 3/2 5 / 3 15/8 2 / 1 24/24 27 / 24 30/24 32 / 24 36/24 40 / 24 45/24 48 / 24 24/24 26.5 / +24 29,3 / 24 32,3 / 24 35,7 / +24 39,4 / 24 43,5 / 24 48/24  , из «натуральных»,
, из «натуральных»,  , примечания).Мы можем сравнить результат с базовым принципом октавы, что отношение любого интервала
, примечания).Мы можем сравнить результат с базовым принципом октавы, что отношение любого интервала
Born Приблизительно 569 г. до н.э., Самос, Греция Died Приблизительно 500 — 475 г. до н.э., Метапонт Италия 

