Формулы правильных многоугольников: Правильный многоугольник. Формулы, признаки и свойства правильного многоугольника
Правильный многоугольник. Формулы, признаки и свойства правильного многоугольника
Навигация по странице: Определение правильного многоугольника Признаки правильного многоугольника Основные свойства правильного многоугольника Правильный n-угольник — формулы — длина стороны — радиус вписанной окружности — радиус описанной окружности — площадь — периметр — угол между сторонами Правильный треугольник Правильный четырехугольник Правильный шестиугольник Правильный восьмиугольник
Определение. Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.
Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.
Многоугольники отличаются между собой количеством сторон и углов.
 1 |
Рис.2 |
Признаки правильного многоугольника
Многоугольник будет правильным, если выполняется следующее условие:
Все стороны и углы одинаковы:
a1 = a2 = a3 = … = an-1 = an
α1 = α2 = α3 = … = αn-1 = αn
Основные свойства правильного многоугольника
1. Все стороны равны:
2. Все углы равны:
3. Центр вписанной окружности Oв совпадает з центром описанной окружности Oо, что и образуют центр многоугольника O
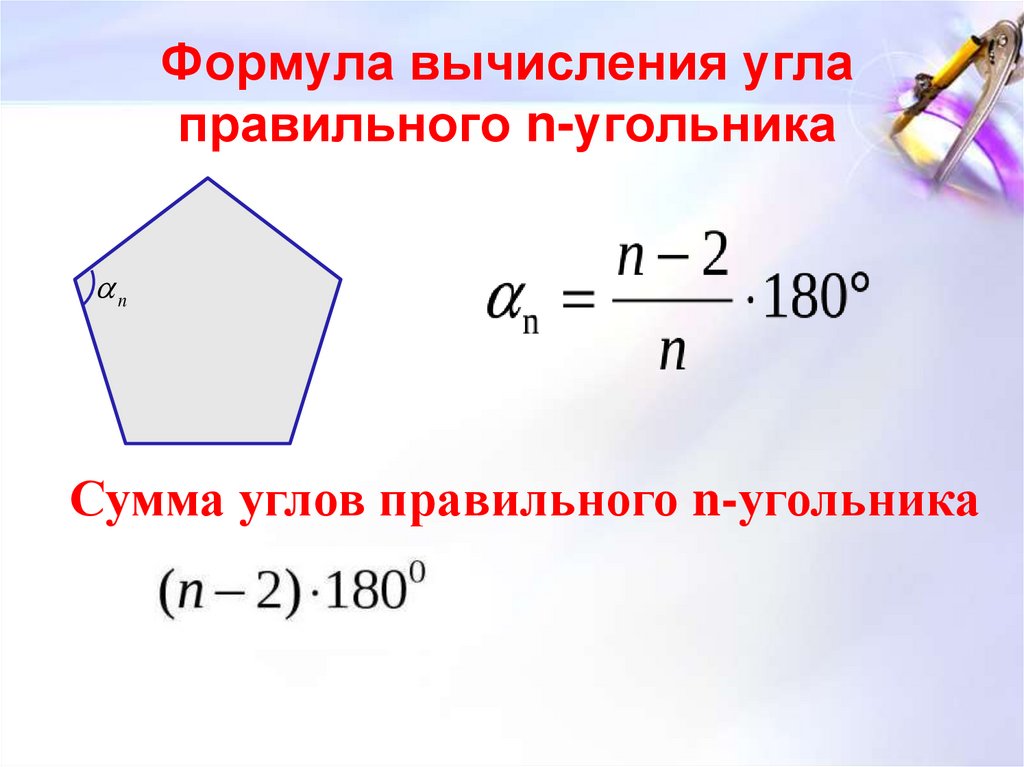
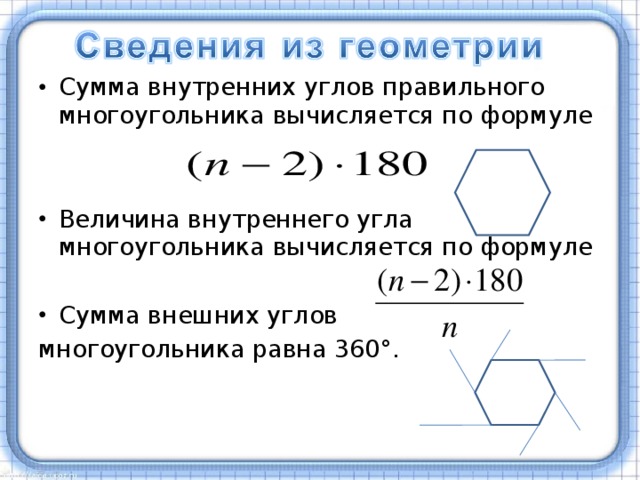
4. Сумма всех углов n-угольника равна:
180° · (n — 2)
5.
Сумма всех внешних углов n-угольника равна 360°:
β1 + β2 + β3 + … + βn-1 + βn = 360°
6. Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины:
| Dn = | n · (n — 3) |
| 2 |
7. В любой многоугольник можно вписать окружность и описать круг при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника:
| S = | π | a2 |
| 4 |
8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника
Правильный n-угольник — формулы
Формулы длины стороны правильного n-угольника
1. Формула стороны правильного n-угольника через радиус вписанной окружности:
| a = 2r · tg | 180° |
| n |
| a = 2r · tg | π |
| n |
2.
Формула стороны правильного n-угольника через радиус описанной окружности:
| a = 2 R · sin | 180° |
| n |
| a = 2 R · sin | π |
| n |
Формула радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны:
| r = a : (2tg | 180° | ) |
| n |
| r = a : (2tg | π | ) |
| n |
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны:
| R = a : (2sin | 180° | ) |
| n |
| R = a : (2sin | π | ) |
| n |
Формулы площади правильного n-угольника
1.
Формула площади n-угольника через длину стороны:
| S = | na2 | · ctg | 180° |
| 4 | n |
2. Формула площади n-угольника через радиус вписанной окружности:
| S = | nr2 · tg | 180° |
| n |
3. Формула площади n-угольника через радиус описанной окружности:
| S = | nR2 | · sin | 360° |
| 2 | n |
Формула периметра правильного многоугольника:
Формула периметра правильного n-угольника:
P = na
Формула определения угла между сторонами правильного многоугольника:
Формула угла между сторонами правильного n-угольника:
| αn = | n — 2 | · 180° |
| n |
Рис. 3 |
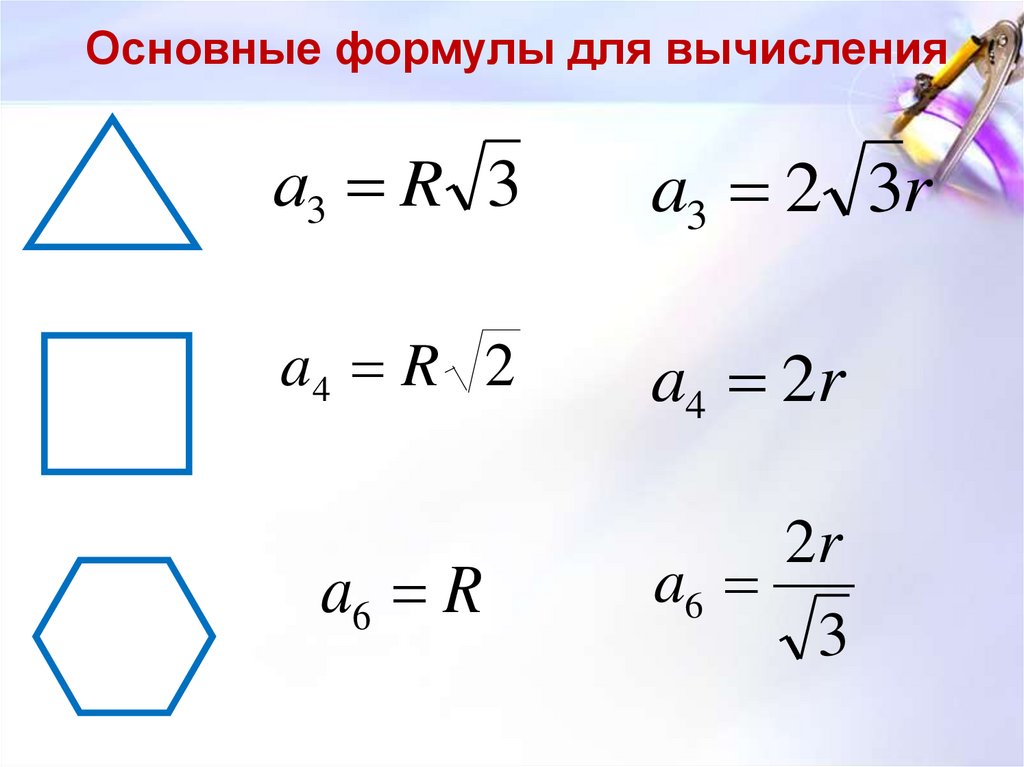
Правильный треугольник
Формулы правильного треугольника:
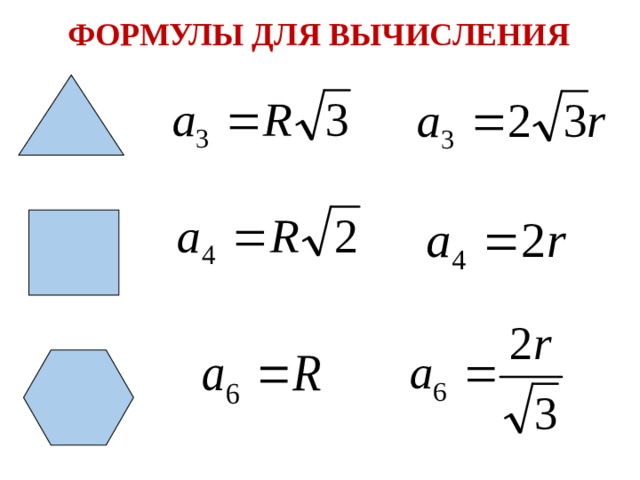
1. Формула стороны правильного треугольника через радиус вписанной окружности:
a = 2r √3
2. Формула стороны правильного треугольника через радиус описанной окружности:
a = R√3
3. Формула радиуса вписанной окружности правильного треугольника через длину стороны:
| r = | a√3 |
| 6 |
4. Формула радиуса описанной окружности правильного треугольника через длину стороны:
| R = | a√3 |
| 3 |
5. Формула площади правильного треугольника через длину стороны:
| S = | a2√3 |
| 4 |
6. Формула площади правильного треугольника через радиус вписанной окружности:
S = r2 3√3
7.
Формула площади правильного треугольника через радиус описанной окружности:
| S = | R2 3√3 |
| 4 |
8. Угол между сторонами правильного треугольника:
α = 60°
| Рис.4 |
Правильный четырехугольник
Правильный четырехугольнику — квадрат.
Формулы правильного четырехугольника:
1. Формула стороны правильного четырехугольника через радиус вписанной окружности:
a = 2r
2. Формула стороны правильного четырехугольника через радиус описанной окружности:
a = R√2
3. Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:
| r = | a |
| 2 |
4.
Формула радиуса описанной окружности правильного четырехугольника через длину стороны:
| R = | a√2 |
| 2 |
5. Формула площади правильного четырехугольника через длину стороны:
S = a2
6. Формула площади правильного четырехугольника через радиус вписанной окружности:
S = 4 r2
7. Формула площади правильного четырехугольника через радиус описанной окружности:
S = 2 R2
8. Угол между сторонами правильного четырехугольника:
α = 90°
Смотрите также формулы и свойства квадрата
Правильный шестиугольник
Формулы правильного шестиугольника:
1. Формула стороны правильного шестиугольника через радиус вписанной окружности:
| a = | 2√3 | r |
| 3 |
2.
Формула стороны правильного шестиугольника через радиус описанной окружности:
a = R
3. Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:
| a√3 | |
| 2 |
4. Формула радиуса описанной окружности правильного шестиугольника через длину стороны:
R = a
5. Формула площади правильного шестиугольника через длину стороны:
| S = | a2 3√3 |
| 2 |
6. Формула площади правильного шестиугольника через радиус вписанной окружности:
S = r2 2√3
7. Формула площади правильного шестиугольника через радиус описанной окружности:
| S = | R2 3√3 |
| 2 |
8. Угол между сторонами правильного шестиугольника:
α = 120°
Правильный восьмиугольник
Формулы правильного восьмиугольника:
1.
Формула стороны правильного восьмиугольника через радиус вписанной окружности:
a = 2r · (√2 — 1)
2. Формула стороны правильного восьмиугольника через радиус описанной окружности:
a = R√2 — √2
3. Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны:
| r = | a(√2 + 1) |
| 2 |
4. Формула радиуса описанной окружности правильного восьмиугольника через длину стороны:
| R = | a√4 + 2√2 |
| 2 |
5. Формула площади правильного восьмиугольника через длину стороны:
S = a2 2(√2 + 1)
6. Формула площади правильного восьмиугольника через радиус вписанной окружности:
S = r2 8(√2 — 1)
7. Формула площади правильного восьмиугольника через радиус описанной окружности:
S = R2 2√2
8.
Угол между сторонами правильного восьмиугольника:
α = 135°
Все таблицы и формулы
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Поиск по сайту:
| Справочник по математике | Геометрия (Планиметрия) | Многоугольники |
| Формулы для стороны, периметра и площади правильного n – угольника |
| Формулы для стороны, периметра и площади правильного треугольника |
| Формулы для стороны, периметра и площади правильного шестиугольника |
| Формулы для стороны, периметра и площади квадрата |
Фигуру называют выпуклой, если для любых двух точек этой фигуры соединяющий их отрезок полностью принадлежит фигуре.
Правильными многоугольниками называют выпуклые многоугольники, у которых все углы равны и все стороны равны.
Замечание 1. В любой правильный многоугольник можно вписать окружность.
Замечание 2. Около любого правильного многоугольника можно описать окружность.
Замечание 3. Центры вписанной в правильный многоугольник окружности и описанной около правильного многоугольника окружности совпадают. Эту точку называют центром правильного многоугольника.
Используемые обозначения
| Число вершин правильного многоугольника | Сторона правильного многоугольника | Радиус вписанной окружности | Радиус описанной окружности | Периметр | Площадь |
| n | a | r | R | P | S |
| Число вершин правильного многоугольника | n |
| Сторона правильного многоугольника | a |
| Радиус вписанной окружности | r |
| Радиус описанной окружности | R |
| Периметр | P |
| Площадь | S |
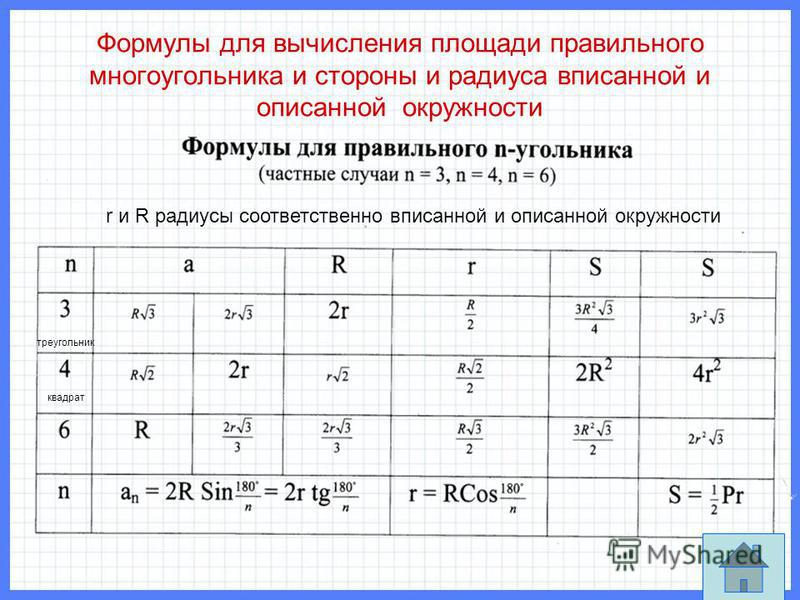
Формулы для стороны, периметра и площади правильного
n – угольника| Величина | Рисунок | Формула | Описание |
| Периметр | P = an | Выражение периметра через сторону | |
| Площадь | Выражение площади через сторону и радиус вписанной окружности | ||
| Площадь | Выражение площади через сторону | ||
| Сторона | Выражение стороны через радиус вписанной окружности | ||
| Периметр | Выражение периметра через радиус вписанной окружности | ||
| Площадь | Выражение площади через радиус вписанной окружности | ||
| Сторона | Выражение стороны через радиус описанной окружности | ||
| Периметр | Выражение периметра через радиус описанной окружности | ||
| Площадь | Выражение площади через радиус описанной окружности |
| Формулы для периметра правильного n – угольника |
Выражение периметра через сторону P = an Выражение периметра через радиус вписанной окружности Выражение периметра через радиус описанной окружности |
| Формулы для площади правильного n – угольника |
Выражение площади через сторону и радиус вписанной окружности Выражение площади через сторону Выражение площади через радиус вписанной окружности Выражение площади через радиус описанной окружности |
| Формулы для стороны правильного n – угольника |
Выражение стороны через радиус вписанной окружности Выражение стороны через радиус описанной окружности |
Формулы для стороны, периметра и площади правильного треугольника
| Величина | Рисунок | Формула | Описание |
| Периметр | P = 3a | Выражение периметра через сторону | |
| Площадь | Посмотреть вывод формулы | Выражение площади через сторону | |
| Площадь | Выражение площади через сторону и радиус вписанной окружности | ||
| Сторона | Выражение стороны через радиус вписанной окружности | ||
| Периметр | Выражение периметра через радиус вписанной окружности | ||
| Площадь | Посмотреть вывод формулы | Выражение площади через радиус вписанной окружности | |
| Сторона | Выражение стороны через радиус описанной окружности | ||
| Периметр | Выражение периметра через радиус описанной окружности | ||
| Площадь | Посмотреть вывод формулы | Выражение площади через радиус описанной окружности |
| Формулы для периметра правильного треугольника |
Выражение периметра через сторону P = 3a Выражение периметра через радиус вписанной окружности Выражение периметра через радиус описанной окружности |
| Формулы для площади правильного треугольника |
Выражение площади через сторону Посмотреть вывод формулы Выражение площади через сторону и радиус вписанной окружности Выражение площади через радиус вписанной окружности Посмотреть вывод формулы Выражение площади через радиус описанной окружности Посмотреть вывод формулы |
| Формулы для стороны правильного треугольника |
Выражение стороны через радиус вписанной окружности Выражение стороны через радиус описанной окружности |
Формулы для стороны, периметра и площади правильного шестиугольника
| Величина | Рисунок | Формула | Описание |
| Периметр | P = 6a | Выражение периметра через сторону | |
| Площадь | Выражение площади через сторону | ||
| Площадь | S = 3ar | Выражение площади через сторону и радиус вписанной окружности | |
| Сторона | Выражение стороны через радиус вписанной окружности | ||
| Периметр | Выражение периметра через радиус вписанной окружности | ||
| Площадь | Выражение площади через радиус вписанной окружности | ||
| Сторона | a = R | Выражение стороны через радиус описанной окружности | |
| Периметр | P = 6R | Выражение периметра через радиус описанной окружности | |
| Площадь | Выражение площади через радиус описанной окружности |
| Формулы для периметра правильного шестиугольника |
Выражение периметра через сторону P = 6a Выражение периметра через радиус вписанной окружности Выражение периметра через радиус описанной окружности P = 6R |
| Формулы для площади правильного шестиугольника |
Выражение площади через сторон Выражение площади через сторону и радиус вписанной окружности S = 3ar Выражение площади через радиус вписанной окружности Выражение площади через радиус описанной окружности |
| Формулы для стороны правильного шестиугольника |
Выражение стороны через радиус вписанной окружности Выражение стороны через радиус описанной окружности a = R |
Формулы для стороны, периметра и площади квадрата
| Величина | Рисунок | Формула | Описание |
| Периметр | P = 4a | Выражение периметра через сторону | |
| Площадь | S = a2 | Выражение площади через сторону | |
| Сторона | a = 2r | Выражение стороны через радиус вписанной окружности | |
| Периметр | P = 8r | Выражение периметра через радиус вписанной окружности | |
| Площадь | S = 4r2 | Выражение площади через радиус вписанной окружности | |
| Сторона | Выражение стороны через радиус описанной окружности | ||
| Периметр | Выражение периметра через радиус описанной окружности | ||
| Площадь | S = 2R2 | Выражение площади через радиус описанной окружности |
| Формулы для периметра квадрата |
Выражение периметра через сторону P = 4a Выражение периметра через радиус вписанной окружности P = 8r Выражение периметра через радиус описанной окружности |
| Формулы для площади квадрата |
Выражение площади через сторону S = a2 Выражение площади через радиус вписанной окружности S = 4r2 Выражение площади через радиус описанной окружности S = 2R2 |
| Формулы для стороны квадрата |
Выражение стороны через радиус вписанной окружности a = 2r Выражение стороны через радиус описанной окружности |
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Правильный многоугольник для школьников и студентов
- формулы, признаки и свойства правильного многоугольника
- формулы правильного n-угольника
- правильный треугольник
- правильный четырехугольник
- правильный шестиугольник
- правильный восьмиугольник
Формулы, признаки и свойства правильного многоугольника
Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.
Многоугольники отличаются между собой количеством сторон и углов.
Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.
Признаки правильного многоугольника
Многоугольник будет правильным, если выполняется следующее условие: все стороны и углы одинаковы.
a1=a2=a3=…=an-1=an ,
α1=α2=α3=…=αn-1=αn
где a1…an — длины сторон правильного многоугольника,
Основные свойства правильного многоугольника
- Все стороны равны: a1=a2=a3=…=an-1=an
- Все углы равны: α1=α2=α3=…=αn-1=αn
- Центр вписанной окружности Oв совпадает с центром описанной окружности Oо, что и образуют центр многоугольника O.
- Сумма всех углов n-угольника равна:180°·n-2
- Сумма всех внешних углов n-угольника равна 360°: β1+β2+β3+…+βn-1+βn=360°
- Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины: Dn=n·n-32
- В любой многоугольник можно вписать окружность и описать круг; при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника: S=π4·a2
- Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O.
Формулы правильного n-угольника
Формулы длины стороны правильного n-угольника
Формула стороны правильного n-угольника через радиус вписанной окружности
a=2·r·tg180°n (через градусы),
a=2·r·tgπn (через радианы)
Формула стороны правильного n-угольника через радиус описанной окружности
a=2·R·sin180°n (через градусы),
a=2·R·sinπn (через радианы)
Формулы радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны
r=a:2·tg180°n (через градусы),
r=a:2·tgπn (через радианы)
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны
R=a:2·sin180°n (через градусы),
R=a:2·sinπn (через радианы)
Формулы площади правильного n-угольника
Формула площади n-угольника через длину стороны
S=n·a24·ctg180°n
Формула площади n-угольника через радиус вписанной окружности
S=n·r2·tg180°n
Формула площади n-угольника через радиус описанной окружности
S=n·R22·sin360°nФормула периметра правильного многоугольника
Формула периметра правильного n-угольника
Периметр правильного n-угольника равен произведению длины одной стороны правильного n-угольника на количество его сторон.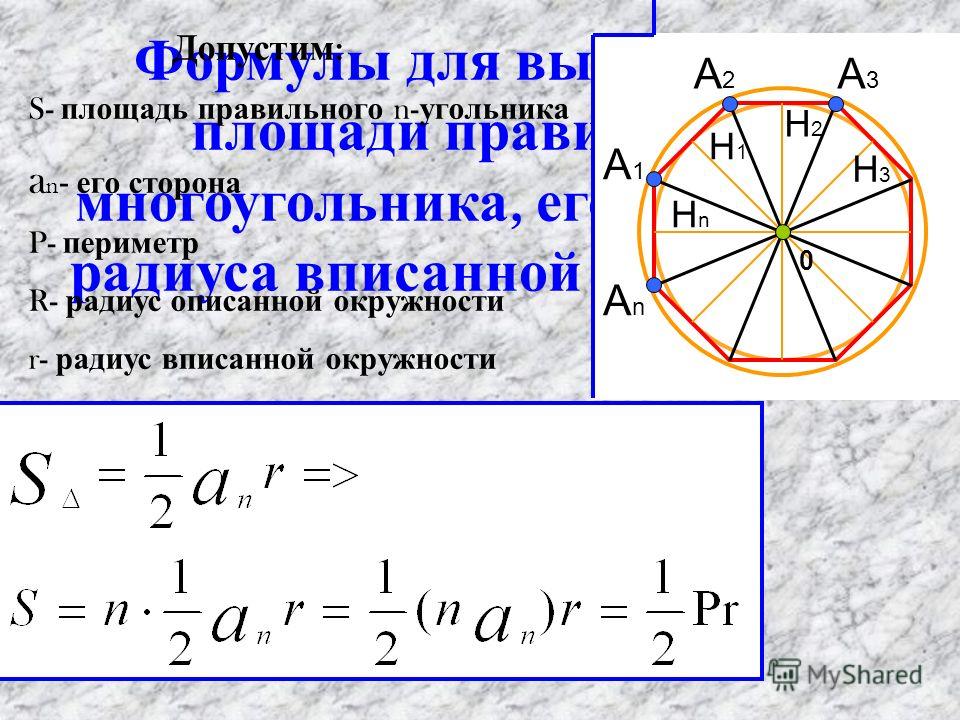
P=n·a
Формула определения угла между сторонами правильного многоугольника
Формула угла между сторонами правильного n-угольника
αn=n-2n·180°Правильный треугольник
Правильный треугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.
Формулы правильного треугольника
Формула стороны правильного треугольника через радиус вписанной окружности
Сторона правильного треугольника равна удвоенному произведению радиуса вписанной окружности на корень из трёх.
a=2·r·3
Формула стороны правильного треугольника через радиус описанной окружности
Сторона правильного треугольника равна произведению радиуса описанной окружности на корень из трёх.
a=R·3
r=a·36
R=a·33
Формула площади правильного треугольника через длину стороны
S=a2·34
Формула площади правильного треугольника через радиус вписанной окружности
S=r2·3·3
Формула площади правильного треугольника через радиус описанной окружности
S=R2·3·34
Углы между сторонами правильного треугольника
α1=α2=α3=60°Правильный четырехугольник
Правильный четырехугольник — это квадрат.
Формулы правильного четырехугольника
Формула стороны правильного четырехугольника через радиус вписанной окружности
Сторона правильного четырехугольника равна двум радиусам вписанной окружности.
a=2·r
Формула стороны правильного четырехугольника через радиус описанной окружности
Сторона правильного четырехугольника равна произведению радиуса описанной окружности на корень из двух.
a=R·2
Формула радиуса вписанной окружности правильного четырехугольника через длину стороны
Радиус вписанной окружности правильного четырехугольника равен половине стороны четырехугольника.
r=a2
Формула радиуса описанной окружности правильного четырехугольника через длину стороны
Радиус описанной окружности правильного четырехугольника равен половине произведения стороны четырехугольника на корень из двух.
R=a·22
Формула площади правильного четырехугольника через длину стороны
Площадь правильного четырехугольника равна квадрату стороны четырехугольника.
S=a2
Формула площади правильного четырехугольника через радиус вписанной окружности
Площадь правильного четырехугольника равна четырем радиусам вписанной окружности четырехугольника.
S=4·r2
Формула площади правильного четырехугольника через радиус описанной окружности
Площадь правильного четырехугольника равна двум квадратам радиуса описанной окружности.
S=2·R2
Углы между сторонами правильного четырехугольника
α1=α2=α3=α4=90°Правильный шестиугольник
Правильный шестиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного шестиугольника равны между собой, все углы также равны и составляют 120°.
Формулы правильного шестиугольник
Формула стороны правильного шестиугольника через радиус вписанной окружности
a=2·r·33Формула стороны правильного шестиугольника через радиус описанной окружности
Длина стороны правильного шестиугольника равна радиусу описанной окружности.
a=R
Формула радиуса вписанной окружности правильного шестиугольника через длину стороны
r=a·32
Формула радиуса описанной окружности правильного шестиугольника через длину стороны
R=a
Формула площади правильного шестиугольника через длину стороны
S=a2·3·32
Формула площади правильного шестиугольника через радиус вписанной окружности
S=r2·2·3
Формула площади правильного шестиугольника через радиус описанной окружности
S=R2·3·32
Углы между сторонами правильного шестиугольника
α1=α2=α3=α4=α5=α6=120°Правильный восьмиугольник
Правильный восьмиугольник — это правильный многоугольник с тремя сторонами.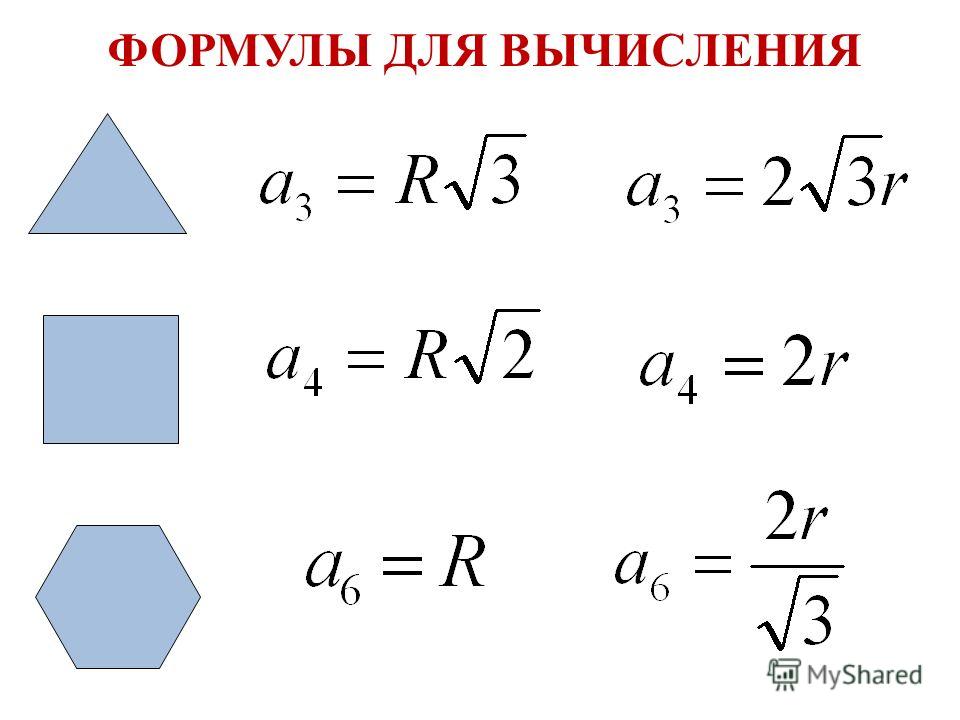
Все стороны правильного восьмиугольник равны между собой, все углы также равны и составляют 135°.
Формулы правильного восьмиугольника
Формула стороны правильного восьмиугольника через радиус вписанной окружности
a=2·r·2-1
Формула стороны правильного восьмиугольника через радиус описанной окружности
a=R·2-2
Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны
r=a·2+12
Формула радиуса описанной окружности правильного восьмиугольника через длину стороны
R=a·4+222
Формула площади правильного восьмиугольника через длину стороны
S=a2·2·2+1
Формула площади правильного восьмиугольника через радиус вписанной окружности
S=r2·8·2-1
Формула площади правильного восьмиугольника через радиус описанной окружности
S=R2·2·2
Углы между сторонами правильного восьмиугольника
α1=α2=α3=α4=α5=α6=α7=α8=135°- Коротко о важном
- Таблицы
- Формулы
- Формулы по геометрии
- Теория по математике
Формула многоугольника — Что такое формула многоугольника?, Примеры
Прежде чем начать с формулы многоугольника, давайте вспомним определение многоугольника.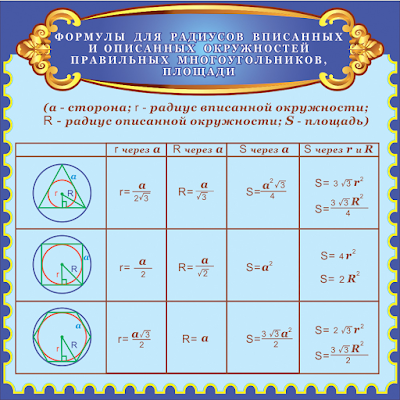
Многоугольник – это замкнутая двумерная фигура, состоящая из трех или более прямых линий. Многоугольник должен иметь как минимум три стороны. Каждая сторона отрезка пересекается с другим отрезком в вершине. Давайте узнаем больше о различных многоугольниках и их формулах.
Типы многоугольников
В зависимости от величины угла и сторон многоугольника многоугольники подразделяются на:
- Правильный многоугольник – все внутренние углы и стороны имеют одинаковую меру
- Неправильный многоугольник — все внутренние углы и стороны имеют разные значения
- Выпуклый многоугольник — все внутренние углы многоугольника < 180 градусов
- Вогнутый многоугольник — многоугольники, которые имеют один или несколько внутренних углов с размером> 180 градусов
Количество сторон многоугольника определяет его форму, и он назван в честь количества сторон. Типичными примерами многоугольников являются треугольники, квадраты, пятиугольники, шестиугольники и т.
д. Ниже перечислены многоугольники в зависимости от количества сторон.
Что такое Формула многоугольника?
Важные формулы, связанные с правильным многоугольником, приведены ниже:
Формула 1: Для правильного многоугольника с n сторонами сумма внутренних углов равна 180°(n-2)
Формула 2: число диагоналей «n-стороннего» многоугольника = [n(n-3)]/2
Формула 3: мера каждого внутреннего угла правильного n-стороннего многоугольника = [(n-2)180 °]/n
Формула 4. Мера внешних углов правильного n-стороннего многоугольника = 360°/n
Формула 5: Площадь правильного многоугольника = (количество сторон × длина одной стороны × апофема)/2, где длина апофемы задается как \(\dfrac{l}{ 2\tan(\dfrac{180}{n})}\) и где l — длина стороны, а n — количество сторон правильного многоугольника.
Формула 6. Периметр правильного многоугольника – площадь правильного многоугольника задается как Площадь = (Периметр × апофема)/2, где периметр = количество сторон × длина одной стороны
Свойства многоугольника
Важными свойствами многоугольника являются
- Сумма внутренних углов всех четырехугольников = 360°.
- Если хотя бы один из внутренних углов больше 180 градусов, то такой многоугольник называется вогнутым.
- Если многоугольник не пересекает сам себя и имеет только одну границу, он называется простым многоугольником. В противном случае это сложный многоугольник.
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Забронируйте бесплатный пробный урок
Примеры использования формул многоугольника
Пример 1. Найдите сумму внутренних углов шестиугольника.
Решение:
Мы знаем, что шестиугольник имеет шесть сторон.
Используя формулу многоугольника, мы знаем, что сумма внутренних углов определяется как:
Сумма внутренних углов = 180°(n-2)
= 180°(6-2)
= 180° (4)
= 720°
Следовательно, сумма внутренних углов шестиугольника равна 720°.
Пример 2. Многоугольник представляет собой восьмиугольник, длина стороны которого составляет 7 см. Вычислите периметр и величину одного внутреннего угла.
Решение:
Многоугольник является восьмиугольником. Отсюда n = 8
Длина каждой стороны, s = 7 см
Периметр восьмиугольника равен P = n × s
P = 8 × 7
= 56 см
Теперь, чтобы найти каждый внутренний угол, используя формулу многоугольника,
Внутренний угол = [(n-2)180°]/n
= [(8 — 2)180°] / 8
= (6 × 180°) / 8
= 135°
Таким образом, периметр данного восьмиугольника равен 56 см, а величина каждого внутреннего угла равна 135 градусам.
Пример 3. Используя формулу многоугольника, найдите сумму внутренних углов треугольника.
Решение:
Мы знаем, что у треугольника три стороны.
Используя формулу многоугольника, мы знаем, что сумма внутренних углов определяется как:
Сумма внутренних углов = 180°(n-2)
= 180°(3-2)
= 180° (1)
= 180°
Следовательно, сумма внутренних углов треугольника равна 180°.
Часто задаваемые вопросы о формуле многоугольника
Что означает формула многоугольника?
Многоугольник — это замкнутая двумерная фигура, состоящая из трех или более прямых линий. Многоугольник имеет по крайней мере три стороны. Каждая сторона отрезка пересекается с другим отрезком только в его конечной точке. Основываясь на количестве сторон многоугольника, мы можем легко определить форму многоугольника. Типичными примерами многоугольников являются треугольники, квадраты, пятиугольники, шестиугольники и т. д.
Сколько существует типов полигонов?
В зависимости от величины угла и сторон многоугольника он подразделяется на:
- Правильный многоугольник – Все внутренние углы и стороны имеют одинаковую величину.
- Неправильный многоугольник. Все внутренние углы и стороны имеют разные размеры.
- Выпуклый многоугольник. Все внутренние углы многоугольника строго < 180°.
- Вогнутый многоугольник — многоугольники, имеющие один или несколько внутренних углов с величиной > 180 °.
Каковы различные формулы полигонов?
Формулы, связанные с правильным многоугольником, приведены ниже:
Формула 1: Сумма внутренних углов многоугольника с «n» сторонами = 180°(n-2) «n-сторонний» многоугольник = [n(n-3)]/2
Формула 3: Мера каждого внутреннего угла правильного n-стороннего многоугольника = [(n-2)180°]/n
Формула 4: Мера внешних углов правильного n-стороннего многоугольника = 360°/n
Каковы свойства многоугольника?
Важными свойствами многоугольника являются
- Сумма внутренних углов всех четырехугольников равна 360°
- Если хотя бы один из внутренних углов больше 180°, то такой многоугольник называется вогнутым.
- Если многоугольник не пересекает сам себя и имеет только одну границу, он называется простым многоугольником. В противном случае это сложный многоугольник.
Правильные многоугольники — Свойства
Многоугольник
Многоугольник — это плоская фигура (двумерная) с прямыми сторонами.
Примеры включают треугольники, четырехугольники, пятиугольники, шестиугольники и так далее.
Обычный
«Правильный многоугольник» имеет:
В противном случае неправильный . |
|
Здесь мы рассматриваем только Правильные многоугольники .
Свойства
Итак, что мы можем знать о правильных многоугольниках? Прежде всего, мы можем работать с углами.
Внешний угол Внешний угол — это угол между любой стороной фигуры, |
Все внешние углы многоугольника в сумме дают 360°, поэтому:
Каждый внешний угол должен быть равен 360°/n
(где n — количество сторон)
3 Нажмите play кнопку, чтобы увидеть.
Внешний угол
(правильного восьмиугольника)
Пример: Каков внешний угол правильного восьмиугольника?
Восьмиугольник имеет 8 сторон, поэтому:
Внешний угол = 360° / n
= 360° / 8
= 45°
Внутренние уголкиВнутренний угол и Внешний угол измеряются от одной и той же линии, поэтому их в сумме дают 180° . |
Внутренний угол = 180° − Внешний угол
Мы знаем, что Внешний угол = 360°/n , поэтому:
Внутренний угол = 180° − 360°/n
Которые можно переставить следующим образом:
Внутренний угол = 180° − 360°/n
= (n × 180° / n) − (2 × 180° / n)
= (n − 2) × 180°/n
Таким образом, у нас также есть это:
Внутренний угол = (n − 2) × 180° / n
Пример: каков внутренний угол обычный восьмиугольник?
Правильный восьмиугольник имеет 8 сторон, поэтому:
Внешний угол = 360 ° / 8 = 45°
Внутренний угол = 180° − 45° = 9
Или мы могли бы использовать: ° / 8
= 6 × 180° / 8
= 135°
Пример.
Каковы внутренние и внешние углы правильного шестиугольника?Правильный шестиугольник имеет 6 сторон, поэтому:
Внешний угол = 360 ° / 6 = 60°
Внутренний угол = 180 ° − 60° = 120°
А теперь некоторые имена:
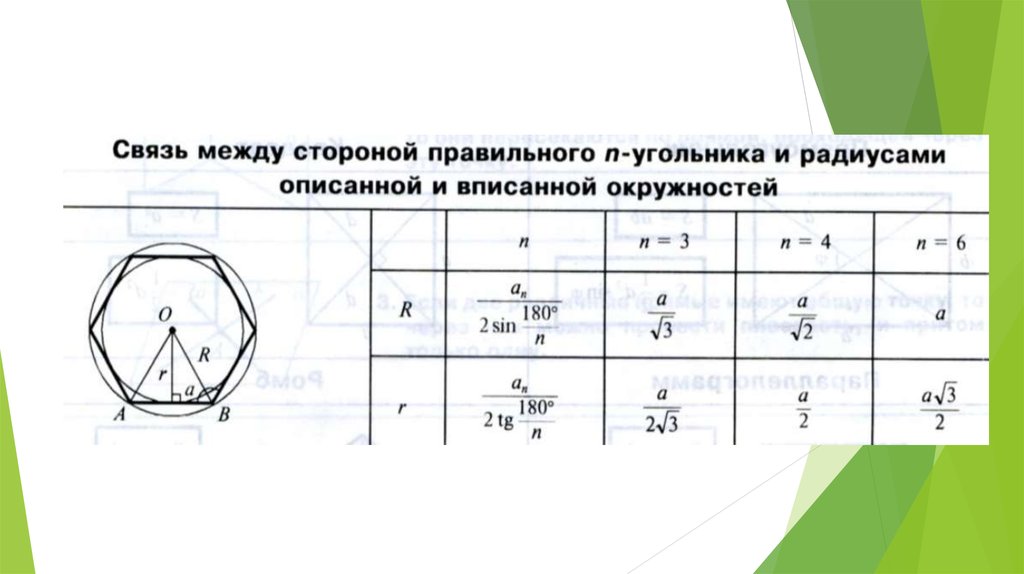
«Описанная окружность, Вписанная окружность, Радиус и Апофема…»
Звучит весьма музыкально, если повторить несколько раз, но они просто названия «внешней» и «внутренней» окружностей (и каждого радиуса), которые можно нарисовать на многоугольнике следующим образом:
«Внешняя» окружность называется описанной окружностью , и она соединяет все вершины (угловые точки) многоугольника.
Радиус описанной окружности также равен радиусу многоугольника.
«Внутренний» круг называется вписанным в окружность , и он просто касается каждой стороны многоугольника в его середине.
Радиус вписанной окружности равен апофеме многоугольника.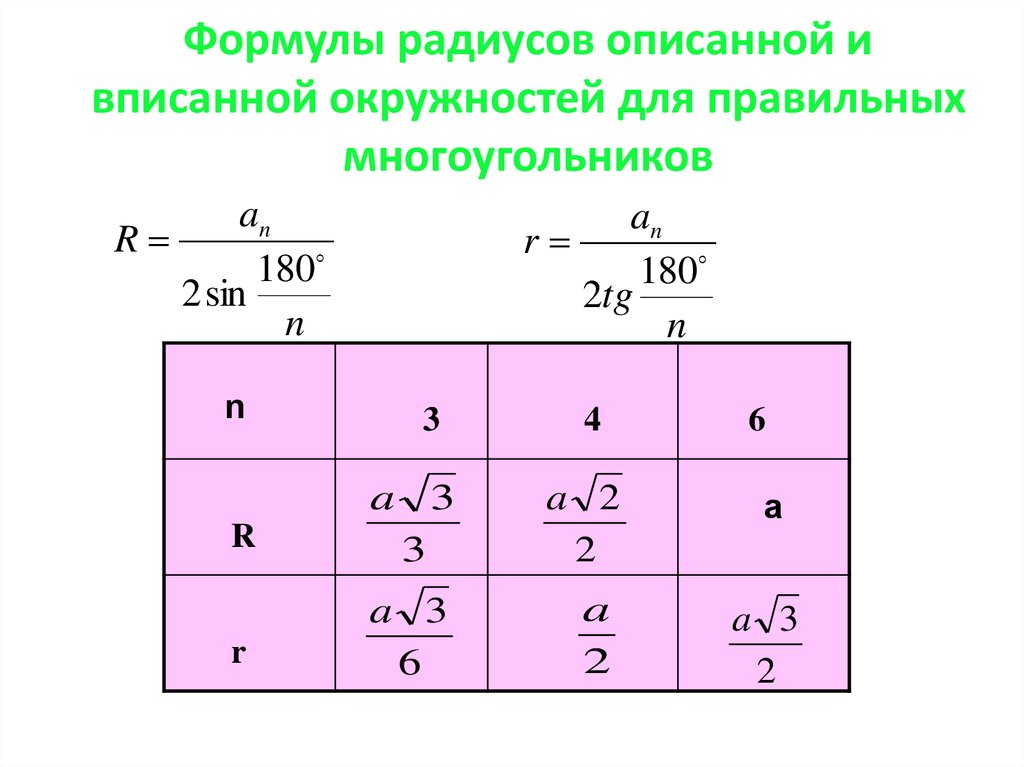
(этими свойствами обладают не все многоугольники, но треугольники и правильные многоугольники).
Разбиение на треугольники
Мы можем многое узнать о правильных многоугольниках, разбив их на треугольники следующим образом:
Обратите внимание, что:
- «основание» треугольника — это одна сторона многоугольника.
- «высота» треугольника является «Апофемой» многоугольника
Теперь площадь треугольника равна половине основания, умноженному на высоту, поэтому:
Площадь одного треугольника = основание × высота / 2 = сторона × апофема / 2
Чтобы получить площадь всего многоугольника, просто добавьте вверх площади всех маленьких треугольников (n из них):
Площадь многоугольника = n × сторона × апофема / 2
А поскольку периметр равен всем сторонам = n × сторона, мы получаем:
Площадь многоугольника = периметр × апофема / 2
Меньший треугольник
Разрезав треугольник пополам, мы получим:
(Примечание: углы указаны в радианах, а не в градусах)
Маленький треугольник прямоугольный, поэтому мы можем использовать синус, косинус и тангенс, чтобы найти, как сторона , радиус , апофема и n (количество сторон) связаны:
| sin(π/n) = (Сторона/2) / Радиус | Сторона = 2 × радиус × sin(π/n) | |
| cos(π/n) = Апофема / Радиус | Апофема = Радиус × cos(π/n) | |
| тангенс (π/n) = (Сторона/2) / Апофема | Сторона = 2 × Апофема × тангенс (π/n) |
Таких отношений гораздо больше (большинство из них просто «перестановки»), но пока что хватит и этих.
Другие формулы площади
Мы можем использовать это для вычисления площади, когда мы знаем только Апофему:
Площадь малого треугольника = ½ × Апофема × (Сторона/2)
И мы знаем (от «tan формула выше), что:
Сторона = 2 × Апофема × тангенс (π/n)
Итак:
Площадь малого треугольника = ½ × Апофема × (Апофема × тангенс (π/n))
= ½ × Apothem 2 × tan(π/n)
И таких треугольников на сторону 2, или 2n для всего многоугольника :
Площадь многоугольника = n × Apothem 2 × tan(π/n)
Когда мы не знаем Apothem, мы можем использовать ту же формулу, но переработанную для радиуса или стороны:
Площадь многоугольника = ½ × n × радиус 2 × sin(2 × π/n)
Площадь многоугольника = ¼ × n × сторона 2 / tan(π/n)
Таблица значений
А вот таблица сторон, апофем и площадей по сравнению с радиусом «1», используя формулы, которые мы разработали:
| Тип | Имя, когда Обычный | стороны (н) | Форма | Внутренний уголок | Радиус | Боковой | Апофема | Район |
|---|---|---|---|---|---|---|---|---|
| Треугольник (или тригон) | Равносторонний Треугольник | 3 | 60° | 1 | 1. 732 (√3) | 0,5 | 1,299 (¾√3) | |
| Четырехугольник (или Тетрагон) | Квадрат | 4 | 90° | 1 | 1,414 (√2) | 0,707 (1/√2) | 2 | |
| Пентагон | Обычный Пентагон | 5 | 108° | 1 | 1,176 | 0,809 | 2,378 | |
| Шестигранник | Обычный Шестигранник | 6 | 120° | 1 | 1 | 0,866 (½√3) | 2,598 ((3/2)√3) | |
| Семиугольник (или Септагон) | Обычный Семиугольник | 7 | 128,571° | 1 | 0,868 | 0,901 | 2,736 | |
| Октагон | Обычный Октагон | 8 | 135° | 1 | 0,765 | 0,924 | 2,828 (2√2) | |
. .. | … | |||||||
| Пятиугольник | Обычный Пентаконтагон | 50 | 172,8° | 1 | 0,126 | 0,998 | 3.133 | |
| (Примечание: значения верны только до 3 знаков после запятой) | ||||||||
График
А вот график таблицы выше, но с числом сторон («n») от 3 до 30.
Обратите внимание, что чем больше «n», тем больше апофема к 1 (равному Радиусу) и что Площадь стремится к π = 3,14159…, как круг.
К чему стремится длина стороны?
Формула внутреннего угла (определение, примеры и видео) // Tutors.com
Формула внутреннего угла (определение, примеры, сумма внутренних углов)
видео Определение Сумма внутренних углов Поиск неизвестных углов Правильные многоугольники
Если вы посмотрите другие уроки по геометрии на этом полезном сайте, то увидите, что при обсуждении многоугольников мы тщательно упомянули внутренние углы, а не только углы.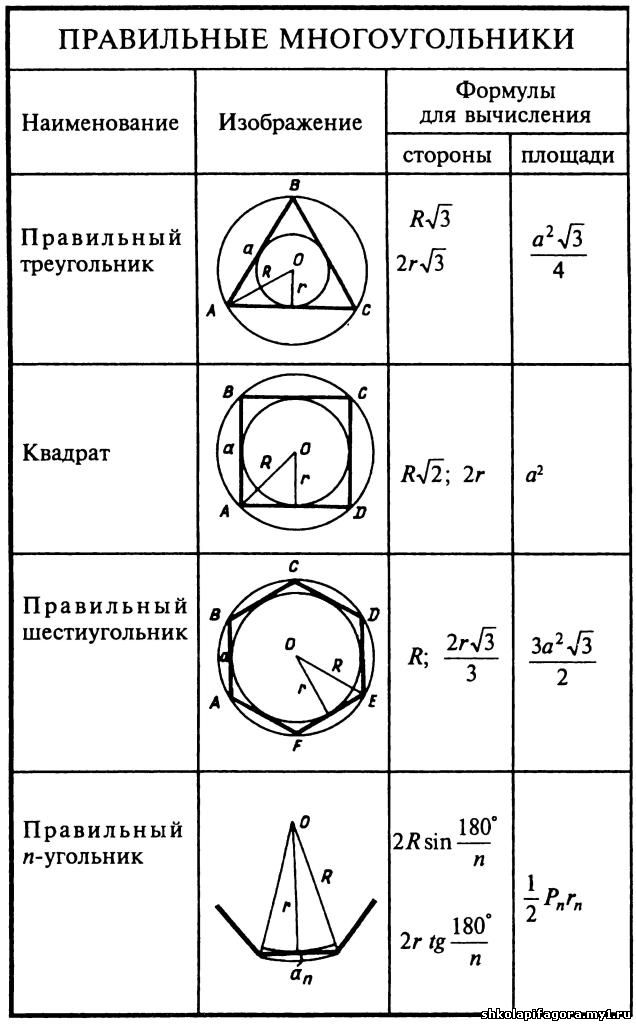
У каждого многоугольника есть внутренние и внешние углы, но все самое интересное происходит во внутренних углах.
Чему вы научитесь:
Проработав этот урок и видео, вы сможете:
- Определять внутренние углы многоугольников
- Вспомните и примените формулу для нахождения суммы внутренних углов многоугольника
- Вспомнить метод нахождения неизвестного внутреннего угла многоугольника
- Вычисление внутренних углов многоугольников
- Найдите количество сторон многоугольника
Внутренний угол Формула
От простейшего многоугольника, треугольника, до бесконечно сложного многоугольника с n сторонами, стороны многоугольников замыкаются в пространстве. Каждое пересечение сторон создает вершину, и эта вершина имеет внутренний и внешний углы. Внутренние углы многоугольников находятся внутри многоугольника.
Хотя Евклид предложил теорему о внешних углах, специфичную для треугольников, теоремы о внутренних углах не существует.
Вместо этого вы можете использовать формулу, которая математически описывает интересную модель многоугольников и их внутренних углов.
Формула суммы внутренних углов
Эта формула позволяет математически разделить любой многоугольник на минимальное количество треугольников. Поскольку каждый треугольник имеет внутренние углы, равные 180°, умножение числа делящихся треугольников на 180° дает сумму внутренних углов.
S = (n — 2) × 180°
S = сумма внутренних углов
n = количество сторон многоугольника
Попробуйте формулу на треугольнике:
90 × 180°
S = (3 — 2) × 180°
S = 1 × 180°
S = 180°
Хорошо, это сработало, но как насчет более сложной формы, например, двенадцатиугольника?
[вставить чертеж десятиугольника]
Он имеет 12 сторон, поэтому:
S = (n — 2) × 180° 180°
S = 1800°
Откуда вы знаете, что это правильно? Возьмите любой додекагон и выберите одну вершину.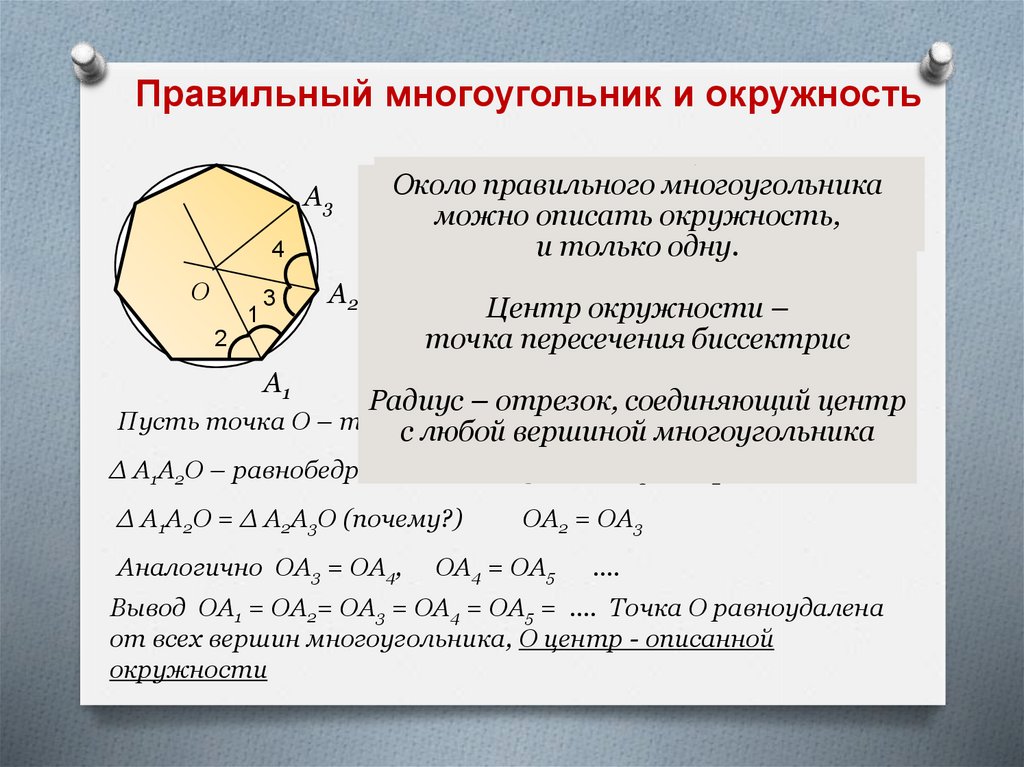
Соедините каждую вторую вершину с этой линейкой, разделив пространство на 10 треугольников. Десять треугольников, по 180° каждый, дают в сумме 1800°!
Нахождение неизвестного внутреннего угла
Та же формула S = (n — 2) × 180° может помочь вам найти недостающий внутренний угол многоугольника. Вот дурацкий пятиугольник, у которого нет двух равных сторон:
[вставьте рисунок пятиугольника с четырьмя отмеченными внутренними углами, имеющими размеры 105°, 115°, 109°, 111°; длина сторон несущественна]
Формула говорит нам, что пятиугольник, независимо от его формы, должен иметь внутренние углы в сумме 540°:
S = (n — 2) × 180°
S = (5 — 2) × 180°
S = 3 × 180°
S = 540°
Таким образом, вычитание четырех известных углов из 540° оставит вам недостающий угол:
540°- 105° — 115° — 109° — 111° = 100°
Неизвестный угол равен 100°.
Нахождение внутренних углов правильных многоугольников
Когда вы знаете, как найти сумму внутренних углов многоугольника, нахождение одного внутреннего угла для любого правильного многоугольника — это просто вопрос деления.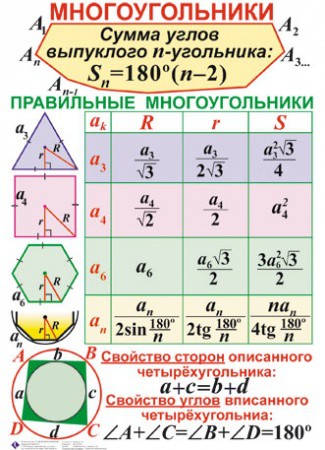
Где S = сумма внутренних углов и n = количество конгруэнтных сторон правильного многоугольника, формула:
Вот восьмиугольник (восемь сторон, восемь внутренних углов). Сначала воспользуемся формулой для нахождения суммы внутренних углов:
S = (n — 2) × 180°
S = (8 — 2) × 180°
S = 6 × 180°
S = 1080°
Затем разделите эту сумму на количество сторон:
- мера каждого внутреннего угла = Sn
- мера каждого внутреннего угла = 1080°8
- мера каждого внутреннего угла = = 135°
Каждый внутренний угол правильного восьмиугольника равен 135°.
Определение количества сторон многоугольника
Вы можете использовать ту же формулу, S = (n — 2) × 180°, чтобы узнать, сколько сторон n имеет многоугольник, если вы знаете значение S, сумма внутренних углов.
Вы знаете, что сумма внутренних углов равна 900°, но понятия не имеете, что это за форма. Используйте то, что вы знаете в формуле, чтобы найти то, что вы не знаете:
Укажите формулу:
S = (n — 2) × 180°
Используйте то, что знаете, S = 900°
900°= (n — 2) × 180°
Разделите обе стороны на 180°
×900°- 180° 180 °) 180 °
Нет необходимости в скобках сейчас
5 = N-2
Добавить 2 к обеим сторонам
5+2 = N-2+2
7 = N
форма была семиугольником!
Итоги урока
Теперь вы умеете определять внутренние углы многоугольников, а также можете вспомнить и применить формулу S = (n — 2) × 180°, чтобы найти сумму внутренних углов многоугольника.