Модуль алгебра 9 класс часть 1 вариант 3 ответы – Карточки. ОГЭ. 9 класс. Модуль («Алгебра»)
Карточки. ОГЭ. 9 класс. Модуль («Алгебра»)
Задание №2.ОГЭ. 9класс
1 вариант
1.На координатной прямой изображены числа и . Какое из следующих неравенств неверно?
1)
2)
3)
4)
2. Какому из данных промежутков принадлежит число
1) [0,5;0,6]
2) [0,6;0,7]
3) [0,7;0,8]
4) [0,8;0,9]
3. На координатной прямой отмечено число Расположите в порядке убывания числа и
1) 2) 3) 4)
4. На координатной прямой отмечено число a.
Из следующих утверждений выберите верное:
1) (a − 6)2 > 1
2) (a − 7)2 > 1
3) a2 > 36
4) a2 > 49
2 вариант
1. Какое из следующих неравенств не следует из неравенства ?
1)
2)
3)
4)
2. На координатной прямой отмечено число Расположите в порядке убывания числа и
1) 2) 3)
4)
3.Одна из точек, отмеченных на координатной прямой, соответствует числу Какая это точка?
1) A
2) B
3) C
4) D
4.На координатной прямой отмечены числа p, q и r.
Какая из разностей p − r, p − q, r − q отрицательна?
1) p − r
2) p − q
3) r − q
4) ни одна из них
infourok.ru
ОГЭ по математике 9 класс 2018. Вариант 3 с решением
ОГЭ по математике 9 класс 2018 года под редакцией И. В. Ященко – Вариант №3
При написании данной работы “ОГЭ по математике 2018. Вариант 3” было использовано пособие “ОГЭ 2018. Математика. 14 вариантов. Типовые тестовые задания от разработчиков ОГЭ / И. Р. Высоцкий, Л. О. Рослова, Л. В. Кузнецова, В. А. Смирнов, А. В. Хачатурян, С. А. Шестаков, Р. К. Гордин, А. С. Трепалин, А. В. Семенов, П. И. Захаров; под редакцией И. В. Ященко. – М.: Издательство “Экзамен”, МЦНМО, 2018″.
Часть 1
Модуль “Алгебра”
- Найдите значение выражения -0,7 ∙ (-10)4-8 ∙ (-10)2-26
Показать решение
Выполняем действия в следующем порядке: возводим в степени, затем выполняем действия с умножением и в последнюю очередь с вычитанием:
-0,7 ∙ (-10)4-8 ∙ (-10)2-26 = -0,7 ∙ 10000-8 ∙ 100-26 = -7000-800-26 = -7826
Ответ:
-7826
- В таблице приведены нормативы по бегу на 30 метров для учащихся 9 класса.
| Мальчики | Девочки | |||||
| Отметка | “5” | “4” | “3” | “5” | “4” | |
| Время (в секундах) | 4,6 | 4,9 | 5,3 | 5,0 | 5,5 | 5,9 |
Какую отметку получит девочка, пробежавшая 30 метров за 5,35 секунды?
- Отметка “5”
- Отметка “4”
- Отметка “3”
- норматив не выполнен
Показать решение
Итак, сравним значение 5,35 секунды с нормативами в таблице. Получаем 5,0 < 5,35 < 5,5 . Т.е девочка получит отметку “4” поскольку уложилась в положенный норматив 5,5 секунд.
Ответ:
Отметка “4” – 2
- Одно из чисел 58/13, 69/13, 76/13, 83/13 отмечено на прямой точкой.
Какое это число?
- 58/13
- 69/13
- 76/13
- 83/13
Показать решение
Решение:
Для начала переведем представленные дроби в десятичные дроби:
58/13 = ~4,46
69/13 = ~5,31
76/13 = ~5,85
83/13 = ~6,38
Между цифрами 5 и 6 на прямой лежат два значения 5,31 и 5,85. Точка, изображенная на прямой, находится ближе к значению 6, значит искома цифра 5,85 – ответ 3.
Ответ:
3.
- Найдите значение выражения
Показать решение
Для начала откроем скобки – перед нами сумма квдратов: (a + b)2 = a2 + 2ab + b2
Корень числа 40 необходимо возвести в квадрат, что дает в результате: 40
Ответ:
56
- При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси – напряжение в вольтах. Определите по графику, на сколько вольт упадёт напряжение за первые 60 часов работы фонарика.
Показать решение
Найдем на графике линию соответствующую 60 часам работы фонарика. Далее определим место её пересечения с кривой зависимости напряжения в цепи от времени работы фонарика. На графике прекрасно видно это место пересечения. Проведем от точки пересечения вниз прямую до шкалы напряжения. Искомая величина 0,6 километров.
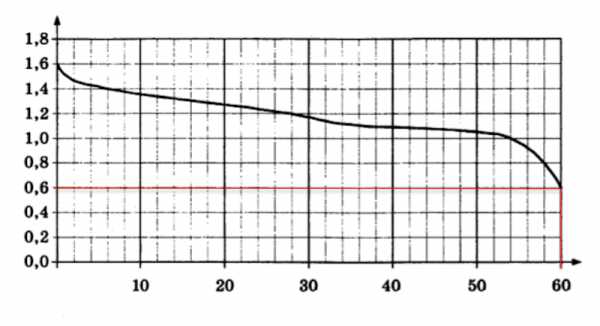
Итак, на начальном этапе заряд батарейки составлял = 1,6 вольт (нулевое значение на графике)
1,6 – 0,6 = 1 (в) – на сколько вольт упал заряд батарейки
Ответ:
1
- Найдите корень уравнения x + x/2 = 12
Показать решение
Для решения данного уравнения умножим все его части на 2, чтобы избавиться от дроби
Выполним проверку:
8 + 8 / 2 = 12
8 + 4 = 12
12 = 12
верно
Ответ
8
- Средний вес мальчиков того же возраста, что и Коля, равен 69 кг. Вес Коли составляет 150% среднего веса. Сколько килограммов весит Коля?
Показать решение
69 кг = 100%
Вес Коли = x = 150%
x = 69 / 100 * 150 = 103,5 (кг) – вес Коли
Ответ
103,5
- Какая из следующих круговых диаграмм показывает распределение грибов в лесу, если белых грибов примерно 22%, мухоморов – примерно 33%, лисичек – примерно 9%, сыроежек – примерно 28% и других грибов – примерно 8%?
В ответе запишите номер выбранного варианта ответа.
Показать решение
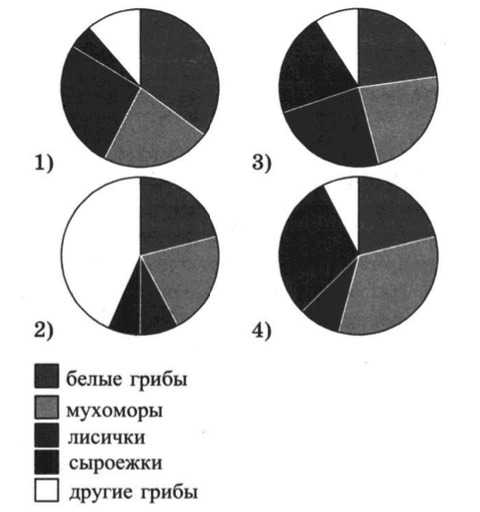
Для начала представим грибы в виде списка по убыванию их распространения:
- мухоморов – примерно 33%
- сыроежек – примерно 28%
- белых грибов примерно 22%
- лисичек – примерно 9%
- других грибов – примерно 8%
Самое малое распространение имеют другие грибы, поэтому круговые диаграммы (2) и (1), на которых они представлены белым цветом, мы не рассматриваем.
Самое большое распространение имеют мухоморы, чему соответсвует круговая диаграмма (4) – сектор закрашенный серым цветом. Значит ответ 4-ая круговая диаграмма.
Ответ
4
- В фирме такси в данный момент свободно 10 машин: 1 чёрная, 1 жёлтая и 8 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
Показать решение
Решение данной задачи основано на классической формуле определения вероятности:
где, m – число благоприятных исходов события, а n – общее количество исходов
Получаем
Ответ
0,1
- На рисунках изображены графики функций вида y = kx + b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ
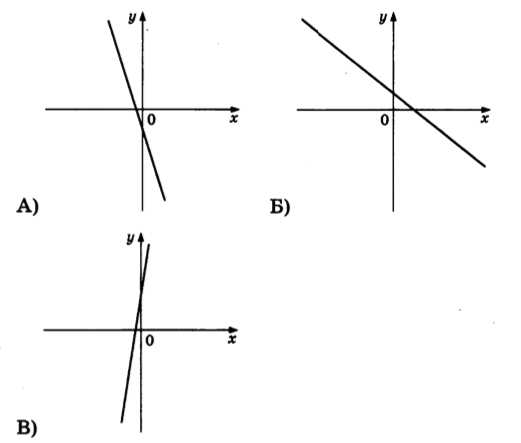
КОЭФФИЦИЕНТЫ
- k < 0, b > 0
- k < 0, b < 0
- k > 0, b > 0
Показать решение
Рассмотрим влияние коэффициента k на результат предложенной нам функции.
- На первом графике показано убывание функции (смотрим слева на право), т.е. функция расположена во второй и четвертой четвертях. Такое поведение функции характерно при значении k < 0.
- На втором графике также показано убывание функции (смотрим слева на право), т.е. функция расположена во второй и четвертой четвертях. Такое поведение функции характерно при значении k < 0.
- На третьем графике показано возрастание функции (смотрим слева на право), т.е. функция расположена в первой и третьей четвертях. Такое поведение функции характерно при значении k > 0.
Теперь рассмотрим постоянную b, представленную в функции y = kx + b. По сути это координата “y” точки пересечения представленной функции и оси “y”. Чтобы определить значение b подставим в функцию значение x = 0, получим:
y = kx + b
y = k * 0 + b
y = b
Как видим из результата, точка b имеет положительное значение. Рассмотрим каждый график:
- на первом графике точка пересечения функции с осью “y” имеет отрицательное значение, значит она соответсвует условию b < 0
- на втором графике точка пересечения функции с осью “y” имеет положительное значение, значит она соответсвует условию b > 0
- на третьем графике точка пересечения функции с осью “y” также имеет положительное значение, значит она соответсвует условию b > 0
Объединив результаты, мы получим следующее:
- первый график соответсвует условию (2) k < 0, b < 0
- второй график соответсвует условию (1) k < 0, b > 0
- третий график соответсвует условию (3) k > 0, b > 0
Ответ
213
- Геометрическая прогрессия (bn) задана условиями:
Найдите b6.
Показать решение
Для решения мы будем использовать формулу:
Для начала найдем значение b2, это поможет нам найти значение q
Теперь находим чему равен q
Ответ
-567
- Найдите значение выражения
при
Показать решение
Для начала необходимо упростить предложенное выражение. Для этого изменим знаменатель первой дроби и найдем значение разности в скобках (не забываем приводить дроби к единому знаменателю).
Знаменатель первой дроби и числитель второй дроби сокращаем
Подставляем значения a и b
Ответ
36
- Площадь четырёхугольника можно вычислить по формуле
где d1 и d2 – длины диагоналей четырёхугольника, a – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d2, если
Показать решение
Помните правило, если у нас трёх-этажная дробь, то нижнее значение переносится наверх
Ответ
17
- Укажите решение неравенства
-3 – x > 4x + 7
Показать решение
Для решения данного неравенства необходимо сделать следующее:
а) перенесём член 4х в левую часть неравенства, а -3 – в правую часть, не забыв поменять знаки на противоположные. Получим:
б) Умножим обе части неравенства на отрицательное число -1 и заменим знак неравенства на противоположный.
в) найдём значение х
г) множеством решений данного неравенства будет числовой промежуток от -∞ до -2, что соответсвует ответу 2
Ответ
2
Модуль “Геометрия”
- Две сосны растут на расстоянии 30 м одна от другой. Высота одной сосны 26 м, а другой – 10м. Найдите расстояние (в метрах) между их верхушками.
Показать решение
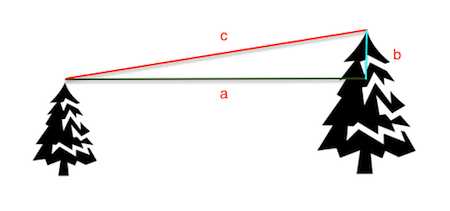
На рисунке мы изобразили две сосны. Расстояние между ними – а = 30 м; разницу в высоте мы обозначили, как b; ну и расстояние между верхушками – это c.
Как видите, у нас получился обычный прямоугольный треугольник состоящий из гипотенузы (c) и двух катетов (a и b). Для нахождения длины гипотенузы воспользуемся теоремой Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов c2 = a2 + b2
отюда
b = 26 – 10 = 16 (м)
a = 30 (м)
Итак, расстояние между верхушками сосен 34 метра
Ответ
34
- В треугольнике ABC известно, что AB = 5, BC = 6, AC = 4. Найдите cos∠ABC
Показать решение
Для решения данной задачи необходимо воспользоваться теоремой косинусов. Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
a2 = b2 + c2 – 2bc cosα
АС² = АВ² + ВС² – 2·АВ·ВС·cos∠ABC
4² = 5² + 6² – 2·5·6·cos∠ABC
16 = 25 + 36 – 60·cos∠ABC
60·cos∠ABC = 25 + 36 – 16
60·cos∠ABC = 45
cos∠ABC = 45 / 60 = 3/4 = 0,75
Ответ
cos∠ABC = 0,75
- На окружности с центром в точке О отмечены точки A и B так, что ∠AOB = 18о. Длина меньшей дуги AB равна 5. Найдите длину большей дуги AB.
Показать решение
Известно, что круг составляет 360о. Исходя из этого, 18о составляет:
360о / 18о = 20 – кол-во сегментов в круге по 18о
Итак, 18о составляют 1/20 часть всей окружности, значит оставшаяся часть круга:
т.е. оставшиеся 342о (360о – 18о = 342о) составляют 19-ю часть всей окружности
Если длина меньшей дуги AB равна 5, то длина большей дуги AB составит:
5 * 19 = 95
Ответ
95
- В трапеции ABCD известно, что AB = CD, ∠BDA = 18о и ∠BDC = 97о. Найдите угол ABD. Ответ дайте в градусах.
Показать решение
По условию задачи перед нами равнобедренная трапеция. Углы в основании равнобедренной трапеции (верхнем и нижним) равны.
∠ADC = 18 + 97 = 115°
∠DAB = ∠ADC = 115°
Теперь рассмотрим треугольник ABD в целом. Нам известно, что сумма углов треугольника равна 180 °. Отсюда:
∠ABD = 180 – ∠ADB – ∠DAB = 180 – 18 – 115 = 47°.
Ответ
47°
- На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.
Показать решение
Площадь треугольника равна произведению половины основания треугольника (a) на его высоту (h):
где,
a – длина основания треугольника
h – высота треугольника.
Из рисунка мы видим, что основание треугольника равно 6 (клеткам), а высота – 5 (клеткам). Исходя из чего получаем:
Ответ
15
- Какое из следующих утверждений верно?
- Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
- Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
- Средняя линия трапеции равна сумме её оснований.
В ответ запишите номер выбранного утверждения.
Показать решение
Данное задание не является задачей. Вопросы, перечисленные здесь необходимо знать наизусть и уметь на них отвечать.
- Это утверждение абсолютно верно по признаку подобия треугольников.
- Неверно, поскольку средняя линия трапеции равна полусумме её оснований.
- Неверно, поскольку сумма углов любого треугольника равна 180о.
Ответ
1
Часть 2
Модуль “Алгебра”
- Решите уравнение
Показать решение
Перенесем выражение √5-x с правой стороны в левую
Сократим оба выражения √5-x
Перенесём 18 в левую часть уравнения
Перед нами обычное квадратное уравнение.
Область допустимых значений в данном случае составляет: 5 – х ≥ 0 ⇒ x ≤ 5
Для решения уравнения, необходимо найти дискриминант:
D = b2 – 4ac
D = 9 + 72 = 81 = 92
х1 = (3 + 9)/2 = 12/2 = 6 – не является решением
х2 = (3 – 9)/2 = -6/2 = -3
х = -3
Ответ
-3
- Теплоход проходит по течению реки до пункта назначения 80 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 23 часа, а в пункт отправления теплоход возвращается через 35 часов после отплытия из него.
Показать решение
Пусть
х – это собственная скорость теплохода, тогда
х + 5 – скорость теплохода по течению
х – 5 – скорость теплохода против течения
35 – 23 = 12 (ч) – время движения теплохода из пункта отправления в пункт назначения и обратно без учета стоянки
80 * 2 = 160 (км) – общее расстояние, пройденное теплоходом
Исходя из выше сказанного получим уравнение:
приводим к общему знаменателю и решаем:
Для дальнейшего решения уравнения, необходимо найти дискриминант:
x=15
Собственная скорость теплохода составляет 15 км/ч
Ответ
15
- Постройте график функции
и определите, при каких значениях m прямая y = m имеет с графиком одну или две общие точки.
Показать решение
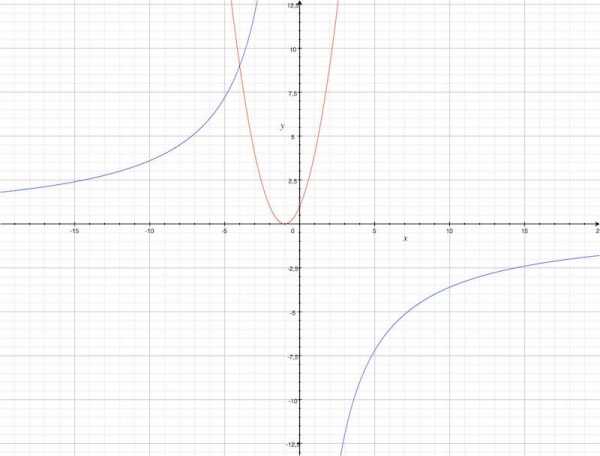
На рисунке выше изображены два графика, соответствующие представленным функциям:
y = x2 + 2x + 1 (график, изображенный красной линией)
y = -36/x (график, изображенный синий линией)
Рассмотрим обе функции:
- y=x2+2x+1 на промежутке [–4;+∞) – это квадратичная функция, графиком является парабола, а=1 > 0 – ветви направлены вверх. Если мы её сократим по формуле квадрата суммы двух чисел, то получим: у=(х+1)2 – сдвиг графика влево на 1 единицу, что и видно из графика.
- у=–36/х – это обратная пропорциональность, график гипербола, ветви расположены во 2 и 4 четвертях.
На графике хорошо видно, что прямая у=m имеет с графиком одну общую точку при m=0 и m > 9 и две общие точки при m=9, т.е. ответ: m=0 и m≥9, проверяем:
Одна общая точка в вершине параболы y = x2 + 2x + 1
x0 = -b/2a = -2/2 = -1
y0 = -12 + 2(-1) + 1 = 1 – 2 + 1 = 0 ⇒ с = 0
Две общие точки при х = – 4 ; у = 9 ⇒ с = 9
Ответ
0; [9;+∞)
- Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB = 18, а расстояние от центра окружности до хорд AB и CD равны соответсвенно 12 и 9.
Показать решение
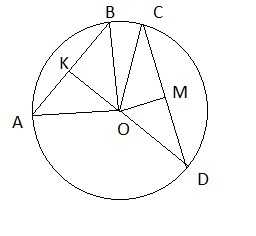 Треугольники ∆АОВ и ∆СОD являются равнобедренными.
Треугольники ∆АОВ и ∆СОD являются равнобедренными.
AK = BK = AB / 2 = 18 / 2 = 9
Отрезки ОК и ОМ являются высотами и медианами.
По теореме Пифагора: квадрат гипотенузы равен сумме квадратов катетов, имеем
OB2 = OK2 + BK2
OB2 = 122 + 92 = 144 + 81 = 225
OB = 15
Учитывая, что OB – это радиус, имеем:
OB = OA = OC = OD = 15
Из треугольника ∆СОМ по теореме Пифагора получаем:
CM2 = OC2 – OM2
CM2 = 152 – 92 = 225 – 81 = 144
CM = 12
CD = CM * 2 = 12 * 2 = 24
Длина хорды CD равна 24.
Ответ
24
- В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке О (или любая другая буква). Докажите, что площади треугольников ∆AOB и ∆COD равны
Показать решение
Пусть AD – нижнее основание трапеции, а BC – верхнее, тогда AD>BC.
Найдем площади треугольников ∆ABD и ∆DCA:
S ∆ABD = 1/2 AD ∙ h2
S ∆DCA = 1/2 AD ∙ h3
Учитывая, что величина основания AD и высота обоих треугольников одинаковые, заключаем, что площади этих треугольников равны:
S ∆ABD = S ∆DCA
Каждый из треугольников ∆ABD и ∆DCA состоят из двух других треугольников:
S ∆ABO + S ∆AOD = S ∆ABD (сумма площадей внутренних треугольников S ∆ABO и S ∆AOD равна площади треугольника S ∆ABD)
S ∆DCO + S ∆AOD = S ∆DCA (сумма площадей внутренних треугольников S ∆DCO и S ∆AOD равна площади треугольника S ∆DCA)
Если площади треугольников S ∆ABD и S ∆DCA равны, то и сумма площадей их внутренних треугольников также равны. Отсюда получаем,:
S ∆ABO + S ∆AOD = S ∆DCO + S ∆AOD
в данном равенстве с обеих сторон фигурирует один и тот же треугольник – S ∆AOD, что позволяет нам сократить его. Получаем следующее равенство:
S ∆ABO = S ∆DCO
Что и требовалось доказать.
Ответ
S ∆ABO = S ∆DCO
- На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD = 80, MD = 64, H – точка пересечения высот треугольника ABC. Найдите AH.
Показать решение
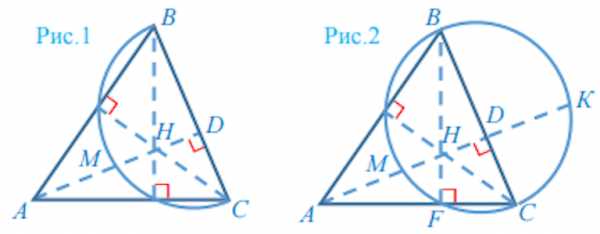
Для начала начертим треугольник и полуокружность, как сказано в условии задачи (рис.1).
Отметим точку пересечения окружности со стороной АС буквой F (рис.2)
BF – является высотой треугольника ∆ABC, так как для окружности ∠BFC – это вписанный угол, который опирается на дугу в 180° (BC – диаметр), следовательно:
∠BFC=180°/2=90°
Согласно теореме “о двух секущих”, имеем: AF * AC = AM * AK
Теперь рассмотрим хорду MK.
Отрезок BC – это перпендикуляр к отрезку MK, проходящий через центр окружности, следовательно BC – это серединный перпендикуляр.
Это значит, BC делит хорду MK пополам, т.е. MD = KD = 64 (см. условие задачи)
Рассмотрим треугольники ∆AHF и ∆ACD.
Угол ∠DAC для обоих треугольников является общим.
А углы ∠AFH и ∠ADC равны, кроме того – это прямые углы.
Следовательно, согласно первому признаку подобия треугольников, данные треугольники подобны.
Отсюда, по определению подобия, мы можем записать: AC / AH = AD / AF => AC * AF = AD * AH
Ранее мы рассматривали равенство (по теореме двух секущих) AF * AC = AM * AK, из которой получаем
AM * AK = AD * AH
AH = (AM * AK) / AD
Из рисунка находим:
AM = AD – MD = 80 – 64 = 16
AK = AD + KD = 80 + 64 =144
Отсюда:
AH = 16 * 144 / 80 = 2304 / 80 = 28,8
Ответ: AH = 28,8
Ответ
28,8
xoge.ru
Итоговый тест по алгебре за курс 9 класса
Информация об итоговом тесте по алгебре за курс 9 класса
Общее время написания работы 45 минут
Работа состоит из двух частей: первая часть содержит 6 заданий с выбором правильного ответа, вторая – одно задание, решение которого необходимо правильно оформить.
1-6 задания по 0,5 баллов, итого 3 балла
7 задание – 2 балла, при условии, что найдены оба неизвестных
Желаю успеха!
Итоговый тест по алгебре 9 класс
Вариант 1
Дана выборка 1, 7, 5, 7, 3, 7, 1, 8, 3. Какое из чисел является модой этой выборки?
А) 3 Б) 7 В) 5 Г) 8
Найдите знаменатель геометрической прогрессии , если 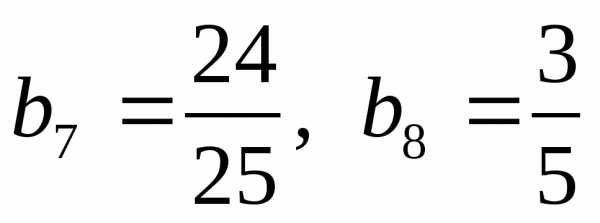
А) 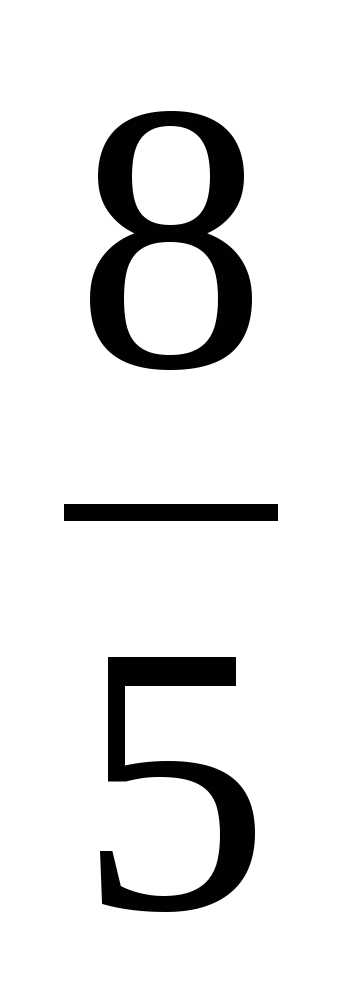 Б)
Б) 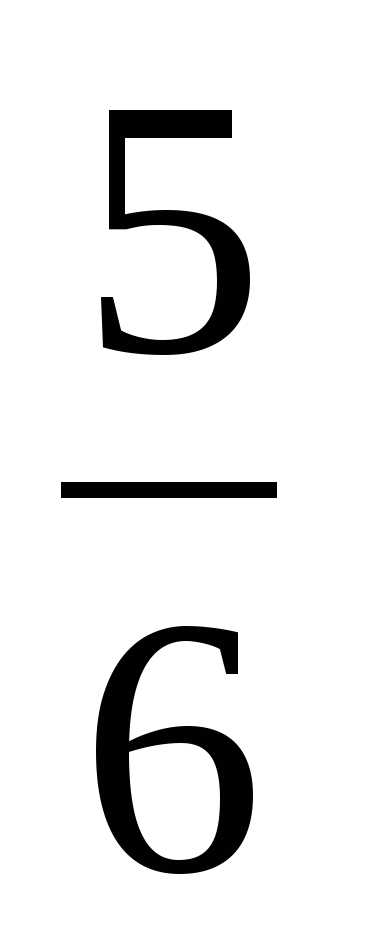 В)
В) 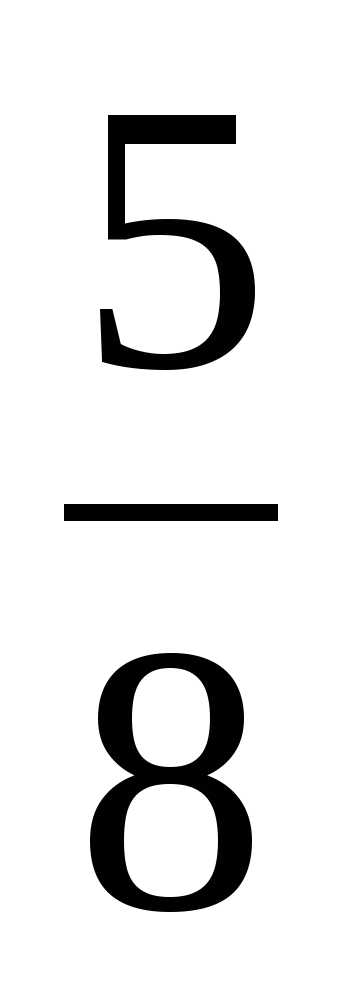 Г)
Г) 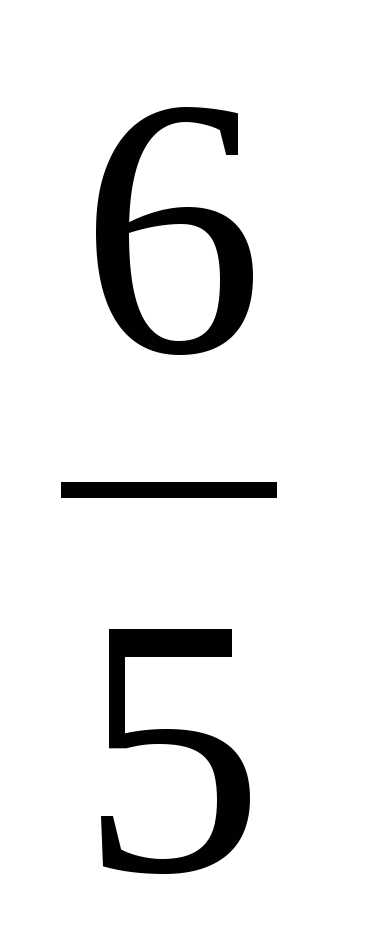
Какой числовой промежуток является решением неравенства
А)  Б)
Б)  В)
В) 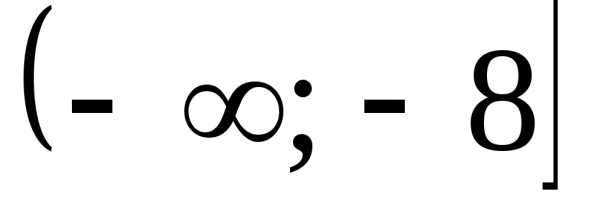 Г)
Г) 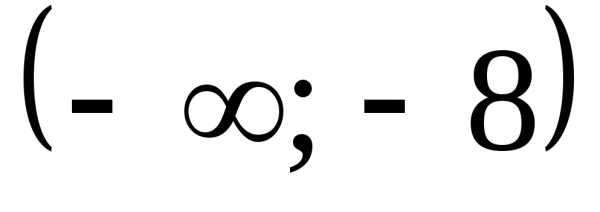
Графиком какой из приведенных функций является парабола?
А) 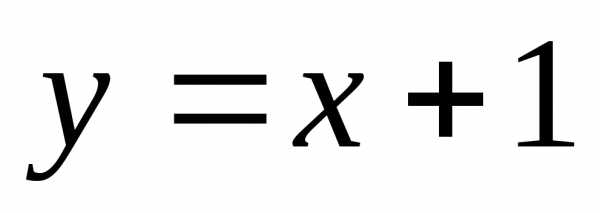 Б)
Б) 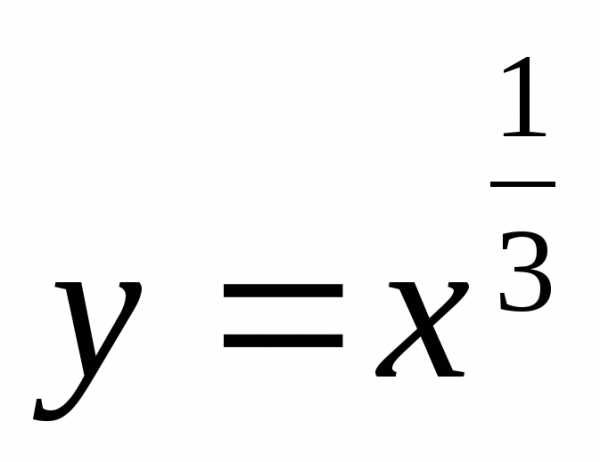 В)
В) 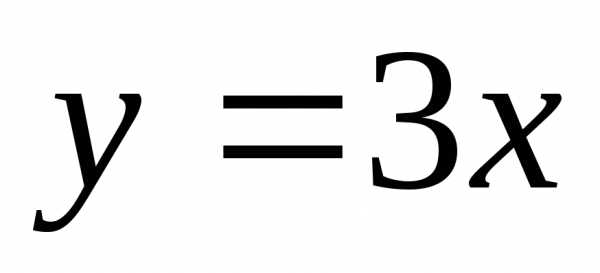 Г)
Г) 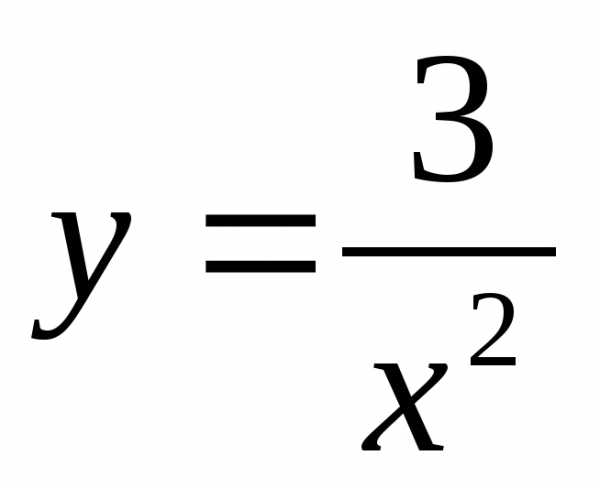
Решите систему неравенств 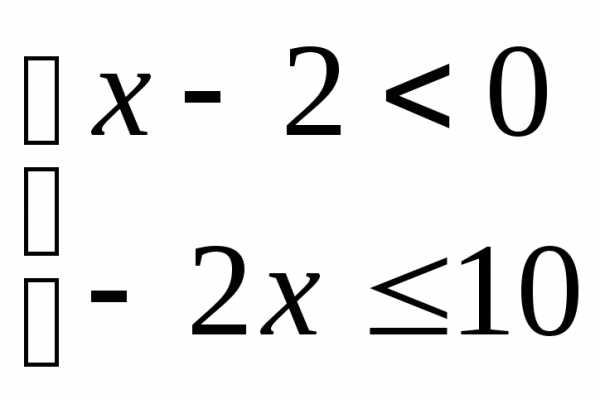
А) Б) 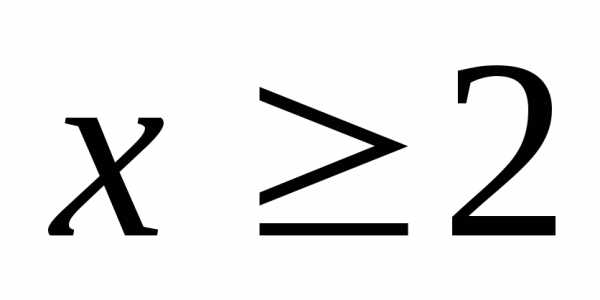 В) Г)
В) Г) 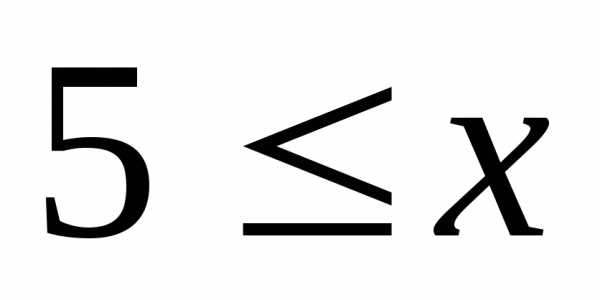
Первый член арифметической прогрессии равен 17, а разность -2. Чему равен пятнадцатый член этой прогрессии?
А) 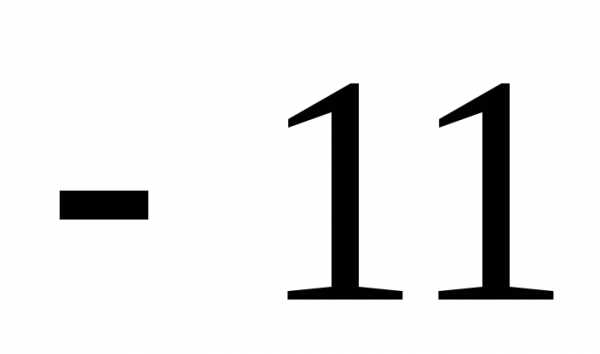 Б)
Б) 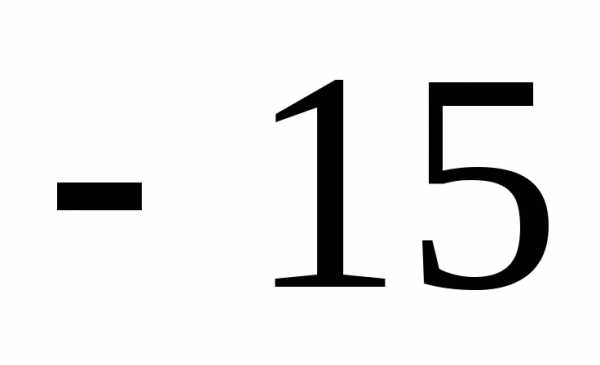 В)
В) 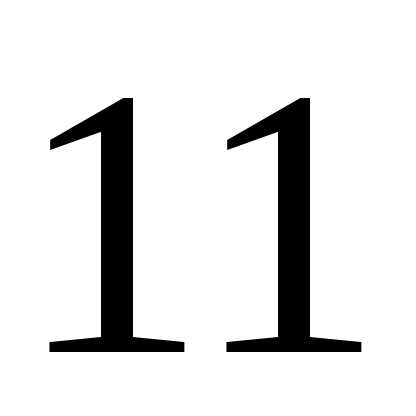 Г)
Г) 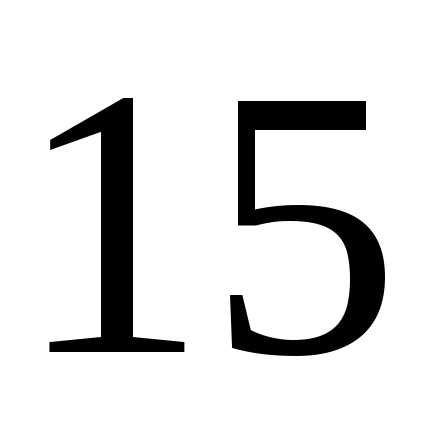
Найдите первый член и знаменатель геометрической прогрессии , если
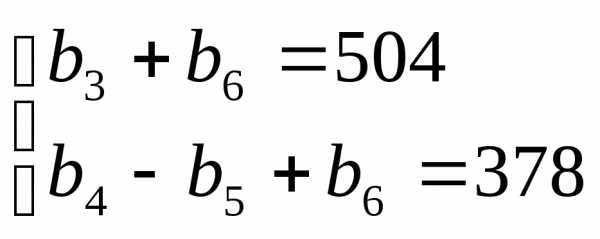
Итоговый тест по алгебре 9 класс
Вариант 2
Дана выборка 7, 4, 5, 7, 4, 7, 5, 7, 3, 3, 2, 1. Какое из чисел является модой этой выборки?
А) 16 Б) 7 В) 4 Г) 3
Найдите знаменатель геометрической прогрессии , если
А) Б) В) Г)
Какой числовой промежуток является решением неравенства
А) 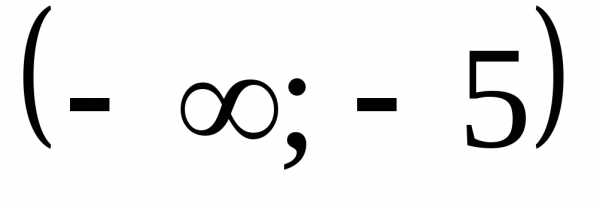 Б)
Б)  В)
В) 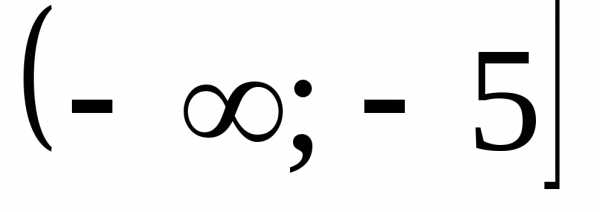 Г)
Г) 
Графиком какой из приведенных функций является парабола?
А) 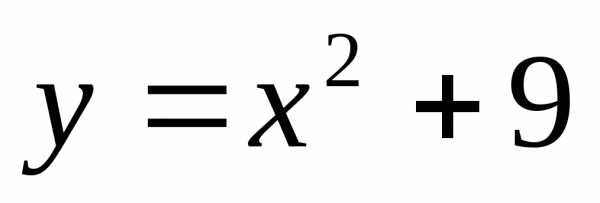 Б) В)
Б) В) 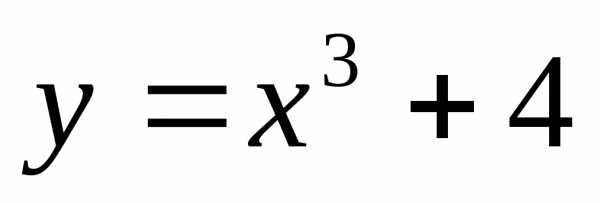 Г)
Г)
Решите систему неравенств 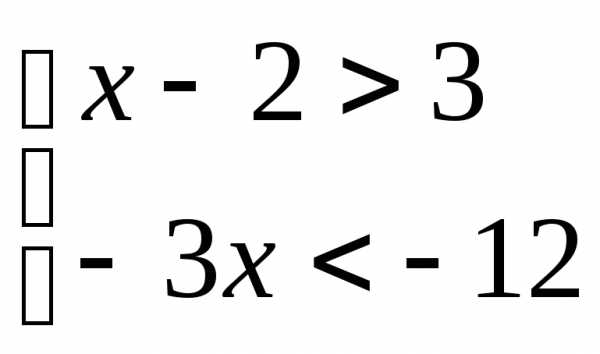
А) 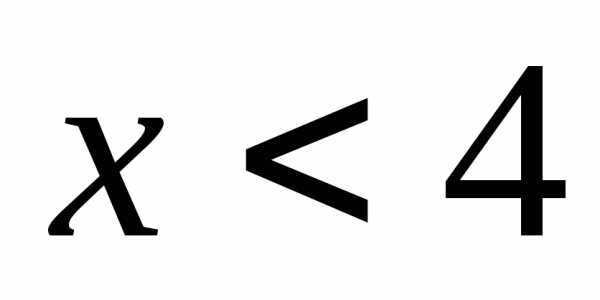 Б)
Б) 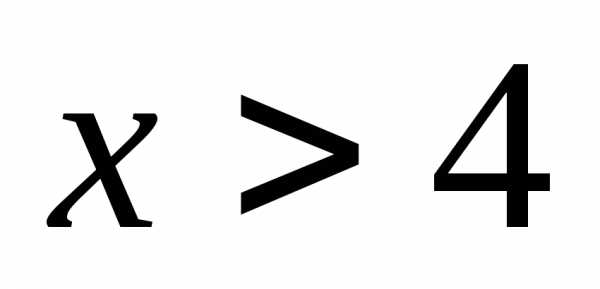 В)
В) 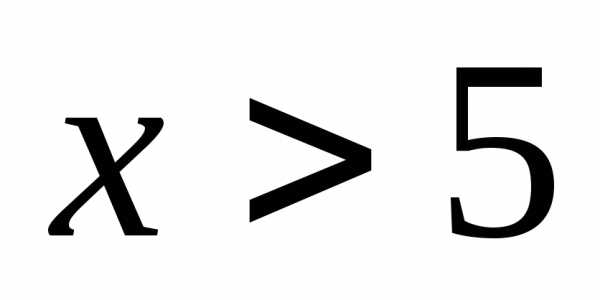 Г)
Г) 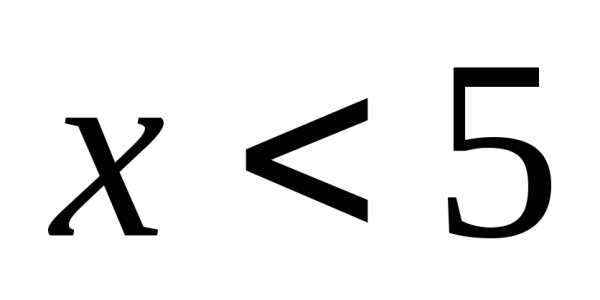
Первый член арифметической прогрессии равен 7, а разность -1. Чему равен десятый член этой прогрессии?
А) Б) 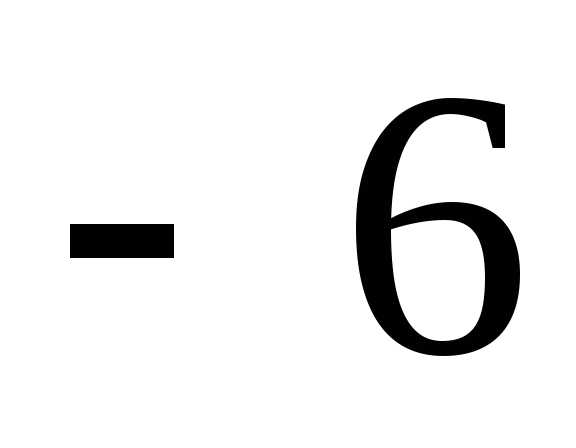 В)
В)  Г)
Г)
Найдите первый член и знаменатель геометрической прогрессии , если
Итоговый тест по алгебре 9 класс
Вариант 3
Дана выборка 2, 7, 7, 6, 2, 5, 2, 1, 3, 2, 4. Какое из чисел является модой этой выборки?
А) 14 Б) 5 В) 7 Г) 2
Найдите знаменатель геометрической прогрессии , если
А) Б) 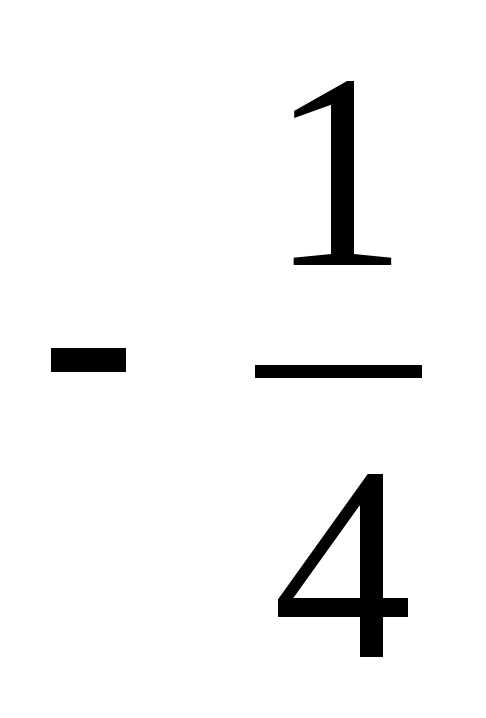 В)
В) 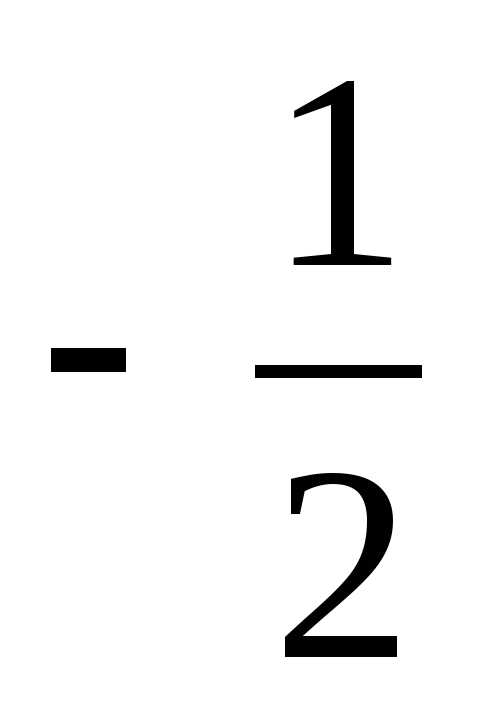 Г)
Г) 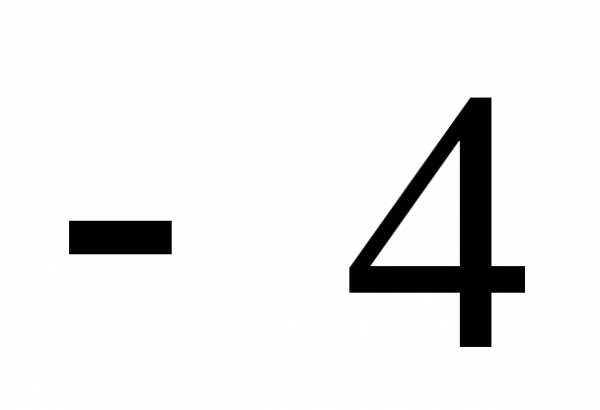
Какой числовой промежуток является решением неравенства
А) 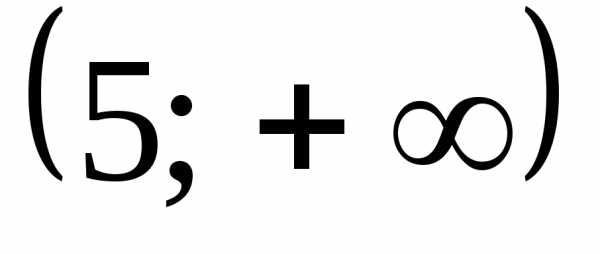 Б)
Б) 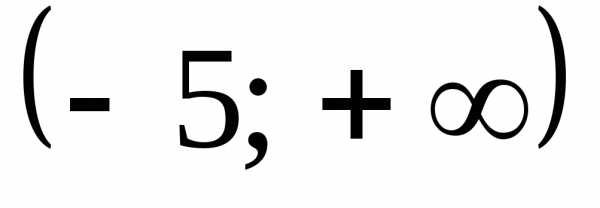 В)
В) 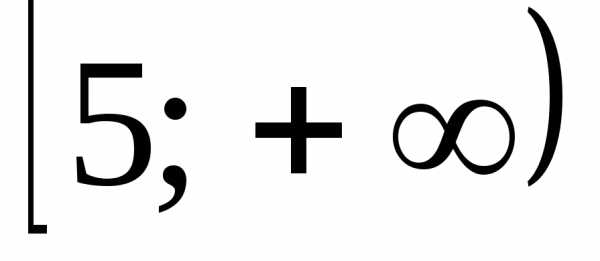 Г)
Г) 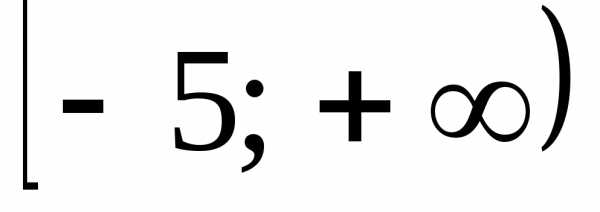
Графиком какой из приведенных функций является парабола?
А) Б) 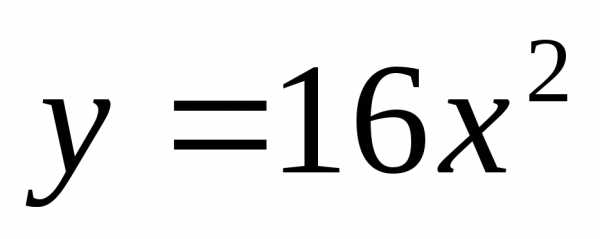 В) Г)
В) Г) 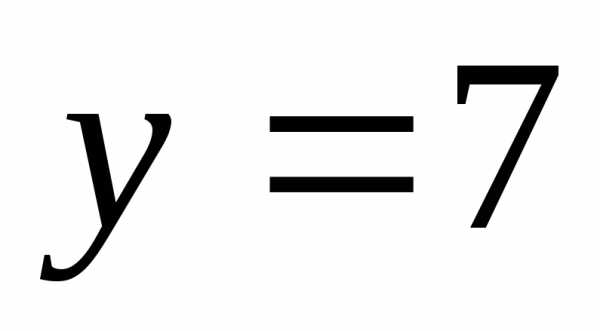
Решите систему неравенств 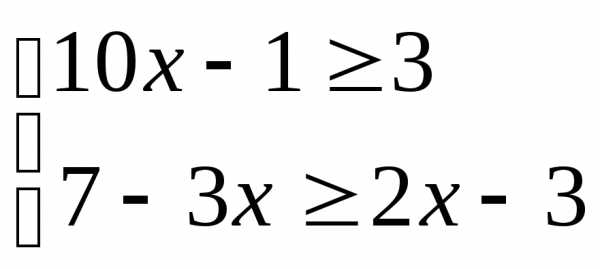
А) 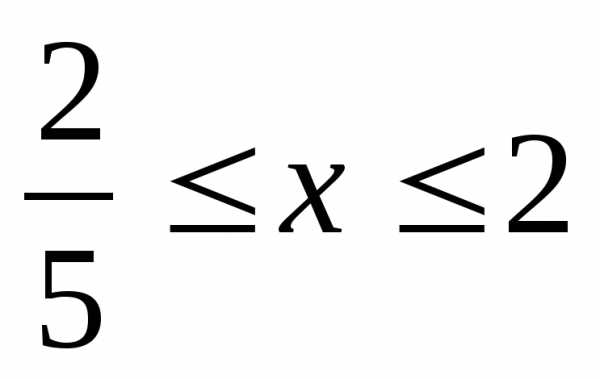 Б)
Б) 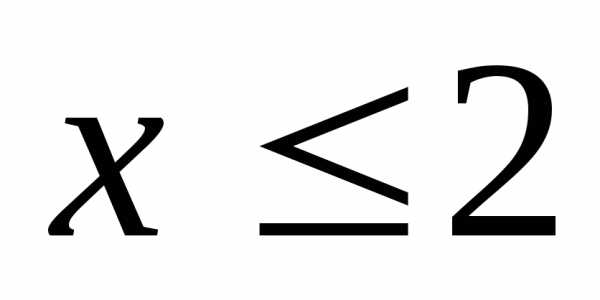 В)
В) 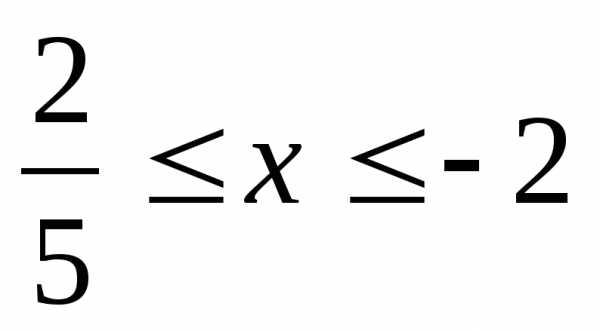 Г)
Г) 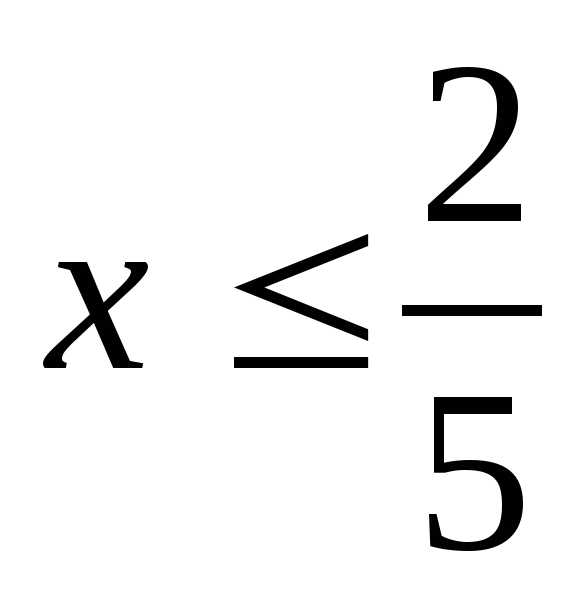
Первый член арифметической прогрессии равен 4, а разность 0,4. Чему равен одиннадцатый член этой прогрессии?
А) Б) 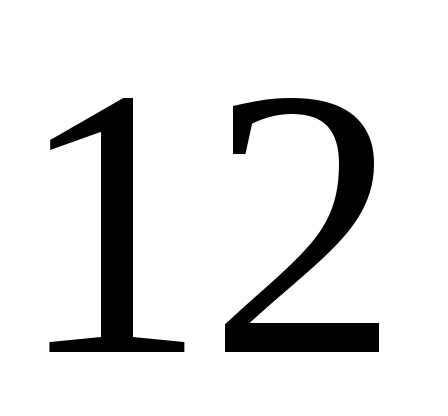 В)
В)  Г)
Г) 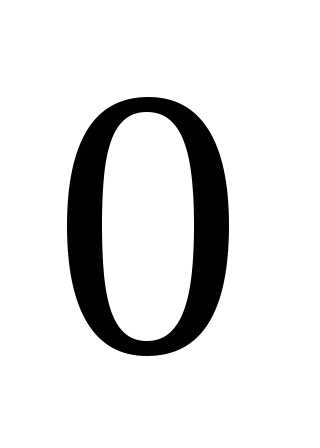
Найдите первый член и знаменатель геометрической прогрессии , если
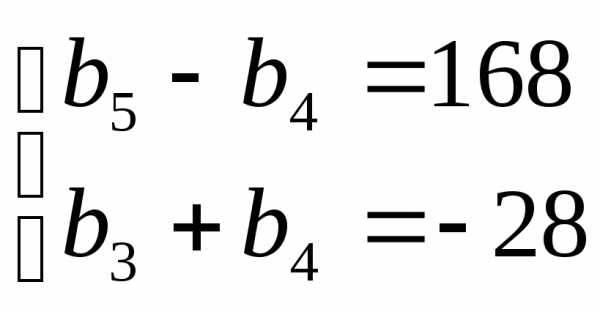
Итоговый тест по алгебре 9 класс
Вариант 4
Дана выборка 7, 4, 2, 6, 4, 4, 1, 3, 5, 4. Какое из чисел является модой этой выборки?
А) 8 Б) 4 В) 1 Г) 5
Найдите знаменатель геометрической прогрессии , если
А) Б) В) Г)
Какой числовой промежуток является решением неравенства
А)  Б)
Б) 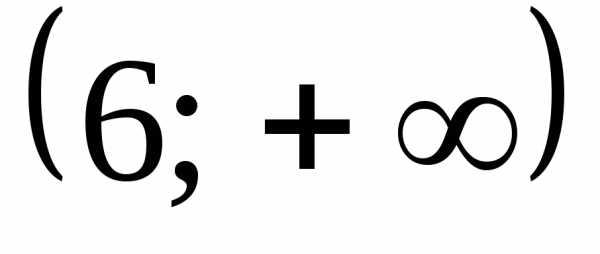 В)
В)  Г)
Г) 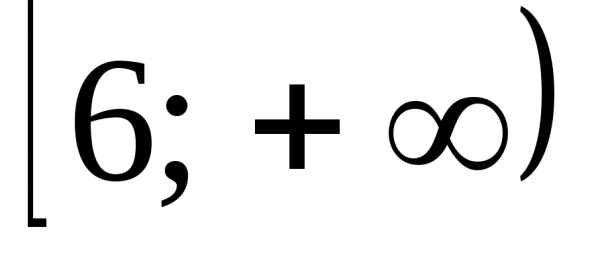
Графиком какой из приведенных функций является парабола?
А) 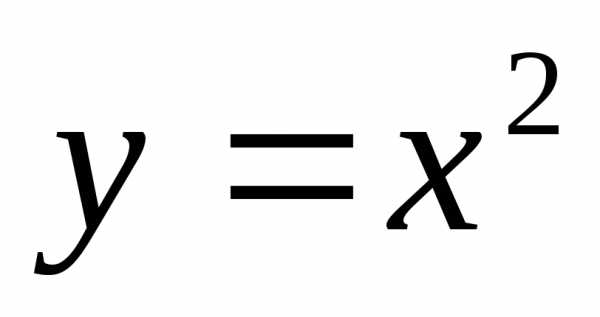 Б)
Б) 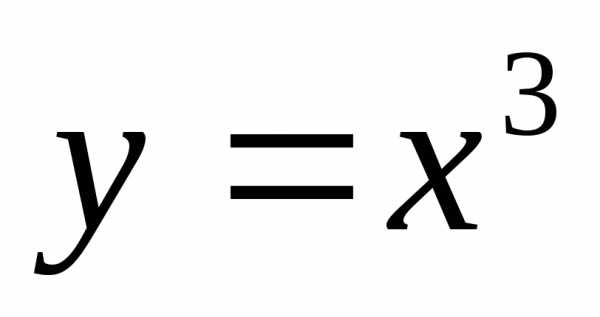 В)
В) 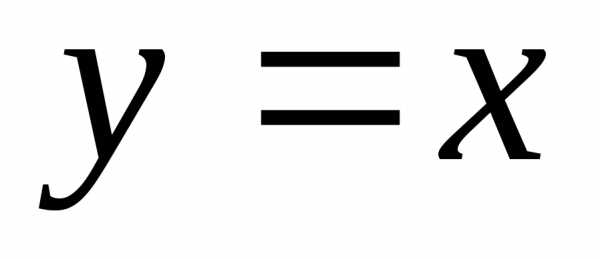 Г)
Г) 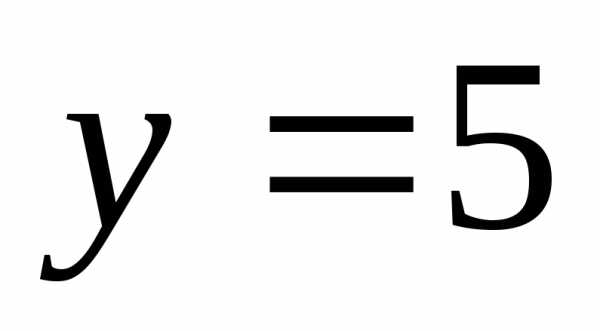
Решите систему неравенств 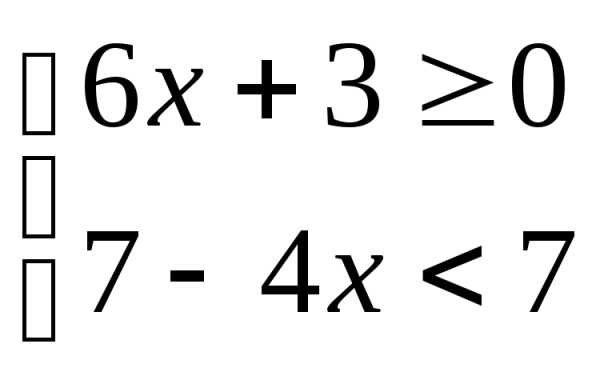
А) 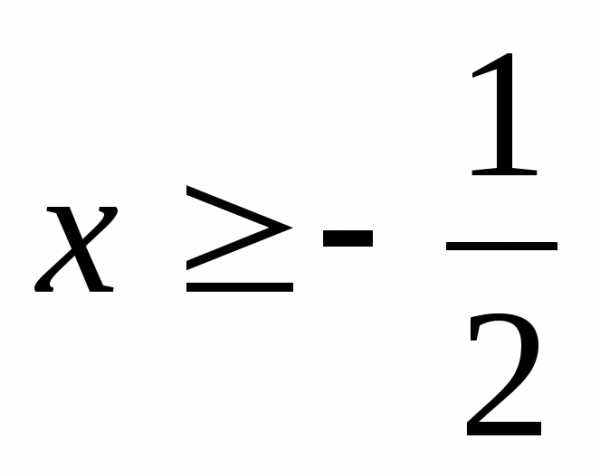 Б)
Б) 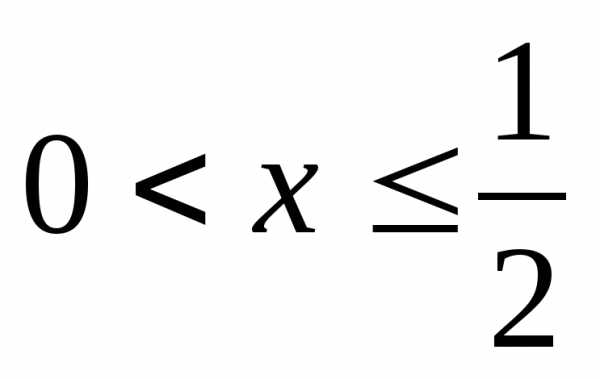 В)
В) 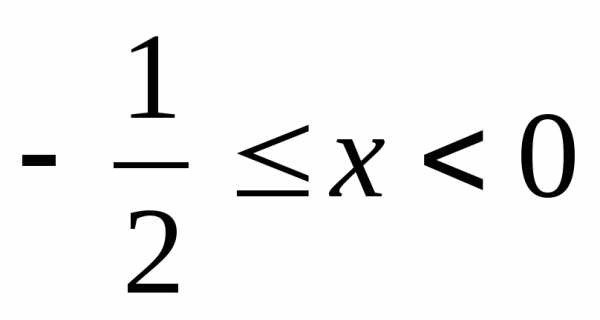 Г)
Г) 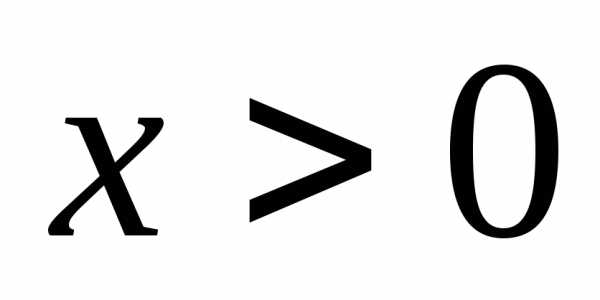
Первый член арифметической прогрессии равен 6, а разность -3. Чему равен пятый член этой прогрессии?
А) 3 Б) 6 В) -6 Г) -3
Найдите первый член и знаменатель геометрической прогрессии , если
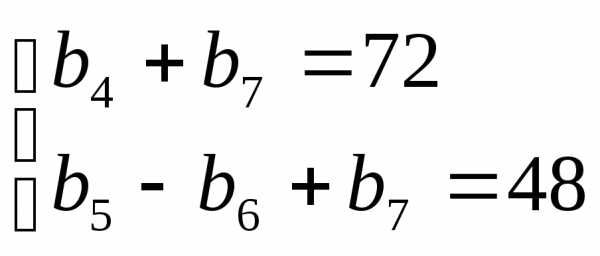
xn--j1ahfl.xn--p1ai
Материал для подготовки к ЕГЭ (ГИА) по математике (9 класс) на тему: Пробный ОГЭ по математике № 1. 9 кл. Вариант 1. Вариант 2. Вариант 3.
Пробный ОГЭ № 1. 9 кл.
Вариант 1
Часть 1
Модуль «Алгебра»
1. Найдите значение выражения .
Ответ: ____________________.
2. В таблице приведены нормативы по бегу на 30м для учащихся 9
класса. Оцените результат девочки, пробежавшей эту дистанцию
за 5,69с.
Мальчики | Девочки | |||||
Оценка | «5» | «4» | «3» | «5» | «4» | «3» |
Время, секунды | 4,6 | 4,9 | 5,3 | 5,0 | 5,6 | 5,9 |
1) отметка «5» 3) отметка «3»
2) отметка «4» 4) норматив не выполнен
Ответ: ____________________.
3. Между какими числами заключено число ?
1) 8 и 9 2) 39 и 40 3) 68 и 70 4) 6 и 7
Ответ: ____________________.
4. Какое из данных ниже выражений при любых n равно произведению
?
1) 2) 3) 4)
Ответ: ____________________.
5. На графике изображена зависимость атмосферного давления от высоты над уровнем моря. По горизонтали указана высота над уровнем моря в километрах, по вертикали – атмосферное давление в миллиметрах ртутного столба. На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 220 миллиметров ртутного столба?
Ответ: ____________________.
6. Квадратный трёхчлен разложен на множители:
х2 + 8х + 12 = (х + 2)(х – а). Найдите а.
Ответ: ____________________.
7. Средний вес мальчиков того же возраста, что и Вова, равен 32кг. Вес Вовы составляет 125% среднего веса. Сколько килограммов весит Вова?
Ответ: ____________________.
8. На диаграмме представлены семь крупнейших по площади территории (в млн км2) стран мира.
Какие из следующих утверждений верны?
1) Алжир входит в семёрку крупнейших по площади территорий стран мира.
2) Площадь территории Бразилии составляет 8,5 млн км2.
3) Площадь территории США больше площади территории Канады.
4) Площадь территории Австралии больше площади территории Индии на 4,4 млн км2.
В ответе запишите номера выбранных утверждений.
Ответ: ____________________.
9. На экзамене 25 билетов, Надя не выучила 5 из них. Найдите вероятность того, что ей попадётся выученный билет.
Ответ: ____________________.
10. Установите соответствие между графиками функций и формулами, которые их задают.
Графики
А) Б) В)
Формулы
1) 2) 3)
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
11. Геометрическая прогрессия (bn) задана условиями:
b1 = – 1, bn+1 = –4bn. Найдите сумму первых шести её членов.
Ответ: ____________________.
12. Найдите значение выражения
при a = – 2,7.
Ответ: ____________________.
13. Центростремительное ускорение при движении по окружности ( в м/с2) можно вычислить по формуле , где – угловая скорость (в с-1), а R – радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 6с-1, а центростреми-тельное ускорение равно 72м/с2.
Ответ: ____________________.
14. Укажите множество решений системы неравенств
Ответ: ____________________.
Модуль «Геометрия»
15. Наклонная крыша установлена на трёх вертикальных опорах, основания которых расположены на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 2,2м, высота большой опоры 2,7м. Найдите высоту средней опоры. Ответ дайте в метрах.
Ответ: ____________________.
16. Катеты прямоугольного треугольника равны 20 и 15. Найдите гипотенузу этого треугольника.
Ответ: ____________________.
17. Найдите площадь квадрата, описанного
около окружности радиуса 32.
Ответ: ____________________.
18. Найдите величину острого угла параллелог-
рамма ABCD, если биссектриса угла А образует
со стороной ВС угол, равный 160.
Ответ дайте в градусах.
Ответ: ____________________.
19. На клетчатой бумаге с размером клетки
изображён параллелограмм.
Найдите его площадь.
Ответ: ____________________.
20. Какие из следующих утверждений верны?
1) Один из углов треугольника всегда не превышает 60 градусов.
2) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
3) Две прямые, параллельные третьей прямой, перпендикулярны друг другу.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ____________________.
Часть 2
Модуль «Алгебра»
21. Решите уравнение .
22. Игорь и паша красят забор за 18 часов. Паша и Володя красят этот же забор за 21 час, а Володя и Игорь – за 28 часов. За сколько минут мальчики покрасят забор, работая втроём?
23. Постройте график функции и определите, при каких значениях m прямая y = m не имеет с графиком ни одной общей точки.
Модуль «Геометрия»
24. Отрезки АВ и СD являются хордами окружности. Найдите длину хорды СD, если АВ = 16, а расстояние от центра окружности до хорд АВ и СD равны соответственно 15 и 8.
25. Основания ВС и АD трапеции АВСD равны соответственно 6 и 24, ВD = 12. Докажите, что треугольники СВD и ВDА подобны.
26. В треугольнике АВС известны длины сторон АВ = 84, АС = 98, точка О – центр окружности, описанной около треугольника АВС. Прямая ВD, перпендикулярная прямой АО, пересекает сторону АС в точке D. Найдите СD.
Вариант 1
Ответы:
1) 2; 2) 3; 3) 1; 4) 2; 5) 9; 6) –6; 7) 40; 8) 24; 9) 0,8; 10) 312;
11) 819; 12) – 0,27; 13) 2; 14) 3; 15) 2,45; 16) 25; 17) 4096;
18) 32; 19) 12; 20) 12.
Вариант 2
Ответы:
1) 3; 2) 2; 3) 4; 4) 1; 5) 6; 6) –4; 7) 35; 8) 13; 9) 0,8; 10) 231;
11) – 547; 12) – 0,56; 13) 3; 14) 1; 15) 2,65; 16) 17; 17) 2304;
18) 38; 19) 12; 20) 23.
Вариант 3
Ответы:
1) 4; 2) 1; 3) 2; 4) 3; 5) 1; 6) –12; 7) 24; 8) 14; 9) 0,6; 10) 132;
11) – 521; 12) – 0,47; 13) 2; 14) 4; 15) 2,95; 16) 15; 17) 2704;
18) 46; 19) 12; 20) 13.
21 22 23 24 26
nsportal.ru
Дидактические материалы для подготовки к ОГЭ 9 класс, модуль «Алгебра. 2 часть»
Кусочно-непрерывные функции
1. Задание 23 № 75. Постройте график функции и определите, при каких значениях параметра прямая имеет с графиком ровно одну общую точку.
2. Задание 23 № 311559. Постройте график функции и найдите все значение , при которых прямая имеет с графиком данной функции ровно одну общую точку.
3. Задание 23 № 311565. Постройте график функции и найдите все значения , при которых прямая не имеет с графиком данной функции общих точек.
4. Задание 23 № 311583. Постройте график функции и определите, при каких значениях прямая имеет с графиком три общие точки.
5. Задание 23 № 311610. Постройте график функции и найдите значения , при которых прямая имеет с ним ровно две общие точки.
6. Задание 23 № 311619. Постройте график функции
и определите, при каких значениях прямая имеет с графиком ровно две общие точки.
7. Задание 23 № 311662. Постройте график функции и определите, при каких значениях прямая не будет иметь с построенным графиком ни одной общей точки.
8. Задание 23 № 311923. Постройте график функции и определите, при каких значениях параметра a он имеет ровно две общие точки с прямой y = a.
9. Задание 23 № 314700. Постройте график функции
и определите, при каких значениях прямая будет пересекать построенный график в трёх точках.
10. Задание 23 № 314702. Постройте график функции и определите, при каких значениях прямая имеет с графиком ровно три общие точки.
11. Задание 23 № 314758. Постройте график функции
и определите, при каких значениях прямая будет иметь с графиком единственную общую точку.
12. Задание 23 № 314777. Постройте график функции
и определите, при каких значениях прямая будет пересекать построенный график в трёх точках.
13. Задание 23 № 316269. Постройте график функции и найдите все значения при которых прямая имеет с графиком данной функции ровно одну общую точку.
14. Задание 23 № 316358. Постройте график функции и найдите все значения при которых он имеет ровно три общие точки с прямой
15. Задание 23 № 333024. Постройте график функции
и определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
16. Задание 23 № 338105. Постройте график функции и определите, при каких значениях прямая имеет с графиком ровно три общие точки.
17. Задание 23 № 338160. Постройте график функции и определите, при каких значениях прямая имеет с графиком ровно две общие точки.
18. Задание 23 № 338253. Постройте график функции и определите, при каких значениях прямая имеет с графиком ровно три общие точки.
19. Задание 23 № 338314. Постройте график функции и определите, при каких значениях прямая имеет с графиком ровно одну общую точку.
20. Задание 23 № 338420. Постройте график функции и определите, при каких значениях прямая не имеет с графиком ни одной общей точки.
21. Задание 23 № 338455. Постройте график функции Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
22. Задание 23 № 338465. Постройте график функции
и определите, при каких значениях прямая имеет с графиком одну или две общие точки.
23. Задание 23 № 340878. Постройте график функции
и определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
24. Задание 23 № 340904. Постройте график функции
и определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
25. Задание 23 № 341284. Постройте график функции и определите, при каких значениях m прямая y = m имеет с графиком ровно одну общую точку.
26. Задание 23 № 341342. Постройте график функции и определите, при каких значениях m прямая y = m не имеет с графиком ни одной общей точки.
1. Задание 23 № 75. Постройте график функции и определите, при каких значениях параметра прямая имеет с графиком ровно одну общую точку.
Решение.
График функции изображён на рисунке.
Прямая будет иметь с графиком единственную общую точку при
Ответ: (−1;0].
2. Задание 23 № 311559. Постройте график функции и найдите все значение , при которых прямая имеет с графиком данной функции ровно одну общую точку.
Решение.
Найдем область определения функции:
.
Поскольку , получаем, что на области определения функция принимает вид .
График изображён на рисунке.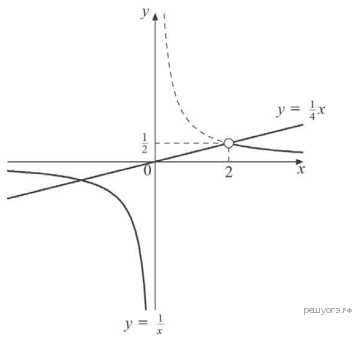
Прямая имеет с графиком данной функции ровно одну общую точку при .
Ответ: .
3. Задание 23 № 311565. Постройте график функции и найдите все значения , при которых прямая не имеет с графиком данной функции общих точек.
Решение.
Найдём область определения функции:
и .
Значит, функция определена при .
Поскольку , получаем, что на области определения функция принимает вид . График изображён на рисунке.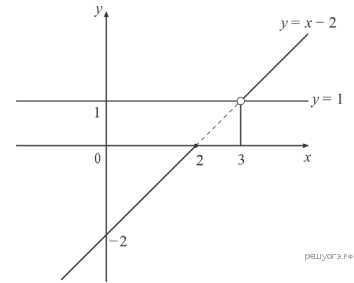 Прямая не имеет с графиком данной функции общих точек при .
Прямая не имеет с графиком данной функции общих точек при .
Ответ: .
4. Задание 23 № 311583. Постройте график функции и определите, при каких значениях прямая имеет с графиком три общие точки.
Решение.
Имеем:
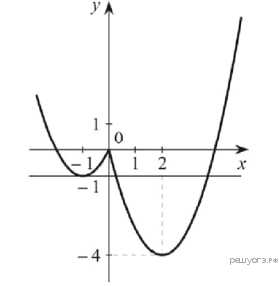 Для построения искомого графика построим график функции на промежутке и график функции на промежутке . Графиком функции является парабола, ветви которой направлены вверх, вершина имеет координаты , точки пересечения с осями координат: . Графиком функции является парабола, ветви которой направлены вверх, вершина имеет координаты , точки пересечения с осями координат: . График данной функции изображен на рисунке. Прямая имеет с построенным графиком ровно три общие точки при и при .
Для построения искомого графика построим график функции на промежутке и график функции на промежутке . Графиком функции является парабола, ветви которой направлены вверх, вершина имеет координаты , точки пересечения с осями координат: . Графиком функции является парабола, ветви которой направлены вверх, вершина имеет координаты , точки пересечения с осями координат: . График данной функции изображен на рисунке. Прямая имеет с построенным графиком ровно три общие точки при и при .
Ответ: график функции изображён на рисунке; прямая имеет с графиком ровно три общие точки при и при .
5. Задание 23 № 311610. Постройте график функции и найдите значения , при которых прямая имеет с ним ровно две общие точки.
Решение.
Раскрывая модули, получаем, что график функции совпадает с прямой при , совпадает с прямой при и совпадает с прямой при .
График изображен на рисунке.
Прямая имеет с графиком данной функции ровно две общие точки при и .
Ответ: .
6. Задание 23 № 311619. Постройте график функции
и определите, при каких значениях прямая имеет с графиком ровно две общие точки.
Решение.
График функции состоит из двух лучей и отрезка.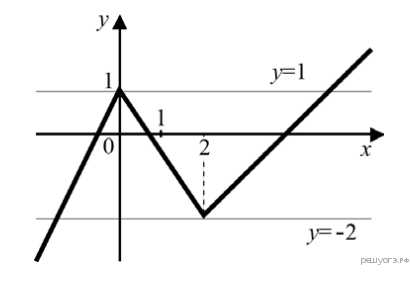 На рисунке видно, что график имеет ровно две общих точки с горизонтальными прямыми и .
На рисунке видно, что график имеет ровно две общих точки с горизонтальными прямыми и .
Ответ: 1; −2.
7. Задание 23 № 311662. Постройте график функции и определите, при каких значениях прямая не будет иметь с построенным графиком ни одной общей точки.
Решение.
Преобразуем выражение: при .
Значит,
Построим ветвь гиперболы при и удалим точку . Затем построим вторую часть графика симметрично первой относительно оси ординат.
На рисунке видно, что прямая не имеет с построенным графиком общих точек, если она горизонтальна, либо проходит через одну из удаленных точек или . Этим случаям соответствуют значения и .
Ответ: .
8. Задание 23 № 311923. Постройте график функции и определите, при каких значениях параметра a он имеет ровно две общие точки с прямой y = a.
Решение.
Построим график функции y = −x2 − 4x − 4 на промежутке (−∞; −1), график функции y = x на промежутке [−1; 1] и график функции y = 2 − x на промежутке (1; +∞).
Прямая y = a имеет с построенным графиком ровно две общие точки при a < −1 и при 0 < a < 1.
Ответ: a < −1, 0 < a < 1.
9. Задание 23 № 314700. Постройте график функции
и определите, при каких значениях прямая будет пересекать построенный график в трёх точках.
Решение.
Построим график функции (см. рисунок).
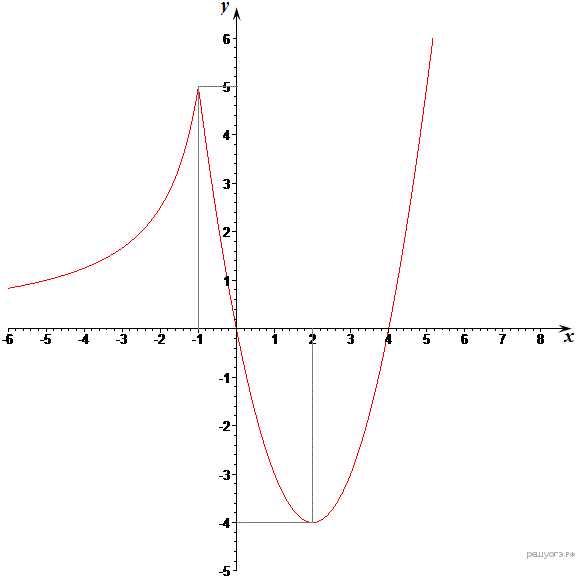
Из графика видно, что прямая будет иметь с графиком ровно три точки пересечения при принадлежащем множеству:
Ответ: (0; 5).
10. Задание 23 № 314702. Постройте график функции и определите, при каких значениях прямая имеет с графиком ровно три общие точки.
Решение.
Раскрывая модуль, получим, что график функции можно представить следующим образом:
Этот график изображён на рисунке:
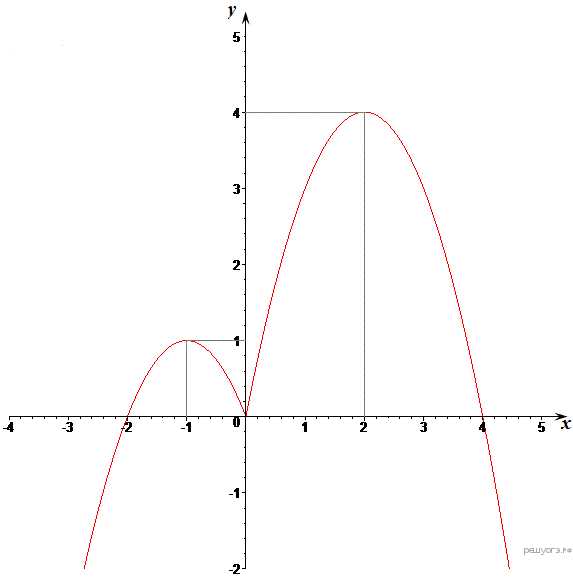
Из графика видно, что прямая имеет с графиком функции ровно три общие точки при и
Ответ: 0; 1.
11. Задание 23 № 314758. Постройте график функции
и определите, при каких значениях прямая будет иметь с графиком единственную общую точку.
Решение.
Построим график функции (см. рисунок).
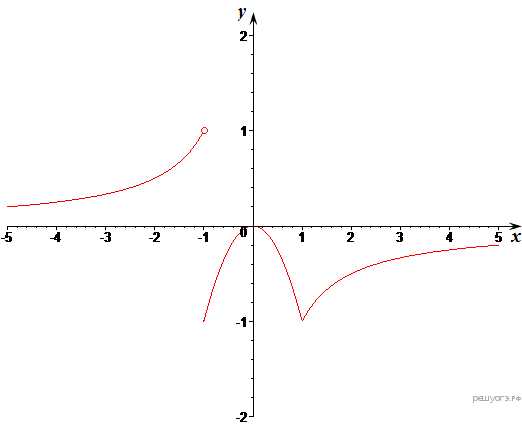
Из графика видно, что прямая будет иметь с графиком функции единственную точку пересечения при принадлежащем множеству [0; 1).
Ответ: [0; 1).
12. Задание 23 № 314777. Постройте график функции
и определите, при каких значениях прямая
infourok.ru
Варианты ОГЭ, «Математика», 9 класс
Вариант 3.
Работа состоит из трёх модулей: «Алгебра», «Геометрия», «Реальная математика». Модуль «Алгебра» содержит
8 заданий. Модуль «Геометрия» содержит 5 заданий. Модуль «Реальная математика» содержит семь заданий. Ответы к заданиям 2, 3, 8, 14 запишите в бланк ответов № 1 в виде одной цифры, которая соответствует номеру правильного ответа. Для остальных заданий части 1 ответом является число или последовательность цифр. Ответ запишите в поле ответа в тексте работы, а затем перенесите в бланк ответов № 1. Если в ответе получена обыкновенная дробь, обратите её в десятичную.
Часть 1 Модуль Алгебра
Запишите в ответе номера выражений, значения которых положительны.
Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.
1)2) –(-0,8)*(-0,6)
3)
4) 0,62-0,6
Сравните числа x и y, если x=(3,5*10-4)*(3*10-3), y=0,0000011. В ответ запишите меньшее из чисел
Найдите значение выражения 0,8*(-7)4-0,3*(-7)2+45
Решите уравнение
Найдите значение b по графику функции y=ax2+bx+c, изображенному на рисунке.
Какое наибольшее число последовательных натуральных чисел, начиная с 1, можно сложить, чтобы получившаяся сумма была меньше 435?
Найдите f(5), если f(x+4)=44-x
Решите неравенство 5x-2(2x-8)<-5. В ответе укажите номер правильного варианта.1) (11;+∞), 2) (-21;+∞), 3) (- ∞;-21), 4) (- ∞;11)
Модуль ГеометрияКатеты прямоугольного треугольника равны 12 и 9. Найдите высоту, проведенную к гипотенузе.
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:7:8. Найдите радиус окружности, если меньшая из сторон равна 20.
В ромбе сторона равна 10, одна из диагоналей — , а угол, из которого выходит эта диагональ, равен 30°. Найдите площадь ромба
Найдите тангенс угла С треугольника ABC, изображённого на рисунке.
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон. Если утверждений несколько, запишите их номера в порядке возрастания.
Модуль Реальная математика
14)В таблице приведены расстояния от Солнца до четырёх планет Солнечной системы. Какая из этих планет ближе всех к Солнцу?
Планета
Юпитер
Марс
Сатурн
Нептун
Расстояние (в км)
7,781 · 108
2,280 · 108
1,427 · 109
4,497 · 109
1) Юпитер; 2) Марс; 3) Сатурн; 4) Нептун
15) В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.
ВеществоДети от 1 года
до 14 лет
Мужчины
Женщины
Жиры
40—97
70—154
60—102
Белки
36—87
65—117
58—87
Углеводы
170—420
257—586
Какой вывод о суточном потреблении жиров, белков и углеводов мужчины можно сделать, если по подсчётам диетолога в среднем за сутки он потребляет 90 г жиров, 90 г белков и 559 г углеводов? В ответе укажите номера верных утверждений.
1) Потребление жиров в норме. 2) Потребление белков в норме. 3) Потребление углеводов в норме. Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Закупив чайные кружки на оптовом складе, магазин стал продавать их по цене на 50% больше закупочной. Перед Новым годом цена кружки была снижена на 40%. Какая цена меньше: та, по которой магазин закупил кружки, или предновогодняя – и на сколько процентов?
Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 10 км/ч и 24 км/ч. Какое расстояние (в километрах) будет между ними через 3 часа?
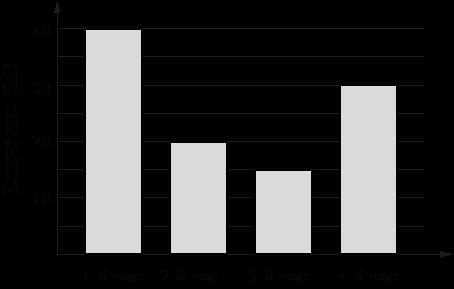
На диаграмме показано количество SMS, присланных слушателями за каждый час четырёхчасового эфира программы по заявкам на радио. Определите, на сколько больше сообщений было прислано за первые два часа программы по сравнению с последними двумя часами этой программы.
Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,06. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
За 40 минут пешеход прошёл 3 километра. За сколько минут он пройдёт
a километров, если будет идти с той же скоростью? Запишите соответствующее выражение.
Вариант 4
Работа состоит из трёх модулей: «Алгебра», «Геометрия», «Реальная математика». Модуль «Алгебра» содержит
8 заданий. Модуль «Геометрия» содержит 5 заданий. Модуль «Реальная математика» содержит семь заданий. Ответы к заданиям 2, 3, 8, 14 запишите в бланк ответов № 1 в виде одной цифры, которая соответствует номеру правильного ответа. Для остальных заданий части 1 ответом является число или последовательность цифр. Ответ запишите в поле ответа в тексте работы, а затем перенесите в бланк ответов № 1. Если в ответе получена обыкновенная дробь, обратите её в десятичную.
Часть 1 Модуль Алгебра
Запишите в ответе номера выражений, значения которых положительны.
Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.
1)2) –(-0,5)*(-0,7)
3)
4) 1,12-1,1
Сравните числа x и y, если x=(9,7*10-3)*(3*10-4), y=0,0000291. В ответ запишите меньшее из чисел
Найдите значение выражения 0,8*(-7)4-0,3*(-7)2+45
Решите уравнение
Найдите значение с по графику функции y=ax2+bx+c, изображенному на рисунке.
Какое наибольшее число последовательных натуральных чисел, начиная с 1, можно сложить, чтобы получившаяся сумма была меньше 496?
Найдите f(6), если f(x+3)=25-х
Решите неравенство 2x-4>7x-1
В ответе укажите номер правильного варианта.1) (1;+∞), 2) (-0,6;+∞), 3) (- ∞;-0,6), 4) (- ∞;1)
Решение.
Последовательно получаем:
Ответ: 2,5.
Ответ: 2,5
Модуль Геометрия
Катеты прямоугольного треугольника равны 18 и 24. Найдите высоту, проведенную к гипотенузе.
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:5:10. Найдите радиус окружности, если меньшая из сторон равна 19.
Сторона ромба равна 73, а диагональ равна 110. Найдите площадь ромба.
Найдите синус угла В треугольника ABC, изображённого на рисунке.
Какие из данных утверждений верны? Запишите их номера.
1) Диагонали любого прямоугольника равны.
2) Если в треугольнике есть один острый угол, то этот треугольник остроугольный.
3) Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла. Если утверждений несколько, запишите их номера в порядке возрастания.
Модуль Реальная математика
В таблице приведены расстояния от Солнца до четырёх планет Солнечной системы. Какая из этих планет дальше всех от Солнца?
Планета
Уран
Сатурн
Юпитер
Нептун
Расстояние (в км)
2,871 · 109
1,427 · 109
7,781 · 108
4,497 · 109
1) Уран; 2) Сатурн; 3) Юпитер; 4) Нептун.
В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.
Дети от 1 года
до 14 лет
Мужчины
Женщины
Жиры
40—97
70—154
60—102
Белки
36—87
65—117
58—87
Углеводы
170—420
257—586
Какой вывод о суточном потреблении жиров, белков и углеводов женщины можно сделать, если по подсчётам диетолога в среднем за сутки он потребляет 90 г жиров, 90 г белков и 559 г углеводов? В ответе укажите номера верных утверждений.
1) Потребление жиров в норме. 2) Потребление белков в норме. 3) Потребление углеводов в норме. Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Магазин закупил на складе футболки и стал продавать их по цене на 60% больше закупочной. В конце года цена была снижена на 50%. Какая цена меньше: та, по которой магазин закупил футболки, или их цена в конце года — и на сколько процентов?
Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 21 км/ч и 28 км/ч. Какое расстояние (в километрах) будет между ними через 4 часа?
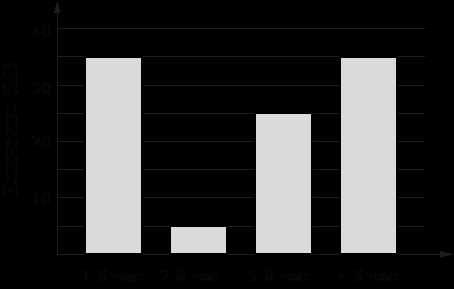
На диаграмме показано количество SMS, присланных слушателями за каждый час четырёхчасового эфира программы по заявкам на радио. Определите, на сколько меньше сообщений было прислано за первые два часа программы по сравнению с последними двумя часами этой программы.
Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,16. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
За 10 минут велосипедист проехал a километров. За сколько минут он проедет 20 километров, если будет ехать с той же скоростью? Запишите соответствующее выражение.
infourok.ru
Б | В | |
| 1)протестанты 2)католики 3)мусульмане 4)прочие |
doc4web.ru


