Как решать рациональные неравенства методом интервалов 9 класс: Решение рациональных неравенств методом интервалов — урок. Алгебра, 9 класс.
Решением рационального неравенства с одной переменной называют такое множество всех значений этой переменной, при подстановке которых в это неравенство вместо неизвестного получается верное числовое неравенство.
При решении неравенств используются свойства неравенств (см. §36 справочника для 8 класса), из которых следует:
- если перенести какое-либо слагаемое неравенства в другую часть, знак неравенства не изменится;
- если разделить обе части неравенства на одно и то же положительное число, знак не изменится; при делении на одно и то же отрицательное число знак нужно поменять.
Алгоритм решения неравенств первой степени
Напомним, что неравенство первой степени также называют «линейным неравенством» (см. Главу 6, §§36-40 справочника для 8 класса)
На входе: неравенство $ax+b \gt 0$ или $ax+b \lt 0$ или аналогичные нестрогие неравенства, где x — переменная, $a \in \Bbb R, b \in \Bbb R$ — некоторые действительные числа, причем $a \neq 0$.
Ход решения:
$$ ax+b \gt 0 \Rightarrow \left[ \begin{array}{cc} {\left\{ \begin{array}{c}a \gt 0 \\ x \gt -\frac{b}{a}, т.е. x \in (-\frac{b}{a};+ \infty)\end{array} \right.} \\ {\left\{ \begin{array}{c} a \lt 0 \\ x \lt -\frac{b}{a}, т.е. x \in(- \infty;-\frac{b}{a} )\end{array} \right.} \end{array} \right. $$
$$ ax+b \ge 0 \Rightarrow \left[ \begin{array}{cc} {\left\{ \begin{array}{c} a \gt 0\\x \ge -\frac{b}{a}, т.е. x \in [-\frac{b}{a};+ \infty) \end{array} \right.} \\ {\left\{ \begin{array}{c} a \lt 0 \\ x \le -\frac{b}{a}, т.е. x \in (- \infty;-\frac{b}{a}]\end{array} \right.} \end{array} \right. $$
Неравенства со знаками $ \lt $ и $ \le $ решаются аналогично.
Например:
1. $5x+8 \gt 0 \Rightarrow 5x \gt -8 \Rightarrow x \gt -1,6 \Rightarrow x \in(-1,6;+ \infty)$
2. $4-2x \le 0 \Rightarrow -2x \le -4 \Rightarrow x \ge 2 \Rightarrow x \in [2;+ \infty)$
Алгоритм решения неравенств второй степени
На входе: неравенство $ax^2+bx+c \gt 0$ или $ax^2+bx+c \lt 0$ или аналогичные нестрогие неравенства, где x — переменная, $a \in \Bbb R, b \in \Bbb R, c \in \Bbb R$ — некоторые действительные числа, причем $a \neq 0$. 2+7x+10 \gt 0 $
2+7x+10 \gt 0 $
D = 49-40 = 9
$x = \frac{-7 \pm 3}{2} = \left[ \begin{array}{cc} x_1 = -5 \\ x_2 = -2 \end{array} \right.$
$a = 1 \gt 0$, парабола ветками вверх, точки над осью OX соответствуют
промежуткам:
$x \in (-\infty;-5) \cup (-2;+\infty)$
Метод интервалов
Исследуем знаки (так называемые, промежутки знакопостоянства) для функции f(x) = x-a. Все x, расположенные левее a, меньше: $x \lt a \Rightarrow x-a \lt 0$. А все x, расположенные правее a, больше: $x \gt a \Rightarrow x-a \gt 0$.
Заметим, что при x = a, f(x) = 0.
Введём понятие «белой» (незакрашенной) и «чёрной» (закрашенной) точек
Cформулируем следующее правило:
При решении строгих неравенств $(>, \lt)$ на числовой прямой следует отмечать «белые» точки, при решении нестрогих неравенств $(\le, \ge)$ на числовой прямой следует отмечать «чёрные» точки .
Получим такое соответствие схем и решений:
$x-a \lt 0, x \in (-\infty;a)$
$ x-a \gt 0, x \in (a;+\infty) $
$x-a \le 0, x \in (-\infty;a]$
$x-a \ge 0, x \in [a;+\infty)$
Теперь понятен смысл «белых» и «чёрных» точек.
Исследуем знаки для функции f(x) = (x-a)(x-b). Это – парабола, ветками вверх, и для неё, как было показано выше:
$$ f(x) \gt 0 при x \lt a \cup x \gt b, \quad f(x) \lt 0 при a \lt x \lt b $$
В качестве примера, для строгих и нестрогих неравенств получаем:
$(x-a)(x-b) \lt 0, x \in (a;b)$
$(x-a)(x-b) \gt 0,$$x \in (- \infty ;a) \cup (b;+ \infty )$
$(x-a)(x-b) \le 0,x \in [a;b]$
$(x-a)(x-b) \ge 0,$
$ x \in (- \infty ;a] \cup [b;+ \infty )$
Посмотрим, как это работает на практике.
Решим неравенство: $(x-3)(x+2) \gt 0$.
Шаг 1. Неравенство строгое, поэтому отметим на числовой прямой «белые» точки -2 и 3.
Вся числовая прямая теперь разделена на три области:
1) левее -2; 2) между -2 и 3; 3) правее 3.
Шаг 2. Возьмём любой x из первой области, левее -2. Например, x = -5. Подставим его в исходное выражение: (-5-3)(-5+2). Не считая, определим знак каждой скобки-сомножителя: $ \underbrace{(-5-3)}_{\lt 0} \underbrace{(-5+2)}_{\lt 0}$. Поскольку «минус на минус даёт плюс», произведение двух скобок $ \gt 0$, т.е. положительное. Помечаем всю первую область знаком «+».
Поскольку «минус на минус даёт плюс», произведение двух скобок $ \gt 0$, т.е. положительное. Помечаем всю первую область знаком «+».
Шаг 3. Возьмём любой x из второй области, между -2 и 3. Например, x = 0. Подставим: $ \underbrace{(0-3)}_{\lt 0} \underbrace{(0+2)}_{\gt 0}$. Произведение двух скобок разных знаков $ \lt 0 $, т.е. отрицательное. Помечаем всю вторую область знаком «-».
Шаг 4. Возьмём любой x из третьей области, правее 3. Например, x = 10. Подставим: $\underbrace{(10-3)}_{\gt 0} \underbrace{(10+2)}_{\gt 0}$. Произведение двух скобок $ \gt 0$, т.е. положительное.
Помечаем всю третью область знаком «+».
Шаг 5. По условию нам нужно выбрать промежутки $\gt 0$, т.е. помеченные «+». Записываем ответ: $x \in (-\infty ;-2) \cup (3;+\infty )$.
Преимущества метода интервалов:
- если левая сторона неравенства может быть представлена в виде произведения линейных сомножителей, ответ получается «автоматически», не нужно задумываться о расположении точек параболы относительно оси OX, не говоря уже о более сложных графиках;
- с помощью метода можно решать неравенства любого порядка, т.
 2+5 \cdot (-2)+6 = 0$
2+5 \cdot (-2)+6 = 0$При этом: $P_2 (x) = (x+3)(x+2)$
Если c — корень многочлена $P_n (x)$, то многочлен делится на (x-c) без остатка.
СЛУЧАЙ 1. Линейные сомножители в 1-й степени
Пусть многочлен $P_n (x)$ имеет n различных корней $c_i,i = \overline{1,n}$. Тогда его можно представить в виде произведения:
$$ P_n (x) = (x-c_1 )(x-c_2 )…(x-c_n ) $$
Алгоритм решения неравенства $(x-c_1 )(x-c_2 )…(x-c_n ) \gt 0$ методом интервалов
Пусть для определенности $c_1 \lt c_2 \lt ⋯ \lt c_n$. Этого всегда можно добиться, т.к. от перестановки сомножителей произведение не изменяется.
Шаг 1. Отметить на числовой прямой корни $c_1,c_2,…c_n$. Т.к. неравенство строгое, точки должны быть «белыми». Числовая прямая будет поделена на n+1 областей:
1) левее $c_1$; 2) между $c_1$ и $c_2$; 3) между $c_2$ и $c_3$; …;n+1) правее $c_n$.
Шаг 2. Из каждой области выбрать произвольный x, подставить в выражение слева, определить его знак, пометить область «+» или «-».

Шаг 3. Выбрать области, помеченные «+». Записать ответ как объединение этих промежутков.
При решении неравенства $(x-c_1 )(x-c_2 )…(x-c_n ) \lt 0$ последовательность шагов аналогична, только в ответ нужно отбирать области, помеченные «-».
Для нестрогих неравенств действуем также, только точки на прямой должны быть «чёрными» и включаться в множество решений (с помощью квадратных скобок).
Например:
Решим неравенство $(x-4)(x+3)(x-1) \lt 0$
Отмечаем на прямой корни (т.е. такие x, которые обращают каждую из скобок в 0).
Неравенство строгое – все точки на числовой прямой «белые»:
Числовая прямая делится на 4 области:
1) левее -3; 2) между -3 и 1; 3) между 1 и 4; 4) правее 4.
Из каждой области выбираем произвольный x, подставляем в (x-4)(x+3)(x-1), и находим знак произведения скобок:
По условию произведение $ \lt 0$, т.е. выбираем промежутки, помеченные «-».
Ответ: $x \in (-\infty;-3) \cup (1;4)$.
 5 \le 0$
5 \le 0$Неравенство нестрогое. Убираем вторую скобку с чётной степенью, добавляем требование равенства корню в совокупность. Заменяем скобку с нечётной степенью на скобку в 1-й степени:
$ \left[ \begin{array}{cc} (x+4)(x+6) \le 0 \\ x = 2 \end{array} \right.$
$x \in [-6;-4] \cup \{2\}$
Решение неравенств через метод интервалов
Определение квадратного неравенства
Неравенство — алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.
Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Квадратное неравенство выглядит так:
где x — переменная,
a, b, c — числа,
при этом а ≠ 0.

Квадратное неравенство можно решить двумя способами:
- графический метод;
- метод интервалов.
Демо урок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Решение неравенства графическим методом
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
Как дискриминант влияет на корни уравнения:
- D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
- D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два различных корня;
- D < 0.
 Если дискриминант меньше нуля, тогда у квадратного уравнения нет корней.
Если дискриминант меньше нуля, тогда у квадратного уравнения нет корней.
Если требуется найти числовой промежуток, на котором квадратный трехчлен ax2 + bx + c больше нуля, то этот числовой промежуток находится там, где парабола лежит выше оси ОХ.
Если нужно найти числовой промежуток, на котором квадратный трехчлен ax2 + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.
Если квадратное неравенство нестрогое, то корни входят в числовой промежуток. А если строгое — не входят.
Обучение на курсах по математике в онлайн-школе Skysmart сделает сложные темы понятными, а высокий балл на экзаменах — достижимым!
Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.

Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, <, ≤, ≥.
Сейчас мы узнаем про интервалы в контексте решения квадратных неравенств.
Интервал — это некий промежуток числовой прямой, то есть все возможные числа, заключенные между двумя числами — концами интервала. Представить эти промежутки не так просто, поэтому интервалы принято рисовать.
Алгоритм решения квадратных неравенств методом интервалов:
- Найти нули квадратного трехчлена
- Изобразить координатную прямую и при наличии корней отметить их на ней.
Если неравенство строгое, нужно отметить корни пустыми (выколотыми) точками.
 Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки.
Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки. - Определить, какие знаки имеют значения трехчлена на каждом промежутке (если на первом шаге нашли нули) или на всей числовой прямой (если нулей нет). И проставить над этими промежутками + или − в соответствии с определенными знаками.
- Если квадратное неравенство со знаком > или ≥ — наносим штриховку над промежутками со знаками +.
Если неравенство со знаком < или ≤, то наносим штриховку над промежутками со знаком −.
В результате получаем геометрический образ некоторого числового множества — это и есть решение неравенства.
Либо вместо штриховки можно нарисовать «арки» для интервалов. Справа налево, начиная с +, проставить чередуя знаки + и −.
- Выбрать необходимые интервалы и записать ответ.
Расскажем подробнее про третий шаг алгоритма.
 Существует несколько подходов для определения знаков на промежутках.
Существует несколько подходов для определения знаков на промежутках.Для примера возьмем трехчлен x2 + 4x — 5, его корнями являются числа -5 и 1, они разбивают числовую ось на три промежутка: (-∞, -5), (-5, 1) и (1, +∞).
Определим знак трехчлена x2 + 4x — 5 на промежутке (1, +∞). Для этого вычислим значение данного трехчлена при некотором значении x из этого промежутка. Можно брать любое значение переменной, главное — чтобы вычисления были простыми. В нашем случае, возьмем x = 2. Подставим его в трехчлен вместо переменной x:
- 22 + 4 * 2 — 5 = 4 + 8 — 5 = 7.
7 — положительное число. Это значит, что любое значение квадратного трехчлена на интервале (1, +∞) будет положительным.
 Так мы определили знак плюс.
Так мы определили знак плюс.Определим знаки на оставшихся двух промежутках. Начнем с интервала (-5, 1). Из этого интервала можем взять x = 0 и вычислить значение квадратного трехчлена при этом значении переменной:
- 02 + 4 * 0 — 5 = 0 + 0 — 5 = -5.
Так как -5 — отрицательное число, то на этом интервале все значения трехчлена будут отрицательными. Так мы определили знак минус.
Осталось определиться со знаком на промежутке (-∞, -5). Возьмем x = -6, подставляем:
- (-6)2 + 4 * (-6) — 5 = 36 — 24 — 5 = 7.
Следовательно, искомый знак — плюс.
Можно расставить знаки быстрее, если запомнить эти факты:
Бесплатные занятия по английскому с носителем
Занимайтесь по 15 минут в день.
 Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.Плюс или минус: как определить знаки
Можно сделать вывод о знаках по значению старшего коэффициента a:
если a > 0, последовательность знаков: +, −, +,
если a < 0, последовательность знаков: −, +, −.
Можно также сделать вывод о знаках по значению старшего коэффициента a:
если a > 0, последовательность знаков: +, +,
если a < 0, последовательность знаков: −, −.
Например -4x2 — 7 не имеет корней и на промежутке (−∞, +∞) его значения отрицательны, так как коэффициент при x2 есть отрицательное число -4, и свободный член -7 тоже отрицателен.
- Когда квадратный трехчлен при D > 0 имеет два корня, то знаки его значений на промежутках чередуются.
 Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.
Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −. - Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −.
- Когда квадратный трехчлен корней не имеет (D < 0), то знаки его значений на всей числовой прямой совпадают как со знаком старшего коэффициента a, так и со знаком свободного члена c.
Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.
 2 — 5x + 6 ≥ 0.
2 — 5x + 6 ≥ 0.Как решаем:
Приравняем квадратный трехчлен к 0 и найдем нули:
x2 — 5x + 6 = 0
(x — 3) (x -2) = 0
x — 3 = 0
x — 2 = 0
x = 3
x = 2Отметим полученные значения на числовой прямой:
Расставим знаки на полученных промежутках:
Ответ: х ≤ 2, х ≥ 3.
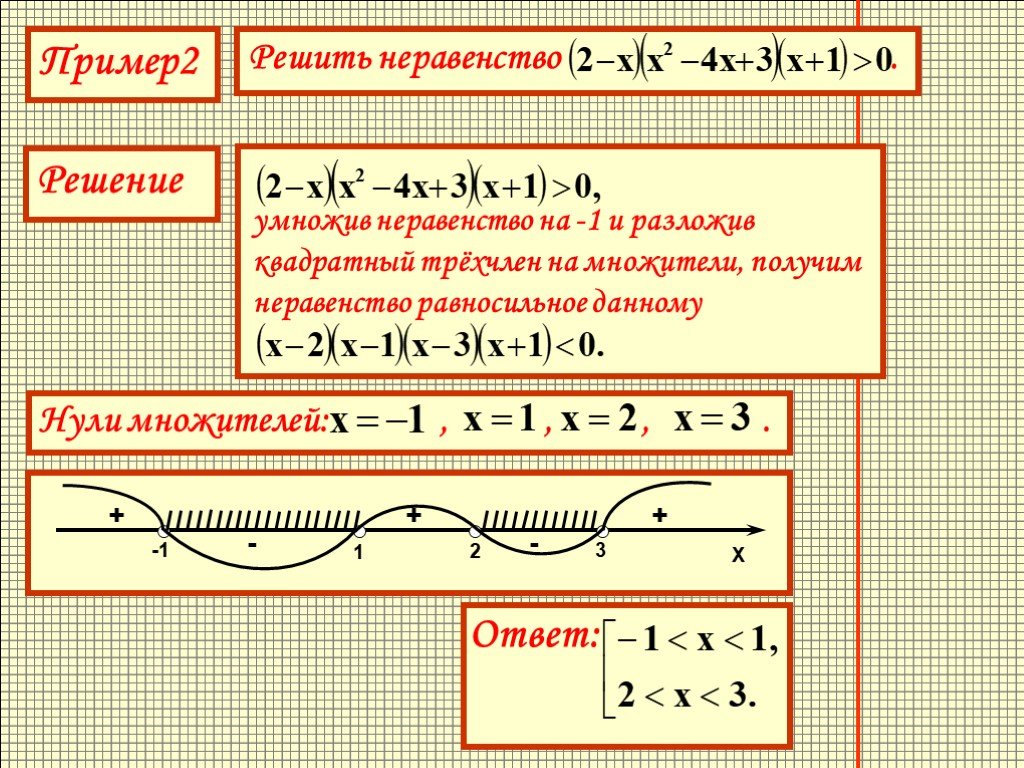
Пример 2. Применить метод интервалов для решения неравенства х2+4х+3 < 0.
Как решить неравенство методом интервалов, нам уже известно. Поэтому можем оформить решение кратко:
Ответ: -3 < x < -2.
Пример 3. Выполнить решение квадратного неравенства методом интервалов:
Как решаем:
- Находим корни квадратного трехчлена, который находится в левой части:
- Так как мы решаем строгое неравенство, то на координатной прямой изображаем выколотую точку с координатой 7:
- Теперь определим знаки на двух полученных промежутках (−∞, 7) и (7, +∞).

Это легко сделать, потому что дискриминант квадратного трехчлена равен нулю, а старший коэффициент со знаком минус. Фиксируем знаки: −, −:
- Так как мы решаем неравенство со знаком <, то изобразим штриховку над интервалами со знаками минус:
Очевидно, решениями являются оба промежутка (−∞, 7), (7, +∞).
Ответ: (−∞, 7), (7, +∞).
9.7: Решение рациональных неравенств — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 49968
- OpenStax
- OpenStax
- Решение рациональных неравенств
- Решите неравенство с рациональными функциями
- Найдите значение \(x-5\), когда ⓐ \(x=6\) ⓑ \(x=-3\) ⓒ \(x=5\)
Если вы пропустили эту задачу, просмотрите пример 1.2. .16. - Решите: \(8-2 x<12\)
Если вы пропустили эту задачу, просмотрите пример 2.6.13. - Запись в интервальной нотации: \(-3 \leq x<5 \)
Если вы пропустили эту проблему, просмотрите пример 2.6.4. - Ответ
\((-\infty,-4) \cup[2, \infty)\)
- Ответ
\((-\infty,-2] \cup(4, \infty)\)
- Ответить
\((3,6)\)
- Ответ
\((-4,2]\)
- Ответ
\([-1,4)\)
- Функция средней стоимости, \(c(x)\)
- Сколько изделий нужно произвести, чтобы их средняя стоимость была меньше 40 долларов.
- \[C(x)=10 x+3000 \номер\]
- Мы хотим, чтобы функция \(c(x)\) была меньше 40.
- Сколько изделий нужно произвести, чтобы их средняя стоимость была меньше 60 долларов.
- Ответ
- \(с(х)=\dfrac{20 х+6000}{х}\)
- Необходимо произвести более 150 единиц товара, чтобы средняя стоимость за единицу не превышала 60 долларов.
- Сколько изделий нужно произвести, чтобы их средняя стоимость была меньше 20 долларов.
- Ответить
- \(с(х)=\dfrac{5 х+900}{х}\)
- Необходимо произвести более 60 единиц продукции, чтобы средняя стоимость не превышала 20 долларов за единицу.

- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Показать страницу TOC
- нет
- Включено
- да
- Теги
- источник[1]-math-5164
- Нули числителя
- Нули знаменателя
- Нули числителя
- Нули знаменателя
- Нули числителя: –1 и 4
- Нули знаменателя: 4
- Нули числителя: -7
- Нули знаменателя: -3
Цели обучения
Будьте готовы
Прежде чем начать, пройдите этот тест на готовность.
Решение рациональных неравенств
Мы научились решать линейные неравенства после того, как научились решать линейные уравнения. Техники были почти такими же, за одним важным исключением. Когда мы умножаем или делим на отрицательное число, знак неравенства меняется на противоположный.
Только что научившись решать рациональные уравнения, мы теперь готовы решать рациональные неравенства. Рациональное неравенство — это неравенство, содержащее рациональное выражение. 9{2}} \leq \dfrac{3}{x}\quad \) являются рациональными неравенствами, поскольку каждое из них содержит рациональное выражение.
Когда мы решим рациональное неравенство, мы будем использовать многие методы, которые мы использовали при решении линейных неравенств. Мы особенно должны помнить, что когда мы умножаем или делим на отрицательное число, знак неравенства должен измениться.
Еще одно отличие состоит в том, что мы должны тщательно рассмотреть, какое значение может сделать рациональное выражение неопределенным и поэтому должно быть исключено.
Когда мы решаем уравнение и получаем \(x=3\), мы знаем, что есть одно решение, которое равно 3.
Когда мы решаем неравенство и получаем \(x>3\), мы знаем, что решений много. Мы графически отображаем результат, чтобы лучше показать все решения, и начинаем с 3. Три становится критической точкой, а затем мы решаем, следует ли заштриховать слева или справа от нее. Числа справа от 3 больше, чем 3, поэтому мы заштриховываем вправо.
Чтобы решить рациональное неравенство, мы сначала должны написать неравенство только с одним частным слева и 0 справа.
Затем мы определяем критические точки, чтобы использовать их для разделения числовой прямой на интервалы. Критическая точка — это число, которое делает рациональное выражение нулевым или неопределенным.
Затем мы оценим множители числителя и знаменателя и найдем частное в каждом интервале. Это позволит определить интервал или интервалы, содержащие все решения рационального неравенства.
Мы записываем решение в интервальной нотации, стараясь определить, включены ли конечные точки.
Пример \(\PageIndex{1}\)
Решите и запишите решение в интервальной записи: \(\dfrac{x-1}{x+3} \geq 0\)
Решение
Шаг 1 . Запишите неравенство в виде одного частного слева и нуля справа.
Наше неравенство имеет следующий вид.\[\dfrac{x-1}{x+3} \geq 0 \nonumber \]
Шаг 2 . Определите критические точки — точки, в которых рациональное выражение будет равно нулю или неопределенно.
Рациональное выражение будет равно нулю, если числитель равен нулю. Так как \(x-1=0\) при \(x=1\), то 1 является критической точкой.
Рациональное выражение будет неопределенным, если знаменатель равен нулю. Поскольку \(x+3=0\) при \(x=-3\), то -3 является критической точкой.
Критические точки 1 и -3.
Шаг 3 . Используйте критические точки, чтобы разделить числовую прямую на интервалы.
Числовая строка делится на три интервала:
\[(-\infty,-3) \quad (-3,1) \quad (1,\infty) \nonumber \]
Шаг 4 . Проверьте значение в каждом интервале. Над числовой прямой показывают знак каждого множителя рационального выражения в каждом интервале. Ниже числовой строки укажите знак частного.
Чтобы найти знак каждого фактора в интервале, мы выбираем любую точку в этом интервале и используем ее в качестве контрольной точки. Любая точка интервала даст выражению тот же знак, поэтому мы можем выбрать любую точку интервала.
\[\text { Интервал }(-\infty,-3) \nonumber \]
Число -4 находится в интервале \((-\infty,-3)\). Проверка \(x=-4\) в выражении в числителе и знаменателе.
Числитель:
\[\begin{array}{l} {x-1} \\ {-4-1} \\ {-5} \\ {\text {Отрицательный}} \end{массив} \номер\]
Знаменатель:
\[\begin{array}{l} {x+3} \\ {-4+3} \\ {-1} \\ {\text {Отрицательный}} \end{массив} \nonumber \]
Над числовой строкой отметьте отрицательный множитель \(x-1\) и отрицательный множитель \(x+3\).
Поскольку отрицательное число, деленное на отрицательное, является положительным, отметьте положительное частное в интервале \((-\infty,-3)\).
\[\text {Интервал } (-3,1) \номер \]
Число 0 находится в интервале \((-3,1)\). Тест \(х=0\).
Числитель:
\[\begin{array}{l} {x-1} \\ {0-1} \\ {-1} \\ {\text {Отрицательный}} \end{массив} \ nonumber \]
Знаменатель:
\[\begin{array}{l} {x+3} \\ {0+3} \\ {3} \\ {\text {Положительный}} \end{массив } \nonumber \]
Над числовой строкой отметьте множитель \(x-1\) отрицательным и отметьте \(x+3\) положительным.
Поскольку отрицательное число, деленное на положительное, равно отрицательному, частное в интервале \((-3,1)\ помечается как отрицательное).
\[\text {Интервал }(1, \infty) \nonumber \]
Число 2 находится в интервале \((1, \infty)\). Тест \(х=2\).
Числитель:
\[\begin{array}{l} {x-1} \\ {2-1} \\ {1} \\ {\text {Positive}} \end{array} \nonumber \]
Знаменатель:
\[\begin{array}{l} {x+3} \\ {2+3} \\ {5} \\ {\text {Положительный}} \end{массив} \nonumber \]
Над числовой строкой отметьте множитель \(x-1\) положительным и отметьте \(x+3\) положительным.
Поскольку положительное число, деленное на положительное, является положительным, отметьте положительное частное в интервале \((1, \infty)\).
Шаг 5 . Определите промежутки, на которых неравенство верно. Запишите решение в интервальной записи.
Мы хотим, чтобы частное было больше или равно нулю, поэтому числа в интервалах \((-\infty,-3)\) и \((1, \infty) \) являются решениями.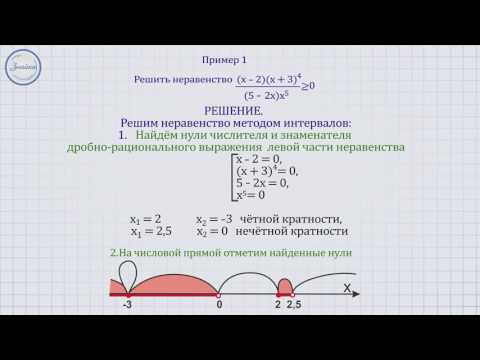
А как же критические точки?
Критическая точка \(x=-3\) делает знаменатель равным 0, поэтому ее нужно исключить из решения и отметить скобкой.
Критическая точка \(x=1\) делает все рациональное выражение равным 0. Неравенство требует, чтобы рациональное выражение было больше или равно. Итак, 1 является частью решения и мы будем отмечать его скобкой.
Вспомните, что когда у нас есть решение, состоящее из более чем одного интервала, мы используем символ объединения \(\cup \), чтобы соединить два интервала. Решение в интервальной записи: \((-\infty,-3) \cup[1, \infty)\).
Упражнение \(\PageIndex{1}\)
Решите и запишите решение в интервальной записи: \(\dfrac{x-2}{x+4} \geq 0\)
Упражнение \(\PageIndex{2}\)
Решите и запишите решение в интервальной записи: \(\dfrac{x+2}{x-4} \geq 0\)
Мы суммируем шаги для удобства.
Как решить рациональное неравенство
Шаг 1. Запишите неравенство в виде одного частного слева и нуля справа.
Шаг 2. Определите критические точки – точки, в которых рациональное выражение будет равно нулю или неопределенно.
Шаг 3. Используйте критические точки, чтобы разделить числовую прямую на интервалы.
Шаг 4. Проверьте значение в каждом интервале. Над числовой прямой показывают знак каждого множителя числителя и знаменателя в каждом интервале. Ниже числовой строки укажите знак частного.
Шаг 5. Определите интервалы, на которых неравенство верно. Запишите решение в интервальной записи.
Следующий пример требует, чтобы мы сначала привели рациональное неравенство в правильную форму.
Пример \(\PageIndex{2}\)
Решите и запишите решение в интервальной записи: \(\dfrac{4 x}{x-6}<1\)
Решение
\[\ dfrac{4 x}{x-6}<1 \nonumber \]
Вычтите 1, чтобы получить ноль справа.
\[\dfrac{4 x}{x-6}-1<0 \nonumber \]
Перепишите 1 в виде дроби с помощью ЖК-дисплея.
\[\dfrac{4 x}{x-6}-\frac{x-6}{x-6}<0 \nonumber \]
Вычтите числители и поместите разницу над общим знаменателем.
\[\dfrac{4 x-(x-6)}{x-6}<0 \nonumber \]
Упростить.
\[\dfrac{3 x+6}{x-6}<0 \nonumber \]
Разложите числитель на множители, чтобы показать все множители.
\[\dfrac{3(x+2)}{x-6}<0 \nonumber \]
Найдите критические точки.
Частное будет равно нулю, если числитель равен нулю. Частное не определено, когда знаменатель равен нулю.
\[\begin{array}{rlrl} {x+2} & {=0} & {x-6} & {=0} \\ {x} & {=-2} & {x} & { =6} \end{массив} \номер \]
Используйте критические точки, чтобы разделить числовую прямую на интервалы.
Проверка значения в каждом интервале.
| \((-\infty,-2)\) | \((-2,6)\) | \((6, \infty)\) | |
|---|---|---|---|
| \(х+2)\) | х+2 -3+2 -1 — | х+2 0+2 2 + | х+2 7+2 9 + |
| \(х-6\) | х-6 -3-6 -9 — | х-6 0-6 -6 — | х-6 7-6 1 + |
Над числовой линией укажите знак каждого множителя рационального выражения в каждом интервале. {2}-2 x-15}>0\). 9{2}-2 x-15}>0 \номер \]
{2}-2 x-15}>0\). 9{2}-2 x-15}>0 \номер \]
Разложите знаменатель на множители.
\[\dfrac{5}{(x+3)(x-5)}>0 \nonumber \]
Найдите критические точки. Частное равно 0, когда числитель равен 0. Поскольку числитель всегда равен 5, частное не может быть 0.
Частное будет неопределенным, если знаменатель равен нулю.
\[\begin{aligned} &(x+3)(x-5)=0\\ &x=-3, x=5 \end{aligned} \nonumber \]
Используйте критические точки для разделения числовую прямую на интервалы. 9{2}=0} && {x-6=0} && {x+1=0} \\ {x=0} && {x=6} && {x=-1} \end{массив} \nonumber \ ]
Используйте критические точки, чтобы разделить числовую прямую на интервалы.
Над числовой линией укажите знак каждого фактора в каждом интервале. Под числовой прямой покажите знак частного.
Поскольку 0 исключен, решение представляет собой два интервала \((-1,0) \cup(0,6)\), \((-1,0)\) и \((0,6) \).
Упражнение \(\PageIndex{7}\) 9{2}}
<\dfrac{3}{x}\).Решение неравенства с рациональными функциями
При работе с рациональными функциями иногда полезно знать, когда функция больше или меньше определенного значения. Это приводит к рациональному неравенству.
Это приводит к рациональному неравенству.
Пример \(\PageIndex{5}\)
Учитывая функцию \(R(x)=\dfrac{x+3}{x-5}\), найдите значения x, при которых функция меньше или равно 0,
Решение
Мы хотим, чтобы функция была меньше или равна 0.
\[R(x) \leq 0 \nonnumber \]
Подставим рациональное выражение вместо \(R(x)\) .
\[\dfrac{x+3}{x-5} \leq 0 \quad x \neq 5 \nonumber \]
Найдите критические точки.
\[\begin{array}{rlrl} {x+3=0} && {x-5=0} \\ {x=-3} && {x=5} \end{array} \nonumber \]
Используйте критические точки, чтобы разделить числовую прямую на интервалы.
Тестовые значения в каждом интервале. Над числовой линией покажите знак каждого фактора в каждом интервале. Под числовой прямой покажите знак частного. Запишите решение в интервальной записи. Поскольку 5 исключено, мы не включаем его в интервал.
\[[-3,5) \nonumber \]
Упражнение \(\PageIndex{9}\)
Учитывая функцию \(R(x)=\dfrac{x-2}{x+4} \), найдите значения \(x\), при которых функция меньше или равна 0.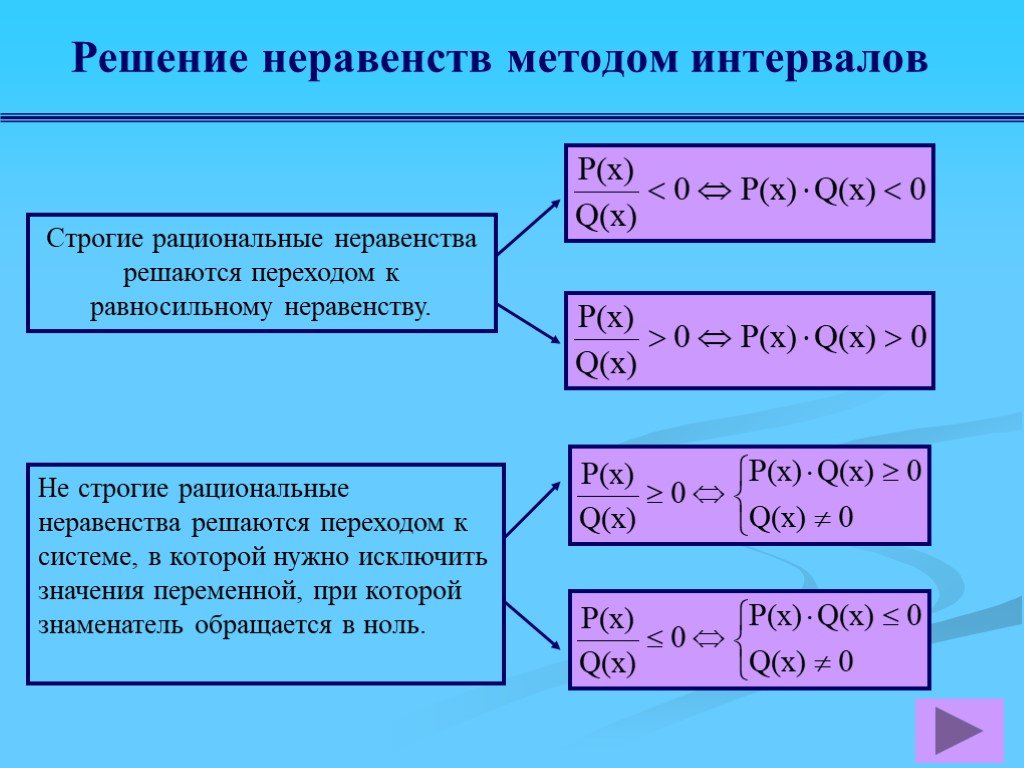
Упражнение \(\PageIndex{10}\)
Учитывая функцию \(R(x)=\dfrac{x+1}{x-4}\), найдите значения \(x\), которые делают функция меньше или равна 0.
В экономике функция \(C(x)\) используется для представления стоимости производства \(x\) единиц товара. Среднюю стоимость единицы можно найти, разделив \(C(x)\) на количество товаров \(x\). Тогда средняя стоимость единицы равна \(c(x)=\dfrac{C(x)}{x}).
Пример \(\PageIndex{6}\)
Функция \(C(x)=10 x+3000\) представляет себестоимость производства \(x\), количество изделий. Найти:
Решение
Функция средней стоимости имеет вид \(c(x)=\dfrac{C(x)}{x})\). Чтобы найти функцию средней стоимости, разделите функцию стоимости на \(x\).
Чтобы найти функцию средней стоимости, разделите функцию стоимости на \(x\).
\[\begin{aligned} &c(x)=\dfrac{C(x)}{x}\\ &c(x)=\dfrac{10 x+3000}{x} \end{aligned} \nonumber \]
Функция средней стоимости равна \(c(x)=\dfrac{10 x+3000}{x} \)
\[c(x)<40 \nonumber \]
Подставить рациональное выражение forc(x).
\[\dfrac{10 x+3000}{x}<40, \quad x \neq 0 \nonumber \]
Вычтите 40, чтобы получить 0 справа.
\[\dfrac{10 x+3000}{x}-40<0 \номер\]
Перепишите левую часть как одно частное, найдя ЖК-дисплей и выполнив вычитание.
\[\begin{align} \dfrac{10 x+3000}{x}-40\left(\dfrac{x}{x}\right) &<0\\ \dfrac{10 x+3000}{ x}-\dfrac{40 x}{x} &<0\\ \dfrac{10 x+3000-40 x}{x} &<0 \\ \dfrac{-30 x+3000}{x} &< 0 \end{aligned} \nonumber \]
Умножьте числитель, чтобы показать все множители.
\[\begin{array}{ll} {\dfrac{-30(x-100)}{x}<0} \\ {-30(x-100)=0} && {x=0} \ конец {массив} \номер \]
Найдите критические точки.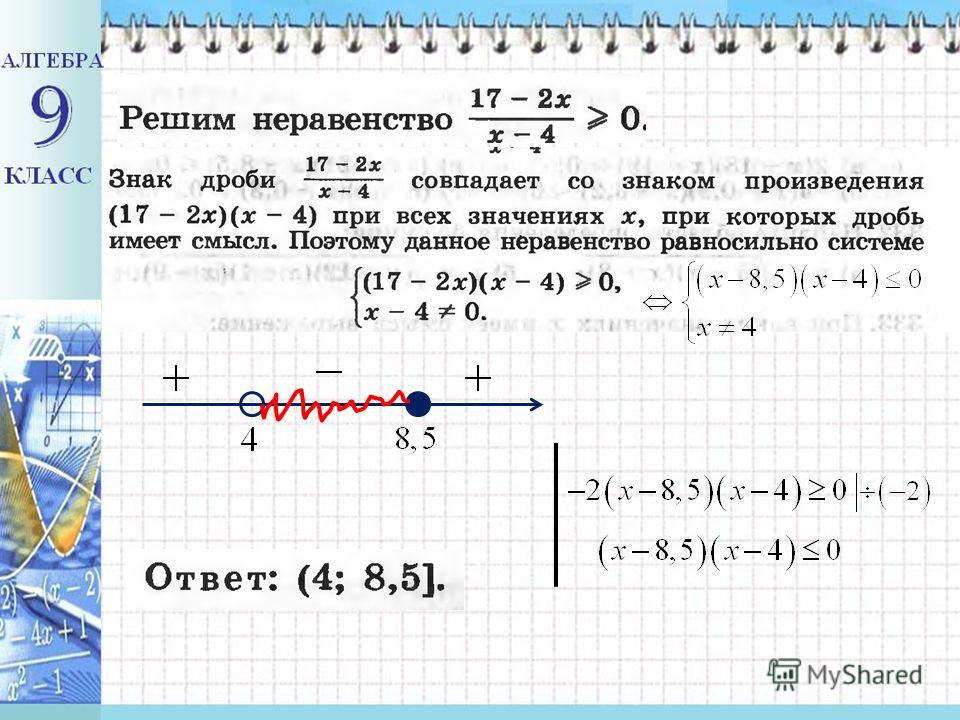
\[\begin{array}{rl} {-30 \neq 0} & {x-100=0} \\ &{x=100} \end{array} \nonumber \]
Более 100 элементов должны быть произведены, чтобы средняя стоимость не превышала 40 долларов за единицу.
Упражнение \(\PageIndex{11}\)
Функция \(C(x)=20 x+6000\) представляет стоимость производства \(x\), количества изделий. Найти:
Упражнение \(\PageIndex{12}\)
Функция \(C(x)=5 x+900\) представляет собой стоимость производства \(x\), количества изделий. Найти:
Эта страница под названием 9.7: Решение рациональных неравенств распространяется по лицензии CC BY и была создана, изменена и/или курирована OpenStax.
Решение рациональных неравенств — ChiliMath
Ключевой подход при решении рациональных неравенств основан на нахождении критических значений рационального выражения, которые делят числовую прямую на отдельные открытые интервалы.
критических значений — это просто нули числителя и знаменателя. Вы должны помнить, что нули знаменателя делают рациональное выражение неопределенным, поэтому их нужно немедленно игнорировать или исключить как возможное решение. Однако нули числителя также необходимо проверять на предмет их возможного включения в общее решение.
В этом уроке я рассмотрю пять (5) проработанных примеров с различными уровнями сложности, чтобы проиллюстрировать как процедуры, так и концепции.
Пример 1: Решите приведенное ниже рациональное неравенство.
Я начинаю решать это рациональное неравенство, записывая его в общем виде. Общая форма подразумевает, что рациональное выражение находится в левой части неравенства, а ноль остается в правой.
Общая форма имеет четыре (4) типа.
Приятно знать, что эта проблема уже в общем виде. Мой следующий шаг — найти нулей числителя и знаменателя .
Я могу найти нули числителя, полностью разложив его на множители, а затем отдельно приравняв каждый множитель к нулю и найдя x. Точно так же нахождение нулей знаменателя выполняется таким же образом.
Теперь я буду использовать нули, чтобы разделить или разделить числовую прямую на интервалы. Нули числителя и знаменателя также известны как критические числа . В этом случае два критических числа делят числовую прямую на три отдельных интервала.
Следующим шагом является выбор числа в каждом интервале и преобразование его обратно в исходное рациональное неравенство; определить, является ли это утверждение истинным или ложным. Верное утверждение означает, что интервал является частью решения, в противном случае — нет.
Как видите, числа, которые я выбрал для каждого интервала, выделены желтым цветом.
Обратите внимание, что открытый интервал между −1 и 3, записанный как \left( { — 1,3} \right), дает верное утверждение , которое подразумевает, что он является частью решения.
Итак, где еще нам искать возможные решения, чтобы покончить с этим?
Проверять нули или критические числа числителей только в исходном уравнении. Если это дает верное утверждение, включите это критическое число как часть общего решения.
Нулей в числителе 3. Сейчас проверю.
Использование квадратной скобки указывает, что это часть решения, а открытая скобка (круглая скобка) означает, что это не так. Я запишу свой окончательный ответ как \left( { — 1,\left. 3 \right]} \right..
Пример 2: Решите приведенное ниже рациональное неравенство.
Во-первых, заданное рациональное неравенство в общем виде, потому что рациональное выражение слева, а ноль справа. Это хорошо!0042
Далее я вынесу числитель и знаменатель. После этого у вас должно получиться что-то вроде этого.
Теперь я могу найти нули числителя и знаменателя.
Эти нули или критические числа делят числовую прямую на отдельные интервалы или части.
Выберите проверочное число для каждого интервала и вернитесь к исходному рациональному неравенству.
Используйте факторизованную форму исходного рационального неравенства для оценки тестовых чисел для упрощения вычислений.
Цифры, выделенные желтым цветом, я выбрал для проверки достоверности каждого интервала.
Интервалы, дающие верные утверждения, равны
Чтобы найти остальную часть решения, проверьте действительность нулей числителя только в исходном рациональном неравенстве.
Если вы все сделали правильно, то согласитесь, что −4 и 2 равны недействительные ответы , потому что они не дают истинных утверждений после проверки.
Окончательный ответ на эту задачу в интервальной записи:
Пример 3: Решите приведенное ниже рациональное неравенство.
Я бы сначала вынес числитель и знаменатель, чтобы найти их нули. В факторизованной форме я получил
Затем определите нули рационального неравенства, приравняв каждый множитель к нулю, а затем найдя x.
Используйте нули в качестве критических чисел, чтобы разделить числовую прямую на отдельные интервалы. Я начинаю проверять правильность каждого интервала, выбирая тестовое значение и оценивая их в исходное рациональное неравенство. Те, что выделены желтым, — это числа, которые я выбрал.
Обратите внимание, что единственным интервалом, дающим истинное утверждение, является \left( { — 1,4} \right).
Более того, нули числителя не согласуются с исходным рациональным неравенством, поэтому я должен их игнорировать.
Окончательный ответ просто \left( { — 1,4} \right).
Пример 4: Решите приведенное ниже рациональное неравенство.
Это рациональное неравенство равно , а не в общем виде. Правая часть должна быть равна нулю. Первый шаг — избавиться от константы на этой стороне, вычитая обе стороны на 1. После этого упростите до одного рационального выражения. У вас должен быть такой же предварительный шаг, как этот.
У вас должен быть такой же предварительный шаг, как этот.
Далее найдите нули числителя и знаменателя.
Используйте нули в качестве критических чисел для разделения числовой строки на участки или интервалы.
Затем выберите тестовые числа для каждого интервала и преобразуйте их в общую форму, чтобы определить их значения истинности. Те, что выделены желтым цветом, являются выбранными значениями. Вы можете выбрать другие числа, если они находятся в проверяемом интервале.
Интервалы, дающие верные утверждения, равны
Между тем, после проверки нуля числителя в точке x = — \,7 это также приводит к истинному утверждению. Используйте квадратную скобку, чтобы указать, что это включено в качестве решения.
Окончательный ответ в интервальной записи должен быть
Пример 5: Решите приведенное ниже рациональное неравенство.
Мне нужно сделать правую часть рационального неравенства равной нулю.


 2+5 \cdot (-2)+6 = 0$
2+5 \cdot (-2)+6 = 0$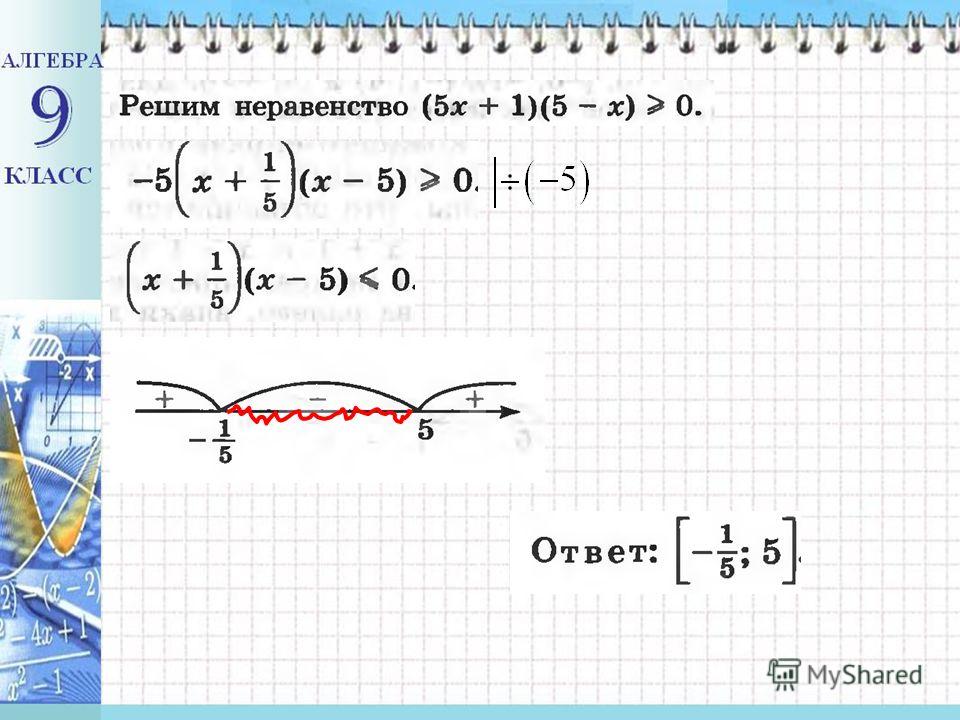
 5 \le 0$
5 \le 0$
 Если дискриминант меньше нуля, тогда у квадратного уравнения нет корней.
Если дискриминант меньше нуля, тогда у квадратного уравнения нет корней.
 Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки.
Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки. Существует несколько подходов для определения знаков на промежутках.
Существует несколько подходов для определения знаков на промежутках. Так мы определили знак плюс.
Так мы определили знак плюс. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.
Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −. 2 — 5x + 6 ≥ 0.
2 — 5x + 6 ≥ 0.
