Система неравенств с одной переменной 8 класс самостоятельная работа: Решение систем неравенств с одной переменной (8 класс) скачать
 © Епифанова Татьяна Николаевна Епифанова Татьяна Николаевна
© Епифанова Татьяна Николаевна Епифанова Татьяна НиколаевнаНеограниченная бесплатная загрука материала Тест «Решение систем линейных неравенств с одной переменной» доступна всем пользователям. Разработка находится в разделе Математика 8 класс и представляет собой проверка знаний, повторение, систематизация.

Скачать материал 0.2Mb
Загрузка началась… Понравился сайт? Получайте ссылки
на лучшие материалы еженедельно!
 Подарок каждому подписчику!
Подарок каждому подписчику! Самостоятельная работа по теме: РЕШЕНИЕ НЕРАВЕНСТВ. 8 класс
Вариант -1
Решите неравенство, ответ запишите в виде промежутка.
1) 5х3,5
2)
3) 6-5х 2
4) –(2-3х)+4(6+х)1
5)
6)
Самостоятельная работа по теме: РЕШЕНИЕ НЕРАВЕНСТВ.8 класс
Вариант -2
Решите неравенство, ответ запишите в виде промежутка.
1) 7х4,2
2)
3) 0,6-2х
4) –(2х+1)3(х+2)
5)
6)
Самостоятельная работа по теме: РЕШЕНИЕ НЕРАВЕНСТВ. 8 класс
Вариант -3
Решите неравенство, ответ запишите в виде промежутка.
1) 6х1,2
2) -12
3) 0,4+3х
4) –(4-х) 2(3+х)
5)
6)
Самостоятельная работа по теме: РЕШЕНИЕ НЕРАВЕНСТВ. 8 класс
Вариант -4
Решите неравенство, ответ запишите в виде промежутка.
1) 0,4х 1,6
2)
3) 6,2+х
4) 4(1-х)0
5)
6)
По теме: методические разработки, презентации и конспекты
Самостоятельная работа по алгебра для 11-го класса по теме «Наибольшее и наименьшее значение функции на отрезке»Самостоятельная работа составлена в шести вариантах одинаковой сложности по материалам для экзаменов, 2-е и 3-е задание из материалов Открытого банка заданий ЕГЭ по математике….
Самостоятельная работа по алгебре для 7-го класса по теме «Координаты»Самостоятельная работа содержит варианты одинаковой сложиности и включает задания на построение точек по координатам, построение точек, симметричных данным относительно осей координат и начала координ…
Самостоятельные работы по алгебре. 1 полугодие. 9 класс.Комплект рейтинговых самостоятельных работ по алгебре. 9 класс. УМК Ю.Н.Макарычева и др….
Контрольные самостоятельные работы по алгебре в 7- 9 классах с углубленным изучение математикиДидактический материал ситематезирован из различных источников…
Самостоятельная работа по алгебре для 8-го класса по теме «Квадратичная функция»Работа составлена в четырех вариантах одинаковой сложности и содержит три задания. Данные задания можно использовать после изучения формул для нахождения координат вершины параболы и рассмотрения част…
Самостоятельная работа по алгебре для 9-го класса по теме «Теория вероятности»Данная самостоятельная работа составлена в двух вариантах одинаковой сложности. В каждом варианте по 7 заданий, взятых из открытого банка заданий ГИА по математике. Работа может быть использована для …
 Самостоятельная работа по алгебре для учащихся 9 класса по теме «Меры разброса»
Самостоятельная работа по алгебре для учащихся 9 класса по теме «Меры разброса»В данном материале содержатся задания для самостоятельной работы учащихся на обобщающем уроке по теме «Меры разброса»….
Проверочная работа по теме: РЕШЕНИЕ НЕРАВЕНСТВ. (8 класс)
Вариант -1
Решите неравенство, ответ запишите в виде промежутка.
1) 5х3,5
2)
3) 6-5х 2
4) –(2-3х)+4(6+х)1
5)
6)
Проверочная работа по теме: РЕШЕНИЕ НЕРАВЕНСТВ. (8 класс)
Вариант -2
Решите неравенство, ответ запишите в виде промежутка.
1) 7х4,2
2)
3) 0,6-2х
4) –(2х+1)3(х+2)
5)
6)
Проверочная работа по теме: РЕШЕНИЕ НЕРАВЕНСТВ. (8 класс)
Вариант -3
Решите неравенство, ответ запишите в виде промежутка.
1) 6х1,2
2) -12
3) 0,4+3х
4) –(4-х) 2(3+х)
5)
6)
Проверочная работа по теме: РЕШЕНИЕ НЕРАВЕНСТВ. (8 класс)
Вариант -4
Решите неравенство, ответ запишите в виде промежутка.
1) 0,4х 1,6
2)
3) 6,2+х
4) 4(1-х)0
5)
6)
№ | Неравенство | Решение на координатной прямой | Решение в виде числового промежутка |
1 | Х ≥ — 17 | _______________________________ | |
2 | Х ≤ 45 | _______________________________ | |
3 | Х ˃ 23 | _______________________________ | |
4 | Х ˂ 8 | _______________________________ | |
5 | Х ≥ 5 | _______________________________ | |
6 | Х ˃- 1 | _______________________________ | |
7 | Х ≤ — 21 | _______________________________ | |
8 | Х ˂ — 18 | _______________________________ | |
ВАРИАНТ 1 | Ф.И. | ||
№ | Неравенство | Решение на координатной прямой | Решение в виде числового промежутка |
1 | Х ˂ 14 | _______________________________ | |
2 | Х ≥ — 4 | _______________________________ | |
3 | Х ≤ — 6 | _______________________________ | |
4 | Х ˃ 23 | _______________________________ | |
5 | Х ≤ 4 | _______________________________ | |
6 | Х ˂ — 8 | _______________________________ | |
7 | Х ˃ — 3 | _______________________________ | |
8 | Х ≥ 30 | _______________________________ | |
ВАРИАНТ 2 | Ф.И. | ||
Самостоятельная работа на тему: «Свойства неравенств»
(Алгебра 8 класс УМК Ю.М. Колягина и др.)
Учитель математики МБОУ «Николаевская СОШ»
Ю. К. Меджидова
Вариант 1
- Сравнить с нулем число а, если
- Записать неравенство, которое получится, если к обеим частям неравенства 8>-2 прибавить число 1
- Записать неравенство, которое получится, если из обеих частей неравенства -5 вычесть число 10
- Записать неравенство, которое получится, если к обеим частям неравенства
прибавить число 3b
- Записать неравенство, которое получится, если из обеих частей неравенства
вычесть число 2c
- Умножить обе части данного неравенства на число m:
- Разделить обе части данного неравенства на число k:
- Доказать, что если
- Доказать, что если
Вариант 2
- Сравнить с нулем число а, если
- Записать неравенство, которое получится, если к обеим частям неравенства 8>-2 прибавить число 9
- Записать неравенство, которое получится, если из обеих частей неравенства -5 вычесть число 8
- Записать неравенство, которое получится, если к обеим частям неравенства
прибавить число 2b
- Записать неравенство, которое получится, если из обеих частей неравенства
вычесть число 3d
- Умножить обе части данного неравенства на число m:
- Разделить обе части данного неравенства на число k:
- Доказать, что если
- Доказать, что если
Вариант 3
- Сравнить с нулем число а, если
- Записать неравенство, которое получится, если к обеим частям неравенства 8>-2 прибавить число -3
- Записать неравенство, которое получится, если из обеих частей неравенства -5 вычесть число -5
- Записать неравенство, которое получится, если к обеим частям неравенства
прибавить число -2a
- Записать неравенство, которое получится, если из обеих частей неравенства
вычесть число -5d
- Умножить обе части данного неравенства на число m:
- Разделить обе части данного неравенства на число k:
- Доказать, что если
- Доказать, что если
Вариант 4
- Сравнить с нулем число а, если
- Записать неравенство, которое получится, если к обеим частям неравенства 8>-2 прибавить число -1
- Записать неравенство, которое получится, если из обеих частей неравенства -5 вычесть число -8
- Записать неравенство, которое получится, если к обеим частям неравенства
прибавить число -3a
- Записать неравенство, которое получится, если из обеих частей неравенства
вычесть число -3c
- Умножить обе части данного неравенства на число m:
- Разделить обе части данного неравенства на число k:
- Доказать, что если 4
- Доказать, что если
Вариант 1 №1. №2. №3. | Вариант 2 №1. №2. №3. |
Вариант 3 №1. №2. №3. | Вариант 4 №1. №2. №3. |
Вариант 5 №1. №2. №3. | Вариант 6 №1. №2. №3. |
Вариант 7 №1. №2. №3. | Вариант 8 №1. №2. №3. |
Вариант 9 №1. №2. №3. | Вариант 10 №1. №2. №3. |
Вариант 11 №1. №2. №3. | Вариант 12 №1. №2. №3. |
Вариант 13 №1. №2. №3. | Вариант 14 №1. №2. №3. |
Вариант 15 №1. №2. №3. | Вариант 16 №1. №2. №3. |
Вариант 17 №1. №2. №3. | Вариант 18 №1. №2. №3. |
Вариант 19 №1. №2. №3. | Вариант 20 №1. №2. №3. |
Вариант 21 №1. №2. №3. | Вариант 22 №1. №2. №3. |
Вариант 23 №1. №2. №3. №4. | Вариант 24 №1. №2. №3. №4. |
Вариант 25 №1. №2. №3. №4. | Вариант 26 №1. №2. №3. №4. |
Неравенство
Раздел неравенств QuickMath позволяет решить практически любое неравенство или систему неравенств в одной переменной. В большинстве случаев вы можете найти точные решения. Даже когда это невозможно, QuickMath может дать вам приблизительные решения практически любого уровня точности, который вам требуется. Кроме того, вы можете построить области, удовлетворяемые одним или несколькими неравенствами, по двум переменным, четко видя, где происходят пересечения этих областей.
Что такое неравенства?
Неравенства состоят из двух или более алгебраических выражений, соединенных символами неравенства. Символы неравенства:| < | менее |
| > | больше |
| <= | меньше или равно |
| > = | больше или равно |
| ! = Или <> | не равно |
Вот несколько примеров неравенства:
|
Решить
Команда Solve может использоваться для решения одного неравенства для одного
неизвестно со страницы основного решения
или одновременно решить систему многих неравенств в одном неизвестном из расширенной страницы решения.2 — 5 <0
Другими словами, QuickMath попытается найти решения, удовлетворяющие обоим неравенствам одновременно.
Перейти на страницу решения
Участок
Команда Plot из раздела Графики построит график любого неравенства две переменные. Для того чтобы построить область, удовлетворяющую одному неравенству с участием х и у, перейдите к основному Страница построения неравенства, где вы можете ввести неравенство и указать верхний и нижний пределы по x и y, которые вы хотите построить график для.Продвинутый Страница построения графика неравенства позволяет построить объединение или пересечение до 8 регионов на одном графике. Вы можете контролировать такие вещи, как или не показывать оси, где должны располагаться оси и какой аспект Соотношение участка должно быть. Кроме того, у вас есть возможность показать каждый отдельный регион сам по себе.
Уравнение говорит, что два выражения равны, а неравенство говорит что одно выражение больше, больше или равно, меньше или меньше или равно другому.Как и в случае с уравнениями, значение переменной для что неравенство истинно, является решением неравенства, и множество всех такими решениями является множество решений неравенства. Два неравенства с В одном и том же наборе решений находятся эквивалентные неравенства. Неравенства решаются с Следующие свойства неравенства.
СВОЙСТВА НЕРАВЕНСТВА
Для действительных чисел a, b и c:
(a) 
(одинаковое число может быть добавлено к обеим сторонам неравенства без изменения решение установлено.)
(б) 
(Обе стороны неравенства могут быть умножены на одно и то же положительное число без изменения набора решений.)
(с) 
(Обе стороны неравенства могут быть умножены на одно и то же отрицательное число
без изменения набора решений, пока направление неравенства
символ перевернут.)
Замена <на> приводит к эквивалентным свойствам.
ПРИМЕЧАНИЕ Поскольку деление определяется в терминах умножения, слово «умноженный» может быть заменен «разделенным» на части (b) и (с) свойств неравенства.
Обратите особое внимание на часть (с): если обе стороны неравенства умноженное на отрицательное число, направление символа неравенства должно быть наоборот. Например, начиная с истинного утверждения — 3 <5 и умножая обе стороны положительным числом 2 дают
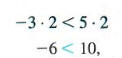
по-прежнему верное утверждение. С другой стороны, начиная с — 3 <5 и умножение обеих сторон на отрицательное число -2 дает истинный результат, только если направление символа неравенства меняется на противоположное.
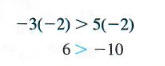
Аналогичная ситуация существует при делении обеих сторон на отрицательное число. В
Таким образом, можно сделать следующее заявление.
При умножении или делении обеих сторон неравенства на отрицательное
число, мы должны изменить направление символа неравенства, чтобы получить
эквивалентное неравенство.
ЛИНЕЙНЫЕ НЕРАВЕНСТВА Линейное неравенство определяется аналогично линейное уравнение.
Линейное неравенство в одной переменной — это неравенство, которое можно записать в форма

, где <> 0.
Пример 1
Решить неравенство -3x + 5> -7.
Используйте свойства неравенства. Добавление — 5 с обеих сторон дает
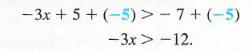
Теперь умножьте обе стороны на -1/3. (Мы также можем разделить на -3.) Поскольку -1/3 < 0, изменить направление символа неравенства.
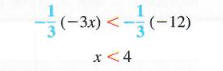
Исходное неравенство удовлетворяется любым вещественным числом меньше 4. множество решений можно записать {x | x <4}. График набора решений показан в Фигура 2.6, где скобка используется, чтобы показать, что само 4 не принадлежит к набору решений.
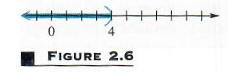
Набор {x | x <4}, решение для неравенства в Примере 1, является примером
интервала. Упрощенная нотация, называемая интервальной нотацией, используется для
интервалы записи. С этим обозначением интервал в Примере 1 может быть записан
как (-оо, 4). Символ -oo не является действительным числом; он используется, чтобы показать, что
интервал включает в себя все действительные числа меньше 4.Интервал (-oo, 4) является примером
открытый интервал, поскольку конечная точка 4 не является частью интервала. Примеры
другие наборы, написанные в интервальной записи, показаны ниже. Квадратная скобка
используется, чтобы показать, что число является частью графика, а скобка используется для
указать, что число не является частью графика. Всякий раз, когда два действительных числа а и
b используются для записи интервала в следующей таблице, предполагается, что
<б.
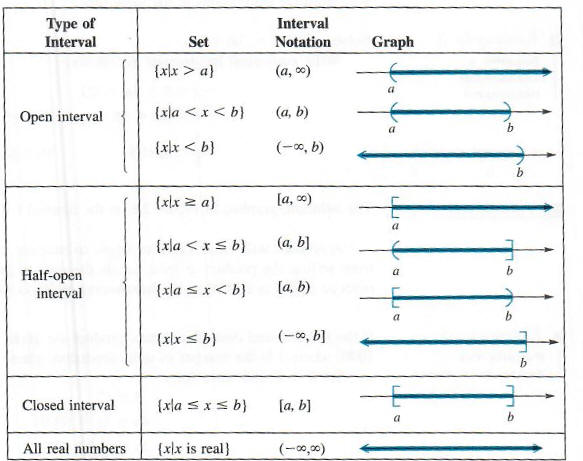
Пример 2
Решить 4 — 3y <7 + 2y.Запишите решение в интервальной записи и графике
решение в строке номера. Напишите следующую серию эквивалентов
неравенства.
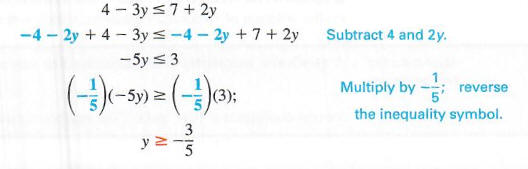
В нотации построителя множеств набор решений {y | y>
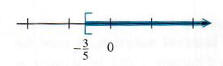
Отныне решения всех неравенств будут записываться с интервалом нотации.
ТРЕХЧАСТНОЕ НЕРАВЕНСТВО Неравенство -2 <5 + 3 м <20 в следующем
пример говорит, что 5 + 3 м между -2 и 20.Это неравенство можно решить
используя расширение свойств неравенства, приведенных выше, работая со всеми
три выражения одновременно.
Решить -2 <5 + 3m <20.
Запишите эквивалентные неравенства следующим образом.
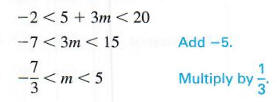
Решение представлено на рисунке 2.8

КВАДРАТИЧЕСКИЕ НЕРАВЕНСТВА Решение квадратичных неравенств зависит от
решение квадратных уравнений.
Квадратичное неравенство — это неравенство, которое можно записать в виде

Мы обсудим квадратные неравенства в следующем разделе.
Перейти на страницу построения графиков неравенства
,учебный план 8 класса
Ниже приведены необходимые навыки со ссылками на ресурсы, которые помогут с этим навыком. Мы также поощряем много упражнений и книжной работы. Curriculum Home
Важно: это только руководство.
Обратитесь в местный орган образования, чтобы узнать их требования.
8 класс | Числа
☐ Понимать двоичные числа
☐ Понимать шестнадцатеричные числа
☐ Преобразовать из базовой десятки в другую базовую цифру и наоборот.
☐ Округлить число до необходимого количества десятичных знаков или до необходимого числа значащих цифр.
☐ Поймите, что существуют другие системы счисления, такие как римские цифры, и как конвертировать из одной системы в другую.
☐ Понимать, что подразумевается под сурдом, и что, если вы не можете упростить число для удаления квадратного корня (или кубического корня и т. Д.), То это — сурд.
☐ Рассчитайте квадратный корень, используя «метод угадывания».
☐ Будьте знакомы с различными методами округления и когда их использовать
8 класс | Проценты
☐ Чтение, запись и определение процентов менее 1% и более 100%
☐ Применить проценты к: * Налог * Простой интерес * Цена продажи * Комиссия * Процентные ставки * Бесплатные
☐ Понять, что означает процентная ошибка, и как ее рассчитать.
☐ Понять, что подразумевается под процентными и базовыми пунктами.
☐ Понять, что подразумевается под процентным изменением (процентное увеличение или процентное уменьшение) и как его рассчитать.
☐ Понять, что подразумевается под процентной разницей, и как ее рассчитать.
8 класс | Соотношения
☐ Знать, как делить количество в заданном соотношении, например, Доля прибыли компании в соотношении инвестиций партнеров
8 класс | Измерение
☐ Решить уравнения / пропорции для преобразования в эквивалентные измерения в метрической системе измерения
☐ Знайте метрические единицы скорости (скорости): метров в секунду (мс-1) и километров в час (км-1)
☐ Распознайте разницу между выражениями «вес» и «масса» и узнайте правильную метрическую единицу веса (Ньютон)
☐ Решите уравнения / пропорции для преобразования в эквивалентные измерения из метрики в обычные системы измерения и наоборот.
☐ Решить уравнения / пропорции для преобразования в эквивалентные измерения в стандартной системе измерений США
☐ Знайте стандартные американские единицы скорости (скорости): футы в секунду (к / с) и мили в час (миль / ч).
☐ Распознайте разницу между выражениями «вес» и «масса» и узнайте правильную стандартную единицу веса США (фунт-сила)
☐ Знать метрические единицы ускорения и как рассчитать ускорение с учетом начальной скорости, конечной скорости и временного интервала.
☐ Преобразовать градусы Фаренгейта в градусы Цельсия и наоборот.
,Система уравнений и неравенств
- Учебный ресурс
- Проводить исследования
- Искусство и Гуманитарные науки
- Бизнес
- Инженерная технология
- Иностранный язык
- история
- математический
- Наука
- Социальная наука
Топ подкатегорий
- Advanced Math
- алгебра
- Basic Math
- Исчисление
- Геометрия
- Линейная Алгебра
- Предварительная алгебра
- Предварительное исчисление
- Статистика и вероятность
- Тригонометрия
- другое →
Топ подкатегорий
- Астрономия
- Астрофизика
- Биология
- Химия
- Науки о Земле
- Наука об окружающей среде
- Наука о здоровье
- Физика
- другое →
Топ подкатегорий
- Антропология
- Закон
- Политология
- Психология
- Социология
- другое →
Топ подкатегорий
- Бухгалтерский учет
- Экономика
- Финансы
- Управление
- другое →
Топ подкатегорий
- Аэрокосмическая Техника
- Биоинженерия
- Химическая инженерия
- Гражданское строительство
- Компьютерные науки
- Электротехника
- Промышленный инжиниринг
- Машиностроение
- Веб-дизайн
- другое →
Топ подкатегорий
- Архитектура
- Связь
- английский
- Гендерные исследования
- Музыка
- исполнительских искусств
- Философия
- Религиоведение
- Написание
- другое →
Топ подкатегорий
- Древняя история
- Европейская история
- История США
- Всемирная история
- другое →
Топ подкатегорий
- хорватский
- чешский
- финский
- греческий
- хинди
Транскрипция
1 Схема учебной программы. Дата пересмотра. Алгебра I. Единица руководства для учебной программы. ЕДИНИЦА 1: 27 ДНЕЙ. Единица 1 — Отдельные переменные Выражения / Уравнения / Неравенства I. Сводная информация по единице / Основные вопросы: К концу восьмого класса учащиеся научились решать линейные уравнения в одной переменной и применили графические и алгебраические методы для анализа и решения систем линейных уравнений от двух переменных.Теперь студенты анализируют и объясняют процесс решения уравнения. Студенты развивают беглое письмо, интерпретацию и перевод между различными формами линейных уравнений и неравенств и используют их для решения проблем. Они осваивают решение линейных уравнений и применяют соответствующие методы решения и законы показателей для создания и решения простых показательных уравнений. Почему возможно не иметь решения или бесконечно много решений уравнения или неравенства? Как решение неравенства похоже / отличается от решения уравнения? Как вы классифицируете и представляете решения уравнения / неравенства? Когда было бы полезно и / или необходимо решить уравнение для другой переменной в этом уравнении? II.Навыки / Концепции: Учащиеся смогут решать линейные уравнения в одной переменной и распознавать особые случаи, в том числе тождества и противоречия (все реалы и решения нет). Студенты смогут писать и интерпретировать выражения и уравнения. Решить линейные неравенства в одной переменной, наборы решений графа и выразить набор решений в интервальной записи. Перестановка формул для выделения интересующего количества (буквальные уравнения). III. Отдельные термины и символы: аддитивный коэффициент пересечения Коэффициент пересечения Обозначение интервала Рациональные числа Составное неравенство Иррациональные числа Решение константы Подобные условия Неравенство Координатная плоскость Буквенное уравнение Уравнение Происхождение Единица Процентная ставка Формула Процент Изменяемая идентичность Процентное изменение Неравенство Доля IV.Конец блока Общая задача: внутренние документы V. Предлагаемая формативная практика оценки: внутренние документы VI. Процесс обучения (до, во время, после): до: учащиеся работали с эквивалентностью между двумя выражениями в третьем классе. В средней школе они работали с одношаговыми линейными уравнениями и многошаговыми линейными уравнениями в одной переменной. Они также решили уравнения вида x + p = q и xp = q для случаев, когда p, q и x были неотрицательными рациональными числами. Кроме того, студенты были ознакомлены с личностями и противоречиями.Студенты также узнали, что неравенства, такие как x> c, имеют бесконечно много решений.
2 VII. VIII. IX. В 7 и 8 классах ученики переводили задачи решения задач в уравнения. Студенты также манипулировали уравнениями, решая различные переменные (буквальные уравнения). После: В последующих единицах и курсах студенты будут решать уравнения и системы уравнений или неравенств и интерпретировать решения алгебраически и графически путем разложения на множители, заполнения квадрата, использования квадратной формулы и построения графиков квадратичных функций для решения квадратных уравнений; путем решения и интерпретации решений уравнений, включающих полиномиальные, рациональные, радикальные и экспоненциальные выражения; и анализируя влияние упрощенных радикальных или рациональных выражений на решение системы уравнений, включающей такие выражения.2 Ресурсы: Алгебра I Учебник Холта: Khan Academy Poll Everywhere Schoology Социальные стандарты: согласованы со следующими общими основными государственными стандартами NQ.1 A-CED2 NQ.3 A-CED4 ASSE-1B A-REI1 A-CED1 A-REI3 UNIT 2 : 25 ДНЕЙ Блок 2 — Линейные уравнения (две переменные) X. Резюме блока / основные вопросы: Этот блок основывается на предыдущем опыте работы с данными с учащихся, предоставляя студентам более формальные средства оценки соответствия модели данным. Студенты используют методы регрессии для описания приблизительно линейных отношений между величинами.Они используют графическое представление и знание контекста, чтобы выносить суждения о целесообразности линейных моделей. Кроме того, они создают и решают уравнения, неравенства и системы линейных уравнений. Как вы решаете оптимальный метод для построения уравнения / неравенства? Как вы решаете, оптимальный метод для решения системы уравнений? Как решения уравнения / неравенства с двумя переменными отличаются от решений с одной переменной? Как вы можете использовать линейные уравнения и неравенства для моделирования результатов реальной ситуации? XI.Навыки / Концепции: Студенты смогут
3 XII. Создайте уравнение линии в стандартной форме, форме точки-наклона и форме пересечения наклона с учетом нескольких представлений (таблица, график и т. Д.). Интерпретируйте скорость изменения в различных контекстах. Решайте системы линейных уравнений графически и алгебраически. Решайте системы линейных неравенств графически. Определите арифметические последовательности. Отдельные термины и символы: Арифметическая последовательность Согласованная / несогласованная система Зависимые / независимые системные перехваты Пересечение Линейная функция Линейное неравенство Параллельные линии Перпендикулярные линии Наклон / скорость изменения Решение системы линейных неравенств Преобразование линейных уравнений XIII.Конец блока Общая задача: внутренние документы XIV. Предлагаемая формативная практика оценки: внутренние документы XV. Прогресс в обучении (до, во время, после): до: учащиеся определили, описали и сравнили ситуации, представляющие постоянные темпы изменений. Кроме того, учащиеся использовали переменные для представления двух величин и определили независимые и зависимые отношения в графиках, таблицах и уравнениях. После: Эти темы также будут пересмотрены в будущих курсах математики. Учащиеся будут представлять и анализировать функции несколькими способами, анализировать характеристики функций (экспоненциальные, логарифмические и тригонометрические) и применять знания о функциях для интерпретации ситуаций.XVI. Заблуждения: анализ таблиц данных, которые увеличиваются через различные интервалы. В стандартной форме (ax + by = c), a представляет наклон, а b — y-пересечение. Неопределенный наклон против отсутствия наклона. Уравнения вертикальных и горизонтальных линий. Перпендикулярные склоны (противоположные обратные). Затенение двух переменных линейных неравенств. XVII. Ресурсы: Algebra I Holt Учебник: Khan Academy Poll Everywhere Schoology Socrative
4 XVIII. Стандарты: Соответствует следующим Общим основным государственным стандартам N-Q.1 F-IF3 NQ.3 F-IF6 A-CED1 F-IF7A A-CED2 F-IF9 A-CED3 F-BF1A A-REI5 F-BF3 A-REI6 F-LE1A A-REI10 F-LE1B A-REI11 F -LE2 A-REI12 F-LE3 F-LE5 S-ID5 S-ID6 S-ID7 S-ID8 S-ID9 БЛОК 3: 20 ДНЕЙ Блок 3 — Функции и взаимосвязи XIX. Краткое содержание / основные вопросы: в более ранних классах учащиеся определяют, оценивают и сравнивают функции и используют их для моделирования отношений между величинами. В этом разделе студенты изучат функциональные обозначения и разработают концепции предметной области и диапазона. Они выходят за пределы функций просмотра как процессов, которые принимают входные данные и дают выходы, и начинают просматривать функции как объекты самостоятельно.Они исследуют множество примеров функций, в том числе последовательности; они интерпретируют функции, данные графически, численно, символически и в устной форме, переводят между представлениями и понимают ограничения различных представлений. Они работают с функциями, представленными графиками и таблицами, имея в виду, что в зависимости от контекста эти представления могут быть приблизительными и неполными. Их работа включает в себя функции, которые могут быть описаны или аппроксимированы формулами, а также те, которые не могут.Когда функции описывают отношения между величинами, возникающими из контекста, учащиеся рассуждают о единицах измерения этих величин. Как вы определяете домен и диапазон функции? Каковы основные характеристики различных изученных функций? Как преобразования влияют на родительские функции? XX. Навыки / Концепции: Учащиеся смогут понять концепцию функции и использовать функцию обозначения. Определите домен и диапазон от различных отношений. Классифицируйте функции по множественным представлениям (линейное, квадратичное, экспоненциальное, радикальное).Преобразуйте различные функции из родительских функций. XXI. Отдельные термины и символы: Обозначение функции функции зависимой переменной домена с общей разницей
5 Диапазон независимых родительских функций переменной Отношение квадратно-корневая функция XXII. Конец блока Общая задача: внутренние документы XXIII. Предлагаемая формативная практика оценки: внутренние документы XXIV. Прогресс в обучении (до, во время, после): до: учащиеся ознакомились с определением функции, но не использовали обозначения функций.Анализируя график, студенты описывали, где функция увеличивалась или уменьшалась, а также была ли функция линейной или нелинейной. Кроме того, студенты должны были различать линейные и нелинейные отношения в графиках, таблицах и контексте. После: Эта тема также будет вновь рассмотрена в будущих курсах, где студенты будут представлять и анализировать функции несколькими способами, анализировать характеристики функций (экспоненциальные, логарифмические и тригонометрические) и применять знания функций для интерпретации ситуаций.XXV. Заблуждения: в обозначениях функций f (x) означает f раз x. Смешение домена и диапазона. Отношение против функции (то есть повторяющиеся значения y не являются функцией). Область и диапазон радикальной функции должны быть [0, бесконечность). Отражения с участием радикальных функций (отрицательные внутри радикала). XXVI. Ресурсы: Algebra I Holt Учебник: Khan Academy Poll Everywhere Schoology Socrative XXVII. Стандарты: Соответствует следующим Общим основным государственным стандартам NQ.1 F-IF1 NQ.2 F-IF2 NQ.3 F-IF4 A-REI10 F-IF5 F-IF7B F-IF9 F-BF3 F-LE1A F-LE1B F -LE1C F-LE2 F-LE3 F-LE5
6 БЛОК 4: 18 ДНЕЙ Блок 4 — Полиномы XXVIII.Подведение итогов / основные вопросы. В этом разделе учащиеся смогут классифицировать многочлены, писать многочлены в стандартной форме и оценивать выражения многочленов. Они смогут выполнять арифметические операции и смогут разложить многочлены, используя различные методы. Работа, которую студенты выполняют с полиномиальной арифметикой и видением структуры в выражениях, подкрепляет их работу линейными, квадратичными, экспоненциальными и радикальными уравнениями. Как факторинг полиномов связан с умножением полиномов? Какие методы и шаблоны используются для разложения многочленов? Как операции и свойства действительных чисел связаны с полиномами? XXIX.Навыки / Концепции: Студенты смогут определить аспекты полиномов. Выполнять арифметические операции над полиномами (за исключением деления). Факторные полиномы с использованием GCF, разности квадратов и триномов. XXX. Отдельные термины и символы: биноминальная степень Наибольший общий множитель, ведущий коэффи- циент Мономиальная полиномиальная совершенная квадратная полиномиальная простая факторизация Стандартная форма Триномиал XXXI. XXXII. XXXIII. Конец блока. Общая задача: Внутренние документы. Предлагаемая практика формативной оценки: Внутренние этапы изучения документов (до, во время, после): До: Студенты написали, оценили и упростили алгебраические выражения с рациональными числами и показателями степени.Они также были подвержены всем законам экспоненты, включая рациональные и отрицательные экспоненты. После: На будущих курсах студенты будут манипулировать, оценивать и упрощать алгебраические и числовые выражения. Они также будут делить многочлены. Студенты также будут складывать, вычитать, умножать и делить рациональные выражения;
7 упрощают сложные дроби; фактор-квадратичные и полиномы высших степеней, включая разность квадратов; и применить свойства логарифмов.Студенты будут решать полиномиальные уравнения графически и алгебраически. XXXIV. Заблуждения: неправильное использование правил экспоненты. Умножение сроков против объединения одинаковых терминов. Пренебрежение методом GCF в начале проблемы. Признавая разницу двух квадратов. Студенты считают, что сумма двух квадратов является факториальной. XXXV. Ресурсы: Algebra I Holt Учебник: Khan Academy Poll Everywhere Schoology Socrative XXXVI. Стандарты: Соответствует следующим Общим основным государственным стандартам. ASSE-1A ASSE-2 A-APR1 A-APR3 ЕДИНИЦА 5: 25 ДНЕЙ Блок 5 — Квадратики XXXVII.Подведение итогов / основные вопросы. В этом разделе учащиеся рассматривают квадратичные функции, сравнивая ключевые характеристики квадратичных функций с характеристиками линейных и экспоненциальных функций. Они выбирают из этих функций для моделирования явлений. Студенты учатся предугадывать график квадратичной функции, интерпретируя различные формы квадратичных выражений. В частности, они идентифицируют действительные решения квадратного уравнения как нули связанной квадратичной функции. Студенты расширяют свой опыт с функциями, чтобы включить более специализированные функции абсолютное значение, шаг и те, которые кусочно определены.Как вершинная форма квадратного уравнения связана с преобразованиями? Когда один метод решения квадратного уравнения может быть более выгодным для использования, чем другой? Каковы основные особенности графика квадратичной функции? Как узнать, когда радикальное выражение находится в простейшей форме? XXXVIII. Навыки / Концепции: Учащиеся смогут идентифицировать вершину, ось симметрии и перехваты квадратичного. График квадратичной функции с использованием таблиц. Решите (найдите нули) квадратики путем проверки, факторинга, заполнения квадрата и квадратичной формулы.
8 XXXIX. Упростите радиканды. Упростите радикальные выражения, включающие сложение, вычитание и умножение. Избранные термины и символы: ось симметрии, дополняющая квадрат, подобный радикалам Максимальный минимум параболы Квадратичное уравнение Квадратичная функция Радикальное уравнение Радикальное выражение Радика и корни Вершина ноль (и) функции XL. XLI. Конец блока Общая задача: Внутренние документы. Предлагаемая практика формативной оценки: Внутренние документы XLII.Прогресс в обучении (до, во время, после): до: учащиеся понимают линейные отношения до этого блока. Ранее в этом году студенты познакомились с графиками, таблицами, уравнениями и преобразованиями, касающимися квадратичных отношений. Студенты написали и оценили алгебраические выражения с рациональными числами и целыми показателями. После: На будущих курсах студенты будут манипулировать, оценивать и упрощать алгебраические и числовые выражения; сложение, вычитание, умножение и деление полиномов и комплексных дробей.Студенты также упростят сложные дроби, множители квадратичных и полиномов высших степеней и применят свойства логарифмов. Студенты будут решать полиномиальные уравнения графически и алгебраически. XLIII. Заблуждения: не узнайте трином, который исходит от идеального квадрата. Корни против нулей. Вытащить неидеальные квадраты из радикалов. При добавлении радикалов учащиеся вместе добавляют коэффициенты и радиканды. Распознайте разницу между четными и нечетными показателями под радикалом. XLIV.Ресурсы: Algebra I Holt Учебник: Khan Academy
9 Социология опроса повсюду Socrative XLV. Стандарты: Соответствует следующим Общим основным государственным стандартам N-RN.3 A-CED1 NQ.1 A-CED2 ASSE-3A A-REI4A ASSE-3B A-REI4B A-APR3 A-REI10 A-REI11 F-IF7A F- IF8A F-IF9 F-BF1A F-BF3 ЕДИНИЦА 6: 15 ДНЕЙ Блок 6 — Экспоненциальный XLVI. Подведение итогов / основные вопросы. До этого момента в алгебре 1 учащиеся сосредоточились на линейных и квадратичных уравнениях и функциях.Теперь они будут включать понятия экспоненциальных уравнений и функций. Студенты научатся оценивать, определять и составлять график экспоненциальных функций. Они будут решать проблемы, связанные с экспоненциальным ростом и распадом. Студенты призывают предварительное знание последовательностей и полиномов, чтобы идентифицировать геометрические последовательности и найти n-й член. Каковы сходства и различия между экспоненциальными функциями и другими, которые мы изучали? Как вы идентифицируете, записываете, отображаете и интерпретируете величины, которые растут или затухают экспоненциально? Каковы характеристики экспоненциальных функций? XLVII.Навыки / Концепции: учащиеся смогут использовать свойства показателей степени для преобразования выражений для показательных функций с целыми показателями. График простых экспоненциальных функций. Интерпретировать графики показательных функций. Создавайте простые экспоненциальные функции для моделирования реального жизненного контекста. Используйте технологии для преобразования экспоненциальных функций. Определите ситуации, которые будут соответствующим образом смоделированы с помощью экспоненциальных функций. Сравните экспоненциальный рост и затухание. Определите геометрические последовательности. XLVIII.Отдельные термины и символы: общий коэффициент Сложный процент Экспоненциальный спад Экспоненциальная функция Экспоненциальный рост Постороннее решение Геометрическая последовательность
10 XLIX. Конец блока Общая задача: внутренние документы L. Предлагаемые методы формативной оценки: внутренние документы LI. Прогресс в обучении (до, во время, после): до: учащиеся имеют практические знания о процентах, включая расчетные чаевые, налоги, скидки и процентное изменение. Они также понимают, что переписывание выражения в различных формах в контексте проблемы может пролить свет на проблему и на то, как соотносятся ее величины.Например, aa = 1,05a означает, что увеличение на 5% аналогично умножению на After: В будущих курсах студенты будут представлять и анализировать функции несколькими способами, анализировать характеристики функций (экспоненциальный, логарифмический и тригонометрический) и применять знание функций для интерпретации ситуаций. Студенты также смогут рассчитывать конкретные значения для независимой переменной, используя технологии и логарифмические функции. LII. Заблуждения: понимание переменных теперь является показателем степени.Время ежегодное. Разнообразие составных интервалов (полугодовой, квартальный, ежемесячный, еженедельный). LIII. Ресурсы: Algebra I Holt Учебник: Технологии Графические калькуляторы Академия хана Опрос везде Schoology Socrative LIV. Стандарты: Соответствует следующим Общим основным государственным стандартам NQ.1 A-CED1 NQ.3 A-CED2 ASSE-1B A-REI10 ASSE-3A F-IF3 ASSE-3C F-IF7E F-IF8B F-IF9 F-BF1A F -LE1A F-LE1C F-LE2 F-LE5 БЛОК 7: 10 ДНЕЙ Блок 7 Одномерная статистика
11 LV.LVI. Подведение итогов / основные вопросы. По мере того, как учащиеся приобретают математические инструменты из изучения алгебры и функций, они применяют эти инструменты в статистических контекстах. Они научатся обобщать, представлять и интерпретировать данные по одной переменной и проводить измерения центральной тенденции и разброса. Кроме того, они будут представлять и интерпретировать данные по двум категориальным и количественным переменным. Наконец, они будут интерпретировать линейные модели, чтобы сделать выводы. Как вы можете оценить статистику по данным, отображаемым в гистограмме? Как вы можете сравнить наборы данных, используя коробочные графики? На какую меру центральной тенденции больше всего влияет выброс? Зачем? Навыки / Концепции: Учащиеся смогут представлять набор данных с помощью блочного графика (прямоугольник и усы), точечного графика (линейный график) и гистограмм.Сравните форму двух или более наборов данных, используя показатели центральной тенденции (среднее значение и медиана). Сравните разброс двух или более наборов данных с использованием стандартного отклонения или межквартильного диапазона. Используйте среднее значение и стандартное отклонение для интерпретации нормального распределения. LVII. Отдельные термины и символы: Комбинированные составные события Зависимые события Экспериментальная вероятность Частота Независимые события Средняя медиана Взаимно исключающая вероятность выброса Квартильный диапазон Теоретическая вероятность LVIII. Конец блока Общая задача: внутренние документы LIX.LX. Предлагаемые формативные методы оценки: внутренние этапы изучения документов (до, во время, после): до: учащиеся создавали изображения и гистограммы для решения проблем. Студенты также представляли и интерпретировали данные на линейном графике. Студенты отображали, анализировали и суммировали данные. Студенты строили и анализировали диаграммы рассеяния и использовали эти представления для решения проблем и прогнозов. Учащиеся ранее анализировали закономерности, тенденции или распределения данных в различных контекстах.Они использовали меры центральной тенденции для анализа ситуаций и решения проблем. После: На будущих курсах студенты расширят свое понимание нормального распределения и будут использовать статистические модели для решения реальных проблем.
12 LXI. Заблуждения: левый против правого перекоса. Представительство каждого квартиля (25%). Смешивая среднее и среднее. Не все максимальные / минимальные значения являются выбросами. Смешайте теоретическую и экспериментальную вероятность. Определение пробного пространства из коллекции предметов.LXII. Ресурсы: Algebra I Holt Учебник: Технологии Графического Калькулятора Khan Academy Poll Everywhere Schoology Socrative LXIII. Стандарты: приведены в соответствие со следующими общими стандартами состояния ядра N-Q.1 N-Q.3 S-ID1 S-ID2 S-ID3 S-ID4
.


















































