Презентация основное свойство дроби сокращение дробей 6 класс: Презентация на тему: «Сокращение дробей» 6 класс – Презентация к уроку по математике (6 класс) по теме: Презентация «Основное свойство дроби». 6 класс
Слайд 1
Основное свойство дроби 1Слайд 2
Назовите числитель и знаменатель каждой дроби. Что показывает знаменатель дроби? Что показывает числитель дроби? На какие группы можно разделить данные числа? Дробные — обыкновенные и десятичные дроби; натуральные числа, число нуль. Вспомним! 2 Прочитайте числа. 2. Переведите дроби в неправильную дробь .
Слайд 3
10 35 Найдите наибольший общий делитель числителя и знаменателя дробей . Когда и как возникли дроби? У людей с древних времен появилась необходимость измерять время, расстояния, площади, углы и другие величины. Потребность в более точном измерении привела к тому, что используемые единицы измерения стали делить на части. А это привело к появлению дробей. Историческая минутка. 3 16 40 8 20 4 28 45 60
Слайд 4
6 3 8 4 4 2 От первого пирога отрезали 3/6 части, от второго – 4/8, от третьего – 2/4. Что вы можете сказать об этих дробях? Пример 4 Вспомним! Равные дроби — различные обозначения одного и того же числа.
Слайд 5
Равные дроби — различные обозначения одного и того же числа. 2 1 6 3 6:3 3:3 6 3 4 2 2 1 8 4 8 4 8:4 4:4 2 1 4 2 4:2 2:2 2 1 Изучение нового материала 5
Слайд 6
Основное свойство дроби: Две равные дроби являются различными записями одного и того же числа. b a b∙c a∙c где с – натуральное число b a b : d a : d где d – натуральное число и общий делитель чисел a и b 6 Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь. Например:
Слайд 7
Практическая работа. 7 I I I I I I I I I I I I I I I I I I I I I
Слайд 8
Они равные, потому, что использовали основное свойство дроби. Умножали числитель и знаменатель дроби на одно и то же число. Что можно сказать об этих дробях и почему? 8
Слайд 9
C D I I I I I I I А В I I I www.konspekturoka.ru 9 Равные дроби изображаются равными отрезками. Что можно сказать об цветных частях данных отрезков? Выделенные части отрезков AB, CD равны
Слайд 10
10 Разделите числитель и знаменатель каждой из дробей на 9.
Слайд 11
11 Умножить числитель и знаменатель каждой из дробей на одно и тоже число.
Слайд 12
НОД (2450;3500) = 2∙5∙5∙7 = 350 НОК (2450;3500) = 2∙5∙2∙5∙5∙7∙7 = 3500∙7=24500 НОД (792;2178) = 2∙3∙3∙11 = 198 НОК (792;2178) = 2178∙2∙2 = 8712 2450 2·5 245 5 49 7 7 7 1 3500 2·5·2·5 35 5 7 7 1 792 2 396 2 198 3 99 3 33 3 11 11 1 2178 2 1089 3 263 3 121 11 11 11 1 НОД (2450;3500) = ? НОК (2450;3500) = ? НОД (792;2178) = ? НОК (792;2178) = ? 12
Слайд 13
Ответить на вопросы: 13 Сформулируйте основное свойство дроби. Чем являются равные дроби? В чем состоит основное свойство дроби? Изменится ли дробь, если ее числитель и знаменатель умножить на 15, а потом разделить на 3?
 Описание слайда:
Описание слайда:Сокращение дробей
2 слайд Описание слайда:
Описание слайда:Из каких частей состоит обыкновенная дробь? Числитель Дробная черта Знаменатель
3 слайд Описание слайда:
Описание слайда:Какая дробь называется правильной? Дробь называется правильной, если ее числитель меньше знаменателя. Т.е. a < b
4 слайд Описание слайда:
Описание слайда: Описание слайда:
Описание слайда:Распределите по столбикам дроби: Правильные дроби Неправильные дроби
6 слайд Описание слайда:
Описание слайда:Проверяем: Правильные дроби Неправильные дроби
7 слайд Описание слайда:
Описание слайда:Сформулируйте основное свойство дроби. Если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится дробь, равная данной.
8 слайд
Найдите равные среди дробей:
9 слайд Описание слайда:
Описание слайда:Сократите дроби = = =
10 слайд Описание слайда:
Описание слайда:Сократите дробь: Нарисуйте получившуюся дробь у себя в тетради.
11 слайд Описание слайда:
Описание слайда:Задания в учебнике: № 243 (а), 244, 245, 246
12 слайд Описание слайда:
Описание слайда:Задания в учебнике: № 247, 249, 252
13 слайд
Домашнее задание: п. 9, № 268, 269, 271
14 слайд Описание слайда:
Описание слайда:Задания в учебнике: №252, 260, 261, 266, 267
15 слайд Описание слайда:
Описание слайда:Домашнее задание: п. 9, № 270, 272, 274
16 слайд Описание слайда:
Описание слайда:Спасибо за урок!!! Спасибо за урок!!!

Курс повышения квалификации
Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДБ-449670
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий









 Предмет: математика Класс:6 «а»
Предмет: математика Класс:6 «а»
Тема урока.Сокращение дробей.
Цель. Способствовать созданию условий для самостоятельного открытия учащимися правила сокращения обыкновенных дробей.
Задачи:
Обучающая: подвести учащихся к «открытию» способа сокращения дробей, разработать алгоритм действий и научиться пользоваться им;
Развивающая: развивать логическое мышление, внимательность, самостоятельность, умение рассуждать, делать выводы;
Воспитывающая:продолжить работу по воспитанию любви к предмету, любознательности, чувства сопереживания и уважительного отношения к мнению одноклассников, культуры общения. воспитывать умение сотрудничать в паре.
Тип урока: урок изучения и первичного закрепления новых знаний.
Методы и приёмы: словесный, наглядный, исследовательский, проблемно-поисковый.
Формы организации познавательной деятельности: индивидуальная, работа в парах.
Средства обучения: учебник, карточки, пословица, мультимедийная доска (проектор)
Место урока в учебном плане. На изучение математики в 6 классе отводится 5 уроков в неделю. Данный урок стоит первым уроком в теме «Сокращение дробей». Всего отводится 3 урока на данную тему
Этапы урока
Организационно – технологический блок
Деятельность учителя
Деятельность учащихся
1. Организационно – психологический настрой детей на урок
Задача:организационная деятельность учащихся.
Форма: фронтальная
Результат: учащиеся настроены на восприятие информации. Подготовленность к уроку.
Прием контроля: наблюдение и самоконтроль.
— Прозвенел звонок для вас
все зашли спокойно в класс
Встали все у парт красиво,
улыбнулись всем учтиво
На меня все посмотрели и за парты тихо сели.
— Откроем тетради, запишем число. Оставили строчку для темы урока.
— Пусть наш урок будет интересным и даст нам возможность открыть новые знания.
Сегодня на уроке вы будете работать в парах, самостоятельно и все вместе.
Подпишите свои оценочные листы.
В верхнем правом углу нарисуйте смайлик своего настроения в начале урока.
Сегодня вы будете оценивать не только свою работу на уроке, но и моё объяснение нового материала. В конце урока вы поставите мне оценку.
Желаю всем нам успеха! В путь!
Никакая наука не приводит в порядок ум так, как это делает математика.
Как вы, ребята, понимаете эти слова?
Не зря утверждал великий русский ученый М.В. Ломоносов, что “Математику уже затем учить надо, что она ум в порядок приводит”. Вот и мы с вами должны регулярно проводить “зарядку для ума”, а значит, заниматься математикой.
Приветствуют учителя.
Настраиваются на работу на уроке.
Активизация
познавательного внимания, его концентрация на словах учителя.
Записывают дату.
Высказывают своё мнение.
2. Актуализация знаний с последующей мотивацией.
Задача: мотивировать учащихся к учебной деятельности.
Форма:работа в парах.
Результат: учащиеся настроены на восприятие информации. Подготовленность к уроку.
Прием контроля: наблюдение и
самоконтроль.
Отгадайте о чём я говорю?
Она бывает охотничья, барабанная и математическая. (дробь)
На протяжении всей своей жизни мы постоянно сталкиваемся с дробями.
Я предлагаю составить кластер: в центре — название дроби, а по сторонам — умения.
Что такое дробь?
Что показывает дробь?
Что вы знаете о дробях?
Какие действия мы умеем выполнять с дробями?
Сегодня на уроке мы научимся выполнять ещё одно действие с обыкновенными дробями и наш кластер умений увеличится.
–В начале урока мы выполним практическую работу:
Исследовательская работа. (работают в парах)
Ну, а теперь проведем небольшое исследование.
На каждой парте лежит круг и записана дробь.
Раскрасьте нужную часть фигуры и вырежете её.
1 ряд:
1 парта1/3
2 парта 2/6
3 парта 6/18
2 ряд:
1 парта: 3/4
2парта: 6/8
3 парта:12/16
Наложите получившиеся части друг на друга
Что вы заметили? Сделайте вывод
— Молодцы! Оцените свою практическую работу.
Мы убедились, что разные дроби могут обозначать одну и ту же часть фигуры.
Как из дроби 1/3 получить дробь 2/6, 6/18?
Что помогает нам утверждать, что эти дроби равны?
Можно ли из дроби 12/16 получить 6/8? Что нужно сделать?
Из дроби 12/16 получить 3/4?
Если числитель и знаменатель дроби делят на одно и тоже число, то в математике говорят данную дробь сократили.
Как вы думаете чему сегодня на уроке чем мы будем учиться?
дроби
Одну долю или несколько равных долей единицы называют дробью или дробным числом.
В дроби число, стоящее над чертой, называют числителем дроби, а число, стоящее под чертой, называют знаменателем дроби. Знаменатель дроби показывает, на сколько равных частей разделена единица, а числитель дроби показывает, сколько таких частей взято.
Работа в паре.
Наблюдают и делают выводы
Умножить числитель и знаменатель дроби на 2
Основное свойство дроби.
Разделить числитель и знаменатель дроби на 2
Разделить числитель и знаменатель дроби на 4
Правильно сокращать дроби.
3. Формулировка темы и цели урока.
Задача.Мотивировать учащихся
на формулировку темы и цели урока.
Форма:беседа.
Результат:
сформирована тема и цель урока
— Попробуйте сформулировать тему нашего урока.
Поставим перед собой цель и задачи.
Как может звучать правило сокращения дробей?
Где мы можем проверить нашу гипотезу?
Откройте учебник на стр. 39
— Прочитаем утверждение, которое здесь записано.
— Сравните данное утверждение с тем, которое мы сделали сами.
Что мы не сказали?
Рассмотрим пример: сократить дробь: 18/24.
Что нужно найти чтобы сократить данную дробь?
Найдем НОД(18,24) = 6
Значить на какое число мы можем сократить дробь?
Разделим числитель и знаменатель на 6.
Какая дробь получилась?
А какой НОД у чисел 3 и 4?
Как называются такие числа?
Дроби, у которых НОД числителя и знаменателя равен 1, называются несократимыми дробями.
Учащиеся в тетради записывают тему урока
Пробуют формулировать правило.
Предлагают в учебнике.
Сравнивают результаты. Убеждаются в совпадении.
Что дроби можно сокращать на НОД
Учащиеся работают в тетрадях, раскладывают числа 18 и24 на простые множители, находят НОД. Один ученик работает на доске
На 6
3/4
1
Взаимно простыми
4.
Физминутка.
Встали все из-за парт. Сейчас я проверю на сколько вы внимательны и всё ли вы знаете о дробях. Я говорю утверждение, если вы с ним согласны вы хлопаете в ладоши над головой 3 раза, если я не права вы топаете ногами1-2.
Дробь ½ меньше 1
Дробь ¾ несократимая
Дробь 4/6 нельзя сократить
6/7 неправильная дробь
15/8 неправильная дробь
12/18 сократимая
5/5 равна единице
165/45 сократимая
5. Первичное закрепление.
Задача. Формирование умения по применению на практике правила сокращения дробей.
Форма:работа у доски и самостоятельно.
Результат:применяют правило сокращения дробей
Спасибо, присаживайтесь.
О чём мы сегодня говорим?
Что значит сократить дробь?
Всегда ли удобно сокращать дроби, находя НОД?
есть и другой способ: сокращать поэтапно.
Сократим дробь эту же дробь, но другим способом.
Чтобы выполнить постепенное сокращение данной дроби, что нам нужно знать?
Давайте вспомним признаки делимости, которые мы знаем.
Сократим постепенно данную дробь, используя признаки делимости.
Общих делителей у этих чисел нет! Получили несократимую дробь.
Сокращение закончилось.
А теперь попробуйте сами сократить дробь:
8/16 = 4/8= 2/4=1/2 (1 у доски)
25/75 = 5/15=1/3(4 чел. У доски)
63/144 = (на 9) 7/16 (2 с обратной стороны ) или на 3 (21/48, 7/16)
322/84 = (на 2) 161/42 (на 7) 23/6
(самостоятельно проверка со слайда)
На каком шаге сокращения было трудно определить, на что числа можно разделить?
Как рассуждали?
Оцените работу над новым материалом, было ли вам всё понятно, или возникли трудности.
О сокращении дробей
Работа в тетрадях
неправильная
на2, на 5, на 10, на 3, на 9
Работа со слайдом.
Физминутка
Задача. Снять напряжение и усталость глаз.
Поднять глазки вверх, вниз. Вправо, влево.
Зажмурить, открыть.
Поморгать.
Физминутка для глаз
6.Самостоятельная работа.
Задача.
Организовать самоконтроль учащихся по умению применять правило сокращения дробей.
Форма: индивидуальная
Результат:
выполнение с.р.
Прием контроля: самопроверка
Как вам больше понравилось сокращать? Почему?
Что нужно знать для правильного сокращения дроби?
Приступаем к самостоятельной работе. Постарайтесь внимательно определить на какое число можно сократить дробь, и правильно выполнить деление.
1 вариант
4/6 15/12 75/100 35/21 198/126
2 вариант
3/9 12/8 25/100 42/35 162/126
После выполнения работы эталон выполнения выводится на экран.
Критерии оценивания.
Оцените свою работу.
— если есть исправь свои ошибки.
7.Итог урока. Д/з
Рефлексия
Ребята, дома вы продолжите закреплять навык применения правила сокращения дробей
Продолжите фразы
Сегодня на уроке я сделал(а) открытие…
Я научился (лась)…
— Так какое правили мы сегодня изучали?
— Как формулируется правило сокращения дробей?
— Давайте вернёмся к нашему кластеру о дробях. Какое умение можно добавить?
— Как вы думаете всё ли мы теперь знаем о обыкновенных дробях?
при дальнейшем изучении математики вы научитесь выполнять сложение, вычитание, сравнение обыкновенных дробей с разными знаменателями, умножать, делить и возводить дроби в степень.
Записывают домашнее задание.
П.9 № 268(а,б) №274(а)
№271(а,б)
Высказывают своё мнение.
Оцените свою работу на уроке.
Нарисуйте смайлик своего настроения.
— На этом мы и заканчиваем наш урок.
Концентрация внимания на словах учителя.
Деятельность учителя
Деятельность учащихся
— Прозвенел звонок для вас
все зашли спокойно в класс
Встали все у парт красиво,
улыбнулись всем учтиво
На меня все посмотрели и за парты тихо сели.
— Откроем тетради, запишем число. Оставили строчку для темы урока.
— Пусть наш урок будет интересным и даст нам возможность открыть новые знания.
Сегодня на уроке вы будете работать в парах, самостоятельно и все вместе.
Подпишите свои оценочные листы.
В верхнем правом углу нарисуйте смайлик своего настроения в начале урока.
Сегодня вы будете оценивать не только свою работу на уроке, но и моё объяснение нового материала. В конце урока вы поставите мне оценку.
Желаю всем нам успеха! В путь!
Никакая наука не приводит в порядок ум так, как это делает математика.
Как вы, ребята, понимаете эти слова?
Не зря утверждал великий русский ученый М.В. Ломоносов, что “Математику уже затем учить надо, что она ум в порядок приводит”. Вот и мы с вами должны регулярно проводить “зарядку для ума”, а значит, заниматься математикой.
Приветствуют учителя.
Настраиваются на работу на уроке.
Активизация
познавательного внимания, его концентрация на словах учителя.
Записывают дату.
Высказывают своё мнение.
Отгадайте о чём я говорю?
Она бывает охотничья, барабанная и математическая. (дробь)
На протяжении всей своей жизни мы постоянно сталкиваемся с дробями.
Я предлагаю составить кластер: в центре — название дроби, а по сторонам — умения.
Что такое дробь?
Что показывает дробь?
Что вы знаете о дробях?
Какие действия мы умеем выполнять с дробями?
Сегодня на уроке мы научимся выполнять ещё одно действие с обыкновенными дробями и наш кластер умений увеличится.
–В начале урока мы выполним практическую работу:
Исследовательская работа. (работают в парах)
Ну, а теперь проведем небольшое исследование.
На каждой парте лежит круг и записана дробь.
Раскрасьте нужную часть фигуры и вырежете её.
1 ряд:
1 парта1/3
2 парта 2/6
3 парта 6/18
2 ряд:
1 парта: 3/4
2парта: 6/8
3 парта:12/16
Наложите получившиеся части друг на друга
Что вы заметили? Сделайте вывод
— Молодцы! Оцените свою практическую работу.
Мы убедились, что разные дроби могут обозначать одну и ту же часть фигуры.
Как из дроби 1/3 получить дробь 2/6, 6/18?
Что помогает нам утверждать, что эти дроби равны?
Можно ли из дроби 12/16 получить 6/8? Что нужно сделать?
Из дроби 12/16 получить 3/4?
Если числитель и знаменатель дроби делят на одно и тоже число, то в математике говорят данную дробь сократили.
Как вы думаете чему сегодня на уроке чем мы будем учиться?
дроби
Одну долю или несколько равных долей единицы называют дробью или дробным числом.
В дроби число, стоящее над чертой, называют числителем дроби, а число, стоящее под чертой, называют знаменателем дроби. Знаменатель дроби показывает, на сколько равных частей разделена единица, а числитель дроби показывает, сколько таких частей взято.
Работа в паре.
Наблюдают и делают выводы
Умножить числитель и знаменатель дроби на 2
Основное свойство дроби.
Разделить числитель и знаменатель дроби на 2
Разделить числитель и знаменатель дроби на 4
Правильно сокращать дроби.
— Попробуйте сформулировать тему нашего урока.
Поставим перед собой цель и задачи.
Как может звучать правило сокращения дробей?
Где мы можем проверить нашу гипотезу?
Откройте учебник на стр. 39
— Прочитаем утверждение, которое здесь записано.
— Сравните данное утверждение с тем, которое мы сделали сами.
Что мы не сказали?
Рассмотрим пример: сократить дробь: 18/24.
Что нужно найти чтобы сократить данную дробь?
Найдем НОД(18,24) = 6
Значить на какое число мы можем сократить дробь?
Разделим числитель и знаменатель на 6.
Какая дробь получилась?
А какой НОД у чисел 3 и 4?
Как называются такие числа?
Дроби, у которых НОД числителя и знаменателя равен 1, называются несократимыми дробями.
Учащиеся в тетради записывают тему урока
Пробуют формулировать правило.
Предлагают в учебнике.
Сравнивают результаты. Убеждаются в совпадении.
Что дроби можно сокращать на НОД
Учащиеся работают в тетрадях, раскладывают числа 18 и24 на простые множители, находят НОД. Один ученик работает на доске
На 6
3/4
1
Взаимно простыми
Встали все из-за парт. Сейчас я проверю на сколько вы внимательны и всё ли вы знаете о дробях. Я говорю утверждение, если вы с ним согласны вы хлопаете в ладоши над головой 3 раза, если я не права вы топаете ногами1-2.
Дробь ½ меньше 1
Дробь ¾ несократимая
Дробь 4/6 нельзя сократить
6/7 неправильная дробь
15/8 неправильная дробь
12/18 сократимая
5/5 равна единице
165/45 сократимая
Спасибо, присаживайтесь.
О чём мы сегодня говорим?
Что значит сократить дробь?
Всегда ли удобно сокращать дроби, находя НОД?
есть и другой способ: сокращать поэтапно.
Сократим дробь эту же дробь, но другим способом.
Чтобы выполнить постепенное сокращение данной дроби, что нам нужно знать?
Давайте вспомним признаки делимости, которые мы знаем.
Сократим постепенно данную дробь, используя признаки делимости.
Общих делителей у этих чисел нет! Получили несократимую дробь.
Сокращение закончилось.
А теперь попробуйте сами сократить дробь:
8/16 = 4/8= 2/4=1/2 (1 у доски)
25/75 = 5/15=1/3(4 чел. У доски)
63/144 = (на 9) 7/16 (2 с обратной стороны ) или на 3 (21/48, 7/16)
322/84 = (на 2) 161/42 (на 7) 23/6
(самостоятельно проверка со слайда)
На каком шаге сокращения было трудно определить, на что числа можно разделить?
Как рассуждали?
Оцените работу над новым материалом, было ли вам всё понятно, или возникли трудности.
О сокращении дробей
Работа в тетрадях
неправильная
на2, на 5, на 10, на 3, на 9
Работа со слайдом.
Поднять глазки вверх, вниз. Вправо, влево.
Зажмурить, открыть.
Поморгать.
Физминутка для глаз
Как вам больше понравилось сокращать? Почему?
Что нужно знать для правильного сокращения дроби?
Приступаем к самостоятельной работе. Постарайтесь внимательно определить на какое число можно сократить дробь, и правильно выполнить деление.
1 вариант
4/6 15/12 75/100 35/21 198/126
2 вариант
3/9 12/8 25/100 42/35 162/126
После выполнения работы эталон выполнения выводится на экран.
Критерии оценивания.
Оцените свою работу.
— если есть исправь свои ошибки.
Ребята, дома вы продолжите закреплять навык применения правила сокращения дробей
Продолжите фразы
Сегодня на уроке я сделал(а) открытие…
Я научился (лась)…
— Так какое правили мы сегодня изучали?
— Как формулируется правило сокращения дробей?
— Давайте вернёмся к нашему кластеру о дробях. Какое умение можно добавить?
— Как вы думаете всё ли мы теперь знаем о обыкновенных дробях?
при дальнейшем изучении математики вы научитесь выполнять сложение, вычитание, сравнение обыкновенных дробей с разными знаменателями, умножать, делить и возводить дроби в степень.
Записывают домашнее задание.
П.9 № 268(а,б) №274(а)
№271(а,б)
Высказывают своё мнение.
Оцените свою работу на уроке.
Нарисуйте смайлик своего настроения.
— На этом мы и заканчиваем наш урок.
Концентрация внимания на словах учителя.
Дроби Дроби
Дроби Дроби

число
Тема урока
№
число
Тема урока
№
число
Тема урока
№
число
Тема урока
№
Лист самоконтроля
На каждом этапе оцени свою работу, выбрав в нужной строке знак «+».
Этап
Учебная деятельность
Выполнил безошибочно
Выполнил с ошибками
Испытывал большие затруднения
Начало урока
Настрой на урок
1 шаг
Повторение пройденного материала
2 шаг
Выполнение пробного задания — действия
3 шаг
Построение проекта выхода из затруднения
4 шаг
Реализация проекта выхода из затруднения
5 шаг
Первичное закрепление
6 шаг
Самостоятельная работа с самопроверкой
7 шаг
Применение нового материала в системе знаний
8 — 9 шаги
Инструктаж по домашнему заданию и итог урока
Оценочный лист в начале урока
Фамилия имя
Практическая
работа
Работа над новой темой
Самостоятельная
работа
самооценка
в конце урока
Оценка за урок :
Я считаю, что поработал на _____
Оценка учителю_________
Оценочный лист в начале урока
Фамилия имя
Практическая
работа
Работа над новой темой
Самостоятельная
работа
самооценка
в конце урока
Оценка за урок :
Я считаю, что поработал на _____
Оценка учителю_________
Оценочный лист в начале урока
Фамилия имя
Практическая
работа
Работа над новой темой
Самостоятельная
работа
самооценка
в конце урока
Оценка за урок :
Я считаю, что поработал на _____
Оценка учителю_________
Оценочный лист в начале урока
Фамилия имя
Практическая
работа
Работа над новой темой
Самостоятельная
работа
самооценка
в конце урока
Оценка за урок :
Я считаю, что поработал на _____
Оценка учителю_________
Оценочный лист в начале урока
Фамилия имя
Практическая
работа
Работа над новой темой
Самостоятельная
работа
самооценка
в конце урока
Оценка за урок :
Я считаю, что поработал на _____
Оценка учителю_________
Оценочный лист урока.
Фамилия имя
Практическая работа
Работа над новой темой
Самостоятельная работа
самооценка
Критерии оценки:
9 баллов
«5»
8-6 баллов
«4»
5 баллов
«3»
Меньше 5
Тема не усвоена
Ответьте на вопросы:
На уроке я работал активно/пассивно
Своей работой на уроке я доволен/не доволен
Материал урока мне был полезен/бесполезен
При решении заданий я испытывал трудности/всё получалось
Считаю, мне нужно обратить внимание на ________________________________
Оценка за урок :
Я считаю, что поработал на _____
Оценка учителя_________
Оценочный лист урока.
Фамилия имя
Практическая работа
Работа над новой темой
Самостоятельная работа
самооценка
Критерии оценки:
9 баллов
«5»
8-6 баллов
«4»
5 баллов
«3»
Меньше 5
Тема не усвоена
Ответьте на вопросы:
На уроке я работал активно/пассивно
Своей работой на уроке я доволен/не доволен
Материал урока мне был полезен/бесполезен
При решении заданий я испытывал трудности/всё получалось
Считаю, мне нужно обратить внимание на ________________________________
Оценка за урок :
Я считаю, что поработал на _____
Оценка учителя_________
Этап урока | Деятельность учителя | Деятельность учащихся | |||
Личностные УУД | Познавательные УУД | Коммуникативные УУД | Регулятивные УУД | ||
Организационный этап | Подведение итогов контрольной работы, анализ типичных ошибок | адекватно воспринимают оценку учителя и одноклассников |
| умение принимать точку зрения другого | обнаруживают и формулируют учебную проблему совместно с учителем |
Постановка цели и задачи урока. Мотивация учебной деятельности учащихся | задача про Витю Верхоглядкина ( слайд 1) | проявляют широкий интерес к новому учебному материалу, способам решения новых учебных задач | анализ с целью выделения признаков (существенных, несущественных) | высказывают свою точку зрения и пытаются её обосновать | обнаруживают и формулируют учебную проблему совместно с учителем |
Актуализация знаний | № 212-211 ( слайды 3-9 ) исследуем чертежи и попробуем сформулировать основное свойство (слайд 5) | проявляют познавательный интерес к изучению математики | выдвижение гипотез и их обоснование | умение отстаивать свою точку зрения, аргументируя её, подтверждать аргументы фактами | определяют цель учебной деятельности с помощью учителя и самостоятельно, осуществляют поиск средств её достижения |
Первичное усвоение новых знаний | № 214( слайды 10) выполнить в тетради и на экране, 216, 217 | проявляют широкий интерес к новому учебному материалу, способам решения новых учебных задач | поиск и выделение информации | умение оформлять свои мысли в устной и письменной речи с учётом своих учебных и жизненных речевых ситуаций | составляют план выполнения заданий совместно с учителем |
Информация о домашнем задании, инструктаж по его выполнению | п.8 № 237, 238 |
|
|
| работают по составленному плану |
Рефлексия (подведение итогов занятия) | А теперь вернёмся к задаче в начале урока и ответим на вопрос задачи. | проявляют широкий интерес к новому учебному материалу, способам решения новых учебных задач | анализ с целью выделения признаков (существенных, несущественных) | высказывают свою точку зрения и пытаются её обосновать |
|
Математика 6 класс
Урок № 1: Дроби. Основное свойство дроби
Цели урока:
1. Образовательные: ввести основное свойство дроби; сформировать умение применять данное свойство на практике; ввести новое действие сокращение дробей.
2. Воспитательные: воспитание аккуратности, дисциплины, настойчивости, ответственного отношения к учебе.
3. Развивающие: развитие памяти, речи, любознательности, познавательного интереса;
формирование представлений о математическом языке, развитие коммуникативных умений и навыков.
Об уроке.
Данный урок является первым по теме «Основное свойство дроби». Цель устного счёта – подготовить учащихся к продуктивной работе на протяжении всего урока, взяты задания на восстановление опорных знаний и умений. На уроке вводится понятие основного свойства дроби, умения — это свойство использовать при выполнении конкретных заданий. Также вводится новое действие с дробями- сокращение дробей. В ходе урока проводится работа по поддержанию и совершенствованию ранее сформированных знаний и умений, в частности, вычислительных навыков. Предлагаются задачи, способствующие развитию учащихся, требующие сообразительности, внимания, анализа и обобщения имеющихся знаний.
Структура урока:
Постановка цели урока.
Устный счёт.
Объяснение нового материала.
Закрепление, отработка нового материала.
Самостоятельная работа.
Итог урока. Домашнее задание.
Ход урока
1. Постановка цели урока.
Добрый день, ребята! Как ваше настроение? Давайте поприветствуем друг друга улыбкой и сохраним хорошее настроение в течение всего урока.
Ребята, нужны ли в жизни человеку математические знания?
А математика может обойтись без дробей?
Почему? Что обозначает слово «дробь?
В русском языке слово «дробь» появилось в 8 веке, оно происходит
от глагола «дробить» — разбивать, ломать на части. В первых учебниках математики (в 17 веке) дроби так и назывались – «ломанные числа».
Современную систему записи дробей с числителем и знаменателем создали в Индии. Только там писали знаменатель сверху, а числитель снизу и не писали дробной черты. На
Руси дроби называли долями, позднее «ломаными числами». Перед вами названия некоторых дробей:
1/2 — половина, полтина;
1/3- треть;
1/6 – полтреть;
1/4 — четь; 1/8 – полчеть:
1/5 – пятина;
1/10 – десятина.
Дробная черта появилась в записи дробей лишь около 300 лет назад. Названия «числитель и знаменатель» ввел в употребление греческий математик Максим Пеануд. Долгое время дроби считались самым трудным разделом математики. У немцев даже сложилась поговорка «попасть в дроби», что означает попасть в трудное положение.
— Хорошо. Итак мы знаем, что дроби можно получить двумя способами. Знаем, что обыкновенная дробь обозначает. (Что-то целое разделили на н частей и взяли таких частей м.)
— Чем же мы сегодня на уроке будем заниматься? Как вы думаете?
2. Устный счёт
С помощью моделей обыкновенных дробей покажите дроби и объясните, что обозначает числитель и знаменатель каждой дроби.
5/12
3/8
5/6
3. Объяснение нового материала.
А сейчас используя модели дробей проиллюстрируйте дроби:
6/8
9/12
3/4
— Что вы можете заметит, какие дроби получились по величине? (Равные.)
— Можно ли между этими дробями поставить знак равенства? (Да.)
6/8 = 9/12 = 3/4
— Как из дроби 3/4 можно получить дробь 6/8? (3 * 2/4 * 2)
— Как из дроби 3/4 можно получить дробь 9/12? (3 * 3/4 * 3)
— Какое действие надо было выполнить чтобы получить дроби равные данным? (Для получения дроби равной данной надо числитель и знаменатель умножить на одно и тоже число.)
— Как из дроби 6/8 получить дробь 9/12? (6 : 2/8 : 2 = 3 * 3/4 * 3 = 9/12)
Т.е. для получения равных дробей можно числитель и знаменатель делить на одно и тоже число.
Вывод: при умножении и делении числителя и знаменателя дроби на одно и тоже число (кроме нуля) ее величина не изменится.
Это свойство очень важное и его называют основным свойством дроби.
Тема нашего урока так и называется «Дроби. Основное свойство дробей».
Открываем тетради, записываем дату, классная работа и тему урока. Открыли учебник на стр. 8 и прочитали данное свойство. Отметили важные слова в этой формулировке. (Числитель, знаменатель и равные.)
Задание: замените дроби 3/12, 15/25, 8/16, 9/15 – равными им дробями с меньшим знаменателем. (Дети выполняют в тетрадях.)
Какое действие вы для этого использовали? (Делили числитель и знаменатель на одно и тоже число.)
Это действие мы будем называть – сокращением дробей.
4. Закрепление нового материала.
Какое действие необходимо выполнить? Проговариваем, на какое число необходимо разделить числитель и знаменатель.
4/10 = 2/5
2/6 = 1/3
9/15 = 3/5
12/16 = 3/4
Следующее задание. Объясните, почему дроби выбранные вами равны дроби 3/7?
6/14
9/21
12/28
Задание «Угадай слово».
Необходимо сократить дроби и каждому правильному ответу найти соответствующую букву. Задание считается выполненным, если слово записано в тетради.
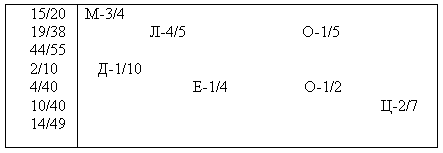
Итак, какое слово у вас получилось. «Молодец».
5. Самостоятельная работа.
Сейчас вы выполните самостоятельную работу на листочках. После выполнения мы работами обмениваемся с соседями по парте и проверяем. Критерии оценивания такие же как всегда:
Без ошибок-5.
Одна ошибка-4.
Две ошибки-3.
Для проверки правильные ответы написаны заранее на обратной стороне доски.
Сдаем листочки с поставленным оценками, я проверю ваши результаты и свои.
2 варианта.
Мы многое успели сегодня на уроке сделать и уже достаточно устали поэтому небольшая игра: дроби написанные на листочках необходимо разложить по двум мешочкам. У каждого мешочка есть своя метка, т.е. в мешок можно положить дроби равные данным.
2/4 2/3 8/12 12/24 3/6 4/6 12/18 9/18 5/10 48/72

Молодцы, к доске можно выбегать бегом. Итак все дроби разложили по своим мешочкам, очень хорошо.
6. Итог урока. Домашнее задание.
— Что нового вы сегодня на уроке узнали? Сформулируйте основное свойство дроби. Молодцы! Сегодня на уроке мы совершенствовали свои знания и умения, применяя полученные знания.
— Откроем дневники и запишем домашнее задание:
Выучить основное свойство дроби и выполнить (стр. 8 — 9), № 6, 7, 8
Самостоятельная работа с взаимопроверкой (10 минут)
Самостоятельная работа«Дроби. Основное свойство дробей»
Вариант №1
Самостоятельная работа
«Дроби. Основное свойство дробей»
Вариант №2
Запишите в виде дроби число:
Две пятых;
Тридцать четыре сорок третьих;
Сто двадцать семь тысячных.
Запишите в виде дроби число:
Семь тринадцатых;
Двадцать две шестидесятых;
Тридцать девять сотых.
Сократите дробь:
24/30
12/48
20/36
14/56
Сократите дробь:
44/100
32/72
36/60
18/90
Приведите дроби:
4/9, 5/6, 7/2 к знаменателю 18
Приведите дроби:
7/8, 5/16, 21/40 к знаменателю 80
Изобразите какую-нибудь геометрическую фигуру (прямоугольник, круг или отрезок) и закрасьте ту ее часть, которая соответствует дроби:
5/8;
15/25
Изобразите какую-нибудь геометрическую фигуру (прямоугольник, круг или отрезок) и закрасьте ту ее часть, которая соответствует дроби:
8/12;
7/9
5*. Какое натуральное число надо вписать вместо буквы, чтобы было верным равенство:
14/21 = x/3
m/18 = 5/9
5*. Какое натуральное число надо вписать вместо буквы, чтобы было верным равенство:
17/51 = 1/n
15/y = 5/6
Для мешочка
2/42/3
8/12
12/24
3/6
4/6
12/18
9/18
5/10
48/72
1/224/36
¾ — м1/10 – д
¼ — е
1/5 – о
½ — о
2/7 — ц
4/5 – л
Выберите документ из архива для просмотра:
Выбранный для просмотра документ Сокращение дробей.pptx
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:6 класс математика Сокращение дробей 10.05.2012
2 слайд Описание слайда:
Описание слайда:Цели: ввести понятие сокращения дробей и дать определение несократимой дроби; учить сокращать дроби, используя признаки делимости чисел и основное свойство дроби
3 слайд Описание слайда:
Описание слайда:На основании чего мы можем умножать числитель и знаменатель дроби? На основании основного свойства дроби мы можем умножать числитель и знаменатель дроби Вспомним! 10.05.2012 www.konspekturoka.ru №261
4 слайд Описание слайда:
Описание слайда:На какие числа можно разделить числитель и знаменатель дроби? На 2, 3, 4, 6, 12. Если разделить числитель и знаменатель дроби на наибольший общий делитель, на 12. Какая дробь получится? = = = — такое преобразование называется сокращением дроби. Определение. Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби. При сокращении дроби ее числовое значение не меняете изменилась только ее запись. Изучение нового материала 10.05.2012 www.konspekturoka.ru 24 36 24 : 12 36 : 12 2 3 24 36 2 3
5 слайд Описание слайда:
Описание слайда:Что можно сказать о числах 2 и 3? Если дробь больше сократить нельзя, то ее называют несократимой Они взаимно простые. Определение. Дробь, числитель и знаменатель которой взаимно простые числа, называется несократимой. 10.05.2012 www.konspekturoka.ru 2 3 4 5 7 8 1 3 15 31 5 39
6 слайд Описание слайда:
Описание слайда:Способы сокращения дробей: 1. Сократить числитель и знаменатель на их НОД. = = 2. Последовательно сокращать на общие делители. = = = = 3. Разложить числитель и знаменатель на множители, а потом сократить. = = 1 1 1 1 1 1 10.05.2012 www.konspekturoka.ru 150 225 150 : 75 225 : 75 2 3 150 225 50 75 3 ∙ 5 ∙ 2 ∙ 5 5 ∙ 5 ∙ 3 ∙ 3 2 3 150 225 15 ∙ 10 25 ∙ 9 2 3 10 15
7 слайд Описание слайда:
Описание слайда:Назвать несократимую дробь. Почему эти дроби являются несократимыми? 10.05.2012 www.konspekturoka.ru 3 7 7 14 10 40 32 48 7 9 3 4
8 слайд Описание слайда:
Описание слайда:10.05.2012 www.konspekturoka.ru Назовите наибольший делитель числителя и знаменателя. Разделите числитель и знаменатель данной дроби на их общий делитель. Как называется получившаяся дробь? = = = = наибольший делитель числителя и знаменателя — 2 наибольший делитель числителя и знаменателя — 3 наибольший делитель числителя и знаменателя -70а наибольший делитель числителя и знаменателя – 7п 4 6 2 3 15 12 5 4 70а 140а 1 2 35п 21п 5 3 №242
9 слайд Описание слайда:
Описание слайда:Какую часть часа составляют 45 мин, 12 мин, 15 мин, 40 мин, 35 мин? 10.05.2012 www.konspekturoka.ru №246
10 слайд Описание слайда:
Описание слайда:Сократите дробь: Общий делитель 3с. = = = Числитель и знаменатель дроби представим в виде множителей: = Назовите общий делитель числителя и знаменателя: = Общий делитель 25b. = Общий делитель 3bc. 10.05.2012 www.konspekturoka.ru 25ab 100bc 25 ∙ a ∙ b 100 ∙b ∙ c a 4c 9abc 30bcd 3a 10d 15ac 18bc 15 ∙a∙c 18∙b∙c 5a 6b 9 ∙ a ∙ b ∙ c 30 ∙ b ∙ c ∙d
11 слайд Описание слайда:
Описание слайда:Сократите дроби:
12 слайд Описание слайда:
Описание слайда:Найдите среди чисел 1, 3, 10, 12, 13, 15, 16, 39 пары взаимно простых чисел. 1 и 3; 1 и 10; 1 и 12; 1 и 13; 1 и 15; 1 и 16; 1 и 39; 3 и 10; 3 и 13; 3 и 16; 10 и 13; 10 и 39; 12 и 13; 13 и 15; 13 и 16; 15 и 16; 16 и 39. 10.05.2012 www.konspekturoka.ru №255
13 слайд Описание слайда:
Описание слайда:Представить в виде обыкновенной несократимой дроби: 0,2 = 0,8 = 0,5 = 0,15 = 0,24 = 0,35 = 0,75 = 0,05 = 0,125 = 0,025 = 0,008 = 0,375 = 10.05.2012 www.konspekturoka.ru №245
14 слайд Описание слайда:
Описание слайда:10.05.2012 www.konspekturoka.ru Сократите дроби: = = = = = 6 = = 1 1 3 4 5 1 3 1 2 5 3 4 2 2 1 17 · 15 12 ·51 48 · 50 25 · 16 12 · 14 16 · 35 1 · 5 4 · 3 5 12 3 · 2 1 · 1 6 1 3 · 2 4 · 5 3 10
15 слайд Описание слайда:
Описание слайда:10.05.2012 www.konspekturoka.ru Сократите дроби: 2 = = = = = = = = = 2 2 3 3 1 3 9 1 1 3 1 1 22 · 12 36 · 33 6·15·4 18·27·10 82·15·16 12·41·20 2 · 1 3 · 3 2 9 1·5·2 3·9·5 1·1·2 3·9·1 2 27 2·3·4 3·1·4 2·1·1 1·1·1 2 1
16 слайд Описание слайда:
Описание слайда:Сократите дроби: 3 = = = = = = 10.05.2012 www.konspekturoka.ru 1 1 1 1 1 1 1 1 3 2 а·b b·c n·8m 12b·n а·d·c d·c·k а c а·1 1·c а·1·1 1·1·k а k 1·2m 3b·1 2m 3b
17 слайд Описание слайда:
Описание слайда:Сократите дроби: = 4 = = = = = = = 10.05.2012 www.konspekturoka.ru 5 6 3 1 2 4 1 2 19·11+19·5 38·20-38·8 19·(11+5) 38·(20-8) 24а·5b 25c·18 a 8·1·1·b 5· c·6·1 8b 30c 19·16 38·12 1·4 2·3 1·2 1·3 2 3
18 слайд Описание слайда:
Описание слайда:Какую часть килограмма составляют 125 г, 250 г, 750 г? Сколько граммов в 1 кг? 125 г = 250 г = 750 г = 10.05.2012 www.konspekturoka.ru №248
19 слайд Описание слайда:
Описание слайда:Ответить на вопросы: 10.05.2012 www.konspekturoka.ru Что значит сократить дробь? Что меняется при сокращении дробей? В каком случае дробь будет несократимой? Какую дробь называют несократимой? Приведите примеры несократимой дроби. На каком свойстве основано сокращение дробей?

Курс повышения квалификации
Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДВ-191543
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:Сокращение дробей.
2 слайд Описание слайда:
Описание слайда:Устная работа. Найдите НОД и НОК чисел: а) 12 и 8 б) 9 и 15 в) 11 и 44 г) 8 и 20 д) 12 и 20 е) 10 и 15 Замените каждую дробь, дробью со знаменателем 36:
3 слайд Описание слайда:
Описание слайда:Сокращение дробей. Как в первых учебниках математики 17 века называли дроби? Какие правила нам помогут в изучении нового материала? Ломанные Основное свойство дроби и делимость чисел.
4 слайд Описание слайда:
Описание слайда:Сокращение дробей. На какие числа можно разделить и числитель и знаменатель? Дана дробь:
5 слайд Описание слайда:
Описание слайда:Разделим и числитель и знаменатель дроби на 12. Равные дроби Сокращение дробей. Такое преобразование называют сокращением дробей. Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дробей.
6 слайд Описание слайда:
Описание слайда:1 способ сокращения дробей. Сокращать дроби можно постепенно, используя признаки делимости чисел. 135 180 27 36 9 12 3 4
7 слайд Описание слайда:
Описание слайда:2 способ сокращения дробей. Сокращать дроби можно используя нахождение НОД. 135 180 3 4 НОД(135; 180) = 45
8 слайд Описание слайда:
Описание слайда:3 способ сокращения дробей. Сокращать дроби можно используя разложение чисел на множители. 135 180 275 1810 935 9225 3 4 3 22
9 слайд Описание слайда:
Описание слайда:ОПРЕДЕЛЕНИЕ: Дробь, числитель и знаменатель которой взаимно простые числа, называется несократимой. Дробь сокращают до тех пор, пока в числителе и знаменателе не получат взаимно простые числа.
10 слайд Описание слайда:
Описание слайда:Закрепление. Назвать несократимые дроби:
11 слайд Описание слайда:
Описание слайда:Закрепление. № 244(а) № 242 № 246 — устно
12 слайд Описание слайда:
Описание слайда:Повторение: № 263 № 266
13 слайд Описание слайда:
Описание слайда:ИТОГ УРОКА. 1.Выпишите несократимые дроби:
14 слайд Описание слайда:
Описание слайда:ИТОГ УРОКА. 2. Какую часть составляет: а) 20 от 70; б) 12 от 60; в) 14 от 49?
15 слайд Описание слайда:
Описание слайда:Домашнее задание. П. 9 № 268 (а, б) № 271 (а, в) № 274 а
16 слайд Описание слайда:
Описание слайда:Спасибо за работу на уроке!

Курс повышения квалификации
Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДБ-640361
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Частичные дроби
Способ «дробления» дробей с полиномами в них.
Что такое частичные дроби?
Мы можем сделать this напрямую:
Как это:
2 x − 2 + 3 x + 1 = 2 (х + 1) + 3 (х − 2) (х-2) (х + 1)
Которое можно упростить с помощью Rational Expressions до:
= 2x + 2 + 3x − 6 x2 + X-2x-2
= 5x-4 x2-X-2
… но как мы пойдем в обратном направлении?
Вот что мы собираемся открыть:
Как найти «части», которые составляют единственную дробь
(«частичные дроби»).
Почему мы хотим их?
Прежде всего … зачем мы их хотим?
, потому что каждая частичная дробь simpler.
Это может помочь решить более сложную дробь. Например, это очень полезно в Integral Calculus.
Частичная дробная часть
Так позвольте мне показать вам, как это сделать.
Метод называется «Частичное разложение дроби» и выглядит следующим образом:
Шаг 1: Коэффициент внизу
Шаг 2: Запишите одну частичную дробь для каждого из этих факторов
Step 3: Умножьте на нижнюю часть, чтобы у нас больше не было дробей
Шаг 4: Теперь найдите константы A1 и A2
Замена корней или «нулей» (x − 2) (x + 1) может помочь:
, и у нас есть ответ:
Это было легко! .Improper: градусов сверху — 2
градусов снизу — 1
Если у вас неправильное выражение, то сначала делайте длинное полиномиальное деление.
Факторинг Низа
Вы должны учитывать нижний полином. См. Факторинг в Алгебре.
Но не делайте их на комплексные числа … вам может потребоваться ограничить некоторые факторы квадратичными (так называемыми неприводимыми квадратичными, потому что любой дальнейший факторинг приводит к комплексным числам):
Example: (x2−4) (x2 + 4)
- x2−4 можно учесть в (x − 2) (x + 2)
- Но x2 + 4 множителей в комплексные числа, так что не делайте этого
Случшее, что мы можем сделать, это:
(X-2) (х + 2) (x2 + 4)
Так факторы могут быть комбинацией
- линейные факторы
- неприводимые квадратичные факторы
Когда у вас есть квадратичный коэффициент, вам нужно включить эту частичную дробь:
B1x + C1 (Ваш квадратичный)
Факторы с экспонентами
Иногда вы можете получить коэффициент с показателем степени, например, (x − 2) 3.
Вы можете выбрать свой собственный способ решения этой проблемы … Я решил вычесть 4-е уравнение из 2-го для начала:
| 0 | = | A1 | + | B | ||
| -2 | = | 2A1 | + | 6B | ||
| 0 | = | 3A1 | + | 9B | + | 6C |
| 1 | = | A1 | + | C |
Затем вычтите 2 раза 1-е уравнение из 2-го:
| 0 | = | A1 | + | B | ||
| -2 | = | 4B | ||||
| 0 | = | 3A1 | + | 9B | + | 6C |
| 1 | = | A1 | + | C |
Теперь я знаю, что B = — (1/2) .

