Примеры по математике на умножение и деление 5 класс: Тренажёр по алгебре (5 класс) на тему: Отработка навыка умножения и деления. Задания для 5 класса

Тренажёр по алгебре (5 класс) на тему: Отработка навыка умножения и деления. Задания для 5 класса

Содержание

По теме: методические разработки, презентации и конспекты

по математике на тему «Умножение и деление степеней», 7 класс

Материал содержит подробный конспект урока….

Умножение и деление дробей 6 класс

Презентация, конспект урока…

Обобщающий урок по теме «Лес». Закрепление вычислительных навыков умножения и деления трехзначных чисел на однозначное число без перехода через разряд.

Пояснение к урокуВ последние годы в педагогической практике остро стал вопрос об активизации познавательной деятельности умственно отсталых школьников. Многолетняя практика педагогической работы в шко…

Урок — путешествие по теме «Умножение и деление степеней» 6 класс

Урок — путешествие по теме «Умножение и деление степеней» 6 класс…

Конспект урока по теме «Умножение и деление степеней» 7 класс

Урок в 7 классе по теме «Умножение и деление степеней»….

Презентация к уроку «Умножение и деление степеней». 7 класс.

Презентация к уроку алгебры в 7 классе по теме «Умножение и деление степеней» (урок — закрепление)….

Тренажер для отработки навыка программирования диалога с компьютером, 9 класс

Любую программу составлять нужно так, чтобы ее выполнение реализовывало диалог между компьютером и пользователем в понятной для человека форме. С этой целью для учащихся 9 класса разработана Пра…

Учебно-методический материал по алгебре (5 класс) на тему: Примеры на умножение и деление натуральных чисел

«Мастер-умножитель»

Предлагаются занимательные примеры. При решении каждого из них получается слово (для этого используем ключ).

1) Ключ 0 1 2 3 4 5 6 7 8 9

И ф л р н а м о г ь

689832 : 67 888982 : 43 181804 : 604

928564 : 91 595161 : 987 965280 : 32

147368 : 169 550940 : 65

767010 : 74 686868 : 546

2) Ключ 0 1 2 3 4 5 6 7 8 9

ь о л с т п а к р е

778 ∙ 73 1398 ∙ 25 102 ∙ 88

25945 ∙ 16 23458 ∙ 37 21333 ∙ 37

166 ∙ 49 83 ∙ 32 4102 ∙ 97

1023 ∙ 71 5489 ∙ 14

3) Ключ 0 1 2 3 4 5 6 7 8 9

к с о в а т е и н р

976968 : 27 947648 : 64 101188 : 82

956662 : 23 638638 : 77 657072 : 18

4) Ключ 0 1 2 3 4 5 6 7 8 9

ь л п е в о н к м а

128520 : 17 238280 : 28 87653 : 37

9972 : 12 73160 : 31 99374 : 22

96930 : 45 151656 : 71

5) Ключ 0 1 2 3 4 5 6 7 8 9

ь к у р п а н о л т

4127 ∙ 111 367 ∙ 34 2026 ∙ 76

3133 ∙ 155 28711 ∙ 16 883 ∙ 15

365 ∙ 131 452 ∙ 15 3367 ∙ 53

751 ∙ 165 1149 ∙ 85

1097 ∙ 443 10084 ∙ 45

328 ∙ 283 485 ∙ 17

6) Ключ 0 1 2 3 4 5 6 7 8 9

о м л ч п я с и а е

49110 : 321 967296 : 352 815670 : 19

81832 : 212 612469 : 143 511225 : 715

178192 : 344 865260 : 23

7) Ключ 0 1 2 3 4 5 6 7 8 9

а х м б н и о к е л

276504 : 984 922507 : 23 196317 : 99

954434 : 26 984256 : 14 778088 : 19

972928 : 32 962090 : 47

205407 : 787 826386 : 209

8) Ключ 0 1 2 3 4 5 6 7 8 9

л о с п р а к е т в

2591 ∙ 111 373 ∙ 244 2179 ∙ 28

1954 ∙ 175 142 ∙ 197 755 ∙ 47

773 ∙ 385 134 ∙ 187 508 ∙ 69

2113 ∙ 432 713 ∙ 905 375 ∙ 827

1477 ∙ 145 1993 ∙ 305

Тренажёр по математике (5 класс) на тему: Умножение и деление десятичных дробей

0,2∙3

0,7∙6

0,03∙2

4∙0,08

1,3∙2

1,2∙3

0,3∙2

0,9∙8

0,02∙3

6∙0,05

0,15∙10

3∙0,7

0,05∙8

0,16∙5

2,5∙4

0,6:2

1,5:3

6:10

7,2:2

0,012:4

1,9:10

0,6:3

29:10

0,64:8

2,8:8

17:100

2,4:12

3:6

0,4:5

4,8:12

0,8:2

2,7:9

0,054:6

32:10

0,16:4

0,04∙3

0,1∙7

0,8∙9

4∙0,006

0,09∙0

0,07∙0

1,3∙4

0,1∙8

0,06∙3

0,7∙8

0,03∙10

1,2∙5

0,07∙8

1,5∙4

0,27∙10

27:10

0,18:9

0,4:2

4,2:7

0,056:8

2,6:13

1,7:10

15:30

7,5:25

2:10

5:25

0,02:4

0,3:2

3,7:100

3,9:13

1,2:40

4:10

20:40

2,3:10

4,5:15

0,2∙6

0,07∙4

0,6∙7

0,5∙2

0,08∙6

7∙0,006

0,3∙5

0,09∙4

0,8∙8

0,23∙1

3∙0,17

0,04∙100

0,18∙5

0,05∙2

4∙0,21

0,14:7

4,8:8

0,28:4

450:100

0,045:9

4,2:14

4:5

0,9:10

0,03:6

0,6:30

0,49:0,7

0,016:0,8

1:0,5

1,6:0,4

100:125

0,7:0,35

0,4:0,8

0,72:0,9

1:0,25

2,8:0,14

0,2∙5

0,9∙7

1∙0,46

2,1∙3

0,004∙7

0,07∙7

0,5∙4

0,4∙5

0,7∙6

3,2∙2

0,07∙100

9∙0,09

5∙1,6

10∙0,46

1,25∙4

2,4:8

0,21:3

1:2

0,35:7

2,9:10

2,4:1000

3,6:18

3:2

0,7:2

31:10

0,7:0,2

4,5:0,9

3:0,1

0,32:0,4

7,5:0,25

3,6:0,04

270:100

0,12:6

0,072:9

0,28:7

0,6∙5

1,2∙5

1,3∙2

0,4∙9

0,004∙5

0,002∙5

0,5∙7

0,8∙5

1,4∙5

2,2∙3

3,5∙2

3∙0,19

0,26∙100

4∙0,17

100∙0,038

34:10

5,6:7

0,8:4

0,025:5

0,81:9

0,04:8

0,2:5

37:100

2:4

28:140

6,4:0,8

0,2:0,04

0,6:0,5

0,7:0,01

2:0,5

5:0,2

0,24:0,6

1:0,125

0,6:0,1

4,8:0,008

Учебно-методический материал по математике (5 класс) на тему: Карточки с примерами на умножение десятичных дробей.

Вариант 4.1.

1) 1,021 · 73,6;

2) 62,027 · 1;

3) 0,723 · 0;

4) 0,0005 · 37;

5) 2,005 · 70,04;

6) 3,0125 · 80;

7) 100 · 67,0036;

8) 80,54 · 51,74;

9) 0,0005 · 100000;

10) 1,28 · 1,5625;

11) 96,6 · 0,0005;

12) 0,0001 · 915.

Вариант 4.2.

1) 0,02 · 70,05;

2) 0,1 · 0,001;

3) 0,025 · 40;

4) 38,006 · 1000;

5) 0,32 · 15,625;

6) 0,5487 · 1;

7) 8,054 · 5;

8) 2,002 · 10,35;

9) 70,08 · 32,66;

10) 0 · 4,2709;

11) 0,04 · 45,02;

12) 10 · 0,003.

Вариант 4.3.

1) 10000 · 0,0058;

2) 0,68 · 35,06;

3) 40,2 · 4,02;

4) 0,0002 · 5000;

5) 6 · 16,0021;

6) 0,55 · 30,04;

7) 2,2018 · 1000;

8) 32,001 · 1;

9) 0,444 · 0,175;

10) 0,128 · 23,4375;

11) 0 · 36,074;

12) 700 · 0,001.

Вариант 4.4.

1) 1000000 · 6,0006;

2) 67,0314 · 1;

3) 0,3363 · 100;

4) 7,4648 · 7,25;

5) 87,6 · 0,001;

6) 0,0003 · 0;

7) 0,016 · 62,5;

8) 0,765 · 13;

9) 12,125 · 8;

10) 4,91 · 70,3;

11) 40,008 · 0,2;

12) 0,116 · 0,525.

Вариант 4.5.

1) 39,0625 · 0,0512;

2) 16,004 · 84,5;

3) 9,0004 · 2,25;

4) 0,008 · 10000;

5) 0,001 · 4;

6) 70,694 · 0,8;

7) 2,075 · 0;

8) 0,36 · 0,73;

9) 16 · 3,0625;

10) 222 · 0,0255;

11) 1 · 97,389;

12) 10 · 51,005.

Вариант 4.6.

1) 0 · 8,1867;

2) 42,5 · 61,008;

3) 2,8125 · 3,2;

4) 0,01 · 0,64;

5) 10000 · 2,0005;

6) 1200 · 0,005;

7) 70,0006 · 70,5;

8) 4,09 · 4,41;

9) 0,07 · 0,43;

10) 2,022 · 3;

11) 41,0009 · 1;

12) 0,008 · 100.

Вариант 4.7.

1) 67,09 · 59,2;

2) 0,005 · 7,08;

3) 0 · 0,004;

4) 100 · 84,082;

5) 2 · 41,0057;

6) 0,0025 · 6800;

7) 5,722 · 1;

8) 6,54 · 3,06;

9) 10000 · 0,0014;

10) 78,125 · 0,128;

11) 0,0001 · 3300;

12) 80,5 · 40,7958.

Вариант 4.8.

1) 3,74 · 0,1;

2) 40 · 3,025;

3) 0,009 · 375;

4) 100 · 0,026;

5) 0,02 · 7,005;

6) 0,0094 · 1;

7) 4,6875 · 1,28;

8) 81,0098 · 0;

9) 49,2 · 41,03;

10) 10,2 · 20,037;

11) 92,72 · 3,05;

12) 88,032 · 100000.

Вариант 4.9.

1) 2,002 · 0;

2) 5 · 0,0183;

3) 0,0001 · 693;

4) 20,096 · 85,025;

5) 1 · 35,121;

6) 3,05 · 95,36;

7) 7,08 · 0,89;

8) 80,4 · 50,004;

9) 0,64 · 3,125;

10) 100000 · 0,095;

11) 7,0005 · 100;

12) 3,0125 · 80.

Вариант 4.10.

1) 93,03 · 9,05;

2) 0,18 · 1,66;

3) 0,0008 · 88,75;

4) 500 · 0,002;

5) 61,0062 · 0;

6) 0,0256 · 78,125;

7) 50,075 · 76,768;

8) 2 · 26,222;

9) 0,639 · 0,1;

10) 10 · 0,057;

11) 10000 · 1,0007;

12) 0,0402 · 1.

4.1.

1) 75,1456; 2) 62,027; 3) 0; 4) 0,0185; 5) 140,4302; 6) 241; 7) 6700,36; 8) 4167,1396; 9) 50; 10) 2; 11) 0,0483; 12) 0,0915.

4.2.

1) 1,401; 2) 0,0001; 3) 1; 4) 38006; 5) 5; 6) 0,5487; 7) 40,27; 8) 20,7207; 9) 2288,8128; 10) 0; 11) 1,8008; 12) 0,03.

4.3.

1) 58; 2) 23,8408; 3) 161,604; 4) 1; 5) 96,0126; 6) 16,522; 7) 2201,8; 8) 32,001; 9) 0,0777; 10) 3; 11) 0; 12) 0,7.

4.4.

1) 6000600; 2) 67,0314; 3) 33,63; 4) 54,1198; 5) 0,0876; 6) 0; 7) 1; 8) 9,945; 9) 97; 10) 345,173; 11) 8,0016; 12) 0,0609.

4.5.

1) 2; 2) 1352,338; 3) 20,2509; 4) 80; 5) 0,004; 6) 56,5552; 7) 0; 8) 0,2628; 9) 49; 10) 5,661; 11) 97,389; 12) 510,05.

4.6.

1) 0; 2) 2592,84; 3) 9; 4) 0,0064; 5) 20005; 6) 6; 7) 4935,0423; 8) 18,0369; 9) 0,0301; 10) 6,066; 11) 41,0009; 12) 0,8.

4.7.

1) 3971,728; 2) 0,0354; 3) 0; 4) 8408,2; 5) 82,0114; 6) 17; 7) 5,722; 8) 20,0124; 9) 14; 10) 10; 11) 0,33; 12) 3284,0619.

4.8.

1) 0,374; 2) 121; 3) 3,375; 4) 2,6; 5) 0,1401; 6) 0,0094; 7) 6; 8) 0; 9) 2018,676; 10) 204,3774; 11) 282,796; 12) 8803200.

4.9.

1) 0; 2) 0,0915; 3) 0,0693; 4) 1708,6624; 5) 35,121; 6) 290,848; 7) 6,3012; 8) 4020,3216; 9) 2; 10) 9500; 11) 700,05; 12) 241.

4.10.

1) 841,9215; 2) 0,2988; 3) 0,071; 4) 1; 5) 0; 6) 2; 7) 3844,1576; 8) 52,444; 9) 0,0639; 10) 0,57; 11) 10007; 12) 0,0402.

Математика 5 класс. Умножение и деление натуральных чисел

Описание презентации по отдельным слайдам:

1 слайд

Описание слайда:

УЧИТЕЛЬ МАТЕМАТИКИ: ГАДАЕВА ЛЮДМИЛА КОНСТАНТИНОВНА Математика 5 класс Муниципальное казенное общеобразовательное учреждение основная общеобразовательная школа с. Синдзикау им. А.Т.Гапбаева Дигорского района РСО-Алания

2 слайд

Описание слайда:

Расшифруйте ребус:

3 слайд

Описание слайда:

Умножение и деление натуральных чисел

4 слайд

Описание слайда:

Умножение натуральных чисел и его свойства 3 7 7 + 7 + 7 = 3 + 3 + 3 + 3 + 3 + 3 + 3 = = 7 ∙ 3 = 3· 7 = 21

5 слайд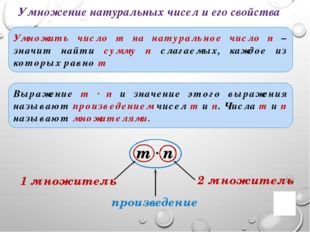

Описание слайда:

Умножение натуральных чисел и его свойства Умножить число m на натуральное число n – значит найти сумму n слагаемых, каждое из которых равно m Выражение m ∙ n и значение этого выражения называют произведением чисел m и n. Числа m и n называют множителями. m ∙ n 2 множитель 1 множитель произведение

6 слайд

Описание слайда:

Умножение натуральных чисел и его свойства 1. Переместительное свойство умножения: а ∙ b = b ∙ a 2. Сочетательное свойство умножения: а ∙ (b ∙ с) = (a ∙ b) ∙ с 3. Свойство умножения на единицу: а ∙ 1 = 1 ∙ а = а 4. Свойство умножения на ноль: а ∙ 0 = 0 ∙ а = 0

7 слайд

Описание слайда:

Умножение натуральных чисел и его свойства 1 + 1 + … + 1 = п 1· п = п 0 + 0 + … + 0 = п 0· п = 0 (a + b) + (a + b) + … + (a + b) = п (a + b)· п

8 слайд

Описание слайда:

Умножение натуральных чисел и его свойства 8· х = 8х a· b = ab 2· (a + b) = 2(a + b) (x + 2)· (y + 3) = (x + 2)(y + 3) (ab)c = abc Когда в записи произведения нет скобок, умножение выполняют по порядку слева направо.

9 слайд

Описание слайда:

ЧТО ЗНАЧИТ УМНОЖИТЬ ОДНО НАТУРАЛЬНОЕ ЧИСЛО НА ДРУГОЕ? КАК НАЗЫВАЮТ ЧИСЛА, КОТОРЫЕ ПЕРЕМНОЖАЮТ? КАК НАЗЫВАЮТ РЕЗУЛЬТАТ УМНОЖЕНИЯ? ЧЕМУ РАВНО 1· N? ЧЕМУ РАВНО 0· N? СФОРМУЛИРУЙТЕ ПЕРЕМЕСТИТЕЛЬНОЕ СВОЙСТВО УМНОЖЕНИЯ. ЗАПИШИТЕ ЕГО С ПОМОЩЬЮ БУКВ. СФОРМУЛИРУЙТЕ СОЧЕТАТЕЛЬНОЕ СВОЙСТВО УМНОЖЕНИЯ. ЗАПИШИТЕ ЕГО С ПОМОЩЬЮ БУКВ. В КАКИХ СЛУЧАЯХ МОЖНО ОПУСТИТЬ ЗНАК УМНОЖЕНИЯ? ЧЕМУ РАВНО ПРОИЗВЕДЕНИЕ Т· 1? ЧЕМУ РАВНО ПРОИЗВЕДЕНИЕ Т· 0? Ответьте на вопросы:

10 слайд

Описание слайда:

Равенство m ∙ (n ∙ k) = (m ∙ n) ∙ k является: а) переместительным свойством умножения; б) сочетательным свойством умножения; в) другим каким-то свойством умножения. Равенство 49 ∙ 0 = 0 при помощи букв записывается: а) b ∙ 0 = 0; б) 0 ∙ b = b; в) b ∙ 49 = 49. Произведение чисел 4 ∙ 222 ∙ 5 равно: а) 8885; б) 4445; в) 4440. Запишите с помощью букв переместительное свойство умножения: а) a + b = b + a; б) a ∙ b = b ∙ a; в) a ∙ 0 = 0 ∙ a Тест

11 слайд

Описание слайда:

5 · 2 = 10 25 ∙ 4 = 100 50 ∙ 2 = 100 125 ∙ 8 = 1000 250 ∙ 4 = 1000 500 ∙ 2 = 1000 Запомни:

12 слайд

Описание слайда:

Расшифруйте ребус:

13 слайд

Описание слайда:

Упрощение выражений

14 слайд

Описание слайда:

Для того чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения. Распределительное свойство умножения относительно сложения (а + b)с = aс + bс Примеры: (3 + 7)a = 10a 3a + 7a = (12 + 6 + 8)x = 26x 12x + 6x + 8x = (11 + 9 + 4)m + 5 = 24m + 5 11m + 9m + 4m + 5 =

15 слайд

Описание слайда:

Распределительное свойство умножения относительно вычитания Для того чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе. (а − b)с = aс − bс Примеры: (26 − 12)x = 14x 26x − 12x = (15 – 8 – 2)a = 5a 15a – 8a – 2a = (31 – 16 – 4)m – 5 = 11m – 5 31m – 16m – 4m – 5 =

16 слайд

Описание слайда:

3у + 7у + 25 = 85 (3 + 7)у + 25 = 85 10у + 25 = 85 10у = 85 – 25 10у = 60 у = 60 : 10 у = 6 3· 6 + 7· 6 + 25 = 85 85 = 85 Решить уравнение: Ответ: 6.

17 слайд

Описание слайда:

В одном мешке было х кг картофеля, а в другом в 2 раза больше. Сколько килограммов картофеля было в двух мешках? а) х; б) 3х; в) 2х; г) 4х. Вася решил а задач, а Миша – на 4 задачи больше. Сколько задач решили Вася и Миша вместе? а) 4а; б) 6а; в) 2а + 4; г) а + 4. Даны два выражения: 9 (856 + 342) и 9 ∙ 856 + 8 ∙ 342. Какое выражение больше? а) равны; б) первое; в) второе. Упростите выражение: 20 · а · 25 · b. а) 50аb; б) 500а; в) 5000аb; г) 500ab. Тест

18 слайд

Описание слайда:

Порядок выполнения действий

19 слайд

Описание слайда:

Сложение и вычитание чисел называют действиями первой ступени, а умножение и деление чисел – действиями второй ступени. Порядок выполнения действий Порядок выполнения действий при нахождении значений выражений определяется следующими правилами: Если в выражении нет скобок и оно содержит действия только одной ступени, то их выполняют по порядку слева направо. Если выражение содержит действия первой и второй ступени и в нем нет скобок, то сначала выполняют действия второй ступени, потом – действия первой ступени. Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2).

20 слайд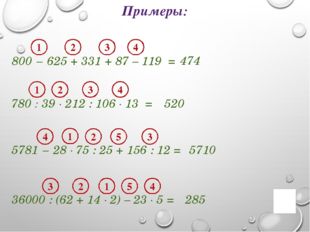

Описание слайда:

Примеры: 474 800 − 625 + 331 + 87 – 119 = 1 2 3 4 520 780 : 39 ∙ 212 : 106 ∙ 13 = 1 2 3 4 5710 5781 − 28 ∙ 75 : 25 + 156 : 12 = 4 1 2 3 5 285 36000 : (62 + 14 ∙ 2) – 23 ∙ 5 = 3 2 1 4 5

21 слайд

Описание слайда:

Порядок выполнения действий В выражениях, содержащих скобки, можно эти скобки не писать, если при этом порядок действий не изменяется: (53 – 12) + 14 = 53 – 12 + 14 (64 : 16) ∙ 25 = 64 : 16 ∙ 25 Изменять порядок действий можно на основе свойств сложения, вычитания и умножения.

22 слайд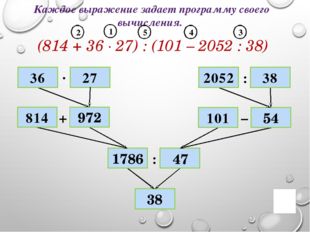

Описание слайда:

1786 38 101 27 814 2052 54 972 47 Каждое выражение задает программу своего вычисления. (814 + 36 ∙ 27) : (101 – 2052 : 38) ∙ + : − : 38 36 1 2 3 4 5

23 слайд

Описание слайда:

КАКИЕ ДЕЙСТВИЯ ОТНОСЯТСЯ К ДЕЙСТВИЯМ ПЕРВОЙ СТУПЕНИ И КАКИЕ – К ДЕЙСТВИЯМ ВТОРОЙ СТУПЕНИ? В КАКОМ ПОРЯДКЕ ВЫПОЛНЯЮТ ДЕЙСТВИЯ В ВЫРАЖЕНИЯХ БЕЗ СКОБОК, ЕСЛИ В НЕГО ВХОДЯТ ДЕЙСТВИЯ ОДНОЙ И ТОЙ ЖЕ СТУПЕНИ; ВСЕ АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ? В КАКОМ ПОРЯДКЕ ВЫПОЛНЯЮТ ДЕЙСТВИЯ В ВЫРАЖЕНИЯХ СО СКОБКАМИ? Ответьте на вопросы:

24 слайд

Описание слайда:

Математика. 5 класс: учеб. для общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М.: Мнемозина, 2012 Использованы ресурсы:

Курс повышения квалификации

Курс профессиональной переподготовки

Учитель математики и информатики

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДБ-507602

Оставьте свой комментарий

Тест: Умножение и деление — Математика 5 класс

Умножение и деление

Умножение и деление натуральных чисел

Математика 5 класс | Автор: Ливанова И.Г. | ID: 3761 | Дата: 31.1.2015

«;} else {document.getElementById(«torf1″).innerHTML=»»;}; if (answ.charAt(1)==»1″) {document.getElementById(«torf2″).innerHTML=»»;} else {document.getElementById(«torf2″).innerHTML=»»;}; if (answ.charAt(2)==»1″) {document.getElementById(«torf3″).innerHTML=»»;} else {document.getElementById(«torf3″).innerHTML=»»;}; if (answ.charAt(3)==»1″) {document.getElementById(«torf4″).innerHTML=»»;} else {document.getElementById(«torf4″).innerHTML=»»;}; if (answ.charAt(4)==»1″) {document.getElementById(«torf5″).innerHTML=»»;} else {document.getElementById(«torf5″).innerHTML=»»;}; if (answ.charAt(5)==»1″) {document.getElementById(«torf6″).innerHTML=»»;} else {document.getElementById(«torf6″).innerHTML=»»;}; if (answ.charAt(6)==»1″) {document.getElementById(«torf7″).innerHTML=»»;} else {document.getElementById(«torf7″).innerHTML=»»;}; if (answ.charAt(7)==»1″) {document.getElementById(«torf8″).innerHTML=»»;} else {document.getElementById(«torf8″).innerHTML=»»;}; if (answ.charAt(8)==»1″) {document.getElementById(«torf9″).innerHTML=»»;} else {document.getElementById(«torf9″).innerHTML=»»;}; if (answ.charAt(9)==»1″) {document.getElementById(«torf10″).innerHTML=»»;} else {document.getElementById(«torf10″).innerHTML=»»;}; if (answ.charAt(10)==»1″) {document.getElementById(«torf11″).innerHTML=»»;} else {document.getElementById(«torf11″).innerHTML=»»;}; if (answ.charAt(11)==»1″) {document.getElementById(«torf12″).innerHTML=»»;} else {document.getElementById(«torf12″).innerHTML=»»;}; if (answ.charAt(12)==»1″) {document.getElementById(«torf13″).innerHTML=»»;} else {document.getElementById(«torf13″).innerHTML=»»;}; if (answ.charAt(13)==»1″) {document.getElementById(«torf14″).innerHTML=»»;} else {document.getElementById(«torf14″).innerHTML=»»;}; if (answ.charAt(14)==»1″) {document.getElementById(«torf15″).innerHTML=»»;} else {document.getElementById(«torf15″).innerHTML=»»;}; if (answ.charAt(15)==»1″) {document.getElementById(«torf16″).innerHTML=»»;} else {document.getElementById(«torf16″).innerHTML=»»;}; if (answ.charAt(16)==»1″) {document.getElementById(«torf17″).innerHTML=»»;} else {document.getElementById(«torf17″).innerHTML=»»;}; if (answ.charAt(17)==»1″) {document.getElementById(«torf18″).innerHTML=»»;} else {document.getElementById(«torf18″).innerHTML=»»;}; if (answ.charAt(18)==»1″) {document.getElementById(«torf19″).innerHTML=»»;} else {document.getElementById(«torf19″).innerHTML=»»;}; if (answ.charAt(19)==»1″) {document.getElementById(«torf20″).innerHTML=»»;} else {document.getElementById(«torf20″).innerHTML=»»;}; } }

Получение сертификата
о прохождении теста

Основные правила математики с примерами. 5 класс

Содержание

Натуральные числа
Сравнение натуральных чисел
Свойства сложения
Формула пути
Корень уравнения
Правила решения уравнений
Отрезок, прямая, луч
Угол, биссектриса угла
Углы: развернутый, прямой, острый, тупой
Многоугольники. Равные фигуры
Треугольники: остроугольный, прямоугольный, тупоугольный
Треугольники: равнобедренный, равносторонний, разносторонний
Прямоугольник. Квадрат. Периметр
Умножение. Свойства умножения
Деление. Деление с остатком
Площадь. Площадь квадрата, прямоугольника
Объем. Объем прямоугольного параллелепипеда, куба
Дроби: правильная, неправильная, сравнение дробей
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание смешанных чисел
Преобразование неправильной дроби в смешанное число
Преобразование смешанного числа в неправильную дробь
Десятичные дроби: свойства, сравнение, округление
Десятичные дроби: сложение, вычитание
Десятичные дроби: умножение, деление
Среднее арифметическое
Процент

Натуральные числа

Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., которые используют при счете предметов, называют натуральными.

Сравнение натуральных чисел

Число меньше любого натурального числа.

$0 < 1,0 < 100$

Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.

$\underbrace {2356}_4 > \underbrace {900}_3$

Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр

$35\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{6} 1 > 35\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{5} 9$

Свойства сложения

Переместительный закон:

Сочетательный закон:

Формула пути

S = Vt ,
где — пройденный путь, — скорость движения, — время, за которое пройден путь .

Корень уравнения

Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.

2 + 10 = 16

= 3 – корень, так как 2 · 3 + 10 = 16

Что значит “Решить уравнение”

Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.

Правила решения уравнений

Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

$\underbrace {20}_{slagaemoe} + \underbrace x_{slagaemoe} = \underbrace {100}_{summa}$

$\begin{array}{*{20}c} {x = 100 - 20} \\ {x = 80} \\ \end{array}$

Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.

$\begin{array}{*{20}c} {\underbrace x_{ymenshaemoe} - \underbrace {10}_{vychitaemoe} = \underbrace {40}_{raznos$

Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

$\begin{array}{*{20}c} {\underbrace {50}_{ymenshaemoe} - \underbrace x_{vychitaemoe} = \underbrace {40}_{raznost$

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

$\begin{array}{l} \underbrace x_{mnozitel$

Чтобы найти неизвестное делимое, надо делитель умножить на частное.

$\begin{array}{l} \underbrace x_{de\lim oe}:\underbrace 8_{delitel$

Чтобы найти неизвестный делитель, надо делимое разделить на частное.

$\begin{array}{l} \underbrace {42}_{de\lim oe}:\underbrace x_{delitel$

Отрезок, прямая, луч

Отрезок

Отрезок – часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)

Свойство длины отрезка

Если на отрезке отметить точку , то длина отрезка равна сумме длин отрезков и .

Равные отрезки

Два отрезка называют равными, если они совмещаются при наложении.

Свойство прямой

Через две точки проходит только одна прямая.

Измерить отрезок

Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается

Ломаная

Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом

Луч

Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча.В названии луча присутствуют две буквы, например, . Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.

Угол, биссектриса угла

Угол

Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.

Равные углы

Два угла называют равными, если они совмещаются при наложении.

Свойство величины угла

Если между сторонами угла ∠ ABC провести луч , то градусная мера ∠ ABC равна сумме градусных мер углов ∠ ABD и ∠ DBC , то есть ∠ ABC = ∠ ABD + ∠ DBC .

DBC

Биссектриса угла

Луч, который делит угол на два равных угла, называется биссектрисой угла.

DBC

Углы: развернутый, прямой, острый, тупой

Развернутый угол

Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.

Прямой угол

Угол, градусная мера которого равна 90°, называют прямым.

Острый угол

Угол, градусная мера которого меньше 90°, называют острым.

Тупой угол

Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.
DBC

Многоугольники. Равные фигуры

Равные многоугольники

Два многоугольники называют равными, если они совмещаются при наложении.

Равные фигуры

Две фигуры называют равными, если они совмещаются при наложении.

Треугольники: остроугольный, прямоугольный, тупоугольный

Остроугольный треугольник

Если все углы треугольника острые, то его называют остроугольным треугольником.

Прямоугольный треугольник

Если один из углов треугольника прямой, то его называют прямоугольным треугольником.

Тупоугольный треугольник

Если один из углов треугольника тупой, то его называют тупоугольным треугольником.
DBC

Треугольники: равнобедренный, равносторонний, разносторонний

Равнобедренный треугольник

Если две стороны треугольника равны, то его называют равнобедренным треугольником.

Равносторонний треугольник

Если три стороны треугольника равны, то его называют равносторонним треугольником.

Периметр равностороннего треугольника

Если сторона равностороннего треугольника равна , то его периметр вычисляют по формуле P=3a

Разносторонний треугольник

Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.
P=3a

Прямоугольник. Квадрат. Периметр

Прямоугольник

Если в четырехугольнике все углы прямые, то его называют прямоугольником.

Свойство прямоугольника

Противоположные стороны прямоугольника равны.

Периметр прямоугольника

Если соседние стороны прямоугольника равны и , то его периметр вычисляют по формуле

Квадрат

Прямоугольник, у которого все стороны равны, называют квадратом.

Периметр квадрата

Если сторона квадрата равна , то его периметр вычисляют по формуле P=4a .
P=4a

Умножение. Свойства умножения

Умножение

$a \cdot b = \underbrace {a + a + \ldots + a}_b$

$5 \cdot 4 = \underbrace {5 + 5 + 5 + 5}_4$

Если один из двух множителей равен 1, то произведение равно второму множителю.

$1 \cdot 25 = 25\quad 25 \cdot 1 = 25$

Если один из множителей равен нулю, то произведение равно нулю.

$0 \cdot 25 = 0\quad 25 \cdot 0 = 0$

Если произведение равно нулю, то хотя бы один из множителей равен нулю.

Свойства умножения

Переместительный закон умножения: $a \cdot b = b \cdot a$

$6 \cdot 3 = 3 \cdot 6$

Сочетательный закон умножения: $(a \cdot b )c= a( b \cdot c)$

$(17 \cdot 5) \cdot 2 = 17 \cdot (5 \cdot 2)$

Распределительное свойство умножения относительно сложения:

2·(3 + 10) = 2 · 3 + 2 · 10

2 · 11 + 2 · 4 = 2·(11 + 4)

Распределительное свойство умножения относительно вычитания:

2·(15 – 7) = 2 · 15 – 2 · 7

3 · 10 – 3 · 4 = 3·(10 – 4)

Деление. Деление с остатком

Деление

Для натуральных чисел a, b, c равенство $a \div b = c$ является правильным, если является правильным равенство

$b \cdot c = a$

15 : 5 = 3 -правильное равенство, так как верно равенство 5 · 3 = 15

В равенстве $a \div b = c$ число называют делимым, число — делителем, число и запись $a \div b$ – частным от деления, отношением, долей.

На ноль делить нельзя.

Для любого натурального числа правильными являются равенства:

$0 \div a = 0$ ,

$a \div a = 1$

Деление с остатком

a=bq+r , где — делимое, — делитель, — неполное частное, — остаток, r < b .

$\underbrace {154}_{de\lim oe} = \underbrace {50}_{delitel$

Если остаток равен нулю, то говорят, что число делится нацело на число .

Площадь. Площадь квадрата, прямоугольника

Свойства площади фигуры

Равные фигуры имеют равные площади;

Площадь фигуры равна сумме площадей фигур, из которых она состоит.

Площадь прямоугольника

Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.

Площадь квадрата

где — площадь квадрата, — длина его стороны.

Объем. Объем прямоугольного параллелепипеда, куба

Свойства объема фигуры

Равные фигуры имеют равные объемы;
Объем фигуры равен сумме объемов фигур, из которых она состоит.

Объем прямоугольного параллелепипеда

где — объем параллелепипеда, , и — его измерения, выраженные в одних и тех же единицах;

, где – площадь поверхности прямоугольного параллелепипеда.

где — площадь основания параллелепипеда, — его высота.

Объем куба

где — объем куба, — длина его ребра.

Дроби: правильная, неправильная, сравнение дробей

Правильная дробь

Дробь, числитель которой меньше знаменателя, называют правильной

$\frac{5} {7},\quad \frac{8} {9}$

Неправильная дробь

Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.

$\frac{{11}} {7},\quad \frac{{27}} {9},\quad \frac{7} {7},\quad \frac{{13}} {{13}}$

Сравнение дробей

Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.

$\frac{3} {4} > \frac{2} {4},\quad \frac{5} {8} < \frac{7} {8}$

Из двух дробей с одинаковыми числителями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.

$\frac{4} {5} > \frac{4} {7},\quad \frac{1} {8} < \frac{1} {5}$

Все правильные дроби меньше единицы, а неправильные — больше или равны единице.

$\frac{4} {5} < 1,\quad \frac{3} {2} > 1$

Любая неправильная дробь больше любой правильной дроби.

$\frac{7} {5} > \frac{4} {5},\quad \frac{7} {7} > \frac{6} {7}$

Сложение и вычитание дробей с одинаковыми знаменателями

Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.

$\frac{3} {7} + \frac{2} {7} = \frac{{3 + 2}} {7} = \frac{5} {7}$

Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.

$\frac{4} {7} - \frac{1} {7} = \frac{{4 - 1}} {7} = \frac{3} {7}$

Сложение и вычитание смешанных чисел

Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.

$2\frac{3} {5} + 1\frac{1} {5} = (2 + 1) + (\frac{3} {5} + \frac{1} {5}) = 3 + \frac{4} {5} = 3\frac{4} {5}$

Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.

$4\frac{6} {7} - 1\frac{1} {7} = (4 - 1) + (\frac{6} {7} - \frac{1} {7}) = 3 + \frac{5} {7} = 3\frac{5} {7}$

Преобразование неправильной дроби в смешанное число

Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно

числитель разделить на знаменатель;
полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.

Преобразование смешанного числа в неправильную дробь

Чтобы преобразовать смешанное число в неправильную дробь нужно

целую часть числа умножить на знаменатель дробной части;
к полученному произведению прибавить числитель дробной части;
эту сумму записать как числитель неправильной дроби;
в его знаменателе записать знаменатель дробной части смешанного числа.

Десятичные дроби: свойства, сравнение, округление

Свойства десятичной дроби

Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.

Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.

Сравнение десятичных дробей

Из двух десятичных дробей больше та, у которой целая часть больше.

Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо

с помощью приписывания нулей справа уравнять количество цифр в дробных частях,
после чего сравнить полученные дроби поразрядно.

Округление десятичных дробей

Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо

все следующие за этим разрядом цифры отбросить.
если при этом первая из цифр, которые отбрасывают равна 0, 1, 2, или 4, то последнюю из цифр, которые оставляют, не меняют;
если же первая из цифр, которые отбрасывют, равна 5, 6, 7, 8 или 9, то последнюю из цифр, которые оставляют, увеличивают на единицу.

Десятичные дроби: сложение, вычитание

Сложение десятичных дробей

Чтобы найти сумму двух десятичных дробей, нужно:

уравнять количество цифр после запятых;
записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
сложить полученные числа так, как складывают натуральные числа;
поставить в полученной сумме запятую под запятыми.

Вычитание десятичных дробей

Чтобы найти разность двух десятичных дробей, нужно:

уравнять количество цифр после запятых;
записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
выполнить вычитание так, как вычитают натуральные числа;
поставить в полученной разности запятую под запятыми.

Десятичные дроби: умножение, деление

Умножение десятичных дробей

Чтобы перемножить две десятичные дроби, надо:

перемножить их как натуральные числа, не обращая внимания на запятые;
в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.

Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.

Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.

Деление десятичных дробей

Чтобы разделить десятичную дробь на десятичную, надо:

перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;
выполнить деление на натуральное число.

Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.

Среднее арифметическое

Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.

Процент

Процентом называют сотую часть величины или числа 1%= $\frac{1}{{100}}$

Данная информация взята из УМК А.Г.Мерзляк, В.Б.Полонский, М.С. Якир

5 класс умножения и деления

Умножение		Пример
Умножьте на 10, 100 или 1000 с отсутствующими коэффициентами		____ x 98 = 98 000
Распределительная собственность		8 х 22 = 8 х 20 + 8 х 2 =
Умножить на части		5 x 71 =
Умножьте числа около 100		9 х 104 =
Умножение 1-значных на 3-значные числа		8 х 223 =
Отдел
Разделите 3-х и 4-х значные числа на 1-значное умственное		812 ÷ 4 =
Деление с остатком, в пределах 1-100		68 ÷ 12 =
Деление с остатком, в пределах 1-1000		981 ÷ 8 =
Деление с остатком, делитель целых десяти		99 ÷ 30 =
Деление с остатком, делитель на целую сотню		5652 ÷ 700 =
Умножение в столбцах
Умножить 4-значные на 1-значные		4 481 x 2
Умножить на 3 цифры х 2 цифры		457 x 21
Умножить 4-значное на 2-значное		2,345 x 23
Умножить 3-значное на 3-значное число		456 x 789
Long Division
Длинное деление (без остатка)
Длинное деление с остатком
Длинное деление с остатками (делители 10-25)
Длинное деление с остатками (делители 10-99)

Отсутствует проблема дивидендов или делителей		1,564 ÷ ___ = 34
Проблемы с отсутствующим фактором (для решения путем длительного деления)		___ x 35 = 1 680
Слово проблемы
Смешанные 4 операции над словами		Слово проблемы

Таблицы умножения и деления дробей

Умножение дроби		Пример
Фракция умножить на целое число		6 х 1/12 =
Фракция, умноженная на целое число (пропущенные факторы)		1/6 x __ = 3

Умножить дроби		2/3 x 3/5 =
Умножить фракции (сложнее)		7/20 x 2/9 =
Умножить дроби (недостающие факторы)		3/4 x ___ = 1/6

Умножение неправильных дробей		5/3 x 3/2 =

Смешанное число раз дробь		2 7/8 x 1/2 =
Смешанное число умноженное на		2 7/8 x 3 1/2 =
Смешанная практика умножения		1 4/5 x 10 =
Фракционное подразделение
Разделите целое число на дробь		3 ÷ 1/3 =
Разделите дробь на целое число		3/4 ÷ 3 =
Делительные дроби и целые числа		4 ÷ 1/2 =
Разделите смешанное число на дробь		5 3/4 ÷ 1/4 =

Фракция, деленная на фракцию		2/3 ÷ 1/6 =
Деление смешанных чисел на дроби		6 2/3 ÷ 1/6 =
Смешанное число, разделенное на смешанное число		6 2/3 ÷ 1 1/6 =
Смешанная практика деления		2 1/3 ÷ 3 =
Слово проблемы
Деление целых чисел (дробные ответы)		Проблемы со словами
Деление на словосочетание по задачам		Проблемы со словами
Умножение дробей на слово		Проблемы со словами
Смешанные операции с дробями		Проблемы со словами
Больше словосочетаний со смешанной дробью		Проблемы со словами

ключевых сдвигов в математике | Единая стандартная государственная инициатива

Введение

Стандартные основные математические стандарты штата основаны на лучших из существующих стандартов и отражают навыки и знания, которые понадобятся учащимся для достижения успеха в колледже, карьере и жизни. Понимание того, как стандарты отличаются от предыдущих стандартов, и необходимые изменения, к которым они стремятся, крайне важно для их реализации.

Ниже приведены ключевые сдвиги, к которым призывает Common Core:

Большой фокус на меньшее количество тем
Общее ядро требует большего внимания в математике.Стандарты, вместо того чтобы мчаться, чтобы охватить многие темы в учебном плане шириной в милю и в дюйм, требуют от учителей математики значительного сужения и углубления способов расходования времени и энергии в классе. Это означает, что необходимо сосредоточиться на основной работе каждого класса следующим образом:
- В классах K – 2: концепции, навыки и решение проблем, связанных с сложением и вычитанием
- В 3–5 классах: концепции, навыки и решение проблем, связанных с умножением и делением целых чисел и дробей
- В 6 классе: отношения и пропорциональные отношения, а также ранние алгебраические выражения и уравнения
- В 7 классе: отношения и пропорциональные отношения, арифметика рациональных чисел
- В 8 классе: линейная алгебра и линейные функции
Этот фокус поможет учащимся обрести прочную основу, в том числе глубокое понимание концепций, высокую степень процедурного мастерства и беглости речи, а также способность применять математику, которую они знают, для решения проблем в классе и за его пределами.
Согласованность : связь тем и мышление между классами
Математика — это не список отдельных тем, уловок или мнемоник; это связная совокупность знаний, состоящая из взаимосвязанных концепций. Таким образом, стандарты разрабатываются вокруг последовательного развития от класса к классу. Обучение тщательно взаимосвязано между классами, чтобы учащиеся могли получить новое понимание на основах, созданных в предыдущие годы. Например, в 4 ^{-м классе} учащиеся должны «применить и расширить прежнее понимание умножения, чтобы умножить дробь на целое число» (Стандарт 4.NF.4). Это распространяется на 5 ^th, когда ожидается, что ученики будут развивать этот навык, чтобы «применять и расширять предыдущее понимание умножения для умножения дроби или целого числа на дробь» (Стандарт 5.NF.4). Каждый стандарт — это не новое событие, а продолжение предыдущего обучения.
Coherence также встроен в стандарты в том, как они усиливают основную тему в классе, используя вспомогательные дополнительные темы. Например, вместо того, чтобы представлять тему отображения данных как самоцель, эта тема используется для поддержки словесных задач на уровне класса, в которых учащиеся применяют математические навыки для решения задач.
Rigor : развивать концептуальное понимание, процедурные навыки и беглость, и применение с равной интенсивностью
Строгость относится к глубокому, аутентичному владению математическими понятиями, не усложняя математику или вводя темы в ранних классах. Чтобы помочь учащимся соответствовать стандартам, преподаватели должны будут с одинаковой интенсивностью выполнять три аспекта строгости в основной работе каждого класса: концептуальное понимание, процедурные навыки и беглость речи, а также применение.
Концептуальное понимание: Стандарты требуют концептуального понимания ключевых понятий, таких как стоимость и соотношения. Студенты должны иметь возможность получить доступ к понятиям с разных точек зрения, чтобы рассматривать математику как нечто большее, чем набор мнемоник или отдельных процедур.
Процессуальные навыки и беглость: Стандарты требуют скорости и точности в расчетах. Студенты должны практиковать основные функции, такие как умножение одной цифры, чтобы иметь доступ к более сложным концепциям и процедурам.Свободное владение языком должно решаться в классе или с помощью вспомогательных материалов, поскольку некоторым учащимся может потребоваться больше практики, чем другим.
Применение: Стандарты требуют от учащихся использования математики в ситуациях, требующих математических знаний. Правильное применение математических знаний зависит от студентов, имеющих глубокое концептуальное понимание и процедурную беглость.

Разделение рабочих листов | K5 Learning

Рабочие листы > Математика > Математика по темам > Отдел

Разделение рабочих листов от 3 до 6 класса

Наши бесплатные рабочие листы деления начинаются с практики простых фактов деления (например, 10 ÷ 2 = 5) и переходят к длинному делению с делителями до 99. Упражнения с и без остатков и с отсутствующими делителями или дивидендами включены. Эти бесплатные рабочие листы организованы по классам; вход в систему не требуется.

Выберите класс / тему:

3-й класс разделение рабочих листов

листы умственного разделения 4 класса

класс 4 длинные листы деления

класс 5 рабочих листов подразделения

6-й класс разделительные листы

Отдел карточек

Темы включают в себя:

Значение деления и разделения предложений
Равные группы
Деление на 2 или 3, 4 или 5, 6 или 7, 8 или 9
Отдел фактов практики (таблицы 1-10)
Отдел фактов практики (таблицы 1-12)
Факты умножения и деления семей
Факты деления с отсутствующими дивидендами или делителями
Деление на 10
Деление на 100
Разделите на целые 10 с
Разделите на целые сотни
Разделите 3 или 4-значные числа на 1-значные числа (без остатка)
Подразделение с остатками (1-100)
Длинное деление: Факты деления (1-100), без остатка
Длинное деление: Факты деления (1-100), с остатком
Отдел словесных задач

(таблицы 1-10, 1-12)
Факты деления с отсутствующим дивидендом или делителем
Разделите на 10 или 100
Разделите на целые десятки или сотни
Разделите целые десятки или сотни на однозначные числа
Разделите числа до 1000 на однозначные числа
Подразделение с остатками (1-1 000)
Разделите на 10 или 100, с остатками
Смешанные задачи на умножение и деление
Смешанные 4 операции слово задач

в форме длинного деления
Двухзначные числа, разделенные на однозначные числа, с / без остатков
Трехзначные числа, разделенные на однозначные числа, с / без остатков
Четырехзначные числа, разделенные на однозначные числа, с / без остатков

Мысленно разделите 3 или 4-значные числа на 1-значные числа
Дивизион с остатком 1-100, 1-1000
Деление на целые десятки или сотни с остатками
Длинное деление с 1-значными делителями, без остатка
Длинное деление с 1-значными делителями, с остатками
Длинное деление с двухзначными делителями (10-25, 10-99)
Отсутствует проблема дивидендов или делителей
Проблемы с отсутствующими факторами (решаем с помощью длинного деления)
Смешанные 4 операции слово задач

1-10 000, разделенные на однозначные числа, без остатка
1-100 000, разделенные на однозначные числа, с остатком
Длинное деление на 2-значные делители
Отсутствует проблема дивидендов или делителей
Проблемы с отсутствующими факторами (решаем с помощью длинного деления)